为了适应经济的发展、缓解我国电煤等大宗物资运输紧张的状况,开行长大重载列车已成为未来发展方向[1].目前我国重载列车上采用的机车无线遥控操作技术虽然能够提高指令传播速度,但仍存在空气制动机所共有的问题[2].因此,为了解决传统空气制动系统对重载运输的制约作用,国外越来越多的重载列车采用了可实现同步制动与缓解的电控空气(electronically controlled pneumatic,ECP)制动系统[3].
针对ECP制动系统的可行性和有效性国内外学者开展了大量研究:国内学者如赵永宾等[4]分析我国重载列车ECP制动系统技术方案;林晖等[2]通过试验进行ECP系统性能测试,体现出ECP制动系统在重载货物运输中的优势;张波等[5]开发了ECP制动仿真模块,并计算表明ECP的采用对于缩短制动距离和降低列车纵向车钩里有显著效果.国外学者如Wright[6]讨论了ECP制动系统实际使用中的问题,并发现采用ECP制动系统可以节省燃料和减少制动盘的磨损;Chou[7]通过试验数据验证了装有ECP制动系统的重载列车纵向动力学模型的有效性.
虽然ECP制动系统能够实现制动缓解的一致性,但是由于线路坡度变化使得同步操控模式下重载列车间的纵向作用力过大,甚至出现断钩危险.为此,许多学者从制动控制角度深入研究.黄志武等[8]分析了重载组合列车同步操控模式存在的缺陷,提出异步操控方式,并进行了仿真验证;Zhuan等[9]设计了能够最小化运行成本的开环和闭环控制器,对比分析3种控制模式下的控制性能;Chou等[10]设计最优控制器以减小列车的纵向冲动和能耗.
在包含文献[4-10]的ECP制动系统研究中,研究者主要是通过传感器检测到的车钩力大小来设计、评估控制器的效果.但在实际运用中车钩力很难通过传感器直接获取,因此研究外界因素对ECP制动系统纵向冲动的影响,并深入分析纵向冲动内在表征形式对于提高列车运行安全有着重要意义.
为此,本文将首先搭建ECP制动系统仿真模型和车钩力计算模型,分析坡道坡度、车钩间隙、制动初速度等因素对列车纵向冲动的影响;然后从传感器布局角度出发分析易检测信号与列车纵向冲动的关系,以提取能够表征列车纵向冲动大小的特征参数,为减小列车纵向冲动提供理论基础.
1 仿真模型简介本文采用AMESim与Simulink软件联合搭建列车ECP制动系统仿真模型与纵向动力学模型,通过软件接口技术将AMESim制动模型中的制动缸压力数据导入到Simulink纵向动力学模型中,实时分析列车制动过程的车钩力等参数变化曲线[11-12].
1.1 ECP制动系统模型ECP制动系统是一种微机控制的直通式制动系统(图 1),可实现列车同步制动、缓解和再制动.其中,AV、RV为制动阀和缓解阀,是实现电控制动的执行部件;CID为车辆识别模块,用于存储车辆特性数据;CCD为车辆控制单元,提供电控常用和紧急制动。因此,根据ECP制动系统工作原理运用AMESim软件对其进行图形化建模,如图 2所示.
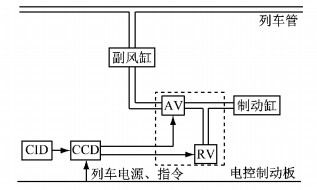
|
图 1 ECP制动系统原理图 Fig.1 simulation model of ECP braking system |

|
图 2 ECP制动系统AMESim仿真模型 Fig.2 Schematic diagram of ECP braking system |
在分析列车纵向动力学行为时,将每个车辆视为一个集中质量,车辆间由弹簧阻尼单元连接,建立单个车辆的运动方程:
| $ {m_i}{a_i} = {F_{G, i-1}} + {F_{ti}}-{F_{Gi}}-{F_{bi}}-{F_{wi}} $ | (1) |
式中:mi为第i辆车的质量;ai为加速度;FG, i-1、FGi分别为前、后车钩力;Fti为牵引力或动力制动力;Fbi为空气制动力;Fwi为运行阻力.本文不考虑机车车辆的动力制动,即:Fti=0.
1.2.1 空气制动力ECP制动系统采用传统的闸瓦制动方式,以压缩空气为动力,通过推动制动缸活塞将闸瓦压紧车轮踏面产生摩擦而形成制动力,制动力计算公式如下:
| $ {F_{{\rm{b}}i}} = \sum {K_i}{\varphi _i} $ | (2) |
| $ {K_i} = \frac{\pi }{4}{d_i}^2{P_{zi}}{\eta _i}{\gamma _i}{n_{zi}} $ | (3) |
| $ {\varphi _i} = 0.41\frac{{{K_i} + 200}}{{4{K_i} + 200}}\cdot\frac{{{v_i} + 150}}{{2{v_i} + 150}} $ | (4) |
式(2)~(4)中:Ki和φi分别为第i辆车中各闸瓦压力和摩擦系数;di、ηi、γi、和nzi分别为制动缸直径以及基础制动装置传动效率、制动倍率、摩擦系数、制动缸数;Pzi为制动缸压强;vi为列车运行速度.
1.2.2 运行阻力运行阻力包括基本运行阻力和附加运行阻力,其中基本运行阻力可根据《列车牵引计算规程》[13]中的规定计算:
滚动轴承重车车辆单位基本阻力为
| $ {\omega _i} = 2.23 + 0.005{v_i} $ |
滚动轴承空车车辆单位基本阻力为
| $ {\omega _i} = 0.92 + 0.005{v_i} $ |
而附加运行阻力主要包括坡道阻力和曲线阻力,本文不考虑曲线阻力.以坡道千分数κi近似表示第i辆车单位坡道阻力.因此,第i辆车在运行过程中所受到的运行阻力为
| $ {F_{{\rm{w}}i}} = {m_i}g\cdot({\omega _i} + {\kappa _i})/{10^3} $ |
机车车辆车钩缓冲装置建模是一个非常复杂的非线性问题,它包含了许多非线性因素.本文将借鉴文献[14]中车钩缓冲器建模方法,将缓冲器特性描述成与非线性刚度、非线性阻尼、相对位移、相对速度相关的函数:
| $ {F_{{\rm{G}}i}} = {K_i}\cdot({x_{i + 1}}-{x_i}) + {C_i}\cdot({v_{i + 1}}-{v_i}) $ | (5) |
| $ {K_i} = {f_1}({x_{i + 1}}-{x_i}) $ | (6) |
| $ {C_i} = {f_2}({v_{i + 1}}-{v_i}) $ | (7) |
式(5)~(7)中:xi、xi+1分别为第i+1和i辆的运动位移;Ki和Ci分别为第i个缓冲器的刚度和阻尼,其中Ki是与xi+1-xi有关的非线性函数f1,而Ci则是关于vi+1-vi的非线性函数f2,本文根据缓冲器单车撞单车试验结果反推得到函数f1和f2.
2 仿真模型验证为了验证基于ECP制动系统的重载列车纵向动力学模型的正确性,本文首先对ECP制动系统性能仿真和车钩缓冲器冲击进行分析,然后研究2万t重载列车在平直道上的纵向冲击.其中,机车采用HXDⅠ型电力机车,车辆以C80型为研究对象,具体参数见表 1.
| 下载CSV 表 1 基础制动装置参数 Tab.1 Parameters of brake rigging device |
本文根据车辆状态和车辆制动率来确定车辆的常用全制动制动缸压力,并根据制动指令的不同以获得各级制动指令的制动缸压力值[15].本文规定最小常用制动为42 KPa;此外,为了保证有充足的压缩空气施行紧急制动,规定最大常用全制动为列车管设定压力的0.71倍.
列车管设定压力为600 KPa,列车车辆均为重车状态,制动率为0.2.以“1节机车+30节货车”组成的列车为研究对象,分别施加最小常用制动、最大常用全制动以及紧急制动,观察机车和货车车辆的制动缸压强变化曲线,如图 3所示.

|
图 3 制动缸压强曲线 Fig.3 Pressure curves of brake cylinder |
由于机车与货车的基础制动参数不一致,所以制动缸目标压强也有所差异.实施最小常用制动时,目标压力均为42 KPa,此时机车制动缸在0.9 s后稳定在40 KPa,而货车均在1.6 s后稳定在39.5 KPa左右(图 3a).实施最大常用全制动时,机车和货车的目标压力分别为406和252 KPa,而仿真结果(图 3b)显示两者分别在9.7和8.8 s后稳定在402和248 KPa附近;缓解后,两者制动缸压强分别需10.3和12.4 s后降至40 KPa以下.施行紧急制动时,机车与货车制动缸目标压力分别为487和302 KPa,而实际(图 3c)中机车和货车分别在11.6和10.3 s后稳定在482和298 KPa左右.进一步研究发现,第1、11以及21节货车的制动缓解响应基本是一致的,这是因为:列车管直接向副风缸供风,此时可将副风缸视为恒压源.
因此,ECP模式下的机车和车辆制动系统仿真结果能较好符合北美铁道协会AAR S—4200的标准[16].
2.2 车钩缓冲器冲击分析以“单车撞单车”模型分析车钩缓冲器装置的纵向冲击,各种初速度下单车撞单车试验仿真结果见表 2,这与文献[17]中HM-1缓冲器单车撞单车试验结果吻合.为此,将此缓冲器模型加入列车纵向动力学仿真程序之中.
| 下载CSV 表 2 各种速度撞击下最大车钩力 Tab.2 Coupler force for variety of initial velocities |
假设重载列车分别以“1+2+1”以及“4×5 000t”编组形式在平直道上实施紧急制动,此时制动初速度为78 km·h-1,列车最大车钩力见表 2.
表 3中“120-1型制动机”指的是大秦线2万t重载列车以制动初速度77.9 km·h-1施加紧急制动时的最大车钩力.由此可知,与传统空气制动方式而言,ECP制动系统可有效减小列车纵向冲击,这是因为ECP制动系统能够实现全列车制动/缓解的一致性.
| 下载CSV 表 3 不同编组方式的列车纵向冲动结果 Tab.3 Longitudinal impact of marshaling modes |
虽然ECP制动系统能够实现重载列车制动/缓解的一致性,但是随着编组数的增加,列车在坡道线路中所处的位置将更加复杂,车辆制动系统的性能差异性更大.因此,有必要研究坡道坡度等参数对列车纵向冲动的影响规律,并深入分析纵向冲动的内在表征形式.
3.1 坡道类型与坡度假设重载列车车钩间隙均为5 mm,列车以120 km·h-1的初速度在不同坡道形式和坡度上实施紧急制动,仿真分析不同工况下列车车钩力的变化.本文研究以下两种典型的坡道形式,分别是“平道+上坡”(图 4a)和“平道+下坡”(图 4b).

|
图 4 线路坡道示意图 Fig.4 Diagram of railway line |
(1) 部分列车在坡道上时
当列车部分处在平直道上、其余处在坡度为5‰的上坡道上,此时施加制动力,观察列车最大车钩力与制动时坡道车辆数的关系,如图 5所示.
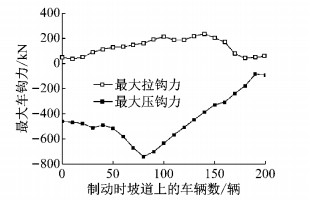
|
图 5 最大车钩力与坡道车辆数的关系 Fig.5 Relationship between maximum coupler force and numbers of vehicles on the ramp |
随着制动时坡道上车辆数目的增加,最大车钩力先增大后减小:当坡道上车辆数为80辆时车钩力最大,为-738 kN.因此,对于同一坡道,不同的制动位置会对列车纵向冲动有着不同影响.
(2) 处在不同类型的坡道上
当列车分别在“平直道+20‰上坡道”和“平直道+20‰下坡道”上实施制动时,最大车钩力与坡道上车辆的关系如图 6所示.

|
图 6 不同坡道的最大车钩力与坡道车辆数的关系 Fig.6 Relationship between maximum coupler force and numbers of vehicles on different ramp |
由图 6可知,上坡道对列车压钩力影响较大,最大可达-3 375 kN;下坡道对列车拉钩力影响较大,最大达到3 098 kN.这是因为:在上坡道时,坡道上车辆的运动减速度比平直道上的大,此时车钩呈压缩状态,因此上坡道对压钩力影响较大;反之亦然.
但是,不同类型的坡道对最大车钩力和坡道车辆数的关系影响是一致的,即:随着坡道上的车辆数的增加,最大车钩力均会先增大后减小.此外,当列车在“平直道+20‰上坡道”上实施制动,当坡道上车辆数为80时,此时车钩力最大;列车在“平直道+20‰下坡道”上时同样如此.
为了进一步研究坡道车辆数与车钩力的关系,列车仍然在“平直道+坡道”的线路上施加制动,改变坡道坡度,观察列车最大车钩力以及对应的坡道车辆数的变化趋势,见表 4.
| 下载CSV 表 4 不同坡度坡道上最大车钩力 Tab.4 Maximum coupler forces in different slope |
不难发现,改变坡道坡度对最大车钩力所对应的坡道车辆数没有明显影响.因此,列车制动的危险位置不会随坡道坡度以及坡道形式的改变而改变,即:当全列车约3/8的车辆处于坡道上,此时施加制动力是最危险的时刻,特别是在坡度较大的坡道上时极易出现断钩等现象.
3.2 车钩间隙和制动初速度重载列车以不同的车钩间隙在“平直道+15‰上坡道”的线路上以不同初速度实施紧急制动,研究车钩间隙、制动初速度等因素对列车纵向冲动的影响.由3.1分析可知,“平直道+上坡道”对列车的压钩力影响较大,因此该处主要分析不同因素对压钩力的影响,见表 5.
| 下载CSV 表 5 不同因素对列车最大压钩力的影响 Tab.5 Maximum coupler forces in different slope |
由表 5知,列车制动的危险位置既不受坡道坡度的影响,也不会随着车钩间隙以及制动初速的改变而改变.当车钩间隙增大时,列车最大压钩力变大;而当制动初速度增大时,最大压钩力的变化无明显趋势.
为了进一步揭示坡道坡度、制动初速度以及车钩间隙等因素与列车纵向冲动的关系,本文选用多元线性回归方法进行相关性分析.设定三个自变量指标分别为:制动初速度x1,km·h-1;车钩间隙x2,mm;以及坡道坡度x3,‰.最大压钩力y,kN,作为因变量,并建立如下的多元线性回归模型:
| $ y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + {\beta _3}{x_3} + \varepsilon $ |
其中β0、β1、β2和β3分别为未知参数;ε为剩余残差,与三个自变量无关,服从正态分布.
通过设置坡道坡度(5‰~20‰)、制动初速度(80~120 km·h-1)和车钩间隙(5~30 mm)等自变量参数,仿真获取列车在最危险制动位置时的最大压钩力,分析结果见表 6.
| 下载CSV 表 6 多元线性回归分析结果 Tab.6 Results of multiple linear regression |
表 6中,T为对回归系数的t检验结果,该值越大,Sig值就越小(Sig代表t检验的显著性).在统计学上,Sig小于0.005一般被认为是系数检验显著.因此,坡道坡度对列车纵向冲动的影响显著,而制动初速度的影响不明显.其中,坡道坡度对纵向冲动的影响最大,坡度越大纵向冲动越大;车钩间隙纵向冲动也有贡献,车钩间隙越大,则纵向冲动越大.
对于“平直道+下坡道”而言,列车制动时车钩最大拉钩力与坡道坡度、车钩间隙以及制动初速也同样存在上述规律,在此将不再赘述.
3.3 纵向冲动与速度差的关系纵向冲动主要通过车钩力反映,而车钩力又是由相邻两车运动状态的不一致引起的.一般地,车辆运动状态可以通过加速度、速度以及位移等参数表征,但是在工程应用中多监测速度信号,这是因为:位移传感器价格贵,加速度传感器易受外界噪音干扰而影响测量精度.同时根据TB/T 1335—1996《铁道车辆强度设计及鉴定规范》[18]可知:通用货车缓冲器最大阻抗力不大于2×103 kN,容量不小于45 kJ.因此,本文主要研究相邻两车的速度差与2×103 kN以上的车钩力之间的内在联系.
当前80辆车在20‰上坡道上、其余车辆在平直道上时实施制动,此时观察第119号车钩的车钩力和该车钩相连的两车速度差的变化曲线,如图 7所示.从图 7a和7b可以看出速度差的每一次突变都会引起车钩力的突变,这是因为:两车之间负的速度差越大,车钩压缩量越大,从而使得车钩力变大;而车钩力作为一个反作用力将阻碍速度差与压缩量的进一步增大.此外,在14 s左右时负的速度差最大,同时压钩力最大,主要原因是:在“平直道+上坡道”线路上车钩多呈压缩状态,此时若速度差为负值则可加剧车钩的压缩程度;负的速度差越大,车钩压缩量越大,车钩工作状态越恶劣,则压钩力也越大.

|
图 7 某车钩的车钩力与速度差变化曲线 Fig.7 Graph of coupler force and speed difference |
为了提取速度差信号中的有用信息、更清晰地反映最大压钩力与最小速度差之间的关系,速度差信号经一阶滤波器处理后如图 7c所示.现分析该工况下2×103 kN以上压钩力与对应的经过滤波后的最小速度差的分布情况,如图 8所示.
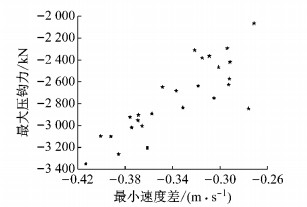
|
图 8 最大压钩力与最小速度差之间的关系 Fig.8 Relationship between maximum coupler force and minimum speed difference |
如图 8所示,当最大压钩力大于2×103 kN时,此时车钩对应的最小速度差均小于-0.26 m·s-1.仔细观察还可发现,最大压钩力与最小速度差之间呈正向线性相关,即:车钩力越小,该车钩所对应的最小速度差越小.为了进一步说明问题,本文模拟列车在“平直道+上坡道”的不同坡度上,以不同车钩间隙和不同制动初速度实施紧急制动,研究2×103 kN以上压钩力所对应的最小速度差的分布情况,如图 9所示.

|
图 9 最小速度差直方图 Fig.9 Histogram of minimum speed difference |
由图 9知,最大压钩力与最小速度差之间呈正态分布,并且服从N(-0.315, 0.001 3).2×103 kN以上压钩力所对应的最小速度差分布在-0.45~-0.2 m·s-1之间,当最小速度差大于-0.25 m·s-1时,最大压钩力大于2×103 kN的概率为3.52%.
对于“平直道+下坡道”路况也可得到同样结论,此时需要观察最大拉钩力与最大速度差之间的关系,其中2×103 kN以上拉钩力所对应的最大速度差分布如图 10所示.

|
图 10 最大速度差直方图 Fig.10 Histogram of maximum speed difference |
通过分析可知,最大拉钩力与最大速度差之间也呈正态分布,服从N(0.349, 0.0025).其中,最大速度差均分布在0.2~0.5 m·s-1之间,当最大速度差小于0.25 m·s-1时,最大拉钩力大于2×103 kN的概率为2.32%.
因此经过一阶滤波后的速度差控制在-0.25~0.25 m·s-1之间时,最大车钩力超过2×103 kN的概率不足5%.
4 总结本文利用ECP制动系统和纵向动力学联合仿真系统,以重载列车为研究对象,研究坡道坡度、车钩间隙和制动初速度对列车纵向冲动的影响规律,并分析纵向冲动与速度差之间的内在联系,得到以下结论:
(1) 在坡道坡度、车钩间隙和制动初速度这三种因素中,坡道坡度对列车纵向冲动的影响最显著,其次是车钩间隙,制动初速度无明显影响;
(2) 当列车前3/8处在坡道上时是最不利的制动位置,且该位置不随坡道坡度、车钩间隙以及制动初速度的变化而变化;
(3) 当压(拉)钩力超过2×103 kN时,最小(大)速度差与最大压(拉)钩力呈正向线性相关;
(4) 最大压(拉)钩力大于2×103 kN的车钩所对应的最小(大)速度差呈正态分布,且经滤波后的速度差控制在-0.25~0.25 m·s-1之间时,车钩力超过2×103 kN的概率不足5%.
| [1] |
王高, 涂智文. ECP技术发展及技术研发探讨[J]. 铁道机车车辆, 2014, 34(5): 21 WANG Gao, TU Zhiwen. Discussion on ECP technology development[J]. Railway Locomotive & Car, 2014, 34(5): 21 |
| [2] |
林晖, 钱立新. 重载列车有线电控空气制动系统的研究[J]. 中国铁道科学, 2007, 28(1): 63 LIN Hui, QIAN Lixin. Study on ECP system for heavy haul train[J]. China Railway Science, 2007, 28(1): 63 |
| [3] |
刘严超, 张国平, 张绍光, 等. 我国铁路发展ECP制动技术的可行性[J]. 铁道车辆, 2014, 52(8): 29 LIU Yanchao, ZHANG Guoping, ZHANG Shaoguang, et al. Feasibility to develop ECP braking technology for railway in China[J]. Rolling Stock, 2014, 52(8): 29 |
| [4] |
赵永宾, 李培曙. 我国重载货物列车采用ECP制动技术的可行性探讨[J]. 铁道车辆, 2007, 45(10): 28 ZHAO Yongbin, LI Peishu. Feasibility discussion on application of ECP braking technology in heavy haul freight cars in our country[J]. Rolling Stock, 2007, 45(10): 28 DOI:10.3969/j.issn.1002-7602.2007.10.009 |
| [5] |
张波, 钱立新, 马大炜, 等. 重载列车ECP_DP系统的仿真研究[C]//铁道科学技术新进展——铁道科学研究院五十五周年论文集. 北京: 铁道科学研究院铁道技术研究发展中心, 2005: 142-152. ZHANG Bo, QIAN Lixin, MA Dawei, et al. Simulation study on ECP system for heavy haul train[C]//New Progress of Railway Science and Technology, Proceedings of the Academy of Railway Science. Beijing: Research Center of Railway Science and Technology, 2005: 142-152. |
| [6] |
Wright E C. ECP brake: Transitioning from development to deployment[C]//2001 ASME International Mechanical Engineering Congress and Exposition, New York: American Society of Mechanical Engineers, Rail Transportation, 2001: 129-134.
|
| [7] |
CHOU Ming. Modelling and model validation of heavy-haul trains equipped with electronically controlled pneumatic brake systems[J]. Control Engineering Practice, 2007, 15(4): 501 DOI:10.1016/j.conengprac.2006.09.006 |
| [8] |
HUANG Zhiwu, QU Xiaohui, LIU Weirong, et al. A high efficient and reliable DC-DC converter for Electronically Controlled Pneumatic brake system applications[C]//40th Annual Conference of the IEEE Industrial Electronics Society. Dallas: IEEE, 2014: 5012-5018.
|
| [9] |
ZHUAN Xiangtao, XIA Xiaohua. Optimal scheduling and control of heavy haul trains equipped with electronically controlled pneumatic braking systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(6): 1159 DOI:10.1109/TCST.2007.899721 |
| [10] |
CHOU Ming, XIA Xiaohua. Optimal cruise control of heavy-haul trains equipped with electronically controlled pneumatic brake systems[J]. Control Engineering Practice, 2007, 15(5): 511 DOI:10.1016/j.conengprac.2006.09.007 |
| [11] |
祝露, 王晓东, 吴萌岭, 等. 备用制动系统性能比较[J]. 交通运输工程学报, 2016, 16(1): 80 ZHU Lu, WANG Xiaodong, WU Mengling, et al. Performance comparison of backup brake system[J]. Journal of Traffic and Transportation Engineering, 2016, 16(1): 80 |
| [12] |
陆强. 重载列车ECP制动系统方案设计及仿真研究[D]. 成都: 西南交通大学, 2009. LU Qiang. Design solution and simulation research of ECP brake system for heavy haul train[D]. Chengdu: Southwest Jiaotong University, 2009. |
| [13] |
杨润栋、王祯、刘继功, 等. 列车牵引计算规程: TB/T 1407—1998[S]. 北京: 中华人民共和国铁道部, 1983. YANG Rundong, WANG Zhen, LIU Jigong, et al. Regulations on railway train traction calculation: TB/T 1407—1998[S]. Beijing: Ministry of Railway of the People's Republic of China, 1983. |
| [14] |
魏伟, 赵连刚. 两万吨列车纵向动力学性能预测[J]. 大连交通大学学报, 2009, 30(2): 39 WEI Wei, ZHAO Liangang. Prediction of longitudinal dynamic coupler force of 2 000 t connected train[J]. Journal of Dalian Jiaotong University, 2009, 30(2): 39 |
| [15] |
姚寿文. 长大货物列车电控空气制动系统及防滑器的智能控制研究[D]. 北京: 铁道部科学研究院, 2006. YAO Shouwen. Research on intelligent control of ECP brake system for long heavy haul freight train and anti-skid system for passenger train[D]. Beijing: China Academy of Railway Sciences, 2006. |
| [16] |
The Association of American Railroads. Manual of standards and recommended practices: AAR S—4200[S]. Washington: The Association of American Railroads, 2007.
|
| [17] |
赵连刚. 基于制动系统仿真的两万吨列车纵向动力学分析[D]. 大连: 大连交通大学, 2008. ZHAO Liangang. Combined simulation of air brake system and longitudinal dynamic of 2 000 t Train[D]. Dalian: Dalian Jiaotong University, 2008. |
| [18] |
洪原山, 周晓峰, 成建民, 等. 铁道车辆强度设计及鉴定规范: TB/T 1335—1996[S]. 北京: 中华人民共和国铁道部, 1996. HONG Yuanshan, ZHOU Xiaofeng, CHENG Jianmin, et al. Code for strength design and test evaluation of railway rolling stock: TB/T 1335—1996[S]. Beijing: Ministry of Railway of the People's Republic of China, 1983. |
 2018, Vol. 46
2018, Vol. 46

