近年来,我国地铁大规模建设,网络规模不断扩大,北京、上海等大城市率先进入网络化运营时代.网络化运营凸显了地铁大运量、准时、便捷等优点,吸引了更多居民乘坐地铁出行.客流的急速增长使网络中某些区段或车站客流承载量过大,网络客流时空分布极度不均衡,尤其在高峰时段,列车满载率过高、乘客留乘等现象已司空见惯.以上海地铁为例,上海地铁成网后客流量不断攀升,工作日均客流量超1 000万人次、双休日超800万人次已成常态,早高峰断面客流量最高超过5万人·h-1,日最大客流量也持续刷新,在2018年3月23日达1 235.5万人次,早高峰列车运行间隔不断缩小,但局部网络区段仍拥挤严重.网络运输能力时空配置与乘客出行需求时空分布不匹配是产生上述现象的根本原因,乘客出行在时空上有特定的需求,一般在个别车站或高峰时段集中分布,受到线路、车站等客观条件的限制,运能无法满足特定时段特定地点的客流需求,从而导致网络客流局部拥挤严重.
受限于地铁网络基础设施设备能力,运能调整缓解高峰常态大客流拥挤逐渐达到极限.在网络化运营条件下,网络可达性增强,乘客的出行路径选择多样化,通过客流路径诱导优化控制网络客流分布为解决此问题提供了新的途径,该方法也更能体现以乘客为本的服务理念.考虑乘客出行需求,将网络中经过拥挤区段的一部分具有替代路径的起止点(orgin and destination,OD)客流,进行路径诱导分流,可有效缓解该区段的拥挤.随着地铁网络规模的不断扩大,针对特定时段特定区段实施有效客流诱导措施的关键是掌握特定时空约束条件下拥挤区段的断面客流构成及来源,即:在时间和路径双重约束下基于断面客流总量推定该断面的OD客流构成.针对此问题,在道路交通领域,通常运用反推技术求解一个智能交通系统难以直接获取的重要输入参数——动态OD矩阵[1],目前该技术已较为成熟,并衍生出多种求解模型.OD矩阵反推是一种由果溯因、与交通分配相逆的过程,所有模型与方法都围绕OD流量与路段流量的内在关系[2],即路段流量是每个OD流量累加的结果.在利用道路交通流量反推动态OD矩阵过程中,Kalman滤波[1]、极大熵[3]、牛顿迭代算法、序列二次规划法(SQP)[4]、改进粒子群算法[5]、贝叶斯推断、极大似然法[6]等都是常用的求解方法.在城市轨道交通领域,主要在网络客流分布计算方面进行了较多研究,将拥挤对乘客产生的影响考虑其中[7-10];或基于自动售检票系统(AFC)采集数据,从多路径、进出站时间、网络化等多角度广泛深入研究网络客流分布理论并在研究过程中对城市轨道交通网络客流分配模型进行不断改进修正[11-13],以及推算客流路径选择概率[14]或基于时空约束生成出行路径集[15],这种“正推”方法旨在计算客流在网络中的分布状态,还不能为实际客流诱导方案的制定提供有效支撑.
本文基于已有理论研究成果,结合地铁网络化运营特点,运用反推思路,研究能够推定地铁网络拥挤区段断面客流构成的模型与算法,为常态大客流压力下的客流路径诱导提供充分理论依据,使客流诱导方案的制定更有针对性、预判性和主动性.
1 问题分析与假设高峰时段由于运能无法满足网络部分区段的客流需求,列车则在该区段超负荷运营.将网络中这样的区段定义为能力限制区段,限制区段可由单个区间或连续的多个区间组成,可以用断面满载率来反映.基于AFC采集数据,通过计算不同时间粒度断面满载率可以识别网络中的能力限制区段,目前最小计算时间粒度为5min,同时高峰时段列车开行间隔为2~3min,因此可选择5min高峰断面满载率反映限制区段拥挤的严重程度;此外,在高峰时段一般会存在15~20min的超高峰时段,随着时间粒度的变大,断面满载率所反映的情况变得较为平均,难以准确识别限制区段,因此本文认为选择30min高峰断面满载率反映限制区段拥挤的持续性较为合适.基于实际调查情况,设定5min高峰断面满载率阈值σ5min=100%进行初步筛选;然后设定30min高峰平均满载率阈值σ30min=85%对初步结果进行二次筛选,通过两次综合考量识别出网络中亟需客流诱导的限制区段.
有效的客流诱导需要根据限制区段的断面客流构成有针对性地对部分客流进行路径分流,从而才能有效缓解限制区段拥挤.在地铁网络化运营条件下,乘客出行有多条路径可选择,且客流在网络上随时间动态变化,而限制区段的形成是在特定地点的特定时段.在网络路径选择多样化、客流网络分布动态化的环境下,利用大规模的OD数据求解特定时段内导致限制区段拥挤的断面客流构成是本文需要解决的关键难点.
本文以地铁网络能力限制区段为研究对象,以高峰运营期[Ta, Tb]为研究时段,求解限制区段S的断面OD客流构成{Q1, Q2, …, Qi, …, QI}(Qi表示一对会包含限制区段的OD,I为OD对的总量)所对应的求解时段经过限制区段的客流量集合{V1, V2, …, Vi, …, VI}.对任一OD,设其乘客集合为UQi={u1, u2, …, un, …, uN},其中N为Qi的乘客总数,设任一OD之间有KQi条有效路径.输入变量分别为限制区段S的断面客流总量VS,乘客选择第k条路径Rk出行的概率Pk(k=1, 2, …, KQi),乘客un在O站的进站时刻TunO,乘客到达限制区段S之前的乘车总时间tktrain、候车总时间tkwait和换乘总时间tktransfer.为便于模型建立与求解,作如下假设:①所有OD数据成对出现,遵循进出站总量守恒原理;②列车运行按照计划运行图执行,不考虑列车延误对客流分布造成的扰动.
2 断面客流构成反推模型 2.1 模型建立在已知限制区段的断面客流总量VS、网络客流出行路径和客流路径选择比例的基础上,建立断面客流构成反推模型,推定求解高峰时段经过限制区段的断面客流构成,即在某高峰时段所有可能包含限制区段S的OD所涉及经过S的客流量集合V.以集合V为求解目标,考虑时间和路径的双重约束条件,建立如下断面客流构成反推模型:
| $ V = \{ {V_1}, {V_2}, \cdots , {V_i}, \cdots , {V_I}\} $ | (1) |
约束:
| $ {V_S} = \sum\limits_{i = 1}^I {{V_i}, i = 1, 2, \cdots , I} $ | (2) |
| $ \forall {Q_i}, {V_i} = \sum\limits_{{u_n} \in {U_{{Q_i}}}} {{P_{{u_n}}}} $ | (3) |
| $ {P_{{u_n}}} = \sum\limits_{k = 1}^{{K_{{Q_i}}}} {{P_k} \cdot {\theta _k}({u_n}), k = 1, 2, \cdots , {K_{{Q_i}}}} $ | (4) |
| $ {\theta _k}({u_n}) = \left\{ \begin{array}{l} 1\;\;{T_{\rm{a}}} \le {T_{{u_n}}} \le {T_{\rm{b}}}且S \in {R_k}\\ 0\;\;其他 \end{array} \right. $ | (5) |
| $ {T_{{u_n}}} = T_{{u_n}}^{\rm{O}} + t_k^{{\rm{train}}} + t_k^{{\rm{wait}}} + t_k^{{\rm{transfer}}} $ | (6) |
式(1)为模型的求解目标,集合V是在高峰时段[Ta, Tb]会包含限制区段S断面OD客流构成所对应的客流量集合.式(2)为限制区段断面客流总量约束.Vi可视为乘客选择包含限制区段S的路径出行的概率累计的结果,由式(3)计算得出.一般情况下,任一OD之间可能存在多条路径可供选择,但并非所有路径都会包含限制区段S,式(4)则用于计算乘客un在高峰时段[Ta, Tb]选择包含限制区段S的路径出行的概率Pun.式(5)为时间路径双重约束条件,θk(un)为0-1变量,若Ta≤Tun≤Tb,则θk(un)=1,为模型的时间约束;若S∈Rk,则θk(un)=1,为模型的路径约束;同时满足时间及路径两个约束可保证乘客un是选择了包含限制区段S的路径出行且在高峰时段[Ta, Tb]内经过限制区段S,则在此约束条件下求得的Vi即为限制区段S的断面客流构成;式(6)用于计算乘客un选择路径Rk到达限制区段S的时刻,用Tun表示.
2.2 迭代算法设计迭代算法是利用计算机解决问题的一种基本方法,确定迭代变量、建立迭代关系式并对迭代过程进行控制是设计迭代算法的关键.基于此,设计求解限制区段断面客流构成的迭代算法如下:
输入数据:以下面3类数据为模型输入数据.
(1) 客流数据:限制区段S的断面客流总量VS;
(2) 路径信息:清分比例表中任一OD之间的有效路径条数KQi、Qi之间的第k条路径Rk的乘客出行选择概率Pk,k=1, 2, …, KQi;
(3) 时间数据:设定求解高峰时段[Ta, Tb]、[Ta, Tb]时段的列车运行时刻表、由AFC获取的乘客un在O站的进站时刻TunO和由调查得到的网络换乘站各换乘方向的换乘时间.
输出结果:限制区段S的断面OD客流构成Qi所涉及的客流量Vi.
步骤1:确定迭代变量Vi,初始化,n=0,Vi=0;
步骤2:n=n+1;
步骤3:对Qi之间的KQi条有效路径,依次判断第k条路径Rk是否包含限制区段S,如果否,则令θk(un)=0;如果是,计算乘客un通过该路径Rk到达限制区段S的时刻Tun,若Ta≤Tun≤Tb,则θk(un)=1;否则,θk(un)=0;
步骤4:根据Qi的客流路径分配比例,计算Pun;
步骤5:根据迭代关系式Vi=Vi+Pun进行计算.判断n是否等于N,如果是,推算结束,返回Vi;否则,转步骤2.
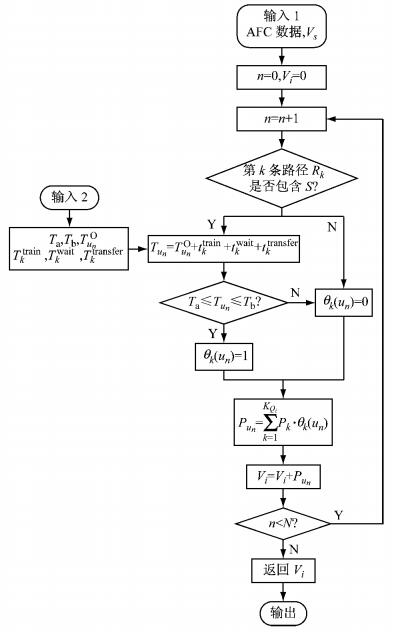
对所有OD进行步骤1~步骤5迭代计算,形成限制区段S的OD客流构成的对应客流量的集合V={V1, V2, …, Vi, …, VI},具体算法流程如图 1所示.
|
图 1 迭代算法流程图 Fig.1 Flow chart of the iterative algorithm |
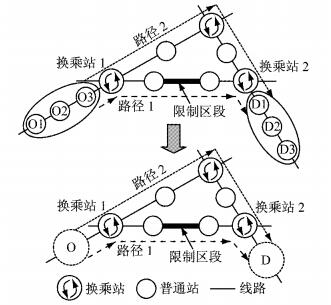
用第2节建立的客流构成反推模型和设计的迭代算法推算出所有经过限制区段OD客流构成对应的客流量的集合V,此时得到的很多OD具有一定的相似特征,如图 2中,乘客从车站O1,O2,O3到车站D1,D2,D3具有相同的替代路径2,并且O1,O2,O3均在第一个换乘站1处开始存在替代路径,车站D1,D2,D3则具有相同的替代路径的最后一个换乘站2.因此可以将具有图 2性质的OD分组为多个类,对一个类中的OD作为一个整体看待,即将车站O1,O2,O3归类为虚拟站点O,将车站D1,D2,D3归类为虚拟站点D.通过OD客流归类排序将具有相同特征的Vi合并的同时,找出具有替代路径的Vi并剔除客流量较小、不足于缓解限制区段拥挤的客流量Vi.
|
图 2 相同特征的OD归类示意 Fig.2 An overview of classification of OD with same characters |
以上海地铁网络为例进行分析,上海地铁(不计磁浮)目前共开通运营线路15条,全网运营里程637 km,车站387座,换乘站52座.网络化运营下全网客流量不断攀升,网络局部区域拥挤严重.
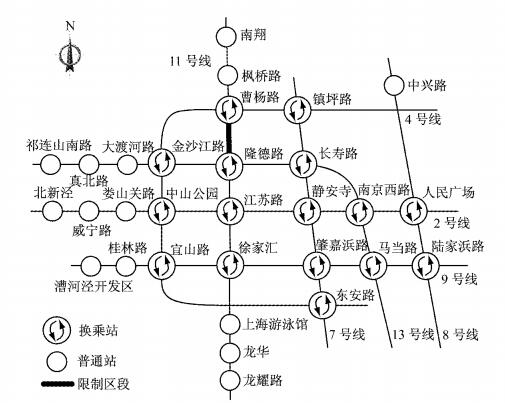
3.1 限制区段识别结合2016年3月3日上海地铁网络车站AFC采集数据,共识别出10个典型能力限制区段,从中选择11号线曹杨路隆德路区段作为研究对象进行模型算法验证.图 3是限制区段曹杨路隆德路在上海地铁网络中的位置(部分车站和线路已省略).
|
图 3 上海地铁局部网络示意图 Fig.3 Part of simplified Shanghai metro network |
根据AFC采集数据和列车开行方案信息,进行一系列计算后得到表 1所示的曹杨路隆德路区段早高峰8:00~9:30时段的满载率情况.分析可知,该区段在其中的8:30~9:00时段存在多个5 min高峰满载率极值超过100%的时段,个别时段甚至超过120%,而30 min高峰平均满载率也远超过85%的阈值.因此,该区段客流拥挤的严重程度和拥挤的持续性都非常突出,有必要求解该区段客流构成,将其中部分客流引导至能力富余的替代路径以缓解该区段的客流拥挤.
| 下载CSV 表 1 限制区段曹杨路-隆德路早高峰时段满载率 Tab.1 Load factor of Caoyang Rd-Longde Rd. in the morning peak |
设定求解时段[Ta, Tb]为早高峰8:30~9:00,运用建立的断面客流构成反推模型,采用VB.net语言编程,在Inter Core TM i5,2.5 GHz主频,内存4 G的计算机上实现算法,得到导致该区段拥挤的OD客流构成,共4 448个ODs在8:30~9:00之间通过了曹杨路隆德路区段.根据上海地铁网络结构特点和2.3中的归类方法,4 448个ODs被归为7类,其中O站被归为2类,D站被归为7类,详细归类结果见表 2.
| 下载CSV 表 2 曹杨路-隆德路限制区段OD客流构成 Tab.2 Detail results of OD composition of Caoyang Rd -Longde Rd. |
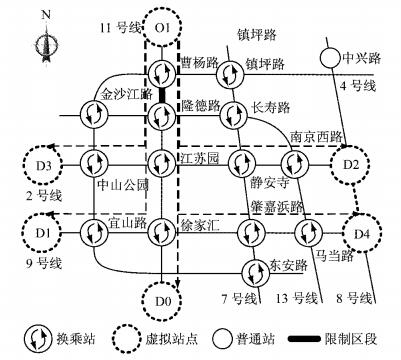
其中2 861个ODs是由11号线曹杨路站以北车站出发,且这些OD的客流量占经过限制区段客流量的84.25%,此类ODs的O站归类为虚拟站点O1,其他O站归类为虚拟站点O2;D站归类为6类虚拟站点D0、D1、D2、D3、D4、D5,如图 4所示,但由于O2、D5包含车站分散,故无法在图上显示.设V'1,V'2,V'3,V'4分别为O1D1,O1D2,O1D3,O1D4涉及的客流量,则V'1=3 169,V'2=2 874,V'3=1 500,V'4=1 330.
|
图 4 OD虚拟站点分布示意图 Fig.4 Distribution of virtual stations of ODs |
根据表 2归类结果和上海地铁网络结构特点,可知导致曹杨路隆德路区段拥挤的OD客流量具有以下特征:
(1) 早高峰8:30~9:00时段经过限制区段的客流,其中的84.25%由11号线曹杨路以北车站出发,因此将此类O站归类为虚拟站点O1;
(2) O1D0的客流为本线客流,即无需换乘即可到达目的地,因此无替代路径,故无法对此类OD实施路径诱导;
(3) 具有替代路径的O1D1,O1D2,O1D3,O1D4所涉及客流量占总量的48.3%,进一步研究此部分客流量,基于替代路径满载率,利用能力富余路径分担其中部分客流量,从而可为制定有效的客流路径诱导方案主动控制网络客流分布奠定基础.
4 结语(1) 针对目前地铁网络高峰时段客流分布不均衡,部分区段满载率过高,供需矛盾突出的现状,基于断面满载率识别网络能力限制区段,并构建断面客流构成反推模型和设计迭代算法求解导致限制区段拥挤的断面客流构成,以上海地铁网络为例,选择限制区段曹杨路隆德路为研究对象验证了模型和算法的可行性,求解得到在早高峰8:30~9:00时段导致该区段拥挤的客流构成,并分析了该区段断面客流构成的主要特征.本文的研究成果可为运营管理部门针对性地制定有效的客流路径诱导方案提供理论依据,从而使客流组织更具人性化和主动性,提出的断面客流构成推定方法同样适用于求解非限制区段的断面客流构成.
(2) 地铁网络客流拥挤作为网络化运营面临的突出问题,需要更多的理论研究和多种客流组织手段的协调运用,下一步的研究重点将是替代路径的搜索和可供实际操作的客流诱导方案的制定.
| [1] |
焦朋朋, 陆化普. 全路网改进动态O-D反推模型[J]. 清华大学学报(自然科学版), 2006, 46(9): 1505 JIAO Pengpeng, LU Huapu. Estimates of dynamic origin-destination flows for general road networks[J]. Journal of Tsinghua University (Science & Technology), 2006, 46(9): 1505 |
| [2] |
陈振起, 王书强. 利用道路交通流量进行OD矩阵反推的模型与方法综述[J]. 物流技术, 2009, 28(8): 89 CHEN Zhenqi, WANG Shuqiang. Summary on models and methods of OD matrix estimation based on road traffic flow[J]. Logistics Technology, 2009, 28(8): 89 |
| [3] |
马广英, 李平, 闻育, 等. 基于极大熵模型的交通出行矩阵解法研究[J]. 浙江大学学报(工学版), 2006, 40(10): 1778 MA Guangying, LI Ping, WEN Yu, et al. Study of solving origin-destination matrix based on maximum entropy model[J]. Journal of Zhejiang University (Engineering Science), 2006, 40(10): 1778 DOI:10.3785/j.issn.1008-973X.2006.10.024 |
| [4] |
郝媛, 徐天东, 杜豫川, 等. 局域路网OD矩阵反推模型研究[J]. 中南公路工程, 2006, 31(5): 107 HAO Yuan, XU Tiandong, DU Yuchuan, et al. Research on OD matrix estimation model of local network[J]. Central South Highway Engineering, 2006, 31(5): 107 |
| [5] |
杜长海, 黄席樾, 杨祖元, 等. 改进的粒子群算法在动态OD矩阵反推中的应用[J]. 计算机工程与应用, 2008, 44(34): 234 DU Changhai, HUANG Xiyue, YANG Zuyuan, et al. Application of improved particle swarm algorithm in dynamic OD matrix estimation[J]. Computer Engineering and Applications, 2008, 44(34): 234 DOI:10.3778/j.issn.1002-8331.2008.34.071 |
| [6] |
吕娜娜. 基于多中心的公交客流OD反推法研究[D]. 重庆: 重庆交通大学, 2009. LV Nana. Study on bus passenger flow OD matrix estimation methods of multi-center cities [D]. Chongqing: Chongqing Jiaotong University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1525049 |
| [7] |
孙捷萍. 城市轨道交通路网客流拥堵控制方法与模型[D]. 北京: 北京交通大学, 2016. SUN Jieping. Methods and models for traffic congestion control in an urban rail transit network [D]. Beijing: Beijing Jiaotong University, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3124836 |
| [8] |
周玮腾. 拥塞条件下的城市轨道交通网络流量分配演化建模及疏导策略研究[D]. 北京: 北京交通大学, 2016. ZHOU Weiteng. Modeling passenger flow assignment and evolution in urban rail transit network with dispersion strategy research under congestion conditions [D]. Beijing: Beijing Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10004-1016059131.htm |
| [9] |
ROBERTO C, JOSE C. Common-lines and passenger assignment in congested transit networks[J]. Transportation Science, 2001, 35(3): 250 DOI:10.1287/trsc.35.3.250.10154 |
| [10] |
SI B F, ZHONG M, YANG X B, et al. Urban transit assignment model based on augmented network with in-vehicle congestion and transfer congestion[J]. Journal of Systems Science and Systems Engineering, 2011, 20(2): 155 DOI:10.1007/s11518-011-5159-9 |
| [11] |
徐瑞华, 罗钦, 高鹏. 基于多路径的城市轨道交通网络客流分布模型及算法研究[J]. 铁道学报, 2009, 31(2): 110 XU Ruihua, LUO Qin, GAO Peng. Passenger flow distribution model and algorithm for urban rail transit network based on multi-route choice[J]. Journal of the China Railway Society, 2009, 31(2): 110 |
| [12] |
ZHOU F, XU R H. Model of passenger flow assignment for urban rail transit based on entry and exit time constraints[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012(2284): 57 |
| [13] |
ZHU W, HU H, XU R H, et al. Modified stochastic user-equilibrium assignment algorithm for urban rail transit under network operation[J]. Journal of Central South University (English Edition), 2013(10): 2897 |
| [14] |
ZHOU F, SHI J G, XU R H. Estimation method of path-selecting proportion for urban rail transit based on AFC data [J]. Mathematical Problems in Engineering, 2015. DOI: http://dx.doi.org/10.1155/2015/350397.
|
| [15] |
徐瑞华, 李伟, 朱炜. 考虑时空约束的地铁乘客出行路径集生成算法[J]. 同济大学学报(自然科学版), 2015, 43(7): 1025 XU Ruihua, LI Wei, ZHU Wei. Path set generation algorithm for schedule based rail transit with constraints of time and space[J]. Journal of Tongji University(Natural Science), 2015, 43(7): 1025 DOI:10.11908/j.issn.0253-374x.2015.07.010 |
 2018, Vol. 46
2018, Vol. 46

