2. 广西交通科学研究院有限公司,广西 南宁 530007;
3. 广东省建筑科学研究院集团股份有限公司,广东 广州 510500
2. Guangxi Transportation Research and Consulting Company, Nanning 530007, China;
3. Guangdong Provincial Academy of Building Research Group, Guangzhou 510500, China
因抗剪性能不足引起的车辙是沥青路面早期破坏中最为常见的病害,严重影响路面的舒适性和安全性,因此,沥青混合料抗剪性能研究一直是业内关注的重点.现阶段,室内三轴剪切试验可以很好地评价沥青混合料的抗剪性能,但三轴剪切试验步骤复杂、成本高、再现性差且无法反映沥青混合料的细观力学特性.杨军等人基于离散元法进行了沥青混合料三轴剪切试验的细观力学数值模拟,但采用二维数值模拟[1]和采用二十四面体表征三维粗集料颗粒[2]皆具有一定的局限性.
近年来,基于算法直接构建虚拟试件的技术得以快速发展,使得低成本、高效率构建虚拟试样并开展细观结构虚拟力学研究成为可能.粗集料占据沥青混合料体积的40%~60%,其棱角性等形态特征、空间位置分布等对沥青混合料的性能有显著影响[3],相对应地,虚拟粗集料颗粒的拟真程度也将会影响数值模拟结果的准确性.
Lu等[4]采用延拓原理生成虚拟颗粒用于评价铁路道砟碎石形状的重要性;田莉[5]通过切割圆球生成虚拟颗粒用于沥青混合料劲度模量虚拟试验;黄晓明等[6]通过切割正方体获得虚拟颗粒并用于沥青混合料单轴蠕变的数值模拟;周长红等[7]使用随机生成的凸多面体及椭球体表示虚拟粗集料颗粒.上述研究中,粗集料颗粒基本是由一定粒径的单元球体堆积而成的球体集合表示.拟真程度受到较大影响,颗粒数量较多,限制计算效率的提升.
本文主要从沥青混合料的组成结构出发,拟采用三维凸包算法及Bubble Pack算法生成粗集料虚拟颗粒用于构建沥青混合料虚拟试样,基于沥青砂浆动态剪切试验确定微观接触模型参数,以三轴剪切试验为切入点,通过对比分析室内与虚拟力学试验数据,验证构建的三维细观力学模型及数值模拟的合理性.
1 三维数值试样构建数值试样的构建分为4部分:①基于Matlab软件平台使用三维凸包算法生成粗集料外壳,并导入PFC 5.0 3D软件中填充生成clump块体表征粗集料颗粒;②筛选出典型的虚拟粗集料颗粒,采用“替换法”确定粗集料颗粒的空间位置进行装配;③试样空间内生成规则排列的单元球体,删除与粗集料颗粒重叠的单元球体,剩余的球体构成沥青砂浆相;④删除部分沥青砂浆颗粒形成空隙.
1.1 虚拟粗集料颗粒生成为减少计算量,将粗集料颗粒简化为凸多面体,使用Matlab软件平台编写代码,在球面上按照均匀分布随机生成若干个点组成“点集”,并基于Quick Hull算法的原理生成“点集”的三维凸多面体,通过控制球面半径及生成点的数量可以实现生成不同大小、不同球度及棱角性的三维凸多面体.图 1所示为生成的三维凸多面体.
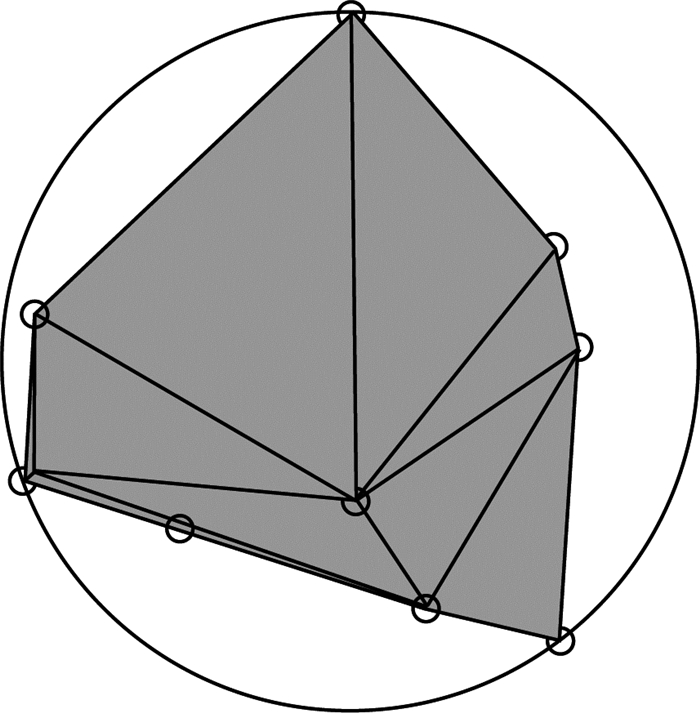
|
图 1 随机生成凸多面体 Fig.1 Generated convex polyhedron randomly |
由于随机生成点集,经过三维凸包算法求解得到的凸多面体的粒径有一定概率小于设定的球体直径,本文采用最小包围壳体的方法对得到的多面体外壳进行尺寸的标定,经过筛选从各档尺寸多面体壳中各筛选出5个接近实体集料颗粒的多面体凸包表示粗集料颗粒.为保证粗集料颗粒多面体外壳能够正常使用,还需要对生成的集料颗粒外壳进行封闭性检验,如果初始生成的集料颗粒外壳存在缺陷,需要对其进行修正和填补处理,得到完全封闭的集料颗粒外壳.如图 2所示为表示各档集料颗粒的多面体外壳.
|
图 2 表示各档集料颗粒的多面体凸包 Fig.2 Polyhedron convex hull representing the particles of each pallet |
最后,将得到的粗集料外壳导入离散元平台PFC 5.0 3D中调用Bubble Pack算法[8],在外壳内部生成具有部分重叠的单元球体,由它们充分填充集料外壳的内部空间,得到的单元球体的集合clump整体轮廓逼近导入的集料外壳,该clump即为具有不规则形状的粗集料颗粒离散元模型.Bubble Pack算法可以通过调整最小球体与最大球体的粒径比R以及单元球体之间的重叠角度A两个变量来对填充精度进行控制[9],图 3a为R=0.1 A=140°时的填充效果,填充球体的数量N=243,图 3b为R=0.2,A=140°时的填充效果,填充球体的数量N=107,图 3c为R=0.2 A=120°时的填充效果,填充球体的数量N=48,图 3d为R=0.3 A=120°时的填充效果,填充球体的数量N=23.当填充参数R越小,A越大,则填充精度越高,使用的单元球体数量N越多,需要的计算时间越长.

|
图 3 粗集料外壳的不同填充效果对比 Fig.3 Comparison of different filling effects of coarse aggregate shell |
沥青混合料力学行为较为复杂,主要表现为沥青砂浆的粘弹性以及粗集料颗粒的离散性,粗集料颗粒在混合料空间内的分布对其性能有显著影响.
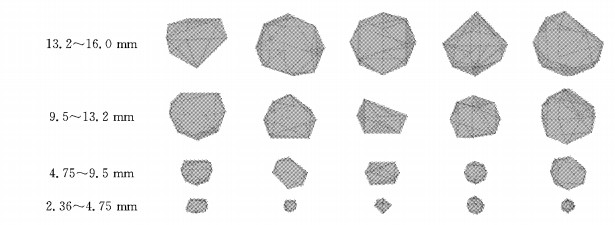
本文根据沥青混合料的级配及油石比计算出各档粗集料与沥青砂浆在试样总体积中的占比,如表 1所示为SUP-13沥青混合料中各档粗集料的占混合料总体积的百分比统计表.为平衡颗粒的填充精度以及虚拟力学模拟计算量,选用R=0.2,A=120°对应的颗粒精度,得到如图 4所示的各档粗集料颗粒离散元模型.
| 下载CSV 表 1 SUP-13各档粗集料占虚拟试件总体积的百分数 Tab.1 The percentage of the total volume of the coarse aggregate in SUP-13 specimen |

|
图 4 各档粗集料颗粒离散元模型 Fig.4 Coarse aggregate particle discreteelement model |
以计算得到的各档粗集料的体积分数作为控制阈值,使用PFC 5.0 3D软件编写代码获取各档粗集料离散元模型的体积,并计算出各档粗集料离散元模型应投放的数量分别为p、q、r、t.为保证粗集料离散元模型装配的随机性及均匀性,首先在PFC软件中生成墙面(wall)组成三维试样空间,然后在试样空间中依次随机生成p、q、r、t数量的直径分别为13.2 mm、9.5 mm、4.75 mm和2.36 mm的圆球.遍历获取所有圆球的位置信息,随机调用相应粒径的粗集料离散元模型将圆球替换,得到粗集料离散元模型装配完成后由clump块体组成的试样,简称clump试样,如图 5所示.

|
图 5 粗集料离散元模型装配形成的clump试样 Fig.5 A clump specimen consisting of a coarse aggregate discrete element models |
分别统计虚拟试样中各档集料颗粒的体积占总体积的比例并计算虚拟试样的VCA值,对clump试样的精准度进行评价.以SUP-13为例,生成clump试样之后,遍历所有的粗集料离散元颗粒并统计各档颗粒的体积,计算各档虚拟颗粒的体积占比如表 2所示.由表中数据可知clump试样中各档虚拟集料颗粒的体积占比分别为2.05%、15.80%、22.28%、17.70%,总的体积占比为57.83%,与通过级配计算得到的粗集料体积占比相比,偏差率为0.77%,符合混合料中粗集料部分的级配要求.
| 下载CSV 表 2 SUP-13 clump试样中虚拟颗粒体积占比与实际级配体积占比对比 Tab.2 Comparison of the proportion of virtual particle volume and actual gradation volume of SUP-13 clump specimen |
沥青砂浆的内部组成过于复杂,且受限于当前计算机及模拟平台的计算能力,精确模拟沥青砂浆的细观结构并进行虚拟力学试验将会耗费巨大的时间成本,因此,国内外学者将沥青砂浆假设为均匀介质,使用单一粒径的单元小球进行模拟[2, 6, 10].
使用单一粒径的单元球体组合表示粗集料颗粒可以解决虚拟粗集料颗粒与砂浆颗粒紧密接触的问题,但与使用clump表示粗集料颗粒相比,前者的颗粒模拟精度大大降低,其中粒径为2.36~4.75 cm之间的颗粒精度降低尤其显著.此外,由于组成粗集料颗粒的整体单元球体的数量增加,后期虚拟力学模拟需要耗费的时间成本也会随之增大.因此,本文选择直接采用clump块体表示粗集料虚拟颗粒.首先,生成与clump试样同等尺寸的完全由粒径1 mm规则排列的单元球体组成的“纯砂浆试样”,如图 6a所示,并使两试样完全重叠;然后,遍历所有单元球体与虚拟粗集料颗粒的重叠情况,若重叠量过大则删除该单元球体,否则将其归为沥青砂浆虚拟颗粒;最后,通过若干时步的循环,调整虚拟砂浆颗粒与粗集料颗粒之间紧密接触.如图 6b所示为经过上述步骤生成的虚拟试样,其中,深色表示虚拟粗集料颗粒,浅色表示虚拟沥青砂浆颗粒.

|
图 6 虚拟砂浆及空隙生成示意图 Fig.6 Mortar virtual specimen and asphalt mixture virtual sample without voids |
在沥青混合料虚拟试样中,删除一定数量的虚拟沥青砂浆单元形成空洞,以对沥青混凝土中的空隙进行模拟.理论上,沥青混合料中空隙应为均匀分布,但使用CT扫描技术获得的真实试样中空隙的空间分布呈上下两端分布密集,中间较为稀疏的规律[11].本文采用三段式的划分方法,将虚拟试样分为上、中、下三等份,根据设计空隙率、试样体积及空隙分布规律[12]可以计算出各个部分的空隙体积.在各部分内按照均匀分布的方式随机删除相应体积的虚拟砂浆颗粒,使虚拟试样的整体空隙分布与真实试样空隙分布更加接近.如图 6c所示为生成虚拟空隙所删除的砂浆球体颗粒平面图,可以直观体现出空隙分布的不均匀性.
2 接触本构模型及参数确定 2.1 PFC接触本构模型简介沥青混合料由集料、沥青胶结料、空隙、矿粉等组成,在外力作用下,其失稳破坏机理较为复杂,采用摩尔-库伦理论进行分析可知,沥青混合料的结构强度主要由集料之间的嵌锁力(内摩擦角)、沥青与集料之间的黏结力以及沥青自身的内聚力构成.从结构组成角度分析,沥青的黏度反映了沥青的内聚力大小,并且沥青与细集料、矿粉充分混合并裹覆在粗集料的表面,所以沥青黏度越大,则沥青混合料的黏结力越大,在相同的集料嵌锁作用下,沥青混合料的强度越大.另外,集料的种类、级配组成、棱角性、表面粗糙程度等也会对沥青混合料的嵌锁力(内摩擦角)产生影响.
离散元法的本质是将连续体适当离散化为离散单元体,为平衡模型精确性及计算量,本文将沥青砂浆离散化为均质的球体,粗集料颗粒采用clump块体表示.PFC离散元平台中,相互接触的离散单元体之间的作用与反作用的响应方式通过其相互之间的连接模式来进行定义,并基于单元体之间的相互作用迭代计算得到整体的运动状态及力学响应.PFC中内置的连接模式分为两种,一种是仅可描述受压状态的接触模式;另一种是可用于描述具有黏结强度的黏结模式.用于描述接触模式的模型包括线性刚度接触模型、滑动接触模型、伯格斯接触模型等,描述黏结模式的模型包括线性接触黏结模型、线性平行黏结模型等[8].
线性刚度接触模型可用于描述离散体之间法向及切向的接触力和相对位移的弹性关系;伯格斯接触模型通过定义法向和切向的微观伯格斯模型来模拟单元体之间的受压状态下连接处的黏弹力学行为.线性接触黏结模型可视为一种点黏结模型,通过接触点将两个单元体连接起来,当两单元体之间的重叠小于0时产生拉力,当拉力大于指定的黏结强度时,线性接触黏结模型失效;线性平行黏结模型相当于通过有限尺寸的圆柱体将两个单元体连接起来,当两单元体产生相对运动时,将在圆柱体连接处产生力和弯矩,当法向或切向应力等于或大于指定的连接强度时,平行黏结模型失效.
2.2 接触本构模型确定在构建的沥青混合料离散元模型中,粗集料颗粒采用clump表示,作为一个不可破碎的整体,内部不需要指定接触,因此,在沥青混合料内部细观组成成分之间有3种连接.如图 7所示,分别为沥青砂浆单元之间的连接、集料单元之间的连接和集料与砂浆单元之间的连接.
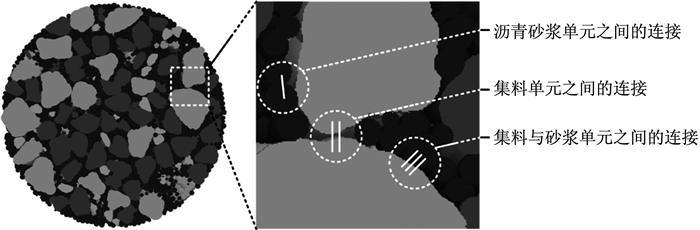
|
图 7 沥青混合料虚拟模型中的连接类型 Fig.7 The connection type of a virtual asphalt concrete model |
基于上述对沥青混合料组成结构、失稳破坏机理及其影响因素的分析,并结合PFC平台内置的模型的功能特点进行接触本构模型的选择.沥青混合料是一种黏弹性材料,其流变性能主要取决于沥青砂浆的黏弹性特征.对于沥青混合料离散元模型来说,在受压状态下,沥青砂浆单元之间及集料与砂浆单元之间可采用伯格斯接触模型来表征混合料的黏弹特性.集料本身符合弹性体的接触特征,在受压状态下,模型中的集料单元相互之间的力学行为可采用线性刚度接触模型描述.沥青的内聚力和沥青与集料之间的黏结力将混合料黏结成为一个整体,因此,混合料模型除指定相应的接触模型,还应当设置适当的黏结模型.由于沥青砂浆具有一定的强度,能够传递力矩,采用线性平行黏结模型描述沥青砂浆单元之间及集料与砂浆单元之间的黏结较为恰当.另外,沥青砂浆裹覆于集料颗粒表面形成一层沥青膜结构将相邻集料黏结在一起,可采用线性平行黏结模型描述相邻集料单元之间的黏结效果.
综上所述,沥青混合料离散元模型中,沥青砂浆单元之间的连接采用伯格斯接触模型及线性平行黏结模型,集料单元之间的连接采用线性刚度接触模型及线性平行黏结模型,集料与砂浆单元之间的连接采用伯格斯接触模型及线性平行黏结模型,能够较为准确地模拟沥青混合料真实的力学特性.
2.3 模型参数确定沥青混合料具有典型的黏弹特性,沥青混合料虚拟试样中的Burgers模型参数的选取会对模拟结果产生较大影响.PFC3D中的微观接触模型参数难以直接通过室内试验获取,需要通过室内试验得到宏观试验参数,进而根据建立的转换关系计算得到微观模型参数[13-14].如图 8所示,Kmn、Cmn、Kkn、Ckn为微观Burgers接触模型法向参数,Kms、Cms、Kks、Cks为微观Burgers接触模型切向参数,m1、m2表示颗粒单元,fs为摩擦系数.
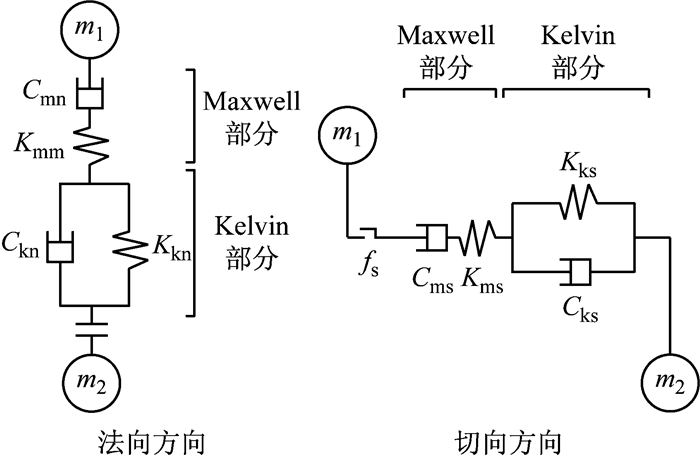
|
图 8 微观Burgers模型 Fig.8 Micro Burgers Model |
沥青砂浆的黏弹性参数可以通过动态剪切流变试验获取特定温度下沥青砂浆蠕变-时间关系曲线,对曲线进行拟合可以得到相应温度下的宏观Burgers模型的4个参数.本文根据《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)中的沥青混合料三轴压缩法抗剪强度试验中对标准试验温度的规定,参考已有的研究[5]选取60℃沥青砂浆黏弹性参数分别为E1=3.11 kPa,E2=0.61 kPa,η1=0.351 kPa,η2=1.24 kPa·s.根据现有的研究成果[15],可将宏观Burgers接触模型参数转换为微观Burgers模型参数
| $ {K_{{\rm{mn}}}} = {E_1}L $ | (1) |
| $ {C_{{\rm{mn}}}} = {\eta _1}L $ | (2) |
| $ {K_{{\rm{kn}}}} = {E_2}L $ | (3) |
| $ {C_{{\rm{kn}}}} = {\eta _2}L $ | (4) |
| $ {K_{{\rm{ms}}}} = \frac{{{E_1}L}}{{2\left( {1 + \nu } \right)}} $ | (5) |
| $ {C_{{\rm{ms}}}} = \frac{{{\eta _1}L}}{{2\left( {1 + \nu } \right)}} $ | (6) |
| $ {K_{{\rm{ks}}}} = \frac{{{E_2}L}}{{2\left( {1 + \nu } \right)}} $ | (7) |
| $ {C_{{\rm{ks}}}} = \frac{{{\eta _2}L}}{{2\left( {1 + \nu } \right)}} $ | (8) |
式中:L为相邻单元的球心距;ν为沥青砂浆泊松比.
本文采用clump块体表示粗集料颗粒,作为一个整体进行计算,集料的宏观弹性模量可通过以下公式转换为微观接触刚度,即
| $ E = \frac{{{k_{\rm{n}}}}}{{2D}} $ | (9) |
| $ {k_{\rm{s}}} = \frac{{{k_{\rm{n}}}}}{{\left( {1 + \nu '} \right)}} $ | (10) |
式中:kn、ks分别为接触刚度模型的法向刚度和切向刚度;E为集料的宏观弹性模量,取55 GPa;D为集料单元的直径;ν′为集料泊松比,取0.25[16].
通过上述公式的换算可以得到沥青砂浆Burgers接触模型的微观参数如表 3所示.
| 下载CSV 表 3 沥青砂浆Burgers模型微观接触参数 Tab.3 Asphalt mortar micro Burgers model parameter |
在上述建立的虚拟试件的基础上构建虚拟三轴剪切试验虚拟平台并进行虚拟三轴剪切试验,虚拟试验的环境参数按照室内三轴剪切试验设定,温度为60 ℃,加载速度为1.27 cm·min-1.利用PFC 3D中的伺服控制机制使虚拟试样在0、138和276 kPa 3个围压下分别进行三轴剪切虚拟试验,试验过程中控制顶面墙体的速度对试件进行轴向加载,并记录试验中所需的数据.
以SUP-13级配型沥青混合料为例,按照上述虚拟试样成型步骤生成直径为60 mm,高度为90 mm的沥青混合料虚拟试样.利用PFC 5.0 3D软件对SUP-13沥青混合料虚拟试样进行三轴剪切试验得到0、138和276 kPa围压下的偏应力-时步曲线,如图 9所示.

|
图 9 SUP-13沥青混合料3种围压水平的虚拟试验结果 Fig.9 Virtual test results of three types of confining pressure of SUP-13 asphalt mixture |
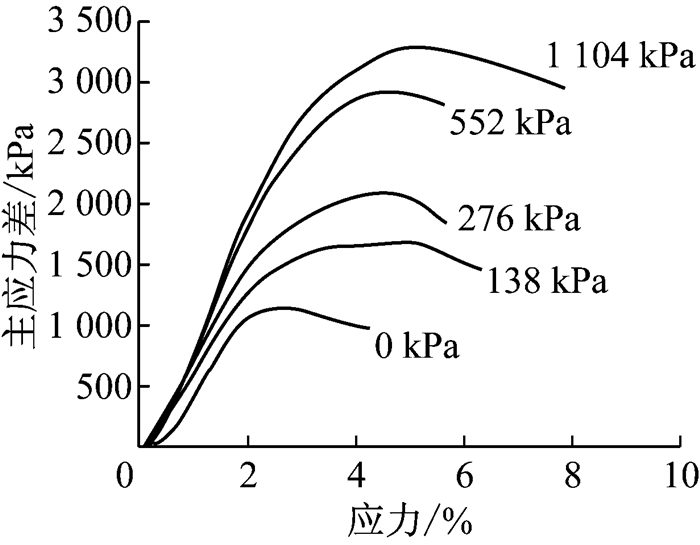
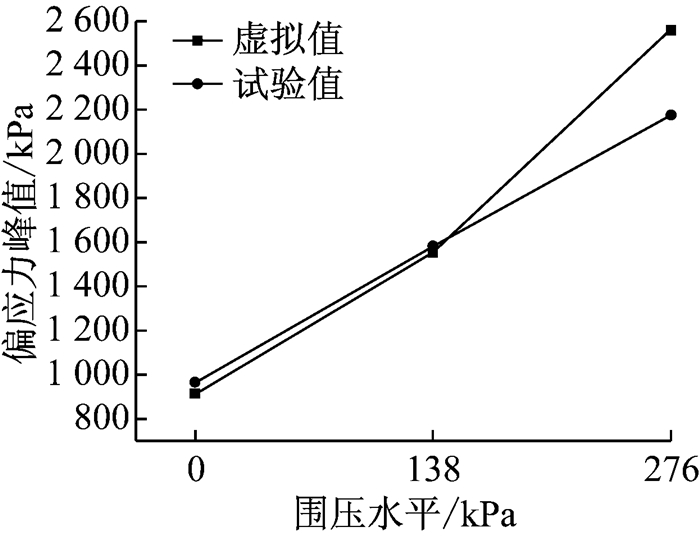
通过分析图 9可知,SUP-13虚拟试样三轴剪切试验中0 kPa围压下试样破坏的时刻最早且偏应力的峰值明显小于138 kPa围压水平及276 kPa围压水平下的偏应力峰值.138 kPa围压及276 kPa围压,偏应力峰值出现的时刻比较接近,而且138 kPa围压下达到偏应力峰值后相对于276 kPa围压水平下衰减速度较慢,这些特征都与现有的如图 10所示的沥青混合料室内三轴剪切试验的研究成果[17]相吻合.SUP-13虚拟三轴试验与室内试验偏应力峰值结果对比如图 11所示,虚拟三轴试验结果相对于室内试验结果具有10.7%的平均偏差,处于合理范围内.
|
图 10 SMA-13室内试验主应力差应变曲线[17] Fig.10 SMA-13 laboratory test principal stress difference-strain curve[17] |
|
图 11 SUP-13虚拟三轴剪切试验与室内试验结果对比 Fig.11 Comparison of virtual triaxial shear test with laboratory test results of SUP-13 |
分析表明虚拟三轴剪切试验的偏应力发展趋势与室内三轴剪切试验规律基本相符,三轴剪切虚拟试件的力学特性与经过实践验证的理论结果保持了较好的一致性,两者的应力应变特性基本相同.虚拟试验的结果与真实试验结果基本吻合,虚拟试验结果处于合理误差范围内,表明基于离散元法的虚拟试验能够有效地描述沥青混合料的剪切破坏行为,建立的沥青混合料细观结构力学模型合理.
4 结论基于三轴剪切试验对沥青混合料三维离散元数值模拟方法开展了相关研究,开发了包括虚拟试样生成、微观接触模型选取及参数标定和伺服控制围压恒定、轴向加载等在内的沥青混合料三维虚拟三轴剪切试验方法,并通过室内三轴剪切试验验证了构建的虚拟试样的合理性及方法的可行性.主要结论如下:
(1) 采用三维凸包算法及Bubble Pack算法生成粗集料虚拟颗粒,得到的颗粒精度可控,模拟效果较好.
(2) 基于PFC 5.0 3D平台,编写代码实现沥青混合料虚拟试样的生成,并通过标定各档集料体积的方法对粗集料投放效果进行验证,可有效控制及评价构建模型的准确性.
(3) 根据动态剪切流变试验数据拟合得到Burgers模型宏观参数,并换算为微观模型参数用于由clump块体表示粗集料颗粒的混合料虚拟试验中,具有一定的可行性及合理性.
(4) 经虚拟及室内三轴剪切试验结果对比验证,构建的沥青混合料三维仿真设计及虚拟三轴剪切试验平台能够准确高效地设计、构建沥青混合料虚拟试件,并可有效描述沥青混合料的力学行为.
本文作为沥青混合料三维离散元试件仿真设计的探索性研究,结果可信,方法过程具有一定借鉴意义及可行性,但对于沥青砂浆的微观接触模型参数的标定、不同类型的沥青混合料构建及力学试验等仍需进一步研究.
| [1] |
杨军, 张旭, 朱浩然. 沥青混合料三轴剪切试验的离散元模拟研究[J]. 建筑材料学报, 2012, 15(1): 64 YANG Jun, ZHANG Xu, ZHU Haoran. Discrete element simulation on tri-axial shear test of asphalt mixtures[J]. Journal of Building Materials, 2012, 15(1): 64 DOI:10.3969/j.issn.1007-9629.2012.01.012 |
| [2] |
杨军, 焦丽亚, 王克利, 等. 基于离散元方法的沥青混合料虚拟三轴剪切试验三维模拟[J]. 东南大学学报(自然科学版), 2014, 44(5): 1057 YANG Jun, JIAO Liya, WANG Keli, et al. Three dimensional simulation of virtual triaxial shear test for asphalt mixture based on discrete element method[J]. Journal of Southeast University(Natural Science Edition), 2014, 44(5): 1057 |
| [3] |
DHARAMVEER S, MUSHARRAF Z, SESH C. Inclusion of aggregate angularity, texture, and form in estimating dynamic modulus of asphalt mixes[J]. Road Materials & Pavement Design, 2012, 13(2): 327 |
| [4] |
LU M, MCDOWELL G R. The importance of modeling ballast particle shape in the discrete element method[J]. Granular Matter, 2007, 1(1-2): 69 |
| [5] |
田莉. 基于离散元方法的沥青混合料劲度模量虚拟试验研究[D]. 西安: 长安大学, 2008. TIAN Li. The virtual test of asphalt mixture stiffness moduli based on DEM[D]. Xi'an: Chang'an University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009066068.htm |
| [6] |
张德育, 黄晓明, 高英. 沥青混合料三维离散元虚拟单轴蠕变试验[J]. 华南理工大学学报(自然科学版), 2012, 40(7): 15 ZHANG Deyu, HUANG Xiaoming, GAO Ying. Three dimension virtual uniaxial creep test of asphalt mixture by using discrete element method[J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(7): 15 DOI:10.3969/j.issn.1000-565X.2012.07.003 |
| [7] |
周长红. 沥青混合料性能分析的PFC实践[M]. 大连: 大连理工大学出版社, 2015 ZHOU Changhong. PFC Practice of performance analysis of asphalt mixture[M]. Dalian: Dalian University of Technology Press, 2015 |
| [8] |
Itasca Consulting Group Inc. PFC Documentation release 5.0[M]. Minneapolis: Itasca Consulting Group Inc, 2014
|
| [9] |
Itasca Consulting Group Inc. KUBRIX® Geo manual & tutorials REV05132015 Version 15[M]. Minneapolis: Itasca Consulting Group Inc, 2015
|
| [10] |
LIU Y, YOU Z, ZHAO Y. Three-dimensional discrete element modeling of asphalt concrete: Size effects of elements[J]. Construction & Building Materials, 2012, 37: 775 |
| [11] |
MASAD E, MUHUNTHAN B, SHASHIDHAR N, et al. Quantifying laboratory compaction effects on the internal structure of asphalt concrete[J]. Transportation Research Record: Journal of the Transportation Research Board, 1999, 1681(1): 179 |
| [12] |
吴文亮, 王端宜, 张肖宁, 等. 基于工业CT技术的沥青混合料内部空隙分布特性[J]. 中南大学学报(自然科学版), 2012, 43(6): 2343 WU Wenliang, WANG Duanyi, ZHANG xiaoning, et al. Air voids distribution of asphalt mixtures based on industrial computerized tomography[J]. Journal of Central South University(Science and Technology), 2012, 43(6): 2343 |
| [13] |
ABBAS A, MASAD E, PAPAGIANNAKIS T, et al. Micromechanical modeling of the viscoelastic behavior of asphalt mixtures using the discrete-element method[J]. International Journal of Geomechanics, 2007, 7(2): 131 |
| [14] |
LIU Y, YOU Z. Simulation of cyclic loading tests for asphalt mixtures using user defined models within discrete element method[J]. Geotechnical Special Publication, 2008(179): 742 |
| [15] |
陈俊, 张东, 黄晓明. 离散元颗粒流软件(PFC)在道路工程中的应用[M]. 北京: 人民交通出版社股份有限公司, 2015 CHEN Jun, ZHANG Dong, HUANG Xiaoming. Application of particle flow code in road engineering[M]. Beijing: China Communicationgs Press Co.Ltd, 2015 |
| [16] |
LIU Y, DAI Q, YOU Z. Viscoelastic model for discrete element simulation of asphalt mixtures[J]. Journal of Engineering Mechanics, 2009, 135(4): 324 DOI:10.1061/(ASCE)0733-9399(2009)135:4(324) |
| [17] |
朱浩然. 采用三轴剪切试验评价沥青混合料的抗剪性能[D]. 南京: 东南大学, 2007. ZHU Haoran. Evaluation on the shear properties of asphalt mixtures through triaxial shear test[D]. Nanjing: Southeast University, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1244341 |
 2018, Vol. 46
2018, Vol. 46

