2. 重庆大学 土木工程学院,重庆 400045;
3. 贵州联建土木工程质量检测监控中心有限公司,贵州 贵阳 550003
2. College of Civil Engineering, Chongqing University, Chongqing 400045, China;
3. Guizhou United Win Civil Engineering Detecting and Monitoring Co. Ltd., Guiyang 550003, China
Mohr-Coulomb强度准则(简记为M-C强度准则)是各种强度准则中历史最久、被研究最多、同时也是一个被争论最多的强度准则,是岩石力学中最常用的强度准则之一,它既适用于塑性岩石的剪切破坏,也适用于脆性岩石的剪切破坏,同时还反映了岩石抗拉强度远小于抗压强度这一特性[1-5].该准则最大缺点是仅考虑了最大主应力和最小主应力的影响,而未考虑中间主应力的影响.从已有的成果来看,Jeremic[3]和Hou[4]认为M-C强度准则适用于大多数硬岩(如花岗岩),但不适用于盐岩;You[5]与黄书岭等[6]认为M-C强度准则对岩石难以达到满意结果,甚至是危险的;马洪岭[7]采用理想弹塑性本构模型对超深地层盐岩地下储气库的稳定性进行了计算,指出M-C强度准则的计算结果偏于安全;邱士利等[8]指出由于低估了岩石的强度水平,M-C强度准则用于工程计算时可能偏于安全,而用于深部硬岩冲击破坏时则可能偏于不安全.在描述岩石卸荷破坏特性方面,不同的研究者的结论同样有所差别,比如,采用线性M-C强度准则时,邱士利等[9]与Wu等[10]结论不一致;而陈卫忠等[11]认为幂函数型M-C强度准则更好.
针对M-C强度准则在岩土工程应用中存在的问题,从能量转化是物质物理过程本质属性出发,本文从弹性应变能角度分析了M-C强度准则的不足之处,并据此建立了广义M-C强度准则.
1 岩石弹性应变能的讨论 1.1 弹性应变能主应力空间弹性应变能Ue为
| $ \begin{array}{l} {U_{\rm{e}}} = \frac{1}{{2E}}\left( {\sigma _1^2 + \sigma _2^2 + \sigma _3^2 - 2\nu \left( {{\sigma _1}{\sigma _2} + {\sigma _2}{\sigma _3} + {\sigma _3}{\sigma _1}} \right)} \right) = \\ \;\;\;\;\;\;\;\;\frac{{3\sigma _1^2}}{{2E}}\left( {1 + k_2^2 + k_3^2 - 2\nu \left( {{k_2} + {k_2}{k_3} + {k_3}} \right)} \right) = \\ \;\;\;\;\;\;\;\;\frac{3}{{2E}}\left( {{J_2} - \frac{{1 - 2\nu }}{3}{I_2}} \right) = {U_{{\rm{e}}{J_2}}} + {U_{{\rm{e}}{I_2}}} \end{array} $ | (1) |
| $ {J_{{\rm{2g}}}} = {J_2} - \frac{{1 - 2\nu }}{3}{I_2} $ | (2) |
| $ {U_{{\rm{e}}{J_2}}} = \frac{3}{{2E}}{J_2} $ | (3) |
| $ {U_{{\rm{e}}{I_2}}} = - \frac{3}{{2E}}\frac{{1 - 2\nu }}{3}{I_2} = \frac{3}{{2E}}\left( {{J_{{\rm{2g}}}} - {J_{\rm{2}}}} \right) $ | (4) |
式(1)~(4)中:σ1、σ2、σ3分别为最大、中间及最小主应力;k2=σ2/σ1;k3=σ3/σ1;E为弹性模量;ν为泊松比;I2为应力张量第二不变量;J2为应力偏量第二不变量;定义J2g为广义应力偏量第二不变量;UeJ2为与J2有关的弹性应变能;UeI2为与I2有关的弹性应变能.
对Ue、UeJ2及UeI2,由公式(1)可以看出:① ν<(1+k22+k32)/2(k2+k2k3+k3)时,Ue满足恒大于零;②与J2有关的弹性应变能UeJ2恒大于等于零;③与I2有关的弹性应变能UeI2,既可大于零、小于零,又可等于零.为使Ue、UeJ2及UeI2正负号所表示的物理意义相同,提出正值表示使岩石屈服的可释放弹性应变能;负值表示不会使岩石屈服的可被吸收的弹性应变能.
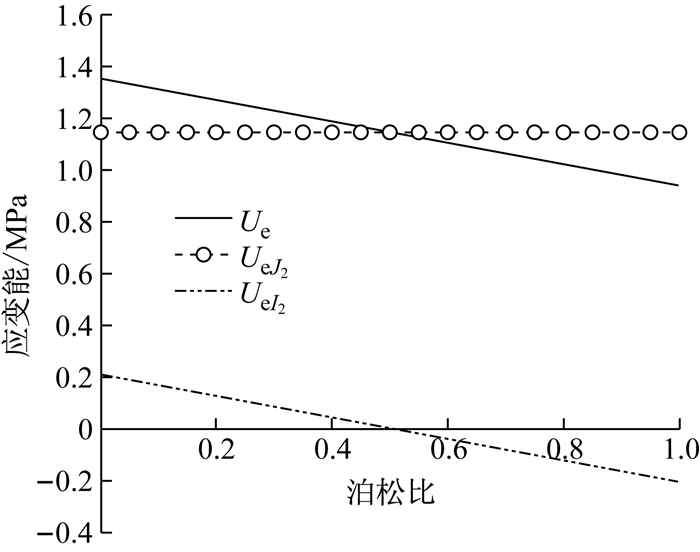
图 1表示某一应力水平(10 MPa, 20 MPa, 200 MPa)条件下,Ue、UeJ2及UeI2随泊松比的变化规律,其中,E=15 GPa.由图 1可以看出,应力水平确定,则UeJ2保持不变;随泊松比增加,Ue及UeI2逐渐减小,即UeI2反映了Ue的变化趋势.基于弹性应变能释放是材料屈服的根本原因[12~13]可知,当UeJ2与UeI2均大于零,仅考虑UeJ2对岩石屈服的影响,将导致理论计算结果偏大;当UeI2<0时,仅考虑UeJ2对岩石屈服与破坏的影响,将导致理论计算结果偏小.
|
图 1 不同泊松比条件下应变能变化规律 Fig.1 Ue、UeJ2、UeI2 and ν |
由式(1)~(4),对应力偏量第二不变量、应力张量第二不变量、泊松比及广义应力偏量第二不变量进行简单讨论.
(1) J2g可反映某一应力状态下岩石所储存的弹性应变能.
(2)由于J2、I2均是不变量,因此J2g是随泊松比的变化而变化的应力不变量;ν=0.5时,J2=J2g,而ν≠0.5时,J2≠J2g.
(3) J2反映了岩石所储存的弹性应变能的一部分,既可大于J2g,又可小于J2g.从本质上讲,UeJ2可看作是泊松比等于0.5时的Ue.从J2g物理意义来看,ν=0.5时, J2g≡J2,相应可得UeJ2=Ue、UeI2=0,可见UeJ2认为材料在任意应力状态下(比如,岩石处于屈服与破坏的极限状态时)泊松比均为0.5.因此,与J2g相比,J2用于岩石是否屈服与破坏,可能会存在一些不足之处.
(4) I2起放大或减小J2的作用;从上述UeI2分析来看,I2的作用可看作是限制(促进)材料的侧向变形,相应地将提高(降低)材料的强度.
(5) 0<ν<0.5.①若I2<0,则UeI2>0、0<UeJ2<Ue.这种应力状态下,UeI2的作用使岩石屈服,相应地, I2作用是促进材料的侧向变形,从而降低材料的强度.因此,若不考虑UeI2的影响,将导致理论计算的结果偏大,不利于工程安全.②若I2>0,则UeI2<0、0<Ue<UeJ2.这种应力状态下,aUeJ2(0<a≤1)释放使岩石屈服,(1-a)UeJ2被UeI2吸收不参与屈服过程,即I2作用是限制材料的侧向变形,相应地提高了材料的强度.因此,若不考虑UeI2的影响,将导致理论计算结果偏小,使工程偏于不经济.
(6) ν>0.5.①若I2<0,则UeI2<0、0<Ue<UeJ2,显然,这与0<ν<0.5、I2>0时的情况相同.②若I2>0,则UeI2>0、0<UeJ2<Ue,显然,这与0<ν<0.5、I2<0时的情况相同.
由此可见,J2、J2g及I2均与Ue有关,J2g反映了Ue,而J2及I2仅表征了部分弹性应变能UeJ2=dUe、UeI2=(1-d)Ue(d可大于1).因此,从能量转化的角度来看,J2g比J2更适合描述岩石的力学特性.
2 岩石变形过程中泊松比的讨论由于Ue、UeI2及J2g均涉及到泊松比,因此,本文利用已有的岩石应力应变曲线对泊松比进行一个简单讨论.
泊松比多通过单轴压缩试验的侧向变形ε3与轴向变形ε1之比确定.式(5)为切线泊松比,为简化计算采用式(6).
| $ \nu = - {\rm{d}}{\varepsilon _3}/{\rm{d}}{\varepsilon _1} $ | (5) |
| $ \nu = - \frac{{{\varepsilon _{3i}} - {\varepsilon _{3\left( {i - 1} \right)}}}}{{{\varepsilon _{1i}} - {\varepsilon _{1\left( {i - 1} \right)}}}} $ | (6) |
| $ {\varepsilon _V} = {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3} = \left( {1 - 2\nu } \right){\varepsilon _1} $ | (7) |
式中:ε3(i-1)、ε1(i-1)、ε3i、ε1i分别为与轴向荷载σ1(i-1)、σ1i相对应的侧向变形与轴向变形;εV为体应变.为简化分析,假定ε2=ε3.
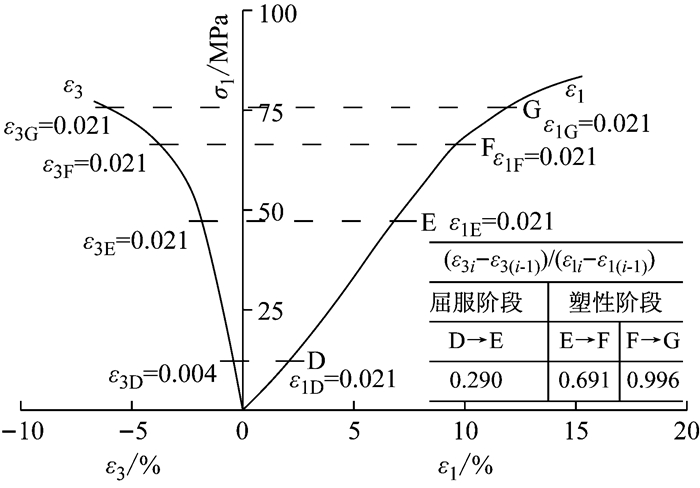
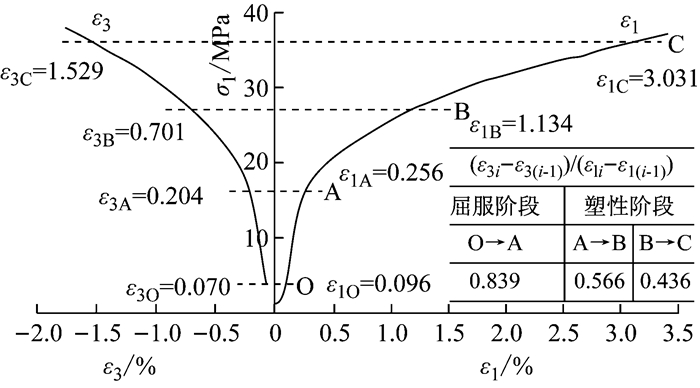
图 2、图 3为图件数字化得到的单轴压缩[14]与三轴压缩条件下[15]岩石的应力应变曲线.单轴压缩条件下大理岩计算的泊松比逐渐增加,最大值接近于1.0;三轴压缩条件下盐岩泊松比逐渐减小.卸荷条件下受裂隙扩展张开变形的影响,泊松比甚至超过了0.8[16].可见,无论是单轴压缩还是三轴压缩条件下,通过试验确定岩石的泊松比都较为困难,且单轴压缩试验结果确定的泊松比,能否适用于复杂的应力状态尚无明确结论[17].另外根据陈卫忠等[18]、刘宁等[19]所作的应力应变曲线可以看出,应力水平不同岩石的泊松比也有所不同.
一方面,在岩石试验过程中观察到岩石存在扩容现象(由式(7)得其泊松比大于0.5是合理的);另一方面理想弹塑性材料极限泊松比为0.5,而岩石,特别是受载后岩石并非理想弹塑性材料,可见岩石泊松比更为复杂.因此,在本文提出的强度准则中泊松比可大于0.5.
由于岩石材料与岩石泊松比均较为复杂,处于弹性极限状态与破坏极限状态的岩石泊松比主要通过数值拟合的方法确定.岩石工程中泊松比确定方法如下:①通过对三轴压缩试验数据拟合,确定不同应力水平条件下岩石泊松比;②根据岩石工程的应力状态,确定实际岩石工程计算的泊松比.
3 M-C强度准则的讨论通过数学处理后,对各向同性材料,强度准则可用统一的表达式(8)进行表示[1].
| $ \sqrt {{J_2}} = f\left( {{I_1},{J_3},{K_1},{K_2},{K_3} \cdots } \right) $ | (8) |
式中:I1为应力张量第一不变量;J3为应力偏量第三不变量;K1、K2、K3为材料参数.
式(8)左右两边同时乘以
| $ \sqrt {\frac{3}{{2E}}} \sqrt {{J_2}} = \sqrt {{U_{{\rm{e}}{J_2}}}} = \sqrt {\frac{3}{{2E}}} f\left( {{I_1},{J_3},{K_1},{K_2},{K_3} \cdots } \right) $ | (9) |
| $ \sqrt {{U_{{\rm{e}}{J_2}}}} = \sqrt {\frac{3}{{2E}}} \sqrt {{J_2} - \frac{{1 - 2 \times 0.5}}{3}{I_2}} $ | (10) |
M-C强度准则可表达为
| $ \sqrt {{J_2}} = \frac{{\left( {\frac{{{I_1}\sin \varphi }}{3} + c\cos \varphi } \right)}}{{\cos {\theta _\sigma } + \frac{{\sin {\theta _\sigma }\sin \varphi }}{{\sqrt 3 }}}} $ | (11) |
式中:θσ为罗德角;c、φ分别为材料的黏聚力与内摩擦角,由M-C强度准则确定.
同理,式(11)左右两边同时乘以
| $ \sqrt {\frac{3}{{2E}}} \sqrt {{J_2}} = \sqrt {{U_{{\rm{e}}{J_2}}}} = \sqrt {\frac{3}{{2E}}} \frac{{\left( {\frac{{{I_1}\sin \varphi }}{3} + c\cos \varphi } \right)}}{{\cos {\theta _\sigma } + \frac{{\sin {\theta _\sigma }\sin \varphi }}{{\sqrt 3 }}}} $ | (12) |
| $ \begin{array}{l} \sqrt {{U_{{\rm{e}}{J_2}}}} = \sqrt {\frac{3}{{2E}}} \sqrt {{J_2} - \frac{{1 - 2\nu }}{3}{I_2}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{3}{{2E}}} \frac{{\left( {\frac{{{I_1}\sin \varphi }}{3} + c\cos \varphi } \right)}}{{\cos {\theta _\sigma } + \frac{{\sin {\theta _\sigma }\sin \varphi }}{{\sqrt 3 }}}} \end{array} $ | (13) |
由式(12)与式(13)可以看出:M-C强度准则仅考虑了UeJ2,而未考虑UeI2对材料屈服与破坏的影响,因此,这可能存在导致违反能量守恒定律的情况出现;或者说M-C强度准则认为岩石屈服与破坏时的泊松比均为0.5.从能量角度来看,M-C强度准则物理意义为:当Ue达到某一临界值,且泊松比必须等于0.5,材料才开始屈服或破坏,这可能是该准则需改进之处.
4 广义M-C强度准则 4.1 广义M-C强度准则的建立根据谢和平等[12-13]提出的能量耗散使材料强度降低,弹性应变能释放使材料破坏的基本原理,并基于上述M-C强度准则的不足之处,提出广义M-C强度准则的物理意义:当Ue达到某一临界值(泊松比不需等于0.5),材料就开始屈服或破坏,据此建立广义M-C强度准则,即将式(13)左侧UeJ2变换为Ue,可得
| $ \begin{array}{l} \sqrt {{U_{\rm{e}}}} = \sqrt {\frac{3}{{2E}}} \sqrt {{J_2} - \frac{{1 - 2\nu }}{3}{I_2}} = \\ \;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{3}{{2E}}} \frac{{\left( {\frac{{{I_1}\sin \varphi }}{3} + c\cos \varphi } \right)}}{{\cos {\theta _\sigma } + \frac{{\sin {\theta _\sigma }\sin \varphi }}{{\sqrt 3 }}}} \end{array} $ | (14) |
相反,式(13)左右两边同时除以
| $ \sqrt {{J_{{\rm{2g}}}}} = \sqrt {{J_2} - \frac{{1 - 2\nu }}{3}{I_2}} = \frac{{\left( {\frac{{{I_1}\sin \varphi }}{3} + c\cos \varphi } \right)}}{{\cos {\theta _\sigma } + \frac{{\sin {\theta _\sigma }\sin \varphi }}{{\sqrt 3 }}}} $ | (15) |
式(15)即为广义M-C强度准则.根据广义应力偏量第二不变量的讨论,与M-C强度准则相比,广义M-C强度准则的计算结果存在4种可能:
(1) 当0<ν<0.5、I2<0时,广义M-C强度准则计算结果小于M-C强度准则计算结果.
(2) 当0<ν<0.5、I2>0时,广义M-C强度准则计算结果大于M-C强度准则计算结果.
(3) 当ν>0.5、I2>0时,广义M-C强度准则计算结果小于M-C强度准则计算结果.
(4) 当ν>0.5、I2<0时,则广义M-C强度准则计算结果大于M-C强度准则计算结果.
广义M-C强度准则具有以下特点:①广义M-C强度准则的各参数c、φ由M-C强度准则确定.②广义M-C强度准则是以泊松比为参数的一族统一屈服准则的集合,而非单一屈服准则.③泊松比等于0.5时,广义M-C强度准则简化为M-C强度准则,即M-C强度准则认为材料在任意应力水平条件下屈服与破坏时的泊松比均为0.5.④可直接利用M-C强度准则的优点与已有的成果,便于广义M-C强度准则的推广和应用.可见,基于弹性应变能的广义M-C强度准则的适用范围更广.
4.2 理论分析图 4为I2<0情况下,广义M-C强度准则在π平面屈服轨迹(括号内为I2>0时的泊松比,σ′1、σ′2、σ′3分别表示有效应力).需要说明:I2>0 (其他条件保持不变条件)时,泊松比越大,广义M-C强度准则在π平面的屈服轨迹越小,与I2<0情况相反.

|
图 4 π平面的屈服轨迹 Fig.4 Trace of yield surfaces on π plane of the generalized M-C criterion |
由图 4可以看出(以I2<0为例进行说明):①泊松比越小,广义M-C强度准则计算的结果越利于安全.②泊松比等于0.5时,广义M-C强度准则屈服轨迹为线性;泊松比不等于0.5时,广义M-C强度准则屈服轨迹为非线性,且泊松比越小,屈服轨迹的非线性愈明显.③随着罗德角的增加,不同泊松比之间应力偏量第二不变量的差值先增加,后减小(其中,θσ=-30°时最小;θσ<30°时差值最大),即广义M-C强度准则与M-C强度准则计算的理论值,在θσ=-30°时差值最小;而在θσ<30°时差值最大.I2>0时结论与I2<0相反.
由广义M-C强度准则π平面屈服轨迹可知,若深部硬岩破坏(或冲击破坏)时的泊松比小于0.5,则M-C强度准则计算结果偏于不安全,这与邱士利等[8]指出由于忽视了中间主应力的影响,M-C强度准则对深部硬岩工程而言,可能造成潜在的不安全相一致;相反,若深部硬岩破坏时的泊松比大于0.5,M-C强度准则计算结果将偏于安全.
综上所述,M-C强度准则是否适用于某类岩石或某一类型的工程,与泊松比是否等于0.5有关,即若处于屈服极限状态或破坏极限状态时岩石的泊松比等于0.5,则M-C强度准则适用性可能较好,反之,M-C强度准则不适用.这也正说明了广义M-C强度准则适用性远高于M-C强度准则适用性.
由图 4可以看出,泊松比小于0.5(I2<0)或大于0.5(I2>0)情况下,强度准则在π平面上屈服轨迹不能保持完全非凸性,同时考虑到广义M-C强度准则也存在尖顶产生的数值计算问题,可采用其他研究者[20]已提出的利用椭圆型、双曲线型和空间滑动面(SMP)的罗德角函数对其屈服面进行修正.
4.3 广义强度准则的验证为验证基于现有强度准则提出的广义强度准则的合理性与有效性,对盐岩(属于软岩)与白云岩的试验数据进行了验证,结果见图 5、图 6.其中,表 1为强度准则计算参数与拟合的泊松比.
| 下载CSV 表 1 盐岩与白云岩的计算参数 Tab.1 Strength parameters for rock salt and granite |
由于M-C强度准则在岩土工程数值计算中具有重要地位,且M-C强度准则是广义M-C强度准则的特例,因此,本文在已有的研究成果的基础上,仅对M-C强度准则与广义M-C强度准则的计算结果进行了对比分析.
泊松比拟合方法:由于应力水平对泊松比的影响,因此,首先将试验数据分为2组,第1组为最小主应力与中间主应力均相对较小的试验数据;第2组为最小主应力与中间主应力均相对较大的试验数据;然后,分别计算第1组与第2组相应于试验最小主应力和中间主应力强度的σCTi(第i样品的最大主应力);最后,分别取对应于第1组与第2组平均误差最小值的ν1、ν2为式(16)在不同应力水平条件下的拟合泊松比.采用均方根误差[24]、平均误差处理的各强度准则第一主应力计算误差见表 2.
| $ {\chi _i} = \frac{{{\sigma _{{\rm{T}}i}} - {\sigma _{{\rm{CT}}i}}}}{{{\sigma _{{\rm{T}}i}}}} \times 100\% $ | (16) |
| $ {{\bar \chi }_1}\left( {{{\bar \chi }_2}} \right) = \frac{{\sum\limits_i {\left| {{\chi _i}} \right|} }}{{{n_1}\left( {{n_2}} \right)}} $ | (17) |
| $ \bar \chi = \frac{{\sum\limits_i {\left| {{\chi _i}} \right|} }}{n} $ | (18) |
| $ \eta = \sqrt {\frac{{\sum\limits_i {{{\left( {{\sigma _{{\rm{T}}i}} - {\sigma _{{\rm{CT}}i}}} \right)}^2}} }}{n}} $ | (19) |
| 下载CSV 表 2 不同准则计算的均方根误差与平均误差 Tab.2 Root-mean-square error of σ1 calculation |
式(16)~(19)中:n1为第1组试验样品的数量;n2为第2组试验样品的数量;n为总的试验样品数量;σTi为第i样品试验的最大主应力;σCTi根据最小主应力与中间主应力计算而得第i样品的最大主应力;χi为第i样品试验值与理论值的计算误差χ1、χ2分别为第1组、第2组试验值与理论值的平均误差;χ为全部试验值与理论值的平均误差;η为均方根误差.
由表 1~2及图 5~6可以看出:①广义M-C强度准则计算的理论强度与试验值更接近,精度更高.②广义M-C强度准则对盐岩与白云岩的破坏强度进行计算,围压较小时泊松比分别为0.53、0.70,而围压较大时泊松比分别为0.44、0.59,这说明受裂隙扩展的影响,考虑岩石破坏时的泊松比不等于0.5可能更合理.③当M-C强度准则(ν=0.5)计算结果大于试验值情况下,则ν<0.5时广义M-C强度准则计算结果精度更高(I2<0);反之,若M-C强度准则计算结果小于试验值,则相应的ν>0.5时广义M-C强度准则计算结果精度更高,这与理论分析相一致.
广义M-C强度准则计算精度较高的原因是从本质上反映了弹性应变能释放是岩石屈服与破坏的根本原因,既考虑了应力张量第二不变量,又考虑了泊松比对岩石屈服与破坏的影响,更符合岩石屈服与破坏时的泊松比不一定为0.5这一情况.
本文根据最小主应力将试验数据分为两组进行拟合,分别计算岩石的破坏强度.若对不同的应力水平采用不同的拟合泊松比,则广义M-C强度准则的计算精度将更高,甚至于试验值及理论值可能完全相同.因此,广义M-C强度准则的关键,就是如何更好确定岩石处于屈服状态或破坏状态时的泊松比.
5 结论(1) 为了建立弹性应变能Ue与应力不变量之间的关系,将Ue看作是与J2有关的弹性应变能UeJ2和与I2有关的弹性应变能UeI2之和,并分析了UeJ2与UeJ2对岩石破坏的影响.
(2) 提出了包含J2、I2及ν的广义应力偏量第二不变量J2g,该物理量能够反映岩石所储存的弹性应变能.
(3) M-C强度准则认为材料屈服与破坏时泊松比均为0.5,这是M-C强度准则计算精度不高的重要原因之一,且违反了能量守恒定律.
(4) 广义M-C强度准则是一族强度准则的集合,泊松比等于0.5时蜕化为M-C强度准则;该准则认为岩石屈服与破坏时泊松比不一定为0.5.
(5) 基于盐岩与白云岩的试验结果,对比分析了M-C强度准则、广义M-C强度准则的计算效果.结果表明,广义M-C强度准则可较好地描述岩石材料的破坏强度,计算结果较为精确.
| [1] |
俞茂宏. 双剪理论及其应用[M]. 北京: 科学出版社, 1998 YU Maohong. Unified strength theory and its applications[M]. Beijing: Science Press, 1998 |
| [2] |
陈景涛.高地应力下硬岩本构模型的研究与应用[D].武汉: 中国科学院武汉岩土力学研究所, 2006. CHEN Jingtao. Study on constitutive model for hard rock under high geostress condition and its applications in engineering[D]. Wuhan: Institute of Rock and Soil Mechanics Chinese Academy of Sciences Wuhan, 2006. http://cdmd.cnki.com.cn/Article/CDMD-80005-2007128266.htm |
| [3] |
JEREMIC M L. Rock mechanics in salt mining[M]. Rotterdam: A A Balkema, 1994
|
| [4] |
HOU Z M.Untersuchungen zum nachweis der standisicherheit füruntertagedeponien im salzgebire[D]. Clausthal: Technische Universitat Clausthal, 1997.
|
| [5] |
YOU M Q. True-triaxial strength criteria for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(1): 115 DOI:10.1016/j.ijrmms.2008.05.008 |
| [6] |
黄书岭, 冯夏庭, 张传庆. 脆性岩石广义多轴应变能准则及其试验验证[J]. 岩石力学与工程学报, 2008, 27(1): 124 HUANG Shuling, FENG Xiating, ZHANG Chuanqing. A new generalized polyaxial strain energy strength criterion of brittle rock and polyaxial test validation[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 124 DOI:10.3321/j.issn:1000-6915.2008.01.019 |
| [7] |
马洪岭.超深地层盐岩地下储气库可行性研究[D].武汉: 中国科学院武汉岩土力学研究所, 2010. MA Hongling. Study on feasibility rock salt underground gas storage in ultra-deep formation[D]. Wuhan: Institute of Rock and Soil Mechanics Chinese Academy of Sciences Wuhan, 2010. http://cdmd.cnki.com.cn/Article/CDMD-80005-2010238548.htm |
| [8] |
邱士利, 冯夏庭, 张传庆, 等. 均质各向同性硬岩统一应变能强度准则的建立及验证[J]. 岩石力学与工程学报, 2013, 32(4): 714 QIU Shili, FENG Xiating, ZHANG Chuanqing, et al. Establishment of unified strain energy strength criterion of homogeneous and isotropic hard rocks and its validation[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 714 DOI:10.3969/j.issn.1000-6915.2013.04.009 |
| [9] |
邱士利, 冯夏庭, 张传庆, 等. 不同卸围压速率下深埋大理岩卸荷力学特性试验研究[J]. 岩石力学与工程学报, 2010, 29(9): 1807 QIU Shili, FENG Xiating, ZHANG Chuanqing, et al. Experimental research on mechanical properties of deep-buried marble under different unloading rates of confining pressures[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1807 |
| [10] |
WU F Q, LIU T, LIU J Y, et al. Excavation unloading destruction phenomena in rock dam foundations[J]. Bulletin of Engineering Geology and the Environment, 2009, 68(2): 257 DOI:10.1007/s10064-009-0202-5 |
| [11] |
陈卫忠, 刘豆豆, 杨建平, 等. 大理岩卸围压幂函数型Mohr强度特性研究[J]. 岩石力学与工程学报, 2008, 27(11): 2214 CHEN Weizhong, LIU Doudou, YANG Jianping, et al. Power function based Mohr strength criterion for marble with unloading confining pressures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2214 DOI:10.3321/j.issn:1000-6915.2008.11.006 |
| [12] |
谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报, 2005, 24(17): 3003 XIE Heping, JU Yang, LI Liyun. Criteria for strength and structural failure of rocks baded on energy dissipation release principles[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003 DOI:10.3321/j.issn:1000-6915.2005.17.001 |
| [13] |
谢和平, 鞠杨, 黎立云, 等. 岩体变形破坏过程的能量机制[J]. 岩石力学与工程学报, 2008, 27(9): 1729 XIE Heping, JU Yang, LI Liyun, et al. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1729 DOI:10.3321/j.issn:1000-6915.2008.09.001 |
| [14] |
李通林, 谭学术, 刘伟. 矿山岩石力学[M]. 重庆: 重庆大学出版社, 1991 LI Tonglin, TAN Xueshu, LIU Wei. Mine rock mechanics[M]. Chongqing: Chongqing University Press, 1991 |
| [15] |
ALKANA H, CINARB Y, PUSCH G. Rock salt dilatancy boundary from combined acoustic emission and triaxial compression tests[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44: 108 DOI:10.1016/j.ijrmms.2006.05.003 |
| [16] |
尤明庆. 岩石的力学性质[M]. 北京: 地质出版社, 2007 YOU Mingqing. Rock mechanics properties[M]. Beijing: Geology Publishing House, 2007 |
| [17] |
黄润秋, 黄达. 卸荷条件下花岗岩力学特性试验研究[J]. 岩石力学与工程学报, 2008, 27(11): 2205 HUANG Runqiu, HUANG Da. Experimental research on mechanical properties of granites under unloading condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2205 DOI:10.3321/j.issn:1000-6915.2008.11.005 |
| [18] |
陈卫忠, 吕森鹏, 郭小红, 等. 基于能量原理的卸围压试验与岩爆判据研究[J]. 岩石力学与工程学报, 2009, 28(8): 1530 CHEN Weizhong, LV Senpeng, GUO Xiaohong, et al. Research on unloading confining pressure tests and rockburst criterion based on energy theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1530 DOI:10.3321/j.issn:1000-6915.2009.08.003 |
| [19] |
刘宁, 张春生, 褚卫江, 等. 深埋大理岩力学特性对岩爆发生条件的影响分析[J]. 岩土力学, 2013, 34(9): 2638 LIU Ning, ZHANG Chunsheng, CHU Weijiang, et al. Influence of mechanical characteristics of deep-buried marble on rockburst occurrence conditions[J]. Rock and Soil Mechanics, 2013, 34(9): 2638 |
| [20] |
朱合华, 张琦, 章连洋. Hoer-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945 ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945 |
| [21] |
KITTITEP F, DECHO P. Effects of cyclic loading on mechanical properties of Maha Sarakham salt[J]. Engineering Geology, 2010, 112: 43 DOI:10.1016/j.enggeo.2010.01.002 |
| [22] |
MOGI K. Experimental rock mechanica[M]. London: Taylor and Francis, 2007
|
| [23] |
Al-AJMI A M, ZIMMERMAN R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 431 DOI:10.1016/j.ijrmms.2004.11.004 |
| [24] |
周辉, 李震, 杨艳霜, 等. 岩石统一能量屈服准则[J]. 岩石力学与工程学报, 2013, 32(11): 2170 ZHOU Hui, LI Zhen, YANG Yanshuang, et al. Unified energy yield criterion of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2170 |
 2018, Vol. 46
2018, Vol. 46