随着世界各国对节能与环保的呼声日益高涨,混合动力汽车的研究成为汽车发展的一大重要方向.于此同时,消费者对汽车传动系统NVH(noise, vibration and harshness)性能也越来越重视.与传统内燃机汽车相比,混合动力汽车增加了驱动电机、起动电机和行星齿轮系统等新总成和零部件,以实现纯电动、混合动力、停车充电、再生制动等工作状态,由此造成传动系统结构的变化,带来了新的振动问题.首先,除了发动机激励外还增加了电机激励,动力源转矩波动也会影响系统的振动响应[1];其次,不同工作模式下传动系统整体的固有特性及传递路径各有不同,容易引发更多的共振问题;最后,系统工况的变化以及工作模式切换会引起严重的瞬态冲击振动,传动系统的扭转振动乃至整车的纵向振动问题更加突出[2-3].因此混合动力传动系统的NVH研究对混合动力汽车的舒适和稳定性变得更加重要.
国内外对于混合动力传动系统的NVH研究中,针对动力传动系统振动问题的研究比较少,主要集中在固定输入下系统响应特性的研究且对混合传动系统建模较为简单,对工作模式及其改变对传动系统瞬态特性造成的影响研究不深入.Tang[4]采用给定周期输入来研究混合动力系统的瞬态响应;Ma等[5]采用定转速输入来研究混合动力系统的瞬态响应;张德久等[6]和于海生等[7]采用多体动力学软件仿真的方法来研究混合动力系统的瞬态响应;Tang[8]采用三质量模型研究混合动力系统的瞬态响应,模型的准确性受到限制.这些研究没有考虑由于工作模式及其改变对传动系统瞬态特性造成的影响,然而这是造成系统瞬态冲击振动的一个重要因素.在典型瞬态工况下更能全面评价系统的NVH性能.因此,研究典型工况和工作模式下混合传动系统振动问题具有十分重要的理论意义和实际应用价值.
本文以包含发动机、电动机和行星齿轮系等子系统的混联式混合动力驱传动系统为研究对象,联合动力控制策略以及典型运行工况,建立了混合动力驱传动系统扭振动力学模型,分析了纯电动、混合动力和停车充电工作模式下系统的固有特性和瞬态响应,找到了影响系统振动性能的主要原因.研究结果对混联式混合动力汽车驱传动系统振动和噪声性能的设计与优化具有重要参考作用.
1 混合动力传动系统结构和工作模式图 1为混联式混合动力传动系统,发动机、电动机、发电机经过功率分流机构——行星齿轮系统耦合输出动力至减差总成,再通过驱动轴驱动车轮,进而驱动车辆.发动机与行星架相联,发电机与太阳轮相联,电动机与内齿圈相联,发动机的动力一部分直接传递给驱动轴,一部分通过发电机发电产生电能,用于驱动电动机或者经过逆变器转换成直流电存储在蓄电池中.
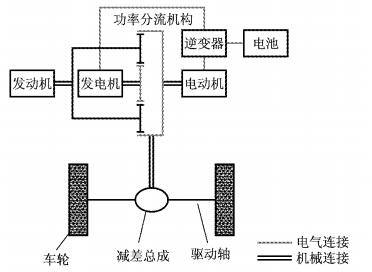
|
图 1 混合动力传动系统结构图 Fig.1 Construction of hybrid powertrain system |
该混合动力系统包含5种类型的运行工况.
(1) 缓起步及低速工况:系统此时为纯电动模式,行星架固定,发动机停机,车辆由电动机提供动力,发电机空转不发电.
(2) 正常行驶工况:此时为混合动力模式,行星齿轮系统基本构件均不固定,发动机一部分功率直接驱动车轮,一部分功率通过发电机发电驱动电动机.
(3) 急加速爬坡工况:此时系统仍为混合动力模式,基本构件均不固定,此时车辆需求功率较大,电动机同时从发电机和电池获得能量.
(4) 减速制动工况:此时系统为再生制动模式,发动机停止工作,车速较高时发动机空转,基本构件均不固定,车速较低时发动机停机,行星架固定;踩下制动踏板后,内齿圈反拖电动机旋转,电动机作为发电机发电,向蓄电池充电,同时产生制动转矩.
(5) 停车充电工况:此时为停车充电模式,内齿圈固定.车辆停止时,电源开关没有关闭,如果此时水温、充电状态、蓄电池温度和电载荷状态不在规定范围之内,发动机将在预定的时间内继续运转后停机;车辆停止后,如果电源控制模块监测到任何不满足条件的项目,电源控制模块将启动发电机和发动机发电.
由系统主要运行工况可知, 混合动力系统主要工作模式包括纯电动模式、混合动力模式、再生制动模式和停车充电模式.从传动系统结构来看,纯电动模式下发动机停机,行星架固定;混合动力模式下,行星齿轮系统基本构件均不固定,行星架、太阳轮和内齿圈均是运动的;再生制动模式下,根据工况的不同存在行星架固定和基本构件均不固定两种情况;停车充电模式下,车辆静止,内齿圈固定,减差总成及轮胎车身都是静止的.因此系统只存在行星架固定、基本构件均不固定及内齿圈固定3种结构,它们所对应的典型工作模式为纯电动模式、混合动力模式及停车充电模式.
2 混合动力传动系统扭转振动动力学模型汽车传动系统是一个连续而复杂的多质量系统,为了能够准确地描述系统的扭转振动特性,本文对系统进行合理简化并建立系统的动力学模型.采用集中质量建模方法将系统简化为当量离散系统.为了将系统简化为一个具有有限自由度的集中质量系统,基本的简化原则和假设如下:①惯量较大且较集中的的部件作为非弹性惯量元件.②惯量较小且分散的部件作为无惯量的弹性元件.③忽略路面不平度对动力传动系统和整车振动的影响,只考虑动力传动系统对整车振动的影响. ④激振载荷只作用在非弹性惯量元件上.
由图 1可知,该混合动力系统动力学模型主要由发动机、电动机、发电机、行星齿轮系统、减速器/差速器、半轴以及轮胎/车身等子模型组成.系统动力学模型架构如图 2所示,其中,发动机、电动机、发电机分别与行星架、内齿圈和太阳轮通过轴连接.由行星齿轮系统变化引起不同的传动结构组合对应不同的工作模式.当行星架固定、基本构件均不固定及内齿圈固定时,系统对应的工作模式分别为纯电动模式、混合动力模式及停车充电模式.
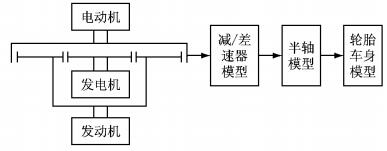
|
图 2 系统总体动力学模型架构 Fig.2 Dynamics model of hybrid powertrain system |
本文采用的是四缸四冲程发动机,考虑气缸曲柄连杆机构的当量转动惯量、飞轮的转动惯量以及彼此间的扭转刚度和阻尼,发动机曲轴系统的扭转动力学模型如图 3所示,其动力学方程如式(1)所示.
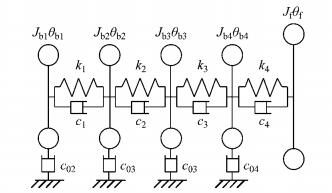
|
图 3 发动机曲轴系统动力学模型 Fig.3 Dynamics model of crankshaft system |
| $ \left\{ \begin{array}{l} {J_{{\rm{b1}}}}{{\ddot \theta }_{{\rm{b1}}}} + {k_1}({\theta _{{\rm{b1}}}} - {\theta _{{\rm{b2}}}}) + {c_1}({{\dot \theta }_{{\rm{b1}}}} - {{\dot \theta }_{{\rm{b2}}}}) + {c_{01}}{{\dot \theta }_{{\rm{b1}}}} = {T_1}\\ {J_{{\rm{b2}}}}{{\ddot \theta }_{{\rm{b2}}}} + {k_1}({\theta _{{\rm{b2}}}} - {\theta _{{\rm{b1}}}}) + {k_2}({{ \theta }_{{\rm{b2}}}} - {{ \theta }_{{\rm{b3}}}}) + {c_1}({{\dot \theta }_{{\rm{b2}}}} - \\ \;\;\;\;\;{{\dot \theta }_{{\rm{b1}}}}) + {c_2}({{\dot \theta }_{{\rm{b2}}}} - {{\dot \theta }_{{\rm{b3}}}}) + {c_{02}}{{\dot \theta }_{{\rm{b2}}}} = {T_2}\\ {J_{{\rm{b3}}}}{{\ddot \theta }_{{\rm{b3}}}} + {k_2}({\theta _{{\rm{b3}}}} - {\theta _{{\rm{b2}}}}) + {k_3}({\theta _{{\rm{b3}}}} - {\theta _{{\rm{b4}}}}) + {c_2}({{\dot \theta }_{{\rm{b3}}}} - \\ \;\;\;\;{{\dot \theta }_{{\rm{b2}}}}) + {c_3}({{\dot \theta }_{{\rm{b3}}}} - {{\dot \theta }_{{\rm{b4}}}}) + {c_{03}}{{\dot \theta }_{{\rm{b3}}}} = {T_3}\\ {J_{{\rm{b4}}}}{{\ddot \theta }_{{\rm{b4}}}} + {k_3}({\theta _{{\rm{b4}}}} - {\theta _{{\rm{b3}}}}) + {k_4}({\theta _{{\rm{b4}}}} - {\theta _{\rm{f}}}) + {c_3}({{\dot \theta }_{{\rm{b4}}}} - \\ \;\;\;\;{{\dot \theta }_{{\rm{b3}}}}) + {c_4}({{\dot \theta }_{{\rm{b4}}}} - {{\dot \theta }_{\rm{f}}}) + {c_{04}}{{\dot \theta }_{{\rm{b4}}}} = {T_4}\\ {J_{\rm{f}}}{{\ddot \theta }_{\rm{f}}} + {k_4}({\theta _{\rm{f}}} - {\theta _{{\rm{b4}}}}) + {c_4}({{\dot \theta }_{\rm{f}}} - {{\dot \theta }_{{\rm{b4}}}}) = {T_{\rm{f}}} \end{array} \right. $ | (1) |
式中:Jbi为发动机4个气缸曲柄连杆机构的当量转动惯量;Jf为飞轮的转动惯量;θbi、θf为各曲拐及飞轮的扭转振动角位移;ki为轴段扭转刚度,ci为轴段内阻尼系数;c0i为作用在惯量元件上的外阻尼系数;Ti、Tf为作用在各个曲拐和飞轮的发动机激振力矩;i=1, 2, 3, 4.
发动机激励主要包括气缸气体压力力矩和曲柄连杆机构往复运动惯性力矩.实际上,由往复惯性力所引起的干扰力矩的值比较小,一般不容易发生共振,往往忽略不计,而只考虑气缸气体压力所产生的干扰力矩Mg,其单缸计算公式为
| $ {M_{\rm{g}}} = \frac{{{\rm{ \mathsf{ π} }}{D^2}}}{4}{P_{\rm{g}}}\frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \beta }}R $ | (2) |
式中:Pg为作用在单位活塞面积上的气缸气体压力;D为气缸直径;R为曲柄半径;α为以上止点为基准的曲柄转角;β为连杆摆角.
2.2 电动机/发电机动力学模型由于电机转子转动时电磁振动频率高,只考虑机械振动而无电磁振动.电机转子的转动惯量很大,不考虑转子的扭转变形.电机轴转动惯量很小,将轴的转动惯量集中到转子上,但将其扭转刚度等效为一根扭转弹簧.由于电机轴为金属材料,不考虑其阻尼.因此,电机的动力学方程可表达为
| $ {J_{\rm{M}}}{{\ddot \theta }_{\rm{M}}} + k({\theta _{{\rm{Mf}}}} - {\theta _{{\rm{Mr}}}}) = {T_{{\rm{M\_ref}}}} + {T_{{\rm{rip}}}} $ | (3) |
式中:JM为电机转子的转动惯量;k为电机轴的等效扭转刚度; θM、θMf、θMr分别为电机转子、电机轴前端面、电机轴后端面的扭转角位移; TM_ref为电机的目标转矩;Trip为谐波转矩.
电机电流基频f=pn/60,p为电机极对数,p=8,n为电机转速.电机转矩波动频率主要为电流基频的6倍,电机转矩谐波分量为
| $ {T_{{\rm{rip}}}} = {T_{{\rm{mag}}}}\sin \left( {12{\rm{ \mathsf{ π} }}ft + \varphi } \right) = {T_{{\rm{mag}}}}\sin (6{\omega _{{\rm{Me}}}}t + \varphi ) $ | (4) |
式中:φ为谐波转矩的初始相位;ωMe为电机的电角速度,ωMe=2πpn/60;Tmag为谐波分量的波动幅值,设定电机转矩波动率为4%[1],则Tmag=0.02TM_ref.
2.3 行星齿轮系统动力学模型行星齿轮系统建模主要假设条件[9]包括:①行星轮沿行星架均匀分布,且行星齿轮参数相同,忽略陀螺效应和向心力的影响;②忽略齿轮啮合的静传递误差以及啮合刚度的时变性,啮合刚度定为常数;③不考虑齿侧间隙.由此建立行星齿轮系统动力学模型如图 4所示.图 4中下标c、r、s分别表示行星架、内齿圈和太阳轮;kj(j=c, r, s)为构件j与外部连接的扭转刚度;θj(j=c, r, s, 1, 2, …, N)为行星架、内齿圈、太阳轮及各行星轮的扭转角位移;krn、ksn分别为第n个行星轮与内齿圈及太阳轮的内外综合啮合刚度;crn、csn分别为第n个行星轮与内齿圈及太阳轮的内外啮合阻尼;ψn为第n个行星轮的初相位.
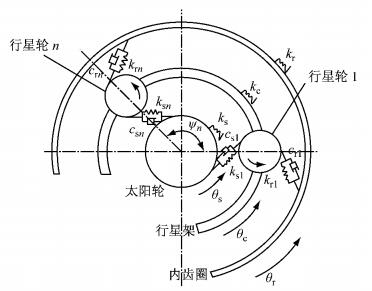
|
图 4 行星齿轮传动系统纯扭转动力学模型 Fig.4 Torsional vibration model of planetary gear system |
因此,各构件的扭转振动微分方程如下:
行星架
| $ \begin{array}{l} ({J_{\rm{c}}} + \mathop \sum \limits_{n = 1}^N {J_n} + N{m_{\rm{p}}}r_{\rm{c}}^2){{\ddot \theta }_{\rm{c}}} + {k_{{\rm{cu}}}}{\theta _{\rm{c}}} - {r_{\rm{c}}}\mathop \sum \limits_{n = 1}^N ({k_{{\rm{r}}n}}{\delta _{{\rm{r}}n}} + \\ {c_{{\rm{r}}n}}{{\dot \delta }_{{\rm{r}}n}})\cos {\alpha _{\rm{r}}} - {r_{\rm{c}}}\mathop \sum \limits_{n = 1}^N ({k_{{\rm{s}}n}}{\delta _{{\rm{s}}n}} + {c_{{\rm{s}}n}}{{\dot \delta }_{{\rm{s}}n}})\cos {\alpha _{\rm{s}}} = {T_{{\rm{p1}}}} \end{array} $ | (5) |
内齿圈
| $ {J_{\rm{r}}}{{\ddot \theta }_{\rm{r}}} + {k_{{\rm{ru}}}}{\theta _{\rm{r}}} + {r_{\rm{r}}}\mathop \sum \limits_{n = 1}^N ({k_{{\rm{r}}n}}{\delta _{{\rm{r}}n}} + {c_{{\rm{r}}n}}{{\dot \delta }_{{\rm{r}}n}}) = {T_{{\rm{p2}}}} $ | (6) |
太阳轮
| $ {J_{\rm{s}}}{{\ddot u}_{\rm{s}}} + {k_{{\rm{su}}}}{\theta _{\rm{s}}} + {r_{\rm{s}}}\mathop \sum \limits_{n = 1}^N ({k_{{\rm{s}}n}}{\delta _{{\rm{s}}n}} + {c_{{\rm{s}}n}}{{\dot \delta }_{{\rm{s}}n}}) = {T_{{\rm{p3}}}} $ | (7) |
行星轮
| $ {J_n}{{\ddot \theta }_n} - {r_n}{k_{{\rm{rn}}}}{\delta _{{\rm{r}}n}} - {r_n}{c_{{\rm{r}}n}}{{\dot \delta }_{{\rm{rn}}}} + {r_n}{k_{{\rm{s}}n}}{\delta _{{\rm{s}}n}} + {r_n}{c_{{\rm{s}}n}}{{\dot \delta }_{{\rm{s}}n}} = {T_{{\rm{p4}}}} $ | (8) |
| $ \left\{ \begin{array}{l} {\delta _{{\rm{s}}n}} = {r_{\rm{s}}}{\theta _{\rm{s}}} + {r_n}{\theta _n} - {r_{\rm{c}}}{\theta _{\rm{c}}}\cos {\alpha _{\rm{s}}}\\ {\delta _{{\rm{r}}n}} = {r_{\rm{r}}}{\theta _{\rm{r}}} - {r_n}{\theta _n} - {r_{\rm{c}}}{\theta _{\rm{c}}}\cos {\alpha _{\rm{r}}} \end{array} \right. $ | (9) |
式(5)~(9)中:下标p表示行星轮;N为行星轮个数;mp为行星轮质量; δrn、δsn分别为太阳轮、内齿圈与第n个行星轮位移沿啮合线方向的分量;αr为内啮合齿轮啮合角;αs为外啮合齿轮啮合角;Jn为行星轮转动惯量; Jj(j=c, r, s, 1, 2, …, N)为构件j的转动惯量;kju(j=c, r, s)为构件j的回转支承刚度; rj(j=c, r, s, 1, 2, …, N)为各行星轮的基圆半径.
对于行星齿轮系统,当系统处于平衡状态时,应满足力矩平衡和功率平衡,即基本构件上的力矩代数和为零,所传递的功率代数和也为零[10].则系统处于平衡状态时,发动机转矩的72%传递到驱动轴上,28%传递到发电机上.
2.4 减速器/差速器-半轴-轮胎/车身动力学模型减速器/差速器齿轮间的连接刚度和啮合刚度很大,可近似看作刚性,不考虑齿轮间的静传递误差和齿侧间隙.根据动能相等及传动比关系[11],可将内齿圈和减速器/差速器总成等效成一个当量转动惯量J′r,对应的扭转角为θr,经减速器/差速器后系统的角度为θ′r=θr/i,i为传动比.
半轴的简化与电机轴类似,将其等效为两根扭转弹簧,不考虑阻尼,其动力学方程为
| $ {T_{{\rm{a}}x}} = {K_{{\rm{a}}x}}({\theta _{{\rm{a}}x{\rm{f}}}} - {\theta _{{\rm{a}}x{\rm{r}}}}) $ | (10) |
式中:Tax为半轴上转矩;Kax为半轴的等效扭转刚度;θaxf、θaxr分别为半轴的前后端扭转角位移.
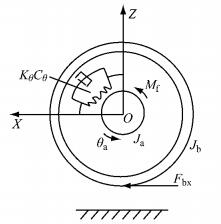
借鉴“刷子”模型,建立轮胎力学模型,如图 5所示.基于子午线轮胎的结构,将轮胎总成分成两个部分,一部分是车轮轮毂的转动惯量Ja,另一部分是车轮总成其他部分的转动惯量Jb.因此,建立轮胎的扭转振动模型,如式(11)所示.
|
图 5 轮胎扭振动力学模型 Fig.5 Tyre model |
| $ \left\{ \begin{array}{l} {J_{\rm{a}}}{{\ddot \theta }_{\rm{a}}} + {C_\theta }({{\dot \theta }_{\rm{a}}} - {{\dot \theta }_{\rm{b}}}) + {K_\theta }({\theta _{\rm{a}}} - {\theta _{\rm{b}}}) = {M_{\rm{f}}}\\ {J_{\rm{b}}}{{\ddot \theta }_{\rm{b}}} + {C_\theta }({{\dot \theta }_{\rm{b}}} - {{\dot \theta }_{\rm{a}}}) + {K_\theta }({\theta _{\rm{b}}} - {\theta _{\rm{a}}}) = - {R_{\rm{d}}}{F_{{\rm{b}}x}} \end{array} \right. $ | (11) |
式中:Kθ为轮胎的扭转刚度;Cθ为轮胎的扭转阻尼;Rd为轮胎的滚动半径;Mf为作用在轮毂上的力矩;Fbx为地面对轮胎的切向作用力,它由地面附着系数和滑移率与车身法向作用力来确定[12];θa、θb分别为轮毂和轮环的角位移.
综上,建立了混合动力传动系统的扭转振动模型构,模型中的关键参数如表 1所示.
| 下载CSV 表 1 子系统动力学模型参数 Tab.1 Subsystem parameters |
混合动力传动系统总体动力学模型见图 6.图 6中JM1、JM2分别为发电机和电动机的转动惯量;J′r为内齿圈和减速器/差速器总成的等效当量转动惯量;Jla、Jra分别为左右车轮轮毂的转动惯量;J′v为车辆平动部分等效到车轮处的当量转动惯量Jv和左右车轮轮冠转动惯量Jla、Jra之和.系统的激励源分别为发动机、电动机和发电机.各子系统通过输入和输出轴的转角和扭矩建立联系.

|
图 6 混合动力传动系统总体动力学模型 Fig.6 Overall model of a hybrid powertrain system |
由于混合动力系统存在纯电动、混合动力及停车充电3种工作模式,不同工作模式下行星齿轮系统的约束不同,因此,基于本文建立的系统扭转振动模型,增加合适的边界条件,满足不同工作模式下系统瞬态扭转振动特性的分析.不同工作模式下行星齿轮系统的边界条件为:
(1) 纯电动模式下行星架固定,发动机停机,传动系统振动力学模型满足以下约束:
| $ \left\{ \begin{array}{l} {\theta _{{\rm{b1}}}} = {\theta _{{\rm{b2}}}} = {\theta _{{\rm{b3}}}} = {\theta _{{\rm{b4}}}} = {\theta _{\rm{f}}} = 0\\ {\theta _{\rm{c}}} = 0 \end{array} \right. $ | (12) |
(2) 混合动力模式下行星齿轮系统基本构件均不固定,传动系统振动力学模型传动系统振动力学模型无约束.
(3) 停车充电模式下车辆静止,内齿圈固定,电动机停机,传动系统振动力学模型满足以下约束:
| $ \left\{ \begin{array}{l} {\theta _{\rm{r}}} = 0\\ {\theta _{{\rm{M2}}}} = 0 \end{array} \right. $ | (13) |
式中:θM2为电机的角位移.
3 典型工况与动力控制策略为了能够考察混合动力系统在各工作模式下的瞬态扭转振动特性,本文提出了包含各种工作模式的典型工况及对应的动力控制策略.
3.1 典型工况混合动力传动系统的典型分析工况,必须包含3个动力源及其工况变化和模式切换.通过设定不同加速度实现加速、匀速和减速的过程,引入发动机启停的瞬态工况实现模式切换.本文提出的典型工况如图 7所示,A、B、C段为不同加速度的匀加速过程,D段为匀速过程,E、F段为不同减速度的匀减速过程.设定匀速阶段车速为60 km·h-1,工况中A、B1段为纯电动模式,然后发动机启动切换至B2、C、D段的混合动力模式,E、F段为再生制动模式且F2段发动机停机.

|
图 7 典型工况 Fig.7 Typical working conditions |
本文采用前向仿真研究方法,图 8为前向仿真流程图,为简化分析,仿真中不考虑蓄电池SOC(state of charge)荷电状态的影响,动力控制策略模型包括驾驶员模型和控制器模型.

|
图 8 前向仿真流程图 Fig.8 Flowchart of forward simulation |
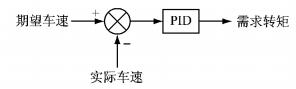
驾驶员模型实际上是个车速控制器,如图 9所示,通过对输入的期望车速与车辆纵向动力学模型反馈的实际车速的差值进行PID(proportion, integral and derivative controller)反馈调节控制,得到驱动轮处所需的转矩.
|
图 9 驾驶员模型框图 Fig.9 Driver model |
(1) 当0≤dv/dt≤a且v≤30 km·h-1时(a为纯电动模式下车辆所能达到的最大加速度,30 km·h-1对应B2阶段发动机点火时刻),系统工作在纯电动模式,发动机停机,发电机空转不工作,系统由电动机驱动.
(2) 当急加速时所需力矩大于此时电动机能提供的最大力矩即期望加速度dv/dt>a时或者当车速达到30 km·h-1(0≤dv/dt≤a且v≤30 km·h-1),发动机启动并工作在最佳油耗曲线上,发电机也开始发电,此时为混合动力模式.
(3) 当车辆减速时(dv/dt < 0),系统处在再生制动模式,发电机和发动机均停止工作且空转,车速降到30 km·h-1以下发动机停机,若制动减速度比较小,则电动机转矩由工况需求决定,若制动减速度较大,电动机工作在最大输出功率曲线上,并由制动器辅助提供制动力.
加速工况下电动机所需提供转矩计算方法为
| $ {T_{{\rm{demand}}}} = \left( {0.72{T_{{\rm{engine}}}} + {T_{{\rm{motor}}}}} \right)i $ | (14) |
式中:Tdemand为驾驶员模型得出的驱动轮处所需的转矩;0.72Tengine为发动机提供给齿圈的力矩,可通过查表获得; Tmotor为电动机所需提供转矩; i为减速器/差速器总成传动比.
减速工况下单个前轮制动力矩Tbf的计算方法为
| $ \begin{array}{l} {T_{{\rm{demand}}}} = i{T_{{\rm{motor}}}} + 2({T_{{\rm{bf}}}} + {T_{{\rm{br}}}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;i{T_{{\rm{motor}}}} + \frac{2}{\beta }{T_{{\rm{bf}}}} \end{array} $ | (15) |
式中:Tbr为单个后轮制动力矩; β为制动器制动力分配系数.
当减速度要求较小时,忽略制动器摩擦制动力矩,电动机按工况需求发电,Tmotor根据加速工况计算方法即式(15)求得;当减速度要求较大时,电动机工作在最大输出功率曲线上,此时Tmotor可通过查表获得.动力控制策略中的参数如表 2所示.
| 下载CSV 表 2 控制模型参数 Tab.2 Parameters of control model |
当发动机与电动机激励源输入为零时,即可得到系统的固有特性.由于系统在纯电动、混合动力及停车充电3种模式下行星齿轮系统工作的部件不同,系统的传递路径和振动模型也不相同.系统在不同模式下的固有频率如表 3所示.由表 3可知:
| 下载CSV 表 3 不同模式下的固有频率 Tab.3 Natural frequencies in different modes |
(1) 纯电动模式下系统共有11个自由度,存在8个非重根和3个重根固有频率.非重根固有频率对应系统整体扭转振动模式,含有一阶刚体模态,296.7 Hz的振型中基本只有行星轮在振动,但不同于3个重根固有频率对应的行星齿轮振动模式.24.0、1 058.8、1 673.9 Hz的振型主要是对应左右车轮、电动机转子、太阳轮在振动.系统整体扭转振动模式中车身振幅几乎为0,轮胎也只有在低频频率5.20、24.0、24.7 Hz处才会有明显振动,24.7和75.9 Hz的振型较为复杂.3重根固有频率为287.8 Hz,对应行星轮振动模式,振型中只有行星轮在振动,其他构件均不振动.
(2) 混合动力模式下系统共有17个自由度,存在14个非重根和3个重根固有频率.非重根固有频率对应系统整体扭转振动模式,含有两阶刚体模态,24.0、296.7、1 058.8和1 673.9 Hz对应的振型与纯电动模式相同,756.5、2 066.6、3 020.4、5 388.4 Hz对应的振型中主要是发动机在振动,25.2、90.3和530.6 Hz对应振型较为复杂.同时,车身振动非常小,车轮只有在低频处(3~5阶)振动.3重根固有频率为287.8 Hz,对应行星轮振动模式,振型中只有行星轮在振动,其他构件均不振动.
(3) 停车充电模式下系统共有12个自由度,存在9个非重根和3个重根固有频率.非重根固有频率对应系统整体扭转振动模式,含有一阶刚体模态,且大部分固有频率及其对应振型与混合动力模式下相同,只有68.8和289.9 Hz不同,同时停车充电模式下的1 058.8 Hz的固有频率消失,这主要是由于电动机不工作导致的.3重根固有频率为287.8 Hz,对应行星轮振动模式,振型中只有行星轮在振动,其他构件均不振动.
(4) 对比各工作模式下系统的固有特性可发现:各模式下非重根固有频率对应的振型中4个行星轮振动状态相同,为整体扭转振动模式;重根固有频率对应的振型中只有行星轮在振动,其他构件均不振动,为行星轮振动模式.由以上对各模式下的固有特性分析可知,系统均具有行星轮振动模式,且对应的3重根固有频率一致,说明固有频率287.8 Hz与行星架和内齿圈的状态无关.
假设行星轮振动模式对应的振型矢量为
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_i} = \left\{ {0\;\; \cdots \;\;0\;\;{a_1}\;\;{a_2}\;\;{a_3}\;\;{a_4}\;\;0\;\; \cdots \;\;0} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, 3 \end{array} $ | (16) |
式中:a1~a4分别为待定常数.
将矢量代入任一工作模式下的主振型方程[13],可得
| $ (\mathit{\boldsymbol{K}} - \omega _i^2\mathit{\boldsymbol{M}}){\mathit{\boldsymbol{A}}_i} = 0 $ | (17) |
式中:K为总体刚度矩阵; ωi为对应阶次固有频率;M为质量矩阵.
通过简化可得方程组
| $ ({k_{{\rm{r}}n}} + {k_{{\rm{s}}n}} - \omega _i^2\frac{{{J_n}}}{{r_n^2}}){a_n} = 0 $ | (18) |
| $ {\omega _i} = \frac{{({k_{{\rm{r}}n}} + {k_{{\rm{s}}n}})r_n^2}}{{{J_n}}}\;\;n = 1, 2, 3, 4 $ | (19) |
由式(18)、(19)可知,固有频率287.8 Hz取决于行星轮转动惯量Jn、基圆半径rn以及行星轮与太阳轮、内齿圈间的啮合刚度ksn、krn.
5 瞬态动力学特性 5.1 车速与转矩特性混合动力系统在典型工况下的实际车速及与期望车速的误差如图 10所示.由图 10可以看出,实际车速与期望车速误差较小,模型可很好地跟随期望车速,系统对工况的响应能力比较强.发动机、电动机、发电机工作状态仿真结果与动力控制策略期望相一致,说明建立的控制模型是有效的.

|
图 10 车速跟随性仿真结果 Fig.10 Simulation results of vehicle speed |
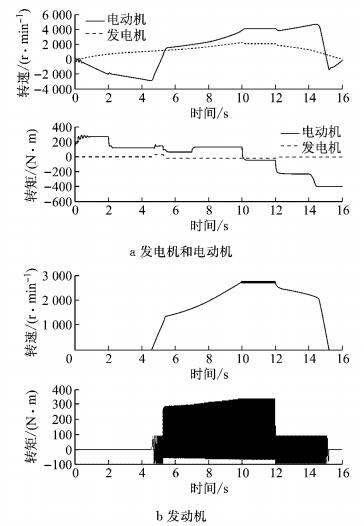
电动机、发电机和发动机的转速、转矩时间历程如图 11所示.由图 11可知,在0~2.0 s内,系统工作在纯电动模式A阶段,电动机启动时转速、转矩存在明显的波动,这是由电机本身结构特性所产生的谐波转矩引起的.发电机的转速与电动机反向,也存在明显的波动且转矩为零,这是由行星齿轮系统各部件的相对运动特性,发电机受到电动机转矩波动影响并空转造成的.该阶段发动机的转速转矩都为零,因为在纯电动模式下行星架固定,发动机并不工作.在2.0 s时,车辆的加速度突然变小,电动机的转矩突然下降并存在小幅波动,这是由于系统对动力需求下降并造成瞬态冲击引起的.
|
图 11 发电机、电动机与发动机转速和转矩时间历程 Fig.11 Speed and torque curves of motor/generator and engine |
在2.0~4.5 s内,车速不断平稳增加,系统工作在纯电动模式B1阶段.发电机转速平稳上升,转矩不变.发电机和发动机仍不工作,发电机的转速依然反向逐渐增大.4.5 s时车辆的速度达到30 km·h-1,系统进入混合动力模式B2阶段,行星齿轮系统的基本构件均不固定.4.5~5.5 s内电动机的转速、转矩都略有升高且存在明显的波动,发动机在发电机的恒转矩带动下,转速、转矩逐渐增大.5.5 s时发动机转速达到1 000 r·min-1并开始点火,其转速、转矩出现了明显的波动.此时,由于发动机开始工作,电动机转矩下降,转速出现明显的波动.发电机转速增大并开始恒转矩发电.在5.5~7.0 s内,系统工作在混合动力模式B2阶段,发动机转速转矩迅速上升,之后转速转矩对应最佳油耗曲线,发电机的转速不断增大,存在明显的波动,主要由发动机转矩波动影响造成.7.0 s时车辆的加速度突然增大,系统进入混合动力模式C阶段,电动机由于系统转矩需求上升,转矩突然增大,发动机的转速转矩持续增大,最终发动机转速维持在2 600 r·min-1,转矩维持在320 N·m.发电机的状态保持不变.在10.0~12.0 s内,车辆的加速度降为零并以最大车速60 km·h-1匀速运行,系统工作在混合动力模式,电动机的转矩明显下降,这是动力系统转矩需求造成的.电动机、发电机和发动机的转速均存在明显的波动.
在12.0~14.5 s内,系统工作在再生制动模式E、F1阶段.内齿圈固定,车辆以固定加速度制动且F1阶段制动加速度较大,车速不断减小.发动机和发电机的转速转矩明显下降,发电机在12.0 s时停止工作.在14.5 s后,发动机停机,发电机和电动机的转速转矩都逐渐降低且电动机转速存在明显波动.
为了分析电动机和发电机转矩波动的频率成分,对其利用短时傅里叶变换开展时频分析,如图 12所示.由图 12可以看出,电动机和发电机转矩波动频率主要为电流基频的6倍,但发电机在低频处存在明显的波动,这与逆变器的非线性和电机本体磁场畸变有关[1].

|
图 12 电动机和发电机转矩三维谱图 Fig.12 Three-dimensional torque spectrum of motor and generator |
图 13为发动机转矩的时频图.由图 13可以看出发动机转矩激励频率存在明显的阶次特性,且以第2、4阶为最主要的阶次成分.

|
图 13 发动机转矩时频图 Fig.13 Time-frequency of engine torque |
整车纵向加速度时间历程及其时频图如图 14所示,并对发生较大纵向振动的时刻进行了标注.由于系统在起步阶段处在纯电动模式,因此,Ⅰ处的纵向振动主要是由电动机启动时系统转速和转矩波动所引起的,如图 10a所示.2.0 s时系统进入加速度较小的B1阶段,电动机转矩突然下降,进而引起Ⅱ处的纵向振动.由于发动机开始工作,引起Ⅲ处和Ⅳ处的纵向振动.通过时频图可以发现,频率成分主要是发动机第2阶和第4阶频率,更有力地说明发动机简谐干扰力矩是引起整车纵向振动的主要原因.由于C阶段加速度较大,所以整车加速度也增大.随后整车进入匀速和制动工况D、E,加速度突然减小,因此整车加速度会突然减小,并引起Ⅴ、Ⅵ处的振动.在停机时刻Ⅶ、Ⅷ处存在明显的波动,主要由发动机停机,行星架锁止转矩突变的影响造成.

|
图 14 整车纵向加速度时间历程及其时频图 Fig.14 Vehicle longitudinal acceleration curve and time-frequency |
综合整个过程,整车纵向加速度在起步、发动机点火和停机时刻存在明显的波动,衰减较慢,如图 14中的Ⅰ、Ⅲ和Ⅷ处,它们主要是由于电动机和发动机转矩突变和行星架锁止转矩突变引起的瞬态冲击造成的.从频域角度看,Ⅰ~Ⅷ处都发生了低频的抖动,主要频率是6 Hz,这与纯电动模式下的一阶固有频率5.20 Hz和混合动力模式下的一阶固有频率6.28 Hz比较一致,从而说明主要是由行星架和行星齿轮引起的共振.
5.3 行星齿轮系统扭振特性行星齿轮系统中行星架、行星轮、太阳轮和内齿圈的角加速度时间历程如图 15所示.从时间历程来看,在0~2.0 s内,系统工作在纯电动模式下的A阶段,除了连同发动机被锁止的行星架,其他部件角加速度波动较大,衰减较慢,主要由于电动机转矩突变造成明显的瞬态冲击;5.5 s时发动机点火,系统进入混合动力模式下的B2阶段,行星齿轮系统的各部件均不固定,各部件角加速度波动幅值明显增大;在6.0~10.0 s混合动力模式加速工况C、D下,各部件均不固定,行星架的角加速度响应不同于其他部件存在多处明显的波动;系统在12.0 s由匀速转入再生制动模式E时,各部件均存在明显的瞬态冲击,由发动机和发电机停止工作并空转造成冲击引起;系统在15.0 s由于发动机停机,导致各部件角加速度波动幅值明显增大,衰减较慢.
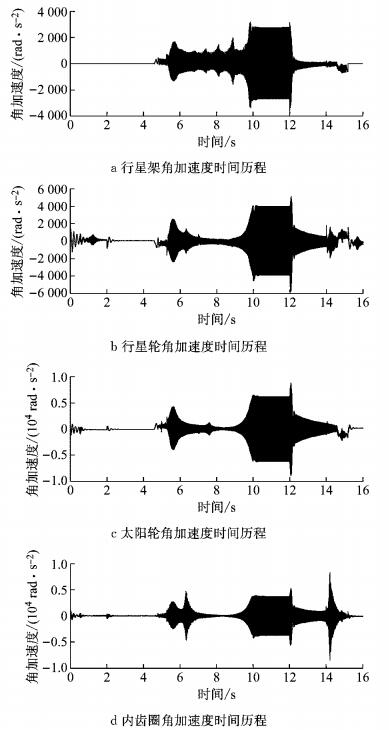
|
图 15 行星齿轮系统各部件角加速度时间历程 Fig.15 Angular acceleration of planetary gear system |
对比行星架、行星轮、太阳轮和内齿圈的角加速度时间历程,发现行星轮的角加速度时间历程最具有代表性,因此以行星轮为例,对行星轮的角加速度响应开展时频分析.
行星轮角加速度时间历程及其时频图如图 16所示,系统在0~2.0 s内,Ⅰ、Ⅱ处角加速度波动以电动机转矩6阶波动频率为主,主要原因是电动机转矩6阶频率接近纯电动模式下的固有频率287.8 Hz,行星轮发生共振.在6.0 s时Ⅴ处角加速度波动剧烈,发动机以第4阶主简谐量波动频率为主,接近混合动力模式下的固有频率90.3 Hz,行星轮发生共振.Ⅲ处角加速度波动剧烈主要原因是电动机转矩6阶频率接近混合动力模式下的固有频率1 058.8 Hz,行星轮发生共振.10.0~12.0 s时,系统稳定在最大车速阶段,Ⅶ处角加速度大幅波动,发动机主简谐量波动频率以第4阶为主,接近混合动力模式下的固有频率90.3 Hz,行星轮发生共振.14.0~16.0 s时Ⅷ、Ⅸ处波动,系统工作在再生制动模式,发动机和发电机停止工作,主要由电机的转矩波动造成.由行星轮角加速度时间历程及其时频图可知,行星轮角加速度响应存在与发动机、电动机、发电机转矩激励对应的频率成分,且行星轮扭振主要体现在由于动力装置转矩波动引起的系统共振.
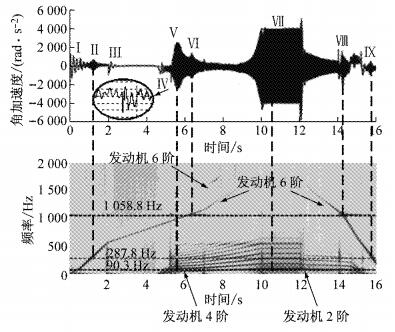
|
图 16 行星轮角加速度时间历程及其时频图 Fig.16 Angle acceleration and time-frequency of planetary wheel |
综合以上行星齿轮系统扭振特性的分析可知,由于电机转矩波动和发动机点火,激励源波动会引起系统振动,应该采取主动控制的优化方法改善激励源波动和冲击,抑制系统的振动;由于激励源频率和系统固有频率接近,系统会产生共振,可采取在电动机或发动机输出端加入扭转减振器的优化方法来改善行星轮的扭振特性.
6 结论(1) 针对发动机、电动机和行星齿轮系等子系统组成的混联式混合动力驱传动系统,提出了一种考虑工作模式和动力控制策略的混合动力驱传动系统扭转动力学模型.
(2) 纯电动、混合动力和停车充电工作模式下下系统的扭转振动模式均可分为整体扭转振动模式和行星轮振动模式两种,整体扭转振动模式下行星齿轮振动状态始终相同,行星齿轮振动模式的固有频率为重根,且与行星轮转动惯量、基圆半径以及行星轮与太阳轮、内齿圈间的啮合刚度有关.混合动力模式与停车充电模式下的固有频率相近.
(3) 在典型运行工况下,混联式混合动力系统瞬态振动主要包括电动机、发电机和发动机的力矩和转速波动、整车纵向低频抖动和行星齿轮系统振动.车辆在起步和发动机点火时存在明显的转矩波动和冲击,容易引起整车纵向低频振动.行星轮扭转振动响应存在与发动机、电动机、发电机转矩激励接近的频率成分,进而引起了系统的共振.
| [1] |
梁锐.电动车动力传动系统扭转振动研究[D].上海: 同济大学, 2008. LIANG Rui. Research on torsional vibration of electric vehicle's powertrain system[D]. Shanghai: Tongji University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1507391 |
| [2] |
熊建强, 黄菊花. 混合动力汽车噪声和振动的分析与控制[J]. 噪声与振动控制, 2009, 29(5): 96 XIONG Jianqiang, HUANG Juhua. Analysis and control of noise and vibration of hybrid electric vehicles[J]. Noise and Vibration Control, 2009, 29(5): 96 DOI:10.3969/j.issn.1006-1355.2009.05.026 |
| [3] |
赵彤航, 卢炳武, 曹蕴涛. 混合动力轿车振动噪声控制技术[J]. 吉林大学学报, 2012, 42(6): 1373 ZHAO Tonghang, LU Bingwu, CAO Yuntao. NVH control technology of hybrid electric vehicle[J]. Journal of Jilin University, 2012, 42(6): 1373 |
| [4] |
TANG X L. Study on the torsional vibration of a hybrid electric vehicle powertrain with compound planetary power-split electronic continuous variable transmission[J]. Archive Proceedings of the Institution of Mechanical Engineers Part C: Journal of Mechanical Engineering Science, 2014, 203-210(17): 228 |
| [5] |
MA X F, LUO K. Modeling and analysis of torsional vibration on engine-generator system of hybrid electric vehicle[C]// Proceedings of SAE-China Congress 2014. Berlin, Heidelberg: Springer, 2015: 59-70.
|
| [6] |
张德久, 于海生, 张建武, 等. 混合动力汽车传动系扭转振动分析及控制[J]. 传动技术, 2014, 28(4): 3 ZHANG Dejiu, YU Haisheng, ZHANG Jianwu, et al. Analysis and control of torsional vibration in HEV[J]. Drive System Technique, 2014, 28(4): 3 DOI:10.3969/j.issn.1006-8244.2014.04.001 |
| [7] |
于海生, 张彤, 马智涛, 等. 行星排式混合动力汽车传动系扭转振动分析[J]. 农业工程学报, 2013, 29(15): 57 YU Haisheng, ZHANAG Tong, MA Zhitao, et al. Torsional vibration analysis of planetary hybrid electric vehicle driveline[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(15): 57 DOI:10.3969/j.issn.1002-6819.2013.15.008 |
| [8] |
TANG X L. A novel simplified model for torsional vibration analysis of a series-parallel hybrid electric vehicle[J]. Mechanical Systems & Signal Processing, 2017, 85(1): 329 |
| [9] |
王世宇, 张策, 宋轶民, 等. 行星传动固有特性分析[J]. 中国机械工程, 2005, 16(16): 1461 WANG Shiyu, ZHANG Ce, SONG Yimin, et al. Natural mode analysis of planetary gear trains[J]. China Mechanical Engineering, 2005, 16(16): 1461 DOI:10.3321/j.issn:1004-132X.2005.16.014 |
| [10] |
王利花.并联混合动力汽车用行星齿轮机构的研究[D].西安: 西安理工大学, 2008. WANG Lihua. Study on planetary gear unit for parallel hybrid electric vehicle[D]. Xi'an: Xi'an University of Technology, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1380519 |
| [11] |
张保成, 苏铁熊, 张林仙. 内燃机动力学[M]. 北京: 国防工业出版社, 2009 ZHANG Baocheng, SU Tiexiong, ZHANG Linxian. Internal combustion engine dynamics[M]. Beijing: National Defense Industry Press, 2009 |
| [12] |
余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009 YU Zhisheng. Internal combustion engine dynamics[M]. Beijing: China Machine Press, 2009 |
| [13] |
靳晓雄, 张立军, 江浩. 汽车振动分析[M]. 上海: 同济大学出版社, 2002 JIN Xiaoxiong, ZHANG Lijun, JINAG Hao. Analysis of vehicle vibration[M]. Shanghai: Tongji University Press, 2002 |
 2018, Vol. 46
2018, Vol. 46

