2. 同济大学 中德学院,上海 200092
2. Sino-German College, Tongji University, Shanghai 200092, China
汽车引起的环境问题越来越受到重视.为了解决汽车尾气排放带来的环境压力,汽车制造商不遗余力地开发新能源汽车,特别是电动汽车[1].随着汽车的电动化和智能化成为汽车发展的主要方向,对汽车主动安全性的要求也越来越高,越来越多的国际主流车厂强制要求其供应商按照道路车辆功能安全标准(ISO26262)[2]对汽车电子控制系统进行功能安全开发.强调汽车功能安全的目的是防止由于控制器功能故障导致的人身伤害.而ISO26262则是以工业功能安全标准IEC61508[3]为基础,专门针对汽车电子行业的功能安全标准, 其内容涉及汽车电子控制系统的概念、系统、软硬件及生产维护部分,覆盖了汽车电子开发的整个生命周期.在中国,汽车电子的功能安全也受到了广泛的关注.目前,由中国汽车技术研究中心制定的国内道路车辆功能安全标准《道路车辆功能安全》(GB/T 34590:2017)[4]也已经开始实施.
功能安全标准对汽车电子功能安全开发的方法和流程进行了规范,但是其具体设计,还是取决于控制系统本身的功能.由于电机和电机控制系统是电动汽车中最关键的部件之一,电动汽车电机控制器的设计开发也得到了广泛的研究[5-9].但是其功能安全开发还是一个较新的问题,文献[10-12]对此展开了相应的研究.文献[10]举例介绍了针对混合动力汽车和电动汽车动力总成的功能安全概念.文献[11]则提出了一种基于标准三层架构的车用永磁同步电机的功能安全概念,通过对电机控制器的功能分层,实现对电机控制系统的实时监控.文献[12]提出了电机的转矩在线监控方法,并指出在检测到电机出现故障时,可以通过触发关断路径,使电机进入安全状态.
在车用电机控制系统中,永磁同步电机,尤其是内置式永磁同步电机由于其高功率密度、高效率和小尺寸得到了广泛的应用[13-14].根据电机控制器的安全目标,要求在电机控制器出现故障时,关闭电机输出,使其转矩接近于零.对于永磁同步电机,在低速条件下,通过关断绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)三相桥臂即可实现这一点.但这种方法的主要缺点是,在电机高速运行时,关闭三相桥臂之后,由于电机反电动势的存在,电机电流通过IGBT的续流二极管向电池整流回馈,会产生较大的制动转矩.另一种关闭永磁同步电机转矩输出的方法是进行电机三相主动短路.实车实验表明,在转速较高的情况下,如果将永磁同步电机三相互短,电机的转矩输出接近零.因此在实际工程开发中,大部分车厂都将主动短路作为电机控制系统的安全路径[12].但是主动短路的主要缺点是,在主动短路过程中,短时间产生电流可能远高于正常运行时的电流;且在低速条件下,主动短路操作会产生一定的制动转矩.在以往的研究中,对永磁同步电机短路过程动态响应缺少深入的理论分析.文献[15]研究永磁同步电机在稳态情况下的电流和转矩输出,但是没有对过程中产生的过电流情况进行分析.文献[16-19]提出了使用主动短路进行电机关断的方法和相关电路设计,但是没有对主动短路过程中电机的状态进行研究.
因此,本文的主要目的是,研究永磁同步电机主动短路的动态过程,分析电机工况、电机参数对主动短路时永磁同步电机电流和转矩输出的影响;提出主动短路状态下电流和转矩的估算公式;一方面为选择主动短路作为关断路径提供理论依据,另一方面也为电机控制器选择合适的IGBT提供参考.
1 电动汽车驱动电机功能安全和安全状态自从ISO26262正式颁布以来,汽车电子电气系统的功能安全研究成为国内外的研究热点.在电动汽车中,广泛使用永磁同步电机作为驱动电机,其驱动总成框图如图 1所示.

|
图 1 电动汽车动力总成框图 Fig.1 Block diagram of powertrain of electric vehicle |
电动汽车电机驱动系统的主要功能要求包括: ①在整车控制器请求加速时输出驱动转矩;②在整车控制器请求减速时输出制动转矩.
针对电机驱动系统的功能,可以对其进行危害和风险分析,以总结可能造成的危害事件,确定其安全完整性等级和安全状态.考虑到驾驶场景和路况的复杂性,本文提供了部分HARA(危害分析和风险评估)的结果作为参考,如表 1所示.
| 下载CSV 表 1 电机控制器的危害和风险分析 Tab.1 Hazard and risk analysis of inverter |
作为电动汽车的主要动力来源,在电机控制系统出现故障时,需要使其进入安全状态,以保证车辆受控或者不会对驾乘人员造成伤害.而当电机控制器出现硬件或软件故障,电机输出异常时,无论是输出制动转矩或者是驱动转矩,都是非常危险的.所以目前针对电动汽车出现上述故障时,通常要求电机在进入安全状态之后,关闭电机的转矩输出,使车辆处于惯性滑行状态,便于驾驶员将车驶离车道以寻求帮助.
在高速条件下(反电动势高于母线电压),如果断开电机的三相桥臂,电机电流会经过续流二极管向高压电池整流回馈,并产生较大的制动转矩.因此,目前常见的电机关断方式为主动短路.即在如图 2所示的逆变器中,通过闭合桥臂T2、T4、T6,打开桥臂T1、T3、T5,使电机三相短路.

|
图 2 三相电压型逆变器的拓扑结构 Fig.2 Topology structure of three phase voltage inverter |
根据以往的实验经验和仿真结果,主动短路操作的主要缺点是:在切换主动短路的过程中,会出现一个较大的瞬态电流,而在进入稳态之后,会输出一定的制动转矩.为了了解瞬态电流是否在逆变器和电机的承受范围之内,以及稳态制动转矩是否可能对驾乘人员造成伤害,需要对电机在切换主动短路之后的电流及转矩输出进行分析.
2 永磁同步电机模型及主动短路电动汽车中常见的电机为内置式永磁同步电机,因为其交直轴电感的差异,可以提供更多的磁阻转矩.
为了对电机数学模型进行简化,先做如下假设:①忽略铁芯饱和,不计涡流和磁滞损耗;②永磁材料的电导率为零;③转子上没有阻尼绕组;④相绕组中感应电动势波形为正弦.
因此,转子磁场定向算法中,dq轴系下的电机模型可以表示为
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{i}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{Ai}} + \mathit{\boldsymbol{Bu}} $ | (1) |
| $ \mathit{\boldsymbol{i}} = \left[ \begin{array}{l} {i_d}\\ {i_q} \end{array} \right] $ | (2) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{s}}}}}{{{L_d}}}}&{\frac{{\omega {L_q}}}{{{L_d}}}}\\ { - \frac{{\omega {L_d}}}{{{L_q}}}}&{ - \frac{{{R_{\rm{s}}}}}{{{L_q}}}} \end{array}} \right] $ | (3) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_d}}}}&0\\ 0&{\frac{1}{{{L_q}}}} \end{array}} \right] $ | (4) |
| $ \mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{u_d}}\\ {{u_q} - \omega {\mathit{\Psi }_{\rm{f}}}} \end{array}} \right] $ | (5) |
式中:id、iq分别为定子电流直、交轴分量;ud、uq分别为定子电压直、交轴分量;Ld、Lq分别为直、交轴电感;Rs为定子电阻;ω为转子的电角速度,机械角速度ωm=ω/pn,pn为电机极对数;Ψf表示转子永磁体产生的磁链.
在dq坐标轴系下的永磁同步电机的转矩方程为
| $ {T_{\rm{e}}} = 1.5{p_{\rm{n}}}[{\mathit{\Psi }_{\rm{f}}}{i_q} + ({L_d} - {L_q}){i_d}{i_q}] $ | (6) |
在电动汽车电机控制系统中,普遍采用磁场定向控制(field-oriented control, FOC)算法,对dq轴电流进行分别控制,如图 3所示.图中, id*、iq*分别为定子直、交轴电流参考值;uα、uβ分别为定子电压α、β轴分量;iα、iβ分别为定子电流α、β轴分量;iA、iB、iC分别为A、B、C三相定子电流.

|
图 3 永磁同步电机FOC控制算法框图 Fig.3 Block diagram of FOC control algorithm for permanent magnet synchronous motor |
在切入主动短路状态之后,电机输入ud、uq变为0.同时,由于在电动汽车中,车辆惯性较大,电机转速变化缓慢,相对于电流的变化,可以近似认为转速是常数.为了将方程简化为齐次微分方程以方便求解电流的表达式,设辅助变量
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }} = \mathit{\boldsymbol{i}} - \left[ {\begin{array}{*{20}{c}} { - \frac{{{\omega ^2}{L_q}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}}}\\ { - \frac{{\omega {R_{\rm{s}}}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}}} \end{array}} \right] $ | (7) |
则电机在主动短路状态下的微分方程可以表示为
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }} $ | (8) |
在主动短路状态下,电机电流时域响应可以表示为
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( t \right) = {{\rm{e}}^{At}}\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( 0 \right) $ | (9) |
将矩阵A转化为约当标准型
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{JT}} $ | (10) |
则电流的时域响应可以表示为
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( t \right) = \mathit{\boldsymbol{T}}{{\rm{e}}^{\mathit{\boldsymbol{J}}t}}{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( 0 \right) $ | (11) |
其中:
| $ \begin{array}{*{20}{c}} \mathit{\boldsymbol{J}} ={\left( { - \frac{{( - \sqrt { - ({L_d}{R_{\rm{s}}} - {L_q}{R_{\rm{s}}} + 2\omega {L_d}{L_q})({L_q}{R_{\rm{s}}} - {L_d}{R_{\rm{s}}} + 2\omega {L_d}{L_q})} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2{L_d}{L_q}}}} \right.}\\ 0\\ 0\\ {\left. { - \frac{{(\sqrt { - ({L_d}{R_{\rm{s}}} - {L_q}{R_{\rm{s}}} + 2\omega {L_d}{L_q})({L_q}{R_{\rm{s}}} - {L_d}{R_{\rm{s}}} + 2\omega {L_d}{L_q})} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2{L_d}{L_q}}}} \right)} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{T}} = \left( { - \frac{{{R_{\rm{s}}}}}{{\omega {L_d}}} + \frac{{( - \sqrt { - ({L_d}{R_{\rm{s}}} - {L_q}{R_{\rm{s}}} + 2\omega {L_d}{L_q})({L_q}{R_{\rm{s}}} - {L_d}{R_{\rm{s}}} + 2\omega {L_d}{L_q})} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2\omega {L_d}}}} \right.}\\ 1\\ {\left. {\frac{{(\sqrt { - ({L_d}{R_{\rm{s}}} - {L_q}{R_{\rm{s}}} + 2\omega {L_d}{L_q})({L_q}{R_{\rm{s}}} - {L_d}{R_{\rm{s}}} + 2\omega {L_d}{L_q})} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2\omega {L_d}}} - \frac{{{R_{\rm{s}}}}}{{\omega {L_d}}}} \right)}\\ 1 \end{array} $ | (13) |
在电动汽车中,电机转速的数量级一般远大于电机的电阻电感等参数,因此,J和T中的表达式可做如下近似:
| $ \begin{array}{l} ( - ({L_d}{R_{\rm{s}}} - {L_q}{R_{\rm{s}}} + 2\omega {L_d}{L_q}) \cdot \\ ({L_q}{R_{\rm{s}}} - {L_d}{R_{\rm{s}}} + 2\omega {L_d}{L_q}){)^{\frac{1}{2}}} \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;2\omega {L_d}{L_q}{\rm{j}} \end{array} $ | (14) |
因此J和T可以近似表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}} \approx \left( { - \frac{{( - 2\omega {L_d}{L_q}{\rm{j}} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2{L_d}{L_q}}}} \right.}\\ 0\\ 0\\ {\left. { - \frac{{(2\omega {L_d}{L_q}{\rm{j}} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2{L_d}{L_q}}}} \right)} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{T}} \approx \left( {\frac{{( - 2\omega {L_d}{L_q}{\rm{j}} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2\omega L_d^2}} - \frac{{{R_{\rm{s}}}}}{{\omega {L_d}}}} \right.}\\ 1\\ {\left. {\frac{{(2\omega {L_d}{L_q}{\rm{j}} + {L_d}{R_{\rm{s}}} + {L_q}{R_{\rm{s}}})}}{{2\omega L_d^2}} - \frac{{{R_{\rm{s}}}}}{{\omega {L_d}}}} \right)}\\ 1 \end{array} $ | (16) |
而电流响应也可以近似表示为
| $ \begin{array}{l} \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( t \right) \approx \left[ {{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t}}{{2{L_d}}}}}{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t}}{{2{L_q}}}}}(2\omega L_q^2{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\sin \left( {\omega t} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;{L_d}{R_{\rm{s}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\sin \left( {\omega t} \right) - {L_q}{R_{\rm{s}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\sin \left( {\omega t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;2\omega {L_d}{L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\cos \left( {\omega t} \right))/2\omega {L_d}{L_q}\\ \;\;\;\;\;\;\;\;\;\;\; - {{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t}}{{2{L_d}}}}}{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t}}{{2{L_q}}}}}(2\omega {L_d}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\sin \left( {\omega t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{L_d}{R_{\rm{s}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\sin \left( {\omega t} \right) - {L_q}{R_{\rm{s}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\sin \left( {\omega t} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\left. {2\omega {L_d}{L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\cos \left( {\omega t} \right)/2\omega {L_d}{L_q}} \right] \end{array} $ | (17) |
式(17)为主动短路后电流的时间函数.
从式(17)中可以看出,在进入主动短路之后,电流振荡衰减.
将电流响应中幅值较小的部分忽略,则可以对电机表达式进一步化简为
| $ \begin{array}{l} \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\left( t \right) \approx \\ \left( {\begin{array}{*{20}{c}} {\frac{{{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}}({L_d}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\cos \left( {\omega t} \right) + {L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\sin \left( {\omega t} \right))}}{{{L_d}}}}\\ {\frac{{{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}}({L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\cos \left( {\omega t} \right) - {L_d}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\sin \left( {\omega t} \right))}}{{{L_q}}}} \end{array}} \right) \end{array} $ | (18) |
将表达式(18)代入式(7),可得
| $ \begin{array}{l} \mathit{\boldsymbol{i}}\left( t \right) \approx \\ \left( {\begin{array}{*{20}{c}} {\frac{{{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}}({L_d}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\cos \left( {\omega t} \right) + {L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\sin \left( {\omega t} \right))}}{{{L_d}}}}\\ {\frac{{{{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}}({L_q}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{q0}}\cos \left( {\omega t} \right) - {L_d}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }_{d0}}\sin \left( {\omega t} \right))}}{{{L_q}}}} \end{array}} \right) + \\ \left( {\begin{array}{*{20}{c}} { - \frac{{{\omega ^2}{L_q}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}}}\\ { - \frac{{\omega {R_{\rm{s}}}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}}} \end{array}} \right) \end{array} $ | (19) |
从式(19)中可以看出,在进入主动短路之后,dq轴电流的响应主要由稳态和瞬态两部分组成.
观察电流的瞬态部分可以发现,在dq轴坐标系下,瞬态电流是一条逐渐收敛的椭圆螺旋曲线,瞬态电流幅值的大小,主要取决于电机的电感和进入主动短路瞬间的起始电流的大小;电机的电阻和电感组成的时间常数,共同决定了瞬态电流幅值的收敛速度,电机的转速则决定了瞬态电流振荡的频率.稳态部分主要取决于电机本身的参数和电机的转速.
此外,还可以推导出电流响应的包络线表达式,用于估计主动短路状态下可能出现的最大电流,即
| $ \mathit{\boldsymbol{I}}\left( t \right) \approx \left( \begin{array}{l} - \frac{{{\omega ^2}{L_q}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}} \pm {{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}} \cdot \\ \sqrt {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} _{d0}^2 + \frac{{L_q^2\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} _{q0}^2}}{{L_d^2}}} \\ - \frac{{\omega {R_{\rm{s}}}{\mathit{\Psi }_{\rm{f}}}}}{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}} \pm {{\rm{e}}^{ - \frac{{{R_{\rm{s}}}t\left( {{L_d} + {L_q}} \right)}}{{2{L_d}{L_q}}}}} \cdot \\ \sqrt {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} _{q0}^2 + \frac{{L_d^2\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} _{d0}^2}}{{L_q^2}}} \end{array} \right) $ | (20) |
将稳态电流响应代入永磁同步电机的转矩方程(6),可以获得电机在主动短路之后的转矩输出表达式为
| $ {T_{\rm{e}}} = - 1.5{p_{\rm{n}}}\left( {\frac{{\omega {R_{\rm{s}}}\mathit{\Psi }_{\rm{f}}^2}}{{{L_d}{L_q}{\omega ^2}}} + R_{\rm{s}}^2 - \frac{{{\omega ^3}{L_q}{R_{\rm{s}}}\mathit{\Psi }_{\rm{f}}^2({L_d} - {L_q})}}{{{{({L_d}{L_q}{\omega ^2} + R_{\rm{s}}^2)}^2}}}} \right) $ | (21) |
从公式(21)中可以看出,电机在主动短路状态下的稳态转矩输出,是关于电机的电感、永磁体磁链、定子电阻、极对数以及电机的转速的复杂函数.可以根据转速对其进行分段分析:在电机转矩较高时(LdLqω2≫Rs2),电机转矩方程可以简化表示为
| $ {T_{\rm{e}}} = - 1.5{p_{\rm{n}}}\left( {\frac{{{R_{\rm{s}}}\mathit{\Psi }_{\rm{f}}^2}}{{{L_d}{L_q}\omega }} - \frac{{{R_{\rm{s}}}\mathit{\Psi }_{\rm{f}}^2({L_d} - {L_q})}}{{L_d^2{L_q}\omega }}} \right) $ | (22) |
可见在高速运行时,电机输出转矩与转速成反比,转速越高,转矩输出越小.而随着电机转速逐渐降低,制动转矩渐渐增大.
而在转速很低的情况下(LdLqω2≪Rs2), 转矩方程可以表示为
| $ {T_{\rm{e}}} = - 1.5{p_{\rm{n}}}\left( {\frac{{\omega \mathit{\Psi }_{\rm{f}}^2}}{{{R_{\rm{s}}}}} - \frac{{{\omega ^3}{L_q}\mathit{\Psi }_{\rm{f}}^2({L_d} - {L_q})}}{{R_{\rm{s}}^3}}} \right) $ | (23) |
可以看出, 在低转速下, 随着转速的降低,制动转矩减小,并在电机转速为0 r·min-1时降到0 N·m.
4 仿真和实验验证为了对分析结果进行验证,对一台4对极内置式永磁同步电机进行了仿真分析和实验验证.电机参数如表 2所示:
| 下载CSV 表 2 电机参数 Tab.2 Motor parameters |
首先, 使用本文推导的公式(19), 计算了在主动短路状态下的电流输出,然后使用仿真及台架实验的方法,绘制出不同转速下的主动短路电流曲线进行对比,以验证本文推导公式的正确性.
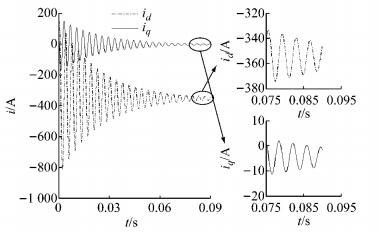
实验工况的选择主要考虑在实际情况下,车速较高时,车辆故障带来的危害更大,因此选取转速为4 000、3 000、2 000 r·min-1(切换过程保持负载电机转速不变),起始电流id0=0 A,iq0=120 A,切换主动短路的情况,分别加以验证,如图 4~12所示.
|
图 4 4 000 r·min-1时主动短路估算结果 Fig.4 Estimated result of active short circuit at 4 000 r·min-1 |

|
图 5 4 000 r·min-1时主动短路仿真结果 Fig.5 Simulation result of active short circuit at 4 000 r·min-1 |

|
图 6 4 000 r·min-1时主动短路实验结果 Fig.6 Experiment result of active short circuit at 4 000 r·min-1 |
|
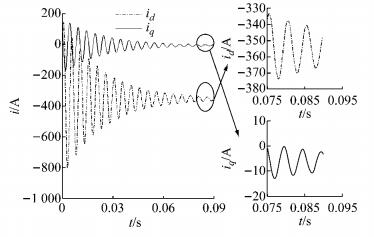
图 7 3 000 r·min-1时主动短路估算结果 Fig.7 Estimated result of active short circuit at 3 000 r·min-1 |

|
图 8 3 000 r·min-1时主动短路仿真结果 Fig.8 Simulation result of active short circuit at 3 000 r·min-1 |
|
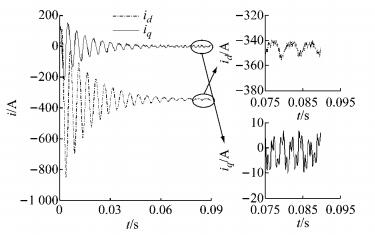
图 9 3 000 r·min-1时主动短路实验结果 Fig.9 Experiment result of active short circuit at 3 000 r·min-1 |
|
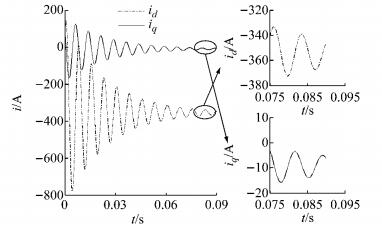
图 10 2 000 r·min-1时主动短路估算结果 Fig.10 Estimated result of active short circuit at 2 000 r·min-1 |

|
图 11 2 000 r·min-1时主动短路仿真结果 Fig.11 Simulation result of active short circuit at 2 000 r·min-1 |
|
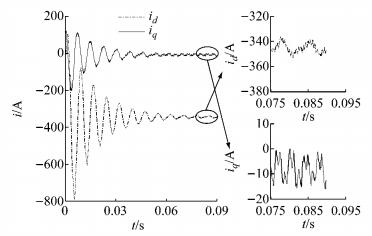
图 12 2 000 r·min-1时主动短路实验结果 Fig.12 Experiment result of active short circuit at 2 000 r·min-1 |
从图 4和图 5可以看出,估算公式(19)和仿真结果几乎完全一致,dq轴电流振荡衰减,最终收敛至稳态值;q轴稳态电流输出约-4.5 A,d轴稳态电流输出约-354.0 A;而对比图 4和图 6可以发现,在台架实验中,主动短路时,d轴电流峰值略大于估算结果和仿真结果.
对比图 7和图 8可以看出,估算结果和仿真结果同样非常接近,dq轴电流振荡频率低于4 000 r·min-1时, q轴稳态电流输出约-6.0 A,d轴稳态电流输出约为-354.0 A;实验测得的d轴电流峰值略大于估算结果和仿真结果.
对比图 10和图 11可以看出,dq轴电流振荡频率比3 000 r·min-1时更低;q轴稳态电流输出接近-9.0 A,d轴稳态电流输出同样约为-354.0 A;实验测得的d轴电流峰值略大于估算结果和仿真结果.
对比3次实验可以发现,虽然d轴电流振荡衰减频率不同,但稳态电流输出都非常接近;q轴稳态电流接近零.
同时可以发现,估算得到的电流结果与仿真结果非常接近,而实际实验中,d轴电流的峰值略大于估算和仿真结果.其主要原因是,在估算和仿真过程中,忽略了电机的磁饱和效应,即电机的电感会随电流变化而变化[20], d轴电感小于空载电感,导致d轴电流峰值比理论计算值偏大.而在解析表达式和仿真中,忽略了磁饱和效应,导致了实验结果和分析结果之间的误差,但两者趋势一致,且误差有限.
根据所得到的电流,利用电机电磁转矩公式(6),还可以计算不同转速下的制动转矩,见表 3.
| 下载CSV 表 3 主动短路制动转矩结果 Tab.3 Result of braking torque at active short circuit |
由表 3可以看出,估算和仿真的转矩结果基本一致,实验中的制动转矩比估计和仿真中的转矩略小,对应q轴电流误差在5 A以内,考虑到实验过程中电流传感器的量程为900 A, 故偏差仍在可接受的范围内.同时分析转矩随转速变化的趋势可以发现,转速越高,输出的制动转矩越小,与分析结果一致.同时可以发现,在较高转速下,主动短路产生的制动转矩非常小.而在较低转速下,驾驶员对故障状况做出反应的时间更为充裕,其他车辆也更容易对故障车辆进行避让,虽然存在一定的制动转矩,但是其危险性也更低.由此可以看出,主动短路适于作为电动汽车电机控制系统的安全关断路径.同时,从分析和实验结果中也可以发现,在进入主动短路的瞬间,电机会产生短时的大电流,电流幅值超过了800 A,进入稳态之后,电流幅值也在350 A左右,这相当于电机满载运行情况下的电流幅值.而从功率器件选择的角度出发,除了要满足电机正常运行的电流要求,还需要能够承受主动短路产生的瞬间电流和稳态电流.因此,为了保证实验正常进行,本实验所采用的是英飞凌公司的IGBT模块FS800R07A2E3,其额定电流为800 A,集电极重复峰值电流为1 600 A,为主动短路操作留出了足够的余量.
5 结语本文针对在电动汽车永磁同步电机控制器的功能安全开发中常见的关断路径、电机主动短路进行了深入的研究.通过对永磁同步电机数学模型的分析,对在主动短路状态下dq轴的电流和转矩输出进行了推导,并且通过仿真和实验进行了验证.分析了永磁同步电机在主动短路状态下的转矩输出,指出其在高速情况下制动转矩很小;低速下虽然存在一定的制动转矩,但是带来的风险在可控范围内,证明了主动短路可以作为车用永磁同步电机控制器的安全关断路径.提出了电机主动短路过程中dq轴电流的时域计算公式,指出在进入主动短路状态时会出现瞬时大电流,并可对主动短路状态下的电机电流进行预测,为选择合适的功率器件提供了理论依据.在未来的研究中,可以在本阶段研究的基础上,进一步研究抑制主动短路瞬间大电流的方法,以提高电机和功率器件的使用寿命.
| [1] |
CHAN C C. The state of the art of electric, hybrid, and fuel cell vehicles[J]. Proceedings of the IEEE, 2007, 95(4): 704 DOI:10.1109/JPROC.2007.892489 |
| [2] |
International Organization for Standardization. Road vehicles-functional safety: ISO 26262: 2011[S].[S.l.]: ISO, 2011.
|
| [3] |
International Electrotechnical Commission. Functional safety of electrical/electronic/programmable electronic safety related system: IEC 61508[S]. [S.l.]: International Electrotechnical Commission, 2010.
|
| [4] |
中国国家标准化管理委员会.道路车辆功能安全: GB/T 34590: 2017[S].北京: 中国标准出版社, 2017. China National Standardization Administration. Road vehicles-functional safety: GB/T 34590: 2017[S].Beijing: China Standard Press, 2017. |
| [5] |
ZHU Z Q, HOWE D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles[J]. Proceedings of the IEEE, 2007, 95(4): 746 DOI:10.1109/JPROC.2006.892482 |
| [6] |
KOMMURI S K. A robust observer- based sensor fault- tolerant control for PMSM in electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7671 DOI:10.1109/TIE.2016.2590993 |
| [7] |
LIU X D. Research on the performances and parameters of interior PMSM used for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3533 DOI:10.1109/TIE.2016.2524415 |
| [8] |
MIYAMA Y. PWM carrier harmonic iron loss reduction technique of permanent-magnet motors for electric vehicles[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2865 DOI:10.1109/TIA.2016.2533598 |
| [9] |
ESTIMA J O. Efficiency analysis of drive train topologies applied to electric/ hybrid vehicles[J]. IEEE Transactions on Vehicular Technology, 2012, 61(3): 1021 DOI:10.1109/TVT.2012.2186993 |
| [10] |
WU Z H, LU K, ZHU Y, et al. Functional safety and secure CAN in motor control system design for electric vehicles[C]// SAE 2017 World Congress Experience. [S.l.]: SAE, 2017: 2017-01-1255.
|
| [11] |
CHRISTIAENS S, OGRZEWALLA J, PISCHINGER S. Functional safety for hybrid and electric vehicles[C]// SAE 2012 World Congress & Exhibition. [S.l.]: SAE, 2012: 2012-01-0032.
|
| [12] |
LI S, CHANG C, ZHAO H. Functional safety development of e-motor drive system for PHEV[C]//SAE 2012 World Congress & Exhibition. [S.l.]: SAE, 2015: 2015-01-0261.
|
| [13] |
GIANMARIO P. Performance comparison between surface-mounted and interior PM motor drives for electric vehicle application[J]. IEEE Transactions on Industrial Electronics, 2011, 59(2): 803 |
| [14] |
GIANMARIO P. Comparison of induction and PM synchronous motor drives for EV application including design examples[J]. IEEE Transactions on Industry Applications, 2012, 48(6): 2322 DOI:10.1109/TIA.2012.2227092 |
| [15] |
暴杰, 赵慧超, 董秀辉, 等. 电动车用永磁同步电机的三相短路稳态分析与应用[J]. 微特电机, 2014, 42(3): 17 BAO Jie, ZHAO Huichao, DONG Xiuhui, et al. Three phase short circuit steady-state analysis and application of PMSM for electric vehicle[J]. Small & Special Electrical Machines, 2014, 42(3): 17 DOI:10.3969/j.issn.1004-7018.2014.03.006 |
| [16] |
王淑旺, 苑红伟, 孙纯哲, 等.一种电动汽车电驱动系统主动短路保护电路: CN104442405A[P].2014-12-04. WANG Shuwang, YUAN Hongwi, SUN Chunzhe, et al. Active short-circuit protection circuit for electric drive system of electric automobile: CN104442405A[P]. 2014-12-04. |
| [17] |
凌欢, 罗晓, 陈茜兵, 等.一种电动汽车的主动短路保护电路: CN105262059A[P].2015-09-30. LING Huan, LUO Xiao, CHEN Qianbing, et al. Active short-circuit protection circuit of electric automobile: CN105262059A[P]. 2015-09-30. |
| [18] |
胡鹏, 肖梦, 艾敬尧, 等.一种主动短路控制电路及控制方法: CN105680417A[P].2016-03-31. HU Peng, XIAO Meng, AI Jingyao, et al. Active short circuit control circuit and control method: CN105680417A[P]. 2016-03-31. |
| [19] |
蒋建军.一种电机三相定子绕组主动短路系统以及方法: CN107124124A[P].2017-04-01. JIANG Jianjun. Motor three-phase stator winding active short circuit system and method: CN107124124A[P]. 2017-04-01. |
| [20] |
STUMBERGER B, STUMBERGER G, DOLINAR D, et al. Evaluation of saturation and cross-magnetization effects in interior permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications, 2003, 39(5): 1264 DOI:10.1109/TIA.2003.816538 |
 2018, Vol. 46
2018, Vol. 46

