沥青应变计,即埋入式沥青路面应变传感器,目前大量应用于道路性能监测以及各类加速加载试验[1], 其测量结果可用于验证基于室内试验提出的疲劳方程、校核数值仿真结果等[2].然而目前市场上沥青应变计测量准确度(即测量值与沥青混合料基准值间的一致程度)高低不一,测量误差相差较大[3].根据谭忆秋等[4]的研究,传感器测量结果与沥青混合料应变基准值可相差60%以上.因此有必要针对不同应变计的准确度进行比对,优选适宜传感器用于试验.
应变计准确度比对的核心问题在于获取沥青混合料的平均应变基准值.已有研究中,Willis等[5]将沥青应变计放入沥青混合料梁试件,在三点加载过程中依据弹性力学计算应变计所在高度的平均应变.庄传仪等[6]对三点加载试验方法加以改进, 使用四点加载方法,将应变计放置于梁的纯弯段,进而消除剪应力对平均应变的影响.吴璨[7]在此基础上做进一步研究,将应变片粘贴于含应变计的沥青混合料梁试件表面,以获取这一位置的平均应变.Wistuba等[8]直接将沥青应变计放入高黏度环氧树脂试件,以确保试件和应变计变形一致,然后利用环氧树脂的表面应变作为平均应变基准值.但是沥青混合料属于黏弹性材料,使用弹性力学法求解黏弹性的沥青混合料平均应变会引入一定系统误差.此外沥青混合料高度不均匀,当使用应变片测量高度不均匀材料的应变时,应变片电阻丝局部扭曲会对测量结果造成较大影响[9].因此有必要研发新方法获取沥青混合料平均应变基准值,进而比对不同种类沥青应变计准确度.
现阶段比较成熟的数字图像关联(digital image correlation,DIC)技术为解决这一问题提供了思路.该方法发轫于光学力学测量[10],广泛应用于试验力学和断裂力学领域.DIC技术通过比较变形前后的两幅数字图像,直接获取被测物体表面不同位置位移和应变信息.一般条件下,DIC技术位移测量误差小于0.01像素或10-4 mm,理论应变测量误差小于10-7[11],能够满足比对沥青应变计测量准确度的要求.并且沥青混合料表面黑色的沥青胶浆与白色的集料断面对比鲜明,形成天然散斑点,容易被DIC技术捕捉.最后在获取被测物表面不同位置的位移和应变的基础上,可以通过建立一定算法求解平均应变,减少混合料不均匀对测量结果的影响.因此本文拟依托DIC技术建立完整沥青混合料平均应变基准值算法(下文简称DIC法), 进而对该方法进行误差分析.最后使用DIC法作为平均应变基准值,比对两款常用沥青应变计的测量准确度.
1 DIC法测量原理 1.1 DIC技术概述DIC技术是目前图像位移/应变测量的主流技术之一,其原理如下:首先从变形前图像中选择以待测点Q(x, y)为中心,以(2n+1)个像素为边长的正方形区域作为图像子区,用f(x, y)表示.发生变形后,以待测点附近每个像素点为中心,建立与图像子区相同大小的区域,称之为变形子区.
为了寻找目标子区g(x′, y′) (即图像子区形成的变形子区,设中心为Q′,如图 1所示),根据已有研究成果的推荐[12],使用“零均值归一化平方距离和”法逐个计算图像子区和不同变形子区的相关系数.相关系数最高的变形子区所在位置即为目标子区,进而实现像素级的目标子区定位.其表达式如公式(1)所示.
| $ \begin{array}{l} c = \sum\limits_{i = 1}^m {\left( {\left( {f\left( {{x_i},{y_i}} \right) - {f_{\rm{m}}}} \right)\left( {g\left( {{{x'}_i},{{y'}_i}} \right) - {g_{\rm{m}}}} \right)} \right.} /\\ \;\;\;\;\;\left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {f\left( {{x_i},{y_i}} \right) - {f_{\rm{m}}}} \right)}^2}} } \cdot } \right.\\ \;\;\;\;\;\left. {\left. {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {g\left( {{{x'}_i},{{y'}_i}} \right) - {g_{\rm{m}}}} \right)}^2}} } } \right)} \right) \end{array} $ | (1) |

|
图 1 图像子区与目标子区示意图 Fig.1 Image sub-region and target sub-region |
式中:fm、gm分别为图像子区、变形子区灰度均值.
实际测量过程中,这种像素级定位不能满足需要,因此需引入亚像素级定位算法.本文选用Newton-Raphson(N-R)算法,其核心思路如下:对待测点Q(x, y)变形后的坐标(x′, y′)进行泰勒级数一阶展开,如公式(2)所示.
| $ \left\{ \begin{array}{l} x' = x + u + \frac{{\partial u}}{{\partial x}}x + \frac{{\partial u}}{{\partial y}}y\\ y' = y + v + \frac{{\partial v}}{{\partial x}}x + \frac{{\partial v}}{{\partial y}}y \end{array} \right. $ | (2) |
式中:u、v分别为Q点的位移分量;
| $ \nabla c = 0 $ | (3) |
| $ \begin{array}{*{20}{c}} {\nabla c\left( {{p^{k + 1}}} \right) = \nabla c\left( {{p^k}} \right) + \nabla \nabla c\left( {{p^k}} \right)\left( {{p^{k + 1}} - {p^k}} \right)}\\ {{p^{k + 1}} = {p^k} - \frac{{\nabla c\left( {{p^k}} \right)}}{{\nabla \nabla c\left( {{p^k}} \right)}}} \end{array} $ | (4) |
解得p1~p6后,即可实现亚像素级定位.该方法误差较小、比较稳定[13],并且可以在图像发生小规模抖动时正常工作.为了降低镜头畸变引发的测量误差,拍摄过程中可依据王助贫[14]研究成果修正镜头畸变对测量结果产生的影响.
1.2 基于二次曲线拟合的平均应变求解算法在实现被测试件表面亚像素级位移场识别的基础上,尚需解决沥青混合料平均应变求解算法.设应变计标距为l0,距离梁底部的距离为h,梁表面相同高度存在一长度为l0的虚拟线段.设线段变形后长度为l1,挠曲线为f(x),对f(x)在区间(x1, x2)上求定积分可得l1的曲线长度,如公式(5)所示.再依平均应变定义式可求解平均应变,如公式(6)所示.
| $ {l_1} = \int_{{x_1}}^{{x_2}} {\sqrt {1 + f'{{\left( x \right)}^2}} {\rm{d}}x} $ | (5) |
| $ \varepsilon = \left( {{l_1} - {l_0}} \right)/{l_0} $ | (6) |
由于沥青混合料为典型的黏弹性材料,变形后挠曲线f(x)形状未知,因此本文使用一般二次曲线表示隐函数f(x),如公式(7)所示.但是在进一步拟合f(x)的过程中,由于混合料表面高度不均匀、局部应变变化剧烈,使用常规最小二乘拟合法效果较差(拟合参数受个别应变畸变点影响过大),有必要进行一定的改进.
| $ A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0 $ | (7) |
一般认为二次曲线拟合的核心问题在于依据一定目标函数I,求解公式(7)中A~F等6个未知数,使得该二次曲线对所有已知点满足目标函数I=Imin[15].根据这一方法,取目标函数I如公式(8)所示,其中(xi, yi)代表线段变形后各点所在位置.为了求解Imin,令A=1并对公式(8)求偏导数,可得方程组(9),求解方程组(9)可得1组A~F解.
| $ I = \sum\limits_{i = 1}^n {Q{{\left( {{x_i},{y_i}} \right)}^2}} $ | (8) |
| $ \frac{{\partial I}}{{\partial K}} = 0 $ | (9) |
式中:K分别代表B、C、D、E、F.同理可分别令B, C, D, E, F =1,得出5组A~F的解,每一组解都对应一条二次曲线.最终待求曲线可表示为这6组解的线性组合.权重确定方法如下:
| $ {I_i} = \sum\limits_{j = 1}^n {\left( {{A_i}x_j^2 + {B_i}{x_j}{y_j} + {C_i}y_j^2 + {D_i}{x_j} + {E_i}{y_j} + {F_i}} \right)} $ | (10) |
| $ S = {\left[ {\sum\limits_{i = 1}^5 {{\alpha _i}{I_i}} + \left( {1 - \sum\limits_{i = 1}^5 {{\alpha _i}} } \right) + {I_6}} \right]^2} $ | (11) |
式中:S为Ii的线性组合;αi(i=1, 2, 3, 4, 5, 6)为所求权重.
对S求偏导数可得
| $ \frac{{\partial S}}{{\partial {\alpha _i}\left( {i = 1,2,3,4,5} \right)}} = 0 $ | (12) |
| $ {\alpha _6} = 1 - \sum\limits_1^5 {{\alpha _i}} $ | (13) |
将公式(12)及(13)联立,可求解αi(i=1, 2, 3, 4, 5, 6)的值.最终二次曲线的A~F等6个系数,可由公式(14)决定.
| $ \begin{array}{*{20}{c}} {A = \sum\limits_{i = 1}^6 {{\alpha _i}{A_i}} }&{B = \sum\limits_{i = 1}^6 {{\alpha _i}{B_i}} }&{C = \sum\limits_{i = 1}^6 {{\alpha _i}{C_i}} }\\ {D = \sum\limits_{i = 1}^6 {{\alpha _i}{D_i}} }&{E = \sum\limits_{i = 1}^6 {{\alpha _i}{E_i}} }&{F = \sum\limits_{i = 1}^6 {{\alpha _i}{F_i}} } \end{array} $ | (14) |
解得二次曲线的参数后,代入公式(5)、(6)即可求解出沥青混合料平均应变,用于比对不同应变计测量准确度.以上即本文构建的DIC法.
2 DIC法误差分析DIC技术理论测量误差很小,但二次曲线拟合算法尚未经误差分析,因此有必要进行这一工作.
首先应确定应变测量的误差上限.根据以往研究者对78只相同沥青应变计测量结果的统计[16],在相同荷载下,90%的应变计测量标准偏差低于12×10-6.而一般认为,用于校准应变计的测量方法与基准值间的误差至少不大于应变计测量结果的标准偏差(否则无法起到校准作用[17]),因此在进行误差分析时,将12×10-6作为DIC法测量误差的上限.
然后使用应变片法获取平均应变基准值,分析DIC法的测量误差.选择Q235型钢材制成小梁试件,进行四点加载试验.将应变片粘贴于小梁底面中心位置,其敏感栅长为30 mm(即测量30 mm内的平均应变),测量误差小于1×10-6.由于Q235型钢材符合均匀物体假设,应变片可以准确测量敏感栅范围内的平均应变,因此能够使用应变片的测量结果作为基准值,分析DIC法的平均应变测量误差.在约35 s的采样过程中,DIC法共获得1 109个有效数据点.两种测量方法的误差分析如表 1所示, 测量结果对比如图 2所示.
| 下载CSV 表 1 测量误差分析结果 Tab.1 Results of test error analysis |

|
图 2 DIC法与应变片法测量结果 Fig.2 Comparison of the results of DIC method and strain gauge method |
依据统计学原理,由于样本满足数据量大、测量误差正态分布性良好(Sig值大于0.05)的条件,可以使用t分布来确定DIC法的测量误差是否超过预定误差上限, 计算应变误差的置信区间.当使用t分布时,一定置信水平α下的拒绝域和单侧置信区间如公式(15)、(16)所示.
| $ \left( {\frac{S}{{\sqrt n }}{t_\alpha }\left( {n - 1} \right), + \infty } \right) $ | (15) |
| $ \min \left( {0,\bar x - \frac{S}{{\sqrt n }}{t_\alpha }\left( {n - 1} \right),\bar x + \frac{S}{{\sqrt n }}{t_\alpha }\left( {n - 1} \right)} \right) $ | (16) |
当α=95%时,待检验假设为测量误差≤12×10-6,拒绝域为t∈(1.68, +∞),而样本t检验量为-47.0.待检验假设成立,置信区间为(0, 3.31+8.04×10-6).因此可以认为本文方法比较可靠,满足比对沥青应变计准确度的需求.
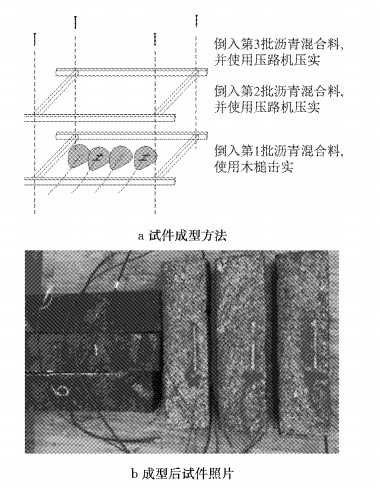
3 基于DIC法的测量准确度比对 3.1 应变计试件制备本文使用DIC法获取的平均应变作为基准值比对某两款常用沥青应变计的测量准确度,以验证准确度比对方法的合理性.为了模拟应变计在真实路面的使用状态,设计双层压实法成型试件以保证试件压实度.在成型过程中采用手扶压路机对沥青混合料两次压实,具体方法如图 3a所示.考虑到应变计所在位置对测量结果具有较大影响,因此采用Seo等[18]根据374只应变计总结出的成熟安装方法安装应变计.即事先刻槽,然后填入沥青以固定应变计水平、垂直方向位置.成型结束后,切去部分沥青混合料测定压实度,其密度为相同条件下马歇尔试件密度的94%,基本满足应变计所在的下面层压实度要求[19].沥青混合料冷却后,将模具取下,切割成450 mm×100 mm×120 mm的大梁试件.每种应变计有3个平行试件,成型后的试件如图 3b所示.依据产品使用说明,A、B类应变计的标称分辨率均为5×10-6.
|
图 3 沥青应变计试件成型方法及部分成型后试件 Fig.3 Schematic of asphalt gage specimen molding method |
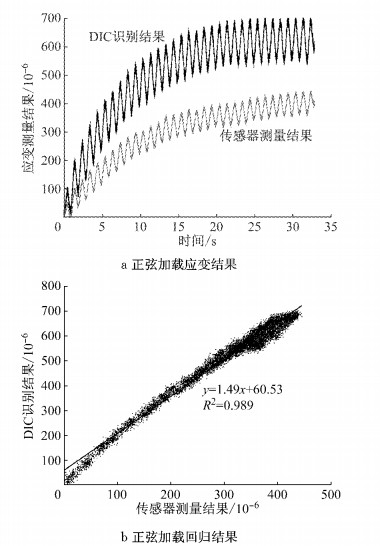
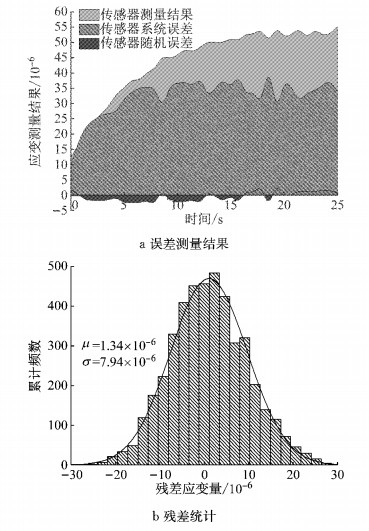
使用四点加载方式对试件分别施加1 Hz的正弦荷载和四级逐级荷载,记录应变计测量结果,同时使用DIC法测量试件表面应变计所在位置的平均应变基准值.在两种荷载作用下,A-1试件的DIC法测量结果和应变计测量结果分别如图 4a、图 5a所示.随后以DIC法应变基准值εDIC为因变量,应变计测量结果εsensor为自变量进行线性回归,获得应变计校准方程.两种荷载下该试件的回归结果、校准方程如图 4b、图 5b所示.此外在误差分析过程中,可将εDIC分解为应变计测量结果εsensor、系统误差εsystem、随机误差εrandom之和,如公式(17)所示.其中εsystem代表可通过校准方程进行补偿的误差,εrandom代表无法消除的残余误差.A-1试件正弦荷载过程中两类误差如图 6所示.
| $ {\varepsilon _{{\rm{DIC}}}} = {\varepsilon _{{\rm{sensor}}}} + {\varepsilon _{{\rm{system}}}} + {\varepsilon _{{\rm{random}}}} $ | (17) |
|
图 4 正弦加载测量结果对比及回归方程 Fig.4 Comparison of measured results and revised equation at sinusoidal load |

|
图 5 逐级加载测量结果对比及回归方程 Fig.5 Comparison of measured results and revised equation at step load |
|
图 6 随机误差、系统误差示意图 Fig.6 Random error and system error |
由图 4a、图 5a可以发现,随着荷载反复作用,沥青混合料的累积塑性应变会占总应变相当大比例.因此在进行误差分析时,应考虑去除累计塑性应变的影响.对于正弦荷载以某次荷载作用下应变峰值和应变谷值之差,即应变波动范围反映由该次荷载引发的弹性应变.对于逐级荷载以本级加载中最大应变与最小应变之差反映弹性应变.此外本文也对经校准方程校准后的测量结果进行误差分析.各试件误差分析结果如表 2所示,其中μ、μ′、σ、σ′、R2、μcalibrated、VC分别代表测量误差均值、弹性应变测量误差均值、测量误差标准差、弹性应变测量误差标准差、测量值与基准值相关系数、校准方程校准后的测量误差均值、测量误差变异系数.
| 下载CSV 表 2 应变计试件测量误差分析结果 Tab.2 Measurement error analysis of sensor sample |
仅就已有测量结果,可得以下初步结论:
(1) 两种应变计测量结果均明显小于DIC法获得的平均应变基准值,推测与应变计与混合料变形不协调有关.由于应变计的弹性模量远大于沥青混合料,导致测量结果明显偏小.
(2) 荷载模式对传感器的测量准确度有一定影响,以A-1传感器为例,在正弦荷载作用下的测量误差和标准差都小于逐级荷载作用下的测量误差和标准差,推测与逐级荷载作用次数较少,变形不充分有关.
(3) 综合考虑两种荷载,B型应变计的测量误差均值小于A型应变计测量误差均值,相差11.7%,表明B型应变计测量结果更接近DIC法获取的基准值,具有更高的测量准确度.
(4) 在提取应变波动范围以消除累计塑性应变的影响后,两种应变计的测量准确度均得到一定程度的提高,测量结果与基准值之间的差异缩小(μ>μ′).综合考虑两种荷载,B型应变计μ′值依然小于A型应变计μ′值,二者相差约9.6%,进一步证明B型传感器的准确度更高.但根据变异系数计算结果,同种传感器个体之间差异性并无明显区别.
(5) 应变计测量结果与DIC法获得平均应变基准值呈显著线性关系(R2>0.9),因此可以通过建立线性校准方程的方法提高测量精度.依据公式(17)及修正方程可计算εsystem与εrandom.由图(6)可知A-1试件加载10个循环之后εsystem基本保持稳定,达300× 10-6. 当使用线性校准方程校准后,测量误差大幅度降低,μcalibrated均值仅为1.34×10-6.排除εsystem后εrandom基本服从正态分布,证明修正方程效果良好.
综上,依据测量准确度的定义可以初步推断B型应变计测量准确度好于A型应变计,表明本文提出的方法基本满足比对应变计测量准确度的需求,达到预期目的.
4 结论本文在DIC技术的基础上,开发基于二次曲线拟合的平均应变计算方法,进而构建沥青应变计准确度比对方法.具体结论如下:
(1) 使用基于二次曲线拟合的应变算法之后,能够求解沥青混合料表面平均应变,基本消除由于沥青混合料变形不均匀带来的不利影响.
(2) 使用应变片对DIC法进行误差分析,可知其测量误差基本服从正态分布,有不低于95%的置信度认定测量误差上限小于沥青应变计测量结果的标准偏差12×10-6.
(3) 通过比较应变计测量结果与DIC法获得应变基准值之间的测量误差,可以比较测量沥青混合料梁底应变时不同应变计测量准确度的优劣,比对方法可以实现预定的目的.
(4) 沥青混合料累积塑性应变会对应变计测量准确度产生影响,消除其影响有利于提高测量应变计测量准确度.
(5) 采用线性校准方程对应变计测量结果进行校准能够显著提高应变计的测量准确度,并且εrandom呈现明显正态分布.在未来研究中,应当考虑不同加载模式对校准方程的影响.
| [1] |
STOFFELS S M, SOLAIMANIAN M, MORIAN D, et al. Field instrumentation and testing data from Pennsylvania's super pave in-situ stress strain investigation[C]// Proceedings of the 2006 Airfield and Highway Pavement Specialty Conference. Reston: ASCE, 2006: 107-118.
|
| [2] |
TIMM D, PRIEST A. Dynamic pavement response data collection and processing at the NCAT test track[R]. Auburn: Auburn University, 2004.
|
| [3] |
国家质量监督检验检疫总局计量司.通用计量术语及定义: 2011-1001-JJF[S].北京: 国家质量监督检验检疫总局, 2011. Department of Metrology, General Administration of Quality Supervision, Inspection & Quarantine. General metrological terms and definitions: 2011-1001-JJF[S]. Beijing: State Administration of Quality Supervision, Inspection and Quarantine, 2011. |
| [4] |
谭忆秋, 董泽蛟, 田庚亮, 等. 光纤光栅传感器与沥青混合料协同变形评价方法[J]. 土木建筑与环境工程, 2009, 31(2): 100 TAN Yiqiu, DONG Zejiao, TIAN Gengliang, et al. Evaluating method of the coordination deformation between asphalt mixture and fiber bragg grating sensor[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(2): 100 |
| [5] |
WILLIS J, TIMM D. Repeatability of asphalt strain measurements under falling weight deflectometer loading[J]. Transportation Research Record: Journal of the Transportation Research Board, 2009(2094): 3 |
| [6] |
庄传仪, 王林, 叶亚丽. 动应变传感器标定方法及与沥青混合料协同变形评价研究[J]. 公路, 2014, 59(4): 179 ZHUANG Chuanyi, WANG Lin, YE Yali. Calibration and evaluation method of synchronized collaborative deformation between asphalt mixture and asphalt strain gauges[J]. Highway, 2014, 59(4): 179 DOI:10.3969/j.issn.1671-8879.2014.04.028 |
| [7] |
吴璨.机场道面状态感知系统构建方法[D].上海: 同济大学, 2014. WU Can. Construction method of pavement condition monitoring system[D]. Shanghai: Tongji University, 2014. |
| [8] |
WISTUBA M, JACQUES P. Comparative strain measurement in bituminous layers with the use of ALT[C]// International Conference on Accelerated Pavement Testing. Minneapolis: University of Minnesota, 2004: 119-125.
|
| [9] |
尚春. 传感器技术及应用[M]. 北京: 北京航空航天大学出版社, 2004 SHANG Chun. Sensor technology and application[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2004 |
| [10] |
BRUCK H, MCNEILL S, SUTTON M, et al. Digital image correlation using Newton-Raphson method of partial differential correction[J]. Experimental Mechanics, 1989, 29(3): 261 DOI:10.1007/BF02321405 |
| [11] |
PAN B, ABEL J, RICCI M S, et al. Comparative oxidation studies of methionine residues reflect a structural effect on chemical kinetics in rhG-CSF[J]. Biochemistry, 2006, 45(51): 15430 DOI:10.1021/bi061855c |
| [12] |
ZHANG Z. Parameter estimation techniques: a tutorial with application to conic fitting[J]. Image and Vision Computing, 1997, 15(1): 59 DOI:10.1016/S0262-8856(96)01112-2 |
| [13] |
ALBERTO G. Probability, statistics, and random processes for electrical engineering[M]. 3rd ed. Upper Saddle River: Pearson/Prentice Hall, 2008
|
| [14] |
王助贫.三轴试验土样变形的数字图像测量方法及其应用[D].大连: 大连理工大学, 2001. WANG Zhupin. Digital image measuring method for deformation of soil samples in three axis test and its application[D]. Dalian: Dalian University of Technology, 2001. http://cdmd.cnki.com.cn/article/cdmd-10141-2002112536.htm |
| [15] |
TAUBIN G. Estimation of planar curves, surfaces, and nonplanar space curves defined by implicit equations with applications to edge and range image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(11): 1115 DOI:10.1109/34.103273 |
| [16] |
WILLIS J R, TIMM D H. Repeatability of asphalt strain measurements under full-scale dynamic loading[J]. Journal of the Transportation Research Board, 2008(2087): 40 |
| [17] |
WENG J, COHEN P, HERNIOU M. Camera calibration with distortion models and accuracy evaluation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(10): 965 DOI:10.1109/34.159901 |
| [18] |
SEO Y, LEE J H. Short-and long-term evaluation of asphalt concrete strain gauge installation methods applied to the KHCTR[J]. Journal of Transportation Engineering, 2011, 138(6): 690 |
| [19] |
交通部公路科学研究所.公路沥青路面施工技术规范: JTG-F40—2004[S].北京: 人民交通出版社, 2004. Institute of Highway Science, Ministry of Communications. Technical specifications for construction of highway asphalt pavement: JTG-F40—2004[S]. Beijing: People's Transportation Press, 2004. |
 2018, Vol. 46
2018, Vol. 46

