2. 大连海事大学 战略管理与系统规划研究所,辽宁 大连 116026
2. Institute of Strategy Management and System Planning, Dalian Maritime University, Dalian 116026, China
国际贸易量的快速增长和集装箱船舶的大型化趋势,对集装箱码头的集港效率和服务能力提出了更高的要求.一方面,大型集装箱船挂靠的码头作业量和作业强度增大,另一方面,大量送箱集卡高峰时间集中在集装箱码头闸口及堆场排队等待作业,消耗了大量的能源,排放了大量的CO2及污染气体,迫切需要应对和解决.服务于集港作业的送箱集卡调度一直是集装箱码头集港作业流程的关键环节,合理优化送箱集卡调度方案对提高车辆资源配置效率、节约能耗、减少碳排放等有直接的影响.目前有关集卡调度的研究多集中于港口码头内集卡的研究,对港外集卡进港提送箱作业的相关研究较少.相对于港口码头内集卡而言,外集卡服务多个码头且运输距离更远,码头调度方案对其等待时间的影响更大,同时由于外集卡资源数量也同样有限,其等待时间过长势必将降低集卡整体周转效率.由于大型集装箱船舶对挂靠港口的停泊时间有严格要求,码头集港时间较短,且集港量大;同时集装箱码头往往服务的航线多、挂靠的船舶多,使得码头作业高峰期有大量集卡在同一时段到达港口进行操作,容易使码头闸口、堆场和作业线路的内外集卡产生排队、拥堵等诸多问题.这一方面是对码头及堆场核心资源的浪费,另一方面也增加了集卡在等待过程中的能耗及CO2排放,提高了运营成本.针对这些问题,一些港口从建立码头预约机制着手,尝试使送箱集卡在可控的规定预约时段内到港,以缓解作业高峰时段码头集卡的拥堵问题,降低堆场码头作业能耗,减少其总碳排放量,提高码头的服务效率和质量.
从1999年加拿大温哥华首先实施预约集港以来,长滩、洛杉矶、新加坡和天津等港口引入了集卡预约系统.一些学者针对预约集港及预约机制下送箱集卡调度进行了研究.曾庆成等[1]利用Baskett-Chandy-Muntz-Palacios排队网络优化了每个时段的预约份额,其可以有效地减少集卡在码头的周转时间,较好地处理到达过程不平稳的排队问题.Namboothiria等[2]以降低车队运输成本为目标构建了集卡调度模型,研究集卡预约系统对提高周转效率的影响.蒋美仙等[3]提出了基于Poisson过程的港口码头集卡预约调度模型,根据到港船舶船期表和预出口集装箱数目, 模型对每艘到港船舶进行了预约时间段和各时间段计划预约集装箱数量分配.Huynh等[4]模拟了集卡在堆场的作业过程,利用数学模型求解了每个时间段最多可接受的预约份额.邵乾虔等[5]构建了码头集疏港联动预约模式,以时间残值矩阵为核心的线性仿真数学模型验证了联动预约模式的有效性.许巧莉等[6]研究了非平稳到达情况下的集卡预约优化问题.Guan等[7]基于M/Ek/c排队模型(顾客到达间隔时间分布为M负指数分布,Ek表示服务时间分布为k阶爱尔兰分布,服务台数目为c)建立了集卡预约优化模型.Chen等[8]建立了预约机制下集卡服务非稳态排队模型,在此基础上设计了包括集卡到达优化、拥堵收费设计的两阶段码头外部集卡管理方法.此外,曾庆成等[9]研究了集装箱码头装卸过程中集卡调度问题,建立了集卡调度动态模型,应用Q学习算法(Q-learning algorithm,一种强化学习算法)进行了求解.丁一等[10]以桥吊调度计划为依据,通过给定轮胎吊和集卡关联任务集与作业要求时间,研究了轮胎吊集卡的调度问题特性.Phan等[11]、Zhang等[12]及Chen等[13]对具有能源约束、集卡到达时间、时间窗限制的集装箱码头集卡调度优化问题进行了分析求解.综上,目前的相关研究多是对单一外堆场与单一码头间的集卡调度问题,而现实中的港外堆场服务能力较强,一般同时为多个码头执行集港服务.本文在考虑堆场、码头节能减排发展要求的基础上,从碳排放和预约机制的视角出发,对单一港外堆场服务多码头的送箱集卡调度问题进行研究,通过合理安排堆场集卡的送箱作业顺序,降低调用集卡数量,提高集卡作业效率,减少其在码头的作业等待时间,从而降低集卡多码头调度作业CO2总排放量,提升堆场与码头的协作水平.
1 送箱集卡调度模型 1.1 问题描述在传统集装箱码头针对远洋运输的集港业务流程中,船方会在船舶到港前一段时间(如前96 h)向码头预报船期,并在船舶到港前24 h还会有船期确报,集装箱码头根据船期以及码头的出口箱量、码头闸口和场内机械的作业效率确定每条船舶的集港时间.港外堆场根据各码头公布的各集装箱对应船舶的集港时间、对应码头的集港箱量大小、集港时间紧迫程度等信息,考虑自身的运力配置情况,制定集卡调度方案将集装箱运抵集装箱码头.
由于船舶集中到达、码头场桥和岸桥等核心调度资源能力不足、码头闸口拥挤等原因,这种传统的集卡调度方案容易产生集卡资源过度占用,在码头闸口、港内堆场等待时间过长等问题,因此传统集卡调度在制定方案时需要堆场保持一定数量的集卡来应付各种突发需求.由于堆场集卡保有量较高,集卡在作业过程中怠速等待时间过长,导致车辆能耗及CO2总排放量较高大,堆场运营成本较高.
依托现代信息和网络通信技术有效建立码头和堆场之间的联系.集装箱码头根据船期以及码头的出口箱量、码头闸口和场内机械的作业效率确定每条船舶的集港时间.码头将集港时间平均分成若干时间间隔相同的预约时段.堆场根据自身运力情况选择合适的预约时段,并给出该时段的集港箱量.码头经过平衡确定最终的集港计划,并通知各个堆场,堆场按照具体的集港计划来安排自身运力并进行集港工作.
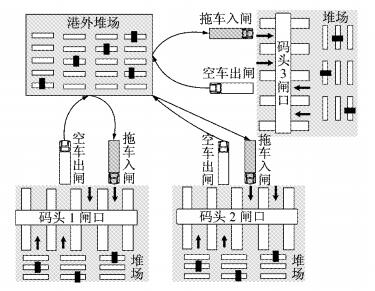
图 1显示了单一港外堆场向多个集装箱码头的送箱集卡作业流程.在码头预约机制下,为了让集卡可以在其所预约时段到达闸口,码头需要保证一定长度的预约时段.码头一般将24 h划分为12个预约时段(每时段2 h),每个时段码头给各个堆场一定的预约份额,堆场可根据各个码头的集港计划以及自身实时运力情况选择预约时段.码头根据各堆场所提交的预约时段及相应预约箱量确定最终的堆场集港计划.堆场按照最终的码头集港计划制定集卡调度计划方案.
|
图 1 单港外堆场对多码头的送箱集卡作业流程示意图 Fig.1 Operation flow of delivery trucks from single outside yard to multi-terminal |
由于码头在预约时段内的集卡预约份额是有限的,码头不允许堆场在全天12个时段均申请集港作业.在预约机制下各码头提前通知堆场其船舶集港计划(一般提前24 h),码头会按照计划为堆场分配相应的送箱时间窗(即可接受其集港的预约时段区间).堆场与码头最终确定集港作业计划.一般船舶在本港的装箱量决定了码头的集港箱量,不同码头船舶的出口箱集港时间对堆场而言可能在预约时段上有所重叠,在该时间窗内堆场运抵码头的集装箱数量必须满足码头集港计划要求.因此本文研究的是在堆场现有集卡资源基础上,在码头预约机制下,单一港外堆场向多集装箱码头的送箱集卡调度的优化问题,满足码头预约时段有限集卡预约份额要求,使堆场最终调用的集卡数量最少的同时节约能耗,减少集卡调度方案中CO2的总排放量,提高堆场的运营效率和效益.
1.2 问题假设(1) 预约机制下码头将每天划分为12个预约时段(每时段2h),各码头时段划分一致.
(2) 预约机制下堆场所调用集卡从1时段0时刻开始计时,其作业时间主要包括装卸箱时间、运输时间、等待时间.在堆场的装箱时间主要由其场桥决定,一般取平均值;码头内卸箱时间及运输时间可统一为码头的集卡操作时间,一般取平均值,各码头操作时间各异;运输时间与堆场和码头间的距离直接相关;等待时间包括堆场等待时间、码头等待时间及闸口排队时间,堆场及码头的等待时间与集卡调度方案有关,码头闸口排队等待时间与码头相关,各码头一般根据其情况取平均值.
(3) 假设多集装箱码头所需要的总箱量一定,集卡从单一堆场对多码头进行送箱作业时其总的路程是不变的,但不同优化方案的码头作业顺序会对堆场集卡调用数量以及由于怠速等待运行造成的碳排放量有直接的影响.
(4) 集卡从堆场出发时仅能装载一个集装箱,在相应码头完成卸箱操作后应返回始发堆场等待继续调度,集卡在码头等待及装卸箱作业时怠速运行,在堆场等待调度时无能耗.
(5) 堆场集卡型号相同,行驶速度、油耗等性能相同,可在一个预约时段内多次往返堆场码头完成集港任务.
(6) 在预约机制下,集卡能准时到达集港作业计划码头,不考虑其他干扰因素对集卡的影响.
(7) 预约机制下,码头会为堆场分配集港时间窗,时间窗所包括的预约时段和预约份额由码头给定,码头堆场共同制定集港作业计划后,堆场出口集装箱必须在码头集港时间窗内到达港口.
1.3 模型建立目标函数分为两部分,K0表示堆场所调用集卡数量,E表示相应集卡调度方案的总CO2排放量.目标函数如下:
| $ \min \left\{ \begin{array}{l} {K_0} = \max \left\{ {\mathop \sum \limits_{k \in K} {y_{i, k}}} \right\}\\ E = \left( {\mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} \mathop \sum \limits_{n \in N} \mathop \sum \limits_{k \in K} {y_{ijn, k}}({t_{j2}} + {t_{j3}} + {t_{ijn2, k}}) \cdot } \right.\\ \;\;\;\;\;\;{c_{il}} + {D_j}({c_{hl}} + {c_{ll}}){e_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} \end{array} \right. $ | (1) |
式中:i为预约时段,将24 h决策期等分为I个预约时段, i=1, 2, …, I;j为集装箱码头编号,j=1, 2, …, J;n为集卡在某一时段的第n次送箱,n=1, 2, …, N;k为堆场集卡编号,k=1, 2, …, K;yi, k为决策变量,表示集卡k在预约时段i是否参与过送箱,若是则其值为1,否则为0;yijn, k为决策变量,若集卡k在i时段的第n次送箱至码头j,则yijn, k=1,否则yijn, k=0;tj2为集卡在码头j闸口的平均等待时间;tj3为集卡在码头j的平均操作时间;tijn2, k为集卡k在i时段第n次送箱到达码头j后,在码头的等待时间;cil为集卡的怠速油耗,L·min-1;Dj为堆场到码头j的距离,km;chl为集卡重载油耗,为L·km-1;cll为集卡轻载油耗,L·km-1;eCO2为燃油CO2排放系数,kg·L-1.
目标函数计算时应首先确定各时段堆场调用的集卡数量,再从中取最大值作为堆场总集卡调用量,取其最大值堆场能保证每个时段各个码头的送箱要求都能得到满足,且未调用集卡可在堆场熄火等待,减少碳排放.其相应集卡调度方案总的碳排放量与集卡调度方案中集卡行驶距离、作业及怠速等待时间直接相关,目标函数优化目标是使两个目标都尽可能达到最优,保证最终的优化调度方案较少占用堆场集卡,减少总碳排放量.
约束条件表示如下:
(1) 数量约束
| $ \mathop \sum \limits_{i \in I} {x_{ij}} = {Q_j}, \;\;\forall j = 1, 2, \cdots , J $ | (2) |
| $ {x_{ij}} = \mathop \sum \limits_{k \in K} \mathop \sum \limits_{n \in N} {y_{ijn, k}}, \;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J $ | (3) |
| $ {x_{ij}} \le {h_{ij}}, \;\forall i = 1, 2, \cdots , I, \;\forall j = 1, 2, \cdots , J $ | (4) |
| $ \begin{array}{l} {y_{ijn, k}} \in \left\{ {0, 1} \right\}, \forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (5) |
| $ {y_{i, k}} \in \left\{ {0, 1} \right\}, \forall i = 1, 2, \cdots , I, \forall k = 1, 2, \cdots , K $ | (6) |
式(2)~(6)中:xij为堆场在预约时段i送达码头j的箱量;Qj为码头j需要的集港总箱量;hij为预约时段i码头j允许堆场运送的最大送箱量.
式(2)表示在码头j的预约送箱时间窗内,堆场各时段总的送箱量应满足码头j的要求.式(3)表示i预约时段下从堆场送往码头j的总箱量.式(4)表示预约时段i内堆场到码头j的送箱量要满足其在该时段内最大送箱量的约束.式(5)、(6)为决策变量属性.
(2) 时间约束
| $ \begin{array}{l} {T_{ijn, k}} = {T_{idn, k}} + {t_{j1}}\\ \;\;\;\;\;\;\;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (7) |
| $ \begin{array}{l} {T_{irn, k}} = {T_{ijn, k}} + {t_{j2}} + {t_{j3}} + {t_{j1}}\\ \;\;\;\;\;\;\;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (8) |
| $ \begin{array}{l} {T_{id1, k}} = {T_{\left( {i - 1} \right)rn, k}} + {t_{ij11, k}} + {t_0}\\ \;\;\;\;\;\;\;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (9) |
| $ \begin{array}{l} {T_{idn, k}} = {T_{ir\left( {n - 1} \right), k}} + {t_{ijn1, k}} + {t_0}\\ \;\;\;\;\;\;\;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (10) |
| $ \begin{array}{l} {T_{\rm{s}}} + \left( {i - 1} \right)L \le {T_{ijn, k}} \le {T_{\rm{s}}} + iL\\ \;\;\;\;\;\;\forall i = 1, 2, \cdots , I, \forall j = 1, 2, \cdots , J, \\ \;\;\;\;\;\;\forall n = 1, 2, \cdots , N, \forall k = 1, 2, \cdots , K \end{array} $ | (11) |
式(7)~(11)中:Tijn, k为集卡k在i时段第n次送箱至码头j的时刻,若Tijn, k处于时段i,则Tidn, k, Tirn, k计入时段i而不考虑其实际所处时段;Tidn, k为集卡k在i时段第n次离开堆场的时刻;Tirn, k为集卡k在i时段第n次返回堆场的时刻;tj1为集卡从堆场到码头j的行驶时间;t0为集卡在堆场的装箱时间,min;L为每个预约时段长度,min;Ts为第一个预约时段开始时刻;tijn1, k为集卡k在i时段第n次送箱至码头j前,在堆场的等待时间.
式(7)表示集卡k第i时段第n次送箱到达码头j的时刻.式(8)表示集卡k第i时段第n次回到堆场的时刻.式(9)表示集卡在第i时段第1次送箱离开堆场的时刻,式中T(i-1)rn, k表示集卡k在第i-1时段最后一次返回堆场的时刻,tij11, k表示集卡k第i时段第1次离开堆场前在堆场内的等待时间.式(10)表示集卡k第i时段第n(n≥2)次离开堆场送箱的时刻,式中Tir(n-1), k表示集卡k第i时段第n-1次送箱返回堆场的时刻.式(11)保证在预约时段i送往码头j的集装箱要满足其预约时段i的时间限制.模型中相关的数量及时间约束能保证堆场集卡在预约时间段内满足各个码头的送箱要求.
2 算法设计本文设计了改进的蚁群算法,采用人工蚂蚁来模拟堆场送箱集卡进行调度优化[14].在每次循环中,每只蚂蚁分别模拟K辆集卡,K即为本次循环中堆场所调用的集卡数量.在所设计算法中,状态转移规则和信息素更新规则是集卡调度模拟的2个重要的规则,直接决定了蚂蚁的搜索状态,结合集卡调度特点, 算法对其做了相应改进,以提高算法对最优方案的搜索效率,保证集卡作业顺序的合理性.
2.1 解的结构设计针对所构建集卡调度模型的特点,本文首先在基本蚁群算法中加入时间窗和分割配送的设计[15].时间窗设置能使蚂蚁有效地判别码头不同预约时段内的送箱需求,进而合理安排最适合的集卡执行相应配送.与车辆路径问题及旅行商问题等不同,在集卡调度问题中车辆往往需要在堆场和各集装箱码头间执行多行程反复配送,因此结合其多行程的调度特点,算法引入了分割配送设计,当蚂蚁在时间窗和运量约束下完成第1辆集卡调度后,从其开始的预约时段对第2辆集卡进行模拟直到所有任务都被完成,以每辆集卡的路径串序列代表部分解方案,所有蚂蚁所模拟集卡路径及时间过程即为完整的求解方案.
改进的蚁群算法初始解路径串由集卡编号、预约时段、送箱序数、送箱码头、前一次送箱完成后返回堆场时刻、堆场等待时间等元素组成,例如(1, 1, 1, 3, 0, 0)→(1, 2, 1, 1, 15, 5)→(1, 2, 2, 4, 30, 0)表示1号集卡的全部调度过程,集卡从0开始,在等待0后进行第1时段的第1次送箱,送箱目标为码头3;返回堆场的时刻为15,等待5后执行第2时段的第1次送箱,送箱目标为码头1;再次返回堆场的时刻为30,等待0后进行第2时段的第2次送箱,送箱目标为码头4.集卡全部路径串即组成了港外堆场在多集装箱码头间的总调度方案.
2.2 信息素更新规则信息素更新规则主要包括集卡行驶后信息素更新时间及更新量.根据模型的特点,算法设定在所有蚂蚁均都遍历一次循环后更新信息素,对每只蚂蚁m,更新规则如下:
| $ {\tau _{ijn, k}}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _{ijn, k}}\left( t \right) + \Delta \tau \left( t \right){y_{ijn, k}} $ | (12) |
式中:τijn, k(t)表示第t次循环集卡k在i时段第n次送箱至码头j的信息素浓度.当蚂蚁完成了一次循环后,路径上的信息素会相应挥发,ρ表示信息素挥发系数.Δτ(t)表示第t次循环时所选定路径的信息素增加量,未选定路径信息素浓度在挥发后不相应增加,考虑到调度方案中集卡数量的重要性,算法将当前方案集卡调用数量引入信息素增加量计算,
算法在求解过程蚂蚁会根据道路上遗留的信息素按照概率来进行下一路段路径的选择,信息素浓度越高,路径被选中的概率越大.因此需要设定状态转移规则来计算路径被选中的概率,完成集卡路径的构造.在蚁群算法中,蚂蚁对于路径的选择主要是由信息素浓度和启发函数决定的,状态转移规则如式(13)所示.
| $ {p_{ijn, k}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\tau _{ijn, k}^a\left( t \right)\eta _{ijn, k}^\beta \left( t \right)}}{{\mathop \sum \limits_{j \in {J_{in, k}}} \tau _{ijn, k}^\alpha \left( t \right)\eta _{ijn, k}^\beta \left( t \right)}}, }&{j \in {J_{in, k}}}\\ {0, }&{j \notin {J_{in, k}}} \end{array}} \right. $ | (13) |
式中:pijn, k(t)表示第t次循环时集卡k在第i时段第n次前往码头j的概率;τijn, k(t)表示第t次循环时集卡k在第i时段第n次送箱前往码头j的路径上的信息素浓度;ηijn, k(t)表示第t次循环时集卡k在第i时段第n次送箱前往码头j的启发函数;α、β分别表示集卡调度过程中信息素浓度和启发函数的相对重要度;Jin, k表示集卡k第i时段第n次送箱所允许前往的码头集合.
2.3.1 启发函数的构造在基本蚁群算法中,启发函数主要与路段的路径长度有关,路径越短其被选中概率越高,由于本问题集卡送箱量是固定的,其送箱与否与路径长度无关,因此在构建启发函数时主要考虑集卡在堆场的等待时间,保证集卡能在各码头间高效周转.集卡相应的启发函数如式(14)、(15)所示.
| $ {\eta _{ijn, k}}\left( t \right) = {w_{ijn, k}} $ | (14) |
| $ {w_{ijn, k}} = 1 - \frac{{{t_{ijn1, k}}}}{{\mathop \sum \limits_{j \in {J_{in, k}}} {t_{ijn1, k}}}} + \varepsilon , \forall j \in {J_{in, k}} $ | (15) |
式(14)、(15)中:wijn, k表示集卡在选择下一前往的码头时能否被选中的概率,与其在堆场的等待时间tijn1, k直接相关,以有等待时间的集卡1和无等待时间的集卡2为例,由于tijn1, 1>0使wijn, 1 < 1,tijn1, 2=0使wijn, 2=1,因此集卡2被选中概率大于集卡1,tijn1, k越大,集卡被选中前往的概率越小;ε为一极小的正数; Jin, k表示蚂蚁k在第i时段第n次送箱时能到达,且满足时间窗及最大送箱量约束的码头集合.
2.3.2 禁忌表设计在满足堆场码头时间窗、预约时段码头最大预约份额以及码头总集港箱量约束下,集卡调度问题并不限制每辆集卡访问某码头的次数.码头禁忌表设计如下:设蚂蚁k在堆场空闲,可以接受任务.若Jin, k=Ø,则表明集卡k在第i时段的送箱任务全部完成;Jin, k≠Ø,则计算码头集合J中的转移概率pijn, k(t).
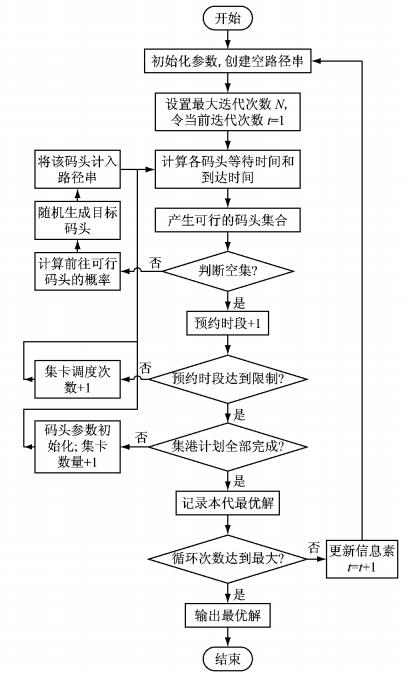
2.4 算法步骤改进的蚁群算法流程如图 2所示.
|
图 2 改进蚁群算法流程图 Fig.2 Modified ant colony algorithm procedure |
算法步骤如下:
Step 1 输入码头初始信息J、I,码头送箱时间窗[Tj, s, Tj, f],其中Tj, s和Tj, f分别表示码头开始接箱时间和码头终止接箱时间,Qj,hij,各时间信息t0、tj1、tj2、tj3,蚂蚁数量M,堆场集卡总量K;设置初始信息素浓度τijn, k(0)、Q、ρ,相对重要度α、β,最大迭代次数N;令当前循环次数t=1.
Step 2 令当前集卡数量km=1,i=1,n=1, xij= 0, qj=0, T1r0, k设置为第1预约时段开始时刻(qj表示码头j已完成的送箱量,km表示蚂蚁m模拟的集卡数量).
Step 3 计算集卡k在第i时段第n次前往码头j之前,在堆场的等待时间tijn1, k和到达码头j的时刻Tijn, k(假设每辆集卡都希望尽早到达码头),判定其可行性,即码头是否有集港需求,堆场在第i时段最大送箱量是否饱和,是否可以在时段i到达,是否有时间窗可以响应.遍历结束后,产生可行的码头集合Jin, k.若Jin, k=Ø,则转入Step 5;若Jin, k≠Ø,则转入Step 4.
Step 4 对Jin, k中的码头,按式(13)计算第t次循环蚂蚁m在第i时段第n次前往的码头j的概率,决定本次前往的码头,计算返回堆场的时刻Tirn, k,将该元素加入路径串序列.令yijn, k=1, n=n+1, xij=xij+1,qj=qj+1,记录蚂蚁m模拟集卡调度的解,返回Step 3.
Step 5 i=i+1.若i≤12,则令n=1,返回Step 3.若i>12,判断所有码头的集港需求是否得到满足,若是则kbest=min{km},记录最优解,转Step 6;若不是,则km=km+1,i=1,n=1,T1r0, k=T1, s,返回Step 3.
Step 6 若t < N,则根据此循环中蚂蚁m路径信息更新信息素,t=t+1转Step 2;若t≥N,则输出历代得到的最优结果,从中选取最优解.
3 算例分析 3.1 算例描述某堆场拥有100辆可调度的集卡,堆场与港口的7个码头建立了相应的预约机制.码头将一天24 h划分为12个预约时段,每个预约时段长度为2 h.集卡平均行驶速度为60 km· h-1,其重载油耗为1.2 L·km-1,轻载油耗为0.8 L·km-1,怠速状态下油耗为2.5 L·h-1,燃油的CO2排放系数为2.65 kg·L-1,集卡在堆场的平均装箱时间t0为3 min.堆场与各码头间的距离lj,码头集港箱量Qj,码头送箱时间窗信息Tj, s、Tj, f,集卡在各码头闸口的平均等待时间tj2,在码头平均操作时间tj3等信息如表 1所示,不同预约时段码头对堆场的最大预约份额如表 2所示.为了便于计算,案例中的时间单位在计算时都用分钟表示.
| 下载CSV 表 1 各码头集港信息 Tab.1 Dependent information of terminals |
| 下载CSV 表 2 各码头预约时段允许堆场的最大送箱量 Tab.2 Maximum delivery volume of container allowed in each terminal at appointment periods |
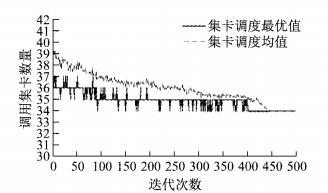
为检验本文调度模型及算法的适用性,算法采用MATLAB2012进行模型求解,在奔腾双核处理器E5400,主频2.7 GHz,内存为3.00 GB的计算机上运行.为了选择较好的算法参数组合,令α、β、ρ在[1, 2]、[1, 3]、[0, 1]中取值[16],通过对算例进行大量实验验证,确定所设计改进蚁群算法的各项参数取值如下:信息素初始浓度设置为1,Kn=30,信息素挥发系数ρ=0.5,相对重要度α=1,相对重要度β=2,蚂蚁数量M=30,信息素增加常量Q=100.当迭代次数设为500时,算法可在迭代次数内找到较优的解,调度结果如图 3所示.
|
图 3 算法迭代500次优化结果 Fig.3 Optimized results of algorithm at iteration 500 |
由图 3可知,随着迭代次数的增加,最优调度方案中集卡数量渐渐趋于稳定,当算法迭代到400代时,所调用的集卡数量波动越来越小,目标值趋于收敛.此时的送箱集卡最优调度方案所使用的集卡数量为34,最优方案中集卡调度顺序及其作业情况如表 3所示.在各集卡的路径方案中,由1×5的数组来标记其送箱及作业情况.数组中的5个数字依次为该集卡本次送箱的预约时段、本时段的送箱序数、送箱码头序号、前一次送箱完成后返回堆场的时刻、本次送箱在堆场的等待时间.表 4中数据给出了表 3各集卡及最终调度方案中运输里程、作业时间及CO2排放量等信息.
| 下载CSV 表 3 预约机制下算法求解最优集卡调度方案 Tab.3 Optimal scheduling plan of truck in appointment system |
| 下载CSV 表 4 预约机制下最优集卡调度方案作业信息表 Tab.4 Job information form of optimal scheduling plan in appointment system |
在通过改进蚁群算法对预约机制下考虑碳排放的多码头集卡调度优化方案进行求解基础上,表 5、6中给出了以往传统模式无预约机制下堆场面对同样的多集装箱码头集港任务时的集卡调度方案及相关的运输距离、作业时间、碳排放等数据.同样的多码头集港需求,传统模式下调度方案需要堆场保有39辆集卡,其集卡最多集港次数为11次,单车最长行驶里程为820 km,其平均堆场等待时间为0 min,平均码头等待时间为403.33 min,其最终返回堆场的平均时间为1 182.41 min,集卡平均CO2排放量为1 888.77 kg.由表 4预约机制最优集卡调度优化方案数据可知,其需求集卡保有量仅为34辆,调度方案中集卡最多服务次数为16次,单车最长行驶里程为1 140 km,堆场平均等待时间为145.26 min,码头平均等待时间为61.65 min,集卡最终返回堆场的平均时间为1 099.62 min,集卡平均CO2排放量为2 122.23 kg.
| 下载CSV 表 5 传统模式送箱集卡调度方案 Tab.5 Traditional truck scheduling plan |
| 下载CSV 表 6 传统模式下集卡调度方案作业信息表 Tab.6 Traditional job information form of scheduling plan |
从调度方案中集卡数量来看,考虑预约机制的新调度模式仅为34台,较传统调度方案少5台;传统方案下CO2排放达73 662.19 kg,基于预约机制优化方案CO2总排放量为72 155.91 kg,碳排放量减少了2.04%;预约机制下集卡总工作时间为37 387 min,较传统模式减少18.92%(传统模式下集卡工作总时间为46 114 min);从等待时间方面来看,预约机制下集卡优化调度与传统模式最大的区别在于,预约机制下某集卡服务路径中等待时间多是在堆场产生的,而传统模式中集卡由于没有预约信息的沟通,只能在完成上一次集港任务返回堆场后马上出发,前往下一码头进行集港,但往往其到达码头后由于码头方面种种原因需要在码头等待较长一段时间,怠速工况下增加了燃油消耗以及CO2排放量.
由此可见,在基于预约机制的单堆场多码头集卡优化调度模式中,由于有对码头集港时间窗及各预约时段最大预约份额等预约信息的沟通,堆场在安排集卡集港服务路径时可以更加方便地安排集卡的服务次序及作业流程,合理规避码头集港作业的高峰时段,避免码头闸口或港内堆场的过长等待.与传统集卡调度模式相比,本文所构建的调度优化方案能降低堆场对集卡数量的要求,提高集卡集港作业效率,有效减少能源消耗,降低集港作业过程中的CO2排放总量,最终减少堆场的运营成本.
4 结论在考虑集卡碳排放和码头预约机制的基础上合理调度集卡车队,完成各码头最终确定的各预约时段及其预约份额的集港任务,可以有效降低堆场集卡的调用数量,提高其运营效率,减少燃油消耗和CO2排放,降低堆场运营成本.本文针对预约机制下单一堆场多集装箱码头间送箱集卡优化调度问题,在考虑碳排放基础上构建了相应的优化模型,设计了改进的蚁群算法对其进行求解.算例求解及对比分析表明了本文所构建模型及算法的有效性.研究成果拓展了堆场、码头相关的理论研究,为堆场企业的集卡调度优化决策和低碳港口建设的相关决策提供了一定参考.
应该指出,由于船舶集港所涉及的各个环节和影响因素较为复杂,在求解分析过程中本文没有考虑集港过程中的集卡在港的排队规律、相关干扰因素以及集卡失约等问题,这些都有待于未来继续研究.
| [1] |
曾庆成, 张笑菊, 陈文浩, 等. 基于BCMP排队网络的码头集卡预约优化模型[J]. 系统工程学报, 2013, 28(5): 592 ZENG Qingcheng, ZHANG Xiaoju, CHEN Wenhao, et al. Optimization model for truck appointment based on BCMP queuing network[J]. Journal of Systems Engineering, 2013, 28(5): 592 |
| [2] |
NAMBOOTHIRIA R, ERERA A L. Planning local container drayage operations given a port access appointment system[J]. Transportation Research Part E: Logistics & Transportation Review, 2008, 44(2): 185 |
| [3] |
蒋美仙, 张晓, 冯定忠, 等. 基于Poisson过程的港口码头集卡预约调度优化[J]. 浙江工业大学学报, 2016, 44(3): 292 JIANG Meixian, ZHANG Xiao, FENG Dingzhong, et al. Study on appointment scheduling model of container port truck based on poisson process[J]. Journal of Zhejiang University of Technology, 2016, 44(3): 292 DOI:10.3969/j.issn.1006-4303.2016.03.012 |
| [4] |
HUYNH N, WATLON C M. Robust scheduling of truck arrivals at information on container terminals[J]. Journal of Transportation Engineering, 2008, 134(8): 347 DOI:10.1061/(ASCE)0733-947X(2008)134:8(347) |
| [5] |
邵乾虔, 靳志宏, 邢磊. 基于联动预约模式的集装箱码头集疏港仿真优化[J]. 交通运输系统工程与信息, 2016, 16(4): 217 SHAO Qianqian, JIN Zhihong, XING Lei. Simulation optimization of consolidation and configuration in container terminals based on cooperative appointment[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 217 DOI:10.3969/j.issn.1009-6744.2016.04.032 |
| [6] |
许巧莉, 孙丽君, 胡祥培, 等. 非平稳到达的码头集卡预约优化模型[J]. 大连理工大学学报, 2014, 54(5): 589 XU Qiaoli, SUN Lijun, HU Xiangpei, et al. Optimization model for appointment of container trucks with non-stationary arrivals[J]. Journal of Dalian University of Technology, 2014, 54(5): 589 |
| [7] |
GUAN C, LIU R R. Container terminal gate appointment system optimization[J]. Maritime Economics & Logistics, 2009, 11(4): 378 |
| [8] |
CHEN X, ZHOU X, LIST G F. Using time-varying tolls to optimize truck arrivals at ports[J]. Transportation Research Part E: Logistics and Transportation Review, 2011, 47(6): 965 DOI:10.1016/j.tre.2011.04.001 |
| [9] |
曾庆成, 杨忠振. 集装箱码头集卡调度模型与Q学习算法[J]. 哈尔滨工程大学学报, 2008, 29(1): 1 ZENG Qingcheng, YANG Zhongzhen. A scheduling model and Q-learning algorithm for yard trailers at container terminals[J]. Journal of Harbin Engineering University, 2008, 29(1): 1 DOI:10.3969/j.issn.1006-7043.2008.01.001 |
| [10] |
丁一, 杨阳, 沙梅, 等. 集装箱港口集卡轮胎吊集成调度方法[J]. 计算机集成制造系统, 2017, 23(4): 892 DING Yi, YANG Yang, SHA Mei, et al. Integrated methodology for scheduling of yard cranes and internal trucks in container terminal[J]. Computer Integrated Manufacturing Systems, 2017, 23(4): 892 |
| [11] |
PHAN M H, KIM K H. Negotiating truck arrival times among trucking companies and a container terminal[J]. Transportation Research Part E: Logistics and Transportation Review, 2015, 75(3): 132 |
| [12] |
ZHANG R, YUN W Y, MOON K. Modeling and optimization of a container drayage problem with resource constraints[J]. International Journal of Production Economics, 2011, 133(1): 351 DOI:10.1016/j.ijpe.2010.02.005 |
| [13] |
CHEN G, YANG Z Z. Optimizing time windows for managing export container arrivals at Chinese container terminals[J]. Maritime Economics & Logistics, 2010, 12(1): 111 |
| [14] |
李广儒, 杨大奔, 任大伟. 集卡动态调度路径优化算法[J]. 交通运输工程学报, 2012, 12(3): 86 LI Guangru, YANG Daben, REN Dawei. Path optimization algorithm of dynamic scheduling for container truck[J]. Journal of Traffic & Transportation Engineering, 2012, 12(3): 86 DOI:10.3969/j.issn.1671-1637.2012.03.015 |
| [15] |
马华伟, 叶浩然, 夏维. 允许分割配送的多时间窗车辆调度问题的改进蚁群算法求解[J]. 中国管理科学, 2012, 20(增刊1): 43 MA Huawei, YE Haoran, XIA Wei. Improved ant colony algorithm for solving split delivery vehicle routing problem with multiple time windows[J]. Chinese Journal of Management Science, 2012, 20(S1): 43 |
| [16] |
李琳, 刘士新, 唐加福. B2C环境下带预约时间的车辆路径问题及多目标优化蚁群算法[J]. 控制理论与应用, 2011, 28(1): 87 LI Lin, LIU Shixin, TANG Jiafu. Vehicle routing problem with time reservation under B2C electronic commerce and ant colony algorithm for multi-objective optimization[J]. Control Theory & Applications, 2011, 28(1): 87 |
 2018, Vol. 46
2018, Vol. 46
