2. 同济大学 岩土及地下工程教育部重点实验室,上海 200092
2. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education, Tongji University, Shanghai 200092, China
边坡稳定性分析是岩土工程研究中的经典问题.目前,关于边坡稳定性研究的方法主要有极限平衡法[1-5]、有限元分析法[6-9]和极限分析法[10-13].极限平衡法作为较早分析边坡稳定性的方法,因其力学概念明确、计算简单等特点一度成为分析边坡稳定性的主要方法[14].但该方法在假设条块间作用力时,往往存在假设过于简单的情况,得到的解答既不是真实解的上限也不是下限,对三维极限平衡法更是如此.随着计算机运算能力和商用有限元分析软件功能的提升,有限元分析法已成为分析边坡稳定性较为全面的一种方法.该方法不仅可以考虑复杂的边坡形式、受荷情况等因素,还能追踪边坡失稳破坏的整个过程.然而,有限元分析法建模过程复杂、用到的本构模型所需参数较难确定,且计算结果的合理性很大程度上取决于本构模型参数取值的准确性,另外,需要花费很多精力来建立的计算模型每次却只能分析某一特定边坡的稳定性,因此,该方法在实际工程中的应用推广还存在许多困难.
极限分析上限法基于塑性极限理论,通过构造合理的速度场破坏机制来求真实解的上限.该方法已被Chen[10]较好地应用于二维土质边坡稳定性分析,合理性得到了充分验证.Michalowski和Drescher[15]在Chen的基础上,将二维土质边坡的破坏模式拓展到三维土质边坡,从而研究了三维土质边坡的稳定性.其后,国内外学者在此基础上研究了三维土质边坡在不同条件下的稳定性:饶平平等[16]研究了边坡沉桩对三维土质边坡稳定性影响,得知前期沉桩导致边坡安全系数不断减小,但当桩体穿过破坏面后,安全系数明显提高;Gao等[17]将三维边坡的坡趾破坏拓展到坡底和坡面破坏,得出边坡在坡角和土体内摩擦角较小的情况下坡底破坏比坡趾破坏更危险;同时,Gao等[18]分析了抗滑桩对三维土质边坡的加固作用,发现当抗滑桩桩间距越小时,抗滑桩对边坡的加固作用较明显;Pan等[19]讨论了土体渗流力对三维土质边坡稳定性的影响,并将计算结果与FLAC 3D数值模拟结果进行了对比验证.从上述研究可以看出,目前利用极限分析法对三维土质边坡稳定性的研究还较少.另外,非均质性是土体具有的固有属性[10, 12],尽管Yang和Xu[20]应用土体二维非均质公式研究了二阶三维土质边坡的稳定性,但其仍未对二维非均质公式进行相应的三维拓展.同时,其他关于土体非均质性对三维土质边坡稳定性影响的研究还鲜见报道.值得指出的是Michalowski和Drescher[15]在研究三维边坡稳定性时考虑了土体体积压缩产生的能量耗散,但当三维土质边坡受荷或环境情况稍显复杂时,土体体积压缩耗能的计算将变得异常复杂而无法计算.因此,大部分研究[16, 18-19]直接忽略了此部分耗能,却未分析不考虑此部分耗能对三维土质边坡稳定性的影响.
在现有三维土质边坡极限分析方法的基础上,把考虑土体非均质性的二维公式拓展到三维情况,研究忽略土体体积压缩耗能对三维土质边坡稳定性系数的影响,并进一步分析不同坡角、不同内摩擦角和不同宽高比的三维土坡稳定性随土体非均质性变化的规律.
1 非均质三维土坡稳定性分析 1.1 三维边坡极限分析的破坏模式Michalowski和Drescher[15]将Chen提出的二维土质边坡对数螺旋线破坏机制成功拓展到如图 1所示牛角状对数螺旋线锥体三维土质边坡破坏机制.图中,
| $ r = {r_0}{{\rm{e}}^{\left( {\theta - {\theta _0}} \right)\tan \varphi }} $ | (1) |
| $ r' = {{r'}_0}{{\rm{e}}^{ - \left( {\theta - {\theta _0}} \right)\tan \varphi }} $ | (2) |

|
图 1 三维土质边坡极限破坏机制示意[15] Fig.1 Schematic of limit failure mechanism of three-dimensional soil slope[15] |
X1、X2和Y可分别表示为
| $ {X_1} = \sqrt {{R^2} - {a^2}} $ | (3) |
| $ {X_2} = \sqrt {{R^2} - {d^2}} $ | (4) |
| $ Y = \sqrt {{R^2} - {x^2}} $ | (5) |
根据图(1)所示几何关系可得a、b和θB的表达式为
| $ a = \frac{{\sin {\theta _0}}}{{\sin \theta }}{r_0} - {r_m} $ | (6) |
| $ d = \frac{{\sin \left( {\beta + {\theta _h}} \right)}}{{\sin \left( {\beta + \theta } \right)}}{r_0}{{\rm{e}}^{\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi }} - {r_m} $ | (7) |
| $ {\theta _B} = {\rm{arctan}}\frac{{\sin {\theta _0}}}{{\cos {\theta _0} - A}} $ | (8) |
式(8)中
| $ \begin{array}{l} A = \frac{{\sin \left( {{\theta _h} - {\theta _0}} \right)}}{{\sin {\theta _h}}} - \\ \;\;\;\;\;\;\frac{{{{\rm{e}}^{\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi }}\sin {\theta _h} - \sin {\theta _0}}}{{\sin {\theta _h}\sin \beta }}\sin \left( {{\theta _h} + \beta } \right) \end{array} $ | (9) |
当三维土质边坡纵向长度趋于一个较大值时,三维边坡稳定性即可视作二维平面问题.基于此,将上述模型沿对称面切开,插入宽度为b的二维边坡破坏模式.当插入宽度b足够大时,三维破坏模式即可转化为二维破坏模式,该拓展的示意图可参见图 2.图中,B为滑动体的最大宽度,H为边坡的高度.
1.2 重力做功计算如图 1所示,重力对三维土块ABC所做的功可表示为
| $ \begin{array}{l} {W_\gamma } = 2\omega \gamma \left[ {\int_{{\theta _0}}^{{\theta _B}} {\int_0^{{X_1}} {\int_a^Y {{{\left( {{r_m} + y} \right)}^2}} } \cos \theta {\rm{d}}x{\rm{d}}y{\rm{d}}\theta {\rm{ + }}} } \right.\\ \;\;\;\;\;\;\;\left. {\int_{{\theta _B}}^{{\theta _h}} {\int_0^{{X_2}} {\int_d^Y {{{\left( {{r_m} + y} \right)}^2}\cos \theta {\rm{d}}x{\rm{d}}y{\rm{d}}\theta } } } } \right] \end{array} $ | (10) |
式中:γ为土体的容重.
重力对图 2中宽度为b的插入体所做的功为
| $ \begin{array}{l} {W_{\gamma ,P}} = b\gamma \omega \left[ {\int_{{\theta _0}}^{{\theta _B}} {\int_a^R {{{\left( {{r_m} + y} \right)}^2}} \cos \theta {\rm{d}}y{\rm{d}}\theta {\rm{ + }}} } \right.\\ \;\;\;\;\;\;\;\left. {\int_{{\theta _B}}^{{\theta _h}} {\int_d^R {{{\left( {{r_m} + y} \right)}^2}\cos \theta {\rm{d}}y{\rm{d}}\theta } } } \right] \end{array} $ | (11) |
由式(10)和式(11)可将重力对滑动土体做的总功表示为
| $ W = {W_\gamma } + {W_{\gamma ,P}} $ | (12) |
根据Michalowski和Drescher的研究可知三维土质边坡在失稳破坏时的内能耗散包括两部分,一部分是土体沿破裂面滑动的摩擦耗能损失,另一部分是土体体积压缩耗能损失[15].为考虑土体在自然沉积过程中形成的非均质性,依据Chen[10]、Nian等[12]和Yang等[20]关于土体非均质性假设的模型,采用黏聚力沿深度直线变化的模式来表示土体的非均质性(见图 3),因此黏聚力大小可表示为
| $ c\left( z \right) = \left[ {{n_0} + \frac{z}{H}\left( {1 - {n_0}} \right)} \right]c $ | (13) |

|
图 3 线性增大的土体非均质性 Fig.3 Soil nonhomogeneity increasing linearly with depth |
式中:c为土体黏聚力;n0为非均质系数,取值范围为0~1.n0越小,土体的非均质性越强.当n0=1时,土体是均质的.
在考虑土体非均质性条件下,土体体积压缩耗能计算将过于复杂而难以得到相应解答.因此,假设滑动土体不可压缩,内能耗散仅发生在滑动面上,那么土体沿三维滑动面(图 1)产生的摩擦耗能可表示为
| $ \begin{array}{l} {D_{3D}} = 2\omega \left[ {\int_{{\theta _0}}^{{\theta _B}} {\int_a^R {\frac{{{{\left( {{r_m} + y} \right)}^2}}}{{\sqrt {{R^2} - {y^2}} }}} cR{\rm{d}}y{\rm{d}}\theta {\rm{ + }}} } \right.\\ \;\;\;\;\;\;\;\left. {\int_{{\theta _B}}^{{\theta _h}} {\int_d^R {\frac{{{{\left( {{r_m} + y} \right)}^2}}}{{\sqrt {{R^2} - {y^2}} }}cR{\rm{d}}y{\rm{d}}\theta } } } \right] \end{array} $ | (14) |
图 2中宽度为b的插入体滑动面产生的摩擦耗能可计算为
| $ {D_{\rm{P}}} = b\omega \int_{{\theta _0}}^{{\theta _h}} {c{{\left( {{r_m} + R} \right)}^2}{\rm{d}}\theta } $ | (15) |
在土体非均质性条件下,黏聚力是沿深度变化的.因此,根据图 3中的几何关系可将坡面黏聚力表示为
| $ {c_{\rm{f}}} = c\left[ {{n_0} + \frac{{{h_{\rm{f}}}}}{H}\left( {1 - {n_0}} \right)} \right] $ | (16) |
式中:H和hf的表达式为
| $ H = {r_h}\sin {\theta _h} - {r_0}\sin {\theta _0} $ | (17) |
| $ {h_{\rm{f}}} = {r_{\rm{f}}}\sin \theta - {r_0}\sin {\theta _0} $ | (18) |
式中:rf为坡面到旋转中心的距离.图 3中对应滑裂面上的黏聚力可表示为
| $ {c_b} = c\left[ {{n_0}\frac{{{h_{\rm{b}}}}}{H}\left( {1 - {n_0}} \right)} \right] $ | (19) |
式中:hb的表达式为
| $ {h_b} = r\sin \theta - {r_0}\sin {\theta _0} $ | (20) |
根据三维边坡破坏模式的几何关系,可得θ0至θB段以及θB至θh段的黏聚力分别为
| $ c = \frac{{y - a}}{{R - a}}{c_b} + \frac{{R - y}}{{R - a}}{n_0}c,{\theta _0} \le \theta \le {\theta _B} $ | (21) |
| $ c = \frac{{y - d}}{{R - d}}{c_b} + \frac{{R - y}}{{R - d}}{c_f},{\theta _B} \le \theta \le {\theta _h} $ | (22) |
将式(21)和式(22)代入式(14),并将式(13)代入式(15),即可计算出考虑土体非均质性的内能耗散.
基于上限分析原理,三维土质边坡处于临界状态时重力所做的功与内能耗散相等,即
| $ W = {D_{3D}} + {D_{\rm{P}}} $ | (23) |
将式(12)、式(14)和式(15)代入式(23)可得
| $ \frac{{\gamma H}}{c} = F\left( {{\theta _0},{\theta _h},\frac{{{{r'}_0}}}{{{r_0}}}} \right) $ | (24) |
式(24)的最小值可被定义为三维土质边坡的稳定性系数Ns[10, 15],即
| $ {N_{\rm{s}}} = \min F\left( {{\theta _0},{\theta _h},\frac{{{{r'}_0}}}{{{r_0}}}} \right) $ | (25) |
当土体的内摩擦角
为了验证本文解答的准确性,将得出的稳定性系数结果与文献[15]不考虑土体体积压缩耗能即内摩擦角
由于本文算法不同于文献[15]算法,因此计算得出的稳定性系数可能与文献[15]的结果存在差异.从图 4的对比结果可以看出,当宽高比较小时(B/H < 2),本文计算结果与文献[15]计算结果存在些许误差,但最大误差仅为5%,且这个误差仅在B/H=1、β=45°时存在.另外,当宽高比较大时(B/H>2),本文计算结果与文献[15]的计算结果基本重合.因此,根据计算结果的比较,本文计算得出的稳定性系数是合理的,解答具有准确性.

|
图 4 本文与文献[15]的稳定性系数对比 Fig.4 Comparison between stability factors of present study and the literature [15] |
如前文所述,本文因考虑土体非均质性对三维土质边坡稳定性影响而无法考虑土体体积压缩产生的能量耗散,所以需要先分析忽略此部分耗能对稳定性系数的影响.图 5和图 6给出了本文只考虑摩擦耗能计算出的稳定性系数与文献[15]不仅考虑摩擦耗能且考虑土体体积压缩耗能的稳定性系数计算结果的对比.由图 5可以看出,当土体内摩擦角
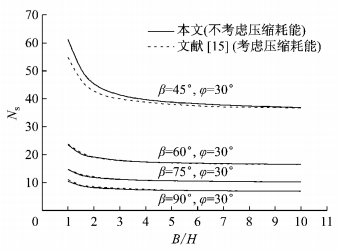
|
图 5 土体内摩擦角为30°时本文与文献[15]的稳定性系数对比
Fig.5 Comparison between stability factors of present study and the literature when |

|
图 6 土体内摩擦角为15°时本文与文献[15]的稳定性系数对比
Fig.6 Comparison between stability factors of present study and the literature when |
因此,可以总结得出当土体内摩擦角较大而边坡坡角较小时,如果三维土质边坡的宽高比也较小,则需考虑土体体积压缩产生的能量耗散;如果三维土质边坡的宽高比较大,则土体体积压缩产生的能量耗散可以忽略.此外,当土体内摩擦角和边坡坡角均较大或者仅土体内摩擦角较小时,土体体积压缩产生的能量耗散对三维土坡稳定性系数的影响也可忽略.
3.2 参数分析图 7为土体非均质性对不同坡角的三维土质边坡稳定性影响结果对比.从图中可以发现,随着土体非均质性的增强,即非均质系数减小,不同坡角的三维土质边坡的稳定性系数都呈现减小趋势,且坡角越小,其稳定性系数减小的趋势越明显,说明土体非均质性对坡角较小的三维土质边坡稳定性影响越强.图 8为土体非均质性对不同内摩擦角的三维土质边坡稳定性影响结果对比.从图中同样可以发现,随着土体非均质性的增强,三维土质边坡的稳定性系数都呈现减小趋势,且内摩擦角较大的三维土质边坡稳定性减弱越明显.因此,对坡角较小或内摩擦角较大的三维土质边坡,土体非均质性对其稳定性的影响较显著.
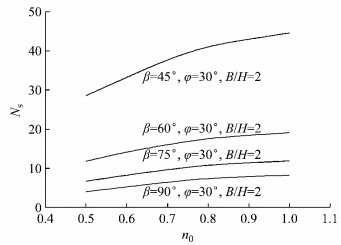
|
图 7 非均质性对不同坡角的三维边坡稳定性系数影响 Fig.7 Influence of nonhomogeneity on stability factors of three-dimensional slopes with different inclination angles |

|
图 8 非均质性对不同内摩擦角的三维边坡稳定性系数影响 Fig.8 Influence of nonhomogeneity on stability factor of three-dimensional slopes with different internal friction angles |
图 9为土体非均质性对不同宽高比的三维土质边坡稳定性影响结果对比.如前文所述,宽高比反映了土质边坡的三维效应,即宽高比越小,边坡三维效应越强.从图中可以发现,土体非均质性对三维效应越强的土质边坡稳定性影响越明显,而对三维效应较弱的边坡稳定性影响较小.同时,从图中可以看出,在不考虑土体非均质性条件下,三维效应强的土质边坡其稳定性系数要大于三维效应较弱的边坡,但在考虑土体非均质性条件下,特别当土体具有很强的非均质性时,三维效应强的边坡其稳定性系数可能会小于三维效应较弱的边坡.

|
图 9 非均质性对不同宽高比的三维边坡稳定性系数影响 Fig.9 Influence of nonhomogeneity on stability factor of three-dimensional slopes with different ratios of width to height |
基于极限分析法探讨了土体非均质性对三维土质边坡稳定性的影响,分析了忽略土体体积压缩耗能对边坡稳定性的影响.主要结论如下:
(1) 当三维土质边坡内摩擦角较大而坡角和宽高比较小时,土体体积压缩产生的能量耗散需要考虑;当三维土质边坡内摩擦角和坡角均较大或仅土体内摩擦角较小时,土体体积压缩产生的能量耗散可以忽略.
(2) 土体非均质性对坡角较小或内摩擦角较大的三维土质边坡稳定性影响较大.三维土质边坡坡角越小、内摩擦角越大,土体非均质性对其稳定性的影响越强.
(3) 边坡三维效应越强,土体非均质性对其稳定性的影响也越强.当土体非均质性很强时,三维效应较强边坡的稳定性系数小于三维效应较弱边坡的稳定性系数.
| [1] |
郑颖人, 赵尚毅, 时卫民, 等. 边坡稳定分析的一些进展[J]. 地下空间, 2001, 21(4): 262 ZHENG Yingren, ZHAO Shangyi, SHI Weimin, et al. Progress in analysis of slope stability[J]. Underground Space, 2001, 21(4): 262 DOI:10.3969/j.issn.1673-0836.2001.04.003 |
| [2] |
杨明成, 郑颖人. 基于极限平衡理论的局部最小安全系数法[J]. 岩土工程学报, 2002, 24(5): 600 YANG Mingcheng, ZHENG Yingren. Local minimum factor-of-safety method based on limit equilibrium theory[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 600 DOI:10.3321/j.issn:1000-4548.2002.05.013 |
| [3] |
卢坤林, 朱大勇, 甘文宁, 等. 一种边坡稳定性分析的三维极限平衡法及应用[J]. 岩土工程学报, 2013, 35(12): 2276 LU Kunlin, ZHU Dayong, GAN Wenning, et al. 3D limit equilibrium method for slope stability analysis and its application[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2276 |
| [4] |
LAM L, FREDLUND D G. A general limit equilibrium model for three-dimensional slope stability analysis[J]. Canadian Geotechnical Journal, 1993, 30(6): 905 DOI:10.1139/t93-089 |
| [5] |
AL-KARNI A A, AL-SHAMRANI M A. Study of the effect of soil anisotropy on slope stability using method of slices[J]. Computers and Geotechnics, 2000, 26(2): 83 DOI:10.1016/S0266-352X(99)00046-4 |
| [6] |
张磊, 张璐璐, 程演, 等. 考虑潜蚀影响的降雨入渗边坡稳定性分析[J]. 岩土工程学报, 2014, 36(9): 1680 ZHANG Lei, ZHANG Lulu, CHENG Yan, et al. Slope stability under rainfall infiltration considering internal erosion[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1680 |
| [7] |
陈金锋, 宋二祥, 徐明. 强度折减有限元法在昆明新机场高填方边坡稳定分析中的应用[J]. 岩土力学, 2011, 32(S1): 636 CHEN Jinfeng, SONG Erxiang, XU Ming. Application of strength reduction FEM to stability analysis of high fill slope in Kunming new airport[J]. Rock and Soil Mechanics, 2011, 32(S1): 636 |
| [8] |
MATSUI T, SAN K C. Finite element slope stability analysis by shear strength reduction technique[J]. Soils and Foundations, 1992, 32(1): 59 DOI:10.3208/sandf1972.32.59 |
| [9] |
DAWSON E M, ROTH W H, DRESCHER A. Slope stability analysis by strength reduction[J]. Géotechnique, 1999, 49(6): 835 DOI:10.1680/geot.1999.49.6.835 |
| [10] |
CHEN W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier, 1975
|
| [11] |
年廷凯, 栾茂田, 杨庆. 阻滑桩加固土坡稳定性分析与桩基的简化设计[J]. 岩石力学与工程学报, 2005, 24(19): 3427 NIAN Tingkai, LUAN Maotian, YANG Qing. Stability analysis of slopes with stabilizing piles and their simplified design[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3427 DOI:10.3321/j.issn:1000-6915.2005.19.004 |
| [12] |
NIAN T K, CHEN G Q, LUAN M T, et al. Limit analysis of the stability of slopes reinforced with piles against landslide in nonhomogeneous and anisotropic soils[J]. Canadian Geotechnical Journal, 2008, 45(8): 1092 DOI:10.1139/T08-042 |
| [13] |
唐高朋, 赵炼恒, 李亮, 等. 基于MATLAB的边坡稳定性极限上限分析程序开发[J]. 岩土力学, 2013, 34(7): 2091 TANG Gaopeng, ZHAO Lianheng, LI Liang, et al. Program development for slope stability using MATLAB software and upper bound limit analysis[J]. Rock and Soil Mechanics, 2013, 34(7): 2091 |
| [14] |
DONALD I B, CHEN Z. Slope stability analysis by the upper bound approach: Fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 853 DOI:10.1139/t97-061 |
| [15] |
MICHALOWSKI R L, DRESCHER A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839 DOI:10.1680/geot.8.P.136 |
| [16] |
饶平平, 赵琳学, 李林, 等. 坡面沉桩边坡动态稳定性三维极限上限分析[J]. 岩石力学与工程学报, 2017, 36(3): 697 RAO Pingping, ZHAO Linxue, LI Lin, et al. Three-dimensional dynamic stability analysis of slope during pile driving using upper-bound limit analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 697 |
| [17] |
GAO Y F, ZHANG F, LEI G H, et al. An extended limit analysis of three-dimensional slope stability[J]. Géotechnique, 2013, 63(6): 518 DOI:10.1680/geot.12.T.004 |
| [18] |
GAO Y, YE M, ZHANG F. Three-dimensional analysis of slopes reinforced with piles[J]. Journal of Central South University, 2015, 22(6): 2322 DOI:10.1007/s11771-015-2757-6 |
| [19] |
PAN Q, XU J, DIAS D. Three-dimensional stability of a slope subjected to seepage forces[J]. International Journal of Geomechanics, 2017, 17(8): 04017035 DOI:10.1061/(ASCE)GM.1943-5622.0000913 |
| [20] |
YANG X L, XU J. Three-dimensional stability of two-stage slope in inhomogeneous soils[J]. International Journal of Geomechanics, 2017, 17(7): 06016045 DOI:10.1061/(ASCE)GM.1943-5622.0000867 |
 2018, Vol. 46
2018, Vol. 46


