虽然通过单天线全球导航卫星系统(GNSS)接收机无法直接获得方位角信息，但是可以对一段连续的GNSS坐标点轨迹拟合求切线，间接求得该段所对应的方位角，即轨迹拟合方位角.由于拟合方位角由轨迹拟合得到，不会受到仪器安置误差的影响，因此可以用来粗略校正惯性传感单元方位角(航向角)的安置误差^[1].

在数学上，符合一定条件的动点所形成的图形，或者说，符合一定条件的点的全体所组成的集合，叫做满足该条件的点的轨迹.移动测量系统的轨迹是由GNSS接收机测得的坐标点的集合.一般来说，车辆的行驶轨迹没有规律，即在不同区域内，它们的形状可以完全不相关，而且轨迹的累积距离也相当长，因而无法直接通过高次拟合函数对车辆的行驶轨迹进行逼近.在分段插值中，分段线性插值在分段点上仅连续但不可导，分段埃尔米特插值只有连续的一阶导数，光滑度不高，而样条函数可以同时解决这两个问题，使插值函数既是低阶分段函数, 又是光滑函数，并且只需在区间端点提供某些导数信息^[2].

样条插值的特点是拟合的曲线通过插值点，即通过GNSS轨迹点.然而，GNSS轨迹点含有1~2 cm左右的平面误差，直接插值的做法会将误差传播到样条函数的参数中，进而对切线结果(即方位角)产生一定的影响.因此，需要以拟合的方式计算方位角.

根据分段得到的一段轨迹点，可以拟合得到一个函数关系式.然而，在这个函数关系式上，拟合的精度不是均匀的，通常中部的精度稍高，两头的精度较差，容易产生“跳变”.因此，将分段拟合得到的曲线简单地拼接起来作为拟合的结果势必是不理想的.姚连璧等^[3]提出整体样条拟合的方法，将连接处的连续性作为条件方程，以附有条件的间接平差来进行整体拟合.当轨迹累积距离太长，参与计算的轨迹点太多时，采用该方法计算会形成一个巨大的矩阵，严重时甚至超过计算机内存容量的限制而导致无法计算，因此这种方法也不适用于移动测量系统的轨迹拟合.

实际上，对于最终要拟合的结果，只需相应地离散坐标点所对应的拟合坐标以及轨迹拟合方位角，因此拟合过程中的拟合曲线是否连续或者拟合结果是否能够组成一条连续的轨迹并不是必须的.根据上述常用方法的问题以及轨迹拟合方位角的特性，尝试采用移动最小二乘法来拟合轨迹，获得轨迹的方位角.

1 移动最小二乘理论

移动最小二乘法是形成无网格方法逼近函数的方法之一, 已在无网格方法中得到广泛应用^[4-5].移动最小二乘法最初由Shepard^[6]以最低阶的形式发展成为一种逼近方法，并由Lancaster等^[7]扩展到更高阶的形式.移动最小二乘法的优点有很好的数学理论支持，对于每个固定点，移动最小二乘法即为通常的最小二乘法^[8].

设在某一个子域Ω⊂R^d上存在参数未知的多项式函数u，并已知该函数关系式在一系列自变量x(x∈Ω)上的对应函数值，则可以通过这些对应值逼近多项式函数u^[9].作为一种逼近方法，移动最小二乘法由三部分组成：基函数、权函数、待求系数.对于一个自变量x，可以得到

$ u\left( \mathit{\boldsymbol{x}} \right) \simeq \hat u\left( \mathit{\boldsymbol{x}} \right) = {\mathit{\boldsymbol{P}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\alpha }} = \sum\limits_{j = 1}^m {{\alpha _j}{p_j}\left( \mathit{\boldsymbol{x}} \right), \mathit{\boldsymbol{x}} \in \mathit{\Omega }} $

(1)

式中: P(x)=(p₁(x), p₂(x), …, p_m(x))^T为一个m项基函数；α为待求参数，其值通过最小二乘法解得.令

$ \begin{array}{l} M\left( \mathit{\boldsymbol{\alpha }} \right) = \sum\limits_{i \in {I_{\mathit{\boldsymbol{x}}, \delta }}} {{{\left( {u\left( {{\mathit{\boldsymbol{x}}_i}} \right) - \sum\limits_{j = 1}^m {{\alpha _j}{p_j}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} } \right)}^2}w\left( {\mathit{\boldsymbol{x}} - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_i}} \right) = \min \end{array} $

(2)

式中：I_{x, δ}={i={1, 2, …, n}:‖x-x_i‖²≤δ}；w:R^d→R为一非负权函数，值域为[0, 1]；δ∈R为紧支系数，约束计算的取值范围.

使Ω_x是以δ为约束参数的一个邻域，则式(2)可以写成

$ \begin{array}{l} M\left( \mathit{\boldsymbol{\alpha }} \right) = \mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} - 2{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}^{\rm{T}}\mathit{\boldsymbol{\alpha }} + \min \end{array} $

(3)

式中：α=(α₁, α₂, …, α_m)^T；$ {\mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} = {\left( {u\left( {{\mathit{\boldsymbol{x}}_i}} \right)|i \in {I_{\mathit{\boldsymbol{x}}, \delta }}} \right)^{\rm{T}}} \in {{\boldsymbol{\rm{R}}}^{{c_\mathit{\boldsymbol{x}}}}} $；$ {\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} = {\left( {{p_j}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right)_{i \in {I_{\mathit{\boldsymbol{x}}, \delta }}, j \in \left( {1, 2, \cdots , m} \right)}} \in {{\boldsymbol{\rm{R}}}^{m \times {c_\mathit{\boldsymbol{x}}}}} $；$ {\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} = {\rm{diag}}\left( {w\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right)|i \in {I_{\mathit{\boldsymbol{x}}, \delta }}} \right) \in {{\boldsymbol{\rm{R}}}^{{c_\mathit{\boldsymbol{x}}} \times {c_\mathit{\boldsymbol{x}}}}} $；c_x为I_x，δ的基数.最后，由M(α)=0可得

$ \left[ {{\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}\;\;{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}\;\;\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}^{\rm{T}}} \right]\mathit{\boldsymbol{\alpha }} = {\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} $

(4)

即

$ \mathit{\boldsymbol{\alpha }} = {\left[ {{\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}\;\;{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}\;\;\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}^{\rm{T}}} \right]^{ - 1}}{\mathit{\boldsymbol{P}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{W}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}}{\mathit{\boldsymbol{U}}_{{\mathit{\Omega }_\mathit{\boldsymbol{x}}}}} $

(5)

式(5)中有m个未知参数，则x的邻域Ω_x应该满足求得最小二乘解的条件.为防止求解运算中矩阵出现奇异，Ω_x邻域内点的数量应该大于基函数P(x)的项数.

2 轨迹拟合切线方位角算法

在基于移动最小二乘法的轨迹拟合切线方位角算法中，为保证拟合质量与后续方位角计算的需要，选择三次多项式p(x)=(1, x, x², x³)为拟合基函数.拟合时，将移动测量车的里程作为拟合参数分别拟合U_X(x)=p^T(x)α_X与U_Y(x)=p^T(x)α_Y，移动测量车的里程由GNSS点的坐标求得.最后，以$ \frac{{\partial {\mathit{\boldsymbol{U}}_X}\left( x \right)}}{{\partial x}}/\frac{{\partial {\mathit{\boldsymbol{U}}_Y}\left( x \right)}}{{\partial x}} $作为拟合曲线的切线值计算轨迹切线方位角.

在拟合中，紧支系数δ作为计算取值范围的约束，决定了纳入拟合计算的坐标点的范围.由于轨迹为线性数据，则δ以距离约束量的方式约束拟合数据点的选取，即选择拟合目标点前后±δ里程范围内的点进行拟合计算.在拟合计算中，权函数决定了各坐标点对拟合结果的影响大小，一般分为等权与不等权，等权时将各坐标点“一视同仁”，而不等权时则一般是离目标点近的点的权重较大，在取值范围边界处的点的权重较小.不等权的权函数有多种取法，下文中将对其做比较.

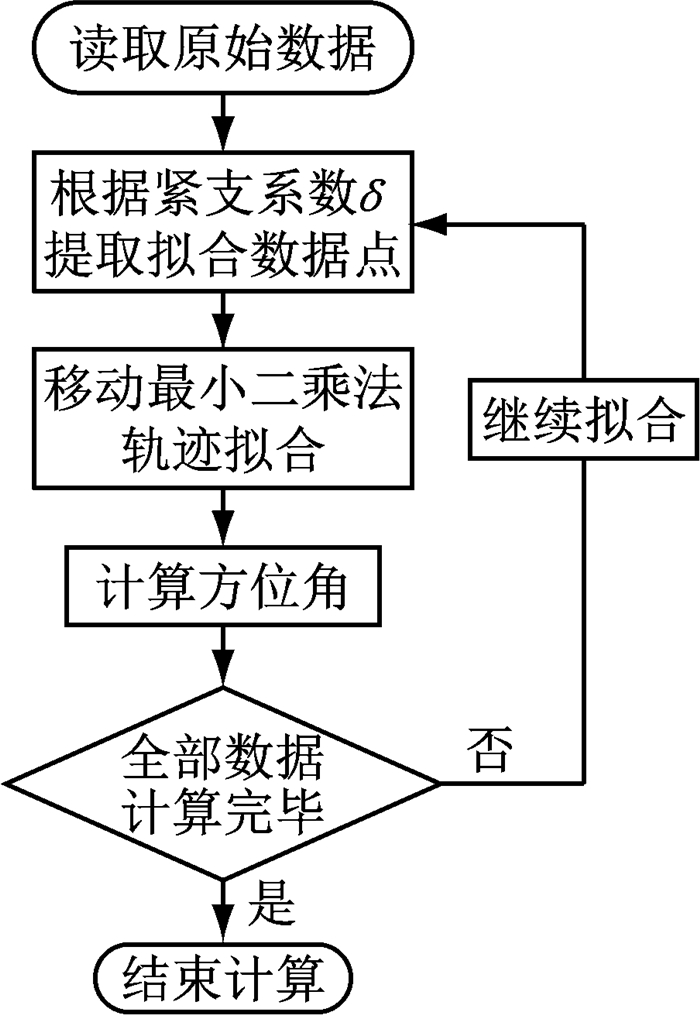
基于移动最小二乘法的轨迹拟合切线方位角的算法流程如图 1所示.

3 算法测试

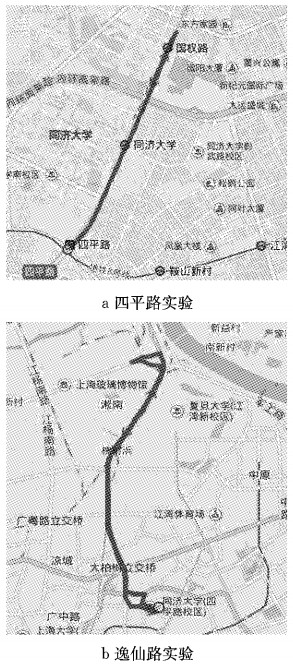
算法测试的主要目的有以下两点：①测试算法的可行性与适用性；②测试紧支系数δ的不同取值及权函数的不同选择对拟合结果的影响.测试数据来源于同济大学测绘与地理信息学院移动测量车的实验数据，实验的时间地点分别为2015年2月5日于上海市四平路大连路至国顺路段(包括四平路隧道)及2015年5月19日于上海市逸仙路高架曲阳路至军工路段，轨迹如图 2所示.选取其中观测精度质量较好的部分作为测试数据.

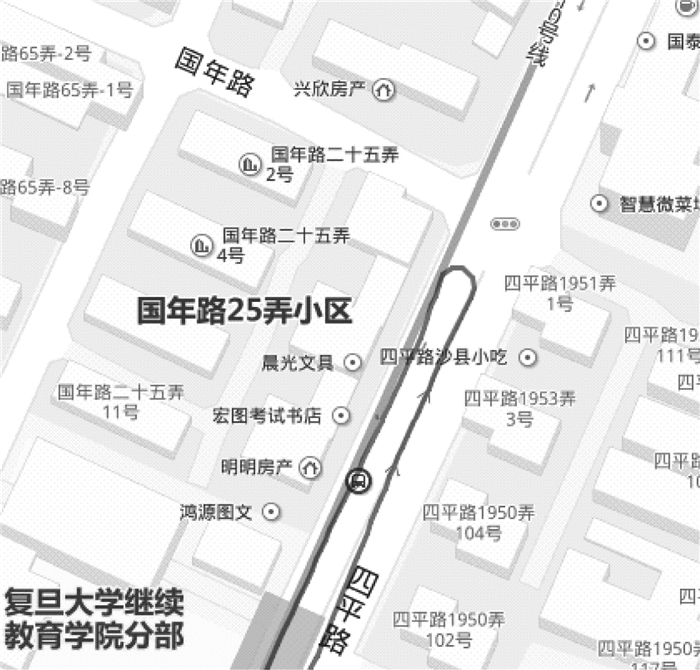
对于算法的可行性与适用性，主要测试算法在不同轨迹形状下的适用性.本文选择的逸仙路实验轨迹主要由直线段与曲率较小(半径达到100 m以上)的路段构成，而四平路隧道部分则提取车辆掉头转弯处曲率较大(转弯半径在几米到几十米)的轨迹进行计算，如图 3所示.

测试时，设定紧支系数δ为2 m，等权计算.将实测坐标、原始惯性导航单元(IMU)方位角与拟合坐标、拟合方位角做差值并计算标准差，结果如表 1所示.

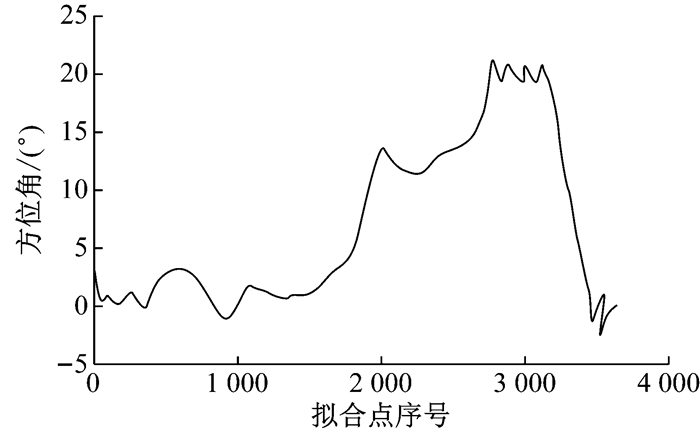
从表 1可以看出，在轨迹形状弯曲变化程度较小的路段，移动最小二乘法的拟合效果较好.在逸仙路实验中，坐标差的平均值都为0 m，标准差分别为0 m及0.001 m，与实测数据几乎一致；方位角差的平均值为0.859°，标准差为0.511°，说明在该段IMU存在着约0.859°的对准误差.在四平路实验掉头处，坐标拟合结果同样优异，坐标差的平均值都为0 m，标准差分别为0.005 m与0.007 m，而方位角拟合结果不甚理想，差值的平均值达7.096°, 标准差达7.119°.如图 4所示，在车辆转弯半径较小的地方，IMU方位角与轨迹的切线方向存在着较大的不同.这主要是由于二轮驱动的桑塔纳在转弯时，其前进方向与IMU反映的车体方向存在一定的夹角，从而导致转弯处拟合角和IMU测量值的偏差较大.

分别以2、3、4、5、10 m紧支系数δ等权计算逸仙路实验数据，与实测数据做差，对比不同紧支系数δ取值对坐标及方位角拟合结果的影响，如表 2和表 3所示.

从表 2和表 3可以看到，紧支系数δ确定了参与拟合计算的轨迹点的范围.当紧支系数δ越小时，坐标拟合的标准差越小，随着紧支系数δ的增大，坐标拟合的标准差逐渐增大.紧支系数δ的增大导致了拟合距离的增大，虽然轨迹接近于光滑的弧线，但是会导致拟合曲线与实际轨迹的差异变大，即方位角标准差逐渐增大；对于方位角，随着紧支系数δ的增大，IMU方位角与拟合方位角差的均值不变，而标准差逐渐减小，说明紧支系数δ越大，拟合方位角的离散程度越小.需要注意的是，由紧支系数δ所确定范围内的点的数量应满足最小二乘求解的条件，因而紧支系数δ不能取得太小，需满足

$ \delta \ge 2.5\frac{{{v_{\max }}}}{f} $

(5)

式中：v_max为移动测量系统的最大车速，m·s^-1；f为传感器数据时间同步后的频率，Hz.最后，选择δ=4 m，分别以等权及不等权的方式计算逸仙路实验数据，与实测数据做差值，对比不同的权函数对拟合结果的影响.等权为在由紧支系数δ确定的范围内，所以测量数据的权都为1，而不等权为根据测量点至拟合点之间的距离，由权函数分配不同的权值给测量点，使得离拟合点较近的测量值对拟合的影响大，远离拟合点的测量值对拟合的影响较小.

在本文中，分别构造以下3种不等权的权函数模型：

$ {W_1}\left( {\Delta s} \right) = 1 - \frac{{\Delta s}}{\delta } $

(6)

$ {W_2}\left( {\Delta s} \right) = \frac{1}{{1 + {{\left( {\Delta s/\delta } \right)}^2}}} $

(7)

$ \begin{array}{l} {W_3}\left( {\Delta s} \right) = \\ \left\{ \begin{array}{l} \frac{2}{3} - 4{\left( {\frac{{\Delta s}}{\delta }} \right)^{ - 2}} + 4{\left( {\frac{{\Delta s}}{\delta }} \right)^{ - 3}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \frac{{\Delta s}}{\delta } \le \frac{1}{2}\\ \frac{3}{4} - 4{\left( {\frac{{\Delta s}}{\delta }} \right)^{ - 1}} + 4{\left( {\frac{{\Delta s}}{\delta }} \right)^{ - 2}} + \frac{4}{3}{\left( {\frac{{\Delta s}}{\delta }} \right)^{ - 3}}, \;\;\;\;\frac{1}{2} < \frac{{\Delta s}}{\delta } \le 1 \end{array} \right. \end{array} $

(8)

式中:Δs为测量点至拟合点的距离.将4种权函数拟合轨迹与方位角的计算结果与实测数据做差值，对比不同权函数模型对坐标及方位角拟合结果的影响，如表 4和表 5所示.

从表 4和表 5可以看出：权函数对坐标拟合标准差的影响较大，根据所采用权函数的不同，拟合的坐标约有5%至25%的提升；轨迹拟合方位角受权函数的影响则较小，平均值在精度范围内未发生变化，标准差的变化也较小.这说明权函数主要影响拟合出的线型，而对该处的切线方向——方位角影响不大.

4 结论

(1) 轨迹形状测试说明本文算法能处理小曲率及大曲率半径下的轨迹拟合.在大曲率半径下，拟合方位角与IMU方位角有较大的差异，所以这种情况下不建议使用该方法拟合的数据；在轨迹弯曲不大的路线上，该算法能够较好地逼近轨迹并计算方位角，为移动测量车的IMU方位角标定提供一个比较精准的原始值.

(2) 随着紧支系数δ的增大，移动最小二乘坐标拟合的精度(标准差)逐渐下降，而方位角拟合的精度逐渐上升.

(3) 权函数能够提高坐标拟合的精度，但对方位角拟合的作用十分有限.

综上所述，在选择紧支系数δ时，本文建议充分考虑实验的具体情况.根据实验中移动测量系统的最大车速、GNSS的频率，选择满足整体最小二乘拟合要求的紧支系数δ，且不宜过大; 然后, 配以适当的权函数模型，对弯曲程度较小的轨迹切线方位角进行拟合计算，以此进行IMU粗对准标定等相关应用.