2. 南昌工程学院 江西省精密驱动与控制重点实验室,江西 南昌 330099
2. Jiangxi Province Key Laboratory of Precision Drive & Control, Nanchang Institute of Technology, Nanchang 330099, China
风电叶片寿命直接影响风力发电成本,而叶片的使用寿命很大程度上取决于其抗疲劳性能,因此风电叶片的疲劳加载试验至关重要[1].在国内风电叶片疲劳加载试验主要采用单激振器,用于对疲劳安全系数较小的危险区域进行针对性测试[2].随着风电叶片规模变大,使用单套加载装置所产生的激振力不足以驱动大型叶片且试验精度较低,因此多激振器加载形式应运而生[3].目前,丹麦LM (LM Glasfiber)公司、美国NREL (National Renewable Energy Lab)和荷兰WMC (Workflow Management Coalition)等对多轴加载和多点加载的方法进行了研究,并对风电叶片进行了疲劳试验.多加载源系统振动过程存在能量传递,多加载源与风电叶片构成了一个复杂的非线性机电耦合系统,而机电耦合作用影响控制效果[4-5].同步控制是实现激振联动的有效方式之一,在实际应用中激振频率工作在共振情况下,同时各加载点间存在较强的机电耦合作用,从而影响同步控制的效果[6].为了提高了控制系统的自适应性和鲁棒性,众多学者提出了若干控制方法应用于风电叶片疲劳试验.文献[7]中提出了一套风轮叶片疲劳试验线性控制系统,将非线性叶片振动模型通过输出振幅的简化等效为线性模型,使叶片以给定的幅值振动.廖高华等[8]设计了大型风电叶片加载试验,并建立了模糊控制系统,试验结果表明该系统应用于叶片加载试验具有良好的控制精度.文献[9]中采用并联交叉耦合架构,设计了滑模变结构跟随误差同步控制算法,并将该控制算法应用于激振试验.文献[10]中论述了两轴共振疲劳加载系统的基本结构和工作原理,设计了一套针对加载源的转速差、相位差及叶片振幅测量方案,并制定了相应的控制策略.
上述研究主要基于偏心块驱动或液压驱动的加载模式,并且激振器控制策略主要采用交叉耦合控制策略和偏差耦合控制策略.然而,在受控激振器数量较多时,这些策略的控制结构也更加复杂,而且补偿规律也难以确定.因此,本文基于电驱动惯性式激振装置,构建了风电叶片两点疲劳加载测试系统.提出虚拟主令同步控制算法,以比例-积分-微分(PID)算法设计误差补偿器,最后试验验证耦合下虚拟主令同步控制算法的有效性.虚拟主令同步控制算法基于无模型的控制方式,能降低系统控制结构的复杂程度并提高鲁棒性.
1 叶片两点疲劳加载试验系统构建系统由电驱动惯性式疲劳加载装置、个人计算机(PC)人机软件、就地控制柜、激光测距仪及应变仪等构成.叶片根部固定在加载基座上,两点电驱动惯性式疲劳加载装置通过木芯及夹具安装于叶片展向不同位置,装置距离根部分别为16 m和32 m.两点疲劳加载试验系统如图 1所示.系统测控模块的上位机采用Labview设计人机界面环境,以实现参数设置与曲线显示、控制器的数据驱动与存储、激光测距仪的数据采集以及与各模块的通信.下位机(就地控制柜)实现叶片共振频率搜索与跟踪,并与上位机通信以及同步控制激振器.试验过程中对频率、应变、位移等进行监控,叶片位移检测采用LDS30系列激光测距仪.采用24组应变片,测量以下位置:叶根及叶根过渡段、剖面变化较大处,材料或厚度变化处,内部接合部、加强筋和梁.

|
图 1 叶片两点疲劳加载试验系统现场 Fig.1 Site of two-point fatigue loading test system of the blade |
在叶片展向不同位置上设置配重来调整载荷分布,得到各剖面所需的载荷.根据叶片特征参数建立模型, 对载荷进行匹配,并设计弯矩分布校验算法.对配重的质量和数量进行优化并校验,得到沿叶片展向的弯矩分布误差小于7%,满足实际工作时弯矩分布.两点疲劳加载试验系统参数如表 1所示.
| 下载CSV 表 1 两点疲劳加载试验系统参数 Tab.1 Parameters of two-point fatigue loading test system |
标准条件(激振器几何尺寸、性能和结构等参数一致)下进行非控制振动特性试验.设定激振器频率同为6.35 rad·s-1,试验曲线如图 2所示.从图 2可看出,相位差有趋于某个固定角度的趋势,叶片振幅则表现为不同程度的波动,不能达到稳定状态.这是由于2台激振器联振时存在耦合特性,导致相位差出现波动,因此叶片振动振幅发生紊乱.
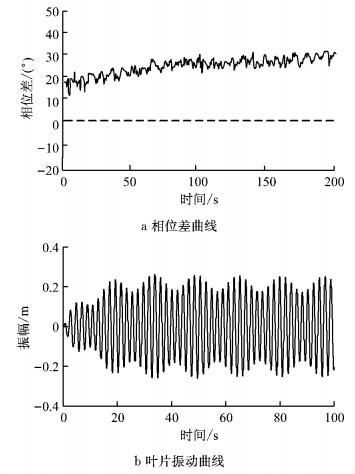
|
图 2 振动耦合特性试验分析 Fig.2 Experimental analysis of coupling characteristics of vibration |
为了消除振动耦合现象,需要设计一种同步控制策略以实现对激振系统的同步控制,从而提高疲劳试验精度.根据运动控制器自身函数库,引入交叉耦合同步结构,设计了虚拟主令相邻耦合同步器.同步控制策略中,先模拟电子虚拟轴,使系统中每个电机都接受同一指令的信号,然后将相邻偏差耦合引入控制器,最后用同步及跟随误差描述系统同步性能, 同步控制算法使跟随误差趋于零.同步控制策略结构如图 3所示.

|
图 3 基于虚拟主令偏差耦合的同步控制策略结构 Fig.3 Synthronization control strategy structure based on virtual master deviation coupling |
对于具有n台激振器的振动系统,设激振器都跟踪同一基准位置θr,定义第i台激振器的跟随误差ei(t)=θr-θi.满足ei(t)=0可保证各旋转轴与基准速度的同步,但由于电机特性差别及耦合的影响,在ei(t)→0的同时,需满足e1(t)=e2(t)=…=en(t).相邻偏差耦合控制中最重要的部分就是位置反馈模块,由它给每台激振器提供位置补偿信号.每个激振器同步误差被定义为与其相邻两轴速度误差的差分值,如下所示:
| $ \left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}}\\ {{\varepsilon _2}}\\ \vdots \\ {{\varepsilon _{n - 1}}}\\ {{\varepsilon _n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 2&{ - 1}&0& \cdots &0&0&{ - 1}\\ 1&2&{ - 1}& \cdots &0&0&0\\ \vdots&\vdots&\vdots &{}& \vdots&\vdots&\vdots \\ 0&0&0& \cdots &{ - 1}&2&{ - 1}\\ { - 1}&0&0& \cdots &0&{ - 1}&2 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{e_1}}\\ {{e_2}}\\ \vdots \\ {{e_{n - 1}}}\\ {{e_n}} \end{array}} \right] $ | (1) |
式中:εi为第i轴的位置同步误差.当式(1)中所有的位置同步误差都等于0,则同步控制目标e1(t)=e2(t)=…=en(t)得以实现.式(1)可进一步表示为
| $ \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{Te}} $ | (2) |
式中:ε = [ε1 ε2 … εn]T;T为同步变换矩阵;e =[e1 e2 … en]T.将式(2)左乘以eT可以得到
| $ \begin{array}{l} {\mathit{\boldsymbol{e}}^2}\mathit{\boldsymbol{Te}} = {\left( {{e_1} - {e_2}} \right)^2} + {\left( {{e_2} - {e_3}} \right)^2} + \cdots + \\ \;\;\;\;\;\;\;\;\;\;{\left( {{e_n} - {e_1}} \right)^2} \ge 0 \end{array} $ | (3) |
用跟随误差及同步误差来描述系统位置同步性能,同步控制的目标是通过同步控制算法使跟随误差ei(t)与同步误差εi(t)都趋于零.引入一个同时包含ei(t)、εi(i+1)(t)、εi(i-1)(t)的信息量Ei(t),称之为相邻耦合误差.按相邻次序定义Ei=ei+Λiεi,其中Λi为一个正的耦合系数,用于权衡控制器的跟踪性能和同步性能.
引入新的变量耦合误差,由E =e+Λε得到
| $ \mathit{\boldsymbol{E}} = \left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T}}} \right)\mathit{\boldsymbol{e}} $ | (4) |
式中:I表示单位矩阵;Λ表示控制增益矩阵,是一个对角正定矩阵.
3 同步控制算法及稳定性控制系统整体结构如图 4所示.控制器以激振器的跟踪误差作为输入,完成振子位移到电机转角的参数转换,以及对电机转角指令的补偿.假设电动缸参数相同,由交流电机磁场定向控制理论可知,系统状态方程式的第i个运动学方程可表示如下:
| $ \left\{ \begin{array}{l} {J_i}{{\ddot \theta }_i} + {B_i}{{\dot \theta }_i} = {T_{{\rm{em}}i}} - {T_{{\rm{L}}i}}\\ {T_{{\rm{em}}i}} = 1.5{p_{\rm{n}}}{\mathit{\Psi }_{\rm{f}}}{i_{\rm{q}}},{T_{{\rm{L}}i}} = \frac{{{P_{\rm{h}}}}}{{2{\rm{ \mathsf{ π} }}}}{F_{{\rm{s}}i}} \end{array} \right. $ | (5) |

|
图 4 伺服控制结构框图 Fig.4 Servo control structure diagram |
式中:Ji为伺服结构等效转动惯量;θi为电机位移;Ph为丝杠导程;iq为电机输入交轴电流;Bi为等效摩擦系数;pn为电机极对数;Ψf为绕组的匝链永磁磁链值;Temi为电机磁转矩;TLi为转轴上承受的负载转矩;Fsi为丝杠承受的负载力.
考虑两点疲劳加载是一个多电机轴控制系统,轴参数为n,系统状态方程(5)可改为以下形式:
| $ \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot \theta }} + \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\dot \theta }} = {\mathit{\boldsymbol{T}}_\tau } $ | (6) |
式中:J(θ)为系统的惯量矩阵且对称正定;Tτ为输入力矩矢量;B(
由式(1)和式(4)可推导得到以下关系:
| $ \mathit{\boldsymbol{\dot e}}\left( t \right) = \mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{\dot \varepsilon }}\left( t \right) = \left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T}}} \right)\mathit{\boldsymbol{\dot \theta }} $ | (7) |
叶片疲劳加载试验系统比例微分型同步控制律可以表示为
| $ {\mathit{\boldsymbol{T}}_\tau } = {\mathit{\boldsymbol{K}}_{\rm{p}}}\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} + {\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)^{ - 1}}{\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{\dot e}} $ | (8) |
式中:T'为同步变换矩阵T的转置且为正定阵;Kp、Kd和Ke为正定的控制增益矩阵.
考虑系统的稳定性,引入式(8)右侧的第3项,并将式(8)代入式(6),得到的同步控制器可以表示为
| $ \begin{array}{l} \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot \theta }} + \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\dot \theta }} = {\mathit{\boldsymbol{K}}_{\rm{p}}}\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E + }}\\ \;\;\;\;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)^{ - 1}}{\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{\dot e}} \end{array} $ | (9) |
定义正定标量函数为
| $ V = \frac{1}{2}\left( {\left( {\mathit{\boldsymbol{\dot e'J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} \dot e'T'J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\dot e}}} \right) + \mathit{\boldsymbol{E'}}{\mathit{\boldsymbol{K}}_{\rm{p}}}\mathit{\boldsymbol{E}}} \right) $ | (10) |
如果控制增益矩阵Λ选择得足够小,式(10)函数是正定的,则对V关于时间t进行求导,可以得到
| $ \begin{array}{*{20}{c}} {\dot V = \mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)\mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot e + }}\frac{1}{2}\mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{I}} + } \right.}\\ {\left. {\mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)\mathit{\boldsymbol{\dot J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{E'}}{\mathit{\boldsymbol{K}}_{\rm{p}}}\mathit{\boldsymbol{\dot E}}} \end{array} $ | (11) |
在式(9)两边同时乘以
| $ \begin{array}{l} \mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)\mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot e}} + \mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)\mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\dot e}} = \\ \;\;\;\;\;\;\; - \left( {\mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{p}}}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} + \mathit{\boldsymbol{\dot e'}}{\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{\dot e}}} \right) \end{array} $ | (12) |
将式(12)代入(11),可得到
| $ \begin{array}{l} \dot V = \mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}} \right)\left( {\frac{1}{2}\mathit{\boldsymbol{\dot J}}\left( \mathit{\boldsymbol{\theta }} \right) - \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)} \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} - \\ \;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\dot e'}}{\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{\dot e'}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}\left( {\frac{1}{2}\mathit{\boldsymbol{\dot J}}\left( \mathit{\boldsymbol{\theta }} \right) - \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)} \right) - {\mathit{\boldsymbol{K}}_{\rm{e}}}} \right)\mathit{\boldsymbol{\dot e}} - \\ \;\;\;\;\;\;\mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} \le \mathit{\boldsymbol{\dot e'}}\left( {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varLambda} T'}}\left( {\frac{1}{2}\mathit{\boldsymbol{\dot J}}\left( \mathit{\boldsymbol{\theta }} \right) - \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)} \right)} \right\|} \right. - \\ \;\;\;\;\;\;\left. {{\lambda _{\min }}\left\{ {{\mathit{\boldsymbol{K}}_{\rm{e}}}} \right\}} \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} \end{array} $ | (13) |
由于
| $ \dot V \le \mathit{\boldsymbol{\dot e'}}\left( {{b_1}\left\| \mathit{\boldsymbol{\theta }} \right\| + {b_2}\left\| {\mathit{\boldsymbol{\dot \theta }}} \right\| - {\lambda _{\min }}\left\{ {{\mathit{\boldsymbol{K}}_{\rm{e}}}} \right\}} \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{\dot E'}}{\mathit{\boldsymbol{K}}_{\rm{d}}}\mathit{\boldsymbol{\dot E}} $ | (14) |
因此,对于式(8)所设计的同步控制器,选择矩阵系数{Ke}满足
利用Matlab软件建立电机矢量控制仿真模型,加入同步控制算法即可建立电机控制仿真模型.假设2台电动缸参数完全相同,设定仿真参数为:额定功率18 kW,额定转速3 000 r·min-1,电机转动惯量Ji=0.8×10-3 kg·m2,等效黏滞摩擦系数Bi=0.003 (N·s)·m-1,传动部件转动惯量JL=1.5 kg·m2.相关控制参数的取值为kp=36, ki=0, kd=19, Λ=0.5.图 5为PID控制器的跟踪误差.从图 5可以看出,本文所提出的同步跟踪控制比标准跟踪控制具有更好的同步性能.
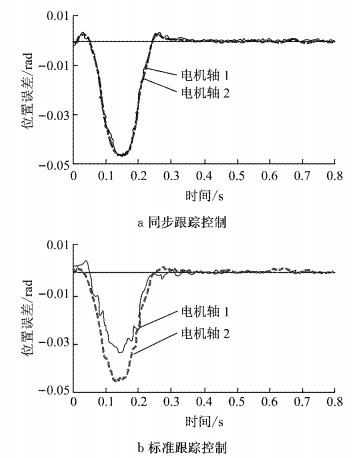
|
图 5 PID控制器的跟踪误差 Fig.5 Tracking error control of PID |
为了验证振动耦合下同步控制算法的有效性,在疲劳加载试验系统机电耦合仿真模型中加入上述同步控制算法模块,构成了机电耦合下的同步控制仿真模型.同步控制仿真模型如图 6所示.

|
图 6 同步控制算法仿真模型 Fig.6 Simulation model of synchronous control algorithm |
基于同步控制的叶片振动系统模型仿真结果如图 7所示.从图 7a可以看出,同步控制能够消除固定相位差,相位差收敛到零附近.虚拟主令同步控制算法响应时间快且超调量小,虚拟主令同步控制算法比标准控制算法更快速地完成相位追赶.从图 7b可以看出,在0.2 s时某作动器的相位受扰,虚拟主令同步控制算法在调整过程中相位波动较小,并能快速地恢复相位同步,抗干扰能力强于标准控制算法.
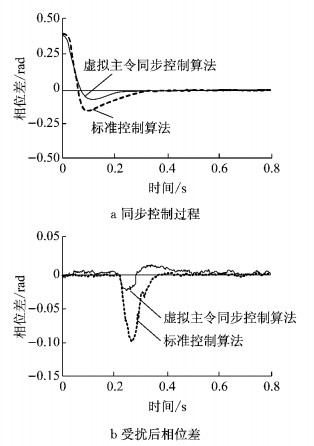
|
图 7 叶片疲劳加载试验系统同步控制算法仿真 Fig.7 Synchronous control algorithm simulation of fatigue loading test system of the blade |
利用如图 1所示的两点疲劳加载试验系统对功率1.5 MW、长度40.3 m的风电叶片进行控制加载,试验验证本文所提出同步控制算法的控制效果.试验环境温度为20 ℃、湿度为30%,测试过程中对频率、应变、位移等进行监控.应变片位置确定为监控关键截面,应变仪精度为0.3%.激光测距仪的分辨率为0.1 mm, 测距为30 m.
图 8为在两激振器频率为6.35 rad·s-1时测量得到的激振器振子位移变化与相位差曲线.从图 8可看出,在近共振时同步控制下的相位差波动较小,其值约±4°左右.
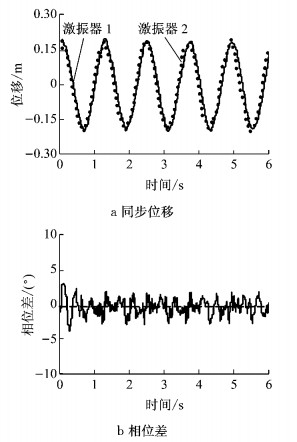
|
图 8 激振器加载的控制结果 Fig.8 Controlling results of excitation loading |
叶片加载点32 m处振幅与时间的关系曲线如图 9所示.振幅随着时间不断增大,系统能很好地捕捉叶片共振点,逐步达到共振峰值后趋于稳定,叶片加载点稳定幅值约为0.3 m.

|
图 9 叶片振幅变化曲线 Fig.9 Amplitude variation curve of the blade |
在加载过程中,改变虚拟主令的频率后得到相位差曲线,如图 10a所示.由于动力源-叶片响应的复杂性,因此相位差在同步过程中会有小波动,相位差在波动后迅速恢复同步.疲劳加载过程中受扰后激振频率及相位差变化情况曲线如图 10b所示.从图 10b可以看出, 在激振器电机受扰后,由于偏差补偿作用,两激振器的电机速度都会进行调整,保证出现较小的相位差波动.由试验可知,利用本文提出的同步控制算法能实现相位差维持在零附近,实现了激振器的同步加载,具有较大的实用性及抗干扰能力.

|
图 10 频率改变及受扰后控制曲线 Fig.10 Control curve after frequency change and disturbance |
(1) 基于电驱动惯性式激振装置,配置叶片加载试验系统参数,构建了兆瓦级风电叶片两点疲劳加载试验系统.振动试验结果表明,激振器之间具有较强的力与能量传递,耦合同步传动是机电耦合的结果,相位差会有趋于零或某个固定角度的趋势.
(2) 风电叶片加载过程中耦合效应影响2台激振器的同步性,因此提出了虚拟主令同步控制算法.以PID算法设计误差补偿器,对同步控制算法的稳定收敛性进行了分析,并数值仿真验证同步控制算法的有效性.本文提出的同步控制算法为一种无模型的耦合控制,实施简单.
(3) 同步控制算法的性能测试结果表明,2台激振器均能快速跟随并保持,耦合作用的固有相位差减小,加载时叶片振幅稳定,误差在设定范围内.
| [1] |
LEE H G, PARK J. Static test until structural collapse after fatigue testing of a full-scale wind turbine blade[J]. Composite Structures, 2016, 136: 251 DOI:10.1016/j.compstruct.2015.10.007 |
| [2] |
MALHOTRA P, HYERS R W, MANWEL J F, et al. A review and design study of blade testing systems for utility-scale wind turbines[J]. Renewable Sustainable Energy Review, 2012, 16: 284 DOI:10.1016/j.rser.2011.07.154 |
| [3] |
LEE H G, PARK J. Linear relationship of damping ratios in resonance-type fatigue testing of a wind turbine blade[J]. Wind Energy, 2014, 17: 1119 DOI:10.1002/we.v17.7 |
| [4] |
闻邦椿, 刘树英, 李鹤, 等. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009 WEN Bangchun, LIU Shuying, LI He, et al. Theory and application of mechanical vibration[M]. Beijing: Higher Education Press, 2009 |
| [5] |
廖高华, 乌建中, 张豪. 风电叶片双惯性激振疲劳加载耦合振动特性[J]. 同济大学学报(自然科学版), 2017, 45(7): 1016 LIAO Gaohua, WU Jianzhong, ZHANG Hao. Coupling characteristics of dual inertia exciter blade fatigue loading system[J]. Journal of Tongji University(Natural Science), 2017, 45(7): 1016 |
| [6] |
来鑫, 乌建中, 周文, 等. 桩锤同步振动系统的机电耦合特性及同步控制[J]. 同济大学学报(自然科学版), 2012, 40(6): 920 LAI Xin, WU Jianzhong, ZHOU Wen, et al. Synchronization control and electromechanical coupling characteristics of pile hammer synchronous vibration system[J]. Journal of Tongji University(Natural Science), 2012, 40(6): 920 DOI:10.3969/j.issn.0253-374x.2012.06.020 |
| [7] |
TOFT A, ROE-POULSEN B, CHRISTIANSEN R, et al. Design of linear control system for wind turbine blade fatigue testing[J]. Journal of Physics, 2016, 753: 1 |
| [8] |
廖高华, 乌建中. 风力机叶片摆锤共振疲劳加载系统及控制研究[J]. 太阳能学报, 2016, 37(11): 2785 LIAO Gaohua, WU Jianzhong. Wind turbine blade resonance fatigue loading system and experiment[J]. Acta Energiae Solaris Sinica, 2016, 37(11): 2785 |
| [9] |
张磊安, 魏修亭, 陶黎明. 风电叶片疲劳加载激振系统解耦控制算法及试验研究[J]. 工程科学与技术, 2017, 49(1): 109 ZHANG Lei'an, WEI Xiuting, TAO Liming. Decoupling control algorithm and experimental study of wind turbine blade fatigue loading excitation system[J]. Advance Engineering Science, 2017, 49(1): 109 |
| [10] |
ZHANG Lei'an, HUANG Xuemei, YAO Jinkai. Vibration characteristic of wind turbine blades in fatigue loading test[J]. Journal of Vibroengineering, 2016, 18(1): 34 |
 2018, Vol. 46
2018, Vol. 46

