双目相机系统由2台相互位置固定并同步曝光的相机组成, 因其对周围环境信息的感知能力以及对三维场景的重建能力,近年来被广泛应用于机器人、深空探测器、无人驾驶车等平台[1-2].为得到准确的感知信息和三维场景模型,使用之前需对双目相机系统进行检校,随后获取精确的相机内、外方位元素.
传统的双目相机检校方法需要特定的检校器材和专门的操作人员,如被广泛使用的基于棋盘格的检校方法[3].该方法要求棋盘格板平整,并且要求相机系统以不同的姿态对棋盘格进行多次拍摄.为了减少拍摄数量,Geiger等[4]在场景中布设多块不同姿态的棋盘格板通过一次拍摄进行检校,该方法虽然简化了传统棋盘格检校方法,但仍需要检校器材和检校场地.Carrera等[5]提出了基于即时定位和地图构建(SLAM)的相机动态检校方法.通过环境中特征点识别来建立环境三维模型,并以此为基准计算相机位置,从而检校双目相机系统.然而,该方法仅检校了相机的外方位元素,未能更新相机的内方位元素和尺度信息,因此得到的内、外方位元素的精度较低.为此,Heng等[6]引入里程计来恢复尺度信息,并联合优化相机的内、外方位元素,但该方法仍需要额外的检校器材即里程计辅助,并且尺度估计的精度由里程计的精度决定,为获取较高的精度需配合价格高昂的高精度里程计.
本文改进了基于SLAM的动态检校方法,提出了基于场景模型的双目相机内、外方位元素动态检校方法.对于相机检校参数未知并且场景模型缺失的情况,通过建立具有绝对尺度的场景三维模型,初步解算内、外方位元素,并采用联合优化对相机系统进行初始检校.若相机在某场景已经完成初始检校,则利用已经建立的场景模型,恢复三维点与二维影像的特征关联,通过联合优化相机检校参数对相机系统进行更新检校.
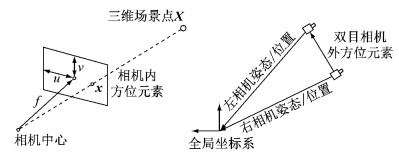
1 双目相机检校原理本文检校方法针对的双目相机模型是由2个基于中心投影的单目相机模型组成.双目相机检校即对2个单目相机各自的相机参数(内方位元素)以及2个相机之间相互的位置与姿态(外方位元素)进行检校.各项参数及其相对关系如图 1所示.
|
图 1 双目相机内、外方位元素示意图 Fig.1 Intrinsic and extrinsic parameters of stereo-camera |
通过中心投影的相机模型[7]建立了场景三维点与像平面点之间的关系,如下所示:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{PX}} $ | (1) |
式中:
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} f&s&{{u_0}}\\ 0&f&{{v_0}}\\ 0&0&1 \end{array}} \right] $ | (2) |
式中:f为相机焦距;(u0, v0)为像主点坐标;s为相机畸变参数.假设第p个三维场景点Xp被n张影像观测到,其对应影像上的二维特征点xnp,并且假设三维场景点和影像的相对位置和姿态即[Rn|tn]是已知的.因此,相机的内方位元素为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{K}} \sum\limits_{n, p} {\left( {{{\left\| {\mathit{\boldsymbol{K}}\left[ {{\mathit{\boldsymbol{R}}_n}|{\mathit{\boldsymbol{t}}_n}} \right]{\mathit{\boldsymbol{X}}_p} - {\mathit{\boldsymbol{x}}_{np}}} \right\|}^2}} \right)} $ | (3) |
式中:K[Rn|tn]Xp代表了三维场景点在n张影像上的投影,其对应的影像同名二维特征点为xnp.理论上三维场景点的投影与同名二维特征点的误差为零,但是由于三维场景点和影像的位置和姿态存在误差,因此借助梯度下降算法优化内方位元素矩阵K,使得投影误差最小.在优化过程中,内方位元素的初始焦距可以从相片的exif信息中获取,初始相主点坐标取影像的中心,通过梯度下降法优化式(3),最后得到的最优K矩阵为内方位元素的初步估计值.
1.2 外方位元素初步估计双目相机所需检校的外方位元素是指右相机相对于左相机的位置和姿态即[RE|tE]并且
| $ {\mathit{\boldsymbol{T}}_{{\rm{L}}n}} = {\mathit{\boldsymbol{R}}_{\rm{E}}}{\mathit{\boldsymbol{T}}_{{\rm{R}}n}} + {\mathit{\boldsymbol{t}}_{\rm{E}}} $ | (4) |
式:(TLn,TRn)为第n个像对中左右相机的位置和姿态,TLn=[RLn|tLn],TRn=[RRn|tRn].假设(TLn,TRn)已知,则外方位元素[RE|tE]可以由第n个像对中左右像片的位置和姿态求得,如下所示:
| $ {\mathit{\boldsymbol{R}}_{\rm{E}}} = {\mathit{\boldsymbol{R}}_{\rm{L}}}\mathit{\boldsymbol{R}}_{\rm{R}}^{\rm{T}}, {\mathit{\boldsymbol{t}}_{\rm{E}}} = {\mathit{\boldsymbol{t}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{\rm{E}}}{\mathit{\boldsymbol{T}}_{\rm{R}}} $ | (5) |
由于(TLn,TRn)存在误差,为获取较精确的外方位元素的初始值,本文通过对所有n个像对求得的[RE|tE]取平均值作为外方位元素的初始值.由于RE是以罗德里格斯旋转矩阵的形式表示,不能直接对其取平均值,因此参考旋转矩阵求平均算法[8].本文将RE转换为对应的四元数qE,再由特征值最大化的方法[9]求解
| $ \overline {{\mathit{\boldsymbol{q}}_{\rm{E}}}} = \mathop {\arg \max }\limits_{{\mathit{\boldsymbol{q}}_{\rm{E}}} \in {S^3}} \mathit{\boldsymbol{q}}_{\rm{E}}^{\rm{T}}\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{q}}_E} $ | (6) |
| $ \mathit{\boldsymbol{M}} \buildrel \Delta \over = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{q}}_{{\rm{E}}i}}\mathit{\boldsymbol{q}}_{{\rm{E}}i}^{\rm{T}}} $ |
由于在现有解算双目相机内、外方位元素的过程中,分别计算并优化了内、外方位元素,未考虑其相互影响,因此本文基于重投影误差最小化建立了目标方程,对相机的内、外方位元素进行联合优化.双目相机的内、外方位元素的检校所要解决的联合优化问题可以表示为
| $ \begin{array}{l} \mathop {\min }\limits_{{\mathit{\boldsymbol{K}}_{\rm{L}}}, {\mathit{\boldsymbol{K}}_{\rm{R}}}, {\mathit{\boldsymbol{R}}_{\rm{E}}}, {\mathit{\boldsymbol{t}}_{\rm{E}}}\mathit{\boldsymbol{, }}{\mathit{\boldsymbol{R}}_{{\rm{L}}n}}, {\mathit{\boldsymbol{t}}_{{\rm{L}}n}}} \sum\limits_{n, p} {\left( {{{\left\| {{\mathit{\boldsymbol{K}}_{\rm{L}}}\left[ {{\mathit{\boldsymbol{R}}_{{\rm{L}}n}}|{\mathit{\boldsymbol{t}}_{{\rm{L}}n}}} \right]{\mathit{\boldsymbol{X}}_p} - {\mathit{\boldsymbol{x}}_{{\rm{L}}np}}} \right\|}^2}} \right.} + \\ \;\;\;\;\;\;\;\left. {{{\left\| {{\mathit{\boldsymbol{K}}_{\rm{R}}}\left[ {\mathit{\boldsymbol{R}}_{\rm{E}}^{\rm{T}}{\mathit{\boldsymbol{R}}_{{\rm{L}}n}}|\mathit{\boldsymbol{R}}_{\rm{E}}^{\rm{T}}\left( {{\mathit{\boldsymbol{t}}_{{\rm{L}}n}} - {\mathit{\boldsymbol{t}}_{\rm{E}}}} \right)} \right]{\mathit{\boldsymbol{X}}_p} - {\mathit{\boldsymbol{x}}_{{\rm{R}}np}}} \right\|}^2}} \right) \end{array} $ | (7) |
(KL, KR)分别为左、右相机的内方位元素,根据左相机位置以及姿态和外方位元素求得右相机的位置和姿态[RETRLn|RET(tLn-tE)].(tLnp,xRnp)为三维场景点Xp在第n个左、右像对中对应的同名二维特征点.通常运动恢复结构(SFM)技术中的光束法平差是将相机作为单独个体,联合优化相机的位置、姿态和场景点,而由于本文中所采用的是双目相机,为保证相机内、外方位元素的一致性,仅优化左相机的位置、姿态以及相机的检校参数.同时,为了防止出现过拟合的情况,在联合优化过程中,不再优化与修正三维场景点坐标.本文通过梯度下降法优化相机内、外方位元素,减小三维投影与其对应的影像特征点之间的误差即重投影误差.由于内、外方位元素的初始值都已经预先求得,因此利用梯度下降优化方法可以快速收敛到最优解,得到精确的检校结果.
2 基于场景模型的双目相机检校流程基于场景模型的双目相机检校可以分为2种情况:初始检校和更新检校.初始检校是指在某未知场景中对未检校的双目相机进行检校,检校过程中场景的全局模型以及相机内、外方位元素未知;更新检校是指在某已知场景中对已经检校的双目相机进行检校,检校过程中相机系统的历史检校参数和全局场景模型均为已知.若选定某一场景作为相机检校场地,则第1次检校对应初始检校,而其后定期的检校对应更新检校.图 2给出了2种情况下动态检校系统的具体工作流程.

|
图 2 双目相机动态检校流程 Fig.2 Calibration process of stereo-camera |
由于初始检校时场景模型未知,因此在检校前需要根据待检校的双目相机获取场景的影像数据,利用SFM技术获取全局场景三维模型[10].因双目相机的检校参数未知,本文在建模阶段将双目相机视为2个单目相机模型,相机的初始焦距从相片的exif信息中获取或由所用镜头的焦距和传感器像元大小估算,初始相主点坐标取影像的中心.本文遵循SFM技术的标准流程:影像特征提取匹配、模型重建初始化、影像配准和光束法平差.根据2个单目相机获得的影像重建场景局部三维模型,同时根据式(3)估计内方位元素初值.此外, 为保证建模精度以及长时间内模型与现实场景的一致性,在选择场景时首选静态刚性结果的场景,如地下车库环境、室内环境等.同时,为了减少建模的累积误差,在数据采集时以轨迹闭合的方式进行,并在构建模型的过程中以环闭的方式去修正建模的累积误差.
本文对2个单目相机在局部模型坐标系分别进行建模,因此建模结果的模型坐标系不统一,并且基于单目视觉的三维重建无法恢复模型的绝对尺度信息,导致所获得的三维结构不具有可量测性.为获取统一的场景模型并且恢复尺度信息,本文在检校场景中布设了视觉标志点,利用全站仪布设观测网来测量三维坐标,为通过单目视觉建立的三维模型提供全局坐标参考和绝对尺度信息.
在识别出影像中视觉标志点后,通过标志点点号查询获取标志点在三维模型中的坐标和由全站仪测量的坐标,采用七参数法[11]进行坐标转换,将2个由单目相机建立的三维模型转换到统一坐标系并恢复尺度信息.考虑到局部三维模型之间存在重叠,为了减少全局场景中重复的三维点,同时降低建模的误差,将统一模型中的三维点投影至二维影像平面,得到影像中关联的二维特征点.若2个三维点之间的二维特征相似度大于一定阈值,则认为空间中的三维点为同一点,且该点的三维坐标为原始2个三维点坐标的平均值.
在SFM技术实施过程中,恢复了各时刻单目相机的位置与姿态,并且在坐标转换过程中将其转换为统一的全局模型坐标系,因此可根据第1.2节估算双目相机外方位元素初值.最后,根据式(7)联合优化内、外方位元素.
2.2 基于场景模型的更新检校在实际使用过程中,双目相机的检校参数可能会随着环境的改变、器材的磨损或形变等发生变化,因此在进行初始检校后,需定期对双目相机进行更新检校,以确保双目相机的检校参数能够更加客观和真实地描述相机系统的几何关系.
当双目相机在某个场景中已经完成了初始检校时,则当前场景的全局模型已经建立,并且相机的内、外方位元素已知.在更新检校过程中,无需再进行三维建模,仅需建立影像中二维特征点与场景模型中三维点的关联.本文场景模型中的三维点是由影像中二维特征点估算的,因此三维点的属性不仅包含三维坐标信息,还包含了对应影像二维点的特征描述子信息.以此作为关联,利用词袋(BoW)法[12]建立模型中三维点与影像同名二维特征点的关联.考虑到关联中可能存在的误匹配,利用N点透视(PnP)算法[13]并结合随机抽样一致性算法(RANSAC)[14]剔除误匹配,估计相机的位置和姿态信息.将相机的位置和姿态以及上一次检校得到的相机参数作为初值代入式(7),以重投影误差最小化为目标进行联合优化,对相机检校参数进行更新.
更新检校是以初始检校为基础,其检校流程更加简便,无需人工参与,且不依赖于检校设备.
2.3 本文方法与现有检校方法对比从检校流程角度来看,本文方法与基于SLAM的检校方法[5]较为接近,但本文方法增加了内方位元素检校、视觉标志点测量过程和联合优化过程.因此,本文的检校方法相比于基于SLAM的检校方法能够更加完整地检校相机系统的内、外方位元素.
本文方法与传统棋盘格检校方法在检校流程上有较大的差异,因此将检校过程中人工参与程度和检校对于特定设备和场地的依赖程度进行对比.首先,对比2种检校方法中人工参与程度.本文提出的基于场景的相机检校方法,为了建立坐标统一且具有绝对尺度参考的场景模型,仅需在初始检校过程中进行人工地布设以及场景中视觉标志点测量,后续更新检校则不需进行重复人工检校,并且其他双目相机也可利用相同场景进行检校而无需重复人工测量.对于传统棋盘格检校方法,不同双目相机在不同时间的检校均需要人工参与,并且检校人员操作的规范程度直接影响了检校的精度.然后,对比2种检校方法的检校流程.本文方法在对双目相机进行多次检校时所需的人工参与较少,就检校的自动化程度而言要优于传统棋盘格检校方法.最后,从检校所需的设备和场地对2种检校方法进行对比.由于本文方法借助于场景模型进行检校,因此要求场景为静态刚性结构,这类场景中地物多为静态且相互位置关系稳定,能为检校提供良好的观测数据;传统棋盘格检校方法则需要以棋盘格板作为检校设备,从中提取棋盘格的角点作为观测数据.本文检校方法中用于检校的场景模型为检校提供更多的观测数据,并且观测数据在三维空间中和二维影像平面中的分布更加均匀,而传统棋盘格检校方法提供的观测数据有限,并且受限于棋盘格的大小,很难同时覆盖双目相机中左右2帧影像.
3 实验与分析 3.1 实验数据准备为验证本文方法,选用1台无人驾驶车作为实验平台,在地下车库环境进行了实验.无人驾驶车平台搭载1组双目相机、数据采集存储系统和辅助照明系统,如图 3所示.其中,双目相机由2个位置关系固定且同步触发的工业相机组成,工业相机的型号为FLIR Blackfly 2.3 MP.考虑到传输带宽和数据采集存储系统的写入速度,采集过程中设置的相机触发频率为2 Hz.数据采集存储系统同步接收拍摄的影像,并根据时序对其进行编号存储.辅助照明系统为光线不足的地下环境提供额外的照明,确保获取影像的质量.实验场地长约35 m,宽约25 m,并且首尾相连为一个环形.实验场景内共布设了90处视觉标志点(见图 4),利用全站仪测量其坐标.为验证本文的初始检校方法,控制无人车在场地中运行了3圈,数据采集时间约为10 min,共采集约600对有效相片.为验证更新检校方法,控制无人车在场地中运行了1圈,共采集200对有效相片.

|
图 3 实验平台 Fig.3 Experiment platform |

|
图 4 实验环境与视觉标志点 Fig.4 Experiment environment and visual marks |
实验中,对同一双目相机分别利用基于场景模型的检校方法、基于SLAM的检校方法[5]和传统棋盘格检校方法[3]进行检校,并对检校结果进行对比.对于传统棋盘格检校方法,通过拍摄60张不同角度、位置的棋盘格影像进行检校.对于基于SLAM的检校方法,利用600对影像进行检校.对于本文基于场景模型的初始检校方法利用600对影像建立场景的三维模型并进行检校,对于本文基于场景模型的更新检校方法,利用200对影像进行检校.几次实验在同一时间段内完成,以确保双目相机的内、外方位元素没有发生较大变化.
3.2 检校实验结果分析4种检校方法得到的双目相机外方位元素比较如表 1所示,内方位元素比较如表 2所示.
| 下载CSV 表 1 外方位元素比较 Tab.1 Extrinsic parameter comparison |
| 下载CSV 表 2 内方位元素数值比较 Tab.2 Intrinsic parameter comparison |
基于SLAM的检校方法和本文检校方法设定的相机内方位元素初值为:f=1 450,u0=960,v0=600,s=0.由于基于SLAM的检校方法仅针对外方位元素进行了检校,因此其检校结果中的内方位元素仍为初值,与本文检校方法和传统棋盘格检校方法相比精度较低.在外方位元素估计中,基于SLAM的检校方法无法恢复绝对尺度信息,其估计得到的外方位元素中平移参数仅表示为单位向量的形式而不具有单位;本文检校方法和传统棋盘格检校方法则均能恢复绝对尺度信息,因此平移参数具有单位.由分析结果可知,基于SLAM的检校方法不能对相机的内、外方位元素进行全面检校,在实际应用中尚需结合其他检校方法以恢复内方位元素以及绝对尺度.
对于本文提出的初始检校方法和更新检校方法,两者实验结果较为接近,说明2次实验期间相机的内、外方位元素未发生变化,与实际情况相符,这也证明了本文初始检校方法和更新检校方法的一致性与可靠性.
对于本文检校方法与传统棋盘格检校方法,两者均能对相机系统进行全面检校并恢复绝对尺度.本文检校方法在联合优化后的平均重投影误差为0.68像素,传统棋盘格检校方法得到的重投影误差为0.59像素,两者较为接近.这表明本文检校方法构建的场景模型精度与传统棋盘格检校方法估计角点的精度相当,均符合检校的需求.比较2种方法得到的内、外方位元素.外方位元素旋转角的差值约为0.03°,平移的差值约为5 mm;内方位元素的差值约为10~20像素.虽然这2种方法得到的检校结果接近,但是仍存在一定的差值.由于2种方法求得的都是内、外方位元素的估计值,内、外方位元素的真实值未知,因此无法仅从参数角度分析和评价2种方法所得结果的精度.为了进一步比较结果精度,本文将这2种方法得到的检校参数应用于双目影像校正、双目视觉定位算法.
(1) 双目影像校正结果验证
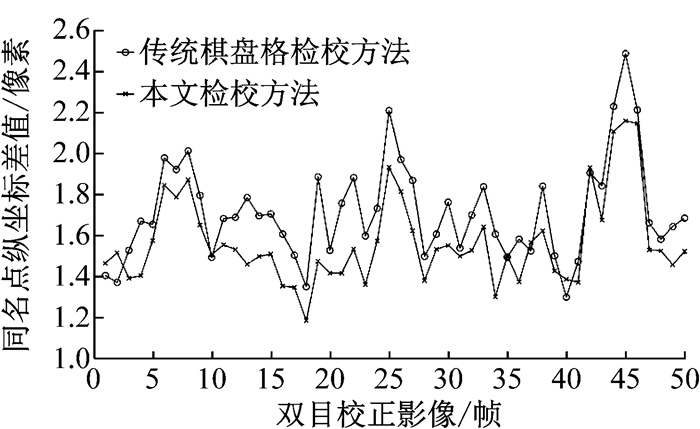
双目影像校正即利用双目相机的内、外方位元素校正双目影像的畸变和光轴位置,最终得到无畸变并且光轴平行的双目影像.理论上经过双目影像校正后的双目影像同名点的纵坐标值相等[15],但是由于检校参数中的误差,校正后的同名点纵坐标存在差值,同名点纵坐标的差值越小说明检校参数的精度越高.本文实验利用待检校的双目相机拍摄了50对双目影像作为测试影像(未参与检校).分别利用2种方法得到的检校参数对测试影像进行双目校正,比较左右相片中同名点纵坐标的差值结果,如图 5所示.
|
图 5 双目影像校正结果 Fig.5 Results of stereo rectification |
如图 5所示,传统棋盘格检校方法对应的左右影像纵坐标平均差值为1.70像素,而本文检校方法的平均差值为1.53像素.比较校正后影像同名点纵坐标的平均差值可知,利用本文检校方法得到的检校结果进行双目校正时,可以得到更加精确的双目校正结果,这也证明了本文检校方法得到的检校结果精度优于传统棋盘格检校方法.
(2) 双目视觉定位结果验证
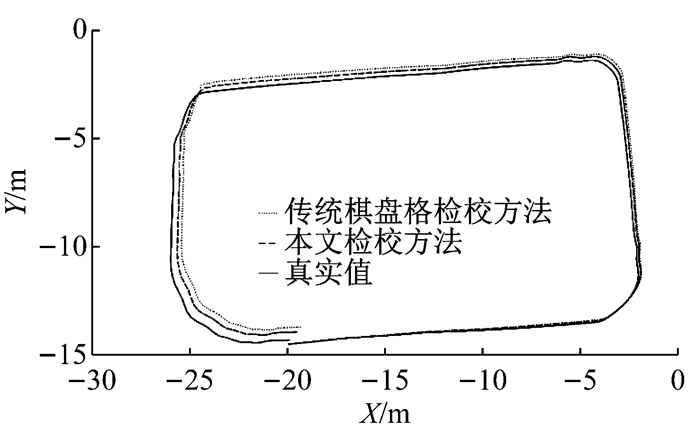
双目视觉定位是双目相机的一个重要应用,双目检校的精度也很大程度上决定了双目定位的精度[16].因此,本文实验将2种方法得到的检校结果应用于双目定位算法,并设定定位算法的其他参数相同,最后通过评估双目视觉定位的精度来评价检校结果,如图 6所示.图 6中,X、Y表示定位在二维平面上的横纵坐标.
|
图 6 双目视觉定位结果 Fig.6 Results of stereo visual odometry |
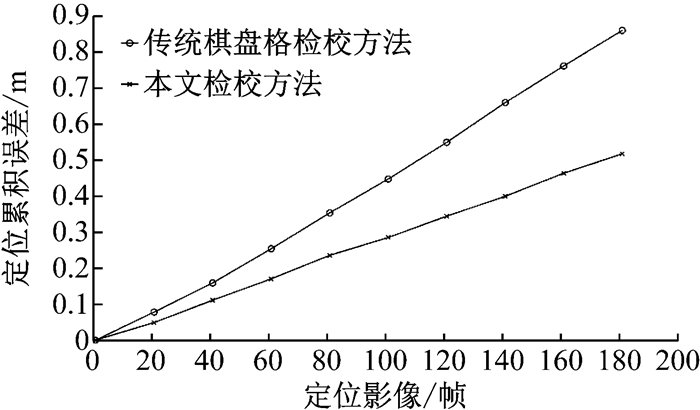
本文实验的位置真实值由全站仪测量场景特征点坐标反算自身位置获取.对比图 6中双目定位结果可以看出,基于场景模型的检校方法对应的双目视觉定位的精度优于传统棋盘格检校方法参数对应的定位结果.传统棋盘格检校方法对应的定位误差为0.87 m, 相对定位误差为1.30%;基于场景模型的检校方法对应的定位误差为0.53 m,相对定位误差为0.08%.进一步分析2种方法对应的定位累积误差,如图 7所示.双目视觉定位算法的定位误差随着解算的像对数量增加而累积,通过提高每一帧影像的定位精度本文检校方法可以有效减少0.05%的累积误差.通过比较双目视觉定位算法的精度,验证了本文检校方法得到的检校结果精度优于传统棋盘格检校方法得到的检校结果精度.
|
图 7 双目视觉定位累积误差对比 Fig.7 Accumulated error comparison of stereo visual odometry |
本文针对双目相机提出了基于场景模型的检校方法.该检校方法通过预先建立场景模型,并利用场景模型对双目相机的内、外方位元素进行检校.根据不同检校需求,本文检校方法可分为初始检校和更新检校,初始检校针对场景和检校参数未知的情况,更新检校针对场景和检校参数已知但需更新的情况.从检校流程角度分析,本文检校方法的自动化程度优于传统棋盘格检校方法,并且为检校提供了数据更多、分布更均匀的三维点.通过在地下车库环境中的实验,验证了本文方法检校的完整性优于基于SLAM的检校方法,检校精度优于传统棋盘格检校方法.
| [1] |
张梁, 徐锦法, 夏青元, 等. 双目立体视觉的无人机位姿估计算法及验证[J]. 哈尔滨工业大学学报, 2014, 46(5): 66 ZHANG Liang, XU Jinfa, XIA Qingyuan, et al. Pose estimation algorithm and verification based on binocular stereo vision for unmanned aerial vehicle[J]. Journal of Harbin Institute of Technology, 2014, 46(5): 66 |
| [2] |
刘昱岗, 王卓君, 王福景, 等. 基于双目立体视觉的倒车环境障碍物测量方法[J]. 交通运输系统工程与信息, 2016, 16(4): 79 LIU Yugang, WANG Zhuojun, WANG Fujing, et al. Vehicle reversing obstacle measurement based on binocular-camera stereo vision[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 79 DOI:10.3969/j.issn.1009-6744.2016.04.012 |
| [3] |
ZHANG Z. Flexible camera calibration by viewing a plane from unknown orientations[C]// The Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999: 666-673.
|
| [4] |
GEIGER A, MOOSMANN F, CARÖ, et al. Automatic camera and range sensor calibration using a single shot[C]// International Conference on Robotics and Automation. Saint Paul: IEEE, 2012: 3936-3943.
|
| [5] |
CARRERA G, ANGELI A, DAVISON A J. SLAM-based automatic extrinsic calibration of a multi-camera rig[C]// International Conference on Robotics and Automation. Shanghai: IEEE, 2011: 2652-2659.
|
| [6] |
HENG L, FURGALE P, POLLEFEYS M. Leveraging image-based localization for infrastructure-based calibration of a multi-camera rig[J]. Journal of Field Robotics, 2015, 32(5): 775 DOI:10.1002/rob.2015.32.issue-5 |
| [7] |
HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2003
|
| [8] |
HARTLEY R, TRUMPF J, DAI Y, et al. Rotation averaging[J]. International Journal of Computer Vision, 2013, 103(3): 267 |
| [9] |
MARKLEY F L, CHENG Y, CRASSIDIS J L, et al. Averaging quaternions[J]. Journal of Guidance Control and Dynamics, 2007, 30(4): 1193 DOI:10.2514/1.28949 |
| [10] |
SCHONBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 4104-4113.
|
| [11] |
李金岭, 刘鹂, 乔书波, 等. 关于三维直角坐标七参数转换模型求解的讨论[J]. 测绘科学, 2010, 35(4): 76 LI Jinling, LIU Li, QIAO Shubo, et al. Discussion on the determination of transformation parameters of 3D Cartesian coordinates[J]. Science of Surveying and Mapping, 2010, 35(4): 76 |
| [12] |
GÁLVEZ-LPEZ D, TARDOS J D. Bags of binary words for fast place recognition in image sequences[J]. IEEE Transactions on Robotics, 2012, 28(5): 1188 DOI:10.1109/TRO.2012.2197158 |
| [13] |
LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: an accurate O(n) solution to the PnP problem[J]. International Journal of Computer Vision, 2009, 81(2): 155 |
| [14] |
FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381 DOI:10.1145/358669.358692 |
| [15] |
FUSIELLO A, TRUCCO E, VERRI A. A compact algorithm for rectification of stereo pairs[J]. Machine Vision and Applications, 2000, 12(1): 16 DOI:10.1007/s001380050120 |
| [16] |
KREŠOI, ŠEGVIC S. Improving the egomotion estimation by correcting the calibration bias[C]//Proceedings of the 10th International Conference on Computer Vision Theory and Applications. Berlin: VISAPP, 2015: 347-356.
|
 2018, Vol. 46
2018, Vol. 46

