2. 中国建筑科学研究院 建筑结构研究所,北京 100020
2. Institute of Building Structures, China Academy of Building Research, Beijing 100020, China
桩-土-结构相互作用已成为高层建筑、桥梁工程、核电站工程等结构抗震设计的研究重点,主要分析方法包括整体分析法和子结构法.整体分析法将上部结构、桩基础和土作为整体进行计算,充分考虑土的非线性、桩和土的相互作用以及土和结构的惯性相互作用,比较符合实际情况.在整体分析法中,场地无限域模拟和土动力模型选择是影响分析精度的2个主要因素.对于无限域模拟,通常在场地四周施加人工边界来模拟远场地基介质的辐射阻尼效应.土动力模型主要有以下2类:等效线性模型(ELM)和基于各向异性运动硬化的塑性模型[1].对于等效线性模型,假定地震过程中土的材料性质是线性的,在每一次迭代计算中土的剪切模量和阻尼比与等效剪切应变相关.与塑性模型相比,等效线性模型能够减少计算难度,同时由于概念明确,因而得到广泛应用.
Ishihara[2]研究发现,强震作用下基础近场区域的土会产生较大的剪切应变,非线性强.若地基土选用等效线性模型,则结构动力分析得到的结果不够精确.Yoshida等[3]也指出,强震作用下土的动力模型采用等效线性模型会使结构的位移峰值增大.然而,当前在进行桩-土-结构相互作用分析时,这些误差往往被忽略.因此,在分析强震作用下桩-土-结构体系的动力响应时,需要对近场区域土的动力模型进行修正.常用的方法是将场地划分为规则的近场区域和远场区域,近场区域采用非线性模型,远场区域采用线性模型.Casciati等[4]建立了桩-土-结构模型并进行动力分析,其中近场区域使用等效线性模型,远场区域使用线性模型,验证了该模型具有良好的精度.然而,地基土的等效剪切模量和阻尼比是通过SHAKE91自由场分析求得后导入三维有限元模型的,未考虑上部结构对地基土的影响.
本文基于已有研究提出一种土动力模型修正方法.首先,建立桩-土-结构有限元模型,其中土动力模型为等效线性模型,并通过分析得到近场区域的尺寸.其次,将近场区域土的剪切模量乘以修正系数,得到修正等效线性模型(MELM),使修正等效线性模型的动力分析结果与摩尔-库伦(MC)模型趋于一致.然后,对100个算例重复上述分析,得到每个模型的修正系数.最终,对修正系数进行回归分析,获得修正系数与结构周期和场地周期的经验公式.
1 有限元模型 1.1 接触结构柱(梁单元)-筏板(实体单元)之间选用动力耦合的方法,耦合梁单元节点和对应柱底面积区域内节点的所有自由度.土(实体单元)-筏板之间选用接触离散算法,法向为硬接触,切向为库伦摩擦模型.桩(梁单元)-土之间采用嵌入模型,土的动力反应将作为位移约束条件施加给桩的节点,实现桩-土动力耦合.
1.2 结构阻尼结构阻尼采用Rayleigh阻尼,阻尼矩阵C写为质量矩阵M和刚度矩阵K的线性比例之和,如下所示:
| $ \mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}} $ | (1) |
由瑞利阻尼理论可知,α和β可以通过下式确定:
| $ {\xi _i} = \frac{\alpha }{{2{\omega _i}}} + \frac{{\beta {\omega _i}}}{2} $ | (2) |
| $ {\xi _j} = \frac{\alpha }{{2{\omega _j}}} + \frac{{\beta {\omega _j}}}{2} $ | (3) |
式中:ξi、ξj为2个振型的阻尼比,取0.02;ωi取结构第1阶频率,ωj取结构第2~20阶频率的平均值[5].
1.3 重力荷载施加已有研究[6]表明:在进行动力分析时,忽略重力将无法考虑初始应力对接触状态的影响,不能真实反映土与结构的受力和变形情况.本文通过2步施加重力荷载:①固定地基土底部边界并对整个模型施加重力加速度场(从0逐渐增加至9.8 m·s-2),得到整个体系的应力状态文件;②将获得的应力状态文件作为初始条件施加到模型上,并同时施加重力加速度9.8 m·s-2,待整个模型的位移趋于稳定,施加地震波进行动力分析.
1.4 等效线性模型在受到地震荷载作用时,土的应力-应变关系表现为复杂的滞回曲线.等效线性模型采用等效剪切模量G和等效阻尼比λ来反映土的滞回曲线,G和λ为应变γ的函数.Hardin等[7]根据试验资料提供了如下经验公式:
| $ \frac{G}{{{G_{\max }}}} = \frac{1}{{1 + \frac{\gamma }{{{\gamma _{\text{d}}}}}}} $ | (4) |
式中:Gmax和γd分别为最大剪切模量和参考应变,可根据试验数据进行确定.λ在工程中通常采用如下经验公式[8]:
| $ \lambda = {\lambda _{\max }}\left( {1 - \frac{G}{{{G_{\max }}}}} \right) $ | (5) |
最大阻尼比λmax可通过试验或经验公式得到.本文中G/Gmax-γ和λ-γ曲线采用孙静[9]对国内不同地区的土样进行共振柱试验的结果.
Abaqus软件中,等效线性模型可以通过Kelvin模型来反映土体在周期载荷下的滞回性.该模型由线弹性弹簧和阻尼装置并联组成,应力-应变关系为
| $ \sigma = E\varepsilon + \eta \dot \varepsilon $ | (6) |
式中:E和η分别为模量系数和黏滞系数;σ为应力;ε为应变.
将一维模型推广至三维模型的情况,如下所示:
| $ {\sigma _{ii}} = v{\varepsilon _V} + {\eta _v}{{\dot \varepsilon }_V} + 2\mu {\varepsilon _{ii}} + 2{\eta _\mu }{{\dot \varepsilon }_{ii}} $ | (7) |
| $ {\sigma _{ij}} = \mu {\gamma _{ij}} + 2{\eta _\mu }{{\dot \gamma }_{ij}} $ | (8) |
式中:ν和μ为拉梅系数;σii和σij分别为正应力和剪应力;εii和γij分别为正应变和剪应变张量;εV=εii+εjj+εkk,ην=2νξ/ω,ημ=2μξ/ω,其中ξ为阻尼比,ω为结构基频.
等效线性模型子程序在Abaqus软件中的开发及使用流程如图 1所示.文献[1]中指出,等效线性模型中,等效剪切应变可取动力作用过程中最大应变与折减系数0.65的乘积.

|
图 1 等效线性模型子程序流程图 Fig.1 Subroutine flow chart of equivalent linear model |
黏弹性人工边界是当前使用较多的一种局部人工边界.刘晶波等[10]基于三维球面波动方程推导出黏弹性边界的法向和切向人工边界条件,并将其等效为人工截断边界上连续分布的并联弹簧-阻尼系统.在Abaqus软件中可以通过在边界节点施加弹簧单元和阻尼器单元来实现,并设置相应的刚度系数Ki和阻尼系数Ci,地震动的输入方法可以通过施加等效荷载来实现[11].
场地范围的选择是桩-土-结构相互作用分析中的重要问题.若截取场地范围过大,则计算时间太长;反之,散射波在人工边界上产生的反射会对计算结果产生较大影响.已有研究对场地的截取范围结论不一[12-13],需要进一步分析场地范围对结构动力响应的影响.
本文结构底部尺寸为20 m×20 m,高度为20 m,对4种场地范围的桩-土-结构模型进行动力分析,得到结构加速度峰值及相对位移峰值(见表 1).结果表明:当场地宽度(100 m×100 m)为结构宽度的5倍时,结构的相对位移及加速度与400 m×400 m场地结果的误差分别为1.42%和1.46%,基本可以消除侧向边界对结构动力响应的影响.
| 下载CSV 表 1 不同场地范围结构的动力响应峰值 Tab.1 Maximum value of structural dynamic response in different site dimensions |
本文研究的是一维地震波输入(x-z截面),故y-z截面方向的宽度可以适当减小,有利于提高计算效率.在表 1选定的场地基础上,增加了2组场地进行了对比分析(见表 2).结果表明:60 m×100 m、80 m×100 m的结果与100 m×100 m的结果十分接近,故最终选用的场地范围为60 m×100 m.
| 下载CSV 表 2 y-z截面不同场地范围结构的动力响应峰值 Tab.2 Maximum value of structural dynamic response in different y-z site dimensions |
本文研究了5层、10层、15层和20层的四跨钢框架.层高3 m,跨度5 m,构件密度7 850 kg·m-3.楼板厚度在0.1~0.2 m之间.5层和10层结构使用筏板基础,15层和20层结构使用桩筏基础.筏板尺寸为22 m×22 m×1 m,群桩按5×5的方式排列,间距为5 m,桩直径为0.5 m.
2.2 场地类型及参数根据《建筑抗震设计规范》,建筑场地类别分为Ⅰ、Ⅱ、Ⅲ、Ⅳ 4类,桩-土-结构相互作用对软土地基上的结构影响较大,故本文只分析Ⅱ、Ⅲ、Ⅳ 3类场地,其中Ⅱ类和Ⅲ类场地各2种.各场地的分层情况和力学参数如表 3所示,泊松比均为0.35.
| 下载CSV 表 3 场地土力学参数 Tab.3 Mechanic parameters of soil at different sites |
已有文献[14]中给出了场地周期的计算公式,如下所示:
| $ T = \sqrt {\sum\limits_{i = 1}^N {{{\left( {\frac{{4{h_i}}}{{{v_i}}}} \right)}^2}\frac{{2{H_i}}}{{{h_i}}}} } $ | (9) |
式中:N为场地土分层数;hi和vi分别为第i层厚度和剪切波速;Hi为第i层中点的深度.
2.3 地震波的筛选及反演本文通过初选(基于台站与地震信息[15])和复选(基于设计反应谱的双频段控制[16])2个步骤筛选符合条件的地震波.
根据各场地的地震反应谱及初选参数从美国太平洋工程地震研究中心数据库(PEER)选出30条地震波,通过文献[15]将我国的地震波参数转换成PEER地震波初选参数,如表 4所示.
| 下载CSV 表 4 地震波初选参数 Tab.4 Primary selection parameters of the earthquake |
复选是将初选的30条地震波调幅至6.2 m·s-2(9度罕遇),分别记录30条地震波的反应谱在[0.1,Tg]和[T1-0.2,T1+0.5]2个区间的值;随后,从30条地震波中选出与目标场地反应谱在2个区间内平均误差最小的5条,用于后续的时程分析.其中,Tg为场地特征周期,T1为结构第1阶周期.
本文采用等效线性水平成层土动力响应分析程序SHAKE91对地表地震波进行反演,该程序基于一维波动理论[12]可以求解出地表层(第N层)和基岩层(第1层)的位移传递函数QN, 1,随后可以确定地基土的底边界(基岩面)的地震波时程(位移、速度、加速度),如下所示:
| $ {Q_{N, 1}} = \frac{{{Q_N}^\prime }}{{{Q_1}^\prime }} = \frac{{{x_1} + {y_1}}}{{{x_N} + {y_N}}} $ | (10) |
式中:QN′和Q1′分别为地表位移和基岩位移相对于入射波的复数传递函数;xi和yi为第i层待定系数,由各层间界面的位移连续和剪应力相等条件确定.
3 近场土修正方法 3.1 地基土修正区域已有文献[2]表明:强震作用下,地基土的剪切应变超过0.9%时,不宜使用等效线性模型.选取100个算例(4种结构、5类场地、5条地震波)计算各桩-土-结构模型超过0.9%剪切应变的地基土区域,并对其中一个算例进行分析(见图 2).水平地震作用下,在基础附近地基土的剪切应变明显大于其他区域,并且数值大于0.9%,需要对该区域的等效线性模型进行修正.其他算例的结果与此算例的分布基本一致.

|
图 2 近场区域土的剪切应变(20层结构,Ⅲ类(1)场地) Fig.2 Shear strain in the near-field soil (20-storey building, soil type Ⅲ(1)) |
基于上述工作进一步确定地基土修正区域的尺寸,可将场地土分成若干区域(SS1~SS5).x-z截面和y-z截面的分区如图 3所示.

|
图 3 场地土分区 Fig.3 Soil partition |
通过动力分析,求出图 3中各区域最大剪切应变的平均值,选取场地土半侧区域的结果进行对比.由图 4可以发现:SS1-1、SS2-1以及SS4-1区域最大剪切应变的平均值大于0.9%,需要对该区域等效剪切模量进行修正.将SS1-1、SS2-1以及SS4-1组合起来,可以得到以下修正区域的范围:宽度为结构宽度的1.5倍,深度为结构宽度的0.5倍.通过对其他算例的分析,发现修正区域的范围和此算例基本一致.
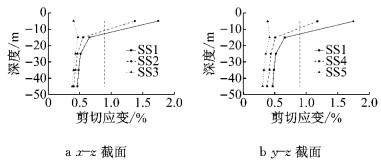
|
图 4 各区域最大剪切应变 Fig.4 Maximum shear strain of each region |
在桩-土-结构模型修正区域中分别采用以下3种土动力模型:①等效线性模型;②修正等效线性模型,修正系数k=Gnew/Gold,其中Gnew和Gold分别为修正后和修正前近场区域土的剪切模量;③摩尔-库伦模型.对每个模型进行动力分析,调节修正等效线性模型的修正系数,直至修正等效线性模型与摩尔-库伦模型中上部结构的动力响应趋于一致.
采用上述方法对100个算例进行分析,并对其中4个算例进行对比,分析不同地基土模型中,上部结构水平位移的比值(见图 5).结果表明:

|
图 5 不同模型结构水平位移对比 Fig.5 Comparison of structural lateral displacement among different models |
(1) 由图 5a和图 5c对比得出,随着场地周期增大,场地变软,等效线性模型与摩尔-库伦模型中结构水平位移的误差越大.
(2) 由图 5a和图 5d对比得出,结构高度越大,等效线性模型与摩尔-库伦模型中结构水平位移的误差越大.
(3) 由图 5a和图 5b对比得出,对相同的桩-土-结构模型,不同地震波作用下位移比ΔELM/ΔMC的值非常接近,表明同一模型下不同地震波对动力分析结果影响很小.
(4) 在强震作用下,采用修正等效线性模型得到的结构水平位移,比等效线性模型更接近摩尔-库伦模型的结果(ΔMELM/ΔMC的值比ΔELM/ΔMC更接近1),故本文针对等效线性模型提出的修正方法是合适的.
3.3 近场区域修正系数及回归公式采用上述方法对100个算例进行动力分析,并分别得到相应的修正系数,以20层结构的分析结果(见表 5)为例,可以发现相同桩-土-结构模型在不同地震波作用下的修正系数非常接近,这是因为在第2.3节中,每一组地震波都是基于相同的目标地震反应谱选出来的.
| 下载CSV 表 5 20层结构不同场地修正系数 Tab.5 Modified coefficients of 20-storey building in different sites |
图 6的点为每一个桩-土-结构模型修正系数的平均值,采用回归分析对每一条曲线进行拟合,得到便于工程使用的经验公式.
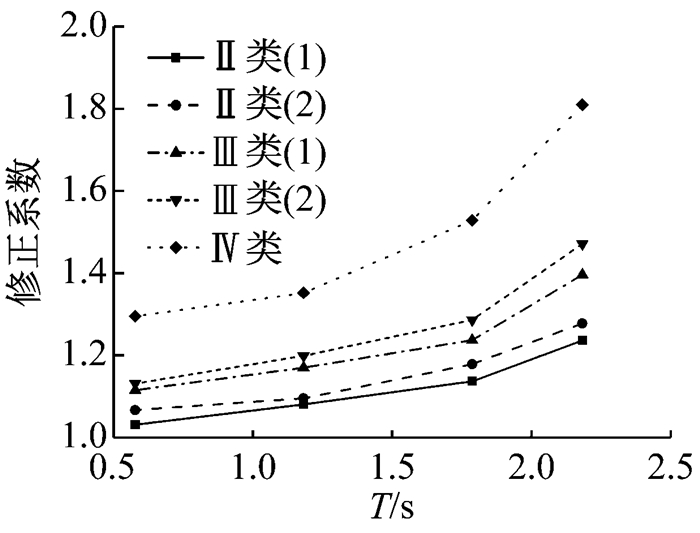
|
图 6 剪切模量修正系数 Fig.6 Modified coefficients of shear modulus |
各曲线的经验公式可统一表示为
| $ k = \left( {a + bT} \right){T^2} + \left( {c + dT} \right){T_1} + e $ | (11) |
式中:a、b、c、d、e为参数,根据不同的场地条件取相应值(见表 6).修正系数的计算值和真实值的平均误差在2%以内.
| 下载CSV 表 6 经验公式参数 Tab.6 Parameters of the empirical equation |
为验证本文提出的修正方法和修正系数经验公式,采用已有试验算例[17]进行验证.选用文献中的模型P4-A2,计算模型如图 7所示,基岩输入地震波为El-Centro波,调幅峰值为0.2g.
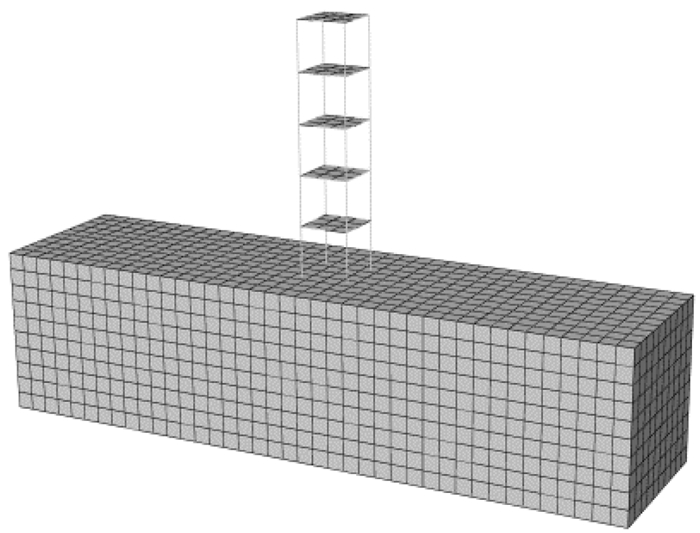
|
图 7 算例的三维有限元模型 Fig.7 Three-dimensional finite element model of the example |
分别采用摩尔-库伦模型、修正等效线性模型和等效线性模型土进行分析,得到结构顶部的加速度峰值如表 7所示.3种有限元模型计算结果与试验结果非常接近,误差分别为2.16%、3.24%、3.96%.这是因为入射地震波峰值仅为0.2g,未能使地基土产生较强的非线性,等效线性模型和非线性模型结果趋于一致,但是分析结果验证了本文有限元模型的正确性.
| 下载CSV 表 7 结构顶部加速度峰值 Tab.7 Peak values of acceleration at the top of structure |
随后将基岩地震波调幅至0.62g,从基岩重新输入,分别采用摩尔-库伦模型、修正等效线性模型和等效线性模型进行分析,得到结构的水平位移和层间剪力,如图 8所示.结果表明:对于试验算例,采用修正等效线性模型得到的水平位移和层间剪力与摩尔-库伦模型的平均误差分别为2.39%和3.57%,小于与等效线性模型的平均误差(6.45%和9.83%),说明了本文提出修正方法的正确性.
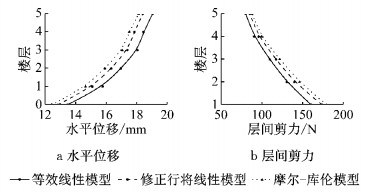
|
图 8 不同模型结构水平位移和层间剪力对比 Fig.8 Comparison of structural lateral displacement and storey shear among different models |
(1) 强震作用下,桩-土-结构模型的基础附近会出现强非线性区域,其宽度为超出结构宽度的50%,深度为结构宽度的50%.
(2) 本文分析了100个算例,得到桩-土-结构模型近场区域的修正系数,范围在1.03至1.81之间,并且随着场地变软,结构变高,修正系数增大.
(3) 本文对所有算例的修正系数进行回归分析,得到修正系数的经验公式,公式计算值和真实值的误差不超过2%.
(4) 在进行桩-土-结构相互作用分析时,相比等效线性模型而言,采用修正等效线性模型得到结构的动力响应与摩尔-库仑模型的结果更为接近,故本文提出的修正方法和经验公式具有较好的适用性和正确性.
| [1] |
郑颖人, 孔亮. 岩土塑性力学[M]. 北京: 中国建筑工业出版社, 2010 ZHENG Yingren, KONG Liang. Geotechnical plastic mechanics[M]. Beijing: China Architecture & Building Press, 2010 |
| [2] |
ISHIHARA K. Soil behavior in earthquake geotechnics[M]. Oxford: Clarendon Press, 1996
|
| [3] |
YOSHIDA N, KOBAYASHI S, SUETOMI I. Equivalent linear method considering frequency dependent characteristics of stiffness and damping[J]. Soil Dynamics & Earthquake Engineering, 2002, 22(3): 205 |
| [4] |
CASCIATI S, BORJA R I. Dynamic FE analysis of South Memnon Colossus including 3D soil foundation structure interaction[J]. Computers & Structures, 2004, 82(20): 1719 |
| [5] |
李曰辰.考虑土-桩-结构相互作用的PHC管桩地震响应研究[D].武汉: 武汉大学, 2013. LI Yuechen. Study on earthquake response of PHC pipe pile considering soil-pile-structure interaction[D]. Wuhan: Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1013210224.htm |
| [6] |
YAZDCHI M, KHALILI N, VALLIAPPAN S. Dynamic soil structure interaction analysis via coupled finite element boundary element method[J]. Soil Dynamics & Earthquake Engineering, 1999, 18(7): 499 |
| [7] |
HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: design equations and curves[J]. Geotechnical Special Publication, 1972, 98(118): 667 |
| [8] |
张克绪, 谢君斐. 土动力学[M]. 北京: 地震出版社, 1989 ZHANG Kexu, XIE Junfei. Soil dynamics[M]. Beijing: Seismological Press, 1989 |
| [9] |
孙静.岩土动剪切模量阻尼试验及应用研究[D].哈尔滨: 中国地震局工程力学研究所, 2004. SUN Jing. Experiment and application studies on dynamic shear modulus and damping of geotechnical media[D]. Harbin: Institute of Engineering Mechanics of China Seismological Bureau, 2004. http://cdmd.cnki.com.cn/Article/CDMD-85406-2004102031.htm |
| [10] |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46 LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three dimensional visco elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46 DOI:10.3969/j.issn.1000-4750.2005.06.008 |
| [11] |
刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998(3): 55 LIU Jingbo, LÜ Yandong. A direct method for analysis of dynamic soil-structure interaction[J]. China Civil Engineering Journal, 1998(3): 55 |
| [12] |
陈波, 吕西林, 李培振, 等. 均匀土-桩基-结构相互作用体系的计算分析[J]. 地震工程与工程振动, 2002, 22(3): 91 CHEN Bo, LÜ Xilin, LI Peizhen, et al. Computational analysis of dynamic homogeneous soil-pile-structure interaction[J]. Earthquake Engineering and Engineering Dynamics, 2002, 22(3): 91 DOI:10.3969/j.issn.1000-1301.2002.03.016 |
| [13] |
楼梦麟, 潘旦光, 范立础. 土层地震反应分析中侧向人工边界的影响[J]. 同济大学学报(自然科学版), 2003, 31(7): 757 LOU Menglin, PAN Danguang, FAN Lichu. Effect of vertical artificial boundary on seismic response of soil layer[J]. Journal of Tongji University (Natural Science), 2003, 31(7): 757 DOI:10.3321/j.issn:0253-374X.2003.07.001 |
| [14] |
齐文浩, 薄景山, 刘红帅. 水平成层场地基本周期的估算公式[J]. 岩土工程学报, 2013, 47(4): 779 QI Wenhao, BO Jingshan, LIU Hongshuai. Fundamental period formula for horizontal layered soil profiles[J]. Chinese Journal of Geotechnical Engineering, 2013, 47(4): 779 |
| [15] |
冀昆, 温瑞智, 任叶飞. 中国抗震规范强震记录选取的初选条件研究[J]. 防灾减灾工程学报, 2016(1): 44 JI Kun, WEN Ruizhi, REN Yefei. Study on the initial of selection criteria strong motion records for Chinese seismic code[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016(1): 44 |
| [16] |
杨溥, 李英民, 赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6): 33 YANG Pu, LI Yingmin, LAI Ming. A new method for selecting inputting waves for time-history analysis[J]. China Civil Engineering Journal, 2000, 33(6): 33 DOI:10.3321/j.issn:1000-131X.2000.06.005 |
| [17] |
楼梦麟, 王文剑, 马恒春, 等. 土-桩-结构相互作用体系的振动台模型试验[J]. 同济大学学报(自然科学版), 2001, 29(7): 763 LOU Menglin, WANG Wenjian, MA Hengchun, et al. Study on soil-pile-structure interaction system by shaking table model test[J]. Journal of Tongji University(Natural Science), 2001, 29(7): 763 DOI:10.3321/j.issn:0253-374X.2001.07.002 |
 2018, Vol. 46
2018, Vol. 46

