2. 武警后勤学院 后勤保障系,天津 300309;
3. 同济大学 土木工程防灾国家重点实验室,上海 200092
2. Logistics Support Department, Logistics University of PAP, Tianjin 300309, China;
3. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
拱形结构受力性能优异,被广泛应用于地下防护结构.现行抗爆规范[1-3]确定:拱表面承受荷载时均视顶部爆炸为最危险点,并且基于单自由度体系,按等效均布荷载进行抗爆计算.计算过程不考虑荷载的偏压效应.洞口部位作为防护工程的重点部位,通常为浅埋,不能再沿用远场等效均布荷载假设.现阶段研究表明,圆拱的最危险受荷点不是拱顶而是1/4跨附近[4],拱结构在不对称荷载作用下的承载能力小于对称荷载作用下的承载能力[5].按照现有设计法对结构承载能力估计结果偏高,结构将偏于危险.因此,亟需针对拱形结构在侧向爆炸下的性能,尤其是塑性破坏过程开展深入研究,为工程设计提供理论指导.
目前地下防护结构在爆炸下响应的理论研究多集中于正向爆炸下的弹性响应阶段[6-7].Weidlinger等[8]用单自由度体系分析地下箱形结构的弹性响应,Ma等[9]和Chen等[10]分别基于连续分布体系分析了地下箱形结构和地下拱形结构的弹性响应.然而,对浅埋拱结构在侧向偏角作用下的理论研究较少.对于呈一定偏角的侧向爆炸,陈海龙等[11]讨论了荷载为均布时拱形结构的受荷范围,得到了远场任意角度爆炸荷载作用下结构弹性响应的解析解,并指出拱结构受远场侧爆时弹性最大位移约出现在40°处.吴永忠[12]的研究表明,波入射角度对结构的影响大于正压作用时长的影响,尤以45°入射时结构动力响应最为剧烈.上述研究未考虑近场侧向荷载非均匀、不对称的特点,而且仅限于弹性范围内的地下拱形结构在侧向爆炸作用下的动力响应,并未涉及塑性破坏阶段.
爆炸荷载具有高频成分丰富、应变速率效应明显等特点,因而钢筋混凝土拱形结构的破坏形态包含整体弯曲破坏、局部脆性剪切破坏等多种形式.20世纪70年代末至80年代初在美国进行的代号为FOAM HEST的一系列现场模型试验也发现,土中浅埋钢筋混凝土结构在脉冲荷载作用下部分结构发生了脆性剪切破坏.国内外学者对拱形结构破坏形态进行了细致研究[13-14].本文研究的塑性破坏为整体弯曲破坏,主要发生在拱结构跨度较大[15]、纵筋配筋率较低而拉筋配筋率较高[16]等情况.
对于满足发生整体弯曲破坏的拱结构的研究,Pippard等[17]认为,当拱内弧面和外弧面上出现4个铰后,结构就会因为失去整体稳定性而发生倒塌,该理论被称为四铰破坏机制.Heyman[18]基于以上机制提出图形方法来计算地下圬工拱结构受力情况,并指出荷载作用在1/4拱跨上为最不利位置,此时拱结构将在拱顶、2个拱脚以及荷载作用点发生塑性铰.以上学者的研究都基于材料不会受压破坏的假设.Chen等[19]基于四铰破坏机制并结合虚功原理,提出了浅埋拱形结构在集中荷载下极限承载力的计算方法,并与试验结果进行对比验证.对于上述结构,四铰破坏机制成为研究拱结构塑性破坏的常用方法,更多学者[20-21]基于该机制开展了研究.以上方法均仅针对地下结构塑性破坏的最终状态,忽略结构塑性破坏的过程,因此无法确定塑性铰的出现顺序以及截面的破坏模式.此外,现阶段研究主要考虑截面弯矩的影响,对于弯矩和轴力的相关关系尚未进行深入研究.
本文取较为典型的圆拱为研究对象,考虑近场侧向荷载的非均布性、不对称性、局部性等特征,根据最大抗力等效原则用动效系数将爆炸动荷载转化为等效静荷载函数.基于理想塑性铰的假设计算结构逐步产生塑性铰的过程,并考虑截面上弯矩和轴力相关的塑性流动法则,进而分析塑性铰截面的破坏模式和结构的塑性破坏过程.
1 侧向爆炸荷载 1.1 自由场荷载拱截面为矩形.设E为弹性模量,A为截面积,I为截面惯性矩,μ为单位长度质量,ρ为结构密度,且μ=ρA.如图 1所示,拱开角为2φ0,r为拱结构内表面半径,R0为爆源O到投影点(规定拱结构上距爆源最近点为投影点)的距离,R为爆源O到拱结构表面任意点的距离,HG为爆源O到地面垂直距离.爆源O(X0, Y0)位于拱结构的侧上方,爆炸偏角为β,计算规定在第一象限为正,第二象限为负;C(Xi, Yi)为土与结构接触点,D(Xj, Yj)为结构与C(Xi, Yi)接触点.φ1表示C点和爆源O的连线与结构圆心O′和爆源O的连线的夹角,φ2表示C点和结构圆心O′的连线与爆源O和结构圆心O′的连线的夹角,θ为结构上的点与Y轴夹角,α为结构迎爆面对应角度的一半,θ1为迎爆左边界与Y轴夹角,θ2为迎爆右边界与Y轴夹角.
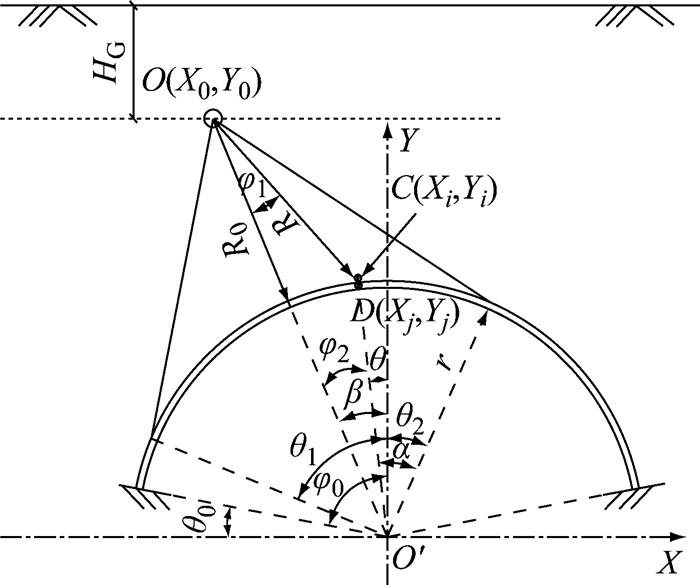
|
图 1 拱结构爆炸受荷示意图 Fig.1 Geometry of arch structure under side blast loads |
点爆炸产生的冲击波在地下介质中传播、衰减,产生的自由场应力σ1i(R, t)可以用空间分布函数σ0(R)和时间分布函数f(t)共同描述[1].空间分布函数
| $ {\sigma _0}\left( R \right) = 48.77F{\rho _{\rm{s}}}{c_{\rm{s}}}{\left( {\frac{{2.78R}}{{\sqrt[3]{{{W_{{\rm{tnt}}}}}}}}} \right)^{ - n}} $ | (1) |
式中:F为耦合系数;ρscs为介质声阻抗;Wtnt为装药量;n为介质衰减系数.时间分布函数
| $ f\left( t \right) = \left\{ \begin{array}{l} 1 - \frac{t}{{{t_{\rm{d}}}}},\;\;\;\;0 \le t \le {t_{\rm{d}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;t > {t_{\rm{d}}} \end{array} \right. $ | (2) |
式中:t为荷载作用时间;td为等效荷载作用时间.因此,自由场应力
| $ {\sigma _{1i}}\left( {R,t} \right) = {\sigma _0}\left( R \right)f\left( t \right) $ | (3) |
爆炸冲击波经过岩土介质传递,作用到拱结构表面.在岩土与结构界面上,通常会发生以下3种界面效应:压缩波的反射、横向稀疏波和边缘效应[22].由于拱结构表面的曲率效应,拱结构界面效应比平顶结构弱[23],因此本文在探讨拱表面荷载分布规律时,忽略横向稀疏波和边缘效应.
当爆炸荷载通过地下介质传递到结构表面时,C点的自由场应力为σ1i(R, t).由于相邻土体的侧向约束作用,C点的侧向土压应力可以表示为
| $ {\sigma _{2i}}\left( {R,t} \right) = \xi {\sigma _{1i}}\left( {R,t} \right) $ | (4) |
式中:ξ为土体的侧压力系数.根据三角形正弦定理
| $ R = \left( {{R_0} + r} \right)\frac{{\sin {\varphi _2}}}{{\sin \left( {{\rm{ \mathit{ π} }} - {\varphi _1} - {\varphi _2}} \right)}} $ | (5) |
将式(1)和式(2)代入式(3)和式(4)中,C点的自由场应力和侧向土压应力分别表示为
| $ \begin{array}{l} {\sigma _{1i}}\left( {{\varphi _1},{\varphi _2},t} \right) = \\ \;\;\;\;\;48.77F{\rho _{\rm{s}}}{c_{\rm{s}}}{\left( {\frac{{2.78\left( {{R_0} + r} \right)\sin {\varphi _2}}}{{\sin \left( {{\rm{ \mathit{ π} }} - {\varphi _1} - {\varphi _2}} \right)\sqrt[3]{{{W_{{\rm{tnt}}}}}}}}} \right)^{ - n}}f\left( t \right) \end{array} $ | (6) |
| $ \begin{array}{l} {\sigma _{2i}}\left( {{\varphi _1},{\varphi _2},t} \right) = \\ \;\;\;\;\;\xi 48.77F{\rho _{\rm{s}}}{c_{\rm{s}}}{\left( {\frac{{2.78\left( {{R_0} + r} \right)\sin {\varphi _2}}}{{\sin \left( {{\rm{ \mathit{ π} }} - {\varphi _1} - {\varphi _2}} \right)\sqrt[3]{{{W_{{\rm{tnt}}}}}}}}} \right)^{ - n}}f\left( t \right) \end{array} $ | (7) |
在自由场应力σ1i和侧向土压应力σ2i的共同作用下,D点的法向入射应力
| $ \begin{array}{*{20}{c}} {{\sigma _{3i}}\left( {{\varphi _1},{\varphi _2},t} \right) = {\sigma _{1i}}\left( {{\varphi _1},{\varphi _2},t} \right)\left( {\xi + \left( {1 - } \right.} \right.}\\ {\left. {\left. \xi \right){{\cos }^2}\left( {{\varphi _2} + {\varphi _1}} \right)} \right)} \end{array} $ | (8) |
如图 1所示,拱结构各相关角度有以下几何关系:
| $ \cos {\varphi _2} = \cos \left( {\beta - \theta } \right) $ | (9) |
| $ \sin {\varphi _2} = \sin \left( {\beta - \theta } \right) $ | (10) |
| $ \cos {\varphi _1} = \frac{{r + {R_0} - r\cos \left( {\beta - \theta } \right)}}{R} $ | (11) |
| $ \sin {\varphi _1} = \frac{r}{R}\sin \left( {\beta - \theta } \right) $ | (12) |
基于式(9)~(12),D点的法向入射应力
| $ \begin{array}{l} {\sigma _{3i}}\left( {\theta ,t} \right) = \\ \;\;\;\;48.77F{\rho _{\rm{s}}}{c_{\rm{s}}}{\left( {\frac{{ - 2.78\left( {{R_0} + r} \right)\sin \left( {\beta - \theta } \right)}}{{\upsilon \sqrt[3]{{{W_{{\rm{tnt}}}}}}}}} \right)^{ - n}}f\left( t \right) \end{array} $ | (13) |
| $ \begin{array}{l} \upsilon = \frac{{r\sin \left( {\beta - \theta } \right)\cos \left( {\beta - \theta } \right)}}{R} + \\ \;\;\;\;\;\;\frac{{r + {R_0} - {R_0}\cos \left( {\beta - \theta } \right)}}{R}\sin \left( {\beta - \theta } \right) \end{array} $ | (14) |
近场爆炸下,结构部分区域受荷.如图 1所示,爆源位于结构侧上方,当忽略波的绕射作用时,荷载在结构上的作用范围边界可以通过爆源和结构外表面的切线求得,具体形式如下所示:
| $ \left[ {{\theta _1},{\theta _2}} \right] = \left\{ \begin{array}{l} \left[ {\beta - \alpha ,\alpha + \beta } \right],\;\;\;\;\;\left| {{X_0}} \right| \le \left| r \right|\\ \left[ { - {\rm{ \mathit{ π} }}/2,\alpha + \beta } \right],\;\;\;\;\;\left| {{X_0}} \right| > \left| r \right| \end{array} \right. $ | (15) |
θ1、θ2、β、α对应范围如图 1所示,且
依据波动理论,在两者界面上,波的传递总满足以下方程:
| $ \left\{ \begin{array}{l} {\sigma _{\rm{j}}} = {\sigma _{\rm{i}}} + {\sigma _{\rm{f}}}\\ {{\dot u}_{\rm{j}}} = {{\dot u}_{\rm{i}}} - {{\dot u}_{\rm{f}}} \end{array} \right. $ | (16) |
式中:σj、
| $ {\sigma _{{\rm{f0}}}}\left( {\theta ,t} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ 2{\sigma _{3i}} - {\rho _{\rm{s}}}{c_{\rm{s}}}\dot u,\\ 0, \end{array}&\begin{array}{l} - {\theta _0} \le \theta < {\theta _1}\\ {\theta _1} \le \theta < {\theta _2}\\ {\theta _2} \le \theta \le {\theta _0} \end{array} \end{array}} \right. $ | (17) |
式中:
对于进入塑性阶段的拱结构,基于延性比设计目标,依据最大抗力等效原则,利用动效系数Kd将爆炸动荷载转化为等效静荷载函数[24].动效系数Kd的计算参考规范推荐方法如下所示:
| $ {K_{\rm{d}}} = \frac{\eta }{{\frac{{2\sqrt {2\left[ \gamma \right] - 1} }}{{\omega {t_0}}} + \frac{{2\left[ \gamma \right] - 1}}{{2\left[ \gamma \right]}}\frac{{\omega {t_0}}}{{\omega {t_0} + 4}}}} $ | (18) |
式中:η为动荷载升压时间对结构动力响应的影响系数;ω为等效单自由度体系的自振圆频率;[γ]为结构或构件的允许延性比;t0为动荷载等效作用时间,一般可取t0=td.Kd受结构截面、边界约束、设计延性比以及荷载作用时间等因素影响.
侧向点爆炸作用下浅埋拱结构受到的荷载具有非均布性、不对称性、局部性等特征,荷载分布如图 2所示.最终作用在结构表面的等效静应力
| $ {\sigma _{{\rm{fd}}}}\left( {\theta ,t} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ {K_{\rm{d}}}\left( {2{\sigma _{3i}} - {\rho _{\rm{s}}}{c_{\rm{s}}}\dot u} \right),\\ 0, \end{array}&\begin{array}{l} - {\theta _0} \le \theta < {\theta _1}\\ {\theta _1} \le \theta < {\theta _2}\\ {\theta _2} \le \theta \le {\theta _0} \end{array} \end{array}} \right. $ | (19) |
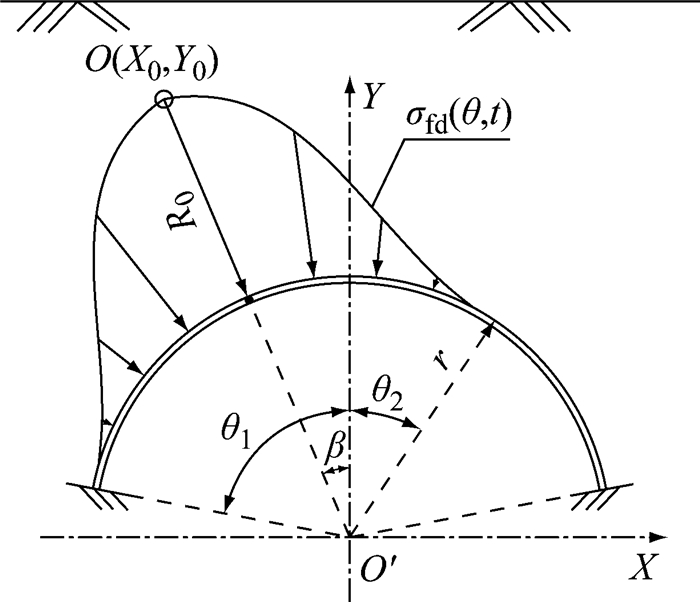
|
图 2 侧向点爆炸作用下拱表面荷载分布 Fig.2 Load distribution of arch structure under side blast loads |
在侧向爆炸等效静荷载作用下,圆拱结构截面在受荷过程中产生塑性变形,截面刚度下降.当变形增加到一定程度时,截面变形增加,但内力不再增加,此时结构截面形成塑性铰.两侧钢筋产生塑性变形,截面发生塑性转动,并提供相应的塑性极限承载力.已有研究表明[4],可以将截面受压边缘混凝土达到极限压应变作为塑性铰的形成条件.钢筋混凝土结构的截面变形主要受到轴力和弯矩共同影响,因此将轴力和弯矩共同作用下的截面内力作为截面塑性破坏的准则.
2.2 偏压状态当轴力为压力时,大小偏压界限状态的破坏特征为受拉侧钢筋达到屈服强度,受压区边缘的混凝土也达到极限压应变而破坏.根据受压区边缘混凝土的极限压应变εcu和受拉钢筋屈服应变εy,可确定混凝土界限受压区高度
| $ {x_{{\rm{cb}}}} = \frac{{\lambda {\varepsilon _{{\rm{cu}}}}}}{{\left( {{\varepsilon _{{\rm{cu}}}} + {\varepsilon _{\rm{y}}}} \right)}}{h_0} = \frac{\lambda }{{\left( {1 + {f_{\rm{y}}}/{\varepsilon _{{\rm{cu}}}}{E_{\rm{s}}}} \right)}} $ | (20) |
式中:λ为混凝土受压区等效为矩形应力分布的系数; fy为钢筋受拉屈服应力设计值; Es为钢筋弹性模量;h0为截面有效高度.将xcb作为判断大小偏压的条件,如下所示:
(1) xc≤xcb,截面发生大偏压破坏.
(2) xc>xcb,截面发生小偏压破坏.
xc为截面实际受压区高度,且x=λxc.截面进入大偏压状态时,受拉侧钢筋先屈服,受压侧的混凝土再达到极限应变,截面被压溃.将受压侧钢筋刚好进入受压屈服的状态作为临界状态,根据平截面假定,大偏压混凝土受压区临界高度满足下式:
| $ {x_{{\rm{cb1}}}} = \frac{{{\varepsilon _{{\rm{cu}}}}{a_{{\rm{s1}}}}}}{{{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{sf}}}}}} $ | (21) |
式中:xcb1为大偏压混凝土受压区临界高度;εsf为钢筋受压屈服应变;as1为受压钢筋形心距受压侧混凝土边缘垂直距离.
当混凝土受压区高度xcb≥xc≥xcb1时,在对称配筋下,两侧钢筋都能进入屈服阶段,截面轴力和弯矩的相关函数表达式为
| $ {M_{\rm{u}}} = - \frac{{N_{\rm{u}}^2}}{{2{\alpha _1}{f_{\rm{c}}}b}} + \frac{h}{2}{N_{\rm{u}}} + {f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) $ | (22) |
式中:Mu、Nu分别为截面塑性极限弯矩和轴力;α1为混凝土强度调整系数;fc为混凝土抗压强度设计值;b、h分别为截面宽度和高度;As为受拉钢筋面积.
当混凝土截面实际受压区高度xc<xcb1时,受压侧钢筋不能屈服,截面轴力和弯矩的相关函数表达式为
| $ \begin{array}{l} {M_{\rm{u}}} = {N_{\rm{u}}}\left( {\frac{h}{2} - {a_{\rm{s}}}} \right) + x\left( {{a_{{\rm{s1}}}} - \frac{x}{2}} \right){\alpha _1}{f_{\rm{c}}}b + \\ \;\;\;\;\;\;\;\;{f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) \end{array} $ | (23) |
式中:x=(Nu-σs1As1+fyAs)/α1fcb,其中As1为受压钢筋面积,σs1为受压钢筋实际应力; as为受拉钢筋形心距受压侧混凝土边缘垂直距离.
当混凝土截面实际受压区高度xc>xcb时,截面形成小偏压破坏,受压侧钢筋先屈服,受压侧混凝土再达到极限应变.截面轴力和弯矩的相关函数表达式为
| $ \begin{array}{l} {M_{\rm{u}}} = - {N_{\rm{u}}}\left( {\frac{h}{2} - {a_{\rm{s}}}} \right) + x\left( {{h_0} - 0.5x} \right){\alpha _1}{f_{\rm{c}}}b + \\ \;\;\;\;\;\;\;\;{f_{{\rm{y1}}}}{A_{{\rm{s1}}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) \end{array} $ | (24) |
式中:x=(Nu+σsAs-fy1As1)/α1fcb, 其中σs为受拉侧钢筋实际应力, fy1为钢筋受压屈服应力设计值.
2.3 偏拉状态当截面轴力为拉力时,对应大小偏拉破坏.判断大小偏拉破坏的条件如下所示:
(1) xc>0,截面发生大偏拉破坏.
(2) xc≤0,截面发生小偏拉破坏.
截面进入大偏拉状态时,靠近轴力的钢筋先进入屈服状态,之后受压区混凝土边缘达到极限压应变,被压溃.当远离轴力的钢筋进入受拉屈服时受压区混凝土边缘也刚好达到极限压应变的状态为临界状态,根据平截面假定,大偏拉混凝土受压区临界高度xcb2满足下式:
| $ {x_{{\rm{cb2}}}} = \frac{{{\varepsilon _{{\rm{cu}}}}{a_{{\rm{s1}}}}}}{{{\varepsilon _{{\rm{cu}}}} + {\varepsilon _{{\rm{sf}}}}}} $ | (25) |
当混凝土截面实际受压区高度0 < xc < xcb2时,两侧钢筋都进入屈服状态,靠近和远离轴力的钢筋均受拉,截面轴力和弯矩的相关函数表达式为
| $ \begin{array}{l} {M_{\rm{u}}} = \left( {2{f_{\rm{y}}}{A_{\rm{s}}} - {N_{\rm{u}}}} \right)\left( {{a_{{\rm{s1}}}} - \frac{{2{f_{\rm{y}}}{A_{\rm{s}}} - {N_{\rm{u}}}}}{{2{\alpha _1}{f_{\rm{c}}}b}}} \right) - \\ \;\;\;\;\;\;\;\;\;\left( {\frac{h}{2} - {a_{{\rm{s1}}}}} \right){N_{\rm{u}}} + {f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) \end{array} $ | (26) |
当混凝土截面实际受压区高度xc≥xcb2时,远离轴力的钢筋未进入受拉屈服状态,截面轴力和弯矩的相关函数表达式为
| $ \begin{array}{l} {M_{\rm{u}}} = - {N_{\rm{u}}}\left( {\frac{h}{2} - {a_{\rm{s}}}} \right) + x\left( {{a_{{\rm{s1}}}} - 0.5x} \right){\alpha _1}{f_{\rm{c}}}b + \\ \;\;\;\;\;\;\;\;{f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) \end{array} $ | (27) |
式中:x=(Nu+σs1As1-fyAs)/α1fcb.
当混凝土截面实际受压区高度xc≤0时,截面对应小偏拉破坏.截面不存在混凝土受压区域,轴向拉力全部由受拉钢筋承担.当两侧钢筋都进入屈服状态,截面变形会持续增加,形成塑性铰.在对称配筋时,靠近轴力的钢筋先进入屈服状态,远离轴力的钢筋随后也进入屈服状态.因此,轴力和弯矩的相关函数表达式为
| $ {M_{\rm{u}}} = \left( {{A_{\rm{s}}} - \frac{{{N_{\rm{u}}}}}{{2{f_{\rm{y}}}}}} \right){f_{\rm{y}}}\left( {{h_0} - {a_{{\rm{s1}}}}} \right) $ | (28) |
综上所述,钢筋混凝土圆拱结构截面在弯矩和轴力共同作用下,会产生不同的破坏模式,对应不同的轴力和弯矩相关函数表达式.考虑对称配筋下,截面能承受的弯矩和轴力极限组合必然在图 3中的曲线上.图中B为矩形截面宽度,H为截面高度.以上各个截面破坏模式下的弯矩和轴力的表达式为
| $ {M_{\rm{u}}} \sim {N_{\rm{u}}} $ | (29) |
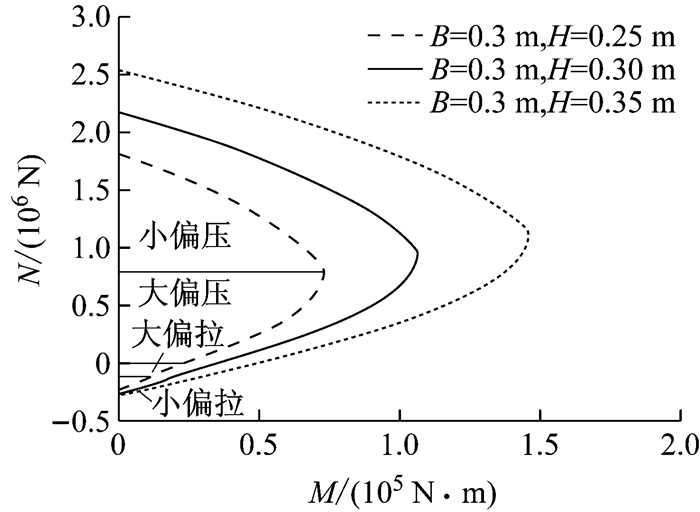
|
图 3 不同截面对应的塑性准则 Fig.3 Plasticity criterion corresponding to different sections |
式(29)称为截面塑性准则.
3 结构塑性破坏 3.1 演化原理如图 4所示,本文预测地下圆拱结构在侧向爆炸荷载作用下仍遵循四铰破坏机制,且结构在塑性发展过程中塑性铰点截面内力满足弯矩-轴力相关曲线,下文重点分析结构在塑性阶段的演化过程.采用理想塑性铰表示结构塑性发展的最大位置,以混凝土截面受压边缘达到极限压应变作为截面塑性发展的极限,具体塑性准则如图 3所示,相关曲线中Mu~Nu数值可根据计算得到.
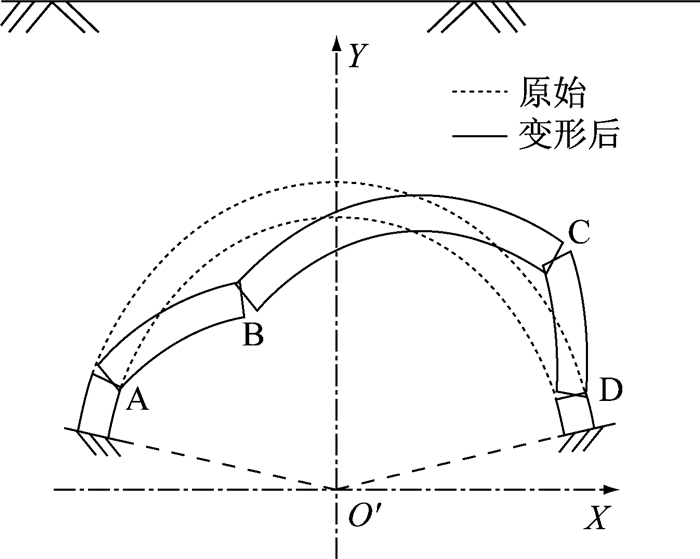
|
图 4 拱结构四铰破坏模式 Fig.4 Four-hinge collapse mode of arch structure |
(1) 假设结构发生整体破坏,在侧向点爆炸作用下结构将产生4个塑性铰.
(2) 假设结构产生的每个塑性铰都为理想塑性铰,塑性段长度为零,除塑性段外结构仍保持弹性.
(3) 结构产生的每个塑性铰始终满足弯矩-轴力塑性准则,即塑性铰内力组合对应的点始终在如图 3所示的弯矩-轴力相关曲线上.
(4) 结构产生的每个塑性铰都始终满足平截面假定,计算时忽略混凝土的抗拉强度.
塑性破坏计算流程的主体为循环迭代阶段,包含以下4个部分:第一部分为结构各截面内力求解,确定结构在不对称性、非均匀性、局部分布的侧向爆炸荷载下每个截面的弯矩、轴力和剪力;第二部分为截面内力状态的判别,基于截面塑性准则确定结构每个截面是否能形成塑性铰,以及对应的截面破坏模式;第三部分为荷载迭代,更新荷载得到新塑性铰形成对应的临界荷载;第四部分为截面剪切破坏验算,确保结构不发生局部剪切破坏.以上4个部分的每一次循环都可确定一个新塑性铰的位置以及铰点内力.形成新塑性铰后,结构整体刚度将更新,但塑性铰截面弯矩和轴力始终满足式(29).当结构尚未形成4个塑性铰时,需循环以上4个部分,直到满足四铰破坏机制,从而得到圆拱结构塑性破坏的全过程.以上迭代过程可基于Matlab编程实现.
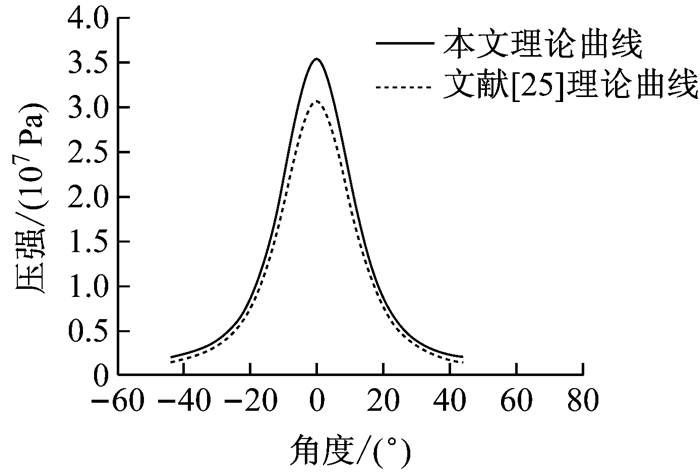
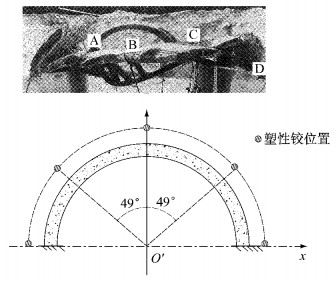
4 参数分析 4.1 有效性验证目前关于侧向点爆炸作用下圆拱结构的理论分析和试验均较少,但当爆炸偏角趋于0°时,上述侧向爆炸下理论可退化为正向爆炸结果.在正向爆炸下,爆炸偏角β=0°.结构表面荷载分布呈现对称性,分布如图 5所示.图中实线为本文理论曲线,虚线为金丰年等[25](取综合反射系数1.6)对于正向爆炸下结构表面荷载的理论计算结果,两者基本吻合.Kiger等[26]对直径为7英尺(2.14 m)、厚度为4英寸(10.16 cm)、开角为180°的两端固支浅埋圆拱结构在正向爆炸(对称荷载)作用下的塑性破坏进行试验研究.结果表明,圆拱结构分别在拱顶、两侧拱脚和两侧45°位置处产生较大裂缝,形成塑性铰,结构破坏满足五铰破坏机制.拱顶和两侧45°位置处的混凝土被压碎,钢筋屈服并裸露,裂缝贯通;两侧拱脚裂缝相对较小,钢筋未裸露,混凝土绕底部墩旋转约5.5°.试验中,拱顶和两侧拱肩破坏明显大于拱脚,初步认定拱脚的塑性铰最后产生.如图 6所示,理论计算下圆拱结构塑性铰开展顺序依次为拱顶、两侧拱肩、两侧拱脚,因此理论计算中塑性铰的位置和开展顺序基本符合试验结果.
|
图 5 正向爆炸下荷载分布 Fig.5 Load distribution of arch structure under vault blast loads |
|
图 6 正向爆炸下塑性铰点位置 Fig.6 Hinge location of arch structure under vault blast loads |
为研究浅埋圆拱结构在侧向点爆炸荷载作用下的塑性破坏规律,取结构开角2φ0=180°的两端固支圆拱.爆炸偏角依次为-15°、-30°、-45°、-60°、-75°、-90°(遵循第一象限为正,第二象限为负的规定),比例爆距为0.5 m·kg-1/3,爆源到地面垂直距离HG=1.2 m;拱结构内表面半径r=10 m,拱结构截面高度H=1.0 m,截面宽度B=0.8 m;拱结构采用C45混凝土,纵筋采用HRB335,双向对称配筋,受拉钢筋和受压钢筋配筋率分别为0.5%,箍筋(含拉筋)采用HPB300,配筋率为0.5%;地下介质为加冷土,土壤参数[9]ρ=1 420 kg·m-3,c=1 350 m·s-1,衰减系数n=2.5.
4.3 塑性铰位置、顺序与爆炸偏角的关系考虑爆炸偏角对于拱结构塑性破坏的影响,将不同的爆炸偏角代入塑性破坏计算流程,计算塑性铰的发展顺序和位置.侧向点爆炸荷载作用下,结构满足四铰破坏模式,并且4个塑性铰的分布随爆炸偏角移动而变化.如表 1所示,规律性地,4个塑性铰一般分布在两端拱脚、爆源投影点处,以及背爆面侧拱肩位置.爆炸偏角较小时,塑性铰先出现于背爆面的拱脚以及爆源投影点位置.随着爆炸偏角的增大,第1个塑性铰出现于迎爆面的拱脚位置,拱脚附近区域内力重分布,投影点对应的塑性铰将会产生于拱脚附近(-60°左右).如图 7所示,背爆面上的塑性铰随着爆炸偏角增大而不断向拱顶方向移动,但始终位于背爆面一侧.该塑性铰产生的顺序通常较晚,当该塑性铰产生后,结构形成机构,发生四铰破坏.因此,可通过该塑性铰的产生位置来预测结构最终破坏的区域,并将该塑性铰对应的承载力作为结构极限承载力.

|
图 7 不同爆炸偏角下塑性铰点位置 Fig.7 Hinge location at different bias angles |
| 下载CSV 表 1 不同爆炸偏角下塑性铰点角度 Tab.1 Angle of plastic hinge at different bias angles |
通过第3节的塑性破坏计算流程,可以确定每个塑性铰点的内力(表 2中以字母M、N、Q分别表示截面弯矩、轴力和剪力,下标数字为塑性铰顺序),以及该内力随着结构塑性破坏而产生的变化.表 2为爆炸偏角β=-30°下,结构4个塑性铰的内力分布和变化趋势.随着荷载增加,结构塑性不断发展,第1个塑性铰的弯矩略有增加,而轴力和剪力会显著上升.第1、3个塑性铰的弯矩方向与第2、4个塑性铰相反,该结论与实际工程相符.
| 下载CSV 表 2 塑性铰处截面内力 Tab.2 Internal force of plastic hinge |
基于表 2中截面内力值,还可计算塑性铰截面的受压区高度,以及对应的界限受压区高度.同理,将不同爆炸偏角下塑性铰对应的截面受压区高度列于表 3中.
| 下载CSV 表 3 塑性铰截面受压区高度 Tab.3 Compressive height of plastic hinge |
各个截面的受压区高度均小于界限受压区高度(44.00 cm),因此截面内力状态都为大偏压.算例工况下截面高度较小,因此在不同爆炸偏角的作用下,截面将始终处于大偏压.在工程上,大偏压破坏时受拉钢筋先屈服,受压侧混凝土再被压溃,是一种较为理想的延性破坏模式.因此,可以依据上述塑性破坏计算流程预测结构的破坏模式,指导工程设计.
5 结论(1) 四铰破坏机制下,结构通常会在2个拱脚附近产生塑性铰,其余2个结构塑性铰的位置会随着爆炸偏角的移动而变化,但通常位于荷载峰值作用处,以及背爆面一侧拱肩位置.塑性铰的产生顺序也和爆炸偏角相关,在爆炸偏角较小时,塑性铰先出现于背爆面的拱脚和爆源投影点位置.随着爆炸偏角的增大,第1个塑性铰出现于迎爆面的拱脚位置.
(2) 结构塑性破坏过程中,各截面内力状态会对塑性铰的破坏模式产生影响.在实际工程中,大偏压是较为理想的破坏模式,利用上述简化算法能判定塑性铰截面破坏模式,从而指导工程设计.
由于爆炸荷载持时短,瞬时超压高,结构进入塑性后处于材料非线性和大变形状态,理论方法求解较为复杂.虽然本文提出了一种解决方向和简化方法,但是在实际应用过程中还存在着诸多问题,尤其是如何真正考虑爆炸荷载动态特性,如何在结构响应求解过程中考虑结构和介质的相互作用等问题,都是后续需要深入研究的方向.
| [1] |
US Army Engineers. TM5-855-1 Fundamentals of protective design for conventional weapons[S]. Vicksburg: Waterways Experimental Station, 1986.
|
| [2] |
Departments of the Army. TM5-1300 Structures to resist the effects of accidental explosions[S]. Washington DC: The Navy and The Air Force, 1990.
|
| [3] |
Departments of the Army. UFC3-340-01 Design and analysis of hardened structures to conventional weapons effects[S]. Washington DC: The Navy and The Air Force, 1990.
|
| [4] |
赵华. 钢筋混凝土拱的承载能力研究[J]. 中南公路工程, 2004, 29(1): 24 ZHAO Hua. Ultimate bearing capacity of reinforced concrete arch[J]. Central South Highway Engineering, 2004, 29(1): 24 DOI:10.3969/j.issn.1674-0610.2004.01.007 |
| [5] |
郑振飞, 张尚杰, 彭大文, 等. 钢筋混凝土拱的极限承载能力试验研究[J]. 福州大学学报(自然科学版), 1982, 2(6): 79 ZHENG Zhenfei, ZHANG Shangjie, PENG Dawen, et al. The experiment on ultimate bearing capacity of reinforced concrete arch[J]. Journal of Fuzhou University(Natural Science Edition), 1982, 2(6): 79 |
| [6] |
魏琏. 超静定圆拱分析[M]. 北京: 科学技术出版社, 1957 WEI Lian. Analysis of statically indeterminate arch[M]. Beijing: Science and Technology Publishing, 1957 |
| [7] |
魏德敏. 拱的非线性理论及其应用[M]. 北京: 科学出版社, 2004 WEI Demin. Nonlinear theory and application of arch[M]. Beijing: Science Press, 2004 |
| [8] |
WEIDLINGER P, HINMAN E. Analysis of underground protective structures[J]. Journal of Structural Engineering: ASCE, 1988, 114(7): 1658 DOI:10.1061/(ASCE)0733-9445(1988)114:7(1658) |
| [9] |
MA G W, ZHOU H Y, LU Y, et al. In-structure shock of underground structures: a theoretical approach[J]. Engineering Structures, 2010, 32: 3836 DOI:10.1016/j.engstruct.2010.08.026 |
| [10] |
CHEN H L, XIA Z C, ZHOU J N, et al. Dynamic response of underground arch structures subjected to conventional blast loads: curvature effects[J]. Archives of Civil and Mechanical Engineering, 2013, 13: 322 DOI:10.1016/j.acme.2013.04.004 |
| [11] |
陈海龙, 金丰年, 夏志成, 等. 侧向爆炸作用下地下拱形结构动力响应[J]. 岩石力学与工程学报, 2012, 31(增2): 3478 CHEN Hailong, JIN Fengnian, XIA Zhicheng, et al. Dynamic response of underground arch structure under side blast load[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S2): 3478 |
| [12] |
吴永忠.爆炸地震波作用下地下结构动力计算模型及对比研究[D].南京: 解放军理工大学, 2014. WU Yongzhong. Dynamic calculation model and comparative study of underground structures under explosion seismic waves [D]. Nanjing: PLA University of Science and Technology, 2014. |
| [13] |
KRAUTHAMMER T, BAZEO S N, HOLMGUIST T J. Modified SDOF analysis of RC box-type structures[J]. Journal of Structural Engineering: ASCE, 1986, 112(4): 726 DOI:10.1061/(ASCE)0733-9445(1986)112:4(726) |
| [14] |
KRAUTHAMMER T, ASSADI-LAMOUKI A, SHANNA H M. Analysis of impulsively loaded reinforced concrete elements Ⅰ: theory[J]. Computers and Structures, 1993, 48(5): 851 DOI:10.1016/0045-7949(93)90507-A |
| [15] |
SUN Huixiang, XU Jinyu, LI Qing. The failure mode study of underground structure subjected to blast load[J]. Journal of Projectiles, Rockes, Missles and Guidance, 2011, 31(5): 89 |
| [16] |
方秦, 吴平安. 爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J]. 计算力学学报, 2003, 20(1): 39 FANG Qin, WU Ping'an. Analysis of the main factors affecting the fracture morphology of RC beams under explosive loading[J]. Chinese Journal of Computational Mechanics, 2003, 20(1): 39 DOI:10.3969/j.issn.1007-4708.2003.01.009 |
| [17] |
PIPPARD A J S, BAKER J F. The anaylsis of engineering structures[M]. London: Edward Arnold and Company, 1936
|
| [18] |
HEYMAN J. The estimation of the strength of masonry arches[J]. Proceedings of the Institution of the Civil Engineers, 1980, 69(4): 921 DOI:10.1680/iicep.1980.2177 |
| [19] |
CHEN Y, ASHOUR A F, GARRITY S W. Modified four-hinge mechanism analysis for masonry arches strengthened with near-surface reinforcement[J]. Engineering Structures, 2007, 29: 1864 DOI:10.1016/j.engstruct.2006.09.023 |
| [20] |
CRISFIELD M A, PACKHAM A J. A mechanism program for computing the strength of masonry arch bridges[R]. London: Transport and Road Research, 1987.
|
| [21] |
BOOTHBY T E. Collapse modes of masonry arch bridges[J]. Masonry International, 1995, 9(2): 62 |
| [22] |
钱七虎. 防护结构计算原理[M]. 南京: 中国人民解放军工程兵工程学院, 1981 QIAN Qihu. Calculation principle of protective structure[M]. Nanjing: PLA Military Engineering Institute, 1981 |
| [23] |
HENRYCH J. The dynamics of arches and frames[M]. Amsterdam: Elsevier, 1981
|
| [24] |
方秦, 柳锦春. 地下防护结构[M]. 北京: 中国水利水电出版社, 2010 FANG Qin, LIU Jinchun. Underground protective structure[M]. Beijing: China Water Conservancy and Hydropower Press, 2010 |
| [25] |
金丰年, 袁小军, 周健南, 等. 爆炸荷载作用下大跨度动被覆结构荷载分布规律[J]. 解放军理工大学学报, 2011, 12(6): 635 JIN Fengnian, YUAN Xiaojun, ZHOU Jiannan, et al. Distribution law of blast loads on large-span compound structure[J]. Journal of PLA University of Science and Technology, 2011, 12(6): 635 |
| [26] |
KIGER S A, DALLRIVA F D, HALL R L. Dynamic skin-friction effects on buried arches[J]. Journal of Structural Engineering: ASCE, 1989, 115: 1768 DOI:10.1061/(ASCE)0733-9445(1989)115:7(1768) |
 2018, Vol. 46
2018, Vol. 46
