在1976年,Merton[1]提出的对数跳扩散模型,将标的资产价格刻画为服从几何布朗运动附加一个偶然离散跳跃的形式.较之标准的几何布朗运动,该模型能够更好地拟合股票收益尖峰厚尾的特性.亚式期权作为具有代表性的新型期权,通过标的资产的平均价格来确定收益,以其便宜的价格和相对较低的风险吸引了许多投资者,目前已成为金融衍生品市场上交易最为活跃的新型期权之一.但是,由于其路径依赖性较强,导致定价问题也特别复杂,解析解很难求得,只能用数值方法对其进行有效的定价.目前对于跳扩散模型下的亚式期权定价,常用的数值方法有有限差分方法、二叉树法、蒙特卡洛方法和半拉格朗日法等.Kim和Qian[2]建立了跳扩散模型下亚式期权的二叉树方法模型,并证明了该二叉树方法的收敛性.二叉树中资产价格节点数呈平方增长,定价亚式期权计算量大,速度慢.Forsyth等[3]首先基于跳扩散模型,利用Itô公式和对冲技巧推导出连续情形下亚式期权的定价公式,然后用半拉格朗日法将二维偏微分问题离散化,转化为在每个时间节点上求解一个一维非线性积分-微分方程,并且证明了迭代方法求解隐式离散格式的收敛性,但实现复杂.Bayraktar等[4]基于Vecer和Xu[5]推导出的跳扩散模型下连续算术平均亚式期权的价格公式,定义了一个函数v来逼近积分-微分方程的解,并使用有限差分方法定价亚式期权.但是,该方法为保证计算精度,迭代次数较多,大大增加了计算量.Glasserman[6]详细介绍了蒙特卡罗法及各种方差减小技术在亚式期权定价中的应用,但是蒙特卡洛方法为保证计算精度,计算量大,耗时很多.近年来,国内学者也对Merton跳扩散模型下亚式期权的定价进行了研究.钱晓松[7]将算术平均亚式期权的定价问题归结为一个与路径无关的一维积分-微分方程的求解问题.刘宣会等[8]采用账户折算与复制的方法将亚式期权的定价转化为类似于欧式期权的定价,然后运用Merton对冲风险的方法,得到原亚式期权的定价.但以上两篇论文都只提供了理论分析,未给出具体的数值解法.张静等[9]推导出亚式期权的价格下界公式,并通过数值实验验证该下界公式可以近似作为亚式期权的定价公式,但是该方法对于虚值期权,定价误差较大.
本文在Merton跳扩散模型下,提出了基于柳树结构的定价亚式期权的方法.柳树法[10]最初通过构造离散的马尔科夫过程来刻画几何布朗运动对欧式期权定价.图 1展示了一个柳树结构的简单例子.该柳树结构从初始时刻0到T,有5个离散时刻,从第2个时刻起,每个时刻有5个可能的资产价格节点.图 1为柳树结构示意图,在实际应用中每一时刻上的资产价格数可以根据模型具体情况任意指定,通常节点个数设为30~50就能够在期权定价问题上保证较高的精度.柳树结构的优点是每个时刻上的资产价格数是常数,因此,随着时间步数的增加,柳树上节点的总个数是线性增长的,而不是二叉树中的平方增长,提高了数值方法的效率.
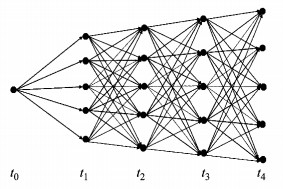
|
图 1 包含5个时刻、5个资产价格节点的柳树结构图 Fig.1 Graphical depiction of the willow tree lattice with 5 space nodes and 5 time nodes |
在Merton跳扩散模型下,本文提出的柳树构造主要分为两部分:首先在计算对数资产价格四阶矩的基础上,通过Johnson曲线,将服从标准正态分布的离散节点转换成服从跳扩散模型的价格节点,得到了资产价格的估计;然后根据跳扩散模型下资产价格满足的条件概率,推导出每两个相邻时刻间的转移概率公式,并对转移概率做了修正,从而保证资产价格满足鞅的性质,同时提高定价精度.在亚式期权定价过程中,平均价格依赖于价格变化的路径.不同于文献[11]中将所有精确的算术平均价格全部计算出来,本文预先计算出每个时刻平均价格的最大值和最小值,在此区间内通过等差数列选取给定个数的平均价格,而对于没有取到的平均价格节点,通过线性插值即可对其进行定价,以起到减少计算量的作用,从而解决了亚式期权定价中的路径依赖问题.另外,本文分析了柳树法的截断误差和插值误差,证明了柳树法的收敛性.最后,本文针对不同参数下的亚式期权进行了数值实验,并将柳树法结果与蒙特卡洛方法进行比较,数值结果显示柳树法与蒙特卡洛方法有相同的计算精度.由于柳树法存储的平均价格节点个数远少于实际的平均价格路径,从而使得运行时间大大减少.
1 跳扩散模型下亚式期权的柳树法定价在Merton跳扩散模型下,假设标的资产价格St满足:
| $ \frac{{{\rm{d}}{S_t}}}{{{S_t}}} = \left( {r - \rho - \lambda k} \right){\rm{d}}t + \sigma {\rm{d}}{W_t} + \left( {y - 1} \right){\rm{d}}{N_t} $ | (1) |
式中:r为无风险利率;ρ为分红率;k为期望;σ为没有发生跳跃情况下的波动率;Wt为标准布朗运动;Nt为强度为λ的泊松过程.这里假定Wt和Nt是相互独立的.资产价格St的跳跃幅度为y-1,且y服从期望为αJ、方差为σJ2的对数正态分布,即ln y~N(αJ, σJ2).因此,y-1的期望k=E[y-1]=eαJ+σJ2/2-1.
下文通过构造在Merton跳扩散模型下的柳树结构描述资产价格变化的随机过程.构造柳树结构包括两部分:资产价格的估计和转移概率的计算.
1.1 资产价格估计在Merton跳扩散模型下,基于方程(1),令X=ln(St/S0),则时刻t的资产价格St即为St=S0·eX,且满足
| $ \begin{array}{*{20}{c}} {X = \left( {r - \rho - \lambda \kappa - \frac{1}{2}{\sigma ^2}} \right)t + \sigma \sqrt t Z + \sum\limits_{i = 1}^{{N_t}} {\ln {y_i}} ,}\\ {Z \sim N\left( {0,1} \right),\;\;\;\ln y \sim N\left( {{\alpha _{\rm{J}}},\sigma _{\rm{J}}^2} \right)} \end{array} $ |
根据Ballotta和Kyriakou[12]的推导,可以得到X的期望μ,方差υ,偏度κ3和峰度κ4分别为
| $ \left\{ \begin{array}{l} \mu = \left[ {r - {\sigma ^2}/2 - \lambda \kappa - \rho + \lambda {\alpha _{\rm{J}}}} \right]t\\ \upsilon = \left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 - \lambda \sigma _{\rm{J}}^2} \right)t\\ {\kappa _3} = \frac{1}{{\sqrt t }}\left( {\frac{{\lambda \left( {\alpha _{\rm{J}}^3 + 3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2} \right)}}{{{{\left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 - \lambda \sigma _{\rm{J}}^2} \right)}^{3/2}}}}} \right)\\ {\kappa _4} = 3 + \frac{1}{t}\left( {\frac{{\lambda \left( {\alpha _{\rm{J}}^4 + 6\alpha _{\rm{J}}^2\sigma _{\rm{J}}^2 + 3\sigma _{\rm{J}}^4} \right)}}{{{{\left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 + \lambda \sigma _{\rm{J}}^2} \right)}^2}}}} \right) \end{array} \right. $ | (2) |
本文在Merton跳扩散模型下,利用Johnson曲线转换公式的逆变换,将一个标准正态分布的随机变量转换成一个满足式(2)中X的四阶矩的随机变量,从而估计资产价格的分布.
Johnson提出的方法[13]可以将任意连续随机变量X转换成正态分布的随机变量Z.其主要原理是通过计算已知变量的四阶矩,然后代入统一的公式中估计该变量的离散值.该模型可以灵活地匹配任意变量的期望、方差、偏度和峰度,并且根据偏度和峰度便可唯一确定模型中所需函数的具体类型.Johnson曲线公式如下:
| $ Z = a + bg\left( {\frac{{X - c}}{d}} \right) $ |
基于Hill提出的算法[14],参数a、b、c、d和函数g(·)的类型都可以根据对应随机变量的四阶矩求得.而根据Johnson曲线的逆变换,则可以将一个标准正态分布的随机变量Z转换成给定的分布X,即
| $ X = c + d \cdot {g^{ - 1}}\left( {\frac{{Z - a}}{b}} \right) $ | (3) |
由此,可以利用Johnson曲线的逆变换,得到基于Merton跳扩散模型(1)的资产价格柳树.该算法总结如下:对于一个标的资产,给定其初始价格S0,将时间区间[0, T]划分为N个时间步数,在每个时刻t有m个可能的资产价格,表示为St,且满足公式(1).时刻t的m个离散值可通过以下步骤得到:
步骤1 定义资产回报X=ln(St/S0),通过式(2)计算X的期望、方差、偏度和峰度.
步骤2 构造序列{(zi, qi)},令qi=(i-0.5)γ/m, γ=0.6,qi=qm+1-i, i=1, 2, …, m/2.标准化qi,即qi=qi/
步骤3 根据步骤2中的{zi},由公式(3)可以计算出随机变量X的离散值,Xi=c+d·g-1
步骤4 估计时刻t的m个标的资产价格值,Sti=S0·eXi, i=1, 2, …, m.其中Sti是St的第i个值.
1.2 转移概率计算在获得资产价格的估计后,本节构造转移概率矩阵来刻画资产价格的变化.假设时刻t的资产价格St已知,则在时刻t+Δt,给定ln St下的ln St+Δt的概率密度函数为
| $ {p_{\rm{J}}}\left( {\ln {S_{t + \Delta t}}\left| {\ln {S_t}} \right.} \right) = \sum\limits_{d = 0}^\infty {\frac{{{{\rm{e}}^{ - \lambda \Delta t}}{{\left( {\lambda \Delta t} \right)}^d}}}{{d!}}{\varphi _N}\left( {{\mu _d},\sigma _d^2} \right)} $ |
其中φN(μd, σd2)是标准正态分布的密度函数,期望μd和方差σd2分别为
| $ {\mu _d} = \ln {S_t} + \left( {r - \rho - \lambda k - 0.5{\sigma ^2}} \right)\Delta t + d{\alpha _{\rm{J}}} $ |
| $ \sigma _d^2 = {\sigma ^2}\Delta t + d\sigma _{\rm{J}}^2 $ |
则对应的累积分布函数为
| $ \begin{array}{l} {P_{\rm{J}}}\left( {\ln {S_{t + \Delta t}} \le A\left| {\ln {S_t}} \right.} \right) = \\ \;\;\;\;\;\;\;\sum\limits_{d = 0}^\infty {\frac{{{{\rm{e}}^{ - \lambda \Delta t}}{{\left( {\lambda \Delta t} \right)}^d}}}{{d!}}N\left( {\frac{{A - {\mu _d}}}{{{\sigma _d}}}} \right)} \end{array} $ |
其中,N(·)是标准正态分布的累积分布函数.
在柳树法结构下,定义时刻t的资产价格SWt=[S1t, S2t, …, Smt],时刻t+Δt的资产价格SWt+Δt=[S1t+Δt, S2t+Δt, …, Smt+Δt],其中资产价格可由1.1节得到.定义从时刻t到t+Δt的转移概率矩阵为[pijt]m×m,矩阵[pijt]m×m中的每个元素pijt,代表资产价格从时刻t的Sit转移到时刻t+Δt的区间[A, B]的概率.这里,pijt可定义为
| $ \begin{array}{l} p_{ij}^t = {P_{\rm{J}}}\left( {\ln S_j^{t + \Delta t} \le B\left| {\ln S_i^t} \right.} \right) - \\ \;\;\;\;\;\;\;{P_{\rm{J}}}\left( {\ln S_j^{t + \Delta t} \le A\left| {\ln S_i^t} \right.} \right), \end{array} $ |
| $ i = 1,2, \cdots ,m,\;\;\;j = 1,2, \cdots ,m $ |
其中
因为对于一个连续随机变量ln St+Δt来说,某个对数资产价格节点处的概率为0,即PJ(ln St+Δt=ln Sjt+Δt|ln Sit)=0,因此pijt实际上表示对数资产价格从时刻t的ln Sit转移到时刻t+Δt的某个区间[A, B]的概率.
另外,根据跳扩散过程的性质,Ste-(r-ρ)t是一个鞅过程,本文通过修正转移概率使柳树构造满足鞅的性质,提高定价精度.由鞅的性质,pijt与Sit需满足如下性质:
(1)
(2)
(3)
在每一个离散时刻,都选取两个最大的转移概率进行修正,以满足鞅的性质.例如,在t时刻,对于第i个资产价格,从pijt中选取两个最大的转移概率,假设为ptij1、ptij2.然后,记修正后的转移概率为
| $ {{\rm{e}}^{ - \left( {r - \rho } \right)\Delta t}}\left[ {xS_{{j_1}}^{t + \Delta t} - xS_{{j_2}}^{t + \Delta t}} \right] = S_i^t - {{\rm{e}}^{ - \left( {r - \rho } \right)\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^tS_j^{t + \Delta t}} $ |
由此,x的表达式如下:
| $ x = \frac{{S_i^t - {{\rm{e}}^{ - \left( {r - \rho } \right)\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^tS_j^{t + \Delta t}} }}{{{{\rm{e}}^{ - \left( {r - \rho } \right)\Delta t}}\left( {S_{{j_1}}^{t + \Delta t} - S_{{j_2}}^{t + \Delta t}} \right)}} $ |
完成以上修正后,即可得到t到t+Δt时刻的转移概率矩阵.
通过资产价格的估计和转移概率的计算,构造了一棵完整的跳扩散模型下的柳树.
1.3 定价跳扩散模型下亚式期权的柳树法对于平均价格路径较多的问题,本文利用插值技术减少计算量,推导亚式期权定价过程,解决了路径依赖问题.
假定标的资产价格S满足微分方程(1),算术平均连续亚式期权的平均价格为
定义欧式亚式期权的价值为关于S、A和t的函数,即Vc=Vc(S, A, t),则在跳扩散模型下Vc满足下列积分-微分方程:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {V^{\rm{c}}}}}{{\partial t}} + \frac{{S - A}}{t}\frac{{\partial {V^{\rm{c}}}}}{{\partial A}} + \frac{{{\sigma ^2}}}{2}{S^2}\frac{{{\partial ^2}{V^2}}}{{\partial {S^2}}} + \left( {r - \rho - \lambda k} \right)S\frac{{\partial {V^{\rm{c}}}}}{{\partial S}} - }\\ {\left( {r + \lambda } \right){V^{\rm{c}}} + \lambda \int_0^\infty {{V^{\rm{c}}}\left( {Sy,t} \right)g\left( y \right){\rm{d}}y} = 0} \end{array} $ | (4) |
式中:g(y)是y的概率密度函数,y服从对数正态分布,即
首先将连续亚式期权离散化,时间区间平均划分为0≡t0 < t1 < … < tN≡T,时间步长为Δt=T/N,N为时间步数,对应的资产价格为:S0, S1, …, SN.假设平均价格A在[tn, tn+1]时间内不变,在时刻tn的平均价格可表示为:
并且存在如下递推公式:
| $ {A^{n + 1}} = {A^n} + \frac{{{S^{n + 1}} - {A^n}}}{{n + 2}},\;\;\;n = 0,1,2, \cdots ,N $ |
在上文中,给定到期日T,离散时间区间[0, T],令tn=nΔt, n=0, 1, …, N,假设在时刻tn,柳树上有m个资产价格节点,可求出在第i个空间节点处的资产价格Sin, i=1, 2, …, m.假设时刻tn的m个资产价格按升序排列,S1n最小,Smn最大.令[Aminn, Amaxn]为从t0到tn的平均价格区间,则
| $ \left\{ \begin{array}{l} A_{\min }^n = \left( {{S^0} + \sum\limits_{q = 1}^n {S_1^q} } \right)/\left( {n + 1} \right)\\ A_{\max }^n = \left( {{S^0} + \sum\limits_{q = 1}^n {S_m^q} } \right)/\left( {n + 1} \right) \end{array} \right. $ | (5) |
假设时刻tn,每个价格节点处有ka个平均价格,取等差数列得到
| $ A_k^n = A_{\min }^n + \left( {k - 1} \right)\frac{{A_{\max }^n - A_{\min }^n}}{{{k_{\rm{a}}} - 1}},\;\;\;\;k = 1,2, \cdots ,{k_{\rm{a}}} $ | (6) |
式(6)表明,从时刻t0到tn的平均价格Akn是分配出来的,不依赖于某个特定的资产价格Sin.令V(Sin, Akn, tn)为亚式期权在时刻tn,股价节点Sin,平均价格为Akn处的期权价值,记为Vikn=V(Sin, Akn, tn),则亚式期权价格可以通过柳树法倒推来得到.
首先,在到期日tN=NΔt=T,平均价格AkN满足式(6),则欧式亚式看涨期权的价值VikN为
| $ V_{ik}^N = \max \left( {A_k^N - K,0} \right),\;\;\;\;i = 1,2, \cdots ,m $ |
这里在时刻T的期权价值不依赖于时刻T的资产价格SiN.
然后,考虑时刻tN-1的期权价值,有m个资产价格节点SiN-1,在每个价格节点SiN-1处,有ka个平均价格AkN-1,由式(6)给出.假设从时刻tN-1到时刻tN,资产价格从SiN-1转移到SjN,那么从时刻t0到tN的平均价格可由AkN-1和SjN计算
| $ \bar A_{jk}^N = A_k^{N - 1} + \frac{{S_j^N - A_k^{N - 1}}}{{N + 1}} $ | (7) |
由于AminN≤ AjkN≤AmaxN,所以存在距离AjkN最近的两个平均价格ANk-与Ak+N,使得Ak-N≤AjkN≤Ak+N,则在时刻tN,资产价格SjN节点处,平均价格为AjkN的期权价值VjkN可以通过Vjk-N和Vjk+N的线性插值得到,即
| $ \bar V_{jk}^N = \alpha _{jk}^NV_{j{k^ + }}^N + \left( {1 - \alpha _{jk}^N} \right)V_{j{k^ - }}^N,\;\;\;\;\;\alpha _{jk}^N = \frac{{\bar A_{jk}^N - A_{{k^ - }}^N}}{{A_{{k^ + }}^N - A_{{k^ - }}^N}} $ | (8) |
因此,在时刻tN-1,资产价格SiN-1节点处,平均价格为AkN-1的期权价值为
| $ \begin{array}{*{20}{c}} {V_{ik}^{N - 1} = {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^{N - 1}\bar V_{jk}^N} ,}\\ {i = 1,2, \cdots ,m,\;\;\;\;k = 1,2, \cdots ,{k_{\rm{a}}}} \end{array} $ |
其中, pijN-1表示从时刻tN-1的SiN-1转移到时刻tN的SjN的概率.依此类推,便可得到时刻t0的欧式亚式看涨期权的价值.
由于在每个时刻tn,价格节点Sjn处有ka个平均价格,对于每个平均价格Akn需要对应计算一个期权价值Vikn,其计算量为O(ka),因此用柳树法定价亚式期权的整体计算量为O(N·ka).
2 误差分析 2.1 柳树法的截断误差在[tn, tn+1]时间内,由于平均价格A不变,亚式期权价格V满足如下微分方程:
| $ \begin{array}{*{20}{c}} {{V_t} = \frac{{{\sigma ^2}}}{2}{S^2}{V_{SS}} + \left( {r - \rho - \lambda k} \right)S{V_S} - \left( {r + \lambda } \right)V + }\\ {\lambda \int_0^\infty {V\left( {Sy,t} \right)g\left( y \right){\rm{d}}y} = 0} \end{array} $ | (9) |
式中:y服从对数正态分布;g(y)是y的概率密度函数.令X=ln S,η=ln y,则dy=eηdη,式(9)作变量代换变为
| $ \begin{array}{*{20}{c}} {{{\tilde V}_t} = \frac{{{\sigma ^2}}}{2}{{\tilde V}_{XX}} + \left( {r - \rho - \lambda k} \right){{\tilde V}_X} - \left( {r + \lambda } \right)\tilde V + }\\ {\lambda \int_0^\infty {\tilde V\left( {x + \eta ,t} \right)f\left( \eta \right){\rm{d}}\eta } = 0} \end{array} $ | (10) |
其中:
使用柳树法定价时,在tn时刻,亚式期权的价格可以由倒推公式求得,即
| $ \tilde V_i^n = {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^n {p_{ij}^n\tilde V_j^{n + 1}} $ | (11) |
其中,
定理1 假设资产价格S满足Merton跳扩散模型,由柳树法定价公式(11)计算的期权价值与方程(10)的真实解之间的全局截断误差为O(Δt)+O(E[η5]),即全局截断误差的大小取决于跳扩散中资产价格S的跳跃幅度ln y的五阶矩.
证明 在Merton跳扩散模型下,时间区间[tn, tn+1]内下式成立:
| $ \begin{array}{*{20}{c}} {{X^{n + 1}} - {X^n} = \left( {r - \lambda \kappa - \frac{1}{2}{\sigma ^2}} \right)\Delta t + }\\ {\sigma \sqrt {\Delta t} Z + \sum\limits_{i = {N_n} + 1}^{{N_{n + 1}}} {\ln {y_i}} } \end{array} $ |
定义ΔXji=Xjn+1-Xin,则在给定Xin的条件下,ΔXji的四阶矩为:
| $ \begin{array}{l} E\left( {\Delta {X_{ji}}\left| {X_i^n} \right.} \right) = \sum\limits_{j = 1}^n {p_{ij}^n\Delta {X_{ji}}} = \\ \;\;\;\;\;\;\;\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)\Delta t \end{array} $ |
| $ \begin{array}{l} E\left( {\Delta X_{ji}^2\left| {X_i^n} \right.} \right) = \sum\limits_{j = 1}^n {p_{ij}^n\Delta X_{ji}^2} = \left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 + } \right.\\ \;\;\;\;\;\;\left. {\lambda \sigma _{\rm{J}}^2} \right)\Delta t + {\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)^2}\Delta {t^2} \end{array} $ |
| $ \begin{array}{l} E\left( {\Delta X_{ji}^3\left| {X_i^n} \right.} \right) = \sum\limits_{j = 1}^n {p_{ij}^n\Delta X_{ji}^3} = \lambda \left( {\alpha _{\rm{J}}^3 + } \right.\\ \;\;\;\;\;\;\;\left. {3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2} \right)\Delta t + {\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)^3}\Delta {t^3} + \\ \;\;\;\;\;\;\;3\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)\left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 + \lambda \sigma _{\rm{J}}^2} \right)\Delta {t^2} \end{array} $ |
| $ \begin{array}{l} E\left( {\Delta X_{ji}^4\left| {X_i^n} \right.} \right) = \sum\limits_{j = 1}^n {p_{ij}^n\Delta X_{ji}^4} = \lambda \left( {\alpha _{\rm{J}}^4 + 6\alpha _{\rm{J}}^2\sigma _{\rm{J}}^2 + } \right.\\ \;\;\;\;\;\;\;\left. {3\sigma _{\rm{J}}^4} \right)\Delta t + 3{\left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 + \lambda \sigma _{\rm{J}}^2} \right)^2}\Delta {t^2} + \\ \;\;\;\;\;\;\;4{\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)^3}\Delta {t^3} + \\ \;\;\;\;\;\;\;3\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)\lambda \left( {\alpha _{\rm{J}}^3 + 3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2} \right)\Delta {t^2} + \\ \;\;\;\;\;\;\;6{\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)^2}\left( {{\sigma ^2} + \lambda \alpha _{\rm{J}}^2 + \lambda \sigma _{\rm{J}}^2} \right)\Delta {t^3} + \\ \;\;\;\;\;\;\;{\left( {r - {\sigma ^2}/2 - \lambda \kappa + \lambda {\alpha _{\rm{J}}}} \right)^4}\Delta {t^4} \end{array} $ | (12) |
将式(11)中
| $ \begin{array}{l} \tilde V_j^{n + 1} = \tilde V\left( {X_i^n + \Delta {X_{ji}},{t_n} + \Delta t} \right) = \tilde V_i^n + \left( {{{\tilde V}_X}\Delta {X_{ji}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\tilde V}_t}\Delta t} \right) + \left( {\frac{1}{2}{{\tilde V}_{XX}}\Delta X_{ji}^2 + \frac{1}{2}{{\tilde V}_{tt}}\Delta {t^2} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\tilde V}_{Xt}}\Delta {X_{ji}}\Delta t} \right) + \frac{1}{6}\left( {{{\tilde V}_{XXX}}\Delta X_{ji}^3 + 3{{\tilde V}_{XXt}}\Delta X_{ji}^2\Delta t + } \right.\\ \;\;\;\;\;\;\;\;\left. {3{{\tilde V}_{Xtt}}\Delta {X_{ji}}\Delta {t^2}} \right) + \frac{1}{{24}}\left( {{{\tilde V}_{XXXX}}\Delta X_{ji}^4 + } \right.\\ \;\;\;\;\;\;\;\;\left. {4{{\tilde V}_{XXXt}}\Delta X_{ji}^3\Delta t + 6{{\tilde V}_{XXtt}}\Delta X_{ji}^2\Delta {t^2}} \right) + O\left( {\Delta {t^3}} \right) \end{array} $ | (13) |
式中:
将式(12)、(13)代入式(11)中,简化之后可以得到
| $ \begin{array}{l} \tilde V_i^n = \tilde V_i^n + \left\{ {{{\tilde V}_t} + \frac{{{\sigma ^2}}}{2}{{\tilde V}_{XX}} + \left( {r - \rho - \lambda \kappa } \right){{\tilde V}_X} - } \right.\\ \;\;\;\;\;\;\;\left( {r + \lambda } \right)\tilde V + \lambda \tilde V + \lambda \left[ {{\alpha _{\rm{J}}}{{\tilde V}_X} + \frac{1}{2}\left( {\alpha _{\rm{J}}^2 + \sigma _{\rm{J}}^2} \right){{\tilde V}_{XX}} + } \right.\\ \;\;\;\;\;\;\;\frac{1}{6}\left( {\alpha _{\rm{J}}^3 + 3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2} \right){{\tilde V}_{XXX}} + \frac{1}{{24}}\left( {\alpha _{\rm{J}}^4 + 6\alpha _{\rm{J}}^2\sigma _{\rm{J}}^2 + } \right.\\ \;\;\;\;\;\;\;\left. {\left. {\left. {3\sigma _{\rm{J}}^4} \right){{\tilde V}_{XXXX}}} \right]} \right\}\Delta t + \varepsilon \Delta t + O\left( {\Delta {t^2}} \right) \end{array} $ | (14) |
其中,当Δt→0时,ε→0.对比式(14)与式(10)可以发现,若要证明柳树法收敛,只需比较
由于η=ln y~N(αJ, σJ2),f(η)是η的概率密度函数,因此η的各阶矩为
| $ \left\{ \begin{array}{l} E\left[ \eta \right] = \int_{ - \infty }^\infty {\eta f\left( \eta \right){\rm{d}}\eta } = {\alpha _{\rm{J}}}\\ E\left[ {{\eta ^2}} \right] = \int_{ - \infty }^\infty {{\eta ^2}f\left( \eta \right){\rm{d}}\eta } = \alpha _{\rm{J}}^2 + \sigma _{\rm{J}}^2\\ E\left[ {{\eta ^3}} \right] = \int_{ - \infty }^\infty {{\eta ^3}f\left( \eta \right){\rm{d}}\eta } = 3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2 + \alpha _{\rm{J}}^3\\ E\left[ {{\eta ^4}} \right] = \int_{ - \infty }^\infty {{\eta ^4}f\left( \eta \right){\rm{d}}\eta } = \alpha _{\rm{J}}^4 + 6\alpha _{\rm{J}}^2\sigma _{\rm{J}}^2 + 3\alpha _{\rm{J}}^4\\ E\left[ {{\eta ^5}} \right] = \int_{ - \infty }^\infty {{\eta ^5}f\left( \eta \right){\rm{d}}\eta } = \alpha _{\rm{J}}^5 + 10\alpha _{\rm{J}}^3\sigma _{\rm{J}}^2 + 15{\alpha _{\rm{J}}}\sigma _{\rm{J}}^4 \end{array} \right. $ |
由
| $ \begin{array}{*{20}{c}} {\tilde V\left( {{X_i} + \eta ,{t_n}} \right) = \tilde V\left( {{X_i},{t_n}} \right) + {{\tilde V}_X}\eta + \frac{1}{2}{{\tilde V}_{XX}}{\eta ^2} + }\\ {\frac{1}{6}{{\tilde V}_{XXX}}{\eta ^3} + \frac{1}{{24}}{{\tilde V}_{XXXX}}{\eta ^4} + {R_4}\left( \xi \right)} \end{array} $ |
其中,
| $ \begin{array}{l} \int_{ - \infty }^\infty {\tilde V\left( {{X_i} + \eta ,{t_n}} \right)f\left( \eta \right){\rm{d}}\eta } = \int_{ - \infty }^\infty {\left[ {\tilde V\left( {x,t} \right) + } \right.} \\ \;\;\;\;\;\;{{\tilde V}_X}\eta + \frac{1}{2}{{\tilde V}_{XX}}{\eta ^2} + \frac{1}{6}{{\tilde V}_{XXX}}{\eta ^3} + \\ \;\;\;\;\;\;\left. {\frac{1}{{24}}{{\tilde V}_{XXXX}}{\eta ^4}} \right]f\left( \eta \right){\rm{d}}\eta = \tilde V\left( {x,t} \right) + {\alpha _{\rm{J}}}{{\tilde V}_X} + \\ \;\;\;\;\;\;\frac{1}{2}\left( {\alpha _{\rm{J}}^2 + \sigma _{\rm{J}}^2} \right){{\tilde V}_{XX}} + \frac{1}{6}\left( {\alpha _{\rm{J}}^3 + 3{\alpha _{\rm{J}}}\sigma _{\rm{J}}^2} \right){{\tilde V}_{XXX}} + \\ \;\;\;\;\;\;\frac{1}{{24}}\left( {\alpha _{\rm{J}}^4 + 6\alpha _{\rm{J}}^2\sigma _{\rm{J}}^2 + 3\sigma _{\rm{J}}^4} \right){{\tilde V}_{XXXX}} + \\ \;\;\;\;\;\;\int_{ - \infty }^\infty {{R_4}\left( \xi \right)f\left( \eta \right){\rm{d}}\eta } \end{array} $ | (15) |
其中余项
| $ \begin{array}{*{20}{c}} {\int_{ - \infty }^\infty {{R_4}\left( \xi \right)f\left( \eta \right){\rm{d}}\eta } = \int_{ - \infty }^\infty {{{\tilde V}^{\left( 5 \right)}}\left( \xi \right)\frac{{{\eta ^5}}}{{5!}}f\left( \eta \right){\rm{d}}\eta } = }\\ {\frac{1}{{120}}{{\tilde V}^{\left( 5 \right)}}\left( \xi \right)\left( {\alpha _{\rm{J}}^5 + 10\alpha _{\rm{J}}^3\sigma _{\rm{J}}^2 + 15{\alpha _{\rm{J}}}\sigma _{\rm{J}}^4} \right)} \end{array} $ |
ξ∈(Xi, Xi+η).假设|
| $ \begin{array}{*{20}{c}} {\lambda \int_{ - \infty }^\infty {{R_4}\left( \xi \right)f\left( \eta \right){\rm{d}}\eta } = O\left( {\alpha _{\rm{J}}^5 + 10\alpha _{\rm{J}}^3\sigma _{\rm{J}}^2 + } \right.}\\ {\left. {15{\alpha _{\rm{J}}}\sigma _{\rm{J}}^4} \right) = O\left( {E\left[ {{\eta ^5}} \right]} \right)} \end{array} $ | (16) |
因此,将式(15)代入式(14)得
| $ \begin{array}{l} \tilde V_i^n = \tilde V_i^n + \left\{ {{{\tilde V}_t} + \frac{{{\sigma ^2}}}{2}{{\tilde V}_{XX}} + \left( {r - \rho - \lambda \kappa } \right){{\tilde V}_X} - } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {r + \lambda } \right)\tilde V + \lambda \int_{ - \infty }^\infty {\tilde V\left( {{X_i} + \eta ,{t_n}} \right)f\left( \eta \right){\rm{d}}\eta } } \right\}\Delta t - \\ \;\;\;\;\;\;\;\;\lambda \int_{ - \infty }^\infty {{R_4}\left( \xi \right)f\left( \eta \right){\rm{d}}\eta } \cdot \Delta t + \varepsilon \Delta t + O\left( {\Delta {t^2}} \right) \end{array} $ |
余项
| $ \begin{array}{*{20}{c}} {{{\tilde V}_t} + \frac{{{\sigma ^2}}}{2}{{\tilde V}_{XX}} + \left( {r - \rho - \lambda \kappa } \right){{\tilde V}_X} - \left( {r + \lambda } \right)\tilde V + }\\ {\lambda \int_{ - \infty }^\infty {\tilde V\left( {{X_i} + \eta ,{t_n}} \right)f\left( \eta \right){\rm{d}}\eta } + \varepsilon + O\left( {E\left[ {{\eta ^5}} \right]} \right) = 0} \end{array} $ |
当Δt→0时,ε=O(Δt)→0,所以柳树法定价的全局截断误差取决于跳扩散中资产价格S的跳跃幅度ln y的五阶矩,
柳树法中的另一大误差来源是插值,即利用插值技术,仅存储一定数量的平均价格节点,起到减少计算量的作用.假设时刻tn,资产价格为Sjn,平均价格为Akn时,期权价值为Vjkn=V(Sjn, Akn, tn).给定一个平均价格
在柳树法中,用线性插值所得期权价值为
| $ \bar V_{jk}^{n + 1} = \alpha _{jk}^{n + 1}V_{j{k^ + }}^{n + 1} + \left( {1 - \alpha _{jk}^{n + 1}} \right)V_{j{k^ - }}^{n + 1} $ |
其中,
则Vjkn+1的插值误差βjkn+1为
| $ \begin{array}{l} \beta _{jk}^{n + 1} = \left| {V_{j\bar k}^{n + 1} - \bar V_{jk}^{n + 1}} \right| = \\ \;\;\;\;\;\;\;\;\;\;\frac{{\left( {\bar A_{jk}^{n + 1} - A_{{k^ - }}^{n + 1}} \right)\left( {\bar A_{jk}^{n + 1} - A_{{k^ + }}^{n + 1}} \right)}}{2}\frac{{{\partial ^2}V_{j\bar k}^{n + 1}\left( \eta \right)}}{{\partial {A^2}}} \end{array} $ | (17) |
假设存在独立于Δt的正常数M2,使得
| $ \left| {\beta _{jk}^{n + 1}} \right| \le \left| {\left( {\bar A_{jk}^{n + 1} - A_{{k^ - }}^{n + 1}} \right)\left( {\bar A_{jk}^{n + 1} - A_{{k^ + }}^{n + 1}} \right)} \right| \cdot {M_2} $ |
在时刻tn+1有ka个平均价格,设平均价格区间长度为
| $ \left\{ \begin{array}{l} A_{\min }^{n + 1} = \left( {{S^0} + \sum\limits_{j = 1}^{n + 1} {S_1^j} } \right)/\left( {n + 2} \right)\\ A_{\max }^{n + 1} = \left( {{S^0} + \sum\limits_{j = 1}^{n + 1} {S_m^j} } \right)/\left( {n + 2} \right) \end{array} \right. $ |
因为
假设存在正常数H,使得Smj-S1j < H, ∀j.则可得
| $ \begin{array}{l} \bar h = \frac{{A_{\max }^{n + 1} - A_{\min }^{n + 1}}}{{{k_{\rm{a}}} - 1}} = \frac{{\sum\limits_{j = 1}^{n + 1} {\left( {S_m^j - S_1^j} \right)} }}{{\left( {n + 2} \right)\left( {{k_{\rm{a}}} - 1} \right)}} < \\ \;\;\;\;\;\;\frac{{n + 1}}{{\left( {n + 2} \right)\left( {{k_{\rm{a}}} - 1} \right)}}H \end{array} $ |
所以
| $ \left| {\beta _{jk}^{n + 1}} \right| \le M \cdot {{\bar h}^2} < M{H^2}\frac{{{{\left( {n + 1} \right)}^2}}}{{{{\left( {n + 2} \right)}^2}{{\left( {{k_{\rm{a}}} - 1} \right)}^2}}} $ | (18) |
根据柳树法倒推公式,在tn时刻,资产价格为Sin,平均价格为Akn的精确的期权价值Vikn可表示为
| $ \begin{array}{l} V_{ik}^n = {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^n\left[ {\alpha _{jk}^{n + 1}V_{j{k^ + }}^{n + 1} + } \right.} \\ \;\;\;\;\;\;\;\left. {\left( {1 - \alpha _{jk}^{n + 1}} \right)V_{j{k^ - }}^{n + 1}} \right] + {i_{{\rm{err}}}} + {t_{{\rm{err}}}} \end{array} $ |
式中:
| $ \begin{array}{l} E_{ik}^n = {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^n\left[ {\alpha _{jk}^{n + 1}E_{j{k^ + }}^{n + 1} + } \right.} \\ \;\;\;\;\;\;\;\left. {\left( {1 - \alpha _{jk}^{n + 1}} \right)E_{j{k^ - }}^{n + 1}} \right] + {i_{{\rm{err}}}} + {t_{{\rm{err}}}} \end{array} $ |
令在tn时刻的最大误差为
| $ \begin{array}{l} \left\| {{E^n}} \right\| \le {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^n\left[ {\alpha _{jk}^{n + 1} + \left( {1 - \alpha _{jk}^{n + 1}} \right)} \right]} \cdot \\ \left\| {{E^{n + 1}}} \right\| + {i_{{\rm{err}}}} + {t_{{\rm{err}}}} \le \left\| {{E^{n + 1}}} \right\| + {i_{{\rm{err}}}} + {t_{{\rm{err}}}} \end{array} $ |
经过N步倒推,在初始时刻t0,期权价值的误差||E0||可以分解为||E0|| = ||E0||I+||E0||T,其中||E0||I是全局插值误差,||E0||T是全局截断误差.本章中定理1已经证明了||E0||T=O(Δt)+O(E[η5]),而全局插值误差||E0||I可根据式(18)得到
| $ \begin{array}{l} {\left\| {{E^0}} \right\|^I} \le {{\rm{e}}^{ - r\Delta t}}\sum\limits_{n = 0}^{N - 1} {\sum\limits_{j = 1}^m {p_{ij}^n \cdot \mathop {\max }\limits_k \left| {\beta _{jk}^{n + 1}} \right|} } \le \\ \;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - r\Delta t}}{M_2}{H^2}\sum\limits_{n = 0}^{N - 1} {\frac{{{{\left( {n + 1} \right)}^2}}}{{{{\left( {n + 2} \right)}^2}{{\left( {{k_{\rm{a}}} - 1} \right)}^2}}}} \le \\ \;\;\;\;\;\;\;\;\;\;\;{M_2}{H^2}{T^2}\frac{1}{{{{\left( {{k_{\rm{a}}} - 1} \right)}^2} \cdot \Delta t}} = O\left( {\frac{1}{{k_{\rm{a}}^2 \cdot \Delta t}}} \right) \end{array} $ |
其中:N=T/Δt.若令ka=C·N,C为常数,则‖E0‖I≤O(Δt).因此,柳树法的整体误差为O(Δt)+O(E[η5]),即整体误差的大小取决于跳扩散中资产价格S的跳跃幅度ln y的五阶矩.
3 Merton跳扩散模型下亚式期权定价的数值实验对不同参数的亚式期权进行分析,比较柳树法与蒙特卡洛方法的数值结果.所有数值实验的程序均在操作系统为64位Windows 7旗舰版的计算机上运行,内存为4 GB,处理器为Intel(R) Core(TM) i5-5200U CPU@2.20GHz,使用的软件版本为Matlab R2016a.
实验中,柳树法中资产价格节点个数m=50,平均价格个数ka=0.6N,离散时间步数N为初始时刻距离到期日的天数,蒙特卡洛方法的模拟路径数为2×104.实验比较了不同参数σ、αJ、σJ、λ以及不同到期日T情况下柳树法和蒙特卡洛方法的表现.
首先,固定跳扩散欧式亚式看涨期权的初始价格S0=100,敲定价格K=100,利率r=0.05,跳扩散的频率λ=1,到期日T为90 d.然后选取了不同的波动率σ,Merton跳扩散运动的期望αJ,标准差σJ.从表 1可以看出,柳树法的定价结果均落在蒙特卡洛模拟的99%置信区间内,说明了柳树法定价期权的精确性.从计算时间上看,在给定资产价格节点个数m和时间节点个数N时,其他参数的变化并没有影响柳树法的计算时间,跳扩散模型的变化对其计算时间影响很小.但是,柳树法的计算时间则远远小于蒙特卡洛方法.
| 下载CSV 表 1 不同σ、αJ、σJ下,柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果 Tab.1 Results of willow tree method and Monte Carlo mothed at different σ, αJ and σJ values |
接下来,讨论跳扩散模型下跳跃的频率λ对数值结果的影响.令λ=1.5和λ=2.0,在固定σ=0.2, S=100, K=100, T=90 d的情况下,分别考虑不同取值的αJ与σJ,结果如表 2所示.表 2的结果表明,用柳树法定价的结果完全落在了蒙特卡洛模拟的99%置信区间内,λ的变化并不会影响柳树法定价跳扩散模型下亚式期权的准确性.
| 下载CSV 表 2 不同λ下柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果 Tab.2 Results of willow tree method and Monte Carlo mothed at different λ values |
另外,当S0=100时,考虑不同敲定价格对亚式期权定价的影响.针对敲定价格K=90, K=95, K=100和K=105的情形,选取了一组σ、λ、αJ、σJ,分别为λ=1,σ=0.2,αJ=-0.02,σJ=0.05.将对应的期权定价结果和计算时间列于表 3.结果说明,敲定价格K的变化不影响柳树法定价亚式期权的表现.定价结果均落在蒙特卡洛模拟的99%置信区间内,而且计算时间也明显少于蒙特卡洛方法.
| 下载CSV 表 3 不同K下,柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果 Tab.3 Results of willow tree method and Monte Carlo mothed at different K values |
最后,考虑期权到期日时间的不同对柳树法定价的影响.以上的数值实验都基于期权的到期日为90 d,表 4给出了到期日为180 d和365 d的实验结果.结果表明,到期日T的变化不影响柳树法定价亚式期权的表现.定价结果均包含在蒙特卡洛模拟的99%置信区间内,而且计算时间也明显少于蒙特卡洛方法.因此,数值实验表明了柳树法在定价跳扩散模型下的亚式期权具有更明显的优势.
| 下载CSV 表 4 不同到期日下,柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果 Tab.4 Results of willow tree method and Monte Carlo mothed at different T values |
亚式期权作为目前金融市场上较活跃的新型期权之一,由于其路径依赖关系,定价公式求解复杂,因此亚式期权的定价问题一直受到众多研究学者的关注.本文基于Merton的跳扩散模型,运用柳树法对亚式看涨期权进行了定价研究.首先,本文介绍了柳树的构造过程,主要分为两步:一是利用Johnson曲线转换公式的逆变换,通过计算随机变量的四阶矩,将一个标准正态分布的随机变量转换成一个服从跳扩散过程的连续随机变量,得到标的资产价格的估计;二是根据跳扩散模型满足的条件概率函数,推导出了相邻两个时间节点间的转移概率矩阵,计算得到相邻时刻间的转移概率.在亚式期权定价过程中,引入了插值技术解决平均价格路径较多的问题,仅存储了一定数量的平均价格节点,大大减少了计算时间,并给出了一种计算复杂度为O(N2)的柳树法.另外,本文还对该算法的截断误差和插值误差分别进行了误差分析,证明了柳树法的整体误差为O(Δt)+O(E[η5]).最后,本文用柳树法定价Merton跳扩散模型下亚式期权的结果与蒙特卡洛方法比较,数值实验的结果表明,柳树法不仅能达到蒙特卡洛方法的计算精度,而且在运行时间上明显少于蒙特卡洛方法,从而说明了柳树法在亚式期权定价中的优势.本文中研究的Merton跳扩散模型只是Levy过程中的一种,除此之外的Levy过程[15]还有Kou提出的双指数跳扩散模型,NIG模型和VG模型等,较之Merton跳扩散模型,这些过程的条件概率的密度函数不存在显示的表达式,将柳树法推广到这些模型,是我们未来的研究方向之一.
| [1] |
MERTON R C. Option pricing when underlying stock returns are discontinuous[J]. Journal of Financial Economics, 1976, 3(1/2): 125 |
| [2] |
KIM K I, QIAN X. Convergence of the binomial tree method for Asian options in jump-diffusion models[J]. Journal of Mathematical Analysis and Applications, 2007, 330(1): 10 |
| [3] |
D'HALLUIN Y, FORSYTH P A, LABAHN G. A semi-Lagrangian approach for American Asian options under jump diffusion[J]. SIAM Journal on Scientific Computing, 2005, 27(1): 315 DOI:10.1137/030602630 |
| [4] |
BAYRAKTAR E, XING H. Pricing Asian options for jump diffusion[J]. Mathematical Finance:An International Journal of Mathematics, Statistics and Financial Economics, 2011, 21(1): 117 |
| [5] |
VECER J, XU M. Pricing Asian options in a semimartingale model[J]. Quantitative Finance, 2004, 4(2): 170 DOI:10.1088/1469-7688/4/2/006 |
| [6] |
GLASSERMAN P. Monte Carlo methods in financial engineering[M]. New York: Springer Science & Business Media, 2013
|
| [7] |
钱晓松. 跳扩散模型中亚式期权的定价[J]. 应用数学, 2003, 16(4): 161 QIAN Xiaosong. Valuation of Asian options in a jump-diffusion model[J]. Mathematica Applicata, 2003, 16(4): 161 DOI:10.3969/j.issn.1001-9847.2003.04.025 |
| [8] |
刘宣会, 徐成贤. 基于跳跃-扩散过程的一类亚式期权定价[J]. 系统工程学报, 2008, 23(2): 142 LIU Xuanhui, XU Chengxian. Asian option pricing based on jump-diffusion prices process[J]. Journal of Systems Engineering, 2008, 23(2): 142 |
| [9] |
张静, 何春雄, 郭艾, 等. 跳跃-扩散模型下亚式期权的定价[J]. 系统工程, 2010(12): 96 ZHANG Jing, HE Chunxiong, GUO Ai, et al. Pricing Asian option under the jump-diffusion model[J]. Systems Engineering, 2010(12): 96 |
| [10] |
CURRAN M. Willow power:optimizing derivative pricing trees[J]. Algo Research Quarterly, 2001, 4(4): 15 |
| [11] |
XU W, HONG Z, QIN C. A new sampling strategy willow tree method with application to path-dependent option pricing[J]. Quantitative Finance, 2013, 13(6): 861 DOI:10.1080/14697688.2012.762111 |
| [12] |
BALLOTTA L, KYRIAKOU I. Convertible bond valuation in a jump diffusion setting with stochastic interest rates[J]. Quantitative Finance, 2015, 15(1): 115 DOI:10.1080/14697688.2014.935464 |
| [13] |
JOHNSON N L. Systems of frequency curves generated by methods of translation[J]. Biometrika, 1949, 36(1/2): 149 DOI:10.2307/2332539 |
| [14] |
HILL I D, HILL R, HOLDER R L. Algorithm AS 99:fitting Johnson curves by moments[J]. Journal of the Royal Statistical Society, 1976, 25(2): 180 |
| [15] |
SATO K. Levy processes and infinitely divisible distributions[M]. Cambridge: Cambridge University Press, 1999
|
 2018, Vol. 46
2018, Vol. 46

