2. 埃克塞特大学 工程、数学与物理科学学院,埃克塞特 EX4 4QF
2. College of Engineering, Mathematics and Physical Science, University of Exeter, Exeter EX4 4QF, UK
随着科学技术的发展和经济全球化的不断深入,企业间的竞争越来越激烈,已从产品间的竞争转化为供应链间的竞争[1].供应商是供应链的重要成员,企业不但要谨慎选择供应商,还应不断对选定的供应商进行动态评价,从而对来自供应商的各种风险进行防范,以确保供应商保质保量地交付,减少企业因供应商失效而产生的损失.因此,供应商的风险评价已成为当代企业经营管理中的一个重要问题.
1 相关研究综述 1.1 供应商风险评价方法研究现状目前国内外专门针对供应商风险评价的研究相对较少, 主要集中在选择或提出一个评价指标体系, 然后用层次分析法AHP或模糊综合评判等方法进行评估, 综合评判出待选供应商们的风险大小, 如丁斌[2]、郭洪仙[3]等人的研究, 这些研究成果是企业进行供应商选择时的重要科学依据.但是, 来自供应商的风险不只存在于选择阶段, 这些风险贯穿于与供应商合作的整个过程, 因此, 企业需不断对选定供应商进行跟踪评价, 找出每一个供应商易发生风险的地方, 防患于未然.目前对此问题进行深入研究的学者较少, 本文试图提花一种供应商风险评价方法, 以此来帮助企业找出各个供应商主要风险及风险产生原因, 进而为企业制定风险管控策略提供支持.
1.2 FMEA研究述评FMEA是常用的风险评估方法之一, 被广泛应用于航天、汽车、机械、医疗等各个领域[4].传统的FMEA通过对故障或风险模式的发生度(occurrence, O)、严重度(severity, S)和检测度(detection, D)进行评分, 并以三者乘积计算风险优先数(risk priority number, RPN), 从而进行风险评估.使用传统FMEA解决实际问题主要存在以下三个缺陷:①实际风险分析中, 失效模式的风险因子难以用数字精确评价.②传统方法没有考虑风险因子的发生度O、严重度S和检测度D之间的相对重要性.③不同的风险因子组合有时会计算出相同的RPN值, 但实际暗藏的风险可能大不相同.
针对传统FMEA存在的第一个缺陷, 国内外许多学者常采用模糊集方法与FMEA结合, Mesut等[5]提出模糊FMEA方法并用其进行风险分析, 门峰等[6]应用模糊集理论和灰色关联理论对FMEA方法进行改进.但模糊集合中元素的隶属度只能定义为一个, 为此多种拓展的模糊集概念被相继提出, Chang等[7]提出基于直觉模糊集的FMEA方法, 该方法允许元素隶属度的确定有一定的偏差, 元素具有隶属度和非隶属度;Bozdag等[8]采用基于区间2型模糊集的FMEA方法对风险进行评估, 2型模糊集允许元素隶属度的确定有一定的概率分布.然而这些拓展模糊集方法均不能解决元素隶属度可能是一组取值的问题, Torra[9]提出的犹豫模糊集方法允许元素的隶属度有多个可选值, 可以解决这一问题.
针对传统FMEA存在的后两个缺陷, 学者们提出各种改善办法, 其中包括灰色关联分析(grey relational analysis, GRA)[10]、逼近理想排序法(technique for order preference by similarity to ideal solution, TOPSIS)[11]、规则库系统(rule base system)[12]和数据包络分析(data envelopment analysis, DEA)[13]等.
为了改进上述缺陷, 本文根据供应商风险评价的需求, 提出了基于犹豫模糊集和灰色关联理论的改进FMEA方法.该方法采用犹豫模糊集和基于语义计算的方法处理专家们对于O、S、D的评价信息, 解决了传统模糊集方法不能处理具有多个可选隶属度函数的问题;运用粗糙集思想将处理后的评价信息转化为区间数形式, 化解了由于犹豫模糊集合粒度不一致带来的计算难题;综合考虑比较O、S和D三者之间的相对重要性, 利用灰色关联理论计算各种风险的关联度, 克服了仅仅以RPN来判断失效模式风险顺序的局限性.
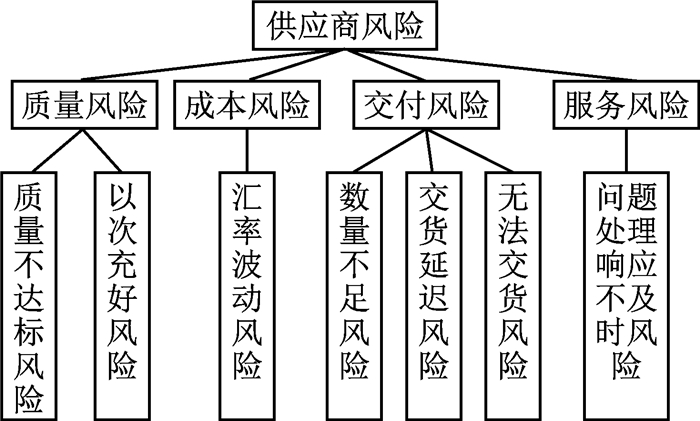
2 改进FMEA模型的构建 2.1 供应商潜在风险识别依据相关论文研究和对某大型跨国公司采购部的调研, 在全球采购的环境下, 从采购商视角将合作供应商在供货期间可能出现的风险划分为质量、交付、成本和服务4个模块, 各模块下的潜在风险见图 1.
|
图 1 供货期间供应商潜在风险 Fig.1 Suppliers' potential risks during delivery |
设犹豫模糊语义术语集HL(ϑi)={lf, …, lu}是有序离散的语义术语集合L={li; i=0, 1, 2, …, g}的有序子集, 其中li代表一个语义评价变量.
请专家们根据自身偏好选择合适的语言粒度的语义术语集合L, 结合自身的工作经验和知识, 参考企业现状和供应商的以下几个方面的数据:是否独家供货、一次提交合格率、交付及时率、报价、问题处理的响应速度、采购订单数, 为供应商各项潜在风险的O、S、D做出评价.评价过程中专家们可根据自己的偏好选择多个语义术语li表达自己的评价意见.将各专家对每项潜在风险的评价意见表示成犹豫模糊语义术语集合HL(ϑi)={lf, …, lu}形式.
2.3 用二元语义处理犹豫模糊语义术语集二元语义是一种有效的词计算方法, 可以直接对语义术语进行计算处理, 根据二元语义处理方法, HL(ϑi)可转化为[14]
| $ {\Delta ^{ - 1}}{H_L}\left( {{\vartheta _i}} \right) = \left\{ {f, \cdots ,u} \right\} $ | (1) |
粗糙集是一种处理模糊和不确定性信息的数学工具, 采用目标集合的下近似和上近似表达模糊信息.粗糙数采用区间数的形式表达信息的不确定性, 利用所需的处理数据确定区间的下限和上限.粗糙数确定过程对数据量的大小没有要求, 不需要任何外部信息以及数据的分析调整, 保持了信息的客观性.
根据粗糙集理论, 在由n位专家评价产生的经过二元语义处理后的n个犹豫模糊集{Δ-1HL(ϑ1), …Δ-1HL(ϑi), …, Δ-1HL(ϑn)}构成的群决策问题中, 假设U是包含在群决策问题评价信息表中的所有对象组成的论域, 所有的对象可以分为n个类, n个类组成集合R, R={C1, C2, …, Cn}.假如n个类的排序为C1<C2<…, Cn, 则对于Ci∈R(1≤i≤n), Ci的下近似域定义为
| $ \underline {{\rm{Apr}}} \left( {{C_i}} \right) = U\left\{ {Y \in U\left| {R\left( Y \right) \le {C_i}} \right.} \right\} $ | (2) |
Ci的上近似域定义为
| $ \overline {{\rm{Apr}}} \left( {{C_i}} \right) = U\left\{ {Y \in U\left| {R\left( Y \right) \ge {C_i}} \right.} \right\} $ | (3) |
Lim(Ci)和Lim(Ci)分别为Ci的下限和上限, 分别定义为
| $ \underline {{\rm{Lim}}} \left( {{C_i}} \right) = \frac{1}{{{M_L}}}\sum {R\left( Y \right)} \left| {Y \in \underline {{\rm{Apr}}} \left( {{C_i}} \right)} \right. $ | (4) |
| $ \overline {{\rm{Lim}}} \left( {{C_i}} \right) = \frac{1}{{{M_U}}}\sum {R\left( Y \right)} \left| {Y \in \overline {{\rm{Apr}}} \left( {{C_i}} \right)} \right. $ | (5) |
式中:ML和MU分别为在Ci下近似域和上近似域中对象的数量.
采用粗糙数的概念将Ci表示为Rnum(Ci), Rnum(Ci)定义为
| $ {R_{{\rm{num}}}}\left( {{C_i}} \right) = \left[ {\underline {{\rm{Lim}}} \left( {{C_i}} \right),\overline {{\rm{Lim}}} \left( {{C_i}} \right)} \right] $ | (6) |
使用上述方法, 将犹豫模糊集Δ-1HL(ϑi)={f, …, u}中的元素转化为对应的粗糙数, Δ-1HL(ϑi)={[Lim (f), Lim (f)], …, [Lim (u), Lim (u)]}.采用算数平均法集成集合Δ-1HL(ϑi)内的所有区间数, 将Δ-1HL(ϑi)转化为一个区间数的形式如下:Δ-1HL(ϑi)=[
n个犹豫模糊集构成的群决策问题结果为
| $ {\Delta ^{ - 1}}{H_L}\left( \vartheta \right) = \left[ {\frac{1}{n}\sum\limits_{i = 1}^n {\underline {{N_i}} } ,\frac{1}{n}\sum\limits_{i = 1}^n {\overline {{N_i}} } } \right] $ | (7) |
Xj表示供应商的第j种风险, 由于每种风险均有O、S、D三个变量, 因此反映第j种风险的数据列可表示为Xj={xj(1), xj(2), xj(3)}.xj(t)(t=1, 2, 3)表示FMEA专家小组对三个变量的群评价结果, 其代表的数值为通过2.4所示过程得到的区间数[
| $ \left\{ {{x_j}\left( t \right)} \right\} = \left( {\begin{array}{*{20}{c}} {{X_1}}\\ {{X_2}}\\ \cdots \\ {{X_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\left[ {\underline {{N_1}} \left( 1 \right),\overline {{N_1}} \left( 1 \right)} \right]}&{\left[ {\underline {{N_1}} \left( 2 \right),\overline {{N_1}} \left( 2 \right)} \right]}&{\left[ {\underline {{N_1}} \left( 3 \right),\overline {{N_1}} \left( 3 \right)} \right]}\\ {\left[ {\underline {{N_2}} \left( 1 \right),\overline {{N_2}} \left( 1 \right)} \right]}&{\left[ {\underline {{N_2}} \left( 2 \right),\overline {{N_2}} \left( 2 \right)} \right]}&{\left[ {\underline {{N_2}} \left( 3 \right),\overline {{N_2}} \left( 3 \right)} \right]}\\ \cdots&\cdots&\cdots \\ {\left[ {\underline {{N_n}} \left( 1 \right),\overline {{N_n}} \left( 1 \right)} \right]}&{\left[ {\underline {{N_n}} \left( 2 \right),\overline {{N_n}} \left( 2 \right)} \right]}&{\left[ {\underline {{N_n}} \left( 3 \right),\overline {{N_n}} \left( 3 \right)} \right]} \end{array}} \right) $ |
供应商的风险排序是相对于一定的参考基准而言的, 可选择每种风险各变量的最优或最差值作为参考基准.本文选择最差值作为参考基准建立参考矩阵, 即描述风险模式短语的最高水平所转化成的区间数[g, g]
| $ \left\{ {{x_0}\left( t \right)} \right\} = \left( {\begin{array}{*{20}{c}} {{X_0}}\\ {{X_0}}\\ \cdots \\ {{X_0}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\left[ {g,g} \right]}&{\left[ {g,g} \right]}&{\left[ {g,g} \right]}\\ {\left[ {g,g} \right]}&{\left[ {g,g} \right]}&{\left[ {g,g} \right]}\\ \cdots&\cdots&\cdots \\ {\left[ {g,g} \right]}&{\left[ {g,g} \right]}&{\left[ {g,g} \right]} \end{array}} \right) $ |
区间数A =[A, A]和B =[B, B]之间的距离为[13]
| $ D\left( {A,B} \right) = \sqrt {\frac{1}{2}\left[ {{{\left( {\overline B - \overline A } \right)}^2} + {{\left( {\underline B - \underline A } \right)}^2}} \right]} $ | (8) |
根据式(8)算出群评价矩阵中每一个区间数和对应的参考矩阵区间数之间的距离Dj(t), 并建立距离矩阵如下:
| $ \left\{ {{D_j}\left( t \right)} \right\} = \left( {\begin{array}{*{20}{c}} {{D_1}\left( 1 \right)}&{{D_1}\left( 2 \right)}&{{D_1}\left( 3 \right)}\\ {{D_2}\left( 1 \right)}&{{D_2}\left( 2 \right)}&{{D_2}\left( 3 \right)}\\ \cdots&\cdots&\cdots \\ {{D_n}\left( 1 \right)}&{{D_n}\left( 2 \right)}&{{D_n}\left( 3 \right)} \end{array}} \right) $ |
根据灰色关联理论, 由下式可以计算出每种风险的3个变量与参考基准的关联系数为
| $ \xi \left( {{X_0}\left( t \right),{X_j}\left( t \right)} \right) = \frac{{\mathop {\min }\limits_j \mathop {\min }\limits_t {D_j}\left( t \right) + \rho \mathop {\max }\limits_j \mathop {\max }\limits_t {D_j}\left( t \right)}}{{{D_j}\left( t \right) + \rho \mathop {\max }\limits_j \mathop {\max }\limits_t {D_j}\left( t \right)}} $ | (9) |
式中:ρ为分辨系数, ρ∈(0, 1).
2.9 计算灰色关联度由于在衡量风险排序时各变量的影响程度不同, 因此, 设风险的3个变量的权重分别为λt, 则第j种风险与参考基准的关联度可由下式得到,即
| $ \gamma \left( {{X_0},{X_j}} \right) = \sum\limits_{t = 1}^3 {{\lambda _t}\left\{ {\xi \left( {{D_j}\left( t \right)} \right)} \right\}} $ | (10) |
式中:
按照各风险关联度从大到小进行排序, 确定风险顺序, 进而有针对性的制定风险管控策略.
3 改进FMEA模型的应用 3.1 应用模型进行风险排序采用基于改进FMEA所构建的供应商风险评价模型对某制造企业A的风险供应商B进行风险评价分析.A公司选择1名供应商管理员(E1), 1名采购经理(E2), 1名质量工程师(E3)组成FMEA专家小组, 依据企业特点对供应商在供货期间的潜在风险进行识别, 分析结果如表 1所示.3位专家采用7粒度的语义术语集合L={l0:很低, l1:低, l2:稍低, l3:一般, l4:稍高, l5:高, l6:很高}对潜在风险进行评价, 评价信息如表 2所示.
| 下载CSV 表 1 供应商各风险模块潜在风险、原因及后果 Tab.1 FMEA of suppliers and its potential risks, reasons and results |
| 下载CSV 表 2 专家们对潜在风险的犹豫模糊语义评价信息 Tab.2 Hesitation fuzzy assessment information of risk from the experts |
采用所提基于粗糙思想的犹豫模糊语义评价信息转化方法对3位专家的评价信息进行转化, 得到的群评价矩阵如下
| $ \begin{array}{l} \left\{ {{x_j}\left( t \right)} \right\} = \\ \;\;\;\left( {\begin{array}{*{20}{c}} {\left[ {0.96,2.04} \right]}&{\left[ {3.67,4.33} \right]}&{\left[ {3.30,4.10} \right]}\\ {\left[ {0.19,1.00} \right]}&{\left[ {3.30,4.10} \right]}&{\left[ {2.54,3.46} \right]}\\ {\left[ {3.67,4.33} \right]}&{\left[ {3.30,4.10} \right]}&{\left[ {3.90,4.70} \right]}\\ {\left[ {5.40,5.87} \right]}&{\left[ {3.90,4.70} \right]}&{\left[ {4.13,4.60} \right]}\\ {\left[ {0.19,1.00} \right]}&{\left[ {3.30,4.10} \right]}&{\left[ {4.13,4.60} \right]}\\ {\left[ {0.19,1.00} \right]}&{\left[ {3.30,4.10} \right]}&{\left[ {2.54,3.46} \right]}\\ {\left[ {4.13,4.60} \right]}&{\left[ {2.54,3.46} \right]}&{\left[ {0.96,2.04} \right]} \end{array}} \right) \end{array} $ |
选择最差值作为参考基准建立参考矩阵, 即描述风险模式短语的最高水平所转化成的区间数[6, 6], 建立参考矩阵如下:
| $ \left\{ {{x_0}\left( t \right)} \right\} = \left( {\begin{array}{*{20}{c}} {{X_0}}\\ {{X_0}}\\ \cdots \\ {{X_0}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\left[ {6,6} \right]}&{\left[ {6,6} \right]}&{\left[ {6,6} \right]}\\ {\left[ {6,6} \right]}&{\left[ {6,6} \right]}&{\left[ {6,6} \right]}\\ \cdots&\cdots&\cdots \\ {\left[ {6,6} \right]}&{\left[ {6,6} \right]}&{\left[ {6,6} \right]} \end{array}} \right) $ |
根据式(8)计算群评价矩阵中每一个区间数和对应的参考矩阵区间数之间的距离Dj(t), 得到距离矩阵如下:
| $ \left\{ {{D_j}\left( t \right)} \right\} = \left( {\begin{array}{*{20}{c}} {6.41}&{2.87}&{3.30}\\ {7.67}&{3.30}&{4.29}\\ {2.87}&{3.30}&{2.47}\\ {0.61}&{2.47}&{2.33}\\ {7.67}&{3.30}&{2.33}\\ {7.67}&{3.30}&{4.29}\\ {2.33}&{4.29}&{6.41} \end{array}} \right) $ |
取ρ=0.5, 根据式(9)计算潜在风险各变量与参考基准之间的关联系数, 得到如下灰色关联矩阵:
| $ \left\{ {\xi \left( {{X_0}\left( t \right),{X_j}\left( t \right)} \right)} \right\} = \left( {\begin{array}{*{20}{c}} {0.43}&{0.66}&{0.62}\\ {0.39}&{0.62}&{0.55}\\ {0.66}&{0.62}&{0.71}\\ {1.00}&{0.71}&{0.72}\\ {0.39}&{0.62}&{0.72}\\ {0.39}&{0.62}&{0.55}\\ {0.72}&{0.55}&{0.43} \end{array}} \right) $ |
由专家确定的潜在风险各变量的系数分别为λ1=0.5 λ2=0.3 λ3=0.2, 根据式(10)计算得到的风险模式相对于参考基准的关联度, 并将各风险模式按关联度由大到小进行排序, 见表 3.
| 下载CSV 表 3 风险排序 Tab.3 Risk ranking |
由表 3排序可以看出供应商B的交货延迟风险和数量不足风险的关联度较高, 说明商家交货能力有待提高,需要重点防控.其次是报价、问题处理响应不及时风险, 说明商家配合程度一般需要注意供应商关系管理.质量不达标风险比较小说明供应商质量体系管控能力可以接受.替代品、数量不足的风险较小, 表明从过去绩效来看供应商信誉良好.无法交货和价格变动的关联度较低表明采购商暂时不用太过关注此两项风险.
从风险供应商B以往的绩效情况来看, 该结果符合实际情况.这验证了该评价方法的有效性和评价结果的合理性.
3.3 风险管控策略的建议采取有效的风险管控策略可以将来自供应商的潜在风险扼杀在摇篮里, 同时也可以帮助提升供应商供货水平, 以确保供应商保质保量地交付和供应链的高效运行.
针对质量差的风险供应商, 要通过QC、精益六西格玛等质量管理工具, 协助供应商查找质量问题, 和供应商一起分析并解决质量问题, 帮助其建立有效的质量管理体系, 最终提升供应商的质量管控水平.
针对交付较差的风险供应商, 通过制定交付及时率提升计划, 备安全库存、提高计划下达的合理性以及要求供应商扩充产能、到供应商现场跟催等方法控制交付风险.
针对响应速度较低的供应商应侧重关系管理, 积极主动与供应商协调, 努力解决在合作中出现的问题, 主动改善与供应商的关系, 确保供应商的合作积极性, 同时开发新供应商资源以降低对其的依赖.
针对国外供应商可能出现的成本变动问题, 企业应注意各国货币的汇率的变动,充分考虑贸易壁垒、不同的付款方式可能引发的财务损失.
针对信誉不良或公司财务状况不好的供应商,企业应加紧对供应商的监督,同时制定好应对措施,寻找替代供应商,以便在合适时机选择放弃该类供应商.
4 结语使用有效的方法对供应商风险进行动态评价, 可帮助企业更好地管控来自供应商的风险.FMEA方法具有事先预警的作用, 常被用于风险评价, 但传统的基于计算RPN的FMEA风险评价方法存在很多缺陷.本文针对供应商风险评价的需求对传统FMEA进行改进, 提出了基于犹豫模糊集和灰色关联理论的改进FMEA方法.首先基于全球采购的环境, 从采购商视角, 识别出供应商的主要风险模式;然后专家根据供应商以往绩效等信息, 选择合适粒度语义术语集在O、S、D三个维度上对供应商的主要风险进行评价;接下来采用犹豫模糊集和词计算方法处理评价信息,改进了传统模糊集方法不能处理具有多个可选隶属度函数的缺陷;利用粗糙集方法将犹豫模糊语义术语集转化为区间数形式, 解决了犹豫模糊语义术语集合粒度不一致带来的计算难题;最后综合考虑各变量的相对重要程度并结合灰色关联理论决定风险排序, 克服了仅通过计算RPN来确定风险排序的局限性.通过应用于某制造企业的供应商评价问题, 表明所提评价方法有助于企业识别供应商的主要风险, 进而可以为企业制定风险管控策略提供支持.
| [1] |
彭静, 李永华, 彭勇. 网络经济时代企业财务危机预警指标体系的构建[J]. 生产力研究, 2008(6): 133 PENG Jing, LI Yonghua, PENG Yong. Research on index system of prediction of enterprises' financial distress in the internet era[J]. Productivity Research, 2008(6): 133 |
| [2] |
丁斌, 孙政晓, 桂斌. 基于粗糙集与未确知模型的供应商风险评估方法研究[J]. 中国管理科学, 2008, 16(S1): 507 DING Bin, SUN Zhengxiao, GUI Bin. Research on supplier risk assessment based on rough set and unascertained measure model[J]. Chinese Journal of Management Science, 2008, 16(S1): 507 |
| [3] |
郭洪仙, 李晓峰. 供应链环境下供应商风险的评估[J]. 现代经济探讨, 2011(9): 60 GUO Hongxian, LI Xiaofeng. Evaluation of supplier risk in supply chain environment[J]. Modern Economic Research, 2011(9): 60 DOI:10.3969/j.issn.1009-2382.2011.09.013 |
| [4] |
LIU H C. FMEA using uncertainty theories and MCDM methods[M]. Sigapore: Springer, 2016
|
| [5] |
KUMRU M, KUMRU P Y. Fuzzy FMEA application to improve purchasing process in a public hospital[J]. Applied Soft Computing, 2013, 13(1): 721 |
| [6] |
门峰, 姬升启. 基于模糊集与灰色关联的改进FMEA方法[J]. 工业工程与管理, 2008, 13(2): 55 MEN Feng, JI Shengqi. An improved FMEA based on fuzzy set theory and grey relational theory[J]. Industrial Engineering and Management, 2008, 13(2): 55 DOI:10.3969/j.issn.1007-5429.2008.02.012 |
| [7] |
CHANG Kueihu, CHENG Chinghsue. A risk assessment methodology using intuitionistic fuzzy set in FMEA[J]. International Journal of Systems Science, 2010, 41(12): 1457 DOI:10.1080/00207720903353633 |
| [8] |
BOZDAG E, ASAN U, SOYER A, et al. Risk prioritization in failure mode and effects analysis using interval type-2 fuzzy sets[J]. Expert Systems with Applications An International Journal, 2015, 42(8): 4000 DOI:10.1016/j.eswa.2015.01.015 |
| [9] |
TORRA V. Hesitant fuzzy sets[J]. International Journal of Intelligent Systems, 2010, 25(6): 529 |
| [10] |
WEI C, LIU P, CHANG C. Failure mode and effects analysis using grey theory[J]. Integrated Manufacturing Systems, 2001, 12(12): 211 |
| [11] |
LIU H C, YOU J X, SHAN M M, et al. Failure mode and effects analysis using intuitionistic fuzzy hybrid TOPSIS approach[J]. Soft Computing, 2015, 19(4): 1085 DOI:10.1007/s00500-014-1321-x |
| [12] |
SANKAR N R, PRABHU B S. Modified approach for prioritization of failures in a system failure mode and effects analysis[J]. International Journal of Quality & Reliability Management, 2001, 18(3): 324 |
| [13] |
CHANG D, SUN K P. Applying DEA to enhance assessment capability of FMEA[J]. International Journal of Quality & Reliability Management, 2009, 26(6): 629 |
| [14] |
HERRERA F, MARTINEZ L. A 2-tuple fuzzy linguistic representation model for computing with words[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(6): 746 DOI:10.1109/91.890332 |
| [15] |
耿秀丽, 张永政. 基于犹豫模糊集的改进FMEA风险评估方法[J]. 统, 2017, 23(2): 340 GENG Xiuli, ZHANG Yongzheng. Improved FMEA approach for risk evaluation based on hesitant fuzzy set[J]. Computer Integrated Manufacturing Systems, 2017, 23(2): 340 |
 2019, Vol. 47
2019, Vol. 47

