2. 上海大学 悉尼工商学院,上海 201899
2. SHU-UTS SILC Business School, Shanghai University, Shanghai 201899, China
现代有轨电车作为一种绿色环保、运量及成本均适中的轨道交通方式, 近两年广受欢迎, 在我国许多城市进行了规划和建设.有轨电车由于运行线路并不是完全封闭, 较其他形式的轨道交通方式存在更多的安全隐患, 有轨电车系统由驾驶员进行操作, 安全责任重大, 基于发现障碍物与常用制动(或紧急制动)的安全驾驶模式, 驾驶员视野距离限制了列车在某些区段的行驶速度上限.同时在夜晚或者雨、雪、雾等恶劣天气条件下, 驾驶员的视野范围受到极大的限制和削弱, 难以发现潜在的障碍物, 一旦不能及时制动, 将会导致碰撞甚至脱轨的严重后果.因此为现代有轨电车研究开发一套具有视觉增强效果的辅助安全防护系统, 具有很大的意义.
本文提出了一种基于异态检测的现代有轨电车辅助安全防护技术, 为有轨电车选取适用性较高的前向检测器, 实时获取前方障碍物的信息, 并通过列车定位技术求得障碍物与轨道限界之间的相对位置, 对于入侵轨道限界的障碍物, 确定其与列车的轨内相对距离, 并以此为行车许可终点实时计算列车防护曲线.如果当前检测周期并无轨内障碍物, 辅助安全防护系统会选取线路上调度计划制定的停车点(如车站等)作为行车许可终点进行防护曲线的计算.
1 异态检测技术研究异态检测技术一般指利用传感器获取周围环境中目标的信息.用于有轨电车的异态检测技术是一种车载检测技术.目前车载检测技术多应用于智能车领域, 主要分为主动检测和被动检测两种技术[1], 其中主动检测需要向待测区域发射一定功率、频段的电磁波, 利用回波分析完成障碍物目标的检测, 代表技术为各类雷达技术[2]; 被动检测主要指视觉检测技术, 利用CCD摄像机一类的设备, 直接从环境中接收信息, 并通过相关算法处理得出感兴趣数据.被动检测是非侵犯式检测, 不增加环境噪声, 功耗低, 获取信息量大, 但其信息来源完全依靠外界, 在恶劣环境如夜晚或大风、雨、雪、雾的条件下基本失效[3].
有轨电车应用环境一般在城市内部, 在某些区段与城市道路交通共享路权, 因此可能入侵有轨电车轨道限界的障碍物一般包括社会车辆、行人以及落入轨道并停留的其他目标.应选取前向检测器, 对列车前方障碍物情况进行检测, 根据EN13452-1标准, 现代有轨电车运营速度一般取50 km·h-1, 对于钢轨钢轮制式有轨电车, 常规制动减速度取1.2 m·s-2, 紧急制动减速度要求达到至少2.8 m·s-2(胶轮导轨制式减速度更高)[4, 5-12].若列车以50 km·h-1速度运行, 一般常规制动的制动距离在100 m以内, 紧急制动距离在50 m左右, 因此所选取检测器需要探测前方至少200 m.同时检测器需要一定的水平角及俯仰角, 能够探测车身高度内的障碍物.
根据上述检测器的需求, 表 1分析了目前比较成熟的几种检测器技术在各个方面的特性对比.
| 下载CSV 表 1 各类异态检测技术特性对比 Tab.1 Feature comparison of different kinds of obstacles detection technologies |
经过研究, 雷达技术中的毫米波雷达在全天候使用、检测距离、检测稳定性、低成本等方面具有一定的优势, 因此本文选取毫米波雷达作为有轨电车前向检测器.
2 辅助安全防护功能设计 2.1 功能需求分析有轨电车辅助安全防护主要提供避撞预警的功能, 不同于汽车能够进行换道等避让行为, 有轨电车只能够进行轨道内的运动, 因此需要判断前述雷达所检测到的前方障碍物与轨道限界的相对位置关系, 从而评估其对于列车行驶的威胁, 本文将通过列车定位信息进行上述匹配的相关运算.
为了保让避撞预警功能的实现, 相关设备及算法需满足如下条件:
(1) 所选取雷达检测器需能较为准确地给出列车与当前目标的位置关系.
(2) 列车定位技术能够提供定位误差较小的列车定位及速度信息.
(3) 相关算法能够确定线路入侵物距离列车的轨内距离, 并提供列车防护曲线.
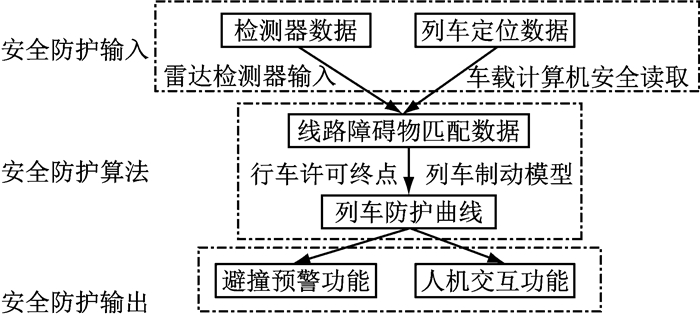
2.2 辅助安全防护构架设计辅助安全防护构架如图 1所示.
|
图 1 辅助安全防护构架 Fig.1 The frame of auxiliary safety protection |
避撞预警功能的实现, 依赖于列车防护曲线的实时计算.列车防护曲线是列车制动模型的直观表达, 表征列车在制动过程中速度下降与距离之间的关系.辅助驾驶系统需实时确定行车许可终点, 并根据行车许可终点确定列车防护曲线, 本文借鉴ETCS系统的列车防护方法[13], 建立了一簇防护曲线.
EBD(emergency brake deceleration)曲线为紧急制动曲线, 列车运行过程中每个行车许可终点都对应一条EBD曲线, EBD曲线是一簇防护曲线中的最外层, 一般不会被触发, 一旦超过EBD曲线, 列车的停车位置将超过行车许可终点, 也即会发生碰撞.
因此需要考虑列车制动建立、驾驶员反应时间、列车定位测速误差等因素, 计算紧急制动触发曲线EBI(emergency brake intervention), 当列车行驶状态越过EBI曲线, 需自动施加紧急制动.
利用相同的原理, 列车还设有最大常用制动曲线SBD(bervice brake deceleration)以及最大常用制动触发曲线SBI(service brake intervention), 当列车运行状态触发该曲线之后, 施加最大常用制动.
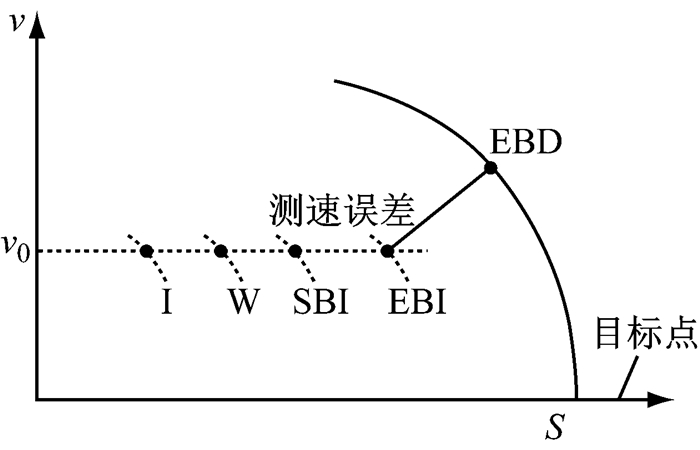
同时为了实现对于驾驶员的提示和警告, 设立了提示点I与警告点W, 通过SBI曲线反推得出, 图 2表征了几条曲线之间的关系.
|
图 2 EBD以及其他几条曲线关系图 Fig.2 The relationship between EBD and other curves |
当驾驶员驾驶列车接近确定的行车许可终点时, 辅助驾驶系统会向驾驶员提示安全引导速度, 本策略中设提示点I与警告点W, 其中I点的作用为提示驾驶员即将超过允许限速, 该点提供足够的时间让驾驶员进行相关操作, 当列车超过I点后, 会通过声音、灯光等提示驾驶员进行减速操作; 如果超过W点意味着即将触及最大常用制动曲线, 若越过W点仍旧没有任何操作, 列车将在越过SBI监督点时自动触发最大常用制动, 如果列车速度仍旧未降低到安全值, 超过了EBI监督点, 则会触发紧急制动, 确保行车安全.
制动过程中的人机交互设计为提示—询问—制动三层:当行车触发I点, 进行声光提示, 若直到触发W点驾驶员仍旧没有进行制动, 给出解释界面, 如果直到触发SBI监视曲线驾驶员没有进行选择, 则自动进行列车最大常用制动, 根据人体工程学结合驾驶员的反应思考时间, 可以设I点、W点以及SBI曲线之间的触发时间为5 s.
由于有轨电车线路部分区段封闭性较差, 有可能会出现突然闯入的障碍物离列车较近, 通过其作为行车许可终点的防护曲线会使得现有状态直接超过I点的包络线, 鉴于这种情况多为行人闯入, 而行人闯入的持续时间一般为2 s左右, 因此这种情况下的制动策略需要驾驶员帮助完成, 具体过程如图 3所示.

|
图 3 入侵物过近的制动策略 Fig.3 The braking strategy when obstacles are too close |
如果闯入障碍物确实有威胁且位于vc>vEBI, (vc指当前车速)等效于列车已经位于EBI曲线之外, 即是紧急制动也会触碰行车许可终点, 则列车将无法避免此次碰撞, 这种情况一般较少.
如果是行人闯入的情况, 驾驶员可以通过按钮解除警报, 继续正常行驶, 系统也将在行人离开轨道限界范围之后自动撤销该行车许可终点.
上述人机交互过程中需要驾驶员进行选择, 告知系统当前由算法得出的威胁情况是否属实, 由于给驾驶员的反应时间较短, 界面的选择设备建议使用更为稳定的物理按钮.
3 辅助安全防护算法设计 3.1 算法输入 3.1.1 雷达数据输入假定选取的雷达检测器所检测到的原始数据经过波形解析、背景噪音过滤等算法处理手段, 能够至少为辅助安全防护系统提供合理采样频率的如下数据输入, 即
| $ \left[{\alpha, \theta, \rho } \right] $ | (1) |
其中:α表示目标障碍物俯仰角; θ表示目标障碍物水平方向航向角; ρ表示目标障碍物到雷达的距离.
根据极坐标转换公式, 剔除高度范围在车辆高度之外的目标, 可以得到二维平面的坐标:
| $ \left[\begin{gathered} {x_{{\text{OB}}}} \hfill \\ {y_{{\text{OB}}}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} \rho \cos \alpha \cos \theta \hfill \\ \rho \cos \alpha \sin \theta \hfill \\ \end{gathered} \right] $ | (2) |
式中:xOB为目标障碍物在二维平面中的x轴坐标; yOB为目标障碍物在二维平面中的y轴坐标.
3.1.2 列车定位数据输入(1) 线路坐标系的构建
使用车载雷达作为检测器, 雷达坐标系会以列车当前运行速度与地面有一个相对运动, 为了便于研究障碍物基于地面以及轨道限界的绝对位置关系, 应用地方坐标系的参数构建线路坐标系, 精度能够达到使用要求.
其中地方坐标系(local coordinate system)是因建设、城市规划和科学研究需要而在局部地区建立的相对独立的平面坐标系统.
(2) 列车运行线路建模
在地方坐标系的基础上, 根据以下模型假设进行线路建模:①将线路形式经过抽象分析, 分为直线线路、曲线线路和交叉口区域线路三类; ②忽略缓和曲线的影响, 假设直线线路与固定曲率半径的曲线线路直接连接.可以将线路每个区段用表示如下:
| $ \left[{n, {x_1}, {y_1}, {s_1}, {x_2}, {y_2}, {s_2}, r, {x_{\text{o}}}, {y_{\text{o}}}, d, i, c, s, m} \right] $ | (3) |
其中:n为区段编号; (x1, y1)(x2, y2)为区段中心线起讫点坐标; s1、s2为区段起讫点所对应的里程数; r为区段曲率半径; (x0, y0)为曲线区段的圆心坐标; d为列车该曲线区段运行方向, 若为顺时针方向运行曲线线路, d取0, 若为逆时针方向运行线路d取1;i为区段坡度值; s为该区段里程数; m为该区段内查询应答器个数.另外定义轨道限界范围W=车辆最大宽度w+2δ, δ为安全余量.
(3) 列车定位数据输入方式
据此给出列车实时定位信息的输入值
| $ \left[{n, {n_1}, {n_2}, x, y, {s_{\text{d}}}, s, {v_{{\text{cur}}}}} \right] $ | (4) |
其中:n为上一个查询应答器编号; n1为上一个查询应答器所处区段的编号; n2为当前列车所处区段编号; (x, y)为上一个查询应答器的地面坐标; sd为以线路起点作为里程0点的上一个查询应答器所对应的里程; s为上一个查询应答器到列车当前位置的累积里程; vcur为列车当前运行速度.
3.2 障碍物绝对位置算法 3.2.1 列车坐标确定模型算法中, 列车需要实时获取自身位置, 假定列车位于区段n2, 则可读取当前区段信息如下:
| $ \left[\begin{gathered} {x_1}, {y_1}, {s_1}, {x_2}, {y_2}, {s_2}, r, \hfill \\ {x_{\text{o}}}, {y_{\text{o}}}, d, i, c, s, m \hfill \\ \end{gathered} \right] $ | (5) |
分别针对直线区段与曲线区段的情况, 计算列车当前位置坐标(xtr, ytr)以及行驶方向β.
(1) 直线区段:通过式(6)式(7)求得当前位置情况.
| $ \left[\begin{gathered} {x_{{\text{tr}}}} \hfill \\ {y_{{\text{tr}}}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} \frac{{{x_1} + \lambda {x_2}}}{{1 + \lambda }} \hfill \\ \frac{{{y_1} + \lambda {y_2}}}{{1 + \lambda }} \hfill \\ \end{gathered} \right], 其中\lambda = \frac{{{s_{\text{d}}} + s -{s_1}}}{{{s_2} -{s_{\text{d}}} -s}} $ | (6) |
| $ \beta = \left\{ \begin{gathered} {\tan ^{-1}}\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}, {x_2} - {x_1} > 0 \hfill \\ {\tan ^{ - 1}}\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} + \pi, {x_2} - {x_1} < 0且{y_2} - {y_1} \geqslant 0 \hfill \\ {\tan ^{ - 1}}\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} - \pi, {x_2} - {x_1} < 0且{y_2} - {y_1} < 0 \hfill \\ \frac{\pi }{2}, {x_2} - {x_1} = 0且{y_2} - {y_1} > 0 \hfill \\ - \frac{\pi }{2}, {x_2} - {x_1} = 0且{y_2} - {y_1} < 0 \hfill \\ \end{gathered} \right. $ | (7) |
(2) 曲线区段:根据式(8)式(9)求得当前位置情况.其中σ通过(xtr, ytr)与区段起点的相对位置进行计算.
| $ \left[\begin{gathered} {x_{{\text{tr}}}} \hfill \\ {y_{{\text{tr}}}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} {x_{\text{o}}} + r \cdot \cos \sigma \hfill \\ {y_{\text{o}}} + r \cdot \sin \sigma \hfill \\ \end{gathered} \right] $ | (8) |
| $ \beta = \left\{ \begin{gathered} \sigma + \frac{\pi }{2}, d = 1 \hfill \\ \sigma-\frac{\pi }{2}, d = 0 \hfill \\ \end{gathered} \right. $ | (9) |
将障碍物从雷达坐标系坐标转化为线路坐标系公式如下:
| $ \left[\begin{gathered} {x_{{\text{OB}}}} \hfill \\ {y_{{\text{OB}}}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} {x_{{\text{tr}}}} + {x_{{\text{ob}}}} \cdot \cos \beta-{y_{{\text{ob}}}} \cdot \sin \beta \hfill \\ {y_{{\text{tr}}}} + {x_{{\text{ob}}}} \cdot \sin \beta-{y_{{\text{ob}}}} \cdot \cos \beta \hfill \\ \end{gathered} \right] $ | (10) |
利用解析几何公式, 可以求得(xob, yob)距离最近的轨道区段中心线的距离, 若该距离小于
| $ {S_{{\text{ob}}}} = \sqrt {{{\left( {{x_{{\text{ob}}}}-{x_{\text{o}}}} \right)}^2} + {{\left( {{y_{{\text{ob}}}}-{y_{\text{o}}}} \right)}^2}-{{\left( {\frac{{\left| {n{x_{{\text{ob}}}} + m{y_{{\text{ob}}}} + c} \right|}}{{\sqrt {{n^2} + {m^2}} }}} \right)}^2}} $ | (11) |
| $ {S_{{\text{ob}}}} = ar + s $ | (12) |
(1) 紧急制动曲线EBD
紧急制动曲线EBD描述列车在最不利情况下从当前速度到完全停止或进入某一个限速区间上限速度所需要的制动距离, 制动曲线的目标点一般可以分为两类, 第一种为行车许可终点, 即列车需要在行车许可终点之前达到完全制动状态才能够保证安全.第二种为最上限速度曲线的变化, 列车到达某一点时速度应该控制在该点最限速度之下.取轨内障碍物作为行车许可终点来计算实时防护曲线, 根据运动学制动模型从行车许可点反算紧急制动曲线, 并与线路最上限速度相交.
| $ {S_{{\text{eb}}}} = \frac{{\left( {v_{{\text{end}}}^2-v_{{\text{org}}}^2} \right)}}{{2{\alpha _{{\text{ebr}}}}}} $ | (13) |
式中:vorg为列车制动初始速度; vebr为列车制动目标速度, 对于以行车许可终点为障碍物目标的情况, 取0;αebr为列车最大制动减速度(考虑回转质量系数以及坡度影响); Seb为紧急制动状态距离.
(2) 紧急制动触发曲线EBI
紧急制动触发曲线EBI通过紧急制动曲线推算, 紧急制动触发曲线与紧急制动曲线之间相差了列车切断牵引与生成制动的过程, 包括司机反应延迟、牵引切断延迟与惰行直至建立制动三个阶段.图 2描述了从EBD到其他几条监控曲线的变化, EBI计算如下:
| $ \Delta v = {\alpha _{{\text{tr}}\gamma }}{t_{{\text{tr}}}}\left( {1 + {r_{\text{V}}}} \right) $ | (14) |
| $ \Delta s = \Delta v{t_{{\text{tr}}}} + {S_{{\text{lo}}}} $ | (15) |
| $ {S_{{\text{EBI}}}}\left( {{v_0}} \right) = {S_{{\text{EBD}}}}\left( {{v_0} + \Delta v} \right) + \Delta s $ | (16) |
式中:αtrγ为列车最大牵引加速度(考虑回转质量系数以及坡度影响); ttr为制动建立延时与驾驶员反应时间之和; rV为测速误差系数; Δs为考虑最不利情况下的距离增量.
(3) 最大常用制动曲线SBD及其触发曲线SBI
与式(1)、式(2)同理, 可得SBD曲线求解式(17)以及SBI曲线的求解式(18), 从SBD到SBI的变换为直接平移.
| $ {S_{{\text{sb}}}} = \frac{{\left( {v_{{\text{end}}}^2-v_{{\text{org}}}^2} \right)}}{{2{\alpha _{{\text{sb}}\gamma }}}} $ | (17) |
| $ {S_{{\text{SBI}}}}\left( {{v_0}} \right) = {S_{{\text{SBD}}}}\left( {{v_0}} \right) + {v_0}{t'_{{\text{tr}}}} $ | (18) |
(4) 报警提示曲线
该模型设两个提示功能点:提示点I与警告点W, 其与SBI曲线之间具有一定的时间间隔, 通过式(22)、式(23)求解, 即
| $ {S_W}\left( {{v_0}} \right) = {S_{{\text{SBI}}}}\left( {{v_0}} \right) + {v_0}{t_{\text{W}}} $ | (19) |
| $ {S_I}\left( {{v_0}} \right) = {S_{{\text{SBI}}}}\left( {{v_0}} \right) + {v_0}{t_{\text{I}}} $ | (20) |
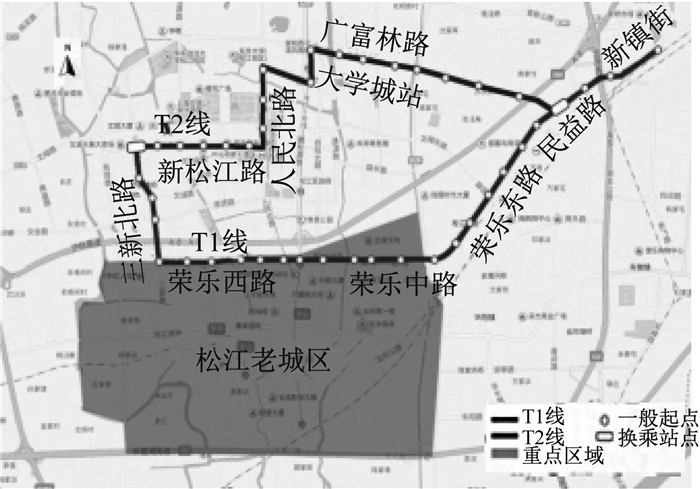
现代有轨电车项目应用前景广泛, 如松江现代有轨电车项目规划建设6条线路, 总长约90km, 设站约118座.目前T1、T2线完成建设, 如图 4所示.T4、T5线2017—2018年开始实施建设, T3、T6线计划2018年起办理前期立项、规划等手续, 实施建设.为了配合有轨电车系统的建设, 松江区配套建设了智能交通管理系统, 涵盖松江城区共382个路口, 建设信号控制、流量采集、交通诱导、停车诱导等设备.
|
图 4 有轨电车T1、T2线建设分布 Fig.4 The map of tramcar Line T1 and Line T2 |
利用Python程序开发语言, 对提出的策略算法进行了验证, 初步构建了现代有轨电车的运行场景, 并着重针对策略算法中的障碍物影响分析、列车防护曲线生成进行了试验设计, 基本验证了策略算法的有效性.
4.1 仿真环境构建(1) 线路建模
相比于传统轨道交通验证程序设计只考虑列车运行一维的情况, 由于本文中有轨电车需要检测线路沿线的障碍物情况, 因此需要建立二维的线路, 如图 5是根据某实际线路进行抽象提取的一条有轨电车线路.

|
图 5 仿真线路示意图 Fig.5 The sketch map of emulational path |
(2) 程序设计
程序主流程为控车程序, 其他子函数包括坐标转换模块、障碍物生成模块、坐标反转换模块、防护曲线生成模块.
4.2 实验结果(1) 列车防护曲线生成模块的验证
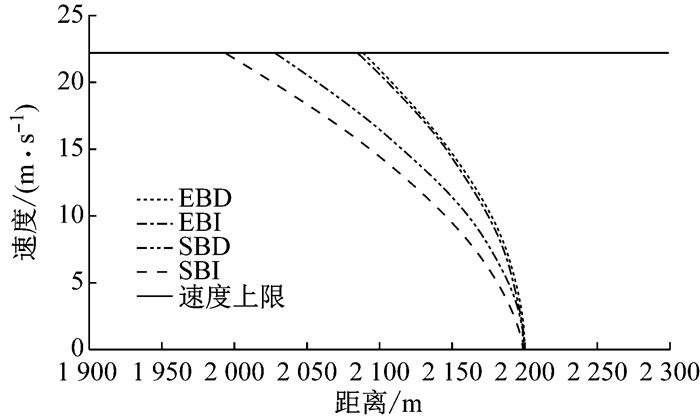
如图 6所示, 为行车许可终点位于轨道里程2 200 m处的4条防护曲线, 算法根据障碍物的位置与列车定位的输入, 能够输出防护曲线情况.
|
图 6 仿真防护曲线 Fig.6 The emulational protection curves |
(2) 防护曲线生成实时性验证
如图 7所示, 仿真实验假定列车检测器停在轨道某处, 随机生成一个具有固定方向匀速运行的目标, 当其进入轨道限界时可以被检测到, 因而影响当前测量周期的列车防护曲线, 并持续一段时间.本次试验的障碍物在轨道内部逗留了14 s, 影响轨道的里程范围为3 143 m~3 156 m, 在一段时间内生成具有突变性的一簇列车防护曲线, 可以在图中看到有一段防护曲线明显向列车靠近, 表明这段时间障碍物进入轨道, 使得行车许可终点有所变化, 另外这一簇曲线所构成的曲面并不完全平行于t轴, 说明障碍物是斜穿经过轨道限界.

|
图 7 防护曲线变化趋势 Fig.7 The variation trend of protection curves |
实验结果可以证明辅助安全防护算法对于雷达检测到的障碍物是实时监测的(探测周期取100 ms), 并且能够实时生成列车防护曲线.
(3) 列车运行验证
图 8为实验行人穿越轨道限界的情景, 所生成的速度记录曲线, 实验中驾驶员根据辅助安全防护系统提供的障碍物及制动信息进行驾驶, 选取线路某一区段, 当列车出站加速引导到某一速度之后, 前方发现障碍物, 而后触发最大常用制动, 4 s后障碍物消失, 列车重新牵引加速, 直至停车进入车站.

|
图 8 速度记录曲线 Fig.8 The curve of velocity change |
实验结果表明, 对于生成的障碍物, 被检测器较为准确地检测到之后, 辅助安全防护算法能够实时计算列车防护曲线, 并提出减速制动的策略.
实验过程中均认为驾驶员遵从相关控制策略.
基于较为准确的雷达检测数据及列车定位数据, 当前的辅助驾驶策略算法设计能够实时确定障碍物目标与轨道限界的位置关系, 并将有威胁的障碍物转化为列车防护曲线的行车许可终点, 从而根据防护曲线给出各个制动监督点, 进行防撞预警.
5 结论现代有轨电车系统由驾驶员进行操作, 驾驶员视野距离限制了列车在某些区段的行驶速度上限.同时在夜晚或者雨、雪、雾等恶劣天气条件下, 驾驶员的视野范围受到极大的限制和削弱, 难以发现潜在的障碍物, 一旦不能够及时制动, 会造成不可挽回的损失.
针对上述问题, 为了保障现代有轨电车运行安全, 提出了一种基于异态检测的有轨电车辅助安全防护技术.主要成果如下:
(1) 雷达技术中的毫米波雷达在全天候使用、检测距离、检测稳定性、低成本等方面具有一定的优势, 因此提出采用毫米波雷达作为有轨电车异态检测器.
(2) 考虑列车制动建立、驾驶员反应时间、列车定位测速误差等因素, 计算紧急制动触发曲线EBI, 当列车行驶状态越过EBI曲线, 需自动施加紧急制动.从功能需求分析、辅助安全防护架构设计、避撞预警功能设计三方面入手, 设计辅助安全防护功能.
(3) 在基于雷达数据输入、列车定位数据输入、列车坐标确定和障碍物等效行车许可终点技术基础上, 从紧急制动曲线EBD、紧急制动触发曲线EBI、最大常用制动曲线SBD、触发曲线SBI四个方面构建辅助安全监控曲线算法.
最后, 利用Python程序开发语言, 对提出的策略算法进行了仿真验证, 初步构建了现代有轨电车的运行场景, 并着重针对策略算法中的障碍物影响分析、列车防护曲线生成进行了实验设计, 最后通过编程仿真实验验证了算法的实时性以及有效性.
| [1] |
陈若望.列车前方障碍物图像检测算法研究[D].成都: 西南交通大学, 2012. CHEN Ruowang. The algorithm of image processing based on obstacle detection in front of train[D]. Chengdu: Southwest Jiaotong University, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10613-1012391600.htm |
| [2] |
郑锐.毫米波汽车防撞雷达的设计与实现[D].南京: 江苏大学, 2010. ZHEN Rui. Design and realization of automotive anti-collision radar[D]. Nanjing: Jiangsu University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-80138-2006184657.htm |
| [3] |
徐友春, 李克强, 连小珉. 智能车辆机器视觉发展近况[J]. 汽车工程, 2003, 25(5): 438 XU Youchun, LI Keqiang, LIAN Xiaomin. The recent development of machine vision for intelligent vehicle[J]. Automotive Engineering, 2003, 25(5): 438 DOI:10.3321/j.issn:1000-680X.2003.05.005 |
| [4] |
STRMTG. GT3-DTW-obstades fixers V2: ref. 4[S]. Paris: [s.n.], 2010.
|
| [5] |
沈拓.基于车-车通信的城轨列车追踪预警研究与实现[D].上海: 同济大学, 2017. SHEN Tuo. Research and realization of city rail train tracking and warming based on inter-vehicle communication[D]. Shanghai: Tongji University, 2017. https://wenku.baidu.com/view/24da0d17793e0912a21614791711cc7930b77837.html |
| [6] |
袁志鹏.基于复合序列的城轨列车射频测距与防撞研究[D].上海: 同济大学, 2014. YUAN Zhipeng. Method of using radio frequency to ranging and anti-collision in city rail train based on composite sequences[D]. Shanghai: Tongji University, 2014. |
| [7] |
WANG Gang, LI Shu, FANG Yungen, et al. Research on improving the accuracy of speed and distance measurement of train by redundant convolution fault-tolerant analysis and multiple data fusion[J]. Journal of Applied Sciences, 2013, 13(12): 2300 DOI:10.3923/jas.2013.2300.2305 |
| [8] |
WANG Gang, ZENG Xiaoqing, LI Jian. Method for evaluation of railway dynamic safety based on 5M model and neural network algorithm[J]. Applied Mechanics and Materials, 2015, 743: 445 DOI:10.4028/www.scientific.net/AMM.743 |
| [9] |
WANG Gang, LIU Huaxiang, ZENG Xiaoqing. Study on train headway in different turn-back mode of urban mass transit station[C]//14th World Conference on Transport Research, WCTR2016. Shanghai: Tongji University, 2016: 600-610.
|
| [10] |
方云根, 曾小清, 王刚. 轨道交通列控系统共因失效分析[J]. 上海交通大学学报, 2015, 49(7): 1052 FANG Yungen, ZENG Xiaoqing, WANG Gang. Common cause failure analysis of automatic train control system[J]. Journal of Shanghai Jiaotong University, 2015, 49(7): 1052 |
| [11] |
ZHENG Wenyi, NAI Wei, DONG Decun, et al. A prognosis method evaluating fault occurance percentage for signaling system in urban rail transit based on naive bayesian classifying[J]. Engineering Letters, 2013, 25(6): 100 |
| [12] |
NAI Wei, DONG Wei, MAO Jieyi, et al. Performance analysis of broadband multimedia access for vehicles based on optimized IEEE 802.11p[C]//The 79th IEEE Vehicular Technology Conference (VTC-Spring). Qingdao: [s.n.], 2014: 1901-1905.
|
| [13] |
ERA. Introduction to ETCS braking curves: ERTMS_040026[S]. Paris: [s.n.], 1996.
|
 2019, Vol. 47
2019, Vol. 47

