振动台缩尺试验是通过模型在试验中的反应反推原型结构的抗震性能,因此要求模型与原型之间有一定的相似关系[1].对于包含钢结构的振动台缩尺模型试验,当缩尺比例较大,为保证精度,对模型加工有较高的要求.紫铜材料特性能够满足钢材的相似比要求,同时又具有可裁剪、拼接和焊制的优点,对于缩尺比较大的振动台试验,通常用紫铜来模拟钢材[2-3].对于小尺寸箱型截面构件,采用焊接加工时,铜片之间通常不会完全焊接,而是采用点焊替代[4].在大部分情况下,点焊连接可以保证构件的正常受力.然而,当试验中构件受较大轴力时,点焊这一加工方式使得构件的承载能力有所下降,构件失效模式表现为局部失稳引起的整体失效,可能造成构件提前破坏,与实际结构的情况不符.目前,国内外关于点焊箱型截面构件的轴压屈曲性能研究较少,为此,本文设计了两种截面尺寸的点焊箱型铜构件,对其进行轴压试验,并在试验的基础上建立有限元模型进行参数分析,得出了一些有益的结论,为振动台试验中点焊箱型截面构件的加工使用提供参考.
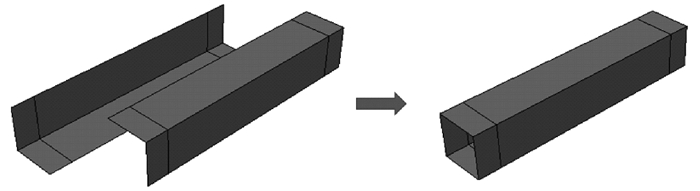
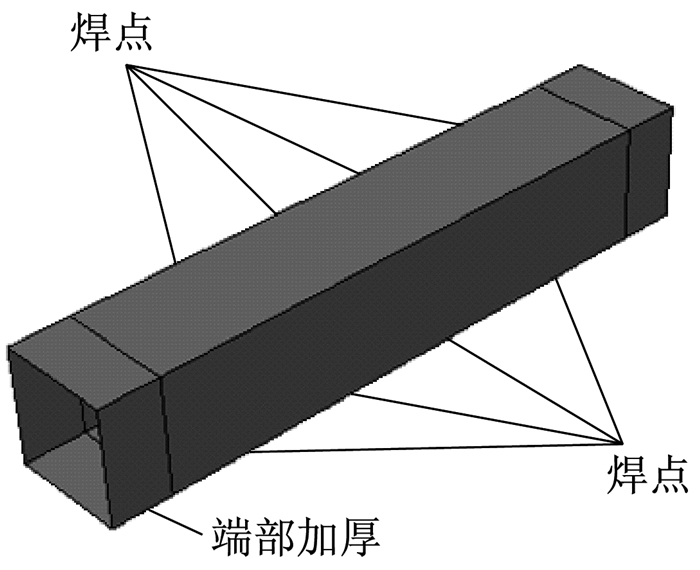
1 试验研究 1.1 试验试件本文设计了两种截面尺寸的点焊箱型铜构件,为方便说明,将这两种试件分别称作1号试件和2号试件.试件编号及相关尺寸如表 1所示.试件的加工方法是将两片铜板分别折为L形截面板材,再将两块板材通过点焊连接成一个箱型截面试件,如图 1a、1b所示,焊点间距为30 mm,实际加工后的点焊连接如图 1c所示.
| 下载CSV 表 1 试件编号及尺寸 Tab.1 Serial number and size of each component |
|
图 1 点焊箱型铜试件加工示意图 Fig.1 Processing method of spot welding square copper tubular components |
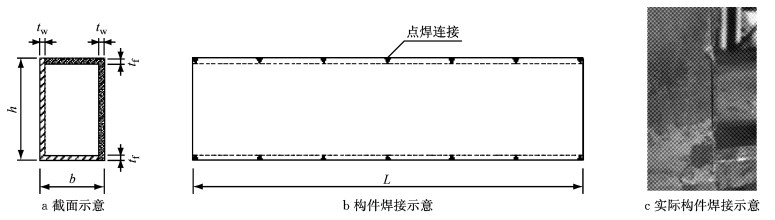
为便于观察试验中试件的变形情况,在试件上画上白色网格,对试件端部进行了加强.在试件中部4个面上贴有应变片,用于记录试验中的应变数据,图 2为加载示意图.
|
图 2 轴压试验示意图(单位:mm) Fig.2 Diagram of axially compressed experiment(unit: mm) |
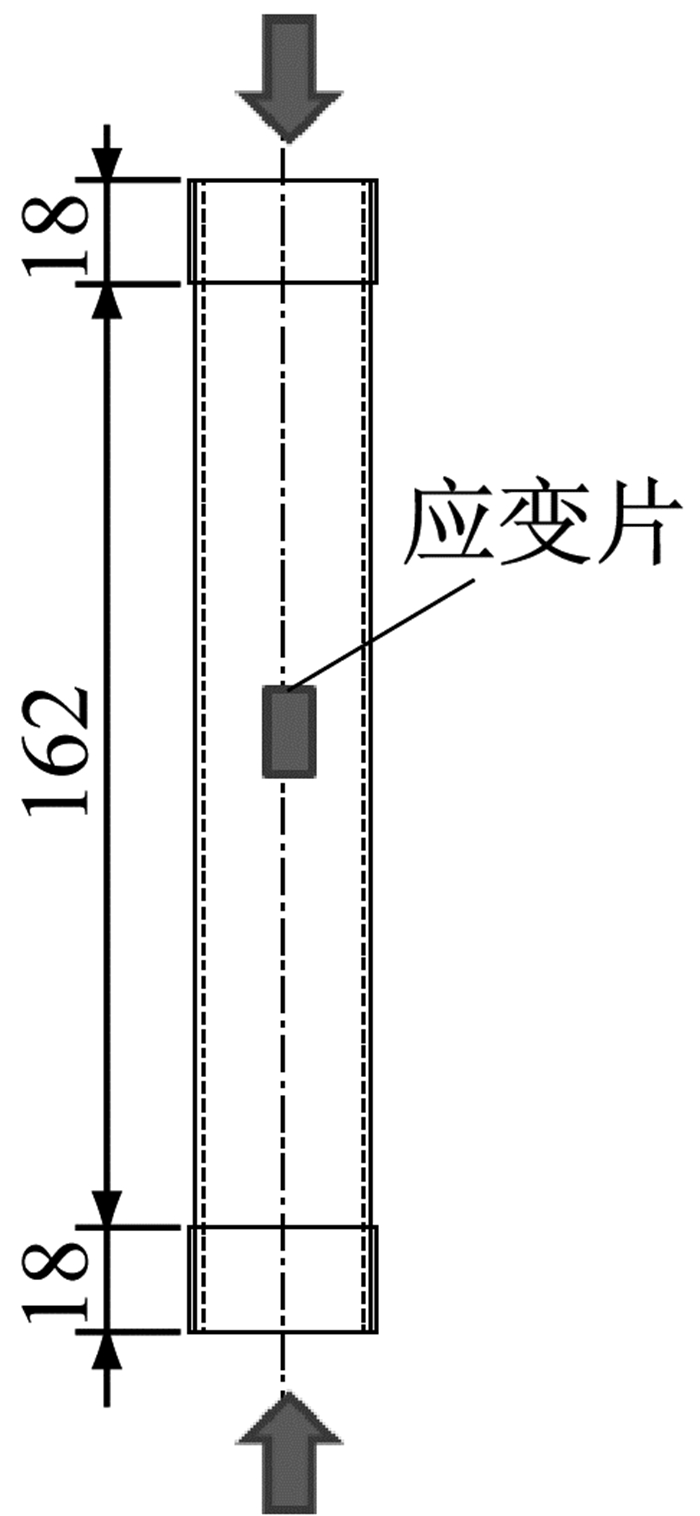
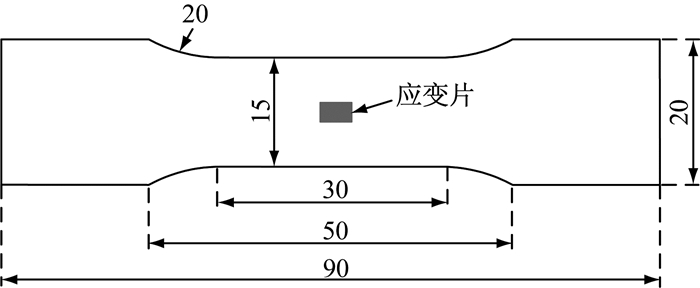
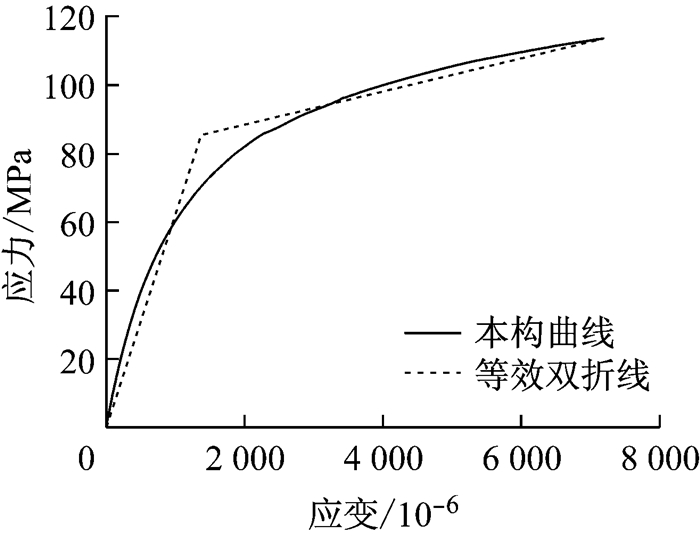
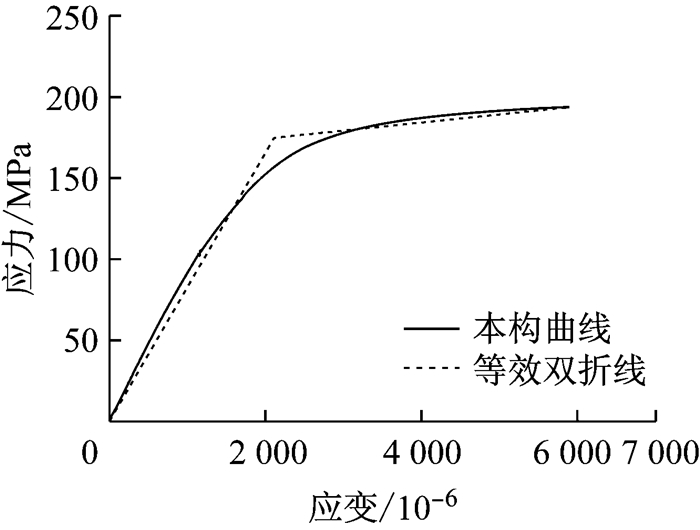
对两种厚度的铜片材料分别做了轴向拉伸试验,其试件尺寸分别如图 3、图 4所示,两种试件各有3个,得到本构曲线分别如图 5、图 6实线所示.图 5、图 6中虚线表示应用能量等效原则得到的等效双折线本构关系,将双折线拐点对应的应变看作材料的屈服应变,其值分别为1 372×10-6和2 114×10-6,用于下文屈曲特性的判别.试验中,同一厚度的3个试件的拉伸结果相近,而从上述两个应变值可以看出,不同厚度的紫铜材性离散度较大.
|
图 3 1号试件本构试验试件尺寸(单位:mm) Fig.3 Specimen dimension of No.1 component in constitutive experiment(unit: mm) |
|
图 4 2号试件本构试验试件尺寸(单位:mm) Fig.4 Specimen dimension of No.2 component in constitutive experiment(unit: mm) |
|
图 5 1号试件材料本构曲线 Fig.5 Constitutive curve of No.1 material |
|
图 6 2号试件材料本构曲线 Fig.6 Constitutive curve of No.2 material |
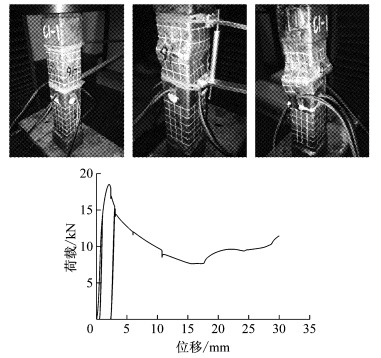
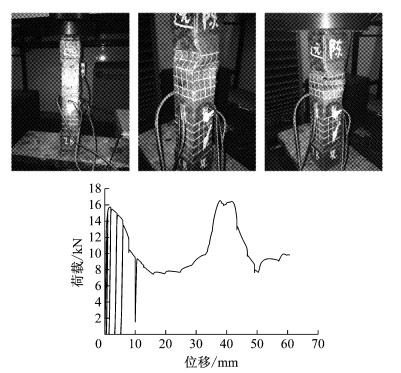
采用5 t万能试验机对试件进行轴向静力加载.1号试件从加载到破坏的形态及其荷载-位移曲线如图 7~10所示,2号试件从加载到破坏的形态及其荷载-位移曲线如图 11、图 12所示.表 2是对试验中所有试件的极限承载力及其对应位移、承载力均值及其对应位移均值的整理统计.试验中两种试件的破坏均是由焊点之间铜片的局部屈曲引起的,在加载后期屈曲处的铜片相互叠合,这也就是加载曲线后期承载力增大的原因.由于仪器原因,C1-3试件只记录了加载到8 mm左右的数据,所以图 7中没有后期承载力增大现象.试验过程中对试件进行了若干次卸载后再加载,以观察其卸载后再加载的刚度,结果显示卸载后再加载的刚度基本不变.
|
图 7 C1-1加载过程及荷载-位移曲线 Fig.7 Loading procedure of C1-1 and its loading curve |
|
图 8 C1-2加载过程及荷载-位移曲线 Fig.8 Loading procedure of C1-2 and its loading curve |
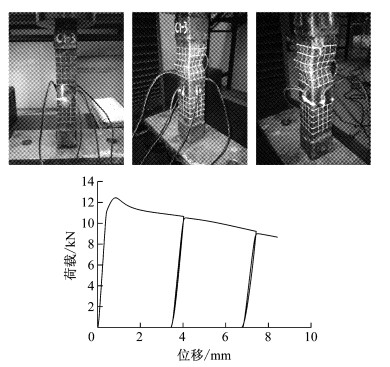
|
图 9 C1-3加载过程及荷载-位移曲线 Fig.9 Loading procedure of C1-3 and its loading curve |
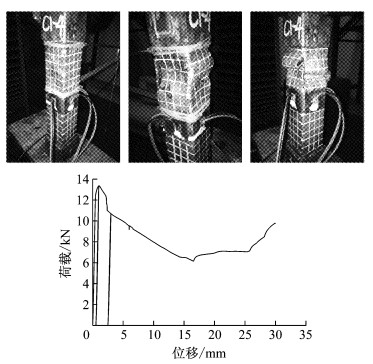
|
图 10 C1-4加载过程及荷载-位移曲线 Fig.10 Loading procedure of C1-4 and its loading curve |
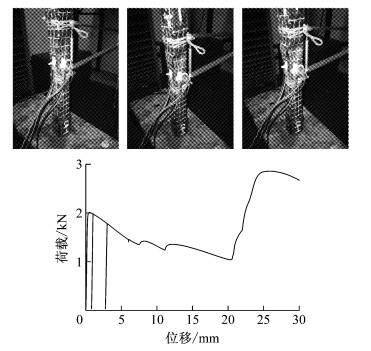
|
图 11 C2-1加载过程及荷载-位移曲线 Fig.11 Loading procedure of C2-1 and its loading curve |
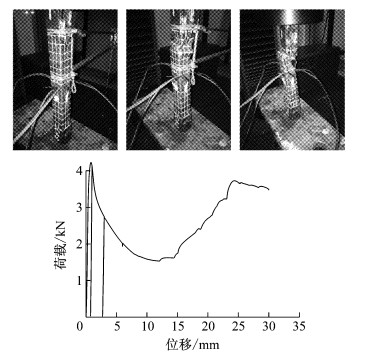
|
图 12 C2-2加载过程及荷载-位移曲线 Fig.12 Loading procedure of C2-2 and its loading curve |
| 下载CSV 表 2 各试件的极限承载力及其对应位移、极限承载力均值及其位移均值 Tab.2 Bearing capacity and displacement of each component |
提取试验中的应变数据以明确试件在屈曲时铜片处于弹性还是塑性.由于C1-2、C1-3的应变数据无效,所以剔除.在承载力达到峰值时,4个试件的中部平均应变如表 3所示.从表 3可以看出,4个应变值均小于材料的屈服应变,所以认为试件均是发生了弹性屈曲.但两种尺寸试件屈曲情况存在一定差别,C1-1、C1-4的应变达到了其屈服应变的一半以上,而C2-1、C2-2的应变不到其屈服应变的三分之一,这说明相对于2号试件,1号试件在屈曲之前应变发展得更充分,即认为1号试件相对来说更晚发生屈曲.这一差异可能由两种试件的宽厚比不同造成的.
| 下载CSV 表 3 承载力达到峰值时试件的中部平均应变 Tab.3 Average strain at the middle of each component when reaching the bearing capacity |
本文采用ABAQUS有限元软件对试验进行模拟.采用S4R壳单元,分别建立两个L形截面的模型再拼装得到箱型截面模型,如图 13所示.按照实际试件情况,模型中试件端部设置较大的厚度.
|
图 13 有限元模型拼装 Fig.13 Assembly of square tubular components |
在试验中,随着加载的进行,试件上的焊点会发生破坏而分离,这一现象都是出现在试件屈曲以后且即将压溃的加载后期,而本文的研究重点是加载前期及中期阶段试件的屈服状态,所以在数值模拟中不考虑焊点的破坏.利用绑定约束(Tie)来模拟点焊连接,这样在分析过程中,试件在点焊处始终保持连接.焊点实际上是一个小区域,设置长度为3 mm,焊点部位网格划分较细.模型中焊点的布置与实际情况相同,焊点间距为30 mm,如图 14所示.两种模型分别采用图 5、图 6实线所示的试验本构曲线,泊松比均取0.35.
|
图 14 焊点布置情况 Fig.14 Distribution of welding spots |
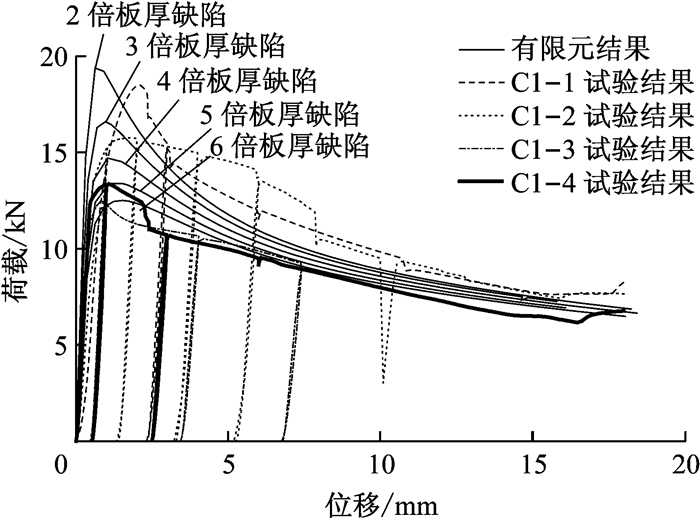
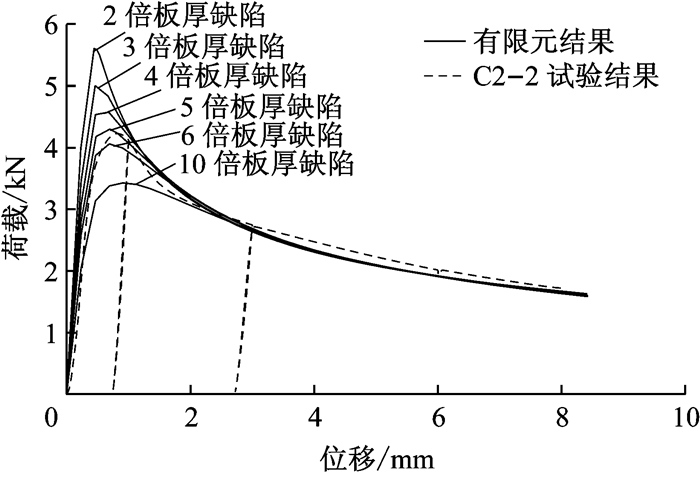
首先进行特征值屈曲分析,求得其屈曲模态,引入一阶屈曲模态作为初始缺陷.分析中模型一端固定,另一端施加轴向位移,考虑几何非线性.对于初始缺陷的取值,若仅考虑初始几何缺陷,参照钢构件缺陷幅值取试件长度的千分之一[5].有限元分析结果中极限荷载较试验结果大许多,这是由于紫铜材料缺陷敏感,而实际试件初始缺陷存在多种缺陷又比较复杂.在此,尚且无法获得试验构件实际初始缺陷大小及分布,有限元分析中将所有初始缺陷全部等效为初始几何缺陷[6],取不同板厚倍数的缺陷幅值进行分析,得到加载曲线及其与试验的对比如图 15、图 16所示.
|
图 15 1号试件模型荷载-位移曲线与试验曲线对比 Fig.15 Comparison of computing loading curve and test loading curve of No.1 component |
|
图 16 2号试件模型荷载-位移曲线与试验曲线对比 Fig.16 Comparison of computing loading curve and test loading curve of No.2 component |
从结果可以看出,对于1号试件,当等效几何缺陷幅值取3~5倍板厚时,有限元结果同试验结果吻合较好.对于2号试件,当缺陷取到10倍板厚时,有限元结果曲线仍高出试件C2-1试验曲线许多,并且继续增大缺陷,极限荷载减小不明显,始终无法达到和试件C2-1接近的极限荷载值,因此认为试件C2-1试验存在异常;剔除问题数据后,当等效初始几何缺陷幅值取4~6倍板厚时,有限元结果与试验结果较为接近.综上,本试验中模型取4~5倍板厚缺陷作为等效初始几何缺陷进行有限元分析较为合理.有限元分析结果与试验结果的承载力及位移的对比如表 4所示,有限元结果与试验结果较为接近.
| 下载CSV 表 4 有限元分析结果与试验结果的对比 Tab.4 Comparison of computing results and test results |
有限元分析得到模型的最终屈曲形态及Mises应力分布如图 17、图 18所示.有限元分析结果中,屈曲都发生在模型中部,而在试验中,许多试件的屈曲是发生在试件上半部或者下半部,这主要是由于有限元模型的初始缺陷只引入一阶屈曲模态,而实际试件尺寸较小,紫铜材料比较敏感,初始缺陷分布比较复杂造成的.

|
图 17 1号试件模型屈曲形态及Mises应力分布 Fig.17 Buckling form and distribution of Mises stress of No.1 component |

|
图 18 2号试件模型屈曲形态及Mises应力分布 Fig.18 Buckling form and distribution of Mises stress of No.2 component |
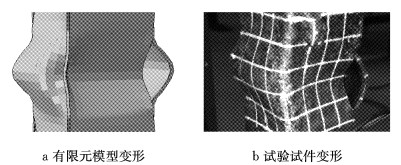
有限元分析与试验中试件的变形形态对比如图 19所示.可以看出,与试验情况一致,在有限元分析中试件也是因为某两个焊点之间的铜片发生局部屈曲而破坏的,其变形形态与试验相符.
|
图 19 有限元模型与试验试件变形形态对比 Fig.19 Comparison of computing and test of deformation of components |
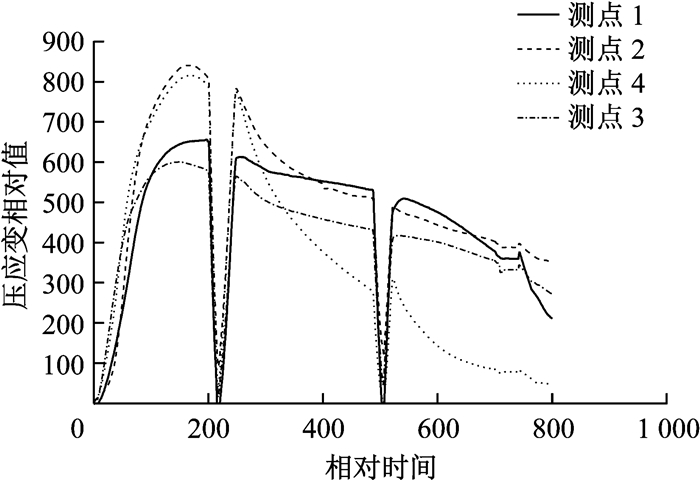
在试验中,试件中部4个表面上都贴有1个应变片以记录应变数据.观察应变数据,发现有如下现象:4个应变数据中,有2个应变数据比另外2个应变数据大,且大应变与小应变处于相邻的表面上.以C2-2试件为例,试件中部4个面上的应变随时间变化情况如图 20所示,可以看出,在变形不大的情况下,测点2和测点4、测点1和测点3采集的应变数据值分别相接近,且测点2、4的数据大于测点1、3的数据.其中,测点1与测点2处于相邻的两个面上,而与测点3处于相对的两个面上.有限元分析中,模型在最大承载力时刻对应的塑性应变发展情况如图 21所示,图中黑色部分表示材料处于弹性.从图 21中可以看出,由于点焊箱型构件本身的屈曲特点,同一焊点区间的4个面各自的应变发展是不同的,有两个面受力较小,基本处于弹性,而另两个面受力较大,部分区域已进入塑性,且相邻两个面应变发展情况不同,这与上述试验现象相符.
|
图 20 试件中部4个面的应变数据变化情况 Fig.20 Strain curves at middle four faces of a component |

|
图 21 试件在最大承载力时刻对应的塑性应变发展情况 Fig.21 Distribution of plastic strain when reaching bearing capacity |
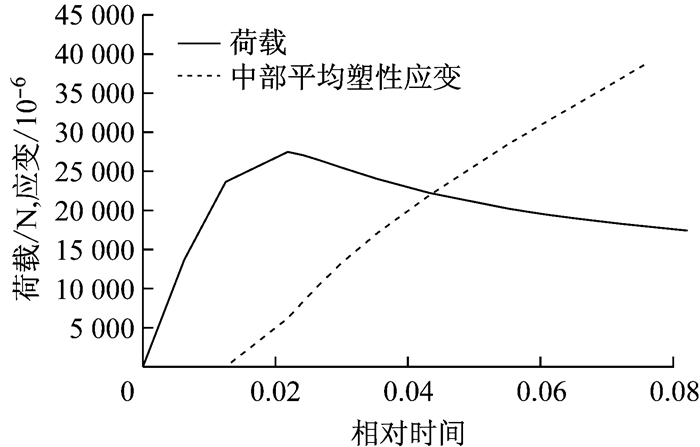
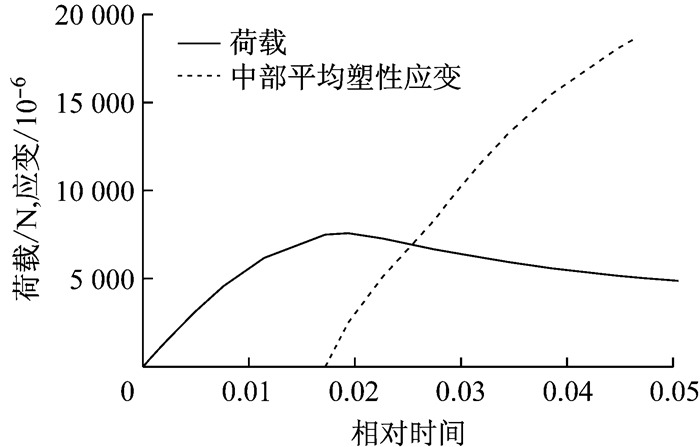
有限元结果中试件达到最大承载力时刻的塑性应变分布如图 22、23所示.从图 22、23中可以看出,在试件开始屈曲时,两个试件中均有部分靠近试件中部的区域已经进入塑性,但两个试件的塑性发展程度存在差别,1号试件比2号试件塑性发展程度更大,2号试件相比1号试件,有更多区域处于弹性状态.这与试验结果中,1号试件在屈曲时中部应变值更接近其屈服应变情况相符.图 24、25分别为两个试件荷载与中部平均塑性应变的变化曲线.从图 24、25中可以看出,在加载前期试件中部处于弹性状态,随着加载进行,材料逐渐进入塑性.对比图 24与图 25可以发现,两个试件是有差异的,2号试件相对1号试件进入塑性更晚,这也与试验结果相符.在钢结构中,试件的局部屈曲与其宽厚比有较大关系[7-8],已知2号试件宽厚比比1号试件稍大,因此从宽厚比角度来说,1号试件更不容易发生局部屈曲,所以在发生屈曲之前应变较大.

|
图 22 荷载达峰值时1号试件塑性发展情况 Fig.22 Distribution of plastic strain of No.1 component when reaching bearing capacity |

|
图 23 荷载达峰值时2号试件塑性发展情况 Fig.23 Distribution of plastic strain of No.2 component when reaching bearing capacity |
|
图 24 1号试件荷载与中部平均塑性应变变化曲线 Fig.24 Load and average middle part plastic strain curve of No.1 component |
|
图 25 2号试件荷载与中部平均塑性应变变化曲线 Fig.25 Load and average middle part strain curve of No.2 component |
有限元计算所得的结果与试验结果存在偏差的主要原因有:
(1) 紫铜材料本身易变形,而本试验中铜片厚度较小,试件通过冷弯后焊接而成,其弯折部位冷加工特征明显.在点焊加工后,会产生较复杂的初始缺陷和残余应力.在有限元模型中,对点焊连接做了简化处理,没有考虑点焊加工对试件产生的影响,初始缺陷只引入一阶屈曲模态,与实际试件的初始缺陷情况有区别[9-10].这一因素反映在计算结果中就是,有限元结果中局部屈曲都发生在模型中部,而试验结果中局部屈曲多发生在试件上半部或下半部.
(2) 紫铜材料对温度较为敏感,焊接加工使材料受到一定程度的损伤,并产生残余应力,反映在计算结果中就是,有限元分析结果中模型轴向刚度比试验结果略大,对应的峰值时刻的应变也比试验结果大.
(3) 不同厚度、不同生产批次的铜板材料性质相差较大.在材性试验中得到的不同厚度铜板的本构曲线相差较大,说明薄壁铜板材料性质本身离散性较大,使有限元分析中使用的本构曲线,与试件真实的本构曲线有差别.
(4) 试验本身也存在加工和加载等方面的误差,从而造成与有限元模型有一定的差别.
通过以上有限元分析结果与试验结果的对比,可知在“等效初始几何缺陷”概念的基础上合理调整缺陷取值后,有限元模型荷载-位移曲线与试验吻合较好;有限元得到的屈曲特性、破坏模式与试验相同;模型破坏后的变形也与试验相符,因此可以认为本文的有限元模型能够准确地分析点焊箱型铜构件受压屈曲性能,运用该模型对点焊试件进行参数分析较为合理.需要指出的是, 如何根据实际工艺和参数条件确定等效初始几何缺陷的取值需要进一步研究.
3 点焊边界条件下的薄板屈曲研究 3.1 四边简支薄板在轴压下的屈曲在弹性力学中,对于单向均匀受压简支板,其屈曲平衡方程为
| $ D\left( {\frac{{{\partial ^4}\omega }}{{\partial {x^4}}} + 2\frac{{{\partial ^4}\omega }}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}\omega }}{{\partial {y^4}}}} \right) + {p_x}\frac{{{\partial ^2}\omega }}{{\partial {x^2}}} = 0 $ | (1) |
式中:D为板单位宽度的抗弯刚度; ω为板的挠度;px为在x轴方向沿板周边中面单位宽度上所承受的力,压力为正,拉力为负.
对于四边简支板,其临界荷载的解为
| $ {p_x} = \frac{{{\pi ^2}D}}{{{b^2}}}{\left( {\frac{{mb}}{a} + \frac{{{n^2}a}}{{mb}}} \right)^2} $ | (2) |
式中:m和n分别是板屈曲时在x和y方向的半波数,即板件在x和y方向分别屈曲成m个和n个正弦半波曲线; a、b分别为板沿x、y方向长度.
临界荷载是保持板微弯状态的最小荷载,只有n=1才能使px具有最小值,因而临界荷载为
| $ {p_x} = \frac{{{\pi ^2}D}}{{{b^2}}}{\left( {\frac{{mb}}{a} + \frac{a}{{mb}}} \right)^2} = \frac{{{\pi ^2}D}}{{{b^2}}}\beta $ | (3) |
式中:
当单向均匀受压板的两个加载边是简支的,有一非加载边也是简支的,而另一非加载边是自由的,文献[7]给出了x轴方向沿板周边中面单位宽度上所承受的力为
| $ {p_x} = \left[{\frac{{{m^2}{\pi ^2}{b^2}}}{{{a^2}}} + 6\left( {1{\rm{-}}\nu } \right)} \right]\frac{D}{{{b^2}}} $ | (4) |
当m=1时可以得到px的最小值,若取泊松比ν=0.35(紫铜材料),可得到板的屈曲荷载
| $ {p_{{\rm{cr}}x}} = \left( {0.395 + \frac{{{b^2}}}{{{a^2}}}} \right)\frac{{{\pi ^2}D}}{{{b^2}}} = \beta \frac{{{\pi ^2}D}}{{{b^2}}} $ | (5) |
屈曲系数β=0.395+b2/a2,当a远大于b时,β≈0.395.
3.3 点焊箱型铜构件的屈曲对于点焊箱型构件,其每一面上的铜片的边界条件可以看作一边简支一边焊点支撑,这种边界条件介于四边简支和三边简支之间,因此猜想其屈曲系数的值是介于4和0.395之间,当保持其他条件不变,改变焊点间距,屈曲系数也将发生变化.为了验证上述猜想,利用有限元软件对点焊箱型铜构件进行特征值屈曲分析.
参照试验试件建立有限元模型,弹性模量取E=1.13×1011 N·m-2,铜片厚度t=1.5 mm,泊松比ν=0.35,得到
改变焊点间距,分别计算得到屈曲荷载,进而根据公式
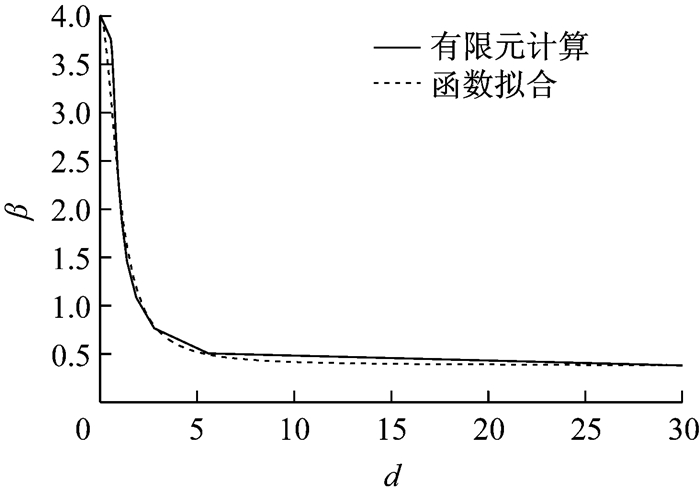
|
图 26 有限元计算得到的d与β的关系曲线及相应函数拟合曲线 Fig.26 Curve d versus β calculated by finite element analysis and the fitting curve 0 |
根据曲线形式,使用函数
由上文已知,宽厚比对点焊构件屈曲性能影响较大,因此对该参数做进一步研究.设置构件厚度均为1.5 mm,宽度为20~60 mm,间隔5 mm,共得到9个不同的试件模型,对其进行有限元轴压模拟.
由于构件上存在应力集中现象,因此不管宽厚比多大,始终会有一定区域进入塑性,即得到的中部点焊区段的平均塑性应变始终大于零.为了便于直观分析宽厚比与塑性发展的关系,取构件中部点焊区段及其相邻区段的平均塑性应变作为衡量指标,通过这种方式得到的平均塑性应变就有可能接近零.
在有限元分析结果中得到最大荷载时刻的中部区段及其相邻区段的平均塑性应变,如表 5所示.从表 5中可以看出,随着宽厚比增大,最大荷载时刻的塑性发展程度逐渐降低,这与上文分析及试验结果相符.以上述平均塑性应变为纵坐标,以宽厚比为横坐标,得到宽厚比对试件塑性发展的影响曲线如图 27所示.从图 27中可以看出,平均塑性发展与宽厚比之间近似呈现为线性关系.
| 下载CSV 表 5 不同宽厚比时构件中部平均塑性应变 Tab.5 Average middle part plastic strain with different width-to-thickness ratios |
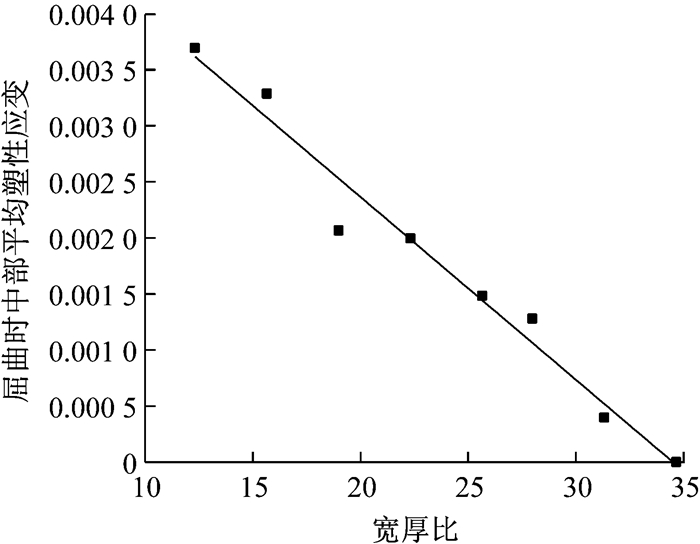
|
图 27 宽厚比对塑性发展的影响曲线 Fig.27 Influence of width-to-thickness ratio on plastic deformation |
除了宽厚比之外,点焊构件的受力性能还会受焊点间距影响[11].取1号试件,改变其焊点间距,共得到9个不同的试件模型,对其进行有限元轴压模拟,所得结果如表 6所示,其中焊点间段数为0时表示构件的两个L形铜板只在端部连接,中间没有焊点,而“全焊”指构件的两个L形铜板边缘完全连接,表中α表示焊点间距与铜片厚度的比值,γ表示点焊试件承载力与全焊试件承载力的比值.图 28为γ随α的变化曲线.由图 28可以看出,随着α的增大,γ不断下降; 当α值较小时,γ随对α变化较为敏感; α逐渐增大后,γ变化速度将逐渐减小,最后趋于不变.
| 下载CSV 表 6 不同α对应的γ Tab.6 Values of γ at different α values |
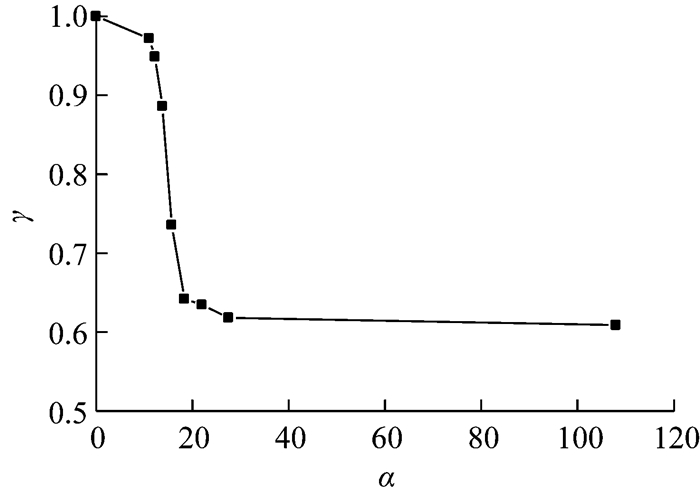
|
图 28 γ随α的变化曲线 Fig.28 Influence of α on γ |
从γ随α的变化曲线来看,在加工点焊构件时,焊点间距越小越好,但是在实际加工中,若焊点间距取得太小,会产生较大的残余应力,使构件受到较大损伤,构件的初始变形会比较复杂.因此,实际焊点间距不能过小.
不同宽厚比的情况下,γ随α的变化规律可能存在差异.上文是采用1号试件对应的有限元模型,该试件截面宽厚比为23.30,在此基础上,增加三组有限元模型,分别设置宽厚比为20.00、27.00、30.00,进行与上文相同的分析,得到不同宽厚比对应的γ随α变化曲线,如图 29所示.由图 29可以看出,不同宽厚比下,γ与α的变化关系基本上呈现以下现象:当α值较小时,宽厚比越大,对应的γ值也越大; 当α值较大时,宽厚比越大,对应的γ值就越小.
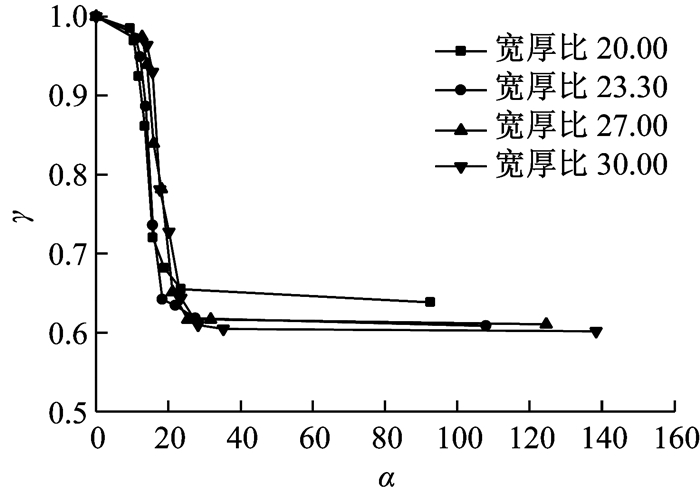
|
图 29 不同宽厚比对应的γ随α的变化曲线 Fig.29 Influence of α on γ at different width-to-thickness ratios |
为了研究振动台试验中常用的点焊构件与实际构件的受力性能差异,本文对两种尺寸的点焊箱型铜构件进行了静力轴压试验,得到其加载曲线,并分析了其屈曲性能.在试验的基础上建立有限元模型,利用试验结果验证该模型.同时,对点焊边界条件下的薄板屈曲展开研究.最后进行了参数分析,研究点焊构件的宽厚比和焊点间距对其受力性能的影响,主要得到以下结论:
(1) 试验中,点焊箱型铜构件的破坏均是由两个相邻焊点之间铜片的局部屈曲引起的,两种尺寸的试件在轴压下都发生弹性屈曲,但1号构件比2号构件更晚发生屈曲,这一差异主要是由构件的宽厚比不同造成的.
(2) 通过在“等效初始几何缺陷”概念基础上调整缺陷取值,能够达到有限元分析结果与试验结果相吻合,本文有限元模拟中,取4~5倍板厚缺陷幅值较为合理,后续工作需深入研究如何根据实际工艺和参数条件确定等效初始几何缺陷的取值.
(3) 轴心受压的点焊箱型铜构件的每一面铜片的边界条件是介于四边简支和三边简支之间,得到了屈曲系数关于焊点间距与铜片宽度比值的函数关系式.
(4) 宽厚比对试件屈曲特性有重要影响,宽厚比越大,试件塑性发展程度就越低.焊点间距影响试件的承载能力,焊点间距相对越小,试件承载力就越大,且宽厚比不同时,焊点间距对点焊构件的影响也有差异.
| [1] |
周明华. 土木工程结构试验与检测[M]. 南京: 东南大学出版社, 2002 ZHOU Minghua. Civil engineering structure testing and detection[M]. Nanjing: Southeast University Press, 2002 |
| [2] |
姚振纲. 建筑结构试验[M]. 武汉: 武汉大学出版社, 2001 YAO Zhengang. Architectural structure experiment[M]. Wuhan: Wuhan University Press, 2001 |
| [3] |
周颖, 卢文胜, 吕西林. 模拟地震振动台模型实用设计方法[J]. 结构工程师, 2003(3): 30 ZHOU Ying, LU Wensheng, LÜ Xilin. Practical model design method of shaking table tests[J]. Structural Engineers, 2003(3): 30 DOI:10.3969/j.issn.1005-0159.2003.03.006 |
| [4] |
钟卫佳. 铜加工技术实用手册[M]. 北京: 冶金工业出版社, 2007 ZHONG Weijia. Copper processing technology handbook[M]. Beijing: Metallurgical Industry Press, 2007 |
| [5] |
彭雄, 杨娜, 猛庆桐. 冷弯薄壁型钢组合截面构件试验研究与数值模拟[J]. 工程力学, 2012, 29(9): 272 PENG Xiong, YANG Na, MENG Qingtong. Experimental research and numerical analysis on the combination effects of cold-formed steel specimens[J]. Engineering Mechanics, 2012, 29(9): 272 |
| [6] |
PASTOR M M, CASAFONT M, BONADA J, et al. Imperfection amplitudes for nonlinear analysis of open thin-walled steel cross-sections used in rack column uprights[J]. Thin-Walled Structures, 2014, 76(76): 28 |
| [7] |
陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社, 2008 CHEN Ji. Stability of steel structure theory and design[M]. Beijing: Science Press, 2008 |
| [8] |
中华人民共和国住房和城乡建设部.钢结构设计规范: GB50017—2003)[S].北京: 中国计划出版社, 2003. Ministry of Construction of the People's Republic of China. Code for design of steel structures: GB50017—2003[S]. Beijing: China Planning Press, 2003. |
| [9] |
WIKANDER L, KARLSSON L, NASSTROM M, et al. Finite element simulation and measurement of welding residual stresses[J]. Modeling and Simulation in Material Science and Engineering, 1984, 2(4): 62 |
| [10] |
赵锐.焊接残余应力的数值模拟及控制消除研究[D].大连: 大连理工大学, 2006. ZHAO Rui. Study of welding residual stress's numerical simulation and relieving[D]. Dalian: Dalian University of Technology, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1029986 |
| [11] |
祁建.点焊构件焊点布置的优化设计[D].沈阳: 东北大学, 2008. QI Jian. Weld spot disposal optimization design of spot welding part[D]. Shenyang: Northeastern University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10145-2010256349.htm |
 2019, Vol. 47
2019, Vol. 47

