2. 同济大学 上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804
2. Shanghai Key Laboratory of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China
制冷剂侧两相流流量分配不均是平行流蒸发器的共性问题.有研究表明,对于制冷剂R134a,制冷剂侧流量分配不均会导致其性能降低20%~30%.现阶段,主要通过试验来探索改善蒸发器内制冷剂流量分配不均的问题.Tompkins等[1]、Zou等[2]发现集管水平或垂直放置时,相较于其他流型,塞状流或混沌流的流量分配均匀性较好.Lee等[3]以及Kim等[4]发现当扁管插入集管深度为集管半径时流量分配均匀性最好.Kim等[5]则发现当集管内插入分流管或分流板时,集管内的流量分配不均匀性可以得到明显的改善.少数研究者利用数值模拟方法来探索改善流量分配不均匀性的方法,如Wang等[6]、Yang等[7]通过试验和CFD(computational fluid dynamics)对Z型和U型换热器液相在换热器中的流量分配展开分析.Ramadevi等[8]用CFD模拟了制冷剂R22、R134a、R407C在高压(最高压力2 MPa)蒸发器换热管段中,不同质量流量下的蒸发过程,模拟结果表明, VOF(volume of fluid)模型可以预测所有流型;且制冷剂在质量流量较小时,模拟压降与实验值的误差要比大多数关联式与实验值的误差小;但是对于R134a,质量流量为200 kg· (m2·s)-1且低干度或质量流量为400 kg· (m2·s)-1且中干度时,所对应的两相流型分别为泡状流和塞状流,气液之间没有明显的界限,此时,适用于有明显两相界面情况的VOF模型误差较大.
试验研究虽然是探索流量分配不均匀方法的最可靠途径,但成本大、周期长,而且要获取更多的信息难度很大.本文将利用CFD模拟蒸发器集管中两相流的流量分配问题,解释流量分配不均的原因,并就改善集管中流量分配不均匀性的措施展开分析.
1 两相流模型验证 1.1 两相流模型简介[9-10]两相流模型的模拟方法主要分为两类:欧拉拉格朗日法和欧拉欧拉法.拉格朗日法不能模拟多相流中每一相的分布,如DPM(discrete phase model)模型.欧拉法主要包括3种模型:VOF模型、Mixture模型,Eulerian模型,可以模拟多相流中每一相的分布.
稳态的VOF模型主要用于计算结果依赖初始条件和每一相进口边界条件不同的情况.VOF模型是一种固定在欧拉网格下的表面追踪方法,当需要得到每一种或多种互不相融流体间的交界面时,可以采用该模型.Mixture模型可用于两相或多相流(流体或颗粒),其应用包括低负载的负载粒子流、气泡流、沉降和旋风分离器等.Mixture模型也可用于没有离散相,相对速度均匀的多相流.Eulerian模型是Fluent中最为复杂的多相流模型,它包含有n个动量方程和连续方程,可以用来求解每一相的情况,其中压力项和各界面交换系数耦合在一起.耦合的方式则依赖于所含相的情况,颗粒流(流固)的处理与非颗粒流(流流)是不同的.欧拉模型可以用在包括气泡柱、上浮、颗粒悬浮和流化床等的场合.
1.2 模型选择 1.2.1 湍流模型、制冷剂物性及边界条件采用标准k-ε湍流模型,非平衡壁面函数,分离求解器及隐式格式求解.制冷剂物性及边界条件分别见表 1和表 2.模型设置中,重力加速度为9.81m·s-2;若是气体在液相中的上升,其操作密度为0;若是液相在气相中的重力下降,操作密度为气相密度.
| 下载CSV 表 1 制冷剂物性表 Tab.1 Physical properties of refrigerant |
| 下载CSV 表 2 边界条件 Tab.2 Boundary condition |
Schwarzkope等[11]指出两相流模型的选择与颗粒荷载、Stokes数有关.
颗粒荷载β是影响相间相互作用的主要因素.它的定义如下:
| $\mathit{\beta = }\frac{{{\mathit{\alpha }_{\rm{d}}}{\mathit{\rho }_{\rm{d}}}}}{{{\mathit{\alpha }_{\rm{c}}}{\mathit{\rho }_{\rm{c}}}}} $ | (1) |
式中:下标d和c分别代表离散相和连续相;αd为离散相体积分数;αc为连续相体积分数;ρd为离散相密度,kg·m-3;ρc为连续相密度,kg·m-3.
假设离散相的体积分数为αd= 0.1,则连续相的体积分数αc= 0.9;气相为连续相,液相为离散相.故β的值大约为4.6.
两相密度比γ的定义为
| $\mathit{\gamma = }\frac{{{\mathit{\rho }_{\rm{d}}}}}{{{\mathit{\rho }_{\rm{c}}}}} $ | (2) |
文中气相为连续相,液相为离散相,液滴气流体的γ值大约为41.4.利用这些参数,液滴间的平均距离可根据文献[12]估算,颗粒间距L/D定义为
| $\frac{L}{D} = {\left( {\frac{{\rm{ \mathit{ π} }}}{6}\frac{{1 + k}}{k}} \right)^{\frac{1}{2}}} $ | (3) |
式中:L为液滴平均距离,mm;D为液滴直径,mm;k=β/γ;
计算得到L/D大约为1.47.在低荷载流体流动中,相间耦合是单向的,连续相通过拽力和湍动能影响液滴,离散相对连续相没有反作用,拉格朗日法和欧拉法都可以处理这种问题;对于中级荷载,耦合是双向的,欧拉法可以处理该问题;而对于高荷载,相间耦合与颗粒间的相互作用都应考虑在内,在这种情况下,只有欧拉法中的Eulerian模型可以处理该问题.
Schwarzkope等[11]指出,当荷载为1,颗粒平均间距为10时,颗粒可以作为孤立的个体处理,属于低级荷载.当荷载大于1,颗粒间距小于10时,属于中级或高级荷载.本文中,颗粒荷载β为4.6,颗粒间距L/D大约为1.74,因此本文两相流颗粒属于中级荷载或高级荷载.
对于颗粒属于中级荷载的流体系统,Stokes数的计算可以帮助选择模型.当St
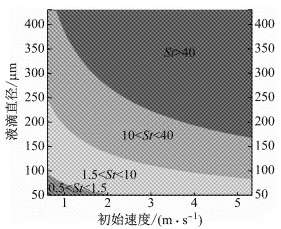
根据PDPA(phase doppler particle analyzer)测量法[13]得到液滴尺寸在50~430 μm之间,所以Stokes数的计算采用Fei等[12]提出的公式
| $St = \frac{{{\mathit{\tau }_{\rm{p}}}}}{{{\mathit{\tau }_{\rm{f}}}}} $ | (4) |
式中:τp为颗粒响应时间,s;τf为流体响应时间,s.
颗粒响应时间计算公式为
| ${\mathit{\tau }_{\rm{p}}} = \frac{{\left( {2{\mathit{\rho }_{\rm{p}}} + {\mathit{\rho }_{\rm{f}}}} \right)d_{\rm{p}}^2}}{{36{\mathit{\mu }_{\rm{f}}}}} $ | (5) |
式中:ρp、ρf分别为液滴与蒸汽的密度,kg·m-3;dp为液滴尺寸,m;μf为蒸汽黏度,Pa·s.
流体响应时间计算公式为
| $\mathit{\tau }{\rm{f = }}\frac{{5H}}{{{U_0}}} $ | (6) |
式中:H为管半径,m;U0是管子中心线处的速度,m·s-1.
本文模拟的制冷剂流动中,质量流量范围为35~50 g·s-1,入口干度范围为0.1~0.3,入口直径为9.5 mm.由图 1[12]、图 2[12]可知,St大部分处于大于1.0的区域,所以Mixture模型并不合适,因此选择欧拉-欧拉法中的Eulerian模型进行模拟计算.
1.2.3 相间作用力在气液两相流的模拟中,第二相一般假设有液滴或气泡,所以制冷剂气相为第一相,液相为第二相.本文升力模型采用Moraga模型,拽力模型采用Symmetric模型,且不考虑虚拟质量力.
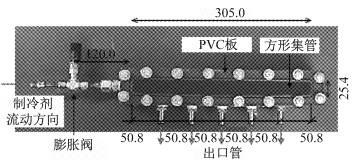
1.3 模型验证采用文献[12]中的实验结果进行模型验证,该文献采用如图 3所示的方形集管配合5个圆形出口的分流结构进行试验,集管中未插入分流管.试验用工质为R134a,入口流量及干度范围分别为35~50 g·s-1和0.1~0.3,通过进口压力的调整,保持左侧制冷剂入口温度与环境温度相同.
|
图 3 验证用物理模型[12](单位:mm) Fig.3 Physical model for validation (unit:mm) |
图 4为质量流量分别为35、40、50 g·s-1,干度为0.2时的实验数据与模拟结果的对比结果.总体而言,除个别管子外,大多数管子的流量分配情况与实验结果较为吻合.文献[12]的分析表明,实验中管子1中的制冷剂主要包括两部分:一是液相制冷剂射流进入集管时,一部分液相制冷剂以离散液滴的形式落在集管入口附近,流入管子1;另一部分是液相制冷剂由下游回流形成.而在CFD模拟中,液相制冷剂入口射入集管时,直接掠过第1根管子,与第1根管子没有直接接触,欧拉模型自身的局限性使得在模拟过程中没有这部分离散液滴出现.模拟结果与实验中的质量流量分布规律较为一致,只有个别管子流量误差稍大,基于两相流的复杂性,认为该误差在可以接受的范围内.

|
图 4 模型验证 Fig.4 Validation of numerical calculation |
本文数值计算采用水平集管带12根扁管的基本结构,对在该结构中插入分流管前后的情况进行流量分配规律的分析,制冷剂进口温度与环境温度一致.图 5为基本结构插入分流管后的示意图,具体参数描述如下:马蹄形集管水平放置,制冷剂上进下出,集管宽度和长度分别为12.0 mm和234.0 mm;12根扁管的长、宽、高分别为150.0 mm、11.0 mm和2.5 mm;入口段长120.0 mm,直径9.4 mm;集管内分流管孔口数量为12,孔口位于两扁管中间位置,扁管插入集管深度为0 mm.定义开孔率为分流管孔口总面积与扁管总流通面积的比值.

|
图 5 集管插入分流管示意图 Fig.5 Head with inserted perforated tube |
网格划分如图 6所示.为了提升计算的稳定性,采用六面体网格对模型进行划分.入口圆管及孔口处采用Oblock的网格处理方式,如图 6a、6b所示,圆管与集管连接处采用两次Oblock对网格进行划分,如图 6c所示.计算域总体网格数量约为70万~90万,扁管在集管内深度不同或分流管孔径不同时,网格数量有所不同.

|
图 6 网格划分图 Fig.6 Grid system |
定义第i根扁管出口质量流量与平均质量流量的比值为
| ${R_\mathit{i}} = \frac{{{m_\mathit{i}}}}{{{m_{\rm{a}}}}} $ | (7) |
式中:mi为第i根扁管气(液相)质量流量;ma为扁管气(液)相平均质量流量;文献[5]中用流量分配的标准差Ds来衡量不均匀程度,Ds值越接近0,流量分配均匀性越好,其定义如下:
| ${D_{\rm{s}}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{R_\mathit{i}} - 1.0} \right)}^2}} }}{N}} $ | (8) |
式中:N为扁管数量,本文中N=12.
3.1 分流管对流量分配的影响定义开孔率为0.46,对应孔径4 mm,当扁管伸入集管深度为0 mm时,对比集管加入分流管前后的流量分配如图 7所示.可以看出,未插分流管时,Ds值随质量流量增大而减小,这与文献[12]得到的结论一致.集管内未加分流管时,Ds平均值大小为0.80,集管内插入分流管后,Ds平均值为0.59,Ds平均值减小26.3%.图 8表明,固定流量而改变干度时,集管内未加分流管时,Ds平均值为0.79,集管内插入分流管后,Ds平均值为0.64,Ds平均值减小19.0%.两种情况均表明,插入分流管可以明显改善平行流蒸发器的流量分配不均匀性.

|
图 7 插入分流管前后Ds对比(干度为0.2) Fig.7 Ds with/without a perforated tube(constant quality) |

|
图 8 插入分流管前后Ds对比(质量流量为35 g·s-1) Fig.8 Ds with/without a perforated tube (constant mass flow rate) |
图 9中纵坐标Rg和Rl分别代表液相流量比和气相流量比,即每根扁管内气相(液相)质量流量与平均气相(液相)质量流量的比值.从图 9可以看出,无论集管中是否加入分流管,液相制冷剂流量分配都是中间扁管流量大两端扁管流量小,气相制冷剂流量分配规律与液相制冷剂的分配规律基本相反.集管中有无分流管时,各个扁管中液相制冷剂Rl最大值与最小值的差分别为1.97和2.30;集管中插入分流管后,各个扁管液相制冷剂Rl值较无分流管时更加接近1,表明集管中加入分流管后液相分配均匀性变好.

|
图 9 加入分流管前后的流量分配(质量流量为35 g·s-1, 干度为0.2) Fig.9 Flow distribution with/without a perforated tube (35 g·s-1, 0.2) |
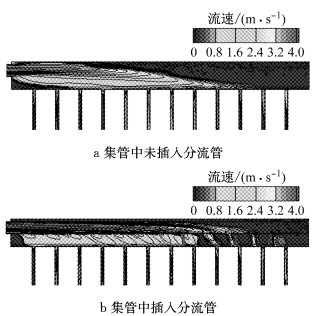
插入分流管对制冷剂分配不均匀性的改善,可以通过集管中的液相速度云图和压力云图作进一步的解释.由图 10可知,集管内插入分流管之后,制冷剂的流动形态发生了显著的改变.未加分流管时,液相制冷剂在入口处形成射流,在重力作用下与气相制冷剂分离,使得液相制冷剂分配主要集中在上游扁管,而下游扁管分配得到的液相制冷剂的量微乎其微;集管中插入分流管后,气液分离滞后,流量分配不均匀性较不插分流管时有明显的改善.集管中压力梯度的存在是造成流量分配不均的一个重要因素[14].图 11表明,集管中未加入分流管时,集管内部最大静压差为115 Pa;而集管中插入分流管时,集管内最大静压差为60 Pa,管内静压压力梯度明显降低,流量分配不均程度减小.
|
图 10 集管中加入分流管前后的液相速度分布图(质量流量为35 g·s-1, 干度为0.2) Fig.10 Velocity distribution in head(35 g·s-1, 0.2) |

|
图 11 集管中加入分流管前后的液相压力分布(质量流量为35g·s-1, 干度为0.2) Fig.11 Pressure distribution in head(35 g·s-1, 0.2) |
插入节流管后,会引起集管压降的增加.定义集管压降为集管入口处与最远扁管入口之间的压力差,包括分流管引起的压降.集管插入分流管前后集管压降如表 3所示.由表 3可以看出,由于分流管管径较小,制冷剂流速快,集管中插入分流管时压降明显增大,约为不插分流管压降的2倍左右.分流管在制冷系统中相当于起了两次节流的作用,只要合理设计系统的节流阀,集管压降的增加并不会增加制冷系统的能耗.
| 下载CSV 表 3 不同工况下插入分流管前后集管压降 Tab.3 Pressure drop in manifold |
从图 9还可以看出,集管中加入分流管后,虽然流量分配的总体不均匀性得到了改善,但集管两端扁管液体流量依然较小.为改善这种状况,将扁管伸入集管一定深度,研究插入深度对流量分配的影响.扁管伸入集管深度分别为0、3、6和9 mm,定义开孔率为0.46,对应孔径4 mm.
从图 12可以看出,随着扁管伸入集管深度的增大,Ds平均值先变小后变大,对应的流量分配均匀性先变好后变差.扁管伸入集管深度为6 mm时,对应Ds平均值最小值为0.47,且Ds最小值0.22也出现在扁管伸入集管深度为6mm的结构中;扁管伸入集管深度为0 mm时,对应Ds最大平均值为0.59.故4种扁管伸入集管深度下,深度为6 mm的情况,集管流量分配均匀性最好,插入深度为0时流量分配均匀性最差.

|
图 12 扁管伸入集管不同深度下的Ds值 Fig.12 Ds at different insert depth of microchannel tube in head |
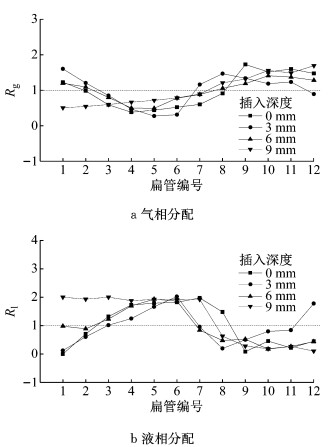
4种扁管深度下的流量分配如图 13所示,其区别主要集中在入口附近扁管和尾部扁管.当扁管伸入集管深度为0、3 mm时,入口附近第1根扁管内的液相质量流量接近0 g·s-1;扁管伸入集管深度为6 mm时,第1根扁管液相Rl接近1.00,扁管流量适中;深度为9 mm时,第1根扁管Rl接近2.00,流量较大.对于尾部扁管质量流量分配,当扁管伸入集管深度为3 mm时,从扁管8到扁管12,液相Rl由0.20不断增大到1.77,涨幅比较剧烈;其余深度下尾部扁管液相Rl在0.10~0.50之间波动.总体而言,质量流量为35 g·s-1,干度为0.2,当扁管插入深度为6 mm时,第1根扁管和最后1根扁管的液相Rl和气相Rg均较其余深度更接近1.00.图 14进一步给出了扁管插入深度为6 mm时,不同流量和干度下,各扁管的液相Rl和气相Rg分布.从图 14可以看出,不同进口状态下,第1根和最后1根扁管的气相和液相流量均较为合理.
|
图 13 不同扁管伸入深度下的流量分配(质量流量为35 g·s-1, 干度为0.2) Fig.13 Flow distribution at different microchannel tube depths (35 g·s-1, 0.2) |

|
图 14 扁管伸入集管深度6mm时流量分配 Fig.14 Flow distribution at 6mm depth of microchannel tubes |
本文所研究的工况及扁管插入深度下,集管压降在0.229~1.904 kPa之间,可见扁管插入集管的深度对集管压降影响不大,在此不再一一列出.
3.3 开孔率对流量分配的影响设定扁管伸入集管深度为6 mm,进一步分析分流管开孔率对流量分配的影响.开孔率分别为0.11、0.26、0.46、0.71、1.00时,对应的均匀布置孔径分别为2、3、4、5和6 mm.
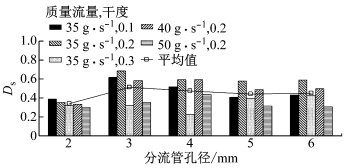
图 15为分流管在不同开孔孔径下的Ds值对比.由图 15可知,Ds在孔径为2~6 mm范围内先增大后缓慢减小,之后在6 mm时稍有上升.分流管孔径为2 mm时,Ds的平均值最小,对应值为0.34,流量分配的均匀性最好;分流管孔径为3 mm时,Ds平均值最大,对应数值为0.51,流量分配均匀性最差.当孔径为4~6 mm时,Ds平均值在0.44~0.47之间波动,波动范围较小,说明开孔率对流量分配的影响不大.干度为0.2,质量流量分别为35、40、50 g·s-1时,Ds随流量的增大减小,流量分配均匀性与质量流量成正比;质量流量为35 g·s-1,干度为0.3时流量分配均匀性最好,Ds值在0.4以下;干度为0.2时流量分配均匀性最差(分流管孔径为2 mm除外).
|
图 15 分流管在不同孔径下的Ds值 Fig.15 Ds with perforated tubes at different open ratios |
质量流量分别为35 g·s-1和50 g·s-1,干度为0.2时的流量分配如图 16所示.总体而言,随着流量的增加,液相和气相不均匀性均得到改善,同时气相制冷剂的流量分配均匀性要比液相制冷剂好.孔径为2 mm时,流量分配均匀度最高,气相制冷剂流量分配也是最均匀的,这归因于小开孔率下分流管的静压箱效应.分流管孔径为3mm时,流量分配均匀性最差.其余结构流量分配规律相似,流量沿程先增大后减小,但出现波峰的扁管位置有所不同.从图 16中还可以看出,不同孔径下,液相制冷剂在尾部扁管流量分配不足的现象始终存在.一方面是因为分流管中液相制冷剂动量削弱,尾部孔口出流液相流量降低;另一方面则是由于气液分离导致气相尾部孔口出流速度较大,对液面造成冲击,使得尾部液面降低而导致的.

|
图 16 不同孔径下的流量分配 Fig.16 Flow distribution with perforated tubes at different open ratios |
表 4为分流管在不同孔径下的集管压降.从表 4可以看出,分流管孔径越大,集管压降越小.分流管孔径为2 mm时集管压降最大,为8.961 kPa,压降较大;分流管孔径在3 mm及以上时,最大压降为2.021 kPa,压降较小.若分流管作为二次节流管,分流管带来的压降作为节流压降的一部分,可以降低对制冷系统性能的影响.否则,小开孔率时,集管压降相对较大,导致蒸发器压降上升,导致压缩机性能降低,制冷系统性能变差.
| 下载CSV 表 4 分流管在不同孔径下集管压降 Tab.4 Pressure drop in heads with perforated tubes of different open ratios |
(1) 加入分流管后,通过制冷剂气液分离的推迟和集管内静压梯度的降低,制冷剂流量分配不均匀性得到了明显的改善;加入分流管前后,两者的流量分配规律相似,即中间扁管流量大两端扁管流量小.
(2) 扁管伸入集管深度大约为分流管下方的二分之一时,集管两端扁管液相流量不足的现象有了较明显的改善,流量分配整体均匀性最好.
(3) 最佳扁管伸入集管深度下,随着开孔率的增大,流量分配均匀性先变差后变好,随着开孔率进一步增大,流量分配均匀性又变差.分流管在小开孔率下,需要注意与制冷系统中节流阀的匹配.
| [1] |
TOMPKINS D M, YOO T, HRNJAK P, et al. Flow distribution and pressure drop in micro-channel manifolds[C]// International Refrigeration and Air Conditioning Conference. West Lafayette: Purdue University, 2002: No.554.
|
| [2] |
ZOU Y, HRNJAK P. Effects of fluid properties on two-phase flow and refrigerant distribution in the vertical header of a reversible microchannel heat exchanger-comparing R245fa, R134a, R410A, and R32[J]. Applied Thermal Engineering, 2014, 70(1): 966 DOI:10.1016/j.applthermaleng.2014.06.021 |
| [3] |
LEE J K, Lee S Y. Distribution of two-phase annular flow at header-channel junctions[J]. Experimental Thermal and Fluid Science, 2004, 28(2): 217 |
| [4] |
KIM N H, HAN S P. Distribution of air-water annular flow in a header of a parallel flow heat exchanger[J]. International Journal of Heat and Mass Transfer, 2008, 51(5): 977 |
| [5] |
KIM N H, LEE E J, BYUM H W. Improvement of two-phase refrigerant distribution in a parallel flow minichannel heat exchanger using insertion devices[J]. Applied Thermal Engineering, 2013, 59(1): 116 |
| [6] |
WANG C C, YANG K S, TSAI J S, et al. haracteristics of flow distribution in compact parallel flow heat exchangers. Part Ⅰ: typical inlet header[J]. Applied Thermal Engineering, 2011, 31(16): 3226 DOI:10.1016/j.applthermaleng.2011.06.004 |
| [7] |
HUANG C H, WANG C H. The study on the improvement of system uniformity flow rate for U-type compact heat exchangers[J]. International Journal of Heat and Mass Transfer, 2013, 63: 1 DOI:10.1016/j.ijheatmasstransfer.2013.03.039 |
| [8] |
RAMADEVI T, VIJAYANAND P. CFD analysis of dual phase refrigerant flow inside an evaporator tube of refrigerator[J]. International Journal of Advance Induatrial Engineering, 2015, 3(3): 111 |
| [9] |
VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics: the finite volume method[M]. London: Pearson Prentice Hall, 2007
|
| [10] |
SCHEPPER S C K D, HEYNDERICKX G J, MARIN G B. CFD modeling of all gas-liquid and vapor-liquid flow regimes predicted by the Baker chart[J]. Chemical Engineering Journal, 2008, 138(1): 349 |
| [11] |
SCHWARZKOPF J D, SOMMERFELD M, CROWE C T, et al. Multiphase flows with droplets and particles[M]. Boca Raton: CRC Press, 2011
|
| [12] |
FEI P, HRNJAK P. Adiabatic developing two-phase refrigerant flow in manifolds of heat exchangers[D]. Champaign-Urbana: University of Illinois at Urbana-Champaign, 2004.
|
| [13] |
BACHALO W D, HOUSER M J. Phase/doppler spray analyzer for simultaneous measurements of drop size and velocity distributions[J]. Optical Engineering, 1984, 23(5): 583 |
| [14] |
KULKARNI T, BULLARD C W, CHO K. Header design tradeoffs in microchannel evaporators[J]. Applied Thermal Engineering, 2004, 24(5/6): 759 |
 2019, Vol. 47
2019, Vol. 47