2. 同济大学 中德学院,上海 201804
2. Chinesisch-Deutsches Hochschulkolleg, Tongji University, Shanghai 201804, China
车用燃料电池系统(fuel cell system, FCS)的性能可靠性和稳定性是燃料电池汽车大规模商业化应用的必要条件,FCS故障实时在线诊断是提高和保障其可靠性和稳定性的有效途径之一.目前,FCS故障诊断方法大致可分为三类,即基于模型的方法、基于数据驱动的方法和实验测试法[1].基于数据驱动的方法因为无需研究系统的故障机理和进行实验测试,较常用于FCS的在线故障诊断.
Zhao等[2]提出了基于多传感器信号和主成分分析(principle component analysis, PCA)的FCS故障诊断方法,用于区分传感器故障和系统级故障.周苏等[3]以电化学阻抗谱与实轴的两个交点作为特征向量,采用模糊C均值(FCM)和支持向量机(SVM)对样本进行聚类和分类,用于识别FCS故障.Zheng等[4]提出了基于EIS(electrochemical impedance spectroscopy)的双模糊诊断方法,可在线诊断燃料电池堆的健康状态.然而,以上研究工作都未考虑FCS老化对诊断结果的影响.随着时间推移,FCS的工作特性会改变,如性能衰减后电压降低,如果采用静态模型,将会产生误诊.目前,考虑FCS老化的在线故障诊断研究相对较少.Li等[5]提出了基于球形支持向量机的FCS在线诊断方法,可在线更新诊断模型和识别新型故障.
针对上述问题,基于K-means和SVM算法,本文提出了一种FCS在线自适应故障诊断方法,利用实时获取的聚类信息构建自适应分类器,动态调节诊断模型,在FCS性能发生变化的情况下用于故障诊断.采用文献[6]中的数据进行了间接的方法有效性验证.文献[6]中样本集共包括20片单体电池的750组单体电压值,其中正常样本400组,故障样本350组,故障样本包含膜干和水淹两种类型.
1 车用燃料电池系统及故障分类如图 1所示,除核心单元电堆外,车用FCS还包括氢气供应子系统、空气供应子系统、热管理子系统和电能管理子系统.因此,其故障类型多,且不易检测.

|
图 1 车用燃料电池系统原理图 Fig.1 Schematic diagram of automotive FCS |
故障诊断一般包含三个步骤,分别是故障检测与定位、类型区分、故障处理.不同故障类型具有不同的特征和解决方法,如果出现系统级故障须立即停机以避免损坏系统;出现传感器信号故障仅需纠正信号误差.车用FCS主要故障可分为以下两种类型[5]:
(1) 内部故障,主要由于系统的水、热、气控制不当或因电堆内部材料物理、化学特性变化而导致.例如氢、空气供应子系统供气不足导致的欠气故障、水管理子系统湿度控制不当造成水淹或者膜干和催化层活化面积变小等,都会使FCS的性能衰减和寿命下降.因此,燃料电池内部故障研究是FCS故障诊断的主要内容之一.
(2) 外部故障,包括在传感器、执行器等单元上发生的故障.传感器故障将导致FCS控制器输出错误指令,通常可通过冗余措施或重构错误信号予以解决;执行器(泵、电磁阀)故障即使在输入正确控制信号情况下也会导致系统发生错误响应.
FCS是一个典型的集机械、电子电气和电化学过程于一体的系统,随运行时间的变化其性能特性会发生变化,故障产生机理及影响程度也随之发生相应的变化.为了保证或维持在实际的剩余性能条件下FCS的安全、可靠运行,有必要研究FCS在线自适应故障诊断机制和方法.
2 方法理论概述 2.1 K均值聚类算法K-means是一种基于距离的经典聚类算法,因其快速、简单而得到广泛使用.对于给定数据集X={xi|xi∈Rm, i=1, 2, …, n},其中n为样本个数,m为样本维数.样本集的类别空间μ={μj|μj∈Rm, j=1, 2, …, c},c为类别个数.两个样本点的距离采用欧式距离进行度量[7],即
| $D\left( {{x_\mathit{i}}, {x_\mathit{j}}} \right) = \sqrt {{{\left( {{x_\mathit{i}} - {x_j}} \right)}^{\rm{T}}}\left( {{x_\mathit{i}} - {x_\mathit{j}}} \right)} $ | (1) |
聚类中心为
| ${\mathit{\mu }_\mathit{k}} = \frac{{\sum\limits_{i = 1}^{{n_\mathit{k}}} {{x_\mathit{i}}} }}{{{n_\mathit{k}}}} $ | (2) |
式中:nk表示属于第k类的样本个数.
K均值算法的目标是达到簇内样本距离最小化,簇间样本距离最大化,因此其目标函数为
| $\min = \sum\limits_{j = 1}^c {\sum\limits_{i = 1}^{{n_\mathit{j}}} {D\left( {{x_\mathit{i}}, {\mathit{\mu }_\mathit{j}}} \right)} } $ | (3) |
算法的迭代过程如表 1所示,其时间复杂度近似于线性,为O(mnct),其中t代表算法迭代的次数,一般(t, c)≤n;空间复杂度为O((n+c)m).
| 下载CSV 表 1 K-means算法伪代码 Tab.1 K-means algorithm pseudo-code |
支持向量机是一种有监督学习的方法,适用于小样本、非线性和高维数据.其本身是定义在特征空间上间隔最大化的线性二分类器,但通过引入核函数,将原始样本空间映射到希尔伯特空间,使得在原空间线性不可分的问题在特征空间中线性可分.本文采用最常见的高斯径向基核函数.
线性可分支持向量机对于给定线性可分训练数据集,通过间隔最大化或等价求解相应的凸二次规划问题,得到的分离超平面为[7-8]
| ${\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{x} + \mathit{b} = {\rm{0}} $ | (4) |
式中:x为样本数据;w是法向量;b是截距(阈值).
相应的分类决策函数为
| $f\left( x \right) = {\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{x}+ \mathit{b}} \right) $ | (5) |
针对线性不可分的数据集,每个样本点引入一个松弛变量ξi≥0,则线性不可分的SVM可采用如下的优化问题来表示:
| $\begin{array}{l} \;\;\min \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\sum\limits_{i = 1}^N {{\mathit{\xi }_\mathit{i}}} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\mathit{y}_\mathit{i}}\left( {\mathit{\boldsymbol{w}}{\mathit{x}_i} + b} \right) \ge 1 - {\mathit{\xi }_i}, \\ {\mathit{\xi }_i} \ge 0, \mathit{\;\;\;\;i = 112, } \cdots \mathit{, n} \end{array} $ | (6) |
式中:C>0,是惩罚参数,一般由实际问题决定; yi={+1,-1}为xi的类标记.
最后,通过核函数与软间隔最大化,非线性支持向量机的分类决策函数可表示为
| $f\left( x \right) = {\mathop{\rm sgn}} \left( {\sum\limits_{i = 1}^n {{\mathit{\alpha }_\mathit{i}}{y_\mathit{i}}K\left( {x, {x_\mathit{i}}} \right) + b} } \right) $ | (7) |
式中:αi≥0是拉格朗日乘子;K(x, xi)为核函数.
SVM算法的核心在于求解拉格朗日乘子,目前运用最多的是序列最小化优化(sequential minimal optimization, SMO)算法[9].
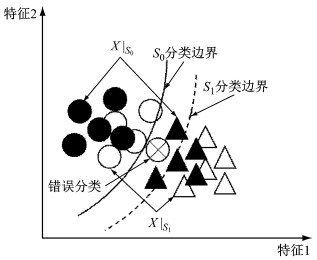
2.3 自适应分类方法传统分类器的分界线在模型训练好后便不再进行调整,因此,不适用于系统特性发生改变后的样本.例如,在图 2所示的特征向量空间中,S0分类边界是在系统初始状态S0下对经初始样本集X|S0={xi|xi∈R2, i=1, 2, …, 10}进行训练后所得的分类边界,但是,当系统特性发生改变,性能状态从S0迁移至S1后,原S0分类边界已不再适用于系统新产生的样本集X|S1={xi|xi∈R2, i=11, 12, …, 20}的分类,也应随性能状态变化移动到S1分类边界(即图 2中虚线所示).如果沿用S0分类边界对性能状态已发生迁移的系统所产生的样本集进行分类,会产生较大的误判率.因此,随FCS系统性能状态变化,有必要引入相应的FCS故障分类器自适应动态调整模型.
|
图 2 自适应方法示意图 Fig.2 Diagram of self-adaptive method |
基于统计学方法的FCS故障诊断方法本质上是一个分类器,即通过在已有的样本集(含正常和故障样本)上训练好的分类器(如SVM分类器)对新测样本进行分类,从而实现FCS的故障诊断.这种诊断方法的问题在于,如上文所述,训练好之后的分类器不再做进一步的调整.
现有燃料电池故障诊断模型原理上大多属于离线静态分类器.但是,FCS长时间运行后有些部件会发生老化,系统性能也会发生衰减.因此,一个更为有效的分类器也应该随系统性能(或特性)变化而变化,具有故障诊断的动态自适应调节功能.
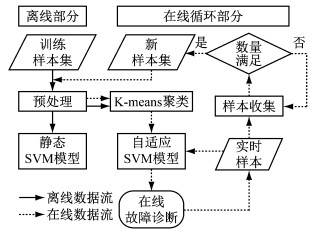
基于静态分类器,通过实时采集样本信息,对诊断模型进行动态更新,这是本文针对以上问题提出的一种在线自适应故障诊断方法,其流程如图 3所示.
|
图 3 在线自适应故障诊断模型流程图 Fig.3 Flowchart of online self-adaptive fault diagnosis model |
在线自适应故障诊断模型由离线和在线循环两部分组成.离线部分首先对已获取的训练样本集(含正常和故障样本)进行数据预处理,然后将其用于训练,得到一个静态SVM模型.在线循环部分是一个循环信息处理过程.首先对采集的新样本集进行批量预处理,然后对其进行K-means聚类,再基于静态SVM模型的标签信息(即正常或故障类型)对聚类后的样本进行标记,最后将带标签信息的样本集用于刷新上一循环的自适应SVM模型.初始模型为静态SVM模型.FCS实时故障诊断与分类器调整过程同步进行.单步实时采集的样本输入至自适应SVM模型进行在线实时诊断.与此同时,一个不断收集实时样本数据的子循环根据给定的某一周期构成一个新样本集.以一个老化周期x的FCS系统为例,若采样频率为f,则设定一个阈值为3 600f,当实时采集的累计样本数达到这个阈值后即构成一个新样本集.
4 诊断实例及仿真分析 4.1 诊断方法实例仿真验证车用燃料电池及系统故障生成的机理具有复杂的多因素相关性.电堆内部的温/湿度、反应物浓度及压力分布等,外部可测变量如单体电压、电堆输出气体温/湿度、电堆实际输出功率等,这些物理、化学变量在不同程度上都隐含了故障发生后的一些特征信息.其中,单体电压是目前最常用的表征FCS实时性能的可测物理量[6, 10],因此,为验证本文提出的在线自适应故障诊断模型,被用作样本变量.
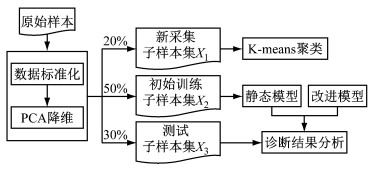
诊断方法实例仿真验证及分析流程如图 4所示.首先对原始样本进行数据预处理,然后随机选择总体样本集X={X1, X2, X3}的20%、50%、30%分别作为新采集子样本集(用于刷新自适应SVM模型)X1={xi|xi∈R20, i=1, 2, …, 150}、初始训练子样本集X2={xi|xi∈R20, i=1, 2, …, 375}和测试子样本集X3={xi|xi∈R20, i=1, 2, …, 225},最后分别采用静态模型和自适应模型进行故障诊断,并对比诊断结果.为简单起见,这里仅考虑正常和故障两种情况.
|
图 4 仿真分析流程图 Fig.4 Flowchart of simulation analysis |
在训练模型之前,首先对仿真数据进行预处理(包括标准化和PCA降维).
数据标准化为降维做准备,采用数据中心化处理,即
| ${\hat x_{\mathit{ij}}} = {x_{ij}} - {\overline x _\mathit{j}}, \;\;i = 1, 2, \cdots n $ | (8) |
式中:xij为第i个样本第j个维度的值(第j片单电池电压);xj为第j个维度的样本均值;
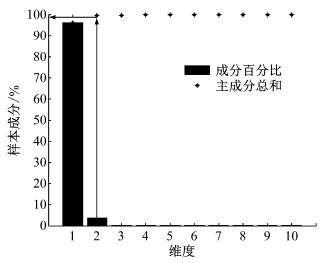
PCA算法是一种常见的数据压缩降维方法,其核心思想是将数据沿方差最大方向投影,保证样本信息足够且样本维数减小[11].燃料电池单体电压尤其是邻近单电池之间具有较强相关性.因此,采用PCA对20个属性(20片单体电压)的原始样本集进行降维处理,结果如图 5所示.样本变量降至2维后,样本集的累计成分达99.55%,已足够表达原始样本变量构成的样本集所包含的信息,既降低了模型的训练和分类时间,也提高了程序运行效率和模型泛化能力,易于实时在线诊断和数据可视化.
|
图 5 PCA降维结果 Fig.5 Results of PCA dimension reduction |
如前所述,根据给定的某一周期构成的新样本集X1中的样本经K-means聚类后尚无标签信息(即正常或故障),因此,需基于带标签的初始训练子样本集X2对新样本集X1的聚类结果进行标签处理.
K-means算法根据统计特征进行聚类,当系统性能状态发生改变时,S1状态下的正常类别样本集可能与初始状态S0下的故障类别样本集发生部分重叠,从而得到错误的样本标记结果.如图 6所示的聚类结果是基于随机选择的采集样本X1,准确率约为77.33%.其中椭圆形区域的聚类结果有误,实际为正常样本,但是却被标记为故障样本.由于新样本集的样本数比初始训练样本集的样本数少得多,且仅用于改进原分类器而非重新训练,所以类似错误不会影响模型最后的诊断准确率.
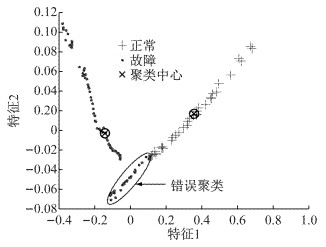
|
图 6 新采集样本聚类结果 Fig.6 Results of acquisition samples clustering |
车用FCS故障诊断模型实质上是一个SVM分类器,因此,通过观察聚类结果分界线的变化可以验证模型是否实现了动态更新.
基于子样本集X2的静态SVM分类器模型能较好地区分此阶段的正常样本与故障样本,如图 7所示.假设系统性能状态发生变化,该分类器便不再适用,需要予以调整.仿真实验采用新子样本集X1模拟上述情况,并将其用于刷新自适应SVM模型(即模拟动态更新),结果如图 8所示.通过增加新样本集X1中的样本并进行K-means聚类,静态分类器模型被刷新为可用于FCS性能状态发生变化后的故障诊断动态分类器.
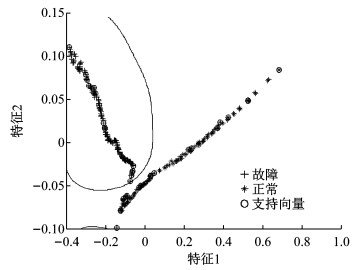
|
图 7 静态分类器 Fig.7 Static classifier |
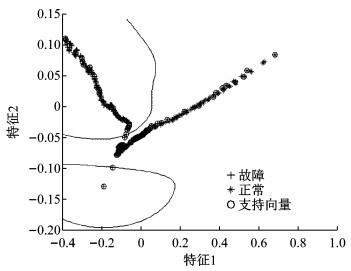
|
图 8 改进分类器 Fig.8 Improved classifier |
通过对比图 7和图 8,可观察到分类器的分界线变化明显.当“新采集样本”引入后,SVM模型的支持向量个数增加,分界线位置和形状均发生改变,这显示诊断模型(即分类器)实现了动态更新.
分别采用初始静态分类器模型和改进后的动态模型对同一测试子样本集X3进行分类识别,结果如图 9所示.
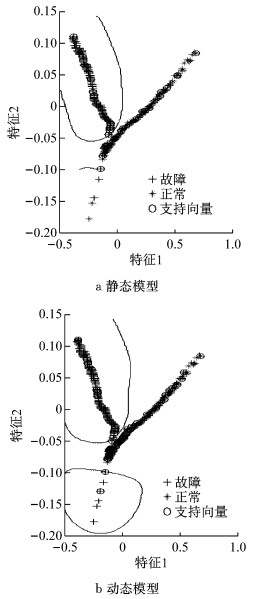
|
图 9 分类结果比较 Fig.9 Comparison of classification results |
本次验证仿真所用的训练数据与测试数据均为同一批实测样本,静态模型已能较好地进行故障诊断(准确率已高达98.22%),模型调整后的诊断准确率为99.11%,较静态模型虽然仅提高了0.89%,但显示了自适应动态故障诊断模型对新样本集包含的新信息(本案例用于模拟FCS性能状态变化)的敏感性.当实际FCS性能状态变化较大时,自适应动态故障诊断模型的故障诊断实时效果将更明显.
5 结论基于K-means和SVM算法,提出了一种FCS在线自适应故障诊断方法,并采用已发表文献中的实验数据对其进行了实例仿真验证及分析.本文建议的方法通过对实时获取的新样本集进行在线聚类,可实现故障分类器的在线自适应调节;针对FCS性能状态变化后的故障诊断,拓展了静态模型的应用范围.
| [1] |
陈维荣, 刘嘉蔚, 李奇, 等. 质子交换膜燃料电池故障诊断方法综述及展望[J]. 中国电机工程学报, 2017, 37(16): 4712 CHEN Weirong, LIU Jiawei, LI Qi, et al. Review and prospect of fault diagnosis methods for proton exchange membrane fuel cell[J]. Proceedings of the CSEE, 2017, 37(16): 4712 |
| [2] |
ZHAO X, XU L, LI J, et al. Faults diagnosis for PEM fuel cell system based on multi-sensor signals and principle component analysis method[J]. International Journal of Hydrogen Energy, 2017, 42(29): 18524 DOI:10.1016/j.ijhydene.2017.04.146 |
| [3] |
周苏, 韩秋玲, 胡哲, 等. 质子交换膜燃料电池故障诊断的模式识别方法[J]. 同济大学学报(自然科学版), 2017, 45(3): 408 ZHOU Su, HAN Qiuling, HU Zhe, et al. Pattern recognition method for proton exchange membrane fuel cell fault diagnosis[J]. Journal of Tongji University (Natural Science), 2017, 45(3): 408 |
| [4] |
ZHENG Z, PÉRA M C, HISSEL D, et al. A double-fuzzy diagnostic methodology dedicated to online fault diagnosis of proton exchange membrane fuel cell stacks[J]. Journal of Power Sources, 2014, 271: 570 DOI:10.1016/j.jpowsour.2014.07.157 |
| [5] |
LI Z, OUTBIB R, GIURGEA S, et al. Diagnosis for PEMFC systems: a data-driven approach with the capabilities of online adaptation and novel fault detection[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 5164 DOI:10.1109/TIE.2015.2418324 |
| [6] |
LI Z, OUTBIB R, HISSEL D, et al. Data-driven diagnosis of PEM fuel cell: a comparative study[J]. Control Engineering Practice, 2014, 28: 1 DOI:10.1016/j.conengprac.2014.02.019 |
| [7] |
DUDA R O, HART P E, STORK D G. Pattern classification[M]. New York: John Wiley & Sons, 2012
|
| [8] |
REBENTROST P, MOHSENI M, LLOYD S. Quantum support vector machine for big data classification[J]. Physical Review Letters, 2014, 113(13): 130503 DOI:10.1103/PhysRevLett.113.130503 |
| [9] |
HU Y C, ANSELL J. Retail default prediction by using sequential minimal optimization technique[J]. Journal of Forecasting, 2019, 28(8): 651 DOI:10.1002/for.v28:8 |
| [10] |
KIM J, LEE I, TAK Y, et al. State-of-health diagnosis based on hamming neural network using output voltage pattern recognition for a PEM fuel cell[J]. International Journal of Hydrogen Energy, 2012, 37(5): 4280 DOI:10.1016/j.ijhydene.2011.11.092 |
| [11] |
HUA J, LI J, OUYANG M, et al. Proton exchange membrane fuel cell system diagnosis based on the multivariate statistical method[J]. International Journal of Hydrogen Energy, 2011, 36(16): 9896 DOI:10.1016/j.ijhydene.2011.05.075 |
 2019, Vol. 47
2019, Vol. 47

