2. 上海市轨道交通结构耐久与系统安全重点实验室, 上海 201804
2. Shanghai Key Laboratory of Rail Infrastructure Durability and System Safety, Shanghai 201804, China
随着我国城市轨道交通的快速发展,为降低地铁列车运行引起的振动对沿线居民、精密仪器等的影响,剪切型减振器曾大量应用于地铁轨道振动控制[1].我国剪切型减振器的设计参考了德国科隆蛋,利用硫化橡胶的剪切变形提供竖向支承刚度,上下铁板与橡胶圈硫化为一体,具有较好的减振效果[2].但是,北京地铁使用剪切型减振器的某些区段,在投入运营一段时间后出现了较为严重的钢轨波磨现象[3].
针对这一问题,国内部分学者利用实验室及现场振动测试,对采用剪切型减振器的钢轨振动特性进行了研究.Zhang等[4]在对北京地铁波磨区段调查测试的基础上指出,采用剪切型减振器地段出现的钢轨波磨应归为特殊轨道结构形式出现的波磨;吴宗臻等[5]通过现场脉冲激励法模态测试得到采用剪切型减振器的轨道结构在200~350 Hz频段内的轨道系统阻尼比在2%以下,此频率范围内的钢轨振动无法得到有效抑制.李伟等[6]通过有限元模型计算,得出在200~400 Hz频段内存在钢轨相对于轨道板的垂向弯曲共振.刘维宁等[7]通过进一步研究发现采用剪切型减振器的轨道结构在200~400 Hz频段内的钢轨振动是引发波磨的主要原因.
为控制采用剪切型减振器的钢轨在200~400 Hz频段内的典型振动,北京地铁在钢轨的轨腰处安装了一种调频式钢轨减振器(TRD)[8].TRD最初是英国南安普顿大学Thompson团队在对钢轨振动特性研究基础上研发的一种阻尼吸振器[9];Maes等[10]通过进一步研究发现,这种阻尼吸振器能有效提高Pinned-Pinned共振频率范围内的钢轨振动衰减率;Wu[11]进一步研究了阻尼吸振器在控制钢轨波磨方面起到的作用;刘卫丰等[8]对北京地铁安装调频式减振器前后钢轨的振动衰减率进行了测试,发现调频式减振器大大提高了使用剪切型减振器的轨道结构在200~400 Hz频段内的钢轨振动衰减率,有效抑制了此频段内的钢轨振动.
综上,有关采用剪切型减振器的钢轨振动特性和TRD调谐作用的研究,主要基于现场振动测试或实验室振动测试,相关的理论分析不足.因此,考虑到轨道结构在纵向上的周期性,本文建立了基于谱元法的钢轨元胞模型,以此分析采用剪切型减振器的钢轨振动特性及TRD调谐机理.
1 基于谱元法的钢轨元胞模型谱元法将整体结构分解为梁、柱、板等简单结构,通过引入简单结构波动方程的精确波动解推导出对应简单结构的谱单元刚度矩阵,采用与有限元类似的方法组装整体结构的谱刚度矩阵,结合谱荷载向量实现频域分析,是一种高精度和高效率的频域分析方法[12].由于谱元法可将材料统一、几何尺寸无间断的同一类型结构划分为一个单元,单元尺寸大小对计算精度没有影响,因此谱元法中结构的自由度数量锐减,计算效率有明显提高[13].考虑到采用剪切型减振器的轨道结构在纵向上的周期性,谱元法在求解这一类型结构的振动传递特性时具有明显的优势,因此这里选用谱元法求解采用剪切型减振器钢轨的垂向振动衰减率.
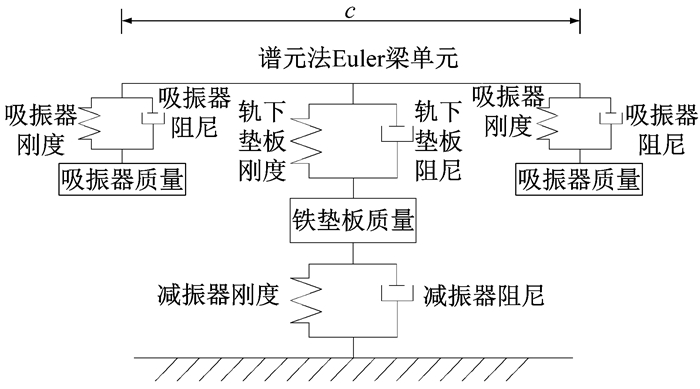
为计算采用剪切型减振器钢轨的垂向振动衰减率,考虑到轨道结构纵向上的周期性,基于周期结构的建模思想,建立如图 1所示的钢轨元胞模型,通过在钢轨元胞模型的两端引入Bloch定理计算钢轨的垂向振动衰减率.钢轨元胞模型中钢轨单元基于Euler梁模型建立;考虑到减振器自身的振动特性对轨道系统的影响[14],扣件连同剪切型减振器被考虑为弹簧-质量-弹簧系统,扣件间距为c;对于调频式钢轨减振器(TRD),一般情况下将其考虑为悬挂在节点处的质量-弹簧系统.
|
图 1 钢轨元胞模型 Fig.1 Cell model of rail |
材料均匀一致、等截面自由振动的欧拉梁的弯曲振动方程可表示为
| $ EIw''''\left( {x,t} \right) + \rho Aw''\left( {x,t} \right) = 0 $ | (1) |
式中:w(x, t)为横向位移;w″″表示位移对时间的四阶导数;w″(x, t)表示位移对时间的二阶导数;E为弹性模量;I为截面惯性矩;ρ为质量密度;A为梁的横截面面积.横向弯矩M和剪力Q分别表示如下:
| $ M\left( {x,t} \right) = EIw''\left( {x,t} \right),Q\left( {x,t} \right) = - EIw''\left( {x,t} \right) $ | (2) |
方程(1)的解可假定为如下的谱形式:
| $ w\left( {x,t} \right) = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {{W_n}\left( {x;{\omega _n}} \right){{\rm{e}}^{{\rm{i}}{\omega _n}t}}} $ | (3) |
将式(3)代入式(1)可得
| $ EIw'''' - {\omega ^2}\rho AW = 0 $ | (4) |
方程(4)的通解可以假定为
| $ W\left( x \right) = a{{\rm{e}}^{ - {\rm{i}}{k_{\rm{F}}}x}} $ | (5) |
将式(5)代入式(4)可得
| $ {k^4} - k_{\rm{F}}^4 = 0 $ | (6) |
式中:kF为梁的振动波数,可以表示为
| $ {k_{\rm{F}}} = \sqrt \omega {\left( {\frac{{\rho A}}{{EI}}} \right)^{1/4}} $ | (7) |
方程(6)有两个实数根和两个虚数根
| $ {k_1} = - {k_2} = {k_{\rm{F}}};{k_3} = - {k_4} = {\rm{i}}{k_{\rm{F}}} $ | (8) |
对于一个长度为L的有限梁单元,方程(4)的通解可以表示为
| $ W\left( {x,\omega } \right) = {a_1}{{\rm{e}}^{ - {\rm{i}}{k_{\rm{F}}}x}} + {a_2}{{\rm{e}}^{ - {k_{\rm{F}}}x}} + {a_3}{{\rm{e}}^{{\rm{i}}{k_{\rm{F}}}x}} + {a_4}{e^{{k_{\rm{F}}}x}} $ | (9) |
即
| $ \mathit{\boldsymbol{W}}\left( {x,\omega } \right) = \mathit{\boldsymbol{e}}\left( {x;\omega } \right)\mathit{\boldsymbol{a}} $ | (10) |
式中:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}\left( {x;\omega } \right) = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{i}}{k_{\rm{F}}}x}}}&{{{\rm{e}}^{ - {k_{\rm{F}}}x}}}&{{{\rm{e}}^{{\rm{i}}{k_{\rm{F}}}x}}}&{{{\rm{e}}^{{k_{\rm{F}}}x}}} \end{array}} \right];}\\ {\mathit{\boldsymbol{a}} = {{\left\{ {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}&{{a_4}} \end{array}} \right\}}^{\rm{T}}}} \end{array} $ | (11) |
梁单元的谱节点位移可以用位移场表示为
| $ \mathit{\boldsymbol{d}} = {\left\{ {\begin{array}{*{20}{c}} {W\left( 0 \right)}&{W'\left( 0 \right)}&{W\left( L \right)}&{W'\left( L \right)} \end{array}} \right\}^{\rm{T}}} $ | (12) |
将式(9)代入式(12)得
| $ \mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}\left( {0;\omega } \right)}&{\mathit{\boldsymbol{e'}}\left( {0;\omega } \right)}&{\mathit{\boldsymbol{e}}\left( {L;\omega } \right)}&{\mathit{\boldsymbol{e'}}\left( {0;\omega } \right)} \end{array}} \right]\mathit{\boldsymbol{a}} $ | (13) |
即
| $ \mathit{\boldsymbol{d}} = {\mathit{\boldsymbol{H}}_{\rm{B}}}\left( \omega \right)\mathit{\boldsymbol{a}} $ | (14) |
将式(13)代入式(9)消去常数向量a得
| $ \mathit{\boldsymbol{W}}\left( x \right) = {\mathit{\boldsymbol{N}}_{\rm{B}}}\left( {x;\omega } \right)\mathit{\boldsymbol{d}} $ | (15) |
式中:
| $ {\mathit{\boldsymbol{N}}_{\rm{B}}}\left( {x;\omega } \right) = \mathit{\boldsymbol{e}}\left( {x;\omega } \right)\mathit{\boldsymbol{H}}_{\rm{B}}^{ - 1}\left( \omega \right) $ | (16) |
弯矩和剪力的谱分量分别为
| $ M\left( x \right) = EIW''\left( x \right);Q\left( x \right) = - EIW'''\left( x \right) $ | (17) |
谱节点荷载可用下式表示:
| $ \mathit{\boldsymbol{f}} = {\left\{ {\begin{array}{*{20}{c}} { - Q\left( 0 \right)}&{ - M\left( 0 \right)}&{ + Q\left( L \right)}&{ + M\left( L \right)} \end{array}} \right\}^{\rm{T}}} $ | (18) |
将式(15)和(17)代入式(18)可得Euler梁的谱节点位移向量和谱节点荷载向量的关系为
| $ {\mathit{\boldsymbol{S}}_{\rm{B}}}\left( \omega \right)\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{f}}\left( \omega \right) $ | (19) |
式中:SB是梁的谱单元矩阵,可以写为
| $ {\mathit{\boldsymbol{S}}_{\rm{B}}}\left( \omega \right) = \frac{{EI}}{{{L^3}}}\left[ {\begin{array}{*{20}{c}} \alpha &{\bar \gamma L}&{ - \bar \alpha }&{\gamma L}\\ {\bar \gamma L}&{\beta {L^2}}&{ - \gamma L}&{\bar \beta {L^2}}\\ { - \bar \alpha }&{ - \gamma L}&\alpha &{ - \bar \gamma L}\\ {\gamma L}&{\beta {L^2}}&{ - \bar \gamma L}&{\beta {L^2}} \end{array}} \right] $ | (20) |
式中:
| $ \alpha = \left( {C{S_{\rm{h}}} + S{C_{\rm{h}}}} \right){\left( {{k_{{\rm{F}}n}}L} \right)^3}/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ \beta = \left( { - C{S_{\rm{h}}} + S{C_{\rm{h}}}} \right)\left( {{k_{{\rm{F}}n}}L} \right)/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ \bar \alpha = \left( {S + {S_{\rm{h}}}} \right){\left( {{k_{{\rm{F}}n}}L} \right)^3}/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ \bar \beta = \left( { - S + {S_{\rm{h}}}} \right)\left( {{k_{{\rm{F}}n}}L} \right)/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ \gamma = \left( { - C + {C_{\rm{h}}}} \right){\left( {{k_{{\rm{F}}n}}L} \right)^2}/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ \bar \gamma = S{S_{\rm{h}}}{\left( {{k_{{\rm{F}}n}}L} \right)^2}/\left( {1 - C{C_{\rm{h}}}} \right); $ |
| $ S = \sin {k_{{\rm{F}}n}}L;{S_{\rm{h}}} = \sinh {k_{{\rm{F}}n}}L; $ |
| $ C = \cos {k_{{\rm{F}}n}}L;{C_{\rm{h}}} = \cosh {k_{{\rm{F}}n}}L. $ |
TRD是由具有高阻尼损失系数的弹性体和在弹性体内按确定的几何和物理特性要求设置的质量体组成的阻尼质量弹簧减振系统,通过弹性体和质量体的共同作用有效地提高钢轨系统的阻尼,降低钢轨振动的平均能量水平,抑制轮轨相互作用产生的振动能量在钢轨内传播[7].通过对TRD弹性体内质量体的质量、几何形状进行合理调整能够增加特定频率范围内轨道系统的阻尼.如果将TRD看作质量弹簧共振系统,则其稳态动力学特性可用附加动刚度来描述,弹簧刚度为kr、质量为mr的质量-弹簧共振系统的附加动刚度可以表示为[15]
| $ {D_{\rm{r}}} = \frac{{ - {\omega ^2}{m_{\rm{r}}}}}{{1 - {\omega ^2}/\omega _{\rm{r}}^2}} $ | (21) |
式中:ωr=(kr/mr)1/2.
如果需要考虑结构的阻尼,式(21)可改写为
| $ {D_{\rm{r}}} = \frac{{ - {\omega ^2}{m_{\rm{r}}}}}{{1 - {\omega ^2}/\omega _{\rm{r}}^2\left( {1 + {\rm{i}}{\eta _{\rm{r}}}} \right)}} $ | (22) |
式中:ηr为损耗因子.
注意到梁单元的每个节点有垂向和转动两个位移自由度,而附加质量-弹簧系统仅与其中的垂向位移自由度耦合,所以质量-弹簧系统的谱单元矩阵为
| $ {\mathit{\boldsymbol{D}}_{\rm{r}}} = \left[ {\begin{array}{*{20}{c}} {{D_{\rm{r}}}}&0\\ 0&0 \end{array}} \right] $ | (23) |
式中:Dr为计算得到的附加动刚度.
1.3 扣件单元本文将扣件连同剪切型减振器一同考虑为弹簧-质量-弹簧系统,其谱单元刚度矩阵的推导与TRD谱单元刚度矩阵的推导相似,限于篇幅,不再推导.
2 钢轨振动衰减率的求解钢轨的振动衰减率(decay rate)是指钢轨振动沿钢轨前进方向能量(振幅)传递的变化率(单位为dB·m-1),作为钢轨的动态参数,这一指标在频域范围内表示了振动沿钢轨衰减的能力[16].如果在某一频率范围内钢轨的振动衰减率较小,表示此频率范围内轨道系统的动态阻尼较低,钢轨的振动不能得到有效抑制,振动沿钢轨传播的能力较大;钢轨的振动衰减率越大,表示相应的轨道系统的动态阻尼越大,对钢轨振动的抑制效果越明显.因此可以用振动衰减率描述轨道结构在某频率范围内抑制钢轨振动的能力.
钢轨元胞模型第i个元胞中钢轨的动态运动方程可以表示成如下的形式:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{{\rm{LL}}i1}}}&{{\mathit{\boldsymbol{D}}_{{\rm{LR}}i1}}}\\ {{\mathit{\boldsymbol{D}}_{{\rm{RL}}i1}}}&{{\mathit{\boldsymbol{D}}_{{\rm{RR}}i1}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_{{\rm{L}}i1}}}\\ {{\mathit{\boldsymbol{\delta }}_{{\rm{R}}i1}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{{\rm{L}}i1}}}\\ {{\mathit{\boldsymbol{F}}_{{\rm{R}}i1}}} \end{array}} \right\} $ | (24) |
式中:D为梁的谱单元刚度矩阵SB(ω)中的2×2阶子矩阵;δ为钢轨两端位移向量;F为钢轨两端的力向量;下标L、R表示左、右节点.
经调整,式(24)可以表示为
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_{{\rm{R}}i1}}}\\ {{\mathit{\boldsymbol{F}}_{{\rm{R}}i1}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{D}}_{{\rm{LR}}i1}^{ - 1}{\mathit{\boldsymbol{D}}_{{\rm{LL}}i1}}}&{\mathit{\boldsymbol{D}}_{{\rm{LR}}i1}^{ - 1}}\\ {{\mathit{\boldsymbol{D}}_{{\rm{RL}}i1}} - {\mathit{\boldsymbol{D}}_{{\rm{RR}}i1}}\mathit{\boldsymbol{D}}_{{\rm{LR}}i1}^{ - 1}{\mathit{\boldsymbol{D}}_{{\rm{LL}}i1}}}&{{\mathit{\boldsymbol{D}}_{{\rm{RR}}i1}}\mathit{\boldsymbol{D}}_{{\rm{LR}}i1}^{ - 1}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_{{\rm{L}}i1}}}\\ {{\mathit{\boldsymbol{F}}_{{\rm{L}}i1}}} \end{array}} \right\} $ | (25) |
进一步,式(25)可写为
| $ {\mathit{\boldsymbol{Y}}_{{\rm{R}}i1}} = {\mathit{\boldsymbol{T}}_{i1}}{\mathit{\boldsymbol{Y}}_{{\rm{L}}i1}} $ |
式中:YRi1=[δRi1 FRi1]T、YLi1=[δLi1 FLi1]T分别为钢轨元胞模型中钢轨左、右两端的状态向量.
子胞界面处的力、位移的边界条件满足
| $ {\mathit{\boldsymbol{\delta }}_{{\rm{R}}i1}} = {\mathit{\boldsymbol{\delta }}_{{\rm{L}}i2}},{\mathit{\boldsymbol{F}}_{{\rm{R}}i1}} = - {\mathit{\boldsymbol{F}}_{{\rm{L}}i2}} $ | (26) |
式(26)可表示为如下的矩阵形式:
| $ {\mathit{\boldsymbol{Y}}_{{\rm{R}}i1}} = {\mathit{\boldsymbol{T}}_{12}}{\mathit{\boldsymbol{Y}}_{{\rm{L}}i2}} $ |
式中:
同理扣件左、右两端的状态向量的表达式为
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_{{\rm{R}}i2}}}\\ {{\mathit{\boldsymbol{F}}_{{\rm{R}}i2}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&0\\ \mathit{\boldsymbol{K}}&{ - \mathit{\boldsymbol{I}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_{{\rm{L}}i2}}}\\ {{\mathit{\boldsymbol{F}}_{{\rm{L}}i2}}} \end{array}} \right\} $ | (27) |
式(27)可简化为
| $ {\mathit{\boldsymbol{Y}}_{{\rm{R}}i2}} = {\mathit{\boldsymbol{T}}_{i2}}{\mathit{\boldsymbol{Y}}_{{\rm{L}}i2}} $ |
利用上述关系可以得到钢轨元胞模型左右两端状态向量的传递矩阵为
| $ \mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{T}}_{i3}}{\mathit{\boldsymbol{T}}_{23}}{\mathit{\boldsymbol{T}}_{i2}}{\mathit{\boldsymbol{T}}_{12}}{\mathit{\boldsymbol{T}}_{i1}} $ |
如果考虑TRD,钢轨元胞模型中钢轨的动态运动方程为
| $ {\mathit{\boldsymbol{D}}_{\rm{b}}} = {\mathit{\boldsymbol{D}}_{\rm{a}}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{\rm{r}}}}&0\\ 0&0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{{\rm{LL}}}} + {\mathit{\boldsymbol{D}}_{\rm{r}}}}&{{\mathit{\boldsymbol{D}}_{{\rm{LR}}}}}\\ {{\mathit{\boldsymbol{D}}_{{\rm{RL}}}}}&{{\mathit{\boldsymbol{D}}_{{\rm{RR}}}}} \end{array}} \right] $ | (28) |
式中:Da为钢轨的谱单元刚度矩阵;Dr为吸振器单元的附加动刚度矩阵;其余推导过程同上.
根据求得的钢轨元胞模型左右两端状态向量传递矩阵,由Bloch定理可得标准矩阵特征值问题为
| $ \left| {\mathit{\boldsymbol{T}} - {{\rm{e}}^{{\rm{i}}{k_{\rm{x}}}\alpha }}\mathit{\boldsymbol{I}}} \right| = {0^{\left[ {15} \right]}} $ |
式中: I为4×4阶单位矩阵;kx为一维Bloch波矢.通过求解特征值问题,即可得波矢kx与频率ω之间的频散关系,对于本模型中的钢轨弯曲问题,Bloch波矢的解总是以±kx的形式成对出现,分别刻画同一种波沿相反方向的传播特性.
对有复波数k=kr+iki(ki为负数)的一个单波,每传播1 m的距离,振幅减少exp(ki),因此,衰减率可表示为Δ=-20lg[exp(ki)]=-8.686ki,即衰减率为波矢虚部的-8.686倍.因此,钢轨的振动衰减率可通过如下的关系表达式求得:
| $ \mathit{\Delta} = - 8.686{\mathop{\rm Im}\nolimits} \left( {{k_{\rm{x}}}} \right) $ |
根据建立的钢轨元胞模型计算采用剪切型减振器钢轨的垂向振动衰减率的理论解,计算时采用的参数如表 1所示.
| 下载CSV 表 1 计算参数 Tab.1 Calculation parameters |
根据上述参数计算得到的以三分之一倍频程的形式表示的采用剪切型减振器钢轨的垂向振动衰减率如图 2所示.

|
图 2 采用剪切型减振器钢轨的垂向振动衰减率 Fig.2 Vertical decay rate of rail using egg fastening system |
从图 2可以看出,由本文的钢轨元胞模型计算得到的采用剪切型减振器的钢轨纵向存在两种形式的波.第1种波在全频段的衰减率都超过10 dB·m-1,且呈现出随频率的增大而增大的趋势,说明这种波很难沿着钢轨传播,属于近场波;第2种波衰减率随频率变化的趋势与第1种波有明显不同,可以看出第2种波在200~400 Hz范围内的衰减率小于0.15 dB·m-1,在630 Hz附近首次出现衰减率的峰值,在1 300 Hz附近再次出现一个较小的衰减率的峰值.
由于近场波在全频段衰减率都超10 dB·m-1,因此近场波对钢轨振动传递特性的影响较小,钢轨垂向弯曲波传播特性主要由第2种波(传播波)决定,因此本文只关注计算得到的采用剪切型减振器钢轨垂向传播波的衰减率.
3 钢轨振动特性分析在实际测量时,钢轨的振动响应通常被分解为与轮轨接触面法向(垂向)激励对应的垂向弯曲波的响应和与车轮轴向(横向)激励对应的横向弯曲波的响应.同时,相较于测量钢轨中近场波和传播波各自的衰减率,测量基于所有波的响应的钢轨总体的横向或垂向衰减率是更为直接有效的手段.
假设钢轨振动被分解为竖向和横向振动,且振动波幅值沿钢轨纵向按照指数衰减,则与采样点的距离为x的点处钢轨轨头的某1/3倍频程带宽内的频响函数幅值可以表达为
| $ A\left( x \right) = A\left( {{x_0}} \right){{\rm{e}}^{ - \beta x}} $ | (29) |
式中:A(x0)为钢轨轨头0点处的频响函数幅值;β为频响函数幅值衰减系数,用对数坐标表示,即为钢轨衰减率,单位为dB·m-1,如下所示:
| $ {R_{\rm{D}}} = 20\lg {{\rm{e}}^\beta } = 8.686\beta $ | (30) |
则钢轨辐射振动能量与振动衰减率的关系可以表达为
| $ \int_0^\infty {{{\left| {A\left( x \right)} \right|}^2}{\rm{d}}x} = {\left| {A\left( {{x_0}} \right)} \right|^2}\int_0^\infty {{{\rm{e}}^{ - 2\beta x}}{\rm{d}}x} $ | (31) |
进一步化简式(30)可得
| $ \int_0^\infty {{{\left| {A\left( x \right)} \right|}^2}{\rm{d}}x} = {\left| {A\left( {{x_0}} \right)} \right|^2}\frac{1}{{2\beta }} $ | (32) |
由于在实际采样时钢轨的振动响应被分解为钢轨对垂向和横向弯曲波各自的响应,导致幅值的实际变化不是简单的指数衰减形式,因此,采用基于离散点锤击测试的钢轨轨头频响函数能更好地计算衰减率的实际值.
| $ \int_0^\infty {\frac{{{{\left| {A\left( x \right)} \right|}^2}}}{{{{\left| {A\left( {{x_0}} \right)} \right|}^2}}}{\rm{d}}x} = \frac{1}{{2\beta }} = \sum\limits_{n = 0}^{{n_{\max }}} {\frac{{{{\left| {A\left( {{x_n}} \right)} \right|}^2}}}{{{{\left| {A\left( {{x_0}} \right)} \right|}^2}}}\Delta {x_n}} $ | (33) |
式中:A(xn)为第n点锤击时在0点的频响函数;Δxn为第n个锤击点到0点的距离.
综合式(29)和式(32)可得钢轨的振动衰减率为
| $ {R_{\rm{D}}} = \frac{{4.343}}{{\sum\limits_{n = 0}^{{n_{\max }}} {\frac{{{{\left| {A\left( {{x_n}} \right)} \right|}^2}}}{{{{\left| {A\left( {{x_0}} \right)} \right|}^2}}}\Delta {x_n}} }} $ | (34) |
根据欧洲标准BS EN 15461:2008+A1:2010[17],测量钢轨的振动衰减率时,为测量方便,可采取移动激励点的方法,沿着钢轨的走向设置至少28个锤击点.如果钢轨的振动衰减率过低,可视情况在第28个锤击点以外再设置若干个锤击点.
文献[8]基于上述测试方法,得到了使用剪切型减振器钢轨的垂向振动衰减率.分析文献中的数据可知,钢轨垂向振动衰减率在100~400 Hz频率范围内很低(低于0.1 dB·m-1),在400 Hz后钢轨垂向振动衰减率逐渐提高,在800 Hz处达到峰值,随后再次呈现下降趋势,在1 300 Hz出现一个较小的峰值.
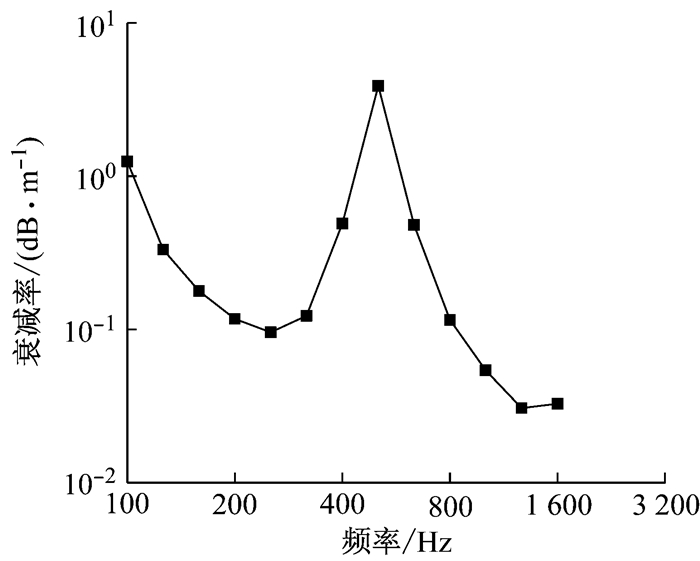
本文基于钢轨元胞模型计算得到的钢轨垂向振动衰减率如图 3所示.从图 3可以看出,钢轨垂向振动衰减率在200~400 Hz频率范围内较低(低于0.15 dB·m-1),在500 Hz附近达到峰值,在1 300 Hz附近出现一个较小的峰值,这和文献[8]中测试结果所体现的规律基本吻合,可以认为本文所采用的计算方法是正确的,得到的结果是合理的.
|
图 3 采用剪切型减振器钢轨的垂向振动衰减率 Fig.3 Vertical decay rate of rail using egg fastening system |
进一步分析采用剪切型减振器钢轨的垂向振动衰减率存在峰值的原因,采用剪切型减振器钢轨的垂向振动衰减率两个峰值的成因各不相同.
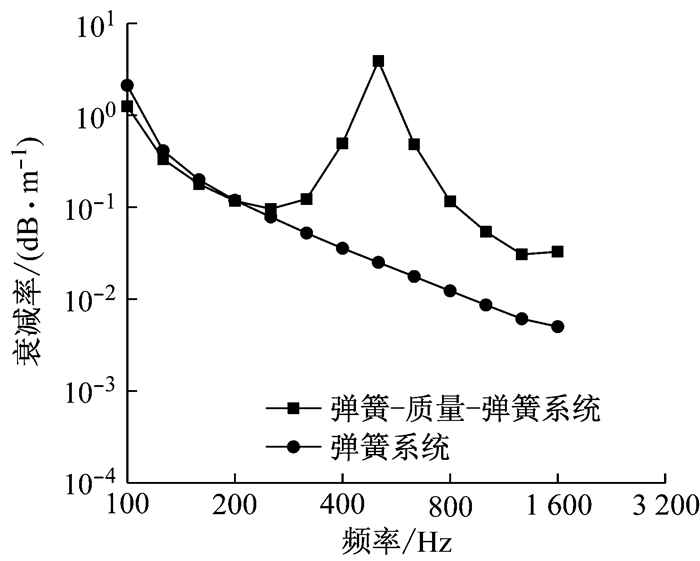
钢轨垂向振动衰减率的第1个峰值是由剪切型减振器自身的振动特性决定的,分别建立将扣件连同剪切型减振器考虑为弹簧系统和弹簧-质量-弹簧系统的钢轨元胞模型,计算得到两种不同简化方式的钢轨垂向振动衰减率的结果如图 4所示.
|
图 4 不同简化方式对钢轨垂向振动衰减率的影响 Fig.4 Effect of different simplified methods on vertical decay rate of rail |
从图 4可以看出,当扣件连同剪切型减振器被考虑成弹簧系统时,计算出来的钢轨垂向振动衰减率在全频段范围内呈现下降趋势.当扣件连同剪切型减振器被考虑成弹簧-质量-弹簧系统时,计算得到的结果在500 Hz附近出现峰值.从图 4还可以看出,当扣件连同剪切型减振器被考虑成弹簧-质量-弹簧系统时,钢轨衰减率从400 Hz起呈现出与当扣件连同剪切型减振器被考虑成弹簧系统时明显不同的变化趋势,这说明剪切型减振器自身的振动特性会对钢轨的振动传递特性产生影响.
钢轨垂向振动衰减率的第2个峰值是由一阶Pinned-Pinned共振产生的[18].从图 4可以看出,不论是将扣件连同剪切型减振器考虑为弹簧系统还是弹簧-质量-弹簧系统,钢轨的垂向振动衰减率在1 300 Hz附近都存在一个峰值,这正是钢轨的一阶Pinned-Pinned共振频率.钢轨在一阶Pinned-Pinned共振频率垂向振动衰减率出现峰值但峰值的值较小,说明钢轨在此频率附近的振动受到了一定的抑制.
4 剪切型减振器的参数敏感性分析以上通过与文献[8]中的实测数据的对比,解释了钢轨振动特性并验证了基于谱元法建立的钢轨元胞模型的合理性.本节利用建立的钢轨元胞模型分析减振器参数变化对钢轨垂向振动衰减率的影响.
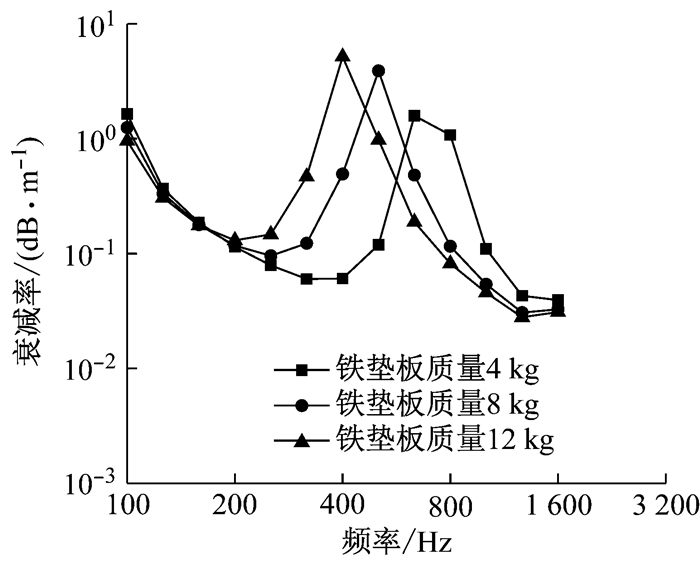
铁垫板质量变化对钢轨垂向振动衰减率的影响如图 5所示.从图 5可以看出,铁垫板的质量增大会使钢轨垂向振动衰减率的第1个峰值向低频移动,同时第1个峰值对应的钢轨垂向振动衰减率也会增加;铁垫板的质量变化对钢轨垂向振动衰减率第2个峰值的影响较小,说明铁垫板的质量对钢轨一阶Pinned-Pinned共振的影响较小.
|
图 5 铁垫板质量对钢轨垂向振动衰减率的影响 Fig.5 Effect of iron pad weight on vertical decay rate of rail |
铁垫板质量对200~400 Hz频率范围内钢轨垂向振动衰减率的影响主要体现在随着铁垫板质量的减小,在靠近400 Hz的一定范围内钢轨的垂向振动衰减率会有所增加,但增加的幅度有限,说明通过减小铁垫板的质量控制钢轨在200~400 Hz频率范围内的振动的效果不明显.
轨下垫板刚度变化对钢轨垂向振动衰减率的影响如图 6所示.从图 6可以看出,轨下垫板刚度的改变对400~1 000 Hz频率范围内钢轨垂向振动衰减率的影响较大;钢轨垂向振动衰减率的第1个峰值随轨下垫板刚度的增加呈现出向高频移动的趋势,峰值所对应的值也有所增加,但随着轨下垫板刚度的进一步增加,这一规律体现得越来越不明显;轨下垫板刚度的改变对钢轨垂向振动衰减率的第2个峰值的位置几乎没有影响.

|
图 6 轨下垫板刚度对钢轨垂向振动衰减率的影响 Fig.6 Effect of rail pad stiffness on vertical decay rate of rail |
轨下垫板刚度改变对400 Hz以内钢轨的垂向振动衰减率的影响较小,随着轨下垫板刚度的减小,仅在靠近400 Hz附近的小部分频率范围内的钢轨垂向振动衰减率会增加但增加的幅度有限.
减振器的刚度变化对钢轨垂向振动衰减率的影响如图 7所示.从图 7可以看出,减振器刚度的变化对500 Hz以上高频范围内钢轨的垂向振动衰减率几乎没有影响;减振器刚度的变化对钢轨垂向振动衰减率的影响主要体现在200 Hz以下的低频部分,随着减振器刚度增加,钢轨在200 Hz以内的垂向振动衰减率增加且增加的幅度较大.

|
图 7 减振器刚度对钢轨垂向振动衰减率的影响 Fig.7 Effect of damper stiffness on vertical decay rate of rail |
减振器刚度变化对200~400 Hz频率范围内钢轨振动的影响很小,不论减振器的刚度如何变化,钢轨在200~400 Hz频率范围内垂向振动衰减率始终小于0.2 dB·m-1.
轨下垫板阻尼对钢轨垂向振动衰减率的影响如图 8所示,可以看出,轨下垫板阻尼对200~400 Hz频率范围内的钢轨垂向振动衰减率几乎没有影响;轨下垫板阻尼对钢轨垂向振动衰减率的影响主要体现在500 Hz以上的高频部分.

|
图 8 轨下垫板阻尼对钢轨垂向振动衰减率的影响 Fig.8 Effect of rail pad damping on vertical decay rate of rail |
轨下垫板阻尼变化几乎不会引起钢轨垂向振动衰减率两个峰值位置的变化,但两峰值之间钢轨的垂向振动衰减率随轨下垫板阻尼的增加呈现出增加的趋势,因此,适当增加轨下垫板阻尼对于控制500 Hz以上的高频范围内的钢轨振动是有利的.
减振器阻尼对钢轨垂向振动衰减率的影响如图 9所示.从图 9可以看出,减振器阻尼变化几乎不会引起钢轨垂向振动衰减率两个峰值的变化;减振器阻尼变化对钢轨500 Hz以上的高频部分的垂向振动衰减率几乎没有影响.减振器阻尼的增加会使200~400 Hz频率范围内钢轨的垂向振动衰减率增加,因此,为控制钢轨在200~400 Hz频率范围内的振动,应适当增加减振器的阻尼.

|
图 9 减振器阻尼对钢轨垂向振动衰减率的影响 Fig.9 Effect of damper damping on vertical decay rate of rail |
根据以上结果可以看出,铁垫板质量、轨下垫板刚度及阻尼对钢轨垂向振动衰减率的影响主要体现在500 Hz以上的高频部分,合理选取铁垫板质量、轨下垫板的刚度和阻尼能够有效控制钢轨在高频范围内的振动.相比于减振器的刚度,减振器的阻尼对200~400 Hz频率范围内钢轨的垂向振动衰减率的影响更明显,适当增加减振器的阻尼对于控制钢轨在200~400 Hz频率范围内的振动是有利的.
综上所述,剪切型减振器自身的振动特性对钢轨垂向振动衰减率的影响主要体现在500 Hz以上的高频部分,对200~400 Hz频率范围内钢轨的垂向振动衰减率的影响很有限,需要选取合理的方式对200~400 Hz频率范围内钢轨的振动进行控制.
5 TRD调控机理分析为探究TRD对采用剪切型减振器钢轨的垂向振动衰减率的影响,进一步建立了考虑TRD的钢轨元胞模型.北京地铁所采用的TRD是英国Corus公司研发生产的专利产品,其固有频率约为800 Hz,每套TRD由2块长360 mm重13.6 kg的阻尼块、4个金属卡以及喷涂于钢轨轨腰表面的声学耦合剂组成[19].
经计算得到以1/3倍频程的形式表示的钢轨振动衰减率如图 10所示.

|
图 10 TRD对钢轨垂向振动衰减率的影响 Fig.10 Effect of TRD on vertical decay rate of rail |
从图 10可以看出,TRD能够显著改变采用剪切型减振器钢轨的垂向振动衰减率.未安装TRD时,采用剪切型减振器的钢轨垂向振动衰减率在200~400 Hz频段内很低(小于0.1 dB·m-1),这对于控制钢轨振动是不利的.安装TRD之后,采用剪切型减振器的钢轨垂向振动衰减率在200~400 Hz频段内有了很大的提高,效果如表 2所示.
| 下载CSV 表 2 TRD对钢轨垂向衰减率的影响 Tab.2 Effect of TRD on vertical decay rate of rail |
TRD阻尼对钢轨垂向振动衰减率的影响如图 11所示.从图 11可以看出,增加TRD的阻尼略微地降低了由于引入TRD产生的钢轨垂向振动衰减率的峰值,对钢轨垂向振动衰减率峰值对应的频率几乎没有影响.TRD阻尼的增加使钢轨振动衰减率之间的峰谷变小,因此适当增加TRD的阻尼能够提高衰减率.

|
图 11 TRD的阻尼对钢轨垂向振动衰减率的影响 Fig.11 Effect of TRD damping on vertical decay rate of rail |
综上,TRD作为附加动刚度使用在钢轨上时,能够大幅度提高钢轨的垂向振动衰减率(TRD工作频率附近).因此,TRD工作频率和阻尼的合理设计能够实现对钢轨振动的全频段控制.
6 结论为研究采用剪切型减振器钢轨的振动传递特性,本文利用谱单元法建立了钢轨元胞模型,结合Bloch定理计算钢轨的垂向振动衰减率,并在此基础上研究了剪切型减振器参数变化对钢轨垂向振动衰减率的影响以及TRD的调谐机理,得到如下结论:
(1) 剪切型减振器对钢轨垂向振动衰减率的影响主要体现在400 Hz以内的中低频.
(2) TRD能大幅度提高在自身工作频率附近钢轨的垂向振动衰减率,合理选择TRD的参数能更好地控制200~400 Hz频率范围内钢轨的振动.
| [1] |
夏禾, 曹艳梅. 轨道交通引起的环境振动问题[J]. 铁道科学与工程学报, 2004, 1(1): 44 XIA He, CAO Yanmei. Problem of railway traffic induced vibrations of environments[J]. Journal of Railway Science and Engineering, 2004, 1(1): 44 DOI:10.3969/j.issn.1672-7029.2004.01.008 |
| [2] |
任静. Ⅲ型双刚度轨道隔振器扣件的设计[J]. 都市快轨交通, 2007, 20(1): 59 REN Jing. Design of double stiffnes track damper fastening model Ⅲ[J]. Urban Rapid Rail Transit, 2007, 20(1): 59 DOI:10.3969/j.issn.1672-6073.2007.01.018 |
| [3] |
任静, 孙京健, 陈鹏, 等. 从钢轨异常波磨研究反思地铁设计[J]. 都市快轨交通, 2011, 24(3): 2 REN Jing, SUN Jingjian, CHEN Peng, et al. Rethink about metro design from rail abnormal corrugtion research[J]. Urban Rapid Rail Transit, 2011, 24(3): 2 DOI:10.3969/j.issn.1672-6073.2011.03.002 |
| [4] |
ZHANG H, LIU W, LIU W, et al. Study on the cause and treatment of rail corrugation for Beijing metro[J]. Wear, 2014, 317(1): 120 |
| [5] |
吴宗臻, 刘维宁, 张厚贵. 剪切型减振器扣件工作性能及改进[J]. 中南大学学报(自然科学版), 2016, 47(9): 3258 WU Zongzhen, LIU Weining, ZHANG Hougui. Performance and improvement of shear type damper fastener[J]. Journal of Central South University (Natural Science), 2016, 47(9): 3258 |
| [6] |
李伟, 杜星, 王衡禹, 等. 地铁钢轨一种波磨机理的调查分析[J]. 机械工程学报, 2013, 49(16): 26 LI Wei, DU Xing, WANG Hengyu, et al. Investigation into the mechanism of type of rail corrugation of metro[J]. Journal of Mechanical Engineering, 2013, 49(16): 26 |
| [7] |
刘维宁, 任静, 刘卫丰, 等. 北京地铁钢轨波磨测试分析[J]. 都市快轨交通, 2011, 24(3): 6 LIU Weining, REN Jing, LIU Weifeng, et al. In-situ tests and analysis on rail corrugation of Beijing metro[J]. Urban Rapid Rail Transit, 2011, 24(3): 6 DOI:10.3969/j.issn.1672-6073.2011.03.003 |
| [8] |
刘卫丰, 张厚贵, 孟磊, 等. 北京地铁采用调频式钢轨减振器抑制钢轨振动的试验研究[J]. 振动工程学报, 2016, 29(1): 105 LIU Weifeng, ZHANG Hougui, MENG Lei, et al. A test of suppressing rail vibration by tunned rail damper foe Beijing metro[J]. Journal of Vibration Engineering, 2016, 29(1): 105 |
| [9] |
THOMPSON D J, JONES C J C, WATERS T P, et al. A tuned damping device for reducing noise from railway track[J]. Applied Acoustics, 2007, 68(1): 43 DOI:10.1016/j.apacoust.2006.05.001 |
| [10] |
MAES J, SOL H. A double tuned rail damper—increased damping at the two first pinned-pinned frequencies[J]. Journal of Sound & Vibration, 2003, 267(3): 721 |
| [11] |
WU T X. Effect on short pitch rail corrugation growth of a rail vibration absorber/damper[J]. Wear, 2011, 271(1/2): 339 |
| [12] |
DOYLE J F. Wave propagation in structures—spectral analysis using fast discrete fourier transform[J]. Archives of Mining Sciences, 1997, 60(1): 403 |
| [13] |
LEE U. Spectral element method in structural dynamics[M]. Singapore: John Wiley & Sons(Asia) Pte Ltd, 2009
|
| [14] |
耿传智, 王伟鹏. 地铁弹性扣件减振性能的落轴冲击仿真分析[J]. 振动与冲击, 2010, 29(3): 113 GENG Chuanzhi, WANG Weipeng. Simulation on vibration-reduction performance of different subway elastic fastener under wheel load drop[J]. Journal of Vibration and Shock, 2010, 29(3): 113 DOI:10.3969/j.issn.1000-3835.2010.03.027 |
| [15] |
肖勇.局域共振型结构的带隙调控与减振降噪特性研究[D].长沙: 国防科学技术大学, 2012. XIAO Yong. Locally resonant structures: band gap tuning and properties of vibration and noise reduction[D]. Changsha: National University of Defense Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-90002-1014048035.htm |
| [16] |
THOMPSON D. Railway noise and vibration : mechanisms, modelling and means of control[J]. Elsevier Science & Technology, 2008, 153(4): 21 |
| [17] |
London British Standards Institution. Railway applications noise emission-characterisation of the dynamic properties of track sections for pass by noise measurements : BS EN 15461: 2008+A1: 2010[S]. London: London British Standards Institution, 2010.
|
| [18] |
THOMPSON D. Railway noise and vibration[M]. Oxford: Linacre House, 2009
|
| [19] |
孙晓静, 张厚贵, 刘维宁, 等. 调频式钢轨阻尼器对剪切型减振器轨道动力特性的影响[J]. 振动与冲击, 2016, 35(14): 209 SUN Xiaojing, ZHANG Hougui, LIU Weining, et al. Effect of tuning rail damper on dynamic properties of the track structure using egg fastening system[J]. Journal of Vibration and Shock, 2016, 35(14): 209 |
 2019, Vol. 47
2019, Vol. 47

