环形生产线通常是为了实现托盘在生产线中全线回流,多用于体积较大的复杂产品的加工或者装配,利用托盘帮助定位与运输.环形生产线中,M代表工位,B表示缓冲区,待加工零件在第1个工位M1被加载在托盘上,然后随托盘依次单向经过各个缓冲区和工位,在最后一个工位MK,加工好的产品卸载离开托盘,托盘不离开生产线,继续流向最后一个缓冲区BK(存放空托盘缓冲区),以待重新进入第1个工位加载零件.环形生产线与开放型生产线的区别在于,待加工零件于第1个工位是否进入生产线,不仅取决于上料是否充分,还取决最后一个缓冲区中有没有空托盘可用.同样,已加工好的产品,在最后一个工位能否被卸载,不仅取决于是否有库存空间存放已加工的产品,还需考虑最后一个缓冲区是否有空间容纳新的空托盘.这在一定程度上确保了整线中在制品数量的恒定,因此,需要控制在制品数量的生产系统也可以视作是环形生产系统[1].
生产线性能评估对生产线的设计、控制和管理至关重要,尤其是生产率指标,往往被作为缓冲区配置、设备选择、布局规划等的重要约束条件或者目标函数.近50年来,研究者们已经对其做了大量分析并取得了诸多成果.但是,环形生产线的研究相对较少,与开放型生产线相比,生产线中缺料堵料机制不仅由工位节拍差异、机器故障和缓冲区容量决定,还与系统中的托盘总量息息相关,因此求解更为复杂.Frein等[2]于1992年提出了一种求解工位时间近似相同的环形生产线生产率的分解方法.Biller等[3]认为环形生产线和与之对应的开放型生产线相比,托盘数量I和最后一个缓冲区BK的容量NK选择不合理,会大大降低整线生产率,因此提出一种符合精益生产原则的I、NK选择方法,使得环形生产线生产率达到与之对应的开放型生产线的标准.Paik等[4]提出3种方法来估算环形生产线的生产率,并且提出简单估算生产率上限的方法,但是计算精度有限;Maggio等[5]利用分解法研究了机器故障呈几何分布的环形生产系统,引入虚拟故障状态来等效由于上下游机器故障引起的缺料或堵料效应,利用恒定的托盘数量来划分缺料和堵料的范围.然而,由于计算效率较低,这种方法仅适用于三工位系统.Gershwin等[6]在此基础上,拓展出一种近似方法来评估多工位环形生产线的性能.Shi等[7]又针对文献[6]方法计算结果连续性较差的问题,做出两处改进来修正其算法,使其计算结果呈连续一致性.该方法精度较高,但仅适用于工位时间相同的环形生产线.
实际生产过程中,由于工艺、工位等约束,生产线往往无法实现完全平衡.在各工位时间不同的情况下,如果仅仅利用瓶颈工位的节拍作为整线节拍,即忽略了节拍差异以及其可能造成的待堵料现象,其生产率计算结果将有较大误差.因此,亟待一种可以求解非平衡环形生产线生产率的方法来解决实际问题.Levantesi等[8]认为,除非利用均一化等间接转化方法,还没有直接求解离散型不平衡生产线生产率的计算方法,但是利用连续型生产线生产率计算方法来估算离散型不平衡生产线,不会造成太大误差, 因此文献[8]利用连续型生产线生产率计算方法估算工位时间不同的两工位单缓冲区生产单元的状态概率,利用改进的DDX[9]分解方法求解离散型开放生产线的整线生产率,并取得较优的结果.
基于上述思路,利用改进的DDX分解方法将环形生产线分解为多个两工位单缓冲区的生产单元,利用恒定的托盘数量来划分故障传递范围,确定各生产单元的故障状态,然后利用连续型生产线生产率计算方法[10-11]来估算两工位单缓冲区生产单元的生产率,最后利用流失效方程和流修复方程[12]使整线迭代收敛,得到整线稳态下的生产率.
1 模型描述如图 1所示,环形生产线由K个工位Mi(i=1, …, K))和K个容量分别为Ni(i=1, …, K)的缓冲区Bi(i=1, …, K)组成.设在线托盘总数为I.以Gershwin-Werner模型[6]为基础进行改进,先作如下假设和定义:

|
图 1 环形生产线 Fig.1 A closed-loop production line |
(1) 零件随着托盘依次经过M1, M2, …, MK,然后零件卸载,托盘回流至BK.
(2) 每个工位Mi的作业时间Ti确定,定义每个工位的独立作业率μi=1/Ti(i=1, 2, …, K),每台机器一次只能加工一个工件,不考虑报废和返修.
(3) 每个工位Mi有γi种故障状态.任一工位不会同时发生2种以上的故障.每个工位Mi的故障用Fi, j(j=1, …, γi)表示,其故障率为pi, j(j=1, …, γi),修复率为ri, j(j=1, …, γi),故障率、修复率符合负指数分布,并且
(4) 所有故障都是基于操作的故障(ODF),即在待料或者堵料时,故障不会发生.
(5) 假设第1个工位上料充分,最后1个工位有库存空间卸料.因此,零件上下线与否完全由托盘决定,并且零件在线中流动与托盘完全同步,因此忽略零件,只考虑托盘的流动.
(6) 不考虑托盘经过缓冲区的时间,缓冲区不发生故障.
(7) t时刻,各个缓冲区中的在制品容量为ni(t), 0≤ni(t)≤Ni.工位中不设存放零件的容量,即
综上,环形生产线的状态由K、I、Ni(i=1, …, K)、Ti(i=1, …, K)、Fi, j、pi, j和ri, j(i=1, …, K; j=1, …, γi)决定.
开放型生产线中,在只有一台机器故障时间足够久的情况下,该机器上游所有的缓冲区都将逐渐填满,导致上游所有机器堵料;而下游的所有机器也会因为缓冲区中在制品数为零而待料(缺料),最终导致整线停产.而环形生产线中的在制品数量一定,即
最简单的两工位单缓冲区系统如图 2所示,由上游工位Mu、中间缓冲区B和下游工位Md组成,其中上游工位有fu种故障状态,分别为(α1, …, αfu),缓冲区容量为N,下游工位有fd种故障状态,分别为(β1, …, βfd).

|
图 2 两工位单缓冲区生产系统 Fig.2 Two-machines-one-buffer system |
两工位单缓冲区系统的状态可用(n, α, β)表示,其中n为缓冲区中在制品数量,满足0≤n≤N,有
| $ \alpha = \left\{ {\begin{array}{*{20}{c}} 1&{{M^{\rm{u}}}\;正常工作}\\ {{\alpha _1}}&{{M^{\rm{u}}}\;处于第\;{\alpha _1}\;种故障状态}\\ \vdots&\vdots \\ {{\alpha _{{f_{\rm{u}}}}}}&{{M^{\rm{u}}}\;处于第\;{\alpha _{{f_{\rm{u}}}}}\;种故障状态} \end{array}} \right. $ |
| $ \beta = \left\{ {\begin{array}{*{20}{c}} 1&{{M^{\rm{d}}}\;正常工作}\\ {{\beta _1}}&{{M^{\rm{d}}}\;处于第\;{\beta _1}\;种故障状态}\\ \vdots&\vdots \\ {{\beta _{{f_{\rm{d}}}}}}&{{M^{\rm{d}}}\;处于第\;{\beta _{{f_{\rm{d}}}}}\;种故障状态} \end{array}} \right. $ |
因此该系统共有(N+1)×(fu+1)×(fd+1)种离散状态,为计算两工位时间不同的情况,将其作为连续型系统处理,仅分为缓冲区空、缓冲区满和中间状态(缓冲区非空非满),f(X, α, β)为对应状态概率密度函数,其中X为当前时刻缓冲区在制品数量.当缓冲区非空非满时,t时刻系统的状态概率密度函数满足式(1),即t时刻系统状态为s(t)=(X≤x, α=i, β=j)的稳态概率Prob对x求偏导.
| $ \begin{array}{l} f\left( {x,i,j,t} \right) = \frac{\partial }{{\partial x}}{P_{{\rm{rob}}}}\left[ {X\left( t \right) \le x,\alpha \left( t \right) = i,\beta \left( t \right) = j} \right],\\ \;\;\;\;0 < x < N \end{array} $ | (1) |
系统稳态概率密度函数定义为f(x, i, j)=
当工位处于故障状态时,其作业率为零,即μiu=0(i=α1, …, αfu),μjd=0(j=β1, …, βfd).根据上下游工位作业率μiu(i=1, α1, …, αfu)和μjd(j=1, β1, …, βfd)的关系,可将状态空间SM分为3个集合,即S1(μiu>μjd)、S2(μiu < μjd)、S3(μiu=μjd),SM=S1∪S2∪S3.当缓冲区为空时,S0=S2∪S3;当缓冲区为满时,SN=S1∪S3;求得所有状态的概率密度函数和缓冲区空(满)的稳态概率后,可求得系统生产率PR和系统实际工作效率E(即除去待料率和堵料率的实际工作效率).
| $ \begin{array}{l} {P_{\rm{R}}} = \sum\limits_{\left( {i,j} \right) \in {S_0}} {\mu _i^{\rm{u}}p\left( {0,i,j} \right)} + \sum\limits_{\left( {i,j} \right) \in {S_{\rm{M}}}} {\int_0^N {\mu _i^{\rm{u}}f\left( {x,i,j} \right){\rm{d}}x} } + \\ \;\;\;\;\;\;\;\sum\limits_{\left( {i,j} \right) \in {S_{\rm{N}}}} {\mu _j^{\rm{d}}p\left( {N,i,j} \right)} \end{array} $ | (2) |
| $ E = 1 - \sum\limits_{\left( {i,j} \right) \in {S_0}} {p\left( {0,i,j} \right)} - \sum\limits_{\left( {i,j} \right) \in {S_{\rm{N}}}} {p\left( {N,i,j} \right)} $ | (3) |
f(x, i, j)、p(0, i, j)和p(N, i, j)的求解参考Tan等[10]所提的方法,根据缓冲区填充量分别求解.
2.2 利用分解方法估算开放型生产线生产率利用马尔科夫状态转移矩阵精确求解两工位单缓冲区系统的稳态概率密度函数,可求解得到生产率,但是该方法如果扩展到3个及以上的工位,会导致状态数量呈指数激增,求解困难.因此,在求解大型生产线时,只能利用估算的方法来求解.本文运用Tolio-Matta[13]的分解方法,将生产线分解为多个两工位单缓冲区的系统单元,进行迭代估算.
如图 3所示,由K个工位和K-1个缓冲区组成的生产线,每个工位Mi(i=1, …, K)各自含有γi(i=1, …, K)种故障.将其以缓冲区为中心分解为K-1个两工位单缓冲区的虚拟单元,每个单元中的缓冲区B(i)对应整线中的真实缓冲区Bi;单元中的上游机器Mu(i)的状态代表整线中Bi上游所有工位和缓冲区对Bi中托盘流入的影响,单元中的下游机器Md(i)的状态代表整线中Bi下游所有工位和缓冲区对Bi托盘流出的影响.

|
图 3 开放型生产线分解方法 Fig.3 Decomposition of a tandem line |
在任一虚拟单元Mu(i)-B(i)-Md(i)中,B(i)的状态与Bi完全相同.对于Bi而言,零件流入中断可能由2种情况导致:一是Bi的上游邻近工位Mi故障;二是Bi上游除Mi以外的工位Mk(1≤k < i)故障时间足够长,导致Mk与Mi之间所有的缓冲区为空,即Mi待料,造成Bi中无零件流入.
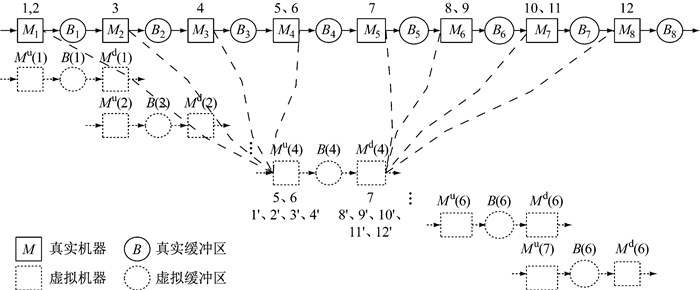
这2类零件流入中断情况对应到虚拟单元Mu(i)-B(i)-Md(i)中,由于没有再上游工位,无零件流入B(i)的状态,无论是由于Mi故障造成或是再上游工位Mk(1≤k < i)造成的,都属于上游工位Mu(i)的故障,于是将前者定义为近程故障(或真实故障),后者定义为远程故障(或虚拟故障).同理,Bi中的零件无法流出可能是由于下游邻近工位Mi+1导致,也可能因为再下游Mk(i+1 < k≤K)机器故障导致,分别对应Md(i)中的近程故障(真实故障)和远程故障(虚拟故障).用Fi, j表示i工位的第j种真实故障;用Ft, j(i)(1≤t < i, j=1, …, γt)来表示t工位的第j种故障造成B(i)零件流入的中断,即Mu(i)的虚拟故障;用Ft, j(i+1)(i+1 < t≤K, j=1, …, γt)来表示t工位的第j种故障造成B(i)零件堆满堵料,即Md(i)的虚拟故障.如图 4所示,数字1~12分别代表图中9个工位的真实故障,比如M1有“1”、“2”两种故障,M2只有“3”一种故障,M3只有“4”一种故障,以此类推.在划分单元Mu(4)-B(4)-Md(4)的故障状态时,“5”、“6”和“7”分别是其上下游工位的真实故障,其他都是虚拟故障,分别用1′、2′、3′、4′、8′、9′、10′、11′、12′表示.F4, 1=5, F4, 2=6, F5, 1=7, F1, 1(4)=1′, F1, 2(4)=2′, F2, 1(4)=3′, F3, 1(4)=4′, F6, 1(5)=8′, F6, 2(5)=9′, F7, 1(5)=10′, F7, 2(5)=11′, F8, 1(5)=12′.
|
图 4 Tolio分解方法故障传递状态示意 Fig.4 Failure modes propagation in Tolio's decomposition |
因此,在每个虚拟单元Mu(i)-B(i)-Md(i)中,Mu(i)的故障就由
根据Tolio-Matta分解方法[13]中流修复方程,远程故障修复的概率与故障本身修复的概率一致,即
| $ \begin{array}{l} {r_{t,j}}\left( t \right) = {r_{t,j}}\;\;\;\left( {i = 1, \cdots ,K;} \right.\\ \;\;\left. {t = 1, \cdots ,K;\;\;\;j = 1, \cdots ,{\gamma _t}} \right) \end{array} $ | (4) |
根据流失效方程,远程故障发生的概率为
| $ \begin{array}{*{20}{c}} {p_{t,j}^{\rm{u}}\left( i \right) = \frac{{P_{t,j}^{{\rm{st}}}\left( {i - 1} \right)}}{{E\left( i \right)}}{r_{t,j}}\left( {i = 1, \cdots ,K;} \right.}\\ {\left. {t = 1, \cdots ,i - 1;\;\;\;j = 1, \cdots ,{\gamma _t}} \right)} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {p_{t,j}^{\rm{d}}\left( i \right) = \frac{{P_{t,j}^{{\rm{bl}}}\left( {i + 1} \right)}}{{E\left( i \right)}}{r_{t,j}}\left( {i = 1, \cdots ,K;} \right.}\\ {\left. {t = i + 2, \cdots ,K;\;\;\;j = 1, \cdots ,{\gamma _t}} \right)} \end{array} $ | (6) |
式中:Pt, jst(i-1)表示在Mu(i-1)-B(i-1)-Md(i-1)单元中,Md(i-1)由于Ft, j(i-1)导致的待料(即n(i-1)=0)的概率; Pt, jbl(i+1)表示在Mu(i+1)-B(i+1)-Md(i+1)单元中,由Ft, j(i+2)导致的堵料(即n(i+1)=Ni+1)的概率; E(i)为Mu(i)-B(i)-Md(i)单元的实际工作效率.
整线生产率的求解是一个迭代收敛的过程,利用改进的DDX[8]进行计算.步骤①,令rt, j(i)=rt, j,(i=1, …, K; t=1, …, K; j=1, …, γt);pt, ju(i)=pt, j,(i=1, …, K;t=1, …, i-1;j=1, …, γt);pt, jd(i)=pt, j,(i=1, …, K;t=i+2, …, K;j=1, …, γt),进行初始化设置.步骤②,从i=1至i=K依次计算各个虚拟单元的状态概率,并将上一单元待料的概率Pt, jst(i-1)根据式(5)转化为下一单元的故障概率pt, ju(i).步骤③,从i=K至i=1依次计算各个虚拟单元的状态概率,并将下一单元的堵料的概率Pt, jbl(i+1)根据式(6)转化为上一单元的故障概率pt, jd(i).步骤④,重复步骤②和步骤③,直到pt, ju(i)与pt, jd(i)不再变化,生产率稳定收敛.这样得到的各个单元生产率不尽相同,根据瓶颈工位决定整线生产率原则,选取最小生产率PR作为整线生产率.
2.3 环形生产线的分解方法在开放型生产线中,一个工位的长时间故障可能导致其上游所有工位堵料、下游所有工位待料,所以在划分两工位单缓冲区虚拟单元的时候,该单元上游所有工位的故障都会对当前单元产生影响,下游亦然.与之不同的是,环形生产线的最后一个工位MK与第1个工位M1之间由一个缓冲区BK联系起来,形成如图 1所示环状,那么一个工位的长时间故障能否导致其他工位待料与堵料,就不是简单的由工位间的相对位置关系决定,而是与两工位间的缓冲区容量与整线中固定的托盘数量有关.
如图 5的环形生产线,设各个缓冲区的容量为10,托盘数量为35.当M1故障时,托盘开始往B6堆积,当B6堆积满后,M6无法再释放托盘,因此堵塞,托盘继续堆积在B5,B5堆满后,M5被堵料,依次类推,B4也被堆积满,B3中剩余5个托盘,而B1、B2为空.也就是说M1故障时间足够长可以导致M6、M5、M4堵料,而导致M2、M3待料.其他工位类推.

|
图 5 六工位环形生产线 Fig.5 A closed-loop of six machines |
总结上述推理,能使M1待料的工位有{M5, M6},能使其堵料的工位有{M2, M3, M4},能使M2待料的工位有{M6, M1},能使其堵料的工位有{M3, M4, M5}.那么,在划分单元Mu(1)-B(1)-Md(1)时,需要考虑的前序工位就是能使M2待料的工位{M6, M1},后续工位是能使M1堵料的工位{M2, M3, M4}.因此,在Mu(1)-B(1)-Md(1)单元中,上游工位Mu(1)的虚拟故障为F6, j(1)(j=1, …, γ6),真实故障为F1, j(j=1, …, γ1),下游工位Md(1)的虚拟故障为F3, j(2)(j=1, …, γ3)、F4, j(2)(j=1, …, γ4),真实故障为F2, j(j=1, …, γ2).其他单元同理类推.接下来,同样利用式(5)、式(6)来迭代虚拟故障的故障率,求解环形生产线整线生产率.
因此,环形生产线在划分两工位单缓冲区单元时,即考虑能对该单元托盘流入流出产生影响的工位范围时,是以能够对当前缓冲区造成空或满为标准判定,而非简单根据相对位置决定.
2.3.1 待料和堵料的范围划分在分解环形生产线时,需要为每个虚拟单元划分待料和堵料范围.若工位Mj在工位Mi的待料范围内,那么在Mj故障时间足够长后,Mi会因两工位间所有的缓冲区为空而停止生产.若工位Mj在工位Mi的堵料范围内,那么Mj故障时间足够长后,Mi会因两工位间所有的缓冲区满而停止生产.设{Ms(i), Ms(i)+1, …, Mi-1}为一系列能导致Mi待料的工位,其中Ms(i)为距离Mi最远的工位.{Mi+1, Mi+2, …, Mb(i)}为一系列能导致Mi堵料的工位,其中Mb(i)为距离最远的工位.s(i)与b(i)的计算为
| $ s\left( i \right) = \mathop {\max }\limits_j \left\{ {j + 1\left| {\mathit{\Psi }\left( {i,j} \right) < I} \right.} \right\} $ | (7) |
| $ b\left( i \right) = \mathop {\min }\limits_j \left\{ {j\left| {\mathit{\Psi }\left( {i,j + 1} \right) > I} \right.} \right\} $ | (8) |
式中:Ψ(i, j)为Mi、Mj间所有缓冲区容量之和.
2.3.2 阈值的消除环形生产线与开放型生产线还有一点不同,一个工位的故障能否导致其他工位待料或者堵料,与它邻近缓冲区中的在制品数量有关.
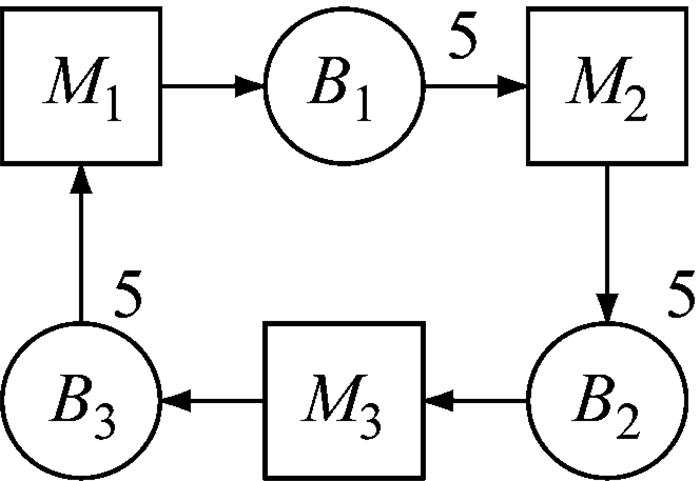
如图 6,3个工位,3个容量均为5的缓冲区,托盘数量为7个.假设M2故障,托盘会堆积在B1中,直到M1堵料.但若此时B3中有2个以上的托盘,那么M1就不会因为B1满而堵料,因为总共只有7个托盘.相反,若B3中的托盘数少于2个,那么B2中的托盘数量必然大于零,那么M3就不会因为M2的故障而待料.因此,B3缓冲区就有一个阈值为2.
|
图 6 带阈值的环形生产线 Fig.6 A closed-loop with thresholds |
通常,定义lj(i)为Bi的一个阈值,lj(i)需要满足能使Mi+1至Mj之间的所有缓冲区同时为满,并且lj(i)最大.
| $ {l_j}\left( i \right) = I - \mathit{\Psi }\left( {i + 1,j} \right) $ | (9) |
对于任意2个工位Mi与Mj,都能计算得到一个lj(i),不过通常只考虑1 < lj(i) < Ni的情况,那么K个工位、K个缓冲区的系统最多能得到K个缓冲区的阈值.在计算大型生产系统时,阈值的存在会导致计算复杂,计算量增大,因此通常利用转化的方法消除阈值来简化计算.借鉴Gershwin-Werner[6]的方法,在阈值出现的位置插入一个理想的机器(作业率无穷大,故障率为零,修复率为1),把原本一个缓冲区分割成2个不含阈值的缓冲区,从而解决了这个问题.例如,将图 6的阈值消除后,可得到如图 7所示的新生产线,由于插入的理想机器M*没有作业时间和故障时间,故不影响整线生产率.

|
图 7 消除阈值后的环形生产线示意 Fig.7 A closed-loop with thresholds eliminated |
以三工位、三缓冲区的环形生产线为例,验证上述方法的有效性.其中,独立作业率用μ表示,每个工位只含1种真实故障状态,其故障率用p表示,修复率用r表示.设生产线基本信息如表 1、表 2.
| 下载CSV 表 1 三工位环形生产线工位参数 Tab.1 Parameters of a 3-machine loop |
| 下载CSV 表 2 三工位环形生产线缓冲区容量和托盘数 Tab.2 Buffer capacity and pallet number of a 3-machine loop |
(1) 根据环形生产线计算方法,先对生产线做基本处理,即消除B1、B2、B3的阈值.计算各缓冲区阈值,分别为5、5、5;插入理想机器M*(u=100, p=10-8, r=1)后,得6个工位、6个缓冲区的生产线,重新编号为M1、M2、M3、M4、M5、M6,其中M1、M3、M5对应原工位M、M2、M3,M2、M4、M6为理想机器M*.转化后的工位参数如表 3,缓冲区容量如表 4.
| 下载CSV 表 3 转化后的工位参数 Tab.3 Parameters of the transferred 3-machine loop |
| 下载CSV 表 4 转化后的缓冲区容量和托盘数量 Tab.4 Buffer capacity and pallet number of transferred 3-machine loop |
(2) 划分工位待料和堵料范围.根据式(7)与(8)计算工位的待料与堵料范围为:st(1)=4;st(2)=5;st(3)=6;st(4)=1;st(5)=2;st(6)=3; bl(1)=4;bl(2)=5;bl(3)=6;bl(4)=1;bl(5)=2;bl(6)=3.
(3) 划分两工位单缓冲区基本单元,确定故障状态.将整线划分为6个基本生产单元Mu(i)-B(i)-Md(i)(i=1, 2, 3, 4, 5, 6),并根据待堵料范围确定各单元的虚拟故障状态.如Mu(1)-B(1)-Md(1)单元中,Mu(1)的故障状态包括能使M2待料的F5, 1(1)、F6, 1(1)、F1, 1;Md(1)的故障状态包括能使M1堵料的F4, 1(2)、F3, 1(2)、F2, 1;其他单元以此类推.
(4) 初始化各虚拟故障状态的可靠性参数pk, ju(i)、rk, ju(i)(k=s(i+1), …, i); pk, jd(i)、rk, jd(i)(k=i+1, …, b(i)).如Mu(1)-B(1)-Md(1)单元中,p1, 1=0.01;p5, 1(1)=p5, 1=0.01;p6, 1(1)=p6, 1=10-8; p4, 1(2)=p4, 1=10-8; p3, 1(2)=p3, 1=0.01;p2, 2=10-8; r1, 1=0.11;r5, 1(1)=r5, 1=0.15;r6, 1(1)=r6, 1=1.00;r4, 1(2)=r4, 1=1.00;r3, 1(2)=r3, 1=0.12;r2, 2=1.00.
(5) 从i=1至i=6,计算每个虚拟单元的状态概率,得E(i)与Pk, jst(i);利用式(5)更新pk, ju(i+1).
(6) 对i=6至i=1,计算每个虚拟单元的状态概率,得E(i)与Pk, jbl(i),利用式(6)更新pk, ju(i-1).
(7) 重复步骤(5)、步骤(6),直到每个虚拟单元的生产率收敛,即pk, ju(i)、pk, jd(i)不再变化.最小的PR即为整线生产率.
为验证生产率计算方法,利用Tecnomatix Plant Simulation软件按照表 1、表 2参数建立三工位环形生产线仿真模型,并进行仿真模拟,仿真结果与数值计算结果比较如表 5,生产率估算误差为0.37%,且计算效率远高于仿真方法.其中,误差为生产率数值计算值相对生产率仿真值的相对误差.
| 下载CSV 表 5 数值计算方法与仿真方法性能对比 Tab.5 Performance comparison between algorithm and simulation |
接下来讨论独立作业率不同的情况.
(1) 以第1个工位独立作业率μ1为变量,验证本文方法的精度.考虑到生产线不平衡率一般控制在20%范围内,因此只取μ1的变化范围在1.0~0.8.部分计算结果如图 8所示,随着μ1的升高,整线生产率随之升高,仿真结果与数值计算结果的相对误差始终控制在2%范围内.

|
图 8 生产率与μ1的关系 Fig.8 Production rate with parameter μ1 varying |
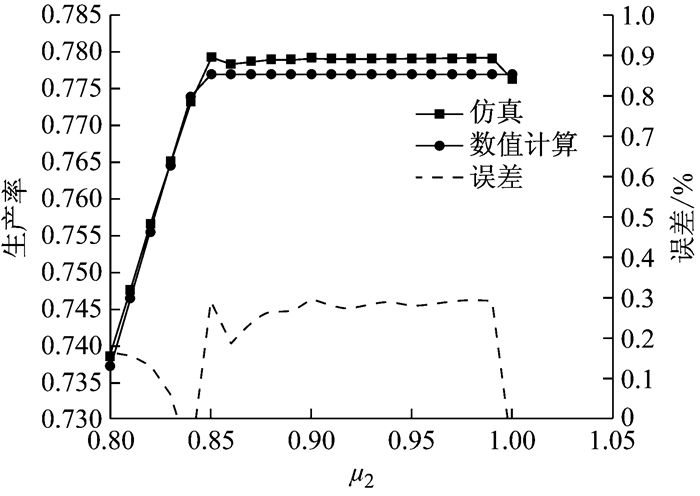
(2) 考虑3个工位独立作业率都不相同的情况.工位参数如表 6,缓冲区配置及托盘数如表 2所示.保持各个参数不变,μ1=0.85,μ2在1.0~0.8范围内变化.计算结果如图 9所示,3个工位独立作业率都不相同的情况下,第2个工位独立作业率变化不超过20%的范围,生产率估算误差不超过1%,说明该方法对于三工位环形系统计算具有有效性.
| 下载CSV 表 6 作业率不同的三工位环形生产线工位参数 Tab.6 Parameters of 3-machine loop with total different efficiency |
|
图 9 独立作业率各不相同的三工位环形生产线生产率 Fig.9 Production rate of 3-machine loop with different independent efficiency |
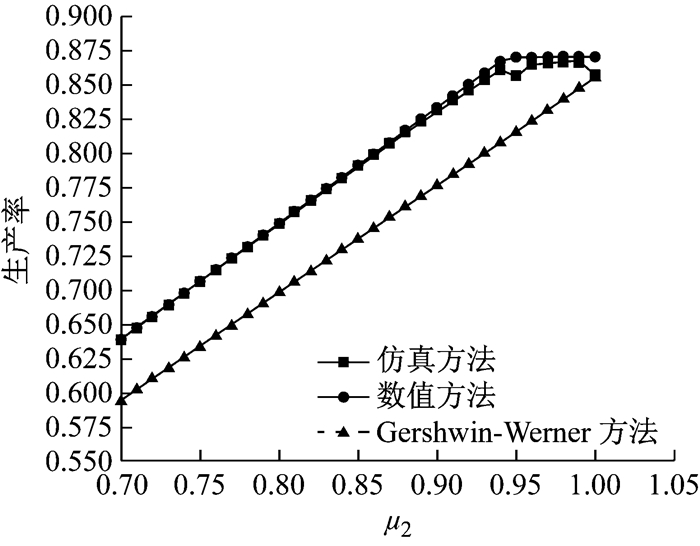
(3) 将上述算法与Gershwin-Werner的算法[6]作比较,假设第1个工位的独立作业率为0.95,而第2个工位的独立作业率在0.7~1.0范围内波动,工位参数如表 7所示,缓冲区配置及托盘数如表 2所示,2种方法的计算结果如图 10所示.Gershwin-Werner的方法能将误差控制在8%范围内,本文方法能将误差控制在2%范围内.Gershwin-Werner方法[6]无法精确计算各工位作业时间不同的情况,只能按照瓶颈节拍作为整线节拍来粗略计算,这将造成较大误差.
| 下载CSV 表 7 独立作业率变化的三工位环形生产线设备参数 Tab.7 Parameters of 3-machine loop with independent efficiency varying |
|
图 10 不同方法比较 Fig.10 Performance comparison between the methods |
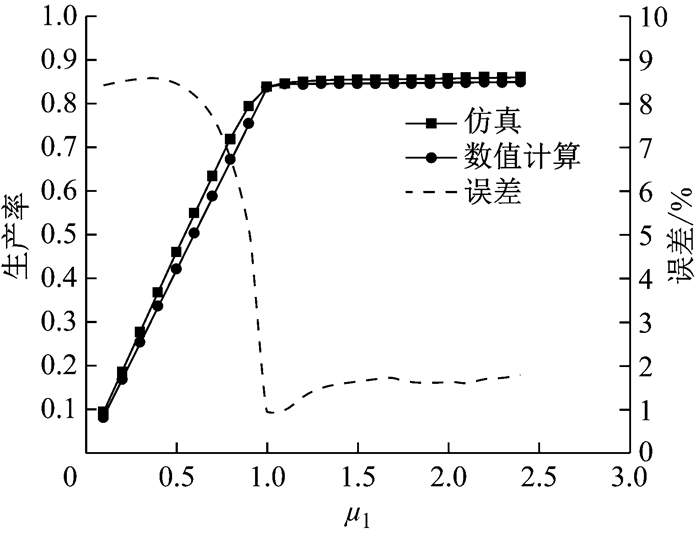
(4) 考虑更多工位的情况.如五工位的生产线,其工位参数如表 8、缓冲区配置及托盘数如表 9,将第1个工位的独立作业率由0.1开始以0.1为增幅逐渐提高至2.5,检验该方法的精确性.计算结果如图 11,与仿真结果相比,计算精度在8%范围内.
| 下载CSV 表 8 五工位环形生产线工位参数 Tab.8 Parameters of 5-machine loop |
| 下载CSV 表 9 五工位环形生产线缓冲区容量及托盘数 Tab.9 Buffer capacity and pallet number of 5-machine loop |
|
图 11 一个工位独立作业率变化的五工位生产线生产率 Fig.11 Production rate of 5-machine loop with one machine's efficiency varying |
如图 9、图 10、图 11,随着工位的独立作业率上升,仿真和数值计算的整线生产率都先上升而后平稳波动,这是比较符合生产实际的.根据瓶颈工位决定整线生产率原则,当一个工位的独立作业率远低于其他工位时,该工位将成为影响整线生产率的最大因素,这个工位通常被叫做瓶颈工位.此时,整线生产率随着该工位的独立作业率升高而升高.但当该工位的独立作业率上升到与其他工位相当后,该工位不再是瓶颈工位,此后,无论该工位作业率如何上升,整线的生产率都只能保持很小范围的波动.
3.2 实例验证某变速箱主箱体分装线共有5个工位,其工艺文件如表 10所示,每2个工位间各有1个缓冲区,缓冲区容量均为4.
| 下载CSV 表 10 某变速箱主箱体分装线工艺参数 Tab.10 Process parameters of main box assembly line of a certain gearbox |
首先将表 10所示生产实例抽象为计算模型:ui=1/Ti,pi=1/(MTBF×60),ri=1/(MTTR×60),i=1, 2, …, 5,其中,MTBF、MTTR分别表示平均故障间隔时间和平均故障修复时间.
| 下载CSV 表 11 某变速箱主箱体分装线工位参数 Tab.11 Workstation parameters of main box assembly line of a certain gearbox |
该分装线各工位间缓冲区容量均为4,以托盘数为变量,根据本文提出的闭环生产线生产率计算方法以及仿真方法,分别计算托盘数从1增加至20时变速箱主箱体分装线的生产率,计算结果如图 12.

|
图 12 某变速线主箱体分装线生产率计算 Fig.12 Production rate of the main box assembly line of a certain gearbox |
当托盘数小于最小缓冲区容量4时,该算法会将托盘数等同于最小缓冲区容量进行计算,从而引起计算误差,这是该算法的固有弊端.但是,在实际生产中,托盘数量少于最小缓冲区容量的情况不利于正常生产,是极其特殊的情况,通常不会发生,并不影响该算法的实用性.
当托盘数量从5继续增长至20的过程中,该分装线的生产率在0.023 6至0.024 2范围内变化,相较于仿真所得生产率,误差在0.15%至2.40%之间,说明本文针对闭环生产线提出的生产率估算方法精确度较高.当托盘数量为20时,缓冲区全满,生产线被卡死,无法正常运作,生产率突降为零.
运用本文方法计算生产率时,每组数据能在3 s内得出收敛值,而仿真方法需要设置大于5 min的物理运行时间来确保数据的稳定性.因此,在一定精度范围内,本文的计算方法相对仿真而言效率更高.计算效率的提高,将有利于生产线性能评估,缩短生产线设计开发周期.
4 结论提出一种环形生产线生产率计算方法,利用连续型生产线的方法计算离散非平衡两工位生产率,根据托盘数量划分故障传递范围,利用分解方法迭代求解整线生产率.经过算例分析和实例验证,并且与仿真结果做对比,证实该方法能够通用性地求解各工位作业时间相同或者不同的多故障环形生产线生产率,计算结果精度较高,且效率远高于仿真,具有实用性.
| [1] |
ANGIUS A, COLLEDÁNI M, HORVATH A, et al. Analysis of the lead time distribution in closed loop manufacturing systems[J]. Ifac Papersonline, 2016, 49(12): 307 DOI:10.1016/j.ifacol.2016.07.622 |
| [2] |
FREIN Y, COMMAULT C, Dallery Y. Analytical performance evaluation of closed transfer lines with limited number of pallets[C]// Proceedings of IEEE International Conference on Robotics and Automation. New York: IEEE, 1992: 1018-1023.
|
| [3] |
BILLER S, MARIN S P, MEERKOV S M, et al. Closed bernoulli production lines: Analysis, continuous improvement, and leanness[J]. IEEE Transactions on Automation Science & Engineering, 2009, 6(1): 168 |
| [4] |
PAIK C H, KIM H G, CHO H S. Performance analysis for closed-loop production systems with unreliable machines and random processing times[J]. Computers & Industrial Engineering, 2002, 42(2/3/4): 207 |
| [5] |
MAGGIO N, MATTA A, GERSHWIN S B, et al. A decomposition approximation for three-machine closed-loop production systems with unreliable machines, finite buffers and a fixed population[J]. ⅡE Transactions, 2009, 41(6): 562 |
| [6] |
GERSHWIN S B, WERNER L M. An approximate analytical method for evaluating the performance of closed-loop flow systems with unreliable machines and finite buffers[J]. International Journal of Production Research, 2007, 45(14): 3085 DOI:10.1080/00207540500385980 |
| [7] |
SHI C, GERSHWIN S B. Improvement of the evaluation of closed-loop production systems with unreliable machines and finite buffers[J]. Computers & Industrial Engineering, 2014, 75(1): 239 |
| [8] |
LEVANTESI R, MATTA A, TOLIO T. Performance evaluation of continuous production lines with machines having different processing times and multiple failure modes[J]. Performance Evaluation, 2003, 51(2/3/4): 247 |
| [9] |
DALLERY Y, DAVID R, XIE X L. Approximate analysis of transfer lines with unreliable machines and finite buffers[J]. IEEE Transactions on Automatic Control, 1989, 34(9): 943 DOI:10.1109/9.35807 |
| [10] |
TAN B, GERSHWIN S B. Analysis of a general Markovian two-stage continuous-flow production system with a finite buffer[J]. International Journal of Production Economics, 2009, 120(2): 327 DOI:10.1016/j.ijpe.2008.05.022 |
| [11] |
刘雪梅, 贾勇琪, 祁国栋, 等. 多失效模式混联生产线生产率估算[J]. 同济大学学报(自然科学版), 2017, 45(2): 281 LIU Xuemei, JIA Yongqi, Qi Guodong, et al. Production rate estimation of series-parallel production line with multiple failure modes[J]. Journal of Tongji University(Natural Science), 2017, 45(2): 281 |
| [12] |
LI Jingshan, BLUMENFELD D E, HUANG Ningjian, et al. Throughput analysis of production systems: Recent advances and future topics[J]. International Journal of Production Research, 2009, 47(14): 3823 DOI:10.1080/00207540701829752 |
| [13] |
TOLIO T, MATTA A, Jovane F. A method for performance evaluation of automated flow lines[J]. CIRP Annals - Manufacturing Technology, 1998, 47(1): 373 DOI:10.1016/S0007-8506(07)62854-6 |
 2019, Vol. 47
2019, Vol. 47
