2. 上海市金融信息技术研究重点实验室,上海 200433;
3. 应用数学福建省高校重点实验室(莆田学院),福建 莆田 351100;
4. 上海财经大学 信息管理与工程学院,上海 200433
2. Shanghai Key Laboratory of Financial Information Technology, Shanghai 200433, China;
3. Key Laboratory of Applied Mathematics, Fujian Province University (Putian University), Putian 351100, China;
4. School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai 200433, China
波动率是金融资产最重要的特征之一,特别是在定价中起决定因素.波动率通常定义为标的资产投资回报率的标准差,通常用来度量标的资产的风险或者不确定性.经典的Black-Scholes模型假设波动率是常数,这与实际金融市场得到的数据不一致.金融实证研究表明:波动率最显著的一个特点就是具有“微笑”或者偏斜的曲线[1].此外,除了具有“微笑”曲线外,人们还发现波动率具有集聚性与时变性,分布呈尖峰厚尾性,还具有杠杆效应、日历效益效应等特性[2].针对市场波动率的这些特性,研究者们提出了一系列随机波动率模型来改进Black-Scholes模型,期望更好地刻画随机波动率特征.估量波动性的模型在过去的半个世纪里成为计量经济学和实证金融学中较为活跃的研究领域之一.概括起来主流的随机波动率模型主要有两类,一类是连续时间的随机波动率模型(SV模型),一类是离散时间的随机波动率模型(GARCH模型).这两类模型被认为是最集中反映全球金融数据时间序列方差波动特点的模型,也是研究现代经济计量学的一个重点.在金融实务操作中,交易都是离散进行的,GARCH模型描述离散时间经济情形,更能反映实务中股票价格运行的实际情况.
GARCH模型是将波动率视为过去信息集的函数,是Bollerslev[3]在Engle[4]在ARCH模型基础上发展起来的.GARCH模型考虑了扰动项的滞后值和扰动项条件方差的滞后值,克服了ARCH模型无法反映波动率的持续性以及不能保证参数非负的缺点,被广泛用于描述金融市场上资产收益的波动变化.1987年,Bollerslev在考虑分布有偏和放宽假设的前提下,使用t分布代替正态分布描述时间序列的偏度和峰度问题,建立了AGARCH模型[4].基于这些研究,考虑到该模型的应用性和扩展性,此后20多年,许多学者针对不同问题构建出多种变形模型,构成GARCH族模型,使条件异方差结构得到完善的诠释.例如,Robert等为解决高风险高收益问题,将风险加入收益方程,建立了MGARCH模型[5].针对冲击非对称效应,Nelson提出了指数模型EGARCH[6], Zakoian提出了门限模型TGARCH[7].大量实证证明GARCH模型对金融时间序列有较好的描述,它充分体现了金融数据的特征,这些GARCH族模型的应用与实证领域双向作用,使得模型在分析波动性和表征宏观、金融高频数据等方面体现出巨大的价值和意义.
GARCH模型描述的是离散时间经济情形,在进行产品定价研究时,不能象连续时间经济情形那样,可以建立期权价格满足的偏微分方程,所以,Monte Carlo模拟方法被普遍用来解决GARCH模型下金融产品的计算问题.Duan等[8]在1995年第一次提出了一个在GARCH模型框架下欧式期权定价的完整理论,运用均衡定价原理证明了当投资者的效用函数满足一定的条件时,就存在一个满足局部风险中性定价关系的概率测度Q,用传统的Monte Carlo模拟算法计算了GARCH模型欧式期权的定价问题[8-9];邵斌和丁娟研究了GARCH模型下美式亚式期权价值的Monte Carlo模拟算法,在Longstaff等的美式期权定价的最小二乘算法的基础上,开发了GARCH模型下美式亚式期权定价的最小二乘模拟算法[10].
波动率衍生产品是一类基于波动率远期水平的特殊金融衍生品,主要代表是方差互换.波动率衍生产品是在1998年经济危机之后顺时而出的产品,它代表了一种新的交易思路——交易波动率,是现今金融工程的热门方向,也是研究的前沿,它的出现为国际资本市场的拓展和融资技术的创新带来了巨大的变化,衍生出了方差和波动率互换市场.1998年,市场开始出现股票指数波动率互换和波动率变动互换的交易;同年,德国出现了波动率指数期货的交易;2001年,基于Nasdaq-100期权的纳斯达克波动率指数(VXN)波动率指数被开发出来;2003年,基于SP500期权的新VIX波动率指数被开发出来;2004年,VIX波动率指数期货与波动率指数变动期货开始交易;2008年,VIX波动率指数期权开始交易.交易波动率除了将不同市场连接起来,同时对于整个资本市场也存在重大的意义,这代表了一种新的研究方向.国内,目前关于波动率衍生产品的关注度也越来越高,上海期货所和上海纽约大学就波动率衍生产品的运用与交易策略已展开多次高层论坛,上海纽约大学专门成立波动研究所(V-Lab),通过对各类金融资产的波动性、相关度及其他风险维度的实时度量、建模和预测,为学界、业界及监管和决策部门提供实时的市场动态资讯及分析,为日后波动率产品的推行做准备.所以,关于波动率及波动率产品的定价和风险管理研究有着重要的现实意义.
方差互换是一种合约,且是期限较长的.买方取得的利润取决于实际资产指数波动率减去敲定波动率,以上各项均应该在与签订方的合约中有限制,包括限定期限等.在合约到期时签订方的偿付额为名义本金与此差值的乘积,即
| $ P = M \cdot \left( {{\sigma ^2} - {K^2}} \right) $ |
式中:M是名义本金;σ2是事实资产指数的方差;K2是方差互换中的敲定方差.
关于波动率衍生产品的定价研究,前人研究思路主要有2个方面:一个方面是在着重刻画产品的性质特征上,如文献[11-12],以期权定价理论为基础,通过一系列标准期权的组合来复制相应的互换[11-12].另一方面是在某些特殊条件下,研究产品价格的半解析解,如文献[13-15],但求半解析解的过程亦是一复杂的数值过程.Ma等[16]使用Monte Carlo技术研究了连续型
Hull-White随机波动率模型下波动率衍生产品的定价问题.
本文着重研究GARCH随机波动率模型下金融衍生产品的加速模拟定价问题,并以方差衍生产品的定价问题为例.
1 Monte Carlo方法及控制变量技术Monte Carlo方法是以概率论为基础,通过计算机生成符合一定概率分布随机数的一种数值计算方法.当要求解的问题是某一事件的概率,或某个随机变量的数学期望时,可以利用Monte Carlo方法求解,假设要估计随机变量V的期望E(V),利用Monte Carlo法,根据随机变量V的概率分布得到n次重复抽样V1, V2, …, Vn,它们独立同分布且有有限期望值E(V)和有限方差值σ2, V1, V2, …, Vn的算术平均值V,它是E(V)的无偏估计值,即
| $ P\left( {\mathop {\lim }\limits_{n \to \infty } \bar V = E\left[ V \right]} \right) = 1 $ |
由中心极限定理,可以得到估计值的误差为
| $ P\left( {\left| {\bar V - E\left[ V \right]} \right| < \frac{{{\lambda _\alpha }\sigma }}{{\sqrt n }}} \right) \approx \mathit{\Phi }\left( {{\lambda _\alpha }} \right) = 1 - \alpha $ |
式中:α为显著水平;λα为分位数;Φ(λα)为正态分布分布函数,这表明不等式
如果标准差σ≠0,那么Monte Carlo法的误差为
假设每次仿真的过程中都存在另一个随机变量X,形成一对独立同分布的随机变量(Xj, Vj),且Xj的期望E(X)是已知的,则对任意确定的常数b,第j次重复试验的结果为
| $ {V_j}\left( b \right) = {V_j} - b\left[ {{X_j} - E\left( X \right)} \right] $ |
那么m次模拟之后,期权价格的控制变量估计值为
| $ \bar V\left( b \right) = \frac{1}{m}\sum\limits_{j = 1}^m {\left( {{V_i} - b\left( {{X_i} - E\left( X \right)} \right)} \right)} $ |
可以看到此时随机变量X的估计值与它的期望值的偏差X-E(X)作为控制变量.显然V(b)是产品价格的一个无偏估计且
| $ \begin{array}{*{20}{c}} {{\rm{Var}}\left( {{V_j}\left( b \right)} \right) = {\rm{Var}}\left( V \right) + {b^2}{\rm{Var}}\left( X \right) - }\\ {2b\sqrt {{\rm{Var}}\left( V \right)} \sqrt {{\rm{Var}}\left( X \right)} {\rho _{XV}}} \end{array} $ |
式中:ρXV为变量X与V的相关系数.欲使上式方差达到最小,需要取到一个最优的控制系数
| $ \frac{{{\rm{Var}}\left( {{V_i}\left( {{b^ * }} \right)} \right)}}{{{\rm{Var}}\left( {{V_i}} \right)}} = 1 - \rho _{XV}^2 $ |
关于控制变量技术的方差分解原理及其他几种方差减小理论可参考文献[17].
2 GARCH模型下方差衍生产品的控制变量加速模拟理论 2.1 GARCH随机波动率模型介绍在风险中性测度Q下,资产收益率过程由式(1)给出[8]:
| $ \ln \frac{{{S_{t + 1}}}}{{{S_t}}} = r - \frac{1}{2}\sigma _{t + 1}^2 + {\sigma _{t + 1}}{\varepsilon _{t + 1}} $ | (1) |
式中:r为无风险利率;St表示t时刻的资产价格;St+1为下一个时刻的资产价格.在测度Q下,εt+1|Φt~N(0, 1),即在风险中性测度Q下,εt+1是一个在时间t时的条件分布为标准正态分布的随机变量,因而时间t时资产收益率的条件方差为σt+12,其变化规则满足下面的GARCH过程:
| $ \sigma _t^2 = {\alpha _0} + {\alpha _1}{\left( {{\varepsilon _{t - 1}} - \left( {\lambda + \gamma } \right)} \right)^2}\sigma _{t - 1}^2 + {\beta _1}\sigma _{t - 1}^2 $ |
式中:α0、α1、β1和γ都是GARCH模型中的参数,α0>0, α1>0, β1>0;λ是风险溢价率.
设0=T0 < T1 < … < TN=T是[0, T]上的N个观察日,记Si=STi是第i个观察日的收盘价, Kstrike2表示敲定方差,该金融衍生产品的到期收益函数也为
| $ \begin{array}{*{20}{c}} {V\left( {{S_T}, T} \right) = M \times \left( {\sum\limits_{i = 1}^N {{{\left( {\ln \frac{{{S_i}}}{{{S_{i - 1}}}}} \right)}^2}} - K_{{\rm{strike}}}^2} \right) \buildrel \Delta \over = }\\ {h\left( {{S_0}, {S_1}, \cdots , {S_N}} \right)} \end{array} $ |
产品的收益函数记为h(S0, S1, …, SN),产品的发行时刻价格为
| $ V\left( {{S_0}, 0} \right) = E\left[ {{{\rm{e}}^{ - rT}}h\left( {{S_0}, {S_1}, \cdots , {S_N}} \right)} \right] $ |
方差衍生产品的定价属于高维的路径依赖型问题,而在GARCH模型下,此类路径依赖问题的解析表达式很难得到,一般情况下只能用数值估计方法估计,若用有限差分方法或者二叉树方法直接求解,计算量极大,因此考虑用Monte Carlo加速模拟技术来研究此定价问题.
2.2 Black-Scholes框架下方差互换产品价格的解析解考虑使用Black-Scholes框架下的辅助方差互换产品,标的资产价格过程服从下面的扩散过程:
| $ \frac{{{\rm{d}}{S_{\rm{t}}}}}{{{S_{\rm{t}}}}} = r{\rm{d}}t + {\sigma _{\rm{c}}}{\rm{d}}{B_{\rm{t}}} $ | (2) |
式中:σc为波动率常数;Bt为标准布朗运动.
记此时产品的价格为W=W(S, t), 到期日的收益函数仍为h(S0,S1,…, SN),使用概率论方法求其解析解.因为
| $ {S_{{T_i}}} = {S_{{T_{i - 1}}}}\exp \left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right)\Delta {T_i} + {\sigma _{\rm{c}}}\sqrt {\Delta {T_i}} {X_i} $ |
式中:Xi~N(0, 1),i=1, 2, …, N,且Xi和Yj相互独立,所以
| $ \begin{array}{l} h\left( {{S_0}, {S_1}, \cdots , {S_N}} \right) = h\left( {{S_0}, {S_0}{{\rm{e}}^{\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right){T_1} + {\sigma _{\rm{c}}}\sqrt {{T_1}} {X_1}}}, } \right.\\ \left. { \cdots , {S_0}{{\rm{e}}^{\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right){T_N} + {\sigma _{\rm{c}}}\sqrt {{T_N}} {X_N}}}} \right) \end{array} $ |
则
| $ \begin{array}{l} W\left( {{S_0}, 0} \right) = E\left[ {{e^{ - rT}}h\left( {{S_0}, {S_1}, \cdots , {S_N}} \right)} \right] = \\ \int { \cdots \int {h\left( {{S_0}, {S_0}{{\rm{e}}^{\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right){T_1} + {\sigma _{\rm{c}}}\sqrt {{T_1}} {X_1}}}, \cdots , } \right.} } \\ \left. {{S_0}{{\rm{e}}^{\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right){T_N} + {\sigma _{\rm{c}}}\sqrt {{T_N}} {X_N}}}} \right) \cdot \\ {\left( {\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} }}} \right)^N}{{\rm{e}}^{ - \frac{{x_1^2 + x_2^2 + \cdots + x_N^2}}{2}}}{\rm{d}}{x_1}{\rm{d}}{x_2} \cdots {\rm{d}}{x_N} \end{array} $ |
将收益函数h(S0,S1,…, SN)的表达式代入上式即可求出解析解为
| $ \begin{array}{l} W\left( {{S_0}, 0} \right) = {{\rm{e}}^{ - rT}}M\left[ {\sigma _{\rm{c}}^2{\rm{T}} + \left( {{r^2} - r\sigma _{\rm{c}}^2 + \frac{1}{4}\sigma _{\rm{c}}^4} \right)\sum\limits_{i = 1}^N {\Delta t_i^2} - } \right.\\ \left. {K_{{\rm{Var}}}^2} \right]. \end{array} $ |
将上述Black-Scholes框架下的辅助方差互换产品的价格作为控制变量来求解GARCH随机波动率模型下方差互换的价格.控制变量Monte Carlo加速模拟算法如下.
(1) 步骤1。n等分时间段[0, T],等分间隔
| $ \left\{ \begin{array}{l} {S_{\left( 1 \right)}}\left( {{t_{i + 1}}} \right) = {S_{\left( 1 \right)}}\left( {{t_i}} \right){{\rm{e}}^{\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right)\Delta t + {\sigma _{\rm{c}}}\sqrt {{\Delta _t}} {\varepsilon _{1, i}}}}\\ {S_{\left( 1 \right)}}\left( {{t_0}} \right) = {S_0} \end{array} \right. $ | (3) |
式中:ε1, i是符合标准正态分布的随机数,每个间隔点产生一个,这样就可以模拟出基于常数波动率下方差互换产品价格的一条路径j.
(2) 步骤2.运用方差互换产品定价模型和步骤1中模拟路径j, 可求出控制变量在零时刻的价格为
| $ {X_j} = M{{\rm{e}}^{ - rT}}\left[ {\frac{1}{T}\sum\limits_{i = 1}^N {{{\left( {\ln \frac{{{S_{1, j}}\left( {{t_i}} \right)}}{{{S_{1, j}}\left( {{t_{i - 1}}} \right)}}} \right)}^2}} - K_{{\rm{Var}}}^2} \right] $ | (4) |
(3) 步骤3.n等分时间段[0, T],基于GARCH模型的收益率变化过程(在于步骤1中相同的随机序列ε1下生成),有式(5):
| $ \left\{ \begin{array}{l} {S_{\left( 2 \right)}}\left( {{t_{i + 1}}} \right) = {S_{\left( 2 \right)}}\left( {{t_i}} \right){{\rm{e}}^{\left( {r - \frac{1}{2}{\sigma ^2}\left( {{t_i}} \right)} \right)\Delta t + \sigma \left( {{t_i}} \right)\sqrt {\Delta t} {\varepsilon _{1, i}}}}\\ {S_{\left( 2 \right)}}\left( {{t_0}} \right) = {S_0} \end{array} \right. $ | (5) |
式中的波动率σ(ti)满足式(6):
| $ \sigma _{i + 1}^2 = {\alpha _0} + {\alpha _1}{\left( {{\varepsilon _{2, i}} - \left( {\lambda + \gamma } \right)} \right)^2}\sigma _i^2 + \beta \sigma _i^2 $ | (6) |
式中:ε2, i取为一个与ε1, i相互独立的服从标准正态分布的随机变量.这样便可以模拟出基于GARCH模型下方差互换产品价格的另一条路径.
(4) 步骤4.运用方差互换产品定价模型和步骤3中模拟的路径推导出方差互换产品初始时刻价格为
| $ V\left( {{S_0}, 0} \right) = M{{\rm{e}}^{ - rT}}\left[ {\sum\limits_{i = 1}^N {{{\left( {\ln \frac{{{S_{\left( 2 \right)i}}}}{{{S_{\left( 2 \right)i - 1}}}}} \right)}^2}} - K_{{\rm{Var}}}^2} \right] $ |
(5) 步骤5.计算V(b)=V-b(X-E(X)),b为一个可以估计出的常数,其中E(X)由下式给出:
| $ \begin{array}{*{20}{c}} {W\left( {{S_0}, 0} \right) = {{\rm{e}}^{ - rT}}M\left[ {\sigma _{\rm{c}}^2T + \left( {{r^2} - r\sigma _{\rm{c}}^2 + } \right.} \right.}\\ {\left. {\left. {\frac{1}{4}\sigma _{\rm{c}}^4} \right)\sum\limits_{i = 1}^N {\Delta t_i^2 - K_{{\rm{Var}}}^2} } \right]} \end{array} $ |
(6) 步骤6.模拟m次(重复步骤1至5 m次),并对每一次模拟所得的V(b)取平均得到GARCH模型下方差互换产品价格的控制变量估计为
| $ \bar V\left( b \right) = \frac{1}{m}\sum\limits_{j = 1}^m {{V_j}\left( b \right)} = \bar V - b\left( {\bar X - E\left( X \right)} \right) $ | (7) |
其中最优系数b*可用样本点估计.
| $ {b^ * } \approx {{\hat b}_m} = \sum\limits_{j = 1}^m {\left( {{V_j} - \bar V} \right)\left( {{X_j} - \bar X} \right)} {\left[ {\sum\limits_{j = 1}^m {{{\left( {{X_j} - \bar X} \right)}^2}} } \right]^{ - 1}} $ |
该Monte Carlo控制变量算法的误差减小效果关键在于要使控制变量与所求GARCH问题模型具有较高的相关性ρXV.加速的效果用2种算法的误差减小倍数R来衡量.
| $ R = \frac{1}{{\sqrt {1 - \rho _{XV}^2} }} $ |
数值结果表明:控制变量技术的加速效果高度依赖于模型参数σc的选取,σc选取的不同,误差减小效果差别很大.图 1描述了R与不同的波动率常数的关系.
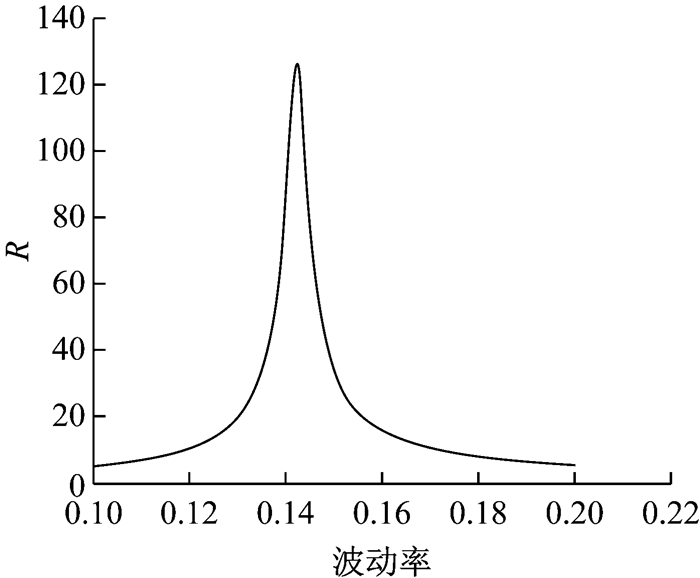
|
图 1 R与波动率的关系(N=1, m=5 000) Fig.1 Relation between the ratio and control variate parameter σc(N=1, m=5 000) |
如何选取高效有代表性的常数波动率σc是该控制变量算法设计的关键问题,使模拟的效果能达到最好.通过对GARCH离散标的过程和Black- Scholes连续标的资产过程的一阶矩和二阶矩的分析,得到下面定理.
定理1 当波动率常数满足
| $ {\sigma _{\rm{c}}} = E\left( {\sigma \left( {{t_{i, j}}} \right)} \right) = \frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {\sigma \left( {{t_{i, j}}} \right)} } $ |
时,过程(3)与(5)所描述的两股票价格的前两阶矩在T时刻近似相等, 其中,σ(ti, j)表示第i条路径上tj时刻对应的波动率.
证明 考虑对[0,T]时间段进行n等分,
若X~N(μ, σ2),则
| $ \begin{array}{*{20}{c}} {E\left( {{{\rm{e}}^X}} \right) = {{\rm{e}}^{\mu + \frac{{{\sigma ^2}}}{2}}}}\\ {{\rm{Var}}\left( {{{\rm{e}}^X}} \right) = \left( {{{\rm{e}}^{{\sigma ^2}}} - 1} \right){{\rm{e}}^{2\mu + {\sigma ^2}}}} \end{array} $ |
所以,对于过程(3)有
| $ \begin{array}{l} E\left( {{S_{\left( 1 \right)T}}} \right) = E\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right)\Delta t + {\sigma _{\rm{c}}}\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}}{{\rm{e}}^{ - \frac{1}{2}\sigma _{\rm{c}}^2T}}E\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n {{\sigma _{\rm{c}}}\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}}{{\rm{e}}^{ - \frac{1}{2}\sigma _{\rm{c}}^2T}}{{\rm{e}}^{\frac{1}{2}\sigma _{\rm{c}}^2T}} = {S_0}{{\rm{e}}^{rT}} \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 1 \right)T}}} \right) = {\rm{Var}}\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}\sigma _{\rm{c}}^2} \right)\Delta t + {\sigma _{\rm{c}}}\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;S_0^2{{\rm{e}}^{2rT}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n {{\sigma _{\rm{c}}}\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;S_0^2{{\rm{e}}^{2rT}}\left( {{{\rm{e}}^{\sigma _{\rm{c}}^2T}} - 1} \right) \end{array} $ |
对于过程(5)有
| $ \begin{array}{l} E\left( {{S_{\left( 2 \right)T}}} \right) = E\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}{\sigma ^2}\left( {{t_i}} \right)} \right)\Delta t + \sigma \left( {{t_i}} \right)\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}}E\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n {\left. { - \frac{1}{2}{\sigma ^2}\left( {{t_i}} \right)} \right)\Delta t + \sigma \left( {{t_i}} \right)\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 2 \right)T}}} \right) = {\rm{Var}}\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}{\sigma ^2}\left( {{t_i}} \right)} \right)\Delta t + \sigma \left( {{t_i}} \right)\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2rT}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n { - \frac{1}{2}{\sigma ^2}\left( {{t_i}} \right)\Delta t + {\sigma _{\rm{c}}}\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) \end{array} $ |
如果
| $ {\sigma ^ * } = E\left( {\sigma \left( {{t_{i, j}}} \right)} \right) = \frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sigma \left( {{t_{i, j}}} \right)} } $ |
则有
| $ \begin{array}{l} E\left( {{S_{\left( 2 \right)T}}} \right) = E\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}{{\left( {{\sigma ^ * }} \right)}^2}} \right)\Delta t + {\sigma ^ * }\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}}{{\rm{e}}^{ - {{\left( {{\sigma ^ * }} \right)}^2}T}}E\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n {{\sigma ^ * }\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}}{{\rm{e}}^{ - {{\left( {{\sigma ^ * }} \right)}^2}T}}{{\rm{e}}^{{{\left( {{\sigma ^ * }} \right)}^2}T}} = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{rT}} = E\left( {S_T^{\left( 1 \right)}} \right) \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 2 \right)T}}} \right) = {\rm{Var}}\left( {{S_0}{{\rm{e}}^{\sum\limits_{i = 1}^n {\left( {r - \frac{1}{2}{{\left( {{\sigma ^ * }} \right)}^2}} \right)\Delta t + {\sigma ^ * }\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2rT}}{{\rm{e}}^{ - {{\left( {{\sigma ^ * }} \right)}^2}T}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{i = 1}^n {{\sigma ^ * }\sqrt {\Delta t} {\varepsilon _{1, i}}} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2rT}}\left( {{{\rm{e}}^{{{\left( {{\sigma ^ * }} \right)}^2}T}} - 1} \right) \end{array} $ |
即当σc2=(σ*)2时有
| $ \left\{ \begin{array}{l} E\left( {{S_{\left( 1 \right)T}}} \right) = E\left( {{S_{\left( 2 \right)T}}} \right)\\ {\rm{Var}}\left( {{S_{\left( 1 \right)T}}} \right) = {\rm{Var}}\left( {{S_{\left( 2 \right)T}}} \right) \end{array} \right. $ |
把满足上面结论的σc所确定的控制变量视为“最优控制”,对应的控制变量估计作为GARCH模型下方差互换产品的价格,此时的误差作为控制变量算法的误差.
3 数值计算模拟结果对算控制变量算法进行数值实现,并验证定理1的最优化结果:即在σc的一个局部区域进行搜索,搜索出满足最优化问题
| $ \mathop {\max }\limits_{{\sigma _{\rm{c}}}} \left\{ {\frac{{{\rm{Var}}\left[ {{V_j}} \right]}}{{\mathop {\min }\limits_b \left\{ {{\rm{Var}}\left[ {{V_j}\left( b \right)} \right]} \right\}}}} \right\} $ |
的最优的常数波动率σc*,比较σc*与定理1所确定的σc,其中b*=
根据方差互换的条款以及GARCH期权定价模型,取下列参数值进行数值实验:M=1 000, r=0.05,n=1 000,T=1,S0=10,σ02=Y0=0.152,α0=0.01,α1=0.005,β1=0.5,λ=0.04,γ=0.3.
由于敲定波动率KVar是一个常数,对实验结果没有影响,所以假设KVar=0;对时间[0, T]做n=1 000次的离散,模拟m次数依次取1 000、2 000、5 000、10 000、15 000、20 000,进行Monte Carlo模拟计算;同时在常数波动率σc附近进行最优化搜索,取最优化搜索区间为[0.15-0.05, 0.15+0.05],以0.000 1为步长,经过最优化搜索,得出一个使误差减小倍数最大时所对应的最优常数波动率σc*,并与定理1计算推导所得的常数波动率进行比较.表 1记录了当观察次数N=1时,由MATLAB软件编程所得的一系列数值分析结果.
| 下载CSV 表 1 N=1时的模拟结果 Tab.1 Simulation results for the case of N=1 |
表中σc1表示由定理1推导所得的常数波动率,σc*表示经最优化搜索后所得的最优常数波动率,V表示模拟出的方差互换产品的价格,Std表示蒙特卡洛模拟的误差,R表示经过控制变量算法模拟加速之后的误差减小倍数,R*表示简单搜索得到的最优波动率对应的模拟误差减小倍数.
由表中数据看出,Monte Carlo控制变量法对于模型的加速效果相当明显,加速后误差减小倍数在126左右,大幅度减小模拟误差;若不使用控制变量法要达到相同的误差减小倍数,模拟次数需要增加到原来的1262倍,所以大幅提高了模拟效率.而随着模拟次数的增加,方差互换产品定价模型的模拟误差逐渐降低,模拟出的标的资产价格V相对稳定(误差小于0.001),这表明Monte Carlo模拟是有效、合理并且稳定的.
关于最优常数波动率的数值分析:σc*与σc1基本相等,相差在0.002左右,差距较小.如当模拟次数m=1 000时,简单搜索得到的最优波动率σc*=0.142 2对应的误差减小倍数为126.234 7,本文推导出的波动率σc1=0.142 4的误差减小倍数为126.542 7,差别很小, 几乎可以忽略不计.因此可以认为经推导得出的常数波动率属于最优常数波动率的范畴.
此外,根据实验模拟结果,还发现了一些其他的结论.如图 2所示为模拟次数m=2 000时方差减小倍数随着常数波动率σc设定值的变化而产生变化的函数图像.可以看到,函数图像是单峰对称分布的,当常数波动率约为0.142 2时,误差减小倍数最大,在对称轴两侧快速递减;当常数波动率以0.142 2为初始点减小或增大时,方差减小倍数下降得很快,常数波动率±0.02的变化引起误差减小倍数下降了100左右.由此可见,在GARCH模型下的方差互换产品定价模型中,用控制变量法进行Monte Carlo模拟时,常数波动率的取值对模拟加速效果影响很大,微小的变化就能使方差减小倍数发生大变,因此在模拟加速时应提升常数波动率取值的精度,提高控制变量法的效率,减小Monte Carlo模拟的模拟误差.
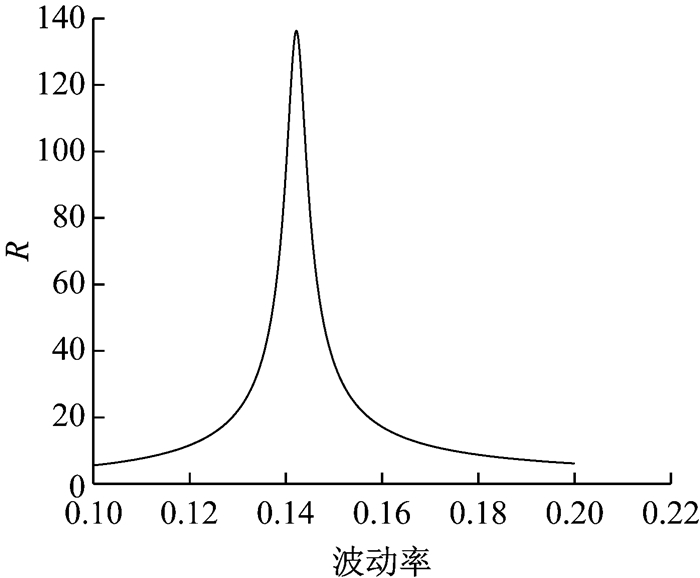
|
图 2 R与波动率的关系(N=1,m=2 000) Fig.2 Relation between R and volatility (N=1, m=2 000) |
为更好进行比较,表 2记录了当观察次数N=10时该Monte Carlo模拟控制变量法的MATLAB数值计算结果.
| 下载CSV 表 2 N=10时的模拟结果 Tab.2 Simulation results for N=10 |
数值实验分析的结果表明:N=10时的模型变化规律与N=1时的模型变化规律基本保持一致,最优波动率均在0.142 2附近取到,且经过推导得出的波动率和最优常数波动率都十分接近,在可接受误差范围内.在N=10时,模拟次数m分别为1 000和2 000时,误差减小与常数波动率取值关系中,和N=1时的情况基本相同,呈单峰对称分布且存在一个最优的常数波动率,使得误差减小倍数达到最大,见图 3.
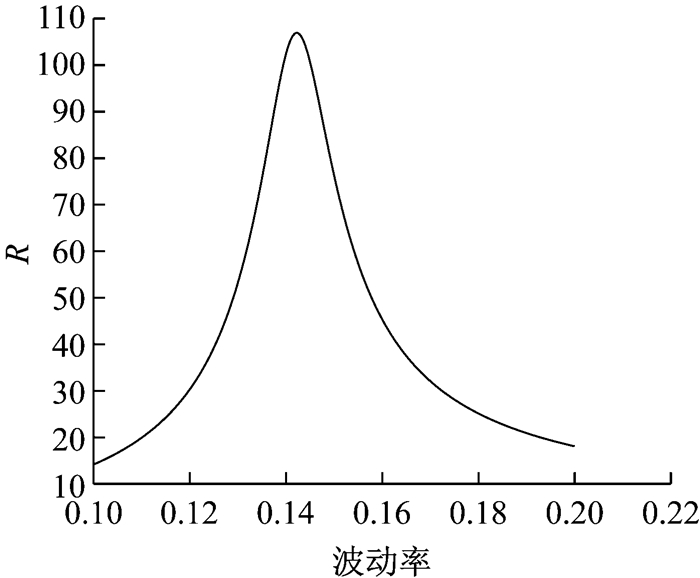
|
图 3 R与波动率关系(N=10,m=2 000) Fig.3 Relation between R and volatility (N=10, m=2 000) |
由上述可见,使用Black-Scholes框架下的确定常数波动率条件下的方差互换的价格作为控制变量,为GARCH模型下的方差互换产品进行加速模拟定价,取得了很好的效果.继续对上述算法进行改进,考虑使用分段常数波动率框架下的产品价格作为控制变量,对原GARCH随机波动率模型下的产品进行加速模拟定价.
考虑式(8)模型:
| $ \frac{{{\rm{d}}{S_{\rm{t}}}}}{{{S_{\rm{t}}}}} = r{\rm{d}}t + {\sigma _{i{\rm{c}}}}{\rm{d}}{B_{\rm{t}}} $ | (8) |
式中:σic为在第i段时间点的波动率常数.同样考虑n等分时间段[0,T],
| $ \left\{ \begin{array}{l} {S_{\left( 1 \right)}}\left( {{t_0}} \right) = {S_0}\\ {S_{\left( 1 \right)}}\left( {{t_{i + 1}}} \right) = {S_{\left( 1 \right)}}\left( {{t_i}} \right){{\rm{e}}^{\sum\limits_{k = i + 1}^{p\left( {i + 1} \right)} {\left( {r - \frac{1}{2}\sigma _{i + 1, {\rm{c}}}^2} \right)\Delta t} }} \cdot \\ \;\;\;\;\;\;{{\rm{e}}^{\sum\limits_{k = i + 1}^{p\left( {i + 1} \right)} {{\sigma _{i + 1, {\rm{c}}}}\sqrt {\Delta t} {\varepsilon _{1, i + 1, k}}} }} \end{array} \right. $ | (9) |
GARCH模型的价格变化过程为
| $ \left\{ \begin{array}{l} {S_{\left( 2 \right)}}\left( {{t_0}} \right) = {S_0}\\ {S_{\left( 2 \right)}}\left( {{t_{i + 1}}} \right) = {S_{\left( 2 \right)}}\left( {{t_i}} \right){{\rm{e}}^{\sum\limits_{k = i + 1}^{p\left( {i + 1} \right)} {\left( {r - \frac{1}{2}{\sigma ^2}\left( {{t_i} + k\Delta t} \right)} \right)\Delta t} }} \cdot \\ \;\;\;\;\;\;{{\rm{e}}^{\sum\limits_{k = i + 1}^{p\left( {i + 1} \right)} {\sigma \left( {{t_i} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, i + 1, k}}} }} \end{array} \right. $ | (10) |
式中:ti表示第i个观测点对应的时刻.
为确保原定价问题与模型(8)下的产品定价问题有较高的相关性,尽量使得两类标的过程(9)和(10)有较高的“相似性”,同样对两类标的过程的一阶矩和二阶矩进行分析,使得它们在任意观测点ti上相等,得到下面的定理.
定理2 当每一段的常数波动率满足
| $ \sigma _{i, {\rm{c}}}^2 = \frac{{{{\left( {E\left( {\sigma \left( {{t_{j, i}}} \right)} \right)} \right)}^2}{t_i} - {{\left( {E\left( {\sigma \left( {{t_{j, i - 1}}} \right)} \right)} \right)}^2}{t_{i - 1}}}}{{{t_i} - {t_{i - 1}}}} $ |
时,可以保证过程(9)和(10)在N个观测点{t1, t2, …, tN}的前两阶矩相等.其中σ(tj, i)表示过程(10)的第j条路径上0~ti之间所有时刻对应的波动率,且
| $ E\left( {\sigma \left( {{t_{j, i}}} \right)} \right) = \frac{1}{{m \times ip}}\sum\limits_{j = 1}^m {\sum\limits_{k = 1}^{ip} {\sigma \left( {{t_0} + k\Delta t} \right)} } $ |
证明 现证明过程(9)与(10)在每一个观测点的一阶矩和二阶矩相等,即期望与方差相等.
因为,若X~N(μ, σ2),则
| $ \begin{array}{*{20}{c}} {E\left( {{{\rm{e}}^X}} \right) = {{\rm{e}}^{\mu + \frac{{{\sigma ^2}}}{2}}}}\\ {{\rm{Var}}\left( {{{\rm{e}}^X}} \right) = \left( {{{\rm{e}}^{{\sigma ^2}}} - 1} \right){{\rm{e}}^{2\mu + {\sigma ^2}}}} \end{array} $ |
在观测点t1, 过程(9)的前两阶矩为
| $ \begin{array}{l} E\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right) = E\left( {{S_0}{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {r - \frac{1}{2}{{\left( {\sigma _{1, {\rm{c}}}^2} \right)}^2}} \right)\Delta t} + \sum\limits_{k = 1}^p {\left( {\sigma _{1, {\rm{c}}}^2\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ {S_0}{{\rm{e}}^{r{t_1}}}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}\sigma _{1, {\rm{c}}}^2} \right)\Delta t} + \sum\limits_{k = 1}^p {\left( {\sigma _{1, {\rm{c}}}^2\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ {S_0}{{\rm{e}}^{r{t_2}}}E\left( {{{\rm{e}}^{ - \frac{1}{2}\sigma _{1, {\rm{c}}}^2{t_1} + {\sigma _{1, {\rm{c}}}}\sqrt {\Delta t} \sum\limits_{k = 1}^p {\left( {{\varepsilon _{1, 1, k}}} \right)} }}} \right) \end{array} $ |
因为ε1, i, k~N(0, 1),所以
| $ \begin{array}{l} E\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right) = {S_0}{{\rm{e}}^{r{t_1}}}E\left( {{{\rm{e}}^{ - \frac{1}{2}\sigma _{1, {\rm{c}}}^2 + {\sigma _{1, {\rm{c}}}}\sqrt {\Delta t} \sum\limits_{k = 1}^p {\left( {{\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_1}}}{{\rm{e}}^{ - \frac{1}{2}\sigma _{1, {\rm{c}}}^2{t_1}}}{{\rm{e}}^{\frac{1}{2}\sigma _{1, {\rm{c}}}^2{t_1}}} = {S_0}{{\rm{e}}^{r{t_1}}} \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right) = \\ \;\;\;\;\;\;\;{\rm{Var}}\left( {{S_0}{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {r - \frac{1}{2}{{\left( {\sigma _{1, {\rm{c}}}^2} \right)}^2}} \right)\Delta t} + \sum\limits_{k = 2}^p {\left( {\sigma _{1, {\rm{c}}}^2\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}\sigma _{1, {\rm{c}}}^2} \right)\Delta t} + \sum\limits_{k = 1}^p {\left( {\sigma _{1, {\rm{c}}}^2\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{{\rm{e}}^{ - \sigma _{1, {\rm{c}}}^2{t_1}}}{\rm{Var}}\left( {{{\rm{e}}^{{\sigma _{1, {\rm{c}}}}\sqrt {\Delta t} \sum\limits_{k = 1}^p {\left( {{\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{{\rm{e}}^{ - \sigma _{1, {\rm{c}}}^2{t_1}}}{{\rm{e}}^{\sigma _{1, {\rm{c}}}^2{t_1}}}\left( {{{\rm{e}}^{\sigma _{1, {\rm{c}}}^2{t_1}}} - 1} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}\left( {{{\rm{e}}^{\sigma _{1, {\rm{c}}}^2{t_1}}} - 1} \right) \end{array} $ |
在观测点t1, 过程(10)的两阶矩为
| $ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = E\left( {{S_0}{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {r - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {r\Delta t} + \sum\limits_{k = 1}^p {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_1}}}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}\sigma \left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{e^{\sum\limits_{k = 1}^p {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = S_0^2{{\rm{e}}^{2r{t_1}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) \end{array} $ |
如果期望
| $ E\left( {\sigma \left( {{t_{0, 1}}} \right)} \right) = \frac{1}{p}\sum\limits_{k = 1}^p {\sigma \left( {{t_0}\left| {k\Delta t} \right.} \right)} $ |
此时有
| $ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = {S_0}{{\rm{e}}^{r{t_1}}}E\left( {{{\rm{e}}^{ - \frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)\sqrt {\Delta t} \sum\limits_{k = 1}^p {{\varepsilon _{1, 1, k}}} }}} \right) = \\ \;\;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_1}}}{{\rm{e}}^{ - \frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}}}{{\rm{e}}^{\frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}}} = \\ \;\;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_1}}} = E\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right) \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = S_0^2{{\rm{e}}^{2r{t_1}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( { - \frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^p {\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} \right.} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{{\rm{e}}^{ - {{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}}} \cdot \\ \;\;\;\;\;\;\;{\rm{Var}}\left( {{{\rm{e}}^{E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)\sqrt {\Delta t} \sum\limits_{k = 1}^p {{\varepsilon _{1, 1, k}}} }}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}{{\rm{e}}^{ - {{\left( {E\left( {\sigma \left( {{t_{0, 1}}} \right)} \right)} \right)}^2}{t_1}}} \cdot \\ \;\;\;\;\;\;\;{{\rm{e}}^{ - {{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}}}\left( {{{\rm{e}}^{\left. {{{\left( {E\left( {\sigma \left( {{t_{0, 1}}} \right)} \right)} \right)}^2}{t_1} - 1} \right)}}} \right) = \\ \;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_1}}}\left( {{{\rm{e}}^{{{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1} - 1}}} \right) \end{array} $ |
此时,当初始条件相等,且σ1, c-E(σ(tj, 1))时,可以保证
| $ \left\{ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = E\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right)\\ {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_1}} \right)} \right) = {\rm{Var}}\left( {{S_{\left( 1 \right)}}\left( {{t_1}} \right)} \right) \end{array} \right. $ |
同理,考虑观测点t2,有
| $ \left\{ \begin{array}{l} E\left( {{S_{\left( 1 \right)}}\left( {{t_2}} \right)} \right) = {S_0}{{\rm{e}}^{r{t_2}}}\\ {\rm{Var}}\left( {{S_{\left( 1 \right)}}\left( {{t_2}} \right)} \right) = S_0^2{{\rm{e}}^{2r{t_2}}}\left( {{{\rm{e}}^{ - \sigma _{1, {\rm{c}}}^2{t_1} - \sigma _{2, {\rm{c}}}^2\left( {{t_2} - {t_1}} \right)}} - 1} \right) \end{array} \right. $ |
且
| $ \left\{ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = {S_0}{{\rm{e}}^{r{t_2}}}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right)\\ {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = S_0^2{{\rm{e}}^{2r{t_2}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) \end{array} \right. $ |
如果期望
| $ E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right. = \frac{1}{{m \times 2p}}\sum\limits_{j = 1}^m {\sum\limits_{k = 1}^{2p} {\sigma \left( {{t_0} + k\Delta t} \right)} } $ |
此时有
| $ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = {S_0}{{\rm{e}}^{r{t_2}}}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_2}}}E\left( {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( { - \frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;\;{S_0}{{\rm{e}}^{r{t_2}}}{{\rm{e}}^{ - \frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}{t_2}}} \cdot {{\rm{e}}^{\frac{1}{2}{{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}{t_2}}} = {S_0}{{\rm{e}}^{r{t_2}}} \end{array} $ |
| $ \begin{array}{l} {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = S_0^2{{\rm{e}}^{2r{t_2}}}{\rm{Var}}\left( {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( { - \frac{1}{2}{\sigma ^2}\left( {{t_0} + k\Delta t} \right)} \right)\Delta t} }} \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\rm{e}}^{\sum\limits_{k = 1}^{2p} {\left( {\sigma \left( {{t_0} + k\Delta t} \right)\sqrt {\Delta t} {\varepsilon _{1, 1, k}}} \right)} }}} \right) = \\ \;\;\;\;\;\;\;\;S_0^2{{\rm{e}}^{2r{t_2}}}\left( {{{\rm{e}}^{ - {{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}{t_2}}} - 1} \right) \end{array} $ |
当初始条件相等,为了保证在观测点t2时刻前两阶矩相等,即
| $ \left\{ \begin{array}{l} E\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = E\left( {{S_{\left( 1 \right)}}\left( {{t_2}} \right)} \right)\\ {\rm{Var}}\left( {{S_{\left( 2 \right)}}\left( {{t_2}} \right)} \right) = {\rm{Var}}\left( {{S_{\left( 1 \right)}}\left( {{t_2}} \right)} \right) \end{array} \right. $ |
则要求
| $ - \sigma _{1, {\rm{c}}}^2{t_1} - \sigma _{2, {\rm{c}}}^2\left( {{t_2} - {t_1}} \right) = - {\left( {E\left( {\sigma \left( {{t_{0, 2}}} \right)} \right)} \right)^2}{t_2} $ |
即
| $ \begin{array}{*{20}{c}} {\sigma _{2, {\rm{c}}}^2\left( {{t_2} - {t_1}} \right) = {{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}{t_2} - \sigma _{1, {\rm{c}}}^2{t_1} = }\\ {{{\left( {E\left( {\sigma \left( {{t_{j, 2}}} \right)} \right)} \right)}^2}{t_2} - {{\left( {E\left( {\sigma \left( {{t_{j, 1}}} \right)} \right)} \right)}^2}{t_1}} \end{array} $ |
依此类推,继续考虑N个观测点,当满足
| $ \sigma _{i, {\rm{c}}}^2\left( {{t_i} - {t_{i - 1}}} \right) = {\left( {E\left( {\sigma \left( {{t_{j, i}}} \right)} \right)} \right)^2}{t_i} - {\left( {E\left( {\sigma \left( {{t_{j, i - 1}}} \right)} \right)} \right)^2}{t_{i - 1}} $ |
则可以保证在N个观测点的前两阶矩相等.证毕.
再次利用与前文相同的初始条件进行数值模拟,并与常数波动率情形进行对比,另外模拟参数α1=0.005.
在表 3中,σc表示分段最优常数波动率(考虑了分N=2段和N=3段的情况),Rc表示分段最优常数波动率下误差减小倍数(相对于原始的Monte Carlo方法).当m=1 000时,分N=2段的话,求出的两段最优波动率常数为:0.142 4和0.142 2,此时控制变量的误差减小倍数为126.68;同样的,当m=1 000时,分N=3段的话,求出的三段最优波动率常数为:0.142 5,0.142 2和0.142 2,此时控制变量的误差减小倍数为127.27.从表 3的结果比较中可以看出,分段波动率常数情形下的误差减小倍数相比常数波动率情形有一定的改进,但改进的幅度并不是很大.分析其主要原因为:从GARCH模型产生的波动率序列的自相关函数逐渐趋于零,当分段考虑不同的波动率时,随着波动率序列的增多,每一段都相当于一个独立的满足过程,即每一段的序列期望值趋于相等,所以针对GARCH模型考虑分段常数波动率时,相比单个常数波动率情形时效果差别不是很大.
| 下载CSV 表 3 常数波动率与分段常数波动率对比(α1=0.005) Tab.3 Constant volatility vs. piecewise constant volatility variance reduction comparison(α1=0.005) |
通过使用Monte Carlo控制变量法对GARCH模型下的方差互换产品的定价问题进行了模拟,讨论了如何选取一个最优常数波动率.借助Black-Scholes模型下的解,选取控制变量使其与所求变量的相关度尽量高,推导出了一个选取最优常数波动率的公式:
数值分析的结果也表明:利用常数波动率下产品价格符合几何布朗运动的一个衍生品的价格作为控制变量,对GARCH模型下的方差互换产品定价是有成效的,推导出的公式也是合理且符合实际的.并且发现:控制变量模型中常数波动率对方差减小的影响具有鲜明的数学特点,方差减小随常数波动率变化的图像呈单峰对称分布.这也为其他模型下对Monte Carlo控制变量法在期权定价中的运用提供了思路.最后,对常数波动率的情形进行了改进,用分段波动率常数的Black-Scholes模型去近似原GARCH模型,并给出了最优分段常数波动率的选取方法.
| [1] |
RUBINSTEIN M. Nonparametric tests of alternative option pricing models using all reported trades and quotes on the 30 most active CBOE option classes from August 23[J]. The Journal of Finance, 1985, 40(2): 455 |
| [2] |
ANDERSEN L, ANDERSEN J. Jump diffusion processes: Volatility smile fitting and numerical methods for option pricing[J]. Review of Derivatives Research, 2000, 4(3): 231 DOI:10.1023/A:1011354913068 |
| [3] |
BOLLERSLEV T. A conditionally heteroscedastic time series model for speculative prices and rates of return[J]. Review of Economics and Statistics, 1987, 69(3): 542 DOI:10.2307/1925546 |
| [4] |
ENGLE F. Autoregressive conditional heterosceda-sticity with estimates of the variance of United Kingdom inflation[J]. Econometrica: Journal of the Econometric Society, 1982, 50(4): 987 DOI:10.2307/1912773 |
| [5] |
ROBERT E, DAVID L, RUSSELL P. Estimating time varying risk premia in the term structure: The Arch-M model[J]. Econometrica, 1987, 55(2): 391 DOI:10.2307/1913242 |
| [6] |
NELSON B. Conditional heteroskedasticity in asset returns: A new approach[J]. Econometrica, 1991, 59: 347 DOI:10.2307/2938260 |
| [7] |
ZAKOIAN M. Threshold heteroscedastic models[J]. Journal of Economic Dynamics and Control, 1994, 18: 931 DOI:10.1016/0165-1889(94)90039-6 |
| [8] |
DUAN J. The GARCH option pricing model[J]. Mathematical Finance, 1995, 5: 13 DOI:10.1111/mafi.1995.5.issue-1 |
| [9] |
DUAN J, SIMONATO J. Empirical martingale simulation for asset prices[J]. Management Science, 1998, 44: 1218 DOI:10.1287/mnsc.44.9.1218 |
| [10] |
邵斌, 丁娟. GARCH模型中美式亚式期权价值的蒙特卡罗模拟算法[J]. 经济数学, 2004, 2: 141 SHAO Bin, DING Juan. Monte Carlo method for pricing American Asian option under GARCH model[J]. Economic Mathematics, 2004, 2: 141 DOI:10.3969/j.issn.1007-1660.2004.02.008 |
| [11] |
DERMAN E, KAMAL M, ZHOU J, et al. A guide to volatility and variance swaps[J]. The Journal of Derivatives, 1999, 6(4): 9 DOI:10.3905/jod.1999.319129 |
| [12] |
CARR P, LEE R. Robust replication of volatility derivatives.[EB/OL].[2018-03-01].http://www.math.nyu.edu/research/carrp/papers.
|
| [13] |
SWISHCHUK A. Modeling of variance and volatility swaps for financial markets with stochastic volatilities[J].[EB/OL].[2018-05-01].http://math.ucalgary.ca/aswish/StochVolatSwap.pdf.
|
| [14] |
ZHU S, LIAN G. A closed-form exact solution for pricing variance swaps with stochastic volatility[J]. Mathematical Finance, 2011, 21(2): 233 |
| [15] |
ZHU S, LIAN G. Analytically pricing volatility swaps under stochastic volatility[J]. Journal of Computational and Applied Mathematics, 2015, 288(2): 332 |
| [16] |
MA J, XU C. An efficient control variate method for pricing variance derivatives[J]. Journal of Computational and Applied Mathematics, 2010, 235(1): 108 DOI:10.1016/j.cam.2010.05.017 |
| [17] |
GLASSERMAN P. Monte Carlo methods in financial engineering[M].[S.l.]: Springer, 2004.
|
 2019, Vol. 47
2019, Vol. 47
