2. 同济大学 新能源汽车工程中心,上海 201804
2. Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China
随着汽车保有量的持续攀升,道路拥堵、交通事故频发等问题日益突出.融合了人工智能、车联网与环境感知传感器等技术的自动驾驶作为一种有效的应对措施,其研究已得到广泛关注.实现自动驾驶是智能汽车控制的终极目标,自动驾驶主要根据当前道路与交通状况,感知并认知出周边环境及障碍物后,决策出车辆合理的运行路径,跟踪该路径并实现车辆的自动加速、制动、转弯、停车等操作.可见,路径跟踪作为自动驾驶执行层的重要组成部分,其研究对于实现车辆的自动驾驶具有重要意义[1].
在传统汽车路径跟踪控制研究领域,李果等设计了一种能够实现对车辆纵向规律进行自适应学习的纵向运动控制系统,该系统考虑了车辆纵向动力学系统的非线性和不确定性问题[2].侯德藻等采用模糊控制和遗传算法相结合的算法设计了纵向运动控制系统,并构造了一种油门和制动切换逻辑[3].孙振平等设计了基于单点预瞄的比例-积分-微分(proportional integrate differential, PID)横向控制器,针对外界扰动对横向控制器的影响添加了补偿扰动观测器,实现了车辆的良好路径跟踪[4].FALCONE等基于主动前轮转向系统,采用模型预测控制算法(model prediction control, MPC)设计了横向路径跟踪控制器,在实现车辆路径跟踪精确跟踪的同时,保证了车辆的稳定性[5-6].
目前车辆路径跟踪控制大多针对常规内燃汽车,对于混合动力汽车,在转弯路径跟踪的同时也存在不同动力源间的转矩分配问题需要解决.论文针对四驱混合动力轿车,提出一种集成横向与纵向运动控制功能的路径跟踪控制策略,并进行离线仿真与台架试验验证,保证了车辆路径跟踪精度与行驶安全性.
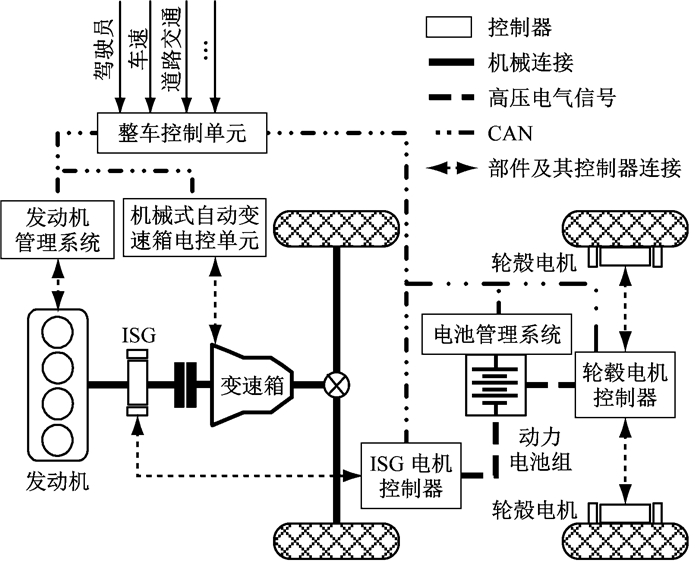
1 四驱混合动力系统及动力学模型 1.1 四驱混合动力系统结构文中研究对象为四驱混合动力轿车,其动力系统配置如图 1所示,在传统内燃发动机基础上,左右后轮各安装轮毂电机及控制器.前轮驱动动力源包括发动机与启动发电一体电机(integrated starter generator, ISG),发动机的输出轴和ISG电机的转子连接,采用并联方式为前轮提供驱动力; 后轴配备的2个轮毂电机直接驱动后轮.其动力传动系统主要包括:离合器、6速变速箱、主减速器、差速器及传动轴.ISG电机和轮毂电机的供电由高压动力蓄电池提供,高压动力蓄电池可通过电机实现充放电.各动力源和执行器都有各自的控制器,与整车控制器通过控制器局域网络(controller area network, CAN)进行通讯.
|
图 1 四驱混合动力轿车动力系统结构 Fig.1 Power system structure of hybrid vehicle |
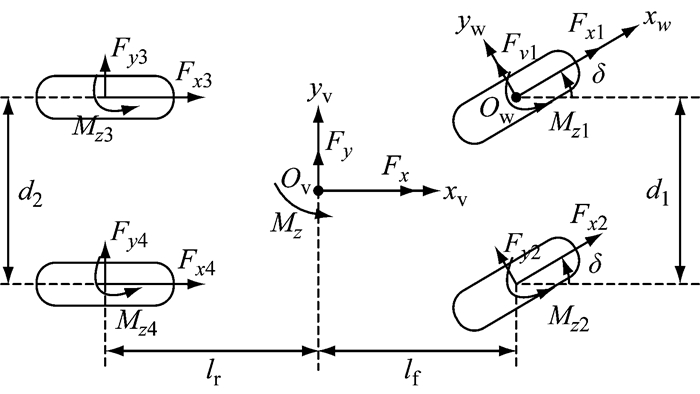
将车身视为刚体,车辆受力分析如图 2所示.根据刚体运动学和动力学原理建立七自由度车辆动力学模型,包括了车身纵向、横向及横摆3个自由度和4个车轮的转动自由度.图 2中, Ovxvyv为车辆坐标系,Owxwyw为车轮坐标系,Fx与Fy分别为车辆纵向与横向力,Mz为车辆横摆力矩.将车体3个方向的合力与力矩代入运动微分方程,整理后得到车体运动的状态方程为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{{\dot v}_x} = \gamma {v_y} + \frac{1}{m}\left[ {\left( {{F_{x1}} + {F_{x2}}} \right)\cos \delta - \left( {{F_{y1}} + } \right.} \right.}\\ {\left. {\left. {{F_{y2}}} \right)\sin \delta + {F_{x3}} + {F_{x4}} - \frac{1}{2}{C_{\rm{d}}}A\rho v_x^2} \right]} \end{array}\\ {{\dot v}_y} = - \gamma {v_x} + \frac{1}{m}\left[ {\left( {{F_{x1}} + {F_{x2}}} \right)\sin \delta + \left( {{F_{y1}} + } \right.} \right.\\ \;\;\;\;{F_{y2}})\cos \delta + {F_{y3}} + {F_{y4}}]\\ \dot \gamma = \frac{1}{{{I_z}}}\left\{ {\left[ {\left( {{F_{x1}} + {F_{x2}}} \right)\sin \delta + \left( {{F_{y1}} + {F_{y2}}} \right)\cos \delta } \right]{l_{\rm{f}}} - } \right.\\ \;\;\;\;\;\;\left( {{F_{y3}} + {F_{y4}}} \right){l_{\rm{r}}} - \left[ {\left( {{F_{x1}} - {F_{x2}}} \right)\cos \delta - } \right.\\ \;\;\;\;\;\;\left( {{F_{y1}} - {F_{y2}}} \right)\sin \delta ]\frac{{{d_1}}}{2} - \left( {{F_{x3}} - {F_{x4}}} \right)\frac{{{d_2}}}{2} + \\ \;\;\;\;\;\;\left. {{M_{z1}} + {M_{z2}} + {M_{z3}} + {M_{z4}}} \right\} \end{array} \right. $ | (1) |
|
图 2 车辆模型 Fig.2 Model of vehicle |
式中:Fxi为各车轮上纵向力; Fyi为各车轮上横向力; Mi为各车轮上回正力矩; lf、lr分别为质心到前、后轴距离; d1、d2分别为前、后轴轮距; Cd为风阻系数; A为车辆横截面面积; ρ为空气密度; δ为前轮转角; Iz为车辆绕z轴转动惯量; vx为车辆纵向速度; vy为车辆横向速度; γ为横摆角速度.
1.3 电池模型电池模型使用常用电路等效模型中的戴维南模型
| $ \begin{array}{*{20}{c}} {{U_{\rm{o}}}\left( t \right) = {V_{\rm{o}}} + {R_0}I\left( t \right) + {U_{\rm{c}}}\left( t \right)}\\ {I\left( t \right) = \frac{{{U_{\rm{c}}}\left( t \right)}}{{{R_1}}} + {C_1}\frac{{{\rm{d}}{U_{\rm{c}}}\left( t \right)}}{{{\rm{d}}t}}} \end{array} $ | (2) |
式中:Vo为输出电压; Uo(t)为电源电动势; I(t)为电流; Uc(t)为极化电压; R0为欧姆内阻; R1为极化内阻; I(t)为电流; C1为极化电容; t为放电时间.
1.4 电机模型四驱混合动力轿车装备的ISG电机和两个轮毂电机皆为永磁同步电机.本文只关注电机的转速转矩输出特性,不考虑电机内部复杂的物理过程和电气过程,利用试验数据查表拟合的方式来表示电机模型.电机实际输出转矩可表示为
| $ {T_{{\rm{r}}1}} = \frac{1}{{1 + {t_1}s}}{T_{{\rm{el}}}} $ | (3) |
| $ T_{\mathrm{r} 2}=\frac{1}{1+t_{2} s} T_{\mathrm{e} 2} $ | (4) |
式中:t1与t2为延时时间常数; Tr1与Tr2分别为ISG电机和轮毂电机扭矩输出; Te1与Te2分别为ISG电机和轮毂电机试验获得的扭矩特性值.
1.5 轮胎模型由于在巡航过程中,自动驾驶车辆存在纵向与横向运动,且危险时可能出现紧急制动.因此,轮胎模型需要综合纵向力与横向力,且考虑轮胎的瞬态特性.本文采用布克哈德轮胎模型,其与大量真实道路试验数据吻合,并可以描述轮胎力非线性摩擦椭圆特性[7].轮胎纵向与横向滑移率为
| $ {s_{x{\rm{i}}}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}} - {v_{\rm{i}}}}}{{{v_{\rm{i}}}}},}&{{v_{\rm{i}}} \ge {\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}}}\\ {\frac{{{\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}} - {v_{\rm{i}}}}}{{{\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}}}},}&{{v_{\rm{i}}} < {\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}}} \end{array}} \right. $ | (5) |
| $ {s_{y{\rm{i}}}} = \left\{ \begin{array}{l} \left( {1 + {s_{x{\rm{i}}}}} \right)\tan {\alpha _{\rm{i}}},\;\;\;\;{v_{\rm{i}}} \ge {\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}}\\ \tan {\alpha _{\rm{i}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{v_{\rm{i}}} < {\omega _{\rm{i}}}{R_{\rm{d}}}\cos {\alpha _{\rm{i}}} \end{array} \right. $ | (6) |
式中:sxi为轮胎纵向滑移率; syi为轮胎横向滑移率; αi为轮胎侧偏角; vi为轮胎中心速度,
上述车辆模型用于本文单点预瞄偏差驾驶员模型开发,同时作为转矩优化的理论基础; 电机模型与轮胎模型一方面用于控制策略开发,另一方面集成于仿真环境内用于控制策略验证.
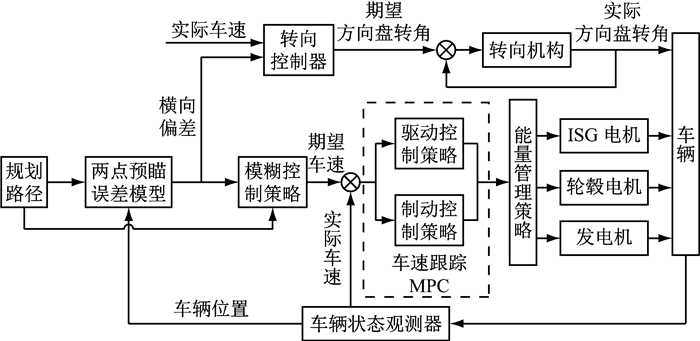
2 路径跟踪控制 2.1 控制系统架构路径跟踪控制系统的架构如图 3所示,车辆在自动驾驶时,通过雷达、摄像头、车车通信、全球定位系统(global positioning system, GPS)等环境感知方式获取交通与车间信息,继而规划出行驶路径.控制系统根据规划路径与车辆当前运行位置的偏差产生期望方向盘转角的同时,综合道路与交通信息产生期望车速.在得到期望车速后,运用模型预测控制设计了车速跟踪控制策略,求解出期望纵向加速度后决策出驾驶员需求驱动力矩或制动力矩,再由能量分配策略将需求转矩分配给各动力源进行实施.
|
图 3 路径跟踪控制系统架构 Fig.3 Control system structure of path tracking |
驾驶员预瞄模型[8]根据自动驾驶时系统规划路径与当前路径的偏差产生转向动作.文中采用的单点驾驶员预瞄模型如图 4所示.其中,OXY为大地坐标系,Cxy为车辆的坐标系,Ld为车辆坐标系下预瞄距离,L为大地坐标系下预瞄距离,f(x)为参考路径,C(XC, YC)、P(XP, YP)分别为车辆质心和预瞄点在OXY坐标系中坐标,

|
图 4 驾驶员预瞄模型 Fig.4 Preview model of driver |
根据图 4中的几何关系,基于运动学关系,得出ye的变化率为
| $ \left. \begin{array}{l} {{\dot y}_{\rm{e}}} = - {v_y} - {L_{\rm{d}}}\gamma + {v_x}{\phi _{\rm{e}}}\\ {{\dot \phi }_{\rm{e}}} = {v_x}\rho - \gamma \end{array} \right\} $ | (7) |
式中:ρ为道路曲率.
2.2.2 前轮转角滑模变结构跟踪控制基于上述路径跟踪偏差,转向控制器决策出期望的车辆前轮转角,控制车辆沿期望路径行驶.由于滑模变结构可以克服参数扰动和不确定因素对车辆行驶稳定性的影响[9],故文中采用其设计转向控制器,求期望的车轮转角δd.
将滑模变结构被控对象表示为
| $ \dot{x}=f(x)+b u+d $ | (8) |
将道路曲率作为外界干扰,d=Wρ,控制输入为车轮转角,即u=δ.
基于滑模变结构的转向控制器以预瞄点P处横向位移误差ye及其变化率
| $ s=\dot{y}_{\mathrm{e}}+\lambda y_{\mathrm{e}} $ | (9) |
式中:λ为滑模参数.
趋近律采用等速趋近率,为减少控制的抖振现象,选用饱和函数g(s)
| $ \dot{s}=-\eta g(s) $ | (10) |
| $ g(s)=\left\{\begin{array}{l}{1, s>\Delta} \\ {k s, s \leqslant|\Delta|, k=1 / \Delta} \\ {-1, s<-\Delta}\end{array}\right. $ | (11) |
式中:η为切换增益; Δ为边界层.
则有
| $ \dot{s}=\ddot{y}_{\mathrm{e}}+\lambda \dot{y}_{\mathrm{e}}=-\eta g(s) $ | (12) |
基于图 4中的几何关系,将预瞄点P在大地坐标系OXY下的位置[XC,YC,
| $ \left[ \begin{array}{l}{x_{\mathrm{e}}} \\ {y_{\mathrm{e}}} \\ {\phi_{\mathrm{e}}}\end{array}\right]=\left[ \begin{array}{ccc}{\cos \phi_{C}} & {\sin \phi_{C}} & {0} \\ {-\sin \phi_{C}} & {\cos \phi_{C}} & {0} \\ {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{l}{X_{P}-X_{C}} \\ {Y_{P}-Y_{C}} \\ {\phi_{P}-\phi_{C}}\end{array}\right] $ | (13) |
结合车辆简化的二自由度模型与式(7)、(13),综合车辆动力学的单点预瞄偏差模型可以表示为
| $ \dot{\boldsymbol{x}}=\boldsymbol{A}_{\mathrm{v}} x+\boldsymbol{B}_{\mathrm{v}} \delta+\boldsymbol{W}_{\rho} $ | (14) |
式中:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{\rm{v}}} = \\ \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&0&0&0\\ {{A_{21}}}&{{A_{22}}}&0&0&0\\ 0&0&1&0&0\\ { - \left( {{A_{11}} + {L_{\rm{d}}}{A_{21}}} \right)}&{ - \left( {{A_{12}} + {L_{\rm{d}}}{A_{22}} + {v_x}} \right)}&0&0&0\\ 0&{ - 1}&0&0&0 \end{array}} \right]; \end{array} $ |
| $ {A_{11}} = \frac{{ - {C_{\rm{f}}} - {C_{\rm{r}}}}}{{m{v_x}}},{A_{12}} = \frac{{b{C_{\rm{r}}} - a{C_{\rm{f}}}}}{{m{v_x}}} - {v_x}; $ |
| $ {A_{21}} = \frac{{b{C_{\rm{r}}} - a{C_{\rm{f}}}}}{{{I_z}{v_x}}},{A_{22}} = - \frac{{{a^2}{C_{\rm{f}}} + {b^2}{C_{\rm{r}}}}}{{{I_z}{v_x}}}; $ |
| $ \boldsymbol{B}_{\mathrm{v}}=\left[ \begin{array}{lll}{B_{1}} & {B_{2}} & {-\left(B_{1}+L_{\mathrm{d}} B_{2}\right)} & {0} & {0}\end{array}\right]^{\mathrm{T}}; $ |
| $ B_{1}=-\frac{C_{\mathrm{f}}}{m}, B_{2}=\frac{a C_{\mathrm{f}}}{I_{z}}; $ |
| $ \boldsymbol{W}=\left[ \begin{array}{lllll}{0} & {0} & {0} & {v_{x}^{2}} & {v_{x}}\end{array}\right]^{\mathrm{T}} $ |
即期望的方向盘转角为
| $ \begin{array}{l} {\delta _{\rm{d}}} = u = - \frac{1}{{{B_1} + {L_{\rm{d}}}{B_2}}}\left[ {\left( {{A_{11}} + {L_{\rm{d}}}{A_{21}} + \lambda } \right){v_y} + } \right.\\ \;\;\;\;\;\;\;\left( {{v_x}\rho - \gamma } \right){v_x} - \lambda {v_x}{\phi _{\rm{e}}} - \eta g(s) + \\ \;\;\;\;\;\;\;\left( {{A_{12}} + {L_{\rm{d}}}{A_{22}} + \lambda {L_{\rm{d}}}} \right)\gamma ] \end{array} $ | (15) |
文中采用基于专家经验的模糊控制器来获取期望车速.模糊控制器的输入量为道路曲率半径和路径跟踪偏差,输出为车辆期望的车速.
当道路曲率较大时,车辆应该降低车速; 道路曲率较小时,车辆应该提高车速; 当路径跟踪偏差较小时,车辆应该提高车速,这样可以使其快速跟踪上给定路径; 当路径跟踪偏差较大时,车辆应该降低车速,给偏差纠正控制留有充足时间.
上述模糊控制器的输入和输出均采用三角形隶属度函数.通过驾驶员操纵驾驶模拟器,收集不同曲率下路径跟踪数据,从而确定隶属度函数参数.模糊推理规则曲面如图 5所示.

|
图 5 模糊推理规则曲面 Fig.5 Rule surface of fuzzy control |
MPC控制方法鲁棒性强,约束处理方便,其在车辆运动控制中已广泛应用[10-11].采用离散形式对车辆纵向运动学特征进行描述,取车辆纵向车速和加速度为系统状态变量,即
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}(k + 1) = {\mathit{\boldsymbol{A}}_{\rm{m}}}\mathit{\boldsymbol{x}}(k) + {\mathit{\boldsymbol{B}}_{\rm{m}}}\mathit{\boldsymbol{u}}(k)}\\ {{\mathit{\boldsymbol{A}}_{\rm{m}}} = \left[ {\begin{array}{*{20}{c}} 1&{{T_{\rm{s}}}}\\ 0&{1 - \frac{{{T_{\rm{s}}}}}{t}} \end{array}} \right],{\mathit{\boldsymbol{B}}_{\rm{m}}} = \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{{T_{\rm{s}}}}}{t}} \end{array}} \right]} \end{array} $ | (16) |
式中:vx为车辆纵向车速; ax为车辆纵向加速度; Ts为采样周期时间; t为下层控制时间常数; u为上层控制算法的输入,即车辆期望加速度.
以速度跟踪误差为观测量
| $ y(k) = \mathit{\boldsymbol{Cx}}(k) - z(k) $ | (17) |
式中:C=[0 1];z表示期望的车速值,即z(k)=vd(k).
基于上述车辆纵向运动学模型的预测模型,对车辆未来状态进行如下预测:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_p}\left( {k + p\left| k \right.} \right) = {{\mathit{\boldsymbol{\bar A}}}_{\rm{m}}}\mathit{\boldsymbol{x}}\left( k \right) + {{\mathit{\boldsymbol{\bar B}}}_{\rm{m}}}\mathit{\boldsymbol{U}}\left( {k + m} \right) + \mathit{\boldsymbol{\bar H}}e\left( k \right)}\\ {{{\mathit{\boldsymbol{\hat Y}}}_p}\left( {k + p\left| k \right.} \right) = \mathit{\boldsymbol{\bar Cx}}\left( k \right) + \mathit{\boldsymbol{\bar DU}}\left( {k + m} \right) + }\\ {\mathit{\boldsymbol{\bar F}}e\left( k \right) - \mathit{\boldsymbol{\bar Z}}} \end{array} $ | (18) |
式中:p为预测时域; m为控制时域,一般存在控制时域不大于预测时域,即
在车辆速度跟随控制中,为了保证速度跟踪动态响应的平顺性,论文采用指数衰减函数φ作为参考轨迹,以速度误差为性能指标,则其参考轨迹可表示为
| $ y_{\mathrm{r}}(k+i)=\varphi^{i} y(k) $ | (19) |
采用二次型优化函数作为滚动优化目标函数,其形式如下:
| $ \begin{array}{*{20}{c}} {J = \sum\limits_{i = 1}^p {{{\left[ {{{\mathit{\boldsymbol{\widehat y}}}_p}(k + i|k) - {y_{\rm{r}}}(k + i|k)} \right]}^{\rm{T}}}} \mathit{\boldsymbol{Q}} \cdot }\\ {\left[ {{{\mathit{\boldsymbol{\widehat y}}}_p}(k + i|k) - {y_{\rm{r}}}(k + i|k)} \right] + }\\ {\sum\limits_{i = 0}^{m - 1} u {{(k + i)}^{\rm{T}}}\mathit{\boldsymbol{R}}u(k + i)} \end{array} $ | (20) |
式中:Q和R为权系数.
在车速跟踪控制中,在保证车速精确跟踪的同时,还将乘坐舒适性考虑进来,故对车辆加速度加以限制,系统的约束可表示为
| $ \left\{\begin{array}{l}{v_{\min } \leqslant v(k) \leqslant v_{\max }} \\ {a_{\min } \leqslant a(k) \leqslant a_{\max }} \\ {u_{\min } \leqslant u(k) \leqslant u_{\max }}\end{array}\right. $ | (21) |
上述MPC算法求解出期望的车辆纵向加速度,而车辆的实际输入为期望的需求驱动力矩和制动力矩,故还需要结合车辆动力学模型进行求解.
驱动工况下存在如下关系:
| $ m{a_x} = \frac{{{i_{\rm{g}}}}}{{{R_{\rm{r}}}}}{T_{\rm{d}}} - {F_x} - \frac{1}{2}{C_{\rm{d}}}A\rho v_x^2 - mg\sin \theta $ | (22) |
制动工况下存在如下关系:
| $ m a_{x}=-\frac{1}{R_{\mathrm{r}}} T_{\mathrm{b}}-F_{x}-\frac{1}{2} C_{\mathrm{d}} A_{\rho} v^{2}-m g \sin \theta $ | (23) |
式中:m为车辆质量; ax为车辆加速度; ig为有效传动比; Rr为车轮有效滚动半径; Td为需求驱动力; Fx为车轮所受纵向力; ρ为空气密度; g为重力加速度; θ为道路坡度角; Tb为需求制动力矩.
4 转弯工况下的转矩优化分配策略 4.1 转矩的分配关系及约束条件在转弯工况中,汽车在转向的同时还具有匀速、制动和加速3种运行状态.本文针对车辆转弯制动情况,对其转矩的分配问题进行优化研究.
转弯制动下转矩优化分配的最终目的是在保证车辆横向稳定性的前提下尽可能满足驾驶员纵向驾驶意图,同时控制耗能最小.在转弯工况车辆稳定性控制中,广义力由轮胎纵向合力Fx和轮胎横向力Fy产生的附加横摆力矩Ma组成.考虑本文采用的直接横摆力矩控制方法以及所研究的四驱混合动力系统结构特点,前轴ISG电机通过半轴与两前轮刚性联结,ISG扭矩调节对车辆横摆运动调节作用基本可以忽略.实际参与车辆动力学稳定性控制的执行器包括2个后轮轮毂电机和4个液压制动器.
车辆高速行驶时,前轮转角较小,因此忽略前轮转角对轮胎纵向力与附加横摆力矩的影响[12],根据车辆动力学方程可得
| $ \left\{\begin{array}{l}{F_{x}=F_{x 1}+F_{x 2}+F_{x 3}+F_{x 4}} \\ {M_{\mathrm{a}}=\frac{l_{\mathrm{w}}}{2}\left(-F_{x 1}+F_{x 2}-F_{x 3}+F_{x 4}\right)}\end{array}\right. $ | (24) |
式中:lw为前后轴等效轮距.
忽略轮胎半径径向变形,可得各轮胎纵向力与电机转矩和液压制动转矩间的关系
| $ \left\{ \begin{array}{l} {F_{x1}} = - {r^{ - 1}}{T_{{\rm{hfl}}}}\\ {F_{x2}} = - {r^{ - 1}}{T_{{\rm{hfr}}}}\\ {F_{x3}} = {r^{ - 1}}\left( {{T_{{\rm{mrl}}}} - {T_{{\rm{hrl}}}}} \right)\\ {F_{x4}} = {r^{ - 1}}\left( {{T_{{\rm{mrr}}}} - {T_{{\rm{hrr}}}}} \right) \end{array} \right. $ | (25) |
式中:Tmrl、Tmrr为各轮毂电机转矩; Thfl、Thfr、Thrl、Thrr为各轮液压制动转矩; r为轮胎半径.
若忽略执行器的动态响应,则转矩指令即为实际执行器转矩u.令u=[Tmrl, Tmrr, Thfl, Thfr, Thrl, Thrr]T,v=[Fx, Ma]T,结合式(24)和(25)可得
| $ \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{Bu}} $ | (26) |
式中:B为效率矩阵,
| $ \boldsymbol{B}=\left[ \begin{array}{ccccc}{\frac{1}{r}} & {\frac{1}{r}} & {-\frac{1}{r}} & {-\frac{1}{r}} & {-\frac{1}{r}} & {-\frac{1}{r}} \\ {-\frac{l_{\mathrm{w}}}{2 r}} & {\frac{l_{\mathrm{w}}}{2 r}} & {\frac{l_{\mathrm{w}}}{2 r}} & {-\frac{l_{\mathrm{w}}}{2 r}} & {\frac{l_{\mathrm{w}}}{2 r}} & {-\frac{l_{\mathrm{w}}}{2 r}}\end{array}\right] $ | (27) |
式(26)即为广义合力分配所需满足的分配关系式.
综合考虑电机及液压执行器能力的约束以及电机优先制动的分配准则,可确定电机和液压制动转矩的约束为
| $ \max \left( {{T_{{\rm{m}}i\_{\rm{min}}}}, - {T_{{\rm{road}}\_i}}} \right) \le {T_{{\rm{m}}i}} \le 0 $ | (28) |
| $ \begin{array}{l} \max \left( {{T_{{\rm{h}}i\_min}}, - {T_{{\rm{road}}\_i}}} \right) - \\ \;\;\;\;\;\;\;\max \left( {{T_{{\rm{m}}i\_\min }}, - {T_{{\rm{road}}\_i}}} \right) \le {T_{{\rm{h}}i}} \le 0 \end{array} $ | (29) |
式中:Tmi为各轮电机转矩; Tmi_min为当前转速下电机的最小制动转矩; Thi为各轮液压转矩; Thi_min为液压制动的最小制动转矩; Troad_i为考虑各轮载荷及路面条件约束的转矩.
4.2 基于加权最小二乘法的转矩分配问题结合转弯工况下车辆稳定性控制需求,本文选择使用加权最小二乘法(weight least square,WLS)来实现转弯工况下执行器转矩的分配,其基本形式如下:
| $ \min J = \left\| {{\mathit{\boldsymbol{W}}_{\rm{v}}}\left( {\mathit{\boldsymbol{Bu}} - {\mathit{\boldsymbol{v}}_{\rm{d}}}} \right)} \right\|_2^2 + \zeta \left\| {{\mathit{\boldsymbol{W}}_{\rm{u}}}\left( {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right)} \right\|_2^2 $ | (30) |
式中:umin≤u≤umax; Wv为广义目标控制力权重矩阵; Wu为执行器权重矩阵; ud为执行器期望达到的控制量;
为了保证广义力跟踪控制目标优先级高于执行器动作最小目标的优先级,ζ权值通常选得很小,故基于WLS的控制分配目标函数可以进行简化
| $ \begin{array}{*{20}{c}} {J = \left\| {{\mathit{\boldsymbol{W}}_{\rm{v}}}\left( {\mathit{\boldsymbol{Bu}} - {\mathit{\boldsymbol{v}}_{\rm{d}}}} \right)} \right\|_2^2 + \zeta \left\| {{\mathit{\boldsymbol{W}}_{\rm{u}}}\left( {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right)} \right\|_2^2 = }\\ {\left\| {\underbrace {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{\rm{v}}}\mathit{\boldsymbol{B}}}\\ {{\zeta ^{\frac{1}{2}}}{\mathit{\boldsymbol{W}}_{\rm{u}}}} \end{array}} \right)}_\mathit{\boldsymbol{A}}\mathit{\boldsymbol{u}} - \underbrace {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{\rm{v}}}\mathit{\boldsymbol{v}}}\\ {{\zeta ^{\frac{1}{2}}}{\mathit{\boldsymbol{W}}_{\rm{u}}}{\mathit{\boldsymbol{u}}_{\rm{d}}}} \end{array}} \right)}_\mathit{\boldsymbol{b}}} \right\|_2^2} \end{array} $ | (31) |
故基于WLS的控制分配问题就可表示为如下形式:
| $ \min \left\| {\mathit{\boldsymbol{Au}} - \mathit{\boldsymbol{b}}} \right\|_2^2 $ | (32) |
式中:umin≤u≤umax.
通过合理选择Wv、ζ值,首先保证广义力跟踪误差最小化,其次力求能量消耗最小,从而满足实际控制需求.
4.3 WLS控制分配问题的求解对于本文所研究的车辆动力学分配问题,积极集法具有计算效率高、保证系统的实时性的优点,故本文采用积极集法来对WLS控制分配问题进行求解运算.
对于一般的二次规划问题如下:
| $ \mathop {\min }\limits_x \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Hx}} + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{x}} $ | (33) |
| $ \begin{array}{*{20}{c}} {{\rm{s}}.{\rm{t}}.\;\;\;{\mathit{\boldsymbol{c}}_i}\left( \mathit{\boldsymbol{x}} \right) = 0,i = 1,2, \cdots ,n}\\ {{g_j}\left( \mathit{\boldsymbol{x}} \right) \ge 0,j = 1,2, \cdots ,m} \end{array} $ |
式中:ci(x)=0,gj(x)≥0分别是二次优化问题对应的等式约束和不等式约束.
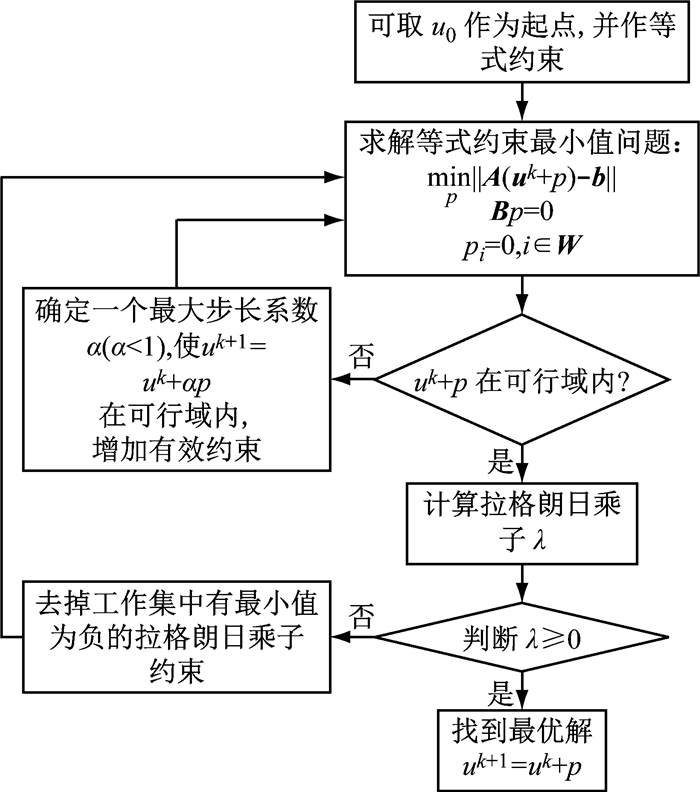
针对本文所讨论的最小二乘求解问题,积极集法流程如图 6所示.
|
图 6 积极集法流程图 Fig.6 Flowchart of active set method |
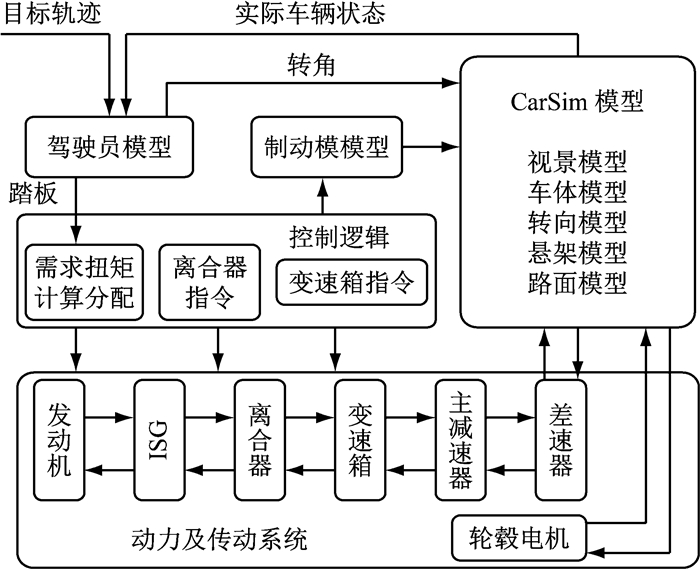
论文采用CarSim-Matlab/Simulink联合建模的方式,在Simulink中搭建车辆动力传动系统、能量分配策略和驾驶员模型等,在CarSim中进行路径跟踪场景的搭建和实时仿真观测.CarSim-Matlab/Simulink联合仿真结构如图 7所示:
|
图 7 CarSim-Matlab/Simulink联合仿真结构图 Fig.7 Co-simulation structure of CarSim-Matlab/Simulink |
为了验证路径跟踪控制策略的有效性,在联合仿真平台上设计路径,对路径跟踪控制进行仿真验证.
5.2 仿真结果路径跟踪控制仿真结果如图 8所示.图 8a为车速变化图,初始时,模糊控制器输出的期望车速为76 km·h-1,在转弯处,模糊控制器输出期望车速分别为50 km·h-1和53.64 km·h-1,车速跟踪整体效果较好,动力系统响应滞后致使车速跟踪存在一定延迟.从图 8b所示路径跟踪误差看出,车辆跟踪精度高,只在弯道处存在较小的横向偏差,且偏差不超过0.1 m.如图 8c与8d所示,车辆加速度整体变化平滑,纵向加速度值总体保持在-2.5~2.0 m·s-2之间变化,保证了乘坐的舒适性.

|
图 8 路径跟踪仿真结果 Fig.8 Result of path tracking simulation |
采用基于CarSim整车模型与视景的自动驾驶模拟器台架进行控制策略验证,台架实物如图 9所示.其主要包括:驾驶员制动与转向输入、助力转向系统(electric power steering, EPS)、稳定性控制系统(electronic stability program, ESP)、雷达、整车模型、实时视景与传感器(方向盘转角、转矩传感器、压力传感器、油门传感器、制动踏板行程等).实时仿真机采用dSPACE公司的MircoAutoBox,实现台架的信号交互.车辆转向由EPS实现,驱动由电子节气门和对托台架实现,制动由ESP液压制动台架实现.

|
图 9 驾驶模拟器 Fig.9 Driving simulator |
台架试验结果如图 10所示,其中图 10a为车辆纵向加速度,实际能够完成对控制器输出跟踪.图 10b、c、d为路径跟踪过程中车辆动力系统响应情况.图 10b为电子节气门响应,节气门实际开度能精确跟踪期望开度,且响应迅速,由于传感器采集精度和测量方式所致,节气门实际开度值存在一定噪声; 图 10c为轮毂电机转矩响应,实际转矩和期望值变化趋势保持一致,且在减速制动过程中,轮毂电机进行了制动能量回收; 图 10d为液压制动系统响应,实际轮缸压力能很好跟踪上目标值,存在一定响应延时,在a车速跟踪减速制动过程中为电液复合制动; 图 10e为车速跟踪,整个过程响应平顺,车辆保持了较好的动力性; 图 10f为路径跟踪误差,由于转向系统存在机械间隙,实际路径跟踪误差保持在±0.25 m之间.台架试验结果对仿真结果进行了验证,试验车速跟踪情况与纵向加速度基本保持一致,路径跟踪误差由于存在间隙而增加0.1 m.

|
图 10 路径跟踪控制驾驶模拟器试验结果 Fig.10 Control strategy validation by simulator |
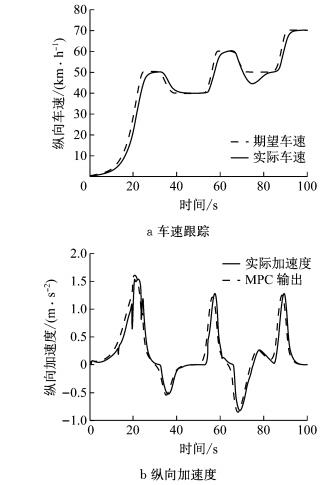
为验证变速箱换挡工况时的车速跟踪情况,将初始速度设置为零,车速跟踪与纵向加速度结果如图 11所示,由于动力系统响应延迟,实际加速度存在一定滞后,总体上能跟上期望加速度,保证了车辆良好的动力输出,整个过程加速度曲线较为平滑,只在挡位变换时存在一定抖动.
|
图 11 换挡路径跟踪控制试验结果 Fig.11 Control strategy validation of shifting |
针对四驱混合动力轿车,在规划路径已知的条件下,研究了其在转弯工况下的路径跟踪控制问题,结论如下:
(1) 基于驾驶员模型设计了滑模变结构转向控制器实现横向路径跟踪,并通过仿真试验证明了其具有良好的跟踪效果.
(2) 根据道路曲率和路径跟踪误差设计了期望车速的模糊控制器,并采用MPC算法实现车速跟踪控制.所提出的基于MPC算法的车辆纵向运动控制,在保证控制目标精确跟踪的同时,通过约束条件兼顾了车辆乘坐舒适性.
(3) 搭建了CarSim-MATLAB/Simulink联合仿真环境,通过仿真验证了提出的控制策略.在硬件在环试验平台对路径跟踪横纵向联合控制算法进行验证,台架试验结果与仿真结果保持了较好的一致性,证明了路径跟踪控制策略的有效性.
| [1] |
RICHARD B. Intelligent vehicle technology and trends[M]. Massachusetts: Artech House Incorporated, 2005
|
| [2] |
李果, 张良起, 张彭, 等. 汽车纵向控制系统的设计与研究[J]. 自动化学报, 1996, 22(5): 582 LI Guo, ZHANG Liangqi, ZHANG Peng, et al. The study and design of the longitudinal control system of automobiles[J]. Acta Automatica Sinica, 1996, 22(5): 582 |
| [3] |
侯德藻, 高锋, 李克强, 等. 基于模型匹配方法的汽车主动避撞下位控制系统的研究[J]. 汽车工程, 2003, 25(4): 399 HOU Dezao, GAO Feng, LI Keqiang, et al. A study on lower layer control of vehicle collision avoidance system with model-match-control method[J]. Automotive Engineering, 2003, 25(4): 399 DOI:10.3321/j.issn:1000-680X.2003.04.022 |
| [4] |
孙振平.自主驾驶汽车智能控制系统[D].长沙: 国防科技大学, 2004. SUN Zhenping. An intelligent control system for autonomous land vehicle[D]. Changsha: National University of Defense Technology, 2004. http://cdmd.cnki.com.cn/Article/CDMD-90002-2005014409.htm |
| [5] |
FALCONE P. Predictive active steering control for autonomous vehicle systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 566 DOI:10.1109/TCST.2007.894653 |
| [6] |
FALCONE P, TSENG H E, ASGARI J. Integrated braking and steering model predictive control approach in autonomous vehicles[J]. IFAC Proceedings Volumes, 2007, 40(10): 273 DOI:10.3182/20070820-3-US-2918.00038 |
| [7] |
李道飞, 喻凡. 基于最优轮胎力分配的车辆动力学集成控制[J]. 上海交通大学学报, 2008, 42(6): 887 LI Daofei, YU Fan. Integrated vehicle dynamics controller design based on optimum tire force distribution[J]. Journal of Shanghai Jiaotong University, 2008, 42(6): 887 DOI:10.3321/j.issn:1006-2467.2008.06.007 |
| [8] |
UNGOREN A, PENG H. An adaptive lateral preview driver model[J]. Vehicle System Dynamics, 2005(43): 245 |
| [9] |
陈海军, 赵治国, 王琪, 等. 干式DCT双离合器联合起步最优协调控制[J]. 机械工程学报, 2014, 50(22): 150 CHEN Haijun, ZHAO Zhiguo, WANG Qi, et al. Dry dual clutch transmission optimal and coordinating launching control with two clutches based on the minimum principle[J]. Journal of Mechanical Engineering, 2014, 50(22): 150 |
| [10] |
REN B, ZHAO H, DENG W, et al. Model predictive control allocation for stability improvement of four-wheel drive electric vehicles in critical driving condition[J]. IET Control Theory & Applications, 2015, 9(18): 2688 |
| [11] |
HIDEHISA Y, SHUNTARO S, MASAO N. Lane change steering maneuver using model predictive control theory[J]. Vehicle System Dynamics, 2008, 46: 669 DOI:10.1080/00423110802033072 |
| [12] |
杨鹏飞. 四轮轮毂电机驱动电动汽车电机/液压系统联合控制策略[J]. 汽车工程, 2013, 35(10): 921 YANG Pengfei. Motor/hydraulic systems combined control strategy for four in-wheel motor driven electric vehicle[J]. Automotive Engineering, 2013, 35(10): 921 DOI:10.3969/j.issn.1000-680X.2013.10.013 |
 2019, Vol. 47
2019, Vol. 47
