制动器制动是典型的热机耦合过程.制动器的热机耦合特性对振动、噪声、热疲劳等现象有很大影响,是汽车制动器的重要设计内容[1-3].制动盘的非均匀热弹性变形与制动抖动、热斑现象有很大的关联性[4-5].因此,深入研究制动盘在制动过程中的温度、应力、热变形的特征及其之间的耦合关系对制动抖动、热斑问题的控制及制动系统的设计与开发有重要的意义.
制动器热机耦合过程是一个非常复杂的多物理场耦合问题.制动器受到机械载荷作用,在接触和摩擦作用下产生摩擦热源,热量在制动器内部进行传导,产生热应力和变形,进而改变了摩擦面的接触状态[6].为了深入研究该问题,学者们主要采用数学模型和有限元数值计算两种方法建立制动器热机耦合模型.制动器热机耦合数学模型,主要考虑了摩擦面热传导与接触耦合,分析系统的热变形和温度[7-10].进而,分析了制动器系统热弹性稳定性问题,发现当制动速度达到临界速度后,制动器会发生热弹性失稳[11].这些数学模型为制动器热机耦合分析提供了理论方法,但是,它们往往将制动器简化为两个接触的半平面,仅包括制动块厚度和长度等结构参数,无法考虑制动器的实际结构,降低了温度和变形分析结果的有效性.
目前,有限元法是制动器热机耦合分析的主流方法.基于有限元数值计算的制动器热机耦合分析方法主要包括2-3维混合有限元模型[12]、三维对称有限元模型[13-17]和三维非对称有限元模型[18-21].从结构的角度分析可知,2-3维混合有限元模型在计算摩擦面热流密度和能量分配时仅使用了制动盘二维断面模型;三维对称有限元模型主要考虑了制动盘与制动块,且制动盘为对称结构,忽略了盘帽部和颈部结构;由于盘颈部和帽部对制动盘温度分布和热翘曲具有重要影响[22],三维非对称有限元模型则不仅考虑制动盘和制动块,还增加了制动盘帽部和颈部结构.由于制动盘和制动块真实结构的引入,导致制动压力的施加方式发生改变,进而影响了盘块间的接触压力、温度场和变形的分布特性[23-24].例如,数学模型、2-3维混合模型、三维对称有限元模型中制动盘高温带主要集中在摩擦面中间区域,而三维非对称模型中制动盘高温度可能集中在大半径区域[20].但是,不难发现,现有三维非对称有限元模型往往忽略了制动钳、保持架、导向销等结构,而这些结构对接触压力的分布有重要的影响,因此,制动钳及其约束对制动器热机耦合特性的作用规律需要进一步加以研究.
本文针对上述前期研究的不足,建立了完整的通风浮钳盘式制动器热机耦合三维有限元模型,分析了制动盘温度、应力和变形等热机耦合特性,研究了制动钳、导向销等关键结构对制动器热机耦合特性的影响.
1 制动器热机耦合有限元建模 1.1 有限元模型本文所建立的热机耦合模型中,不仅包括制动盘、摩擦衬片,而且还包含制动块背板、制动钳、保持架、导向销及其橡胶衬套和活塞等零件.系统有限元模型如图 1所示.其中,制动盘沿周向均布40个通风槽,摩擦衬片中部设有排屑直槽.制动盘、摩擦衬片和制动块背板是主要的摩擦副构件,因此其有限元模型以六面体单元为主,局部复杂结构辅以五边形单元过渡.保持架和制动钳等由于结构复杂,主要使用四面体单元建模.该制动器有限元模型中共包括138 239个单元和64 814个节点.模型中各零件材料参数如表 1所示.其中,各零件的材料密度、杨氏模量和泊松比皆经过模态试验与仿真验证.热膨胀系数、热传导系数和比热等参数通过材料牌号、材料工程手册[25]和文献[26-27]确定.由于本研究中涉及的制动盘温度低于300 ℃,材料参数随温度的变化较小,因此,暂不考虑材料参数随温度的变化.

|
图 1 某通风盘式制动器有限元模型 Fig.1 Finite element model of a ventilated disc brake |
| 下载CSV 表 1 材料的物理特性 Tab.1 Physical parameters of materials |
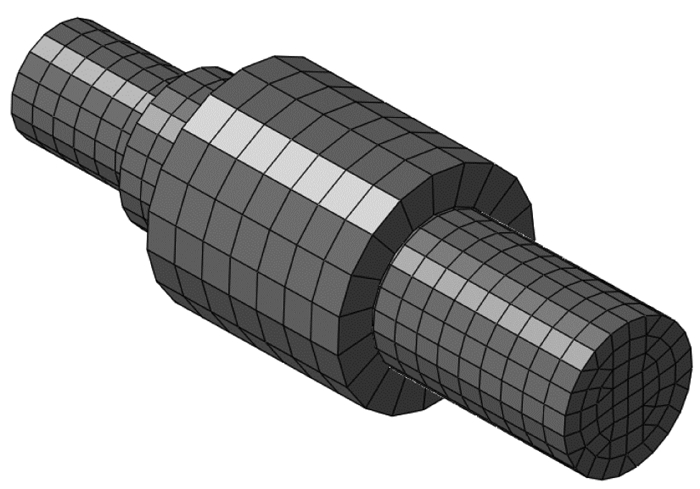
模型中,建立独立的导向销橡胶衬套有限元模型,如图 2所示.衬套在导向销及保持架之间起到减少磨损、隔振等作用,工作中主要受到沿径向的集中力和绕径向的集中力矩.衬套采用Mooney-Rivlin超弹性模型,其材料参数根据文献[26-28]及试验确定,如表 2所示.
|
图 2 导向销橡胶衬套有限元模型 Fig.2 Finite element model of rubber bushing |
| 下载CSV 表 2 橡胶衬套材料的物理特性 Tab.2 Material physical parameters of rubber bushing |
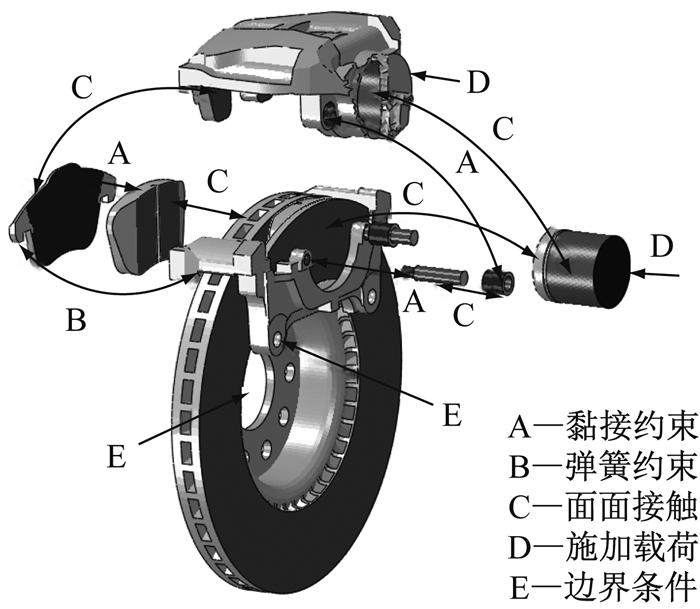
根据制动器的工作原理和结构连接关系,盘式制动器热机耦合模型中各零部件的约束关系如图 3所示.其中,制动盘与摩擦衬片、活塞与内侧制动块背板、活塞与制动钳、外侧制动块与制动钳、导向销与橡胶衬套定义为面-面接触;摩擦衬块与制动背板、制动钳与橡胶衬套、导向销与保持架之间定义为黏接约束;制动背板与保持架间采用弹簧约束连接.
|
图 3 部件约束示意图 Fig.3 Diagram of component constraints |
模型中边界条件主要包括制动盘的旋转、保持架的位移约束和制动压力的施加.其中,在制动盘旋转中心位置约束其自由度,仅保留绕z向的旋转,同时设置转动的角速度;在保持架下部的两个孔处约束其3个方向的平移,实现制动器位置的固定;在活塞背面、与活塞对应的制动钳内表面施加大小相同、方向相反的载荷压力.
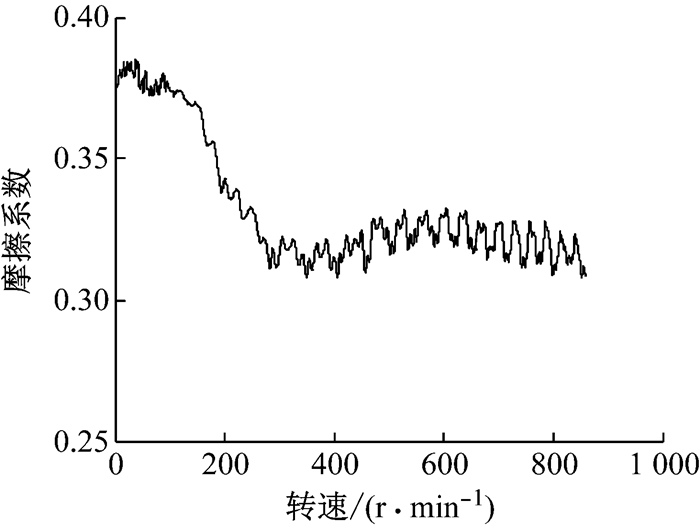
1.3 关键参数的设置实际制动过程中,制动器摩擦系数随着制动速度、制动压力、制动盘温度和制动盘的变形发生变化,其特性极为复杂.为了尽可能地反映制动器摩擦系数的特性,模型中使用制动器热机耦合台架试验测得的摩擦系数-转速曲线进行计算,如图 4所示.
|
图 4 摩擦系数-转速曲线 Fig.4 Friction coefficient and rotating velocity |
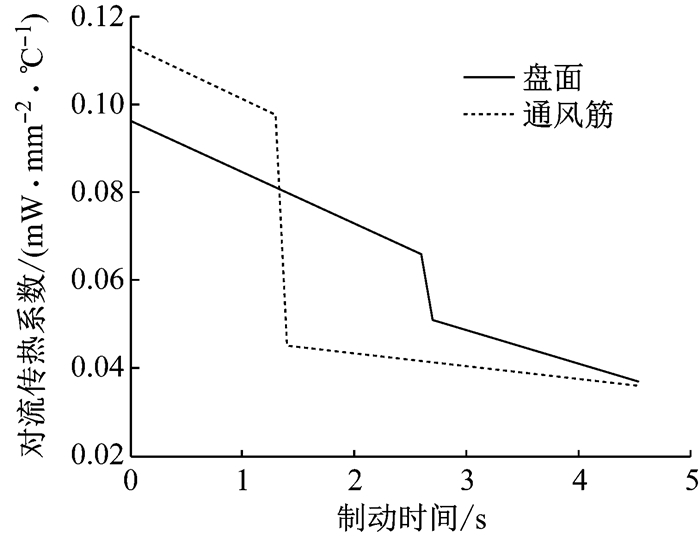
根据传热学原理[29],热能不仅在制动器各零部件内传导,而且与环境具有对流传热作用.制动盘对流传热系数由两部分组成,盘面的对流传热系数如式(1)、(2)所示,通风槽的对流传热系数如式(3)~(5)所示.根据公式(1)~(5),模型中的制动盘与环境的对流传热系数曲线如图 5所示,制动块与环境的对流换热系数设为定值0.005 mW·mm-2·℃-1.其他零件由于温升不大, 不考虑对流换热作用.
| $ \left\{\begin{array}{l}{h_{\mathrm{cl}}=0.7 \frac{k_{\mathrm{a}}}{D} R e^{0.55}, \quad R e \leqslant 2.4 \times 10^{5}} \\ {h_{\mathrm{cl}}=0.04 \frac{k_{\mathrm{a}}}{D} R e^{0.8}, \quad R e>2.4 \times 10^{5}}\end{array}\right. $ | (1) |
|
图 5 对流传热系数变化曲线 Fig.5 Convection heat transfer coefficient |
其中,
| $ R e=\left(\omega R+V_{\mathrm{w}}\right) L \rho_{\mathrm{a}} / \mu_{\mathrm{a}} $ | (2) |
| $ \left\{\begin{array}{ll}{h_{\mathrm{c} 2}=1.86\left(\frac{d_{\mathrm{h}}}{l}\right)^{0.33} R e^{0.33} {Pr}^{0.33} \frac{k_{\mathrm{a}}}{d_{\mathrm{h}}}, } & {R e \leqslant 10^{4}} \\ {h_{\mathrm{c} 2}=0.023\left[1+\left(\frac{d_{\mathrm{h}}}{l}\right)^{0.67}\right] R e^{0.8} {Pr}^{0.33} \frac{k_{\mathrm{a}}}{d_{\mathrm{h}}}, } & {{Re}>10^{4}}\end{array}\right. $ | (3) |
其中,
| $ R e=\left(v_{\mathrm{a}}+V_{\mathrm{w}}\right) d_{\mathrm{h}} \rho_{\mathrm{a}} / \mu_{\mathrm{a}} $ | (4) |
| $ v_{\mathrm{a}}=0.25 \omega \sqrt{D^{2}-D_{0}^{2}}\left(1+\frac{D_{0}}{D}\right) $ | (5) |
式(1)~(5)中:hc1为制动盘盘面对流传热系数; hc2为制动盘通风散热筋对流传热系数; ka为空气导热系数; Re为雷诺数; ω为制动盘转速; ρa为空气密度; R为制动盘盘面中心半径; L为制动盘盘面中心半径周长; μa为空气动力黏度; l为通风散热筋特征长度,取l=(D-D0)/2;D0为制动盘内直径; h为通风槽高度; dh是流体力学直径,dh=2hθR/(h+θR); θ为通风槽包角; R为通风槽中心半径; Pr为普朗特数,Pr=caμa/ka; ca为空气比热; va为通风孔中气流平均速度; Vw为冷却风速.
为分析导向销衬套对制动器热机耦合特性的影响,建立了用弹簧元件代替橡胶衬套有限元模型的对比模型(详见1.4.2).利用图 2中的橡胶衬套有限元模型及表 2中的材料参数,在Abaqus仿真软件中对导向销分别施以径向的集中力和绕径向的力矩,仿真得到导向销的位移量,如图 6所示.根据载荷大小与位移量计算出等效弹簧的径向刚度和扭转刚度分别为Kx = Ky= 794 N·mm-1,KRx = KRy = 20 548 N·mm·rad-1.
|
图 6 橡胶衬套变形仿真 Fig.6 Simulation of rubber bushing deformation |
仿真工况为单次制动工况,制动过程中压力保持不变,具体参数设置与制动器热机耦合台架试验相同,如表 3所示.等效车速为52 km·h-1,制动减速度为6.5 m·s-2.
| 下载CSV 表 3 仿真工况参数 Tab.3 Parameters of simulation conditions |
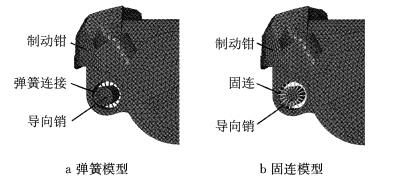
为了便于分析制动钳及其约束对盘式制动器热机耦合特性的影响,将上述建立的盘式制动器热机耦合模型称为完整模型,另外还建立了3个简化模型与其对比.将完整模型中的制动钳、保持架、导向销及其橡胶衬套删除,并在制动块背板直接施加制动压力,称为盘块模型,如图 7所示,具体建模过程详见文献[19];以弹簧单元代替橡胶衬套连接导向销和制动钳,弹簧刚度根据1.3节中的方法计算得出,其他设置与完整模型相同,该简化模型称为弹簧模型,如图 8a所示;删除衬套模型将导向销和制动钳直接固连,其他设置与完整模型相同,该简化模型称为固连模型, 如图 8b所示.通过完整模型与盘块模型的对比,主要分析制动钳对盘式制动器热机耦合特性的影响;通过完整模型、弹簧模型和固连模型的对比,分析导向销橡胶衬套对盘式制动器热机耦合特性的影响.

|
图 7 盘块模型示意图 Fig.7 Schematic of disc-pad model |
|
图 8 弹簧模型、固连模型结构示意图 Fig.8 Schematic of stiffness model and solid model |
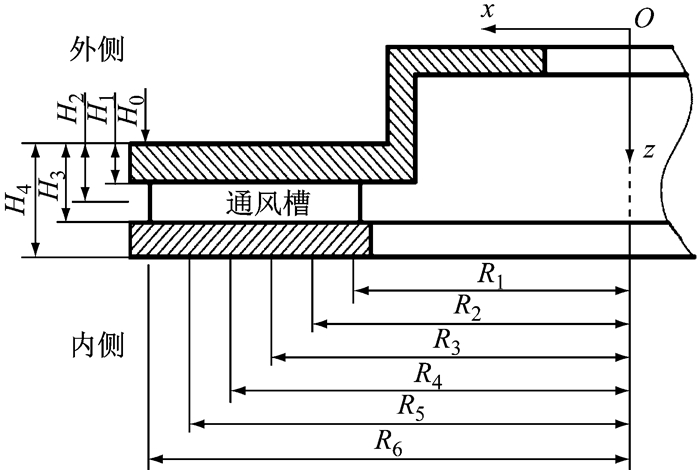
制动器热机耦合特性主要体现在温度、应力、热变形之间的耦合,其与盘块之间的接触特征也紧密相关.因此,选取制动盘等关键部件的温度场、应力场、变形场以及盘块间的接触特性作评价指标.为了便于结果描述与对比,对制动盘关键点处的指标进行评价,关键点的位置如图 9所示.R1~R6代表制动盘摩擦面由小至大的6个圆周;H0~H4代表制动盘法向上的5个位置,其中H0在外侧盘面上,H4在内侧盘面上,H1、H2、H3在通风筋处.选取盘面R4圆周内的节点,作为周向评价点.下面通过完整模型和盘块模型结果的对比,分析制动钳对盘式制动器热机耦合特性的影响.
|
图 9 制动盘关键评价点位置 Fig.9 Position of evaluation points on brake disc |
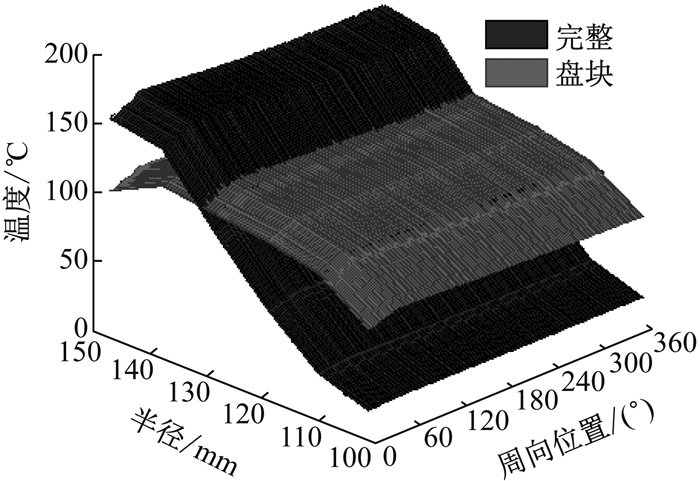
图 10为制动4 s时完整模型和盘块模型的制动盘外侧盘面温度对比图.由图可知:
|
图 10 制动4 s时外侧盘面温度对比 Fig.10 Temperature contrast of outer disc surface at 4 s |
(1) 当考虑制动钳及其约束关系后,盘面高温区域主要分布在大半径区域(R5~R6).完整模型中大半径区域的最高温度达到200 ℃,高于盘块模型的145 ℃,但小半径区域的温度低于盘块模型,从而导致完整模型的径向温度梯度大于盘块模型.盘面径向温度梯度的增大,必然更容易导致制动盘热裂纹和热疲劳.上述现象的产生,主要是制动钳变形改变了接触压力分布特性造成的,具体原因将在2.3节中阐述.
(2) 制动盘面温度在周向上分布不均匀,在0°~60°内存在明显的变化.这一角度区域为制动盘-块间的接触区.制动盘在经过接触区时摩擦生热,温度升高;离开接触区时通过对流散热冷却降温.
图 11为制动盘、摩擦衬片、背板、制动钳、保持架的温升曲线.由图可知,制动盘与摩擦衬片温度相近;制动盘的温度时间历程有明显的锯齿状的波动,摩擦衬片温度波动较小,锯齿状波动的产生原因是制动盘反复进出摩擦接触区,交替受摩擦加热和对流散热作用.而摩擦衬片始终与制动盘摩擦,故温度波动不明显.背板、制动钳、保持架在制动过程中的最高温度没有明显温度变化,基本与环境温度一致.

|
图 11 制动器关键零部件的温升曲线 Fig.11 Temperature rise of key parts of brake |
根据制动盘热弹性失稳理论[11],制动盘周向应力分布与盘面的波纹状变形有密切关系,进而会引起制动盘热点等现象,加剧制动盘的热疲劳发生.因此本节主要分析制动盘面周向应力的分布特性.
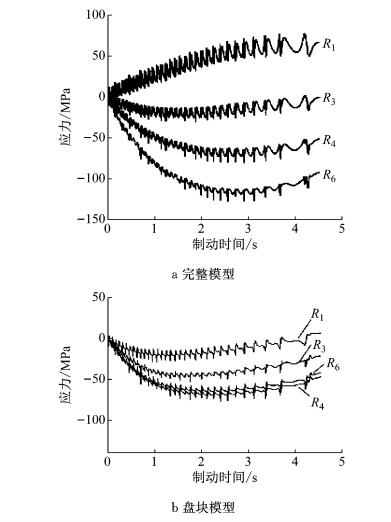
图 12为完整模型与盘块模型在不同半径上的周向应力变化曲线.应力为正值时为拉应力,应力为负值时为压应力.由图可知:完整模型的周向应力随半径增大由拉应力变为压应力,而盘块模型始终为压应力;从R1至R6,完整模型的周向应力在数值上递减,由正变负即为由拉应力变为压应力,径向应力梯度高达200 MPa,而盘块模型始终为负,且变化幅度较小.因此,考虑制动钳时,制动盘更加容易出现热裂纹和热弹性失稳现象.
|
图 12 完整模型、盘块模型周向应力径向分布对比 Fig.12 Contrast of distribution of circumferential stress radial between brake model and disc-pad model |
以上现象是由盘面温度分布特性导致的.盘面的周向应力分布与温度分布密切相关,温度越高膨胀量越大,会产生越大的压应力.完整模型盘面温度的径向梯度较大,产生了大梯度随半径递增的压应力;由于小半径区域压应力较小,在盘毂转矩的作用下会体现为拉应力,因此产生了随半径增加拉应力逐渐变为压应力的现象.盘块模型盘面温度的分布比较均匀,产生的压应力径向梯度不大,小半径区域由膨胀产生的压应力大于转矩产生的拉应力,因此盘面整体均呈现压应力.可见,制动钳的作用会影响温度场分布,进而使应力场的分布发生变化.
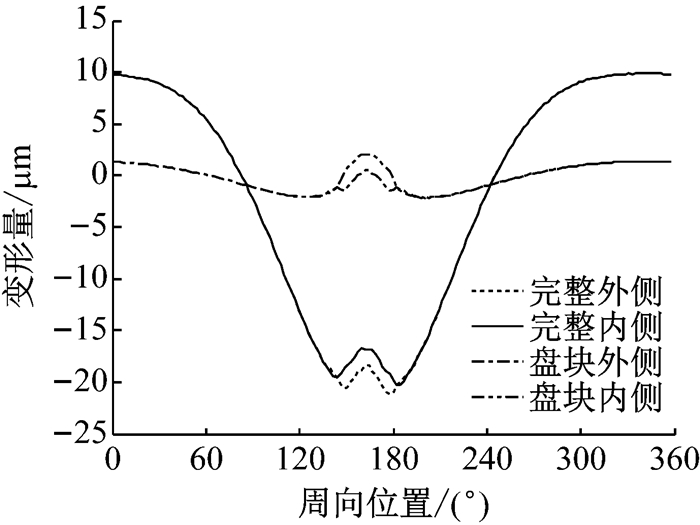
2.3 翘曲变形特性 2.3.1 静态变形特性在制动盘不转动、只施加制动载荷时,完整模型与盘块模型的制动盘翘曲变形周向分布如图 13所示.由图可知,完整模型制动盘的变形量要大于盘块模型,其制动盘与摩擦衬块的接触区向内侧(z负方向)翘曲,接触区对侧向外侧(z正方向)翘曲变形,制动盘整体呈倾斜形态,而盘块模型倾斜变形量较小.产生这种现象的原因是施加载荷时,制动钳活塞一侧会上翘变形,如图 14所示,从而使载荷向制动盘大半径方向移动,使盘面更加倾斜.
|
图 13 完整模型、盘块模型变形周向分布 Fig.13 Deformation circumferential distribution of brake model and disc-pad model |

|
图 14 制动钳加压变形示意图(变形放大150倍) Fig.14 Brake caliper deformation due to pressure (150 times of magnification) |
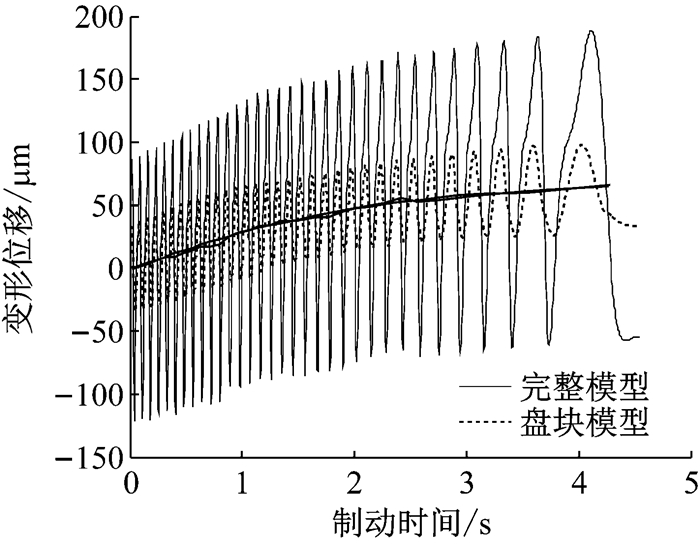
图 15为完整模型、盘块模型制动过程中R4半径上的变形量、变形趋势随时间的变化曲线.分析可知:完整模型的变形量波动较盘块模型大很多,这与静态变形有关,制动的过程中制动盘会一直保持施加载荷产生的变形形态;变形趋势项主要表征热翘曲变形特征,两模型的变形趋势起点不同,完整模型要更偏向内侧(z负方向),这是因为在只施加静态载荷时,完整模型的接触区就更向内侧(z负方向)变形,如图 13所示.
|
图 15 完整模型、盘块模型R4半径处变形量 Fig.15 Deformation at R4 of brake model and disc-pad model |
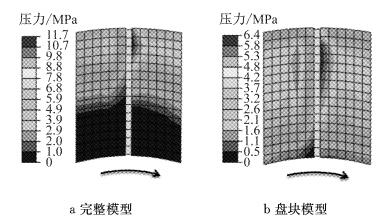
图 16为制动4 s时完整模型、盘块模型制动盘-块间接触压力的对比.由图可知,完整模型接触压力偏向衬块上部,即制动盘大半径区域,原因是制动钳上翘变形,造成制动盘-块下部无法接触,而盘块模型接触良好;同时,完整模型的接触压力最大值较大.接触压力偏上的分布特征使得完整模型制动盘面大半径区域温度较高、温度径向梯度较大,进而出现盘面应力径向梯度较大的现象.
|
图 16 制动4 s时的制动盘-块间接触压力对比 Fig.16 Contrast of contact pressure at 4 s |
下面通过完整模型、弹簧模型和固连模型的结果对比,分析导向销橡胶衬套对盘式制动器热机耦合特性的影响.
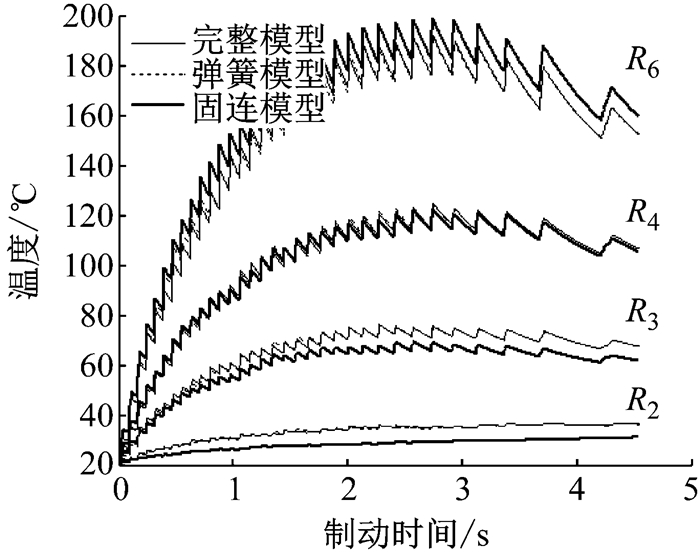
3.1 温度场特性图 17为完整模型、弹簧模型、固连模型制动盘外侧径向的温度变化曲线.由图可知,完整模型与弹簧模型仿真结果比较一致,固连模型与二者的差别稍大.固连模型在小半径区域(R1~R3)温度较低,锯齿波动也较小,半径超过R4之后,温度快速升高,并最终大于完整模型和弹簧模型,即固连模型的盘面温度略向大半径区域偏移.发生此现象的原因是固连模型没有橡胶衬套或弹簧的弹性作用,制动钳的位移特性会发生改变,导致固连模型的压力最大值较其他两模型大,从而导致温度产生差异.
|
图 17 导向销橡胶衬套对温度的影响 Fig.17 Effect of guide pin rubber bushing on temperature |
图 18为完整模型、弹簧模型、固连模型制动盘外侧径向上的周向应力变化曲线.由图可知,完整模型与弹簧模型的曲线仍然十分接近;在不同的半径上,固连模型的周向应力绝对值皆为最大,即固连模型在小半径区域(R1~R3)拉应力更大,大半径区域(R5、R6)压应力更大.这种现象的产生与温度沿径向的分部特性有关,温度越高,制动盘的热膨胀量就越大,会产生越大的周向压应力.

|
图 18 完整模型、弹簧模型、固连模型周向应力径向分布 Fig.18 Distribution of circumferential stress radial of brake model, stiffness model, and solid model |
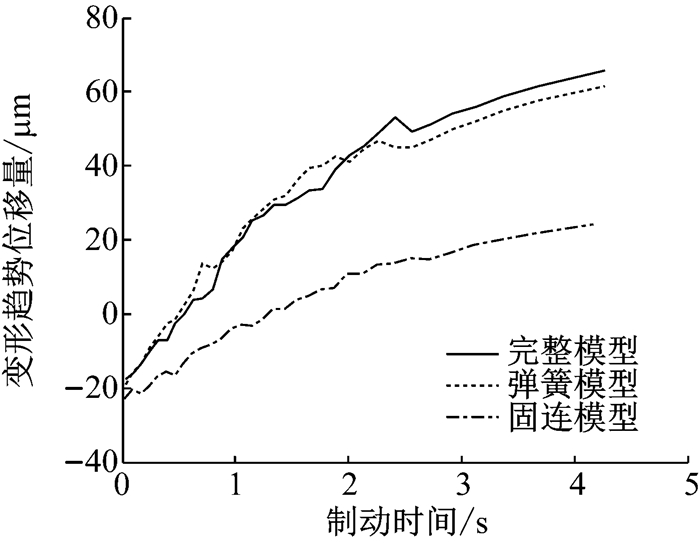
图 19为完整模型、弹簧模型、固连模型制动盘外侧R4半径变形趋势随时间的变化曲线.由图可知,完整模型和弹簧模型的变形趋势项比较相近,而固连模型的变形趋势量明显小于二者.由于在此半径处,3种模型的温度比较接近,则造成变形趋势差别的原因是橡胶衬套的弹性作用对制动钳运动特性的影响.
|
图 19 导向销橡胶衬套对制动盘翘曲的影响(R4) Fig.19 Effect of guide pin rubber bushing on normal deformation of brake disc at R4 |
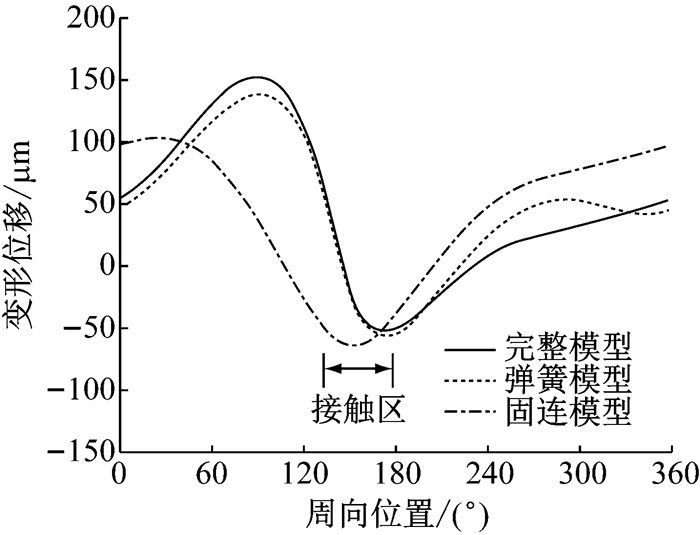
图 20为3种模型制动盘外侧R4半径上4 s时的变形周向分布曲线.由图可知,完整模型与弹簧模型的变化曲线依然相近,说明用弹簧代替橡胶衬套的建模方式比较精确有效;而固连模型的变形周向分布较平缓,且相对接触区对称.说明由于导向销衬套的存在,完整模型和弹簧模型制动钳的连接处变软,导致变形量更大.
|
图 20 导向销橡胶衬套对制动盘周向变形的影响(4 s) Fig.20 Effect of guide pin rubber bushing on circumferential deformation of brake disc at 4 s |
为验证仿真结果的正确性,利用图 21所示的制动器惯量试验台进行了单次制动工况热机耦合特性验证试验.本次台架试验一共采用了3套测试及数据采集系统:Link Model 3900测试及数据采集系统、DASP数据采集系统、热成像仪测试及数据采集系统,具体试验原理如图 22所示.

|
图 21 试验仪器设备 Fig.21 Test equipment |

|
图 22 试验台原理示意图 Fig.22 Schematic diagram of test bench |
试验对象与仿真对象相同.在制动盘外侧有效半径(R4)处设置预埋式热电偶和非接触位移传感器,分别测量外侧盘面的温度和翘曲变形,并利用热成像仪拍摄外侧盘面温度场分布图像.
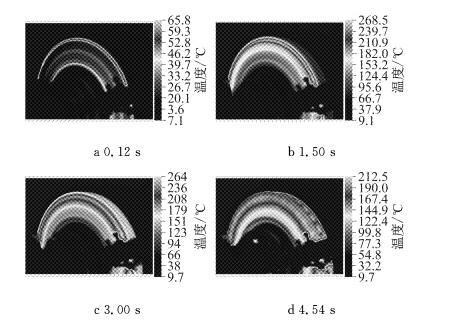
热成像仪拍摄的制动盘面温度场分布特性如图 23所示.由图可知,制动过程中制动盘的高温带分布在大半径区域,在径向上有很大的温度梯度,这与完整模型的仿真结果相近,说明完整模型比盘块模型更贴近试验结果,具有更高的仿真精度.
|
图 23 制动盘温度场分布特性 Fig.23 Distribution of temperature field on brake disc |
图 24为试验与仿真制动盘有效半径处温升曲线对比.由图可知,完整模型的制动盘有效半径上的温度,仿真结果的整体趋势和最高温度基本与试验结果一致,但制动中期仿真结果偏高,可能是热电偶与制动盘面仍有1 mm左右的距离,由于热传导需要一定的时间,热电偶响应有迟滞.

|
图 24 制动盘有效半径处温度变化对比 Fig.24 Temperature variation at effective radius of brake disc in bench test and simulation |
图 25为完整模型中制动盘有效半径处盘面变形与试验结果的对比.由图可知,两模型制动盘有效半径处变形趋势的仿真结果与试验结果吻合较好,说明完整模型有效.

|
图 25 制动盘有效半径处变形趋势对比 Fig.25 Deformation at effective radius of disc in bench test and simulation |
(1) 本文考虑制动盘、摩擦衬片、制动块背板、活塞、制动钳、保持架、导向销及其橡胶衬套等零件,定义了零件间的约束关系和边界条件,设置了制动器摩擦系数、对流散热系数和橡胶衬套刚度等关键参数,建立了制动器热机耦合有限元模型,分析了单次制动工况下制动盘的温度、应力和热变形分布特征,并通过台架试验验证了所建立模型的有效性.
(2) 通过完整制动器模型与盘块模型仿真结果的对比,发现制动钳对热机耦合特性具有重要影响.制动钳在制动压力下会发生弯曲变形,使制动盘面接触压力向大半径区域转移,造成大半径区域处温度和压力增大,且温度、应力的径向梯度增大.同时,制动盘整体变形更加倾斜,制动旋转过程中的法向变形波动也增大.
(3) 在制动器热机耦合模型的基础上,改变导向销橡胶衬套的等效模拟方式发现,橡胶衬套真实结构与等效为弹簧单元的仿真结果差别较小,与不考虑橡胶衬套的仿真结果差别较大,制动器热机耦合仿真中应考虑导向销橡胶衬套.
| [1] |
CANTONI C, CESARINI R, MASTINU G, et al. Brake comfort - a review[J]. Vehicle System Dynamics, 2009, 47(8): 901 DOI:10.1080/00423110903100432 |
| [2] |
高诚辉, 黄健萌, 林谢昭, 等. 盘式制动器摩擦磨损热动力学研究进展[J]. 中国机械工程学报, 2006, 4(1): 83 GAO Chenghui, HUANG Jianmeng, LIN Xiezhao, et al. Research status on heat dynamics of friction and wear for disc-pad braking systems[J]. Chinese Journal of Construction Machinery, 2006, 4(1): 83 |
| [3] |
LE GIGAN G, VERNERSSON T, LUNDEN R, et al. Disc brakes for heavy vehicles: an experimental study of temperatures and cracks[J]. Journal of Automobile Engineering, 2015, 229(6): 684 DOI:10.1177/0954407014550843 |
| [4] |
KAO T K, RICHMOND J W, DOUARRE A. Brake disc hot spotting and thermal judder: an experimental and finite element study[J]. International Journal of Vehicle Design, 2000, 23(3): 276 |
| [5] |
HASSAN M Z, BROOKS P C, BARTON D C. Thermo-mechanical contact analysis of car disc brake squeal[J]. SAE International Journal of Passenger Cars—Electronic and Electrical Systems, 2009.[DOI:10.427112008-01-2566.]
|
| [6] |
BARBER J R. Thermoelasticity and contact[J]. Journal of Thermal Stresses, 1999, 22(4/5): 513 |
| [7] |
ZAGRODZKI P. Analysis of thermomechanical phenomena in multidisc clutches and brakes[J]. Wear, 1990, 140(2): 291 DOI:10.1016/0043-1648(90)90091-N |
| [8] |
EVTUSHENKO A A, GORBACHEVA N V, IVANIK E G. Thermomechanical processes in the friction heating of disk brakes[J]. Journal of Engineering Physics and Thermophysics, 1997, 70(1): 113 DOI:10.1007/s10891-997-0021-0 |
| [9] |
THURESSON D. Thermomechanical analysis of friction brakes[C]//SAE Technical Papers, 18th Annual Brake Colloquium and Engineering Display. San Diego: SAE International, 2000: 358-369.
|
| [10] |
YEVTUSHENKO A A, KUCIEJ M, OCH E. Temperature in thermally nonlinear pad-disk brake system[J]. International Communications in Heat and Mass Transfer, 2014, 57: 274 DOI:10.1016/j.icheatmasstransfer.2014.08.013 |
| [11] |
LEE K, BARBER J R. Frictionally excited thermoelastic instability in automotive disk brakes[J]. Journal of Tribology, 1993, 115(4): 607 DOI:10.1115/1.2921683 |
| [12] |
DUFRENOY P. Two-/three-dimensional hybrid model of the thermomechanical behaviour of disc brakes[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(1): 17 DOI:10.1243/095440904322804402 |
| [13] |
GAO C H, HUANG J M, LIN X Z, et al. Stress analysis of thermal fatigue fracture of brake disks based on thermomechanical coupling[J]. Journal of Tribology, 2007, 129(3): 5363 |
| [14] |
HWANG P, WU X, JEON Y. Repeated brake temperature analysis of ventilated brake disc on the downhill road[C]//26th Annual Brake Colloquium and Exhibition. San Antonio: SAE International, 2008. DOI: doi.org/10.4271/2008-01-2571.
|
| [15] |
黄健萌, 高诚辉, 唐旭晟, 等. 盘式制动器热结构耦合的数值建模与分析[J]. 机械工程学报, 2008, 44(2): 145 HUANG Jianmeng, GAI Chenghui, TANG Xusheng, et al. Numerical modeling and analysis of thermal-structure coupling of disc brake[J]. Journal of Mechanical Engineering, 2008, 44(2): 145 DOI:10.3321/j.issn:0577-6686.2008.02.025 |
| [16] |
杨智勇, 韩建民, 李卫经, 等. 制动盘制动过程的热机耦合仿真[J]. 机械工程学报, 2010, 46(2): 88 YANG Zhiyong, HAN Jianmin, LI Weijing, et al. Thermo-mechanical coupling simulation of braking process of brake disc[J]. Journal of Mechanical Engineering, 2010, 46(2): 88 |
| [17] |
张方宇, 桂良进, 范子杰. 盘式制动器热-应力-磨损耦合行为的数值模拟[J]. 汽车工程, 2014, 36(8): 984 ZHANG Fangyu, GUI Liangjin, FAN Zijie. Numerical simulation of thermal-stress-abrasion coupling behavior of disc brake[J]. Automotive Engineering, 2014, 36(8): 984 |
| [18] |
HWANG P, WU X, JEON Y B. Thermal-mechanical coupled simulation of a solid brake disc in repeated braking cycles[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2009, 223(7): 1041 DOI:10.1243/13506501JET587 |
| [19] |
孟德建, 张立军, 余卓平. 通风盘式制动器热机耦合理论建模与有限元分析[J]. 同济大学学报(自然科学版), 2010, 38(6): 890 MENG Dejian, ZHANG Lijun, YU Zhuoping. Theoretical modeling and FEA of thermo-mechanical coupling dynamics of ventilated disc brake[J]. Journal of Tongji University (Natural Science), 2010, 38(6): 890 DOI:10.3969/j.issn.0253-374x.2010.06.020 |
| [20] |
BELHOCINE A, BOUCHETARA M. Thermomechanical modelling of dry contacts in automotive disc brake[J]. International Journal of Thermal Sciences, 2012, 60: 161 DOI:10.1016/j.ijthermalsci.2012.05.006 |
| [21] |
HAN M J, LEE C H, PARK T W, et al. Coupled thermo-mechanical analysis and shape optimization for reducing uneven wear of brake pads[J]. International Journal of Automotive Technology, 2017, 18(6): 1027 DOI:10.1007/s12239-017-0100-y |
| [22] |
TOSHIKAZU O, HIROYUKI Y. Fundamental study on thermal behavior of brake discs[C]//SAE Technical Papers, 24th Annual Brake Colloquium and Exhibition. Grapevine: SAE International, 2006: 3203-3219.
|
| [23] |
张立军, 陈远, 刁坤, 等. 盘式制动器接触压力与热机耦合特性仿真分析[J]. 同济大学学报(自然科学版), 2013, 44(10): 1554 ZHANG Lijun, CHEN Yuan, DIAO Kun, et al. Computational investigation into disc-pads pressure distribution anf thermomechanical coupling characteristics if brake pads in disc brake[J]. Journal of Tongji University (Natural Science), 2013, 44(10): 1554 DOI:10.3969/j.issn.0253-374x.2013.10.018 |
| [24] |
MENG Dejian, ZHANG Lijun, YU Zhuoping. Influences of pad backplate on thermo-mechnical coupling in disc brake[C]//SAE 2016 World Congress and Exhibition. Detroit: SAE International, 2016: 1354-1363.
|
| [25] |
中国机械工程学会. 中国材料工程大典(第2卷)[M]. 北京: 化学工业出版社, 2006 China Mechanical Engineering Society. China materials engineering canon (Vol. 02)[M]. Beijing: Chemical Industry Press, 2006 |
| [26] |
刘萌, 王青春, 王国权. 橡胶Mooney-Rivlin模型中材料常数的确定[J]. 橡胶工业, 2011, 58(4): 241 LIU Meng, WANG Qingchun, WANG Guoquan. Determination of material constants in rubber Mooney-Rivlin model[J]. Rubber industry, 2011, 58(4): 241 DOI:10.3969/j.issn.1000-890X.2011.04.009 |
| [27] |
邓小强, 邓雄志, 邱俊杰, 等. 汽车悬架橡胶衬套刚度特性分析方法的研究[J]. 客车技术与研究, 2016, 8(4): 1 DENG Xiaoqiang, DENG Xiongzhi, QIU Junjie, et al. Research on stiffness features analysis method of vehicle suspension rubber bushing[J]. Bus and Coach Technology and Research, 2016, 8(4): 1 DOI:10.3969/j.issn.1006-3331.2016.04.001 |
| [28] |
廖抒华, 鲍玉辉, 钟金志, 等.基于Mooney-Rivlin模型的橡胶衬套有限元分析[C]//第五届全国橡胶制品新技术交流暨信息发布会.扬州: 西北橡胶塑料研究设计院, 2014: 172-174. LIAO Shuhua, BAO Yuhui, ZHONG Jinzhi, et al. Finite element analysis of rubber bushing based on mooney-rivlin model[C]//Fifth National Rubber Products New Technology Exchange and Information Conference.Yangzhou: Northwest Rubber and Plastics Research and Design Institute, 2014: 172-174. |
| [29] |
霍尔曼 J P. 传热学[M]. 北京: 机械工业出版社, 2011 HOLMAN J P. Heat transfer[M]. Beijing: Mechanical Industry Press, 2011 |
 2019, Vol. 47
2019, Vol. 47
