既有结构鉴定分析采用的计算模型应为根据结构实际状况建立的二维或三维模型,且该模型符合结构的实际构造和工作状态[1].然而,由于结构正在使用中或建筑装饰形成遮挡等原因,往往难以实现对既有空间结构全部节点位置的测量;同时,测量全部节点位置也不经济.因此,在实际工程应用中,经常采用抽样测量的方法.对于整体结构而言,抽样测量得到的数据是不完备的.然而,既有空间结构的鉴定验算必须基于结构完整的位形信息,因此,选取最佳抽样方法,以及利用抽样测量的节点位置推算结构的整体位形,是既有空间结构检测与鉴定的首要问题.
实际工程中,抽样方法一般是检测人员主观确定的,同时,未测量节点位置往往直接采用设计位置,并按设计采用的一致缺陷模态法[2]等引入节点位置偏差.但是,设计假定缺陷与结构实际位形可能存在很大差异,导致鉴定分析结果不准确.对于此问题,刘俊等[3]提出基于曲面插值的未测节点位置推算方法;吴俊等[4]提出基于马尔可夫随机场理论模型的几何缺陷分布反演算法;罗永峰等[5]提出既有空间结构位形推算的随机偏差方法.曲面插值方法与几何缺陷分布反演算法并未考虑样本的选取对推算结果的影响,无法指导实际工程中最佳样本容量与样本节点位置的确定;随机偏差方法中抽样测量与几何位形推算基于简单随机抽样,简单随机抽样无法考虑样本间的相关关系,对于节点位置偏差存在相关性的既有空间结构,目前尚没有科学的最佳抽样方法以及相应的位形推算方法.
最佳抽样方法的确定应该基于既有空间结构节点位置偏差的分布特性.唐敢[6]、刘学春[7]等先后对几个实际结构的节点位置偏差数据进行了统计分析,验证了节点位置偏差具有正态分布特性.在此基础上,Chen等[8]对某单层网壳结构节点位置偏差数据进行了分析,发现网壳结构部分节点偏差呈现出明显的区域同向性,指出不同节点位置偏差存在一定相关关系.而对于相关样本,即非独立样本,套用基于简单随机样本的统计推断方法可能导致错误的结果[9].
不同于简单随机抽样,空间抽样方法[10]可以考虑样本的相关性,能准确估计总体参数,并提高抽样效率.同时,通过样本相关系数矩阵的等行和分解,可以将非独立样本转换为简单随机样本,并建立平行于简单随机样本情形的假设检验方法[11].基于此,本文提出了基于空间系统抽样的统计推断方法,以推算既有空间结构整体位形,建立结构鉴定计算的几何模型.
1 节点位置偏差相关性 1.1 随机场理论用随机变量Ui表示既有空间结构第i个节点处的位置偏差值,其中i=1, 2, …, N,N为节点总数量,则整个空间结构节点偏差值构成一个离散随机场,记为F(u)={U1, U2, …, UN}, 其中向量u={ u1, u2, …, uN},ui表示随机场中第i个节点的位置坐标.随机场中各点属性的随机分布特性通常采用数字特征(均值、协方差和相关系数)函数描述[12].对于没有明显整体变形的既有空间结构,随机场具有均匀性,即各节点的位置偏差均值函数μ(u)满足μ1=μ2=…=μN=μ,其中μ为常数,且任意两节点位置偏差值的相关系数函数满足如下公式[8]:
| $ \rho\left(\boldsymbol{u}_{i}, \boldsymbol{u}_{j}\right)=\rho\left(\left|\boldsymbol{u}_{i}-\boldsymbol{u}_{\boldsymbol{j}}\right|\right) $ | (1) |
式中:|ui-uj|表示i、j两点间的距离.
随机场的相关结构一般用于考虑随机场中任意两点的相关性,通常用其协方差函数或相关系数函数表示,根据具体问题的性质,随机场的相关结构是一种半经验的假设.常用的随机场相关结构包括三角型相关结构、指数型相关结构和高斯型相关结构[13].其中,空间结构节点位置偏差随机场的指数型相关结构可以表示为
| $ \rho\left(\boldsymbol{u}_{i}, \boldsymbol{u}_{j}\right)=\exp \left(-\frac{\left|\boldsymbol{u}_{i}-\boldsymbol{u}_{j}\right|}{l}\right) $ | (2) |
式中:l为待定系数.
3种相关结构模型曲线如图 1所示.
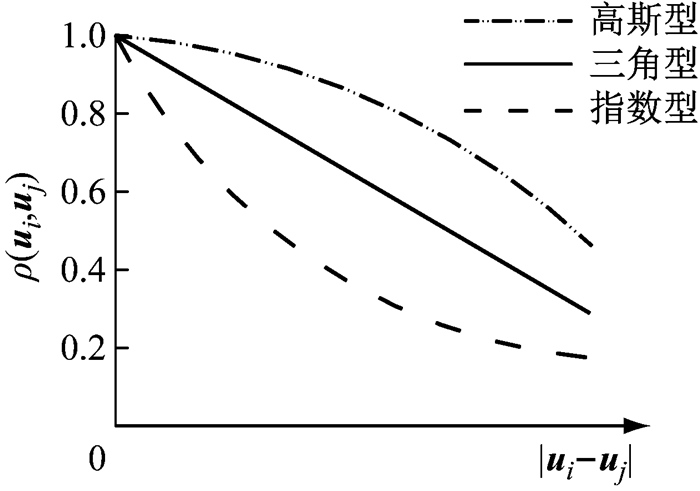
|
图 1 随机场相关结构模型曲线 Fig.1 Correlation structure model of random field |
空间结构节点通过杆件连接,任意两节点间距离由杆件长度和两节点间最小杆件数量决定,在各杆件长度近似相等的条件下,节点间距离主要取决于节点间杆件数量.则任意两节点位置偏差值的相关系数函数满足如下公式[8]:
| $ \rho\left(\boldsymbol{u}_{i}, \boldsymbol{u}_{j}\right)=\rho(m) $ | (3) |
式中:m代表i、j两节点间最小杆件数量.如图 2所示,节点A、B以及C、D分别构成一个节点对,且在这两个节点对中,节点间最小杆件数量均为3根.

|
图 2 节点间最小杆件数量 Fig.2 Minimum number of members between nodes |
既有空间结构节点位置偏差间的相关性分析应基于随机场理论中的相关结构模型,利用实测样本数据可以对节点位置偏差的相关结构模型进行拟合.
在节点位置偏差样本中抽取t对间隔均为m根杆件的节点对的位置偏差值,表示为[(x1, y1), (x2, y2), ..., (xt, yt)],其中(xi, yi)表示第i对节点的位置偏差值.则间距为m根杆件的两节点位置偏差值间的相关系数可以通过下式计算[14]:
| $ \rho_{m}=\frac{s_{x y}}{s_{x} s_{y}} $ | (4) |
| $ s_{x y}=\frac{1}{t-1} \sum\limits_{i=1}^{t}\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right) $ | (5) |
| $ s_{x}=\sqrt{\frac{1}{t-1} \sum\limits_{i=1}^{t}\left(x_{i}-\overline{x}\right)^{2}} $ | (6) |
| $ s_{y}=\sqrt{\frac{1}{t-1} \sum\limits_{i=1}^{t}\left(y_{i}-\overline{y}\right)^{2}} $ | (7) |
| $ \overline{x}=\frac{1}{t} \sum\limits_{i=1}^{t} x_{i} $ | (8) |
| $ \overline{y}=\frac{1}{t} \sum\limits_{i=1}^{t} y_{i} $ | (9) |
式中:ρm表示节点间隔为m根杆件时的相关系数.
然后,分别计算出不同节点间杆件数量下的相关系数,将计算出的相关系数ρm随节点间杆件数量m的变化情况绘制成散点图,观察散点图变化趋势,选择合适的相关结构模型曲线进行拟合.以指数型结构为例,设相关结构模型公式为
| $ \rho=a_{0} \mathrm{e}^{-m / l} $ | (10) |
式中:a0和l均为待定系数;ρ为任意两点间的相关系数.利用计算出的ρm与m对式(10)进行非线性回归分析,即可得到既有结构已测节点位置偏差值间的相关结构模型的拟合公式.
利用拟合得到的相关结构模型公式,可以计算出既有空间结构中已测节点位置偏差值间的相关系数,从而建立其相关系数矩阵P.该矩阵定量地描述了节点位置偏差间的相关性,一般表示为
| $ \mathit{\boldsymbol{P}} = \left( {\begin{array}{*{20}{c}} 1&{{\rho _{12}}}& \cdots &{{\rho _{1n}}}\\ {{\rho _{21}}}&1& \cdots &{{\rho _{2n}}}\\ \vdots & \vdots &{}& \vdots \\ {{\rho _{n1}}}&{{\rho _{n2}}}& \cdots &1 \end{array}} \right) $ | (11) |
式中:ρij表示第i与第j个节点位置偏差间的相关系数,可由拟合公式计算得出;n为样本总数.
对于节点位置偏差具有相关性的既有空间结构,相关系数矩阵P是结构整体位形推算的基础.但是,拟合相关结构模型,并计算相关系数矩阵,需要基于合理的节点位置偏差样本值,目前尚缺乏有效的抽样方法.此外,既有结构位形推算需要样本的均值和方差等统计信息,这些信息的获取必须建立在合理的统计推断理论之上.为此,本文提出一种有效的既有空间结构节点位置测量的抽样方法,即空间系统抽样方法.
2 空间系统抽样 2.1 样本分布模式空间系统抽样是以经典系统抽样为基础的抽样方法[10],旨在将样本点均匀分布在空间结构中,可有效提高抽样效率.空间系统抽样首先根据样本容量与结构节点排列形式确定样本间隔,间隔大小应满足样本均匀分布和最小样本容量的要求;然后,对结构全部节点进行编号,并随机选取一个初始样本点;最后,以初始样本点为中心,按照样本间隔选取其余样本点,得到全部样本.
样本分布模式是抽样的关键因素之一.空间系统抽样分布模式的确定,应根据空间结构的网格形式采用不同的抽样分布方案.对于网格为四边形的空间结构,例如一般的交叉桁架体系网架、四角锥体系网架、联方形柱面网壳等,可参照图 3a形式在初始样本点水平与竖直两个方向等距取样;对于网格为三角形的空间结构,例如三角锥体系网架、一般的柱面和球面网壳以及双曲抛物面和椭圆抛物面网壳等,应根据其网格的具体分布规律,确保相邻的样本点间保持相同间隔,由初始样本点向四周等距扩展取样,直至有效的样本间隔内无法再选取新的样本点,如图 3b所示.

|
图 3 空间系统抽样分布 Fig.3 Distribution of spatial system sampling |
此外,对于三角形网格结构,相同的初始样本点与样本间隔,会有不同的抽样分布模式和不同的样本容量.例如,图 3b中初始样本点相同,但左图样本数为14个,右图样本数为21个.故选择抽样分布模式时,还应根据对样本容量的需求进行合理选择.
2.2 最小样本容量样本容量是抽样的另一关键因素.在考虑样本相关性的空间抽样理论中,样本均值仍是总体均值的无偏估计[10],但是样本均值的方差需要根据空间抽样对象的相关程度进行调整.Ripley[15]提出空间抽样中样本均值方差的期望表达式为
| $ V=\frac{\sigma^{2}}{n}-\frac{E\left[C\left(X_{i}, X_{j}\right)\right]}{n} $ | (12) |
式中:n为样本量;σ2为总体方差;Xi、Xj表示任意两个样本变量,且i≠j;C(Xi, Xj)为协方差,且C(Xi, Xj)=ρ(Xi, Xj)σ(Xi)σ(Xj);ρ(Xi, Xj)为变量Xi、Xj的相关系数;σ2(Xi)、σ2(Xj)为变量Xi、Xj的方差;E[]表示取期望值.
由式(12)可知,空间抽样的样本均值方差比传统的样本均值方差小,减小了E[C(Xi, Xj)]·n-1,进一步调整可得到期望方差条件下的样本量为
| $ n=\frac{\sigma^{2}}{V}\left(1-\frac{R}{\sigma^{2}}\right)=n_{\mathrm{c}}(1-r) $ | (13) |
式中:R=E[C(Xi, Xj)];nc为基于简单随机抽样方法根据样本均值方差的期望计算得到的最小样本量;r=Rσ-2,代表样本相关性带来的影响.
对于有限总体,样本量nc一般由下式求得[16]:
| $ \frac{1}{n_{\mathrm{c}}}=\frac{1}{N_{\mathrm{c}}}+\frac{d^{2}}{Z_{1-\alpha / 2}^{2} \sigma^{2}} $ | (14) |
当样本量很大时,也可以采用下式对样本量nc进行估计[16]:
| $ \frac{1}{n_{\mathrm{c}}}=\frac{d^{2}}{Z_{1-\alpha / 2}^{2} \sigma^{2}} $ | (15) |
式(14)、(15)中:Nc为总体样本总量;d为绝对误差,即期望变量X在X+d和X-d之间;α为置信水平;Z1-α/2为正态分布下对应α的分位数.总体方差σ2需要进行预估计,在参数推断过程中,若σ超过某个限值σcr,则认为节点偏差整体离散性过大,通过统计推断构建既有结构半实测半概率模型的方法将不再适用.因此,空间等距抽样方法应用的前提是σ不超过限值σcr,故将σcr代入式(15)用以计算最小样本容量是合理且偏于安全的.
基于上述空间系统抽样方法获取的数据,经相关结构模型拟合即可确定样本间的相关系数,对于非独立样本,需要建立考虑样本相关性的统计推断方法,才能由样本的分布特性合理推断出总体的分布特性,从而实现对既有结构位形的准确推算.
3 基于空间系统抽样的统计推断 3.1 正态性检验建立既有结构的半实测半概率模型应基于已测数据的分布模式,空间系统抽样方法主要针对正态总体下的非独立样本.因此,在进行参数推断前要先对节点偏差分布的正态性进行检验.
《数据的统计处理和解释——正态性检验:GB/T 4882—2001》中针对无方向检验提供了两个方法,分别是基于样本次序统计量的夏皮洛-威尔克检验和对多种备择假设有较高功效的艾普斯-普利检验.其中,前者主要针对小样本(样本个数8~50),后者可以考虑大样本.
夏皮洛-威尔克检验的统计量为[17]
| $ W = \frac{{{{\left\{ {\sum\limits_{i = 1}^{[n/2]} {{a_i}} \left[ {{X_{(n + 1 - i)}} - {X_{(i)}}} \right]} \right\}}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {{X_{(i)}} - \bar X} \right)}^2}} }} $ | (16) |
| $ \overline{X}=\frac{1}{n} \sum\limits_{i=1}^{n} \overline{X}_{(i)} $ | (17) |
式中:样本值按非降次序排列并记为X(i);系数ai(i≤[n/2], n≤50)在样本容量为n时有特定值.Wα(n)为样本数为n、置信水平为α时所对应的分位数,当W≤Wα(n)时,拒绝样本来自正态分布的假设,否则认为样本服从正态分布.
本文的统计推断方法主要针对正态总体随机偏差样本,若样本正态性检验被拒绝,则本文后面的统计推断方法将不再适用.
3.2 均值假设检验既有空间结构节点位置偏差分布参数未知,但由于节点实际位置是以设计位置为中心形成的随机偏差,故偏差期望应为零,由此需要对样本进行均值为零的假设检验.
对于正态总体的非独立偏差值样本X= {X1, X2, …, Xn},首先根据相关系数的拟合值构建其相关系数矩阵P,将P进行等行和分解[18]得到矩阵A-1,其中,A满足P=AAT,且矩阵A的各行和为常数b,由公式Y=A-1X即可将非独立样本X转换为另一组正态总体下的简单随机样本Y={Y1, Y2, …, Yn}[11].
则对于X的均值检验H0:μ=0等价于对Y的均值检验H0:bμ=0,其检验统计量为[19]
| $ T=\left|\sqrt{n} \frac{\overline{Y}}{\sigma_{y}}\right| $ | (18) |
| $ \overline{Y}=\frac{1}{n} \sum\limits_{i=1}^{n} Y_{i} $ | (19) |
| $ \sigma_{y}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(Y_{i}-\overline{Y}\right)} $ | (20) |
式中:Y为转换后样本均值;σy为转换后样本标准差;b为矩阵A-1的行和.
T服从自由度为n-1的t分布,其否定域为T≥tα/2(n-1).当计算得到的统计量T大于给定样本容量与置信水平α下的tα/2(n-1),则拒绝原样本X均值为零的假设,说明此时的既有结构节点发生某一方向上的整体偏差,基于均值为零假设的统计推断方法将不再适用;否则认为节点偏差满足均值为零的假设.
3.3 方差估计在利用半实测半概率模型进行鉴定分析时,为使结果偏于安全,对于节点偏差程度相关的参数即方差值应进行保守的区间上限估计.基于上节对于非独立样本的转换结果,在总体均值未知的情况下,方差区间估计的统计量为[19]
| $ Q=\frac{(n-1) \sigma_{y}^{2}}{\sigma^{2}} $ | (21) |
式中:σy2为样本方差.
统计量Q服从自由度为n-1的χ2分布,则在置信度为1-α的情况下,既有结构节点偏差的方差区间上限为(n-1)σy2·[χ1-α/22(n-1)]-1,该值偏保守地估计了既有结构节点偏差值的离散程度,可以用于构建既有结构的半实测半概率模型.
4 算例分析 4.1 结构信息本文设计制作了一个单层5环K6型钢网壳试验模型,如图 4所示.

|
图 4 单层网壳模型 Fig.4 Single-layer lattice shell model |
模型跨度3.6 m,矢高0.9 m,杆件均采用ϕ6×1圆钢管,用半径70 mm的焊接球连接,材料均为Q235钢,节点和支座均视为刚性连接.
首先,对节点偏差值的方差进行预估.本文假设节点位置偏差标准差临界值σcr满足σcr=(1/300)L(L为结构最大跨度),计算得σcr=12 mm,置信度1-α取95%,绝对误差d取5 mm,计算得nc=18.取抽样间隔为2根杆件,利用MATLAB软件生成伪随机数的方法,随机选取了7号节点为起始点,通过空间系统抽样方法得到抽样方案如图 5所示,共抽取样本点18个,考虑样本间的相关性,实际最小样本容量一定满足n < nc,现有抽样方案满足最小抽样数量的要求.当取抽样间隔为3根杆件及以上时,发现样本数量已无法满足要求,故采用抽样间隔为2根杆件的方案.网壳结构径向偏差对结构整体稳定性的影响远大于切向偏差[4],为简化计算,试验中提取的节点偏差均指节点沿曲率半径方向的几何偏差.
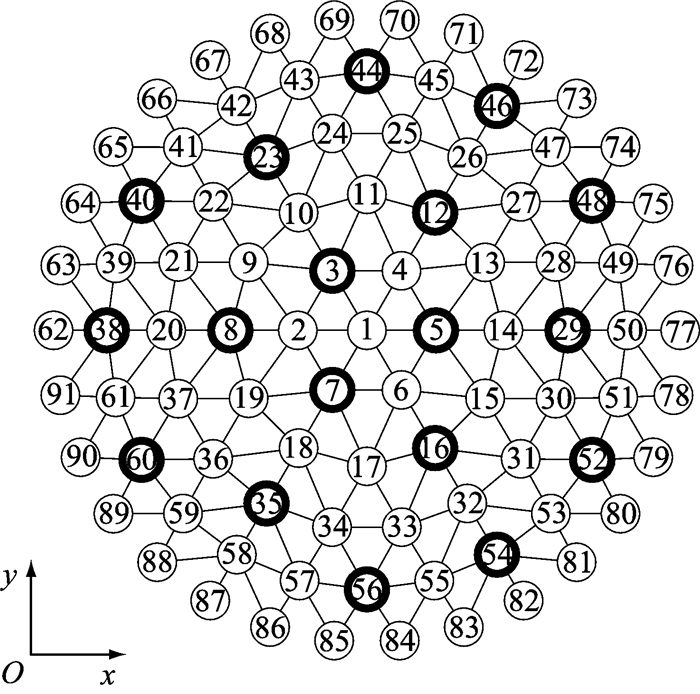
|
图 5 抽样方案 Fig.5 Sampling scheme |
计算不同杆件间距下的样本点间的相关系数,并列于表 1.绘出的相关系数与节点间距的变化趋势如图 6所示.
| 下载CSV 表 1 不同节点间杆件数量下节点偏差值的相关系数 Tab.1 Correlation coefficient of node deviation at different number of connecting members |

|
图 6 相关系数随杆件数量变化趋势 Fig.6 Correlation coefficient versus number of connecting members |
观察图 6可看出,相关系数与节点间杆件数量的相关关系近似呈指数关系,故以指数型相关结构进行拟合,经非线性回归分析得到ρij=1.002 8·e-0.509 4m,利用该公式计算不同杆件间距的节点间相关系数列于表 2,由此构建节点偏差样本的相关系数矩阵.由表 2计算得到r=0.13,则最小样本容量n=nc(1-r)≈16,显然,取18个样本点满足要求.
| 下载CSV 表 2 相关系数拟合值 Tab.2 Fitted values of correlation coefficient |
根据柳毅[18]提出的样本相关系数矩阵等行和分解算法求解A-1,由公式Y=A-1X将原始样本转换为简单随机样本.对样本进行正态性检验和均值假设检验,检验结果列于表 3.
| 下载CSV 表 3 假设检验结果 Tab.3 Results of hypothesis test |
正态性检验中,样本转换前、后统计量Worgin、Wtrans均大于W0.05,未落入拒绝域,说明转换前后的样本值均服从正态分布,且转换过程没有改变样本的正态分布特性.均值假设检验统计量结果T小于T0.025(17),也未落入拒绝域,表明样本满足均值为零的假设.方差σ2的上限估计结果为35.377,标准差σ=5.948小于临界值σcr.因此,基于空间系统抽样方法得到的样本数据可以用于推算结构的整体位形.
4.4 位形推算与鉴定分析利用上节推算出的节点位置偏差特征参数,可以构建出既有结构半实测半概率模型.以结构实际整体稳定承载力为例进行鉴定分析,利用有限元分析软件ANSYS进行数值建模计算,杆件选用beam188单元进行模拟,材料选用Q235钢材,非支座节点设置为刚接节点,支座设置为铰接,荷载选用结构自重,考虑材料和几何双非线性.
采用多种数值建模方法构建既有结构的整体数值模型,进行整体稳定承载力对比分析.全部节点位置信息采用设计值进行计算得到的结构整体稳定系数为2.185;全部节点采用实测值计算得到的稳定系数为2.152,比采用设计值小,说明了实际缺陷对于结构整体稳定性的影响.全部节点采用设计值,用一致缺陷模态法引入缺陷,计算得到的荷载系数为1.749;样本节点采用实测值,其余节点采用设计值,用一致缺陷模态法引入缺陷,计算得到荷载系数为1.817,整体稳定系数更接近实际结果,说明在数值模型中引入部分缺陷的实测值,有助于提高鉴定分析的准确性.样本节点采用实测值,其余节点采用设计值,用随机缺陷模态法,假设每个节点的偏差值均符合2倍均方差范围内的正态概率密度函数,且每个节点的偏差值都是相互独立的,利用ANSYS软件PDS模块进行蒙特卡罗随机有限元分析,经过1 000次随机输入得到具有95%可靠度的计算结果为1.776,且其平均值为2.022,中位数为2.040,众数在2.020~2.059之间.样本节点采用实测值,未测节点以设计坐标为基准,以基于空间系统抽样方法计算得到的5.948 mm为节点偏差的标准差,同样利用ANSYS软件PDS模块进行蒙特卡罗随机有限元分析,经过1 000次随机输入的频率分布结果如图 7所示.具有95%的可靠度的计算结果为1.835,且其平均值为2.046,中位数为2.063,众数在2.054~2.080之间.表明相比于以上各近似建模方法,基于空间系统抽样方法得到的统计参数构建既有结构的数值模型,其整体稳定承载力分析结果更接近于结构实际情况,优于现有的引入缺陷的其他近似建模方法.
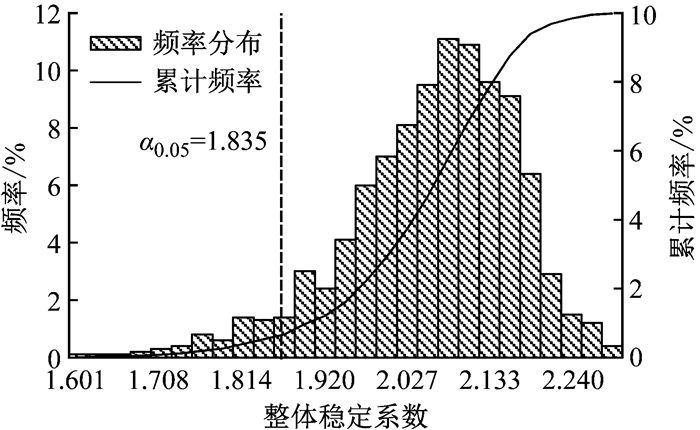
|
图 7 整体稳定系数频率分布图与频率累计图 Fig.7 Frequency distribution and frequency accumulation of overall stability coefficient |
(1) 针对节点位置偏差具有相关性的既有空间结构位形推算问题,提出了空间系统抽样方法及基于空间系统抽样的统计推断方法.此方法可以考虑节点位置偏差的相关性,建立更为准确的鉴定计算模型.
(2) 针对空间网格结构,提出空间系统抽样分布模式的选择原则,保障抽样分布的均匀性,提高抽样效率;同时,提出相应最小样本容量的计算公式.
(3) 建立了基于空间系统抽样的统计推断方法,通过对样本的相关系数矩阵进行等行和分解,准确推断出考虑相关性的总体数据的分布参数,从而构建既有结构半实测半概率模型.
(4) 通过一个算例,验证了基于空间系统抽样方法建立的半实测半概率模型更符合实际结构.
| [1] |
上海市建设和交通委员会.钢结构检测与鉴定技术规程: DG/TJ 08—2011—2007[S].上海: 上海市建筑建材业市场管理总站, 2007. Shanghai Municipal Construction and Transportation Commission. Technical specification for structural inspection and appraisal of steel structure: DG/TJ 08—2011—2007[S]. Shanghai: Shanghai Building Materials Market Management Center, 2007. |
| [2] |
中华人民共和国住房和城乡建设部.空间网格结构技术规程: JGJ 7—2010[S].北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification of space grid structure: JGJ 7—2010[S]. Beijing: China Construction Industry Press, 2010. |
| [3] |
刘俊, 罗永峰, 杨旭. 基于曲面插值的既有网壳结构节点位置推算方法[J]. 上海交通大学学报, 2018, 52(11): 1475 LIU Jun, LUO Yongfeng, YANG Xu. A method of reckoning nodal position of existing grid shell structures based on surface interpolation[J]. Journal of Shanghai Jiaotong University(Science), 2018, 52(11): 1475 |
| [4] |
吴俊, 罗永峰, 王磊. 既有网壳结构几何缺陷分布反演算法[J]. 浙江大学学报(工学版), 2018, 52(5): 864 WU Jun, LUO Yongfeng, WANG Lei. Inversion algorithm for the geometric imperfection distribution of existing reticulated structures[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(5): 864 |
| [5] |
罗永峰, 刘俊. 既有空间结构位形推算的随机偏差方法[J]. 同济大学学报(自然科学版), 2017, 45(6): 791 LUO Yongfeng, LIU Jun. Stochastic deviation method of reckoning geometric shapes of existing spatial structures[J]. Journal of Tongji University(Natural Science), 2017, 45(6): 791 |
| [6] |
唐敢, 黎德琳, 赵才其, 等. 空间结构初始几何缺陷分布规律的实测数据及统计参数[J]. 建筑结构, 2008, 38(2): 74 TANG Gan, LI Delin, ZHAO Caiqi, et al. Statistical regulation and parameter study on initial geometrical imperfections of spatial structures based on measured data[J]. Building Structure, 2008, 38(2): 74 |
| [7] |
刘学春, 张爱林, 葛家琪, 等. 施工偏差随机分布对弦支穹顶结构整体稳定性影响的研究[J]. 建筑结构学报, 2007, 28(6): 76 LIU Xuechun, ZHANG Ailin, GE Jiaqi, et al. Study on the influence of construction deviation random distribution on the integral stability of suspend-dome[J]. Journal of Building Structures, 2007, 28(6): 76 DOI:10.3321/j.issn:1000-6869.2007.06.010 |
| [8] |
CHEN Gengbo, ZHANG Hao, KIM J R, et al. Modeling geometric imperfections for reticulated shell structures using random field theory[J]. Engineering Structures, 2016, 126: 481 DOI:10.1016/j.engstruct.2016.08.008 |
| [9] |
曹胜炎, 严家平. 来自正态总体的常相关样本几个统计量的分布及其应用[J]. 数学的实践与认识, 1990, 20(4): 5 CAO Shengyan, YAN Jiaping. Distribution of several statistics of constant correlation samples from normal population and its application[J]. Mathematics in Practice and Theory, 1990, 20(4): 5 |
| [10] |
王劲峰, 姜成晟, 李连发, 等. 空间抽样与统计推断[M]. 北京: 科学出版社, 2009 WANG Jinfeng, JIANG Chengsheng, LI Lianfa, et al. Spatial sampling and statistical inference[M]. Beijing: Science Press, 2009 |
| [11] |
武坤, 刘业翔. 基于正态总体非独立样本的假设检验[J]. 数学的实践与认识, 1996, 26(3): 193 WU Kun, LIU Yexiang. Hypothesis testing of constant correlation samples under normal population[J]. Mathematics in Practice and Theory, 1996, 26(3): 193 |
| [12] |
VANMARCKE E, SHINOZUKA M, NAKAGIRI S, et al. Random field and stochastic finite elements[J]. Structural Safety, 1986, 3(3/4): 143 |
| [13] |
VANMARCKE E. Random fields:analysis and synthesis[M]. Cambridge: The MIT Press, 1983
|
| [14] |
KREYSZIG E. Advanced engineering mathematics[M]. 10th ed. New York: John Wiley & Sons Inc, 2010
|
| [15] |
RIPLEY B D. Spatial statistics[M]. New York: Wiley Press, 1981
|
| [16] |
金勇进, 杜子芳, 蒋妍. 抽样技术[M]. 3版. 北京: 中国人民大学出版社, 2012 JIN Yongjin, DU Zifang, JIANG Yan. Sampling techniques[M]. 3rd ed. Beijing: China Renmin University Press, 2012 |
| [17] |
国家质量技术监督局.数据的统计处理和解释——正态性检验: GB/T 4882—2001[S].北京: 中国标准出版社, 2001. State Bureau of Quality and Technology Supervision. Statistical intertoretation of data—Normality tests: GB/T 4882—2001[S]. Beijing: China Standard Press, 2001. |
| [18] |
柳毅, 柳力. 关于样本相关系数矩阵等行和分解算法的改进[J]. 武汉理工大学学报, 2009, 31(12): 165 LIU Yi, LIU Li. Improvement on the algorithm of equal line sum decomposition for sample correlation coefficient matrix[J]. Journal of Wuhan University of Technology, 2009, 31(12): 165 DOI:10.3963/j.issn.1671-4431.2009.12.043 |
| [19] |
张帼奋, 黄柏琴, 张彩伢, 等. 概率论、数理统计与随机过程[M]. 杭州: 浙江大学出版社, 2011 ZHANG Guofen, HUANG Baiqin, ZHANG Caiya, et al. Probability theory, mathematical statistics and stochastic processes[M]. Hangzhou: Zhejiang University Press, 2011 |
 2019, Vol. 47
2019, Vol. 47

