2. 上海师范大学 信息与机电工程学院,上海 200234
2. College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China
当前,以大数据和深度学习技术为代表的新型信息技术,为空气污染预测提供了新的技术支撑[1-3].因此,有效利用已有的空气污染监控大数据,融合新型人工智能计算技术,实现准确及时的空气污染预测模型,是当前空气污染治理领域关注的焦点问题.
从模型角度来看,空气污染物浓度预测是一个典型的时间序列数据预测问题,即基于过往时间序列的数据预测未来特定时间内的数据问题[4-6].传统空气污染物浓度预测模型[7-9]主要包括:基于历史数据和统计学方法的经验模型预测,基于数学概率模型预测,利用多维度综合模型预测,以及基于传统机器学习模型预测等.这些模型的主要特点在于:模型计算快速,易于实现; 预测过程计算复杂度低.然而,这些方法还存在以下问题:①将污染物的预测工作建立在局部历史数据和经验规则上,依赖于历史经验归纳污染物变化规律,不能够充分考虑大气环境复杂多变这一问题; ②模型的数据处理能力有限,对历史监测数据的使用不够充分,很难从大数据角度挖掘污染物浓度的分布规律; ③对污染数据内部关联特征不能进行深层次的分析,无法提取数据间深层次的联系.
近年来,随着深度学习在各个领域应用的兴起,深度学习模型所具备的极强的数据序列预测特点也成为一些交叉学科的研究热点[10-12].相对于传统机器学习模型和方法,深度学习在以时间序列为特征的数据预测方面有如下3个优点:①深度学习在大数据处理和分析能力方面可以挖掘历史大数据之间的深层联系,提高空气污染预测的准确性; ②基于深度学习的数据序列预测相比于传统机器学习预测方法,可以将海量监测数据纳入预测体系,实现对大数据的充分利用,同时考虑数据的时间和空间分布的变化,得到数据分布规律,再有效地利用这些分布规律对未来一段时间的数据进行预测; ③通过建立复杂、深层次的神经网络,选择合适的方法解决深层次的网络中易出现的梯度离散和过拟合的问题,通过对模型中参数的调整,可以有效提高神经网络预测的有效性和准确性,以达到精准预测的目的.
为了充分利用深度学习模型特征实现空气污染大数据预测,解决传统的预测模型过分依赖于过去经验、时效性差、局限于浅层数据特征提取等缺点,本文提出了一个自编码深度预测模型[13-14],通过对历史污染浓度大数据分析,总结历史大数据的特征分布,实现时序污染数据的关联性提取,提升预测的准确性.本文提出的自编码预测模型包括编码器和解码器两部分,编码器编码已知时间区间的污染物浓度,总结历史数据特征,取出其最后的隐藏向量,形成一段包含历史数据特征分布的“记忆”; 解码器利用数据特征预测后段未知污染物信息,从而达到短期预测污染物浓度的目的.为了进一步提升预测能力,本文引入LSTM(long short-term memory)[15]模型,以提升编码器的信息采集能力,使得在预测阶段有更多的参考依据,促使模型做出更合理的判断.最后,本文以PM2.5为例,对预测结果与实际测量结果进行比较,检验模型的效果.
1 相关工作机器学习是最早应用于大气污染预测领域的智能算法.学术界在基于传统机器学习的相关模型的空气污染物浓度预测方面展开了大量研究.其中,基于支持向量机[16-17]的浓度预测可以在样本数据比较少时得到比较理想的预报效果.支持向量机回归是一种基于惩罚学习的回归方法[18],通过在训练集上机器学习得到污染物浓度与其他因素之间的回归关系,建立线性回归方程,本质是使回归函数的平面宽度最小化,并结合惩罚情况等构建最终的风险函数,转化为函数最小化问题,最终建立最优回归方程; 利用一种或者多种传统机器学习结合的方法(反向传播神经网络、广义神经网络回归[19]等)建模,对模型进行训练和测试,将符合要求的模型用于预测.
深度学习在大气方面的应用,最早用于天气、温度和风力预测[20-21].Hossain[2]等证实了用深度的神经网络在有噪声的时间序列上比标准的多层前馈神经网络更好地完成天气预报工作; óscar利用深度结构抓取复杂的数据联系,结合图形处理单元(graphical processing units)[20]进行温度预测以避免非凸性等问题的影响; 另有一些将深度学习与风力预测结合的研究表明,深度学习用在风力的时序预测方面十分有效,能够大幅度减少预测误差.这些方法都仅考虑了单一因素,并没有结合与之相关的、有着重大影响的因素.但现实中一种天气状况要受到多种其他自然条件的影响,比如说温度预测,不仅考虑的是一段时间的温度值,还要考虑光照、气候等因素.
在空气污染预测方面,尹文君等[22]基于深度学习进行空气污染预报,实现更充分的大数据集成,充分考虑了污染物的时空变化、空间分布, 得到语义性的污染物变化规律; Kuremoto等利用由两个受限波尔兹曼机(restricted boltzmann machines, RBMs)[23]构成的深度网络进行时序预测[4],并通过利用CATS(competition on artificial time series)基准[5]和原始数据,证明RBMs比线性模型ARIMA(auto regressive integrated moving average)[6]性能更好; 另外,Ong等用早已被学术界多次研究的深度循环神经网络(deep recurrent neural network, DRNN)[24-25]开展空气污染物浓度预测,并证明相同条件下,DRNN比RBMs产生的结果更好[3].但是在该方法中使用的RNN并不能防止梯度消失的状态,随着时间序列的增加,RNN保留之前的信息就越少,这样就会导致模型对长期预测不敏感,对于长序列的预测能力有限.Athira[26]等也提出一种基于RNN的空气污染物预测,与之前的工作一样,这种方法同样无法解决长期预测的问题.Liu等[27]提出了一种基于LSTM的空气污染预测方法,该方法在一定程度上解决了时间序列的问题,但是其对输入输出未做处理,对预测结果有一定的影响.
本文认为如果想对未来一段时间的空气污染浓度做出较为精准的预测,就必须建立在历史观测数据之上,以往的工作都是停留在浅层次的数据分析,并未能充分理解历史数据的分布特征.本文设计了一个自编码深度预测模型,提取历史数据的有效信息,从而对未来污染物浓度进行合理预测.模型采用编码器-解码器的构架,其中编码器采集历史数据信息,解码器用来预测空气污染浓度.为了提升预测能力,本文通过叠加LSTM网络结构提升编码器的信息采集能力,从而在预测的阶段有更多的参考依据,促使模型做出合理的判断.
2 基于自编码网络的空气污染预测模型深度学习最早由Hinton等人提出[28],能够通过合适的训练方法对样本数据进行一系列的训练,并反向调整网络参数,最后得到具有深层次的网络结构的机器学习过程.
空气污染预测问题是典型的时间序列数据预测问题,即通过一段已知时间区间的序列数值,预测随后一段时间区间的数值.本文引入自编码神经网络中编码-解码的构架,结合LSTM[15]网络模型,提出一种基于自编码网络的空气污染预测模型(auto-encoder based pollutant prediction,AEPP),以解决空气污染数据的长序列时间依赖问题,实现时间序列预测.LSTM可以有效地处理时序数据,压缩和提取历史污染物浓度以及同一时刻的气候数据,提取数据中的有效信息,使得网络学习到历史数据的分布特征,同时防止重要信息的弥散,实现对后续一段时间的污染物浓度值的预测.
2.1 数据定义本文首先将时间预测视作一个序列决策过程,选取一个时间区间的数据并按照时间维度将数据输入到预测模型中.假设输入的污染物时间序列为X=(x1, …, xt, …, xm).其中,m为时间序列的长度,xt为包含污染物浓度、温度、风速、风向、湿度、降水量、其他污染物浓度等的因子.依据目标输出的不同,AEPP可选择合适的输入值,即对于以天为单位的时间序列预测,可以选用各个因子的日均值; 对于以小时为单位的时间序列预测,则选用各个因子的小时值.假设Y=(y1, …, yt, …, yn),为相对应的目标时间序列,n为输出序列长度,yt代表某一污染物浓度的观测值.
为了在AEPP中提取污染物数据的特征分布,AEPP中给定训练编码器(Encoder),用于提取输入数据的有效信息; 进一步通过编码器提取隐藏向量(记为C),该隐藏向量C包含过去一段时间输入的有效信息; 相应地,AEPP训练解码器(Decoder),将隐藏向量C注入到Decoder中,利用Decoder获取输入数据的特征信息; 最后使用Decoder按照时间维度预测获得未来一段时间区间的污染物浓度预测值,P={p1, …, pi, …, pm}(规定P向量与目标预测向量Y的长度相等).
2.2 AEPP中的LSTM模型设置LSTM是一种稳定的循环神经网络RNN改进模型.实验表明,LSTM对于长序列依赖预测有比较好的效果.LSTM神经元中内建存储单元用于存储状态信息,通过控制内置的门参数来访问、写入和清除存储单元.这几个门主要是输入门、遗忘门和输出门.与RNN相比,LSTM的优点是可以使用存储单元和门函数控制信息流,因此梯度会被限制在神经元中,达到防止梯度过快消失目标.LSTM的主要参数公式如下:
| $ \begin{array}{l} {i_t} = \sigma ({W_{xi}}{x_t} + {W_{hi}}{h_{t - 1}} + {W_{ci}} \circ {c_{t - 1}} + {b_i})\\ {f_t} = \sigma ({W_{xf}}{x_t} + {W_{hf}}{h_{t - 1}} + {W_{cf}} \circ {c_{t - 1}} + {b_f})\\ {c_t} = {f_t} \circ {c_{t - 1}} + {i_t} \circ {\rm{tanh}}({W_{xc}}{x_t} + {W_{hc}}{h_{t - 1}} + {b_c})\\ {o_t} = \sigma ({W_{xo}}{x_t} + {W_{ho}}{h_{t - 1}} + {W_{co}} \circ {c_t} + {b_o})\\ {h_t} = {o_t} \circ {\rm{tanh}}({c_t}) \end{array} $ |
式中:it、ft、ot、ct、ht分别表示t时刻的输入门、遗忘门、输出门、细胞状态和隐藏层输出; σ为logistic sigmoid函数; W为各个门的循环权重; 代表Hadamard乘积.
本文通过编码器和解码器中多层LSTM堆叠架构形成深度网络模型,从而实现增强提取污染物信息和模拟污染物变化的能力.
2.3 空气污染预测模型本文所提出的AEPP自编码网络模型由两个部分组成,即编码器(Encoder)和解码器(Decoder),分别通过Encoder压缩信息,Decoder预测信息.本文中Encoder通过LSTM实现.在Encoder部分按照时间先后序列将污染物浓度预测数据单元输入到LSTM网络中,其中数据单元指的是每个时刻污染物浓度观测值.然后获取到编码器的最后一个时刻的隐藏向量,也称为语境向量C.C能够代表整个输入时间区间的信息,同时保留重要的特征信息,去除不重要的特征信息.此时,C表达对于已知时间区间内污染物信息的浓缩“记忆”,主要包含污染物信息的特征分布.
进一步地,AEPP中Decoder依据编码器“记忆”,将蕴含在C中的信息解析出来.Decoder也由LSTM构成,将编码器的C输入到解码器中,解码器再根据当前的输入和自身的状态,对下一时刻的污染物浓度进行预测.
AEPP的整体过程如图 1所示.

|
图 1 编码器-解码器模型 Fig.1 Encoder-decoder model |
在编码器-解码器组成的AEPP模型中,编码过程是一个不断学习的过程,每个时间片的学习,都是在丰富自己的记忆(隐藏状态),但是记忆的容量是固定的(隐藏态的维度固定),所以需要不断地过滤之前的知识(可视为遗忘不常用的知识),并更新新加入的知识.经过一段时间序列的学习,获得一定的知识,形成C,然后在解码阶段再将C中蕴含的信息解析出来,对未来一段时间的信息做出预测.
2.3.1 Encoder设计编码器主要是对输入的时序数据进行特征提取.各类长度不同的输入序列X将会经由LSTM构建的编码器编译为C.假设给定输入序列X=(x1, …, xt, …, xT),则隐藏状态C可以通过如下公式得到:
| $ {h_t} = f({x_t}, {h_{t - 1}});{\rm{ }}\mathit{\boldsymbol{C}} = \phi (\{ {h_1}, \ldots , {h_{Ts}}\} ) $ |
式中:xt为t时刻的输入值; ht-1为上一个时刻的隐藏状态; f为LSTM函数; ht为t时刻的隐藏状态;
解码器主要功能是结合C和当前时刻的输入数据预测下一时刻的污染物浓度.
解码器主要公式如下:
| $ \begin{array}{l} {h_t}, {s_t} = f({y_{t - 1}}, {s_{t - 1}}, \mathit{\boldsymbol{C}})\\ {p_t} = {W_{ht}} + b \end{array} $ |
式中:st为当前时刻的预测值; yt-1为上一时刻的输出值; st-1为t-1时刻的隐藏状态; ht为t时刻输出; pt为t时刻污染物的输出; W、b为模型参数.
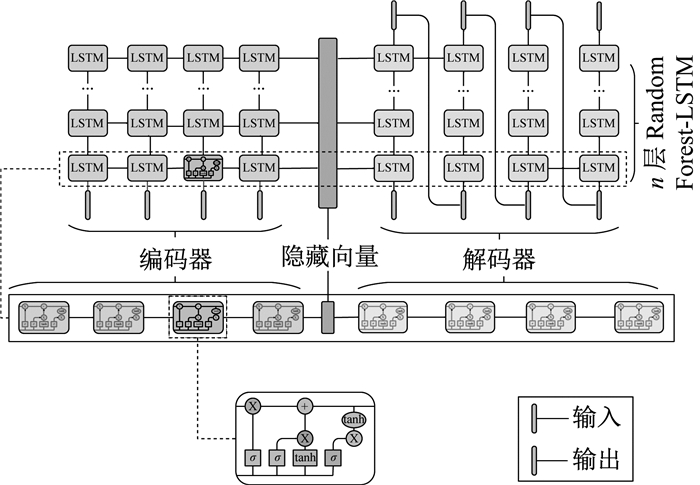
2.3.3 基于Encoder-Decoder的AEPP预测模型本文提出的AEPP模型通过语境向量C连接,通过对网络参数和损失函数的调整和大量数据的训练,实现对污染物浓度时间序列预测的功能.预测模型如图 2所示.
|
图 2 AEPP污染预测模型 Fig.2 AEPP Model |
AEPP模型的预测过程如下:
首先,编码器是由多层LSTM构成,依次将输入序列xi输入到编码器中.经过编码器的过滤和筛选,得到包含输入数据的特征分布的C,得到输入数据的特征表示.
然后,使用C作为解码器的隐藏状态,进行数据解析.在t0时刻,解码器没有输入值,可以使用全零值作为解码器开始的信号.解码器仅依靠C生成t0时刻的预测值; 在ti时刻,解码器结合ti-1时刻的输出值和隐藏状态生成ti时刻的预测值; 依次类推,逐步生成一个时间序列的污染物浓度预测值.
假定输出的预测序列值为P=(p1, …, pi, …, pn), 目标序列预测值为Y=(y1, …, yi, …, yn),定义损失函数为
| $ L = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{({y_i} - {p_i})}^2}} }}{{n}}} $ |
损失函数将误差反向传递到网络中,通过随机梯度下降法调整网络各层的连接权值,直至模型收敛.
在AEPP模型中,编码器和解码器使用同类型LSTM结构:一个用来编码输入序列,另一个用来解码输出序列.其中,编码器和解码器中的LSTM层数是可以调节的.
3 实验及仿真结果本文实验以北京市作为预测目标城市,PM2.5为目标污染物.实验中使用的数据集时间段为2010年1月1日到2014年12月31日,主要观测值分别是年份、月份、天、小时、PM2.5值、露点、温度、气压、风向、风速、累积雪量和累积雨量等.
3.1 数据预处理与量纲一化由于数据的多样性,各种空气状况衡量指标有所不同,观测范围都有很大差别.比如,在本数据集中,PM2.5这一指标的变化范围是0~994,而温度变化范围是-19~42;风向这一观测值是各种方向的标签.观测值变化范围的差异会使数据不平衡,导致神经网络的表达能力下降; 再者,神经网络也不能理解标签化的数据,所以有必要对观测数据进行量纲一化和特征化.具体来说,本实验将风向这一指标转换成数字,比如将东风变换成0、西风变成1、南风变为2、北风变为3等等; 然后将所有观测数据按照观测指标的不同将范围放缩到0~1之间,这样所有的数据在同一范围波动,可以避免观测值过大或者过小导致网络过拟合,有利于网络的收敛.
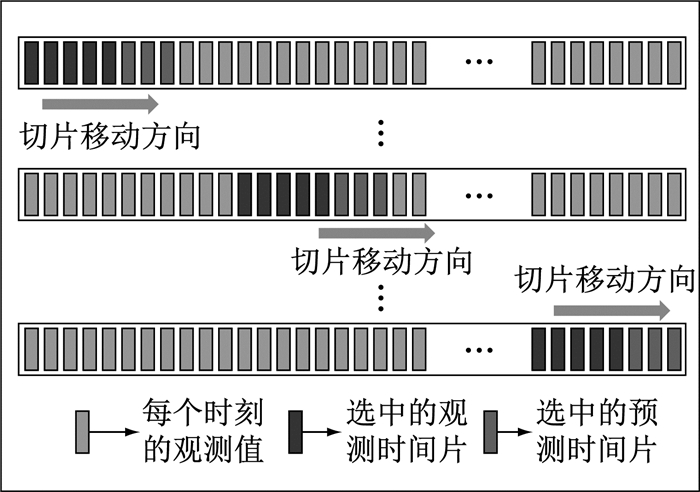
3.2 数据切片本文实验定义已知时间段M为观测时间窗口,预测时间段N为预测时间窗口.那么,实验中模型输入数据的时间窗口为M与N之和.在数据集中从开始位置找M+N时刻的观测值当作一个数据单元,然后逐步向后滑动一个时刻的窗口; 再取M+N时刻的观测值当作另一个数据单元; 按照这种操作直到数据集的时间末尾; 然后将所有数据单元合并构成整个数据集.数据集的格式为[Tsize, M+N, D],观测数据格式应为[Tsize, M, D],目标数据格式应为[Tsize, N, D].其中,Tsize为数据单元的总量,D为特征维度,即同一时刻各种观测值的种类.数据切片如图 3所示.
|
图 3 数据切片图 Fig.3 Data slices |
为了检验本文中模型的有效性,实验中按照经典的训练和测试数据切分方式,即80%的数据用来训练模型,20%用来测试模型的准确性.训练数据和测试数据集结构都是{Xi, Yi}.其中,i∈(0, N),N为集合中的数据总数; Xi={xi1, xi2, …, xim}; Yi={yi1, yi2, …, yin}; m、n分别为已知时间区间和预测时间区间.
为了验证不同RNN结构对AEPP模型的影响,实验中使用了不同的RNN结构,即RNN、GRU(gated recurrent unit)和LSTM等检测模型的性能.由于模型中的编码器和解码器比较灵活,没有固定时间限制,可以自由调整已知时间和预测时间,实验中仅使用前5个时刻的空气观测值和后3个时刻的污染物预测值(简称[5,3]段)训练模型.为了保持和其他模型的统一性,测试阶段使用前72 h的空气观测值预测后24 h的污染物观测值(简称[72,24]段).
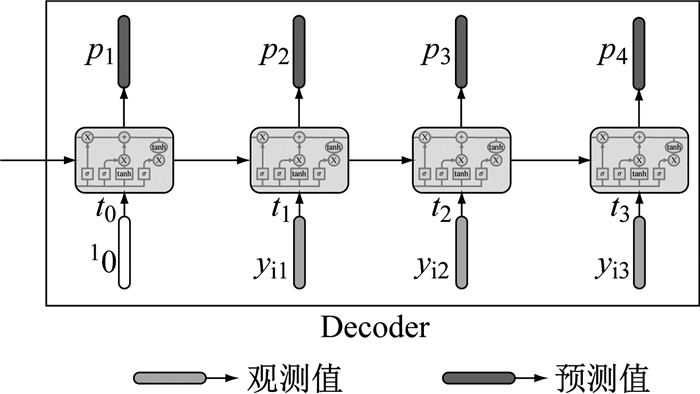
首先,对于模型的编码器部分,把已知时间区间的大气观测值按序列输入到编码器中.然后,对于模型的解码器部分,训练和测试阶段都是一致的,这两个阶段均使用上一时刻的真实值预测下一时刻的污染物浓度.在解码器的开始时刻t0将输入置为10,这就意味着解码器只通过编码器所浓缩的隐藏向量C来预测这一时刻t0的污染物浓度p1.然后,再将数据集中的Yi第一时刻观测值yi1输入到编码器中,用来预测t1时刻的污染物浓度p2; 以此类推,yi2预测p3,yi3预测p4等等.整体效果就是将输入值Yi后延一个时刻,第一时刻补10,即(10, yi1, yi2, …, yi(n-1)),这样就可以达到用上一时刻预测下一时刻污染物浓度的目的.具体结构如图 4所示.
|
图 4 训练阶段和测试阶段解码器的结构 Fig.4 Structures of decoder in training and test |
实验共使用6个模型:RNN模型、GRU模型、LSTM模型、RNN+AEPP模型、GRU+AEPP模型和LSTM+AEPP模型.对于AEPP模型,实验选取前5个时刻的观测值作为模型输入,通过模型预测后3个时刻的PM2.5的浓度.由于RNN模型、GRU模型和LSTM模型在[5,3]段和[72,24]段不可共用模型参数,故需要分别训练.然后,按照上述规则分别对所有模型进行训练和测试,并记录实验结果.
实验结果表明:实验数据集中,PM2.5的质量浓度变化范围是0~994.经过100轮的迭代,所有模型的损失值先有明显下降的趋势,之后保持平稳并基本收敛.本文使用测试集进行测试,实验结果总结见表 1.表中,RMSE表示均方根误差,值越小表示模型性能越好; 相关系数表示真实值和预测值之间的相关程度,越接近1,相关性越好.表中数据均精确到小数点后2位.CAMx(comprehensive air quality model with extensions)、CMAQ(community multiscale air quality modeling system)、NAOPMS(nested air quality prediction modeling system)和WRF-CHEM(weather research and forecasting model coupled with chemistry)表示传统污染物预测模型,RNN、GRU和LSTM表示经典的循环神经网络,最后3个AEPP模型表示本文中的模型和不同神经网络组合.
| 下载CSV 表 1 模型对比表 Tab.1 Comparison of models |
对于单模型RNN、GRU和LSTM来说,[5,3]和[72,24]段模型参数不可共享,需要分别训练.从表 1中可以看出,预测效果并没有太大提升.对于AEPP模型来说,[5,3]段和[72,24]段模型参数可以共享,本实验是用[5,3]段数据训练网络,然后用[72,24]段作测试.
从表 1可以看出:LSTM+AEPP模型预测最准确,相关性最高; RNN+AEPP模型预测不出结果; GRU+AEPP模型预测效果一般.这也说明LSTM对于解决时间序列问题比RNN和GRU好.
为了进一步检测LSTM+AEPP模型的性能,实验继续使用上述[5,3]段保存的模型参数,对不同时间段的数据进行测试.采用的已知时间和预测时间分别是[3,1]、[6,2]、[9,3]、…、[72,24]等,总体比例为3:1.各个预测时间段的RMSE如图 5所示.

|
图 5 不同时间段的污染物质量浓度RMSE值 Fig.5 RMSEs in different periods |
由实验可以看出:预测时间越长,预测精度越高.由此可以看出,LSTM适用于解决长时间依赖的问题.
需要指出的是,由于该模型依赖于长时间序列的数据,在遇到气候或污染源突变(如社会生产导致的污染源变化、交通压力或突然的冷空气等)时,会出现预测错误的情况.这是由LSTM的特性所决定的.
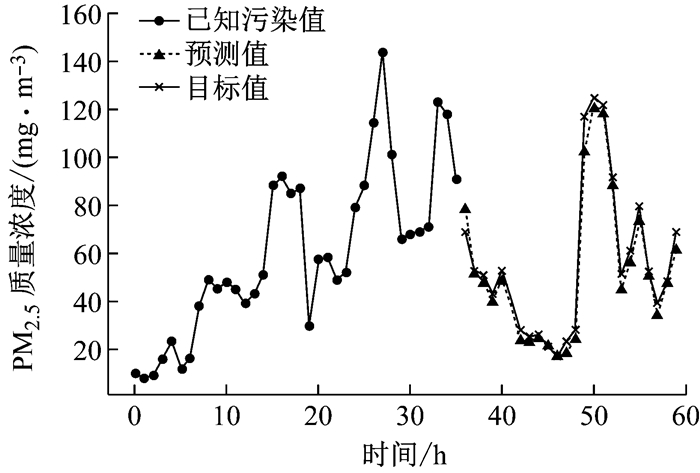
最后,应用LSTM+AEPP模型给出一个PM2.5预测样本,如图 6所示.
|
图 6 PM2.5预测样本 Fig.6 Samples of prediction |
本文介绍了一个基于深度学习的污染物预测模型,主要针对污染物浓度进行序列建模,预测污染物浓度变化趋势.这个预测模型主要用编码器、解码器的方式来总结历史污染物浓度分布,并预测未知时间段的污染物浓度.通过实验证明,本模型在短期污染物浓度预测方面可以取得不错的效果.不足之处是随着预测时间的增加,预测效果越差; 在训练阶段和测试阶段的预测值会有较大差异.当然这也符合天气预测的规律:预测时间区间越短,预测结果越准确; 预测时间区间越长,不确定因素越多,预测准确率就会相对下降.
| [1] |
王俭, 胡筱敏, 郑龙熙, 等. 基于BP模型的大气污染预报方法的研究[J]. 环境科学研究, 2002, 15(5): 62 WANG Jian, HU Xiaomin, ZHENG Longxi, et al. Study on forecasting of air pollution based on bp model[J]. Research of Environmental Sciences, 2002, 15(5): 62 DOI:10.3321/j.issn:1001-6929.2002.05.017 |
| [2] |
HOSSAIN M, REKABDAR B, LOUIS S J, et al. Forecasting the weather of Nevada: a deep learning approach[C]//2015 International Joint Conference on Neural Networks (IJCNN). Killarney: IEEE, 2015: 1-6.
|
| [3] |
ONG B T, SUGIURA K, ZETTSU K. Dynamic pre-training of deep recurrent neural networks for predicting environmental monitoring data[C]//IEEE International Conference on Big Data. Washington D C: IEEE Computer Society, 2014: 760-765.
|
| [4] |
KUREMOTO T, KIMURA S, KOBAYASHI K, et al. Time series forecasting using a deep belief network with restricted Boltzmann machines[J]. Neurocomputing, 2014, 137(15): 47 |
| [5] |
LENDASSE A, OJA E, SIMULA O, et al. Time series prediction competition: the CATS benchmark[J]. Neurocomputing, 2007, 70(13/14/15): 2325 |
| [6] |
BOX G E P, JENKINS G M, REINSEL G C. Time series analysis: forecasting and control[M]. 5th ed. Hoboken N J: John Wiley & Sons, 2015.
|
| [7] |
谢永华, 张鸣敏, 杨乐, 等. 基于支持向量机回归的城市PM2.5浓度预测[J]. 计算机工程与设计, 2015(11): 3106 XIE Yonghua, ZHANG Mingmin, YANG Le, et al. Predicting urban PM2.5 concentration in China using support vector regression[J]. Computer Engineering and Design, 2015(11): 3106 |
| [8] |
陈俏, 曹根牛, 陈柳. 支持向量机应用于大气污染物浓度预测[J]. 计算机技术与发展, 2010, 20(1): 250 CHEN Qiao, CAO Genniu, CHEN Liu. Application of support vector machine to atmospheric pollution prediction[J]. Computer Technology and Development, 2010, 20(1): 250 DOI:10.3969/j.issn.1673-629X.2010.01.065 |
| [9] |
黄思, 唐晓, 徐文帅, 等. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(1): 56 HUANG Si, TANG Xiao, XU Wenshuai, et al. Application of ensemble forecast and linear regression method in improving PM10 forecast over Beijing areas[J]. Acta Scientiae Circumstantiae, 2015, 35(1): 56 |
| [10] |
DENG L, LI X. Machine learning paradigms for speech recognition: an overview[J]. IEEE Transactions on Audio Speech & Language Processing, 2013, 21(5): 1060 |
| [11] |
DAN C, MEIER U, MASCI J, et al. Multi-column deep neural network for traffic sign classification[J]. Neural Networks the Official Journal of the International Neural Network Society, 2012, 32(1): 333 |
| [12] |
BALDI P, SADOWSKI P, WHITESON D. Searching for exotic particles in high-energy physics with deep learning[J]. Nature Communications, 2014, 5(5): 4308 |
| [13] |
LANGE S, RIEDMILLER M. Deep auto-encoder neural networks in reinforcement learning[C]//International Joint Conference on Neural Networks (IJCNN). Barcelona: IEEE, 2010: 1-8.
|
| [14] |
BALDI P. Autoencoders, unsupervised learning and deep architectures[C]//Proceedings of ICML workshop on unsupervised and transfer learning. Edinburgh: Journal of Machine Learning and Research, 2012: 37-49.
|
| [15] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735 DOI:10.1162/neco.1997.9.8.1735 |
| [16] |
NOBLE W S. What is a support vector machine?[J]. Nature Biotechnology, 2006, 24(12): 1565 DOI:10.1038/nbt1206-1565 |
| [17] |
罗瑜.支持向量机在机器学习中的应用研究[D].成都: 西南交通大学, 2007. LUO Yu. Research on application of support vector machine in machine learning[D]. Chengdu: Southwest Jiaotong University, 2007. |
| [18] |
陈晓峰, 王士同, 曹苏群. 自适应误差惩罚支撑向量回归机[J]. 电子与信息学报, 2008, 30(2): 367 CHEN Xiaofeng, WANG Shitong, CAO Suqun. SVR with adaptive error penalization[J]. Journal of Electronics & Information Technology, 2008, 30(2): 367 |
| [19] |
DRAPER N R, SMITH H. Selecting the "best" regression equation[J]. Applied Regression Analysis, 1998(1): 327 |
| [20] |
OSCAR E D Q. Deep learning for temperature prediction using GPUs[D]. Valencia: Universitat Politècnica de València, 2015.
|
| [21] |
SERGIO A T, LUDERMIR T B. Deep learning for wind speed forecasting in northeastern region of Brazil[C]//Brazilian Conference on Intelligent Systems. Natal: IEEE, 2015: 322-327.
|
| [22] |
尹文君, 张大伟, 严京海, 等. 基于深度学习的大数据空气污染预报[J]. 中国环境管理, 2015(6): 46 YIN Wenjun, ZHANG Dawei, YAN Jinghai, et al. Deep learning based air pollutant forecasting with big data[J]. Chinese Journal of Environmental Management, 2015(6): 46 DOI:10.3969/j.issn.1674-6252.2015.06.011 |
| [23] |
HINTON G E. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2010, 9(1): 599 |
| [24] |
KUMAR P R, RAVI V. Bankruptcy prediction in banks and firms via statistical and intelligent techniques-a review[J]. European Journal of Operational Research, 2007, 180(1): 1 DOI:10.1016/j.ejor.2006.08.043 |
| [25] |
DENG L, HINTON G, KINGSBURY B. New types of deep neural network learning for speech recognition and related applications: an overview[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013: 8599-8603.
|
| [26] |
ATHIRA V, GEETHA P, VINAYAKUMAR R, et al. DeepAirNet: applying recurrent networks for air quality prediction[J]. Procedia Computer Science, 2018, 132: 1394 DOI:10.1016/j.procs.2018.05.068 |
| [27] |
LIU X, LIU Q, ZOU Y, et al. A self-organizing LSTM-based approach to PM2.5 forecast[C]//International Conference on Cloud Computing and Security. Haikou: Springer, 2018: 683-693.
|
| [28] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436 DOI:10.1038/nature14539 |
 2019, Vol. 47
2019, Vol. 47

