随着智能汽车发展,理解驾驶员是如何开车的变得越来越重要.一方面,理解驾驶员的驾驶行为对提高智能汽车安全性有重要意义;另一方面,智能汽车在驾驶安全的基础之上还需要具有理解驾驶员,环境,以及周围交通的能力[1].首先,智能汽车应在驾驶中使驾驶员感到舒适.近几年智能汽车在道路测试和行驶中发生的一系列事故表明,在汽车智能驾驶系统完全成熟之前,保持驾驶员时刻在环是非常重要的[2-3].而且当智能汽车和人类驾驶员共同驾驶车辆时,智能汽车的驾驶行为必须考虑驾驶员的接受程度.智能汽车的驾驶行为使驾驶员感到不适应不仅会降低驾驶员对智能汽车驾驶能力的信任感[4],智能汽车与人类驾驶员在驾驶中产生的分歧还可能引发其他安全事故.其次,智能汽车的驾驶行为应当将交通效率和交通安全考虑在内.在未来很长一段时间内,智能汽车与人类驾驶汽车的混合车流将长期存在.因此智能汽车在驾驶中需要将周围交通环境中的人类驾驶汽车的驾驶行为考虑在内.驾驶员的制动反应时间在1.1 s左右[5],而智能汽车的控制频率通常在10 Hz以上.如果不将驾驶员的这种制动特性考虑在内,在跟车工况中智能汽车过快的制动行为会引发后车追尾危险.因此智能汽车应具有类人驾驶的能力以提高驾驶员对智能汽车的接受程度.
驾驶员的驾驶意图主要通过踩制动踏板或加速度踏板,转动方向盘等行为来表达.纵向加速度、侧向加速度、横摆角速度、和速度是描述驾驶员驾驶行为最为直接的几个车辆参数.驾驶员踩制动踏板或加速踏板的行为直接与车辆的纵向加速度相关;驾驶员转动方向盘的行为直接与车辆的侧向加速度和横摆角速度相关.速度是非常重要的车辆状态参数,驾驶员会根据不同的驾驶场景调整车辆行驶速度,并会根据车辆行驶速度调整其驾驶行为.因此选择纵向加速度、侧向加速度、横摆角速度、和速度这几个车辆参数作为描述驾驶员驾驶行为特性的特征参数.
分析驾驶员驾驶行为特征参数的分布特性可以帮助更好地理解驾驶员是如何开车.首先,驾驶员在日常驾驶中并不会达到车辆的物理极限.附着椭圆[6]是车辆加速度的物理极限.文献[7]研究表明驾驶员的加速度分布在菱形区域内,文献[8]研究表明驾驶员的加速度分布在双三角形区域内.这说明驾驶员在日常驾驶中的加速行为并不会达到车辆的附着极限.其次,驾驶员的驾驶行为特征参数也不会达到其驾驶能力极限,并且通常驾驶员的驾驶行为特征参数之间是互相关联的.文献[9]研究表明驾驶员的最大侧向加速度按二次规律随速度增加减小.文献[10]表明驾驶员通过弯道时的速度与弯道半径是相关的,并且使用驾驶员操作误差随速度的变化来解释这一现象.这些都说明驾驶员的驾驶行为特性存在独特的内在规律.
自然驾驶研究(naturalistic driving studies, NDS)可以提供真实可靠的驾驶行为数据.本文使用NDS研究了驾驶员的驾驶行为特征参数的分布特性与相互关系.
1 自然驾驶数据采集本文中所使用的自然驾驶数据(naturalistic driving data, NDD)均来自于China-FOT.China-FOT是由中瑞交通安全研究中心(CTS)发起,由沃尔沃,同济大学,查尔姆斯理工大学等合作在上海市进行的自然驾驶研究.China-FOT从2014年7月持续至2015年12月,分为4个阶段进行,每个阶段有8辆试验车,共32位驾驶员参与测试.试验车全部采用沃尔沃S60L,在试验车上装备有丰富的环境感知系统和数据采集系统,包括地理定位系统(GPS),毫米波雷达,摄像头,速度传感器,加速度传感器等.试验车,数据采集系统,和摄像头图像信息(图 1).测试中所有驾驶员都有大于15 000 km的驾驶经验,因此可认为China-FOT中所有驾驶员都不是新手驾驶员.在测试中每位驾驶员使用试验车约3个月.在这段测试时间中,驾驶员可以在任意时间驾驶试验车去任何地方.因此China-FOT可以采集驾驶员在真实的道路交通环境中的真实驾驶行为.测试中所有32位驾驶员均居住在上海及周边,China-FOT中大部分数据均采集自上海及周边的城市道路,乡村道路,城市高架路等.很多驾驶员也驾驶试验车跨省长途行驶,China-FOT中也有相当比例的高速公路行驶里程.由于驾驶员较少驾驶试验车到上海中环以内的拥堵区域,所以城市拥堵道路所占比例适中.在大约17个月的测试中,China-FOT共收集到7 402段可用行程,共129 935 km的驾驶数据.

|
图 1 测试车、数据采集系统以及摄像头图像信息 Fig.1 Test vehicle, data acquisition systems, and videos information from the camera |
为了准确描述驾驶行为特征参数的概率分布特性,第一步要确定多少驾驶数据可以得到稳定收敛的驾驶行为特征参数的概率分布.如果使用数据太少,无法提取到真实可信的驾驶行为特征参数概率分布;如果使用数据太多,会导致数据采集难度和数据采集成本上升.因此本节讨论驾驶行为特征参数概率分布的收敛性.首先,使用核密度估计得到不同数据量数据集的驾驶行为特征参数在当前采集工况下的概率分布.接着,使用相对熵来衡量各个数据集的核密度估计之间的差别.最后,根据相对熵的变化确定能够得到稳定收敛驾驶行为特征参数概率分布的数据量.
2.1 核密度估计由于事先不知道驾驶行为特征参数服从什么样的概率分布,因此无法使用概率密度函数来描述驾驶员的驾驶行为特征参数概率分布.包括高斯混合模型[11]和核密度估计[12]在内的非参数方法可以通过有限的数据采样点来拟合驾驶员的驾驶行为特征参数的概率分布.非参数估计不利用关于数据分布的先验知识,对数据分布不做附加假定,因而可以用来拟合未知分布.本文使用核密度估计来拟合驾驶行为特征参数的概率分布.记{xi}i=1n为一组观测向量,则核密度函数
| $ {\hat f_n}(x) = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{1}{h}} K\left( {\frac{{x - {x_i}}}{h}} \right) $ | (1) |
式中:K(x)为核函数;n为观测数据的数据量; h为带宽.选择高斯函数作为核密度估计的核函数,则核函数可以表示为
| $ K(x)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{x^{2}}{2}\right) $ | (2) |
在核密度估计中,带宽h的选择对核密度估计的精度有很大影响[13].对于正态分布数据样本,文献[14]中的经验法效果比较好,但该方法并不适用于非正态分布样本.对于非正态分布数据样本,包括插入法(plug-in selector)[15-16]和交叉验证法(cross validation selector)[17-19]在内的以数据为基础的自动带宽选择方法可以得到较好的效果.在本文中,使用文献[15]中提供的方法来估计带宽.
2.2 相对熵相对熵可以用来描述两个概率分布之间差异的大小[20].因此使用相对熵来检验当一组新的数据加入到数据集中,不包含新数据的数据集与包含新数据的数据集之间是否有显著差异.记一组新数据的数据量为m,不包含新数据的数据集中的数据量为n,包含新数据的数据集中的数据量为n+m,则两个数据集的相对熵定义为
| $ \begin{array}{l}{D_{\mathrm{KL}}\left[\hat{f}_{n+m}(x)| | \hat{f}_{n}(x)\right]=} \\~~~~~ {\int_{-\infty}^{\infty} \hat{f}_{n+m}(x) \log \frac{\hat{f}_{n+m}(x)}{\hat{f}_{n}(x)} \mathrm{d} x}\end{array} $ | (3) |
当两个数据集之间的差异越小时,两个数据集的相对熵越趋近于0.而当两个数据集的相对熵充分小时,表明两个数据集之间已经没有显著差异,新加入的一组数据对之前的数据集的分布没有显著的影响.如果向之前数据集中持续加入新数据的过程中相对熵始终保持充分小,则表明分布已趋于稳定.再向数据集中加入新的数据不会显著改变数据分布,新的数据不再提供有用的信息,数据集的分布收敛.若存在一个Γ使式(4)成立,则称Γ为可以得到稳定收敛驾驶行为特征参数概率分布的数据量.
| $ \forall \mathit{\Gamma } \le n \le \mathit{\Omega }, \left\| {{D_{KL}}\left[ {{{\hat f}_{n + m}}(x)||{{\hat f}_n}(x)} \right]} \right\| < \varepsilon $ | (4) |
式中:Ω为数据库中最大的数据量;ε为一充分小的正实数.
2.3 数据处理过程及结果在China-FOT中选取全部32位试验驾驶员的可用驾驶数据作为数据库.数据库中包含驾驶数据的行驶里程为121 951 km,行驶时间为3 432 h.China-FOT中的数据采集系统的采样频率均为10 Hz.数据库中共有123 558 489组观测数据,将该数据库的数据量记为Ω.
驾驶行为特征参数概率分布的收敛性检验算法可以表述为:
(1) 选取1×105组观测数据作为初始数据集.
(2) 将1×105组新的观测数据加入到之前数据集中.旧数据集中包含k×105组观测数据,新的数据集中包含(k+1)×105组观测数据.
(3) 计算旧数据集与新数据集的核密度函数,并计算这两个数据集的相对熵DKL.
(4) 若DKL不满足式(4),跳转到第(2)步;若DKL满足式(4)且Ω-k>50×105,成功并结束,并令Γ=k;若DKL满足式(4)且Ω-k < 50×105,失败并结束,数据库需要更大的数据量.
使用纵向加速度ax、侧向加速度ay、速度v、和横摆角速度ω这4个特征参数来检验驾驶行为的收敛性.对于每一个驾驶行为特征参数,使用收敛性检验算法计算该参数得到收敛分布的数据量.并定义其中最大的一个为得到稳定收敛的驾驶员驾驶行为特性的数据量.即
| $ \mathit{\Gamma } = \max \left\{ {{\mathit{\Gamma }_x}|x \in \left\{ {{a_x}, {a_y}, v, \omega } \right\}} \right\} $ | (5) |
临界值ε的选取对结果有较大影响.较大的ε会导致较小的Γ,较小的ε会导致较大的Γ.ε太大会使算法在驾驶行为特征参数真正收敛之前停止.而ε太小会大大增加需要的数据量,甚至会使算法无法得到有效的结果.通过实际验证,当ε=10-5时,即使非常大的数据集也无法使DKL满足式(4).选择一个非常保守的ε=10-4作为临界值.这与文献[21]中的临界值选择相同.同时,如果数据库需要其中几乎所有的数据才能满足式(4),就无法确定驾驶行为特征参数的概率分布是真正收敛还是数据库不够大.因而使用条件Ω-Γ>50×105来保证有充足数据来验证驾驶行为特征参数概率分布的收敛性.即在又加入了500万新的观测数据到数据集后,新数据集与旧数据集的核密度估计仍没有显著差异.这样就可以保证通过检验算法能够得到稳定收敛的驾驶行为特征参数的概率分布.
不同数据量时纵向加速度、侧向加速度、速度、和横摆角速度的核密度函数如图 2~图 5所示,图中核密度函数是量纲一的.可以看出不同数据量纵向加速度,侧向加速度,横摆角速度的核密度函数差别很小.在数据量较小时,速度的核密度函数在加入新数据后会发生较大变化.当数据量很大时,速度的分布也趋于稳定.

|
图 2 不同数据量时纵向加速度的核密度函数 Fig.2 Kernel density function of the longitudinal acceleration with different amount of data |

|
图 3 不同数据量时侧向加速度的核密度函数 Fig.3 Kernel density function of the lateral acceleration with different amount of data |

|
图 4 不同数据量时速度的核密度函数 Fig.4 Kernel density function of the velocity with different amount of data |

|
图 5 不同数据量时横摆角速度的核密度函数 Fig.5 Kernel density function of the yaw rate with different amount of data |
各个数据集驾驶行为特征参数的相对熵如图 6所示,图中相对熵为量纲一.通过图 6可以看出,4个驾驶行为特征参数的相对熵都随数据量的增加而逐渐减小.其中,纵向加速度、侧向加速度、和横摆角速度只需要很少的数据量就可以保证相对熵小于ε.并且随着数据量增加,这3个参数都逐渐减小并趋近于0.而速度则需要相对较大的数据量才能保证相对熵小于ε.

|
图 6 驾驶行为特征参数的相对熵 Fig.6 Kullback-Leibler divergence of the driving behavior characteristic parameters |
根据收敛性检验算法,得到稳定收敛的驾驶员驾驶行为特性的数据量为
| $ \begin{array}{l} \mathit{\Gamma } = \max \left\{ {{\mathit{\Gamma }_{{a_x}}}, {\mathit{\Gamma }_{{a_y}}}, {\mathit{\Gamma }_v}, {\mathit{\Gamma }_\omega }} \right\} = \\ \begin{array}{*{20}{l}} {\max \left\{ {23 \times {{10}^5}, 45 \times {{10}^5}, 897 \times {{10}^5}, 22 \times {{10}^5}} \right\} = }\\ {897 \times {{10}^5}} \end{array} \end{array} $ | (6) |
式(6)表明约9×107组观测数据组成的数据集可以得到收敛的概率分布.因此本文的数据库可以得到稳定收敛的驾驶员驾驶行为特性.通过式(6)可知,纵向加速度、侧向加速度、和横摆角速度达到收敛标准所需要的数据量都在0.5×107组观测数据之内,并且远远小于速度达到收敛标准所需要的数据量.通过图 2~图 5也可以看出,纵向加速度、侧向加速度、和横摆角速度符合相似的分布样式,而速度则符合完全不同的分布样式.
3 驾驶行为特征参数的分布特性纵向加速度、侧向加速度、和横摆角速度的分布样式比较相似.即在0附近概率密度很大,且概率密度随着参数的数值增加而减小.驾驶员在左转和右转时没有区别[8],因此在后面的分析中总是不区分左右的.而制动减速度和前向加速度通常不对称,因此将制动减速度和前向加速度分别进行分析.使用文献[22]中介绍的Matlab分布拟合工具箱对制动减速度、前向加速度、侧向加速度、和横摆角速度的概率分布进行拟合.该工具箱使用常用的17种分布来拟合经验分布.使用赤池信息量(akaike information criterion, AIC)和贝叶斯信息量(bayesian information criterion, BIC)[23-24]来评价各种分布的拟合效果.使用符号CAIC来表示经验分布的AIC.则CAIC定义为
| $ C_{\mathrm{AIC}}=2 r-2 \ln L $ | (7) |
| $ L=\hat{f}(x | \boldsymbol{\theta}, \boldsymbol{M}) $ | (8) |
式(7)~(8)中:r为概率密度函数的参数个数;L为根据观测数据x确定的统计分布M的最大似然函数;θ为统计分布的参数.
使用符号CBIC来表示经验分布的BIC.则CBIC定义为
| $ C_{\mathrm{BIC}}=r \ln n-2 \ln L $ | (9) |
| $ L=\hat{f}(x | \boldsymbol{\theta}, \boldsymbol{M}) $ | (10) |
式(9)~(10)中:n为观测数据的数据量.
通过式(7)~式(10)可以看出,AIC或BIC越小,表明统计分布M越接近由观测数据决定的经验分布.BIC与AIC的主要区别在于BIC多了一个关于观测数据的数据量的惩罚项,因此BIC在数据量较大时更倾向于选择参数更少的分布.
对于制动减速度、前向加速度、侧向加速度、和横摆角速度,帕累托分布的拟合效果总是最优的,指数分布的拟合效果总是次优的.以侧向加速度为例,图 7和表 1表示了正态分布,帕累托分布,和指数分布这三种典型分布对侧向加速度的拟合效果.表 1中,u, σ, k为分布参数.

|
图 7 不同统计分布侧向加速度拟合效果 Fig.7 Fitting results of the lateral acceleration of different statistical distributions |
| 下载CSV 表 1 不同统计分布侧向加速度拟合结果 Tab.1 Fitting results of different statistical distributions |
通过图 7可以看出,帕累托分布对驾驶行为特征参数的概率分布拟合效果较好.正态分布不能用于拟合驾驶行为特征参数的概率分布.一方面,正态分布的概率密度函数在侧向加速度接近0的地方太小了,其严重低估了侧向加速度在接近0时的分布概率;另一方面,通过图 7的局部放大图可以看到,正态分布在侧向加速度增大时下降太快了,其概率密度函数远比侧向加速度的经验分布更早地下降到了0.通过图 7也可以看出,指数分布也存在下降过快的现象,但要比正态分布稍好一点.这种现象在包括前向加速度,制动减速度,横摆角速度在内的驾驶行为特征参数的概率分布中都存在.
通过表 1可以看出,指数分布的AIC和BIC与帕累托分布差距不大,正态分布的AIC和BIC远远大于帕累托分布或指数分布.这也表明了正态分布不能用于拟合驾驶行为特征参数的概率分布.考虑到指数分布只有1个参数,当对分布拟合效果要求不高时,也可以使用指数分布拟合驾驶行为特征参数的概率分布.
帕累托分布也经常被称为重尾分布.重尾分布通常指概率密度下降比指数分布慢的分布[25].驾驶行为特征参数近似服从帕累托分布表明了较大的制动减速度、前向加速度、侧向加速度、和横摆角速度出现的概率远比正态分布大.如果使用正态分布来描述驾驶行为特征参数的概率分布会产生较大偏差.驾驶员速度的概率分布服从完全不同的分布形式.速度经验分布的概率密度函数在0处值很大,在0~15 m·s-1区间内基本是一条平直的直线,在大于15 m·s-1区间内逐渐下降到0.
对于制动减速度、前向加速度、侧向加速度、和横摆角速度,通常在0附近非常小的区间内就分布着超过50%的数据.比如对于侧向加速度,有61%的观测数据分布在侧向加速度为0~0.2 m·s-2区间内.同时重尾分布表明仍有相当部分数据会分布在较大侧向加速度的范围内.分析制动减速度、前向加速度、侧向加速度、和横摆角速度的百分位对智能汽车舒适性的提高,智能汽车测试场景设计,目标车状态估计等具有一定意义.因此取驾驶行为特征参数的90到99.99百分位进行分析.根据驾驶行为特征参数的经验分布得到的驾驶行为特征参数的百分位见表 2.
| 下载CSV 表 2 驾驶行为特征参数的百分位 Tab.2 Percentile of the driving behavior characteristic parameters |
车辆直行时的驾驶员加速和制动行为是较为关心的.表 3表示了车辆直行工况的前向加速度和制动减速度的百分位,此时侧向加速度为0.
| 下载CSV 表 3 车辆直行时的纵向加速度百分位 Tab.3 Percentile of the longitudinal acceleration when vehicle go straight |
表 4表示了没有加速和制动时的侧向加速度百分位,即纵向加速度为0时的转向操作行为.
| 下载CSV 表 4 没有加速和制动时的侧向加速度百分位 Tab.4 Percentile of the lateral acceleration when longitudinal acceleration is zero |
通过对比表 2和表 3可以看出,所有数据的百分位与侧向加速度为0时的纵向加速度百分位非常接近.同样,对比表 2和表 4可以看出,所有数据的百分位与纵向加速度为0时的百分位非常接近.这是由于纵向加速度或侧向加速度在0附近的数据占所有数据中的大多数,而较大纵向加速度或较大侧向加速度的数据所占的比例较小.
4 驾驶行为特征参数之间的相互影响驾驶员的驾驶行为特征参数之间是存在相互影响的.比如在不同的侧向加速度区间,纵向加速度的概率分布必然会有变化.本节分析了驾驶行为特征参数的条件分布,以此为基础讨论了驾驶行为特征参数之间的相互影响.
4.1 加速度之间的相互影响同样以侧向加速度为例,图 8表示了不同纵向加速度区间的侧向加速度的概率密度.通过图 8可以看出,在不同纵向加速度区间的侧向加速始终符合与全部侧向加速度数据类似的帕累托分布.通过图 8的局部放大图也可看出,不同纵向加速度区间的侧向加速度的概率密度仅仅在细节部分有所区别.这个结论同样适用于制动减速度,前向加速度,和横摆角速度.
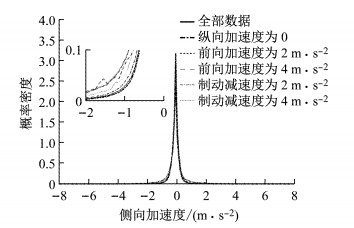
|
图 8 不同纵向加速区间的侧向加速度的概率密度 Fig.8 Density of the lateral acceleration in different longitudinal acceleration intervals |
虽然在不同的纵向加速度区间的侧向加速度始终符合帕累托分布,但概率分布细节差异会使加速度分布百分位产生较大差异.图 9表示了不同纵向加速度区间的侧向加速度百分位.通过图 9可以看出,随着前向加速度或制动减速度增加,侧向加速度百分位上移.这表明了随着前向加速或制动减速度增加,驾驶员的转向越倾向于剧烈.前向加速度对侧向加速度百分位的影响大于制动减速度.

|
图 9 不同纵向加速度区间的侧向加速度百分位 Fig.9 Percentile of the lateral acceleration in different longitudinal acceleration intervals |
这一结果似乎与文献[8]中的结论矛盾.文献[8]研究了驾驶员纵向加速度与侧向加速的联合分布,发现驾驶员的纵向加速度与侧向加速度分布在一个双三角形区域中.当纵向加速度增大时,大侧向加速度的概率是下降的.
分析图 9与图 10之间的差异可知,图 9是针对某一特定纵向加速度区间内的数据的侧向加速度百分位,而图 10是所有数据的二维分布.图 9中表示了不同纵向加速度区间的数据之间的频率比,而图 10中表示了不同纵向加速度区间的数据之间的频数比.因此图 9和图 10都是合理的.对比图 9与图 10可知,随着纵向加速度增加,虽然大侧向加速的绝对频数下降了,但在相同纵向加速度区间内较大侧向加速度的相对频率上升了.这一现象的一种解释是,当驾驶员强烈制动或急加速时,驾驶员更可能会由于自身意愿或受环境所迫进行剧烈的转向操作.比如在路口减速转向,进出停车位,遇到危险等.但纵向加速度和侧向加速度都很大的工况始终是驾驶中的极小概率事件.

|
图 10 纵向加速度与侧向加速的联合分布[8] Fig.10 The multivariate distribution of the longitudinal acceleration and lateral acceleration[8] |
图 11表示了不同侧向加速度区间的前向加速度百分位.可以看到随着侧向加速度增加,前向加速度的百分位上移.这表明当侧向加速度增加时,驾驶员的加速更剧烈.

|
图 11 不同侧向加速度区间的前向加速度百分位 Fig.11 Percentile of the forward acceleration in different lateral acceleration intervals |
图 12表示了不同侧向加速度区间的制动减速度百分位,可以看到不同侧向加速度区间的制动减速度的百分位是一条略有上升的直线.这表明当侧向加速度增加时,驾驶员的制动行为有更剧烈的趋势,但差别不大.

|
图 12 不同侧向加速度区间的制动减速度百分位 Fig.12 Percentile of the brake deceleration in different lateral acceleration intervals |
进一步分析可知,驾驶员的加速行为分布在双三角形区域中也与纵向加速度与侧向加速度之间的这种关系是有关的.通过图 8可知,侧向加速度在不同纵向加速度区间内总符合帕累托分布,反之亦然.因此如果在纵向加速度绝对值变大时侧向加速度的帕累托分布相同或更加集中,那么二维加速度分布的相对密度等高线和边界应当是一条内凹的曲线.通过图 10可以看出,加速行为分布的双三角区域在制动减速部分有一点内凹趋势,而在前向加速部分有一点外凸趋势.这通过图 9~图 12也可以表现出来.即制动减速度与侧向加速度的百分位之间相互促进上移的作用小一点,而前向加速度与侧向加速度的百分位之间相互促进上移的作用大一些.因此图 10所示的双三角形区域是由于前向加速度、制动减速度和侧向加速度这几个变量的帕累托分布和在变量相互影响下帕累托分布参数变化这两种因素共同作用的结果.
4.2 速度对驾驶行为特征参数的影响仍然以侧向加速度为例,图 13表示了不同速度区间的侧向加速度的概率密度.通过图 13可以看出,在不同速度区间的侧向加速度始终符合帕累托分布,并且帕累托分布的参数与全部数据时的分布参数差别不大.同样,该结论也适用于制动减速度,前向加速度,和横摆角速度.

|
图 13 不同速度区间的侧向加速度的概率密度 Fig.13 Density of the lateral acceleration in different velocity intervals |
图 14表示了不同速度区间的前向加速度百分位.图 15表示了不同速度区间的制动减速度百分位.图 16表示了不同速度区间的侧向加速度百分位.图 17表示了不同速度区间的横摆角速度的百分位.通过图 14~图 17可以看出,前向加速度、制动减速度、侧向加速度和横摆角速度这几个参数的百分位都随速度增加先上升后下降.即在低速时驾驶行为特征参数的百分位会随速度增加而上移,在高速时驾驶行为特征参数的百分位会随速度增加而下移.这与文献[8]中的结论一致.文献[8]中的数据等高线也在图 14~图 16中给出.通过对比可知,本文中得到的数据百分位与数据等高线的变化趋势高度一致,并且数据百分位与相应数据等高线也基本重合.通过图 4可知,速度的概率分布在0~15 m·s-1区间内基本是均匀分布的.当速度大于15 m·s-1时,其概率密度近似线性的逐渐下降到0.因此数据等高线的变化主要来源于不同速度区间的帕累托分布参数的变化.所以数据等高线与百分位曲线高度一致.

|
图 14 不同速度区间的前向加速度百分位 Fig.14 Percentile of the forward acceleration in different velocity intervals |

|
图 15 不同速度区间的制动减速度百分位 Fig.15 Percentile of the brake deceleration in different velocity intervals |

|
图 16 不同速度区间的侧向加速度百分位 Fig.16 Percentile of the lateral acceleration in different velocity intervals |

|
图 17 不同速度区间的横摆角速度百分位 Fig.17 Percentile of yaw rate in different velocity intervals |
驾驶员的这种行为特性对智能汽车的乘坐舒适性具有一定指导作用.在辅助驾驶或人机共驾中,当车辆速度越快时,加速、制动、和转向操作应当越平缓.驾驶员操作最为剧烈的速度区间是5~10 m·s-1.因而在中低速时,智能汽车的加速,制动和转向操作可以适当剧烈一些.
5 结论本文使用NDD研究了驾驶员驾驶行为特征参数的概率分布.首先,使用核密度估计得到了驾驶行为特征参数的概率分布,使用相对熵描述不同数据集之间的差异.大约9×107组观测数据点组成的数据集可以得到收敛的驾驶行为特征参数分布,因此使用本文中的数据库可以得到真实可靠的驾驶员驾驶行为特征参数的分布特性.接着,对驾驶行为特征参数进行拟合发现,驾驶员的前向加速度、制动减速度、侧向加速度和横摆角速度均近似服从帕累托分布.帕累托分布表明有超过50%的数据会集中在0附近很小的区域内,但较大加速度或横摆角速度出现的概率却要比正态分布大的多.最后,分析了驾驶行为特征参数之间的相互影响.前向加速度、制动减速度和侧向加速度在不同的加速度和速度区间中总是近似服从帕累托分布,只是帕累托分布参数会有变化.随着制动减速度或前向加速度增加,侧向加速度的百分位上移,驾驶员转向操作趋于更加剧烈.同样,当侧向加速度增加时,驾驶员的制动或加速操作也趋于更剧烈.当速度增加时,前向加速度、制动减速度、侧向加速度和横摆角速度的百分位均先上升后下降.通过对比驾驶行为特征参数的百分位等高线与数据百分位可知,二维加速度分布在双三角形区域中是加速度的帕累托分布和帕累托分布参数变化这两个因素共同作用的结果.
| [1] |
MARINIK A, BISHOP R, FITCHETT V, et al. Human factors evaluation of level 2 and level 3 automated driving concepts[R]. Washington D C: NHTSA, 2014.
|
| [2] |
KHOSRAVANI S, KHAJEPOUR A, FIDAN B, et al. Development of a robust vehicle control with driver in the loop[C]//American Control Conference. Portland: IEEE, 2014: 3482-3487. https://ieeexplore.ieee.org/document/6858845/
|
| [3] |
LI R, LI S, GAO H, et al. Effects of human adaptation and trust on shared control for driver-automation cooperative driving[C/CD]//SAE Technical Paper Series. Detroit: SAE Publication Group, 2017. 2017-01-1987.
|
| [4] |
LEE J D, SEE K A. Trust in automation: designing for appropriate reliance[J]. Human Factors, 2004, 46(1): 50 DOI:10.1518/hfes.46.1.50.30392 |
| [5] |
ZHANG Y, ANTONSSON E K, GROTE K. A new threat assessment measure for collision avoidance systems[C]//Intelligent Transportation Systems Conference. Toronto: IEEE, 2006: 968-975. https://ieeexplore.ieee.org/document/1706870/
|
| [6] |
DUGOFF H, FRANCHER P S, SEGEL L. Tire performance characteristics affecting vehicle response to steering and braking control inputs[R]. Ann Arbor: University of Michigan, 1969.
|
| [7] |
BOSETTI P, DA LIO M, SAROLDI A. On the human control of vehicles: an experimental study of acceleration[J]. European Transport Research Review, 2013, 6(2): 157 |
| [8] |
LIU R, ZHU X. Driving data distribution of human drivers in urban driving condition[C]//International Conference on Intelligent Transportation Systems. Yokohama: IEEE, 2017: 1-6. https://www.researchgate.net/publication/323792440_Driving_data_distribution_of_human_drivers_in_urban_driving_condition
|
| [9] |
REYMOND G, KEMENY A, DROULEZ J, et al. Role of lateral acceleration in curve driving: driver model and experiments on a real vehicle and a driving simulator[J]. Human Factors, 2001, 43(3): 483 DOI:10.1518/001872001775898188 |
| [10] |
VANWINSUM W, GODTHELP H. Speed choice and steering behavior in curve driving[J]. Human Factors, 1996, 38(3): 434 DOI:10.1518/001872096778701926 |
| [11] |
BUTAKOV V A, IOANNOU P. Personalized driver/vehicle Lane change models for ADAS[J]. IEEE Transactions on Vehicular Technology, 2015, 64(10): 4422 DOI:10.1109/TVT.2014.2369522 |
| [12] |
BISHOP C M. Pattern recognition and machine learning[M]. New York: Springer, 2006
|
| [13] |
JONES M C, MARRON J S, SHEATHER S J. Progress in data-based bandwidth selection for Kernel density estimation[J]. Computational Statistics, 1996, 11(3): 337 |
| [14] |
SILVERMAN B W. Density estimation for statistics and data analysis[M]. Boca Raton: CRC Press, 1986
|
| [15] |
BOTEV Z I, GROTOWSKI J F, KROESE D P. Kernel density estimation via diffusion[J]. Annals of Statistics, 2010, 38(5): 2916 |
| [16] |
SHEATHER S J, JONES M C. A reliable data-based bandwidth selection method for kernel density estimation[J]. Journal of the Royal Statistical Society Series B-Methodological, 1991, 53(3): 683 |
| [17] |
RUDEMO M. Empirical choice of histograms and kernel density estimators[J]. Scandinavian Journal of Statistics, 1982, 9(2): 65 |
| [18] |
BOWMAN A W. An alternative method of cross-validation for the smoothing of density estimates[J]. Biometrika, 1984, 71(2): 353 DOI:10.1093/biomet/71.2.353 |
| [19] |
HALL P, MARRON J S, PARK B U. Smoothed cross-validation[J]. Probability Theory and Related Fields, 1992, 92(1): 1 |
| [20] |
MACKAY D J C. Information theory, inference and learning algorithms[M]. Cambridge: Cambridge University Press, 2003
|
| [21] |
WANG Wenshuo, LIU Chang, ZHAO Ding. How much data are enough? a statistical approach with case study on longitudinal driving behavior[J]. IEEE Transactions on Intelligent Vehicle, 2017, 2(2): 85 |
| [22] |
ZHAO D, LAM H, PENG H, et al. Accelerated evaluation of automated vehicles safety in lane-change scenarios based on importance sampling techniques[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(3): 595 DOI:10.1109/TITS.2016.2582208 |
| [23] |
WIT E, VAN DEN HEUVEL E, ROMEIJN J W. All models are wrong...': an introduction to model uncertainty[J]. Statistica Neerlandica, 2012, 66(3): 217 DOI:10.1111/j.1467-9574.2012.00530.x |
| [24] |
AHO K, DERRYBERRY D, PETERSON T. Model selection for ecologists: the worldviews of AIC and BIC[J]. Ecology, 2014, 95(3): 631 DOI:10.1890/13-1452.1 |
| [25] |
FOSS S, KORSHUNOV D, ZACHARY S. An introduction to heavy-tailed and subexponential distributions[M]. New York: Springer, 2011
|
 2019, Vol. 47
2019, Vol. 47

