便携式RGB-D(彩色-深度)传感器因廉价、便携等特点被广泛应用于计算机视觉、同时定位与建图(simultaneous localization and mapping, SLAM)及室内小场景建模等领域,目前针对便携式RGB-D深度传感器的研究,侧重于点云配准、建模算法研究与改进;对其自身的深度测量精度以及重建场景模型精度的定量评价分析很少,一般只基于视觉的逼真程度进行定性分析.与高精度三维激光扫描仪(light detection and ranging, LiDAR)等专业量测设备不同,便携式RGB-D传感器研发是为了游戏并未考虑精确量测的应用.现LiDAR仪器获取的点云精度都有具体的精度指标,但针对RGB-D传感器深度测量质量的定量分析较少,且已有的针对Kinect相机的相关研究多集中在1.0的结构光深度获取方式[1-2].文献[2]通过实验分析了物体不同表面状况(光滑、毛糙)下飞行时间测距法(time of flight, ToF)深度测量的精度,而对采用ToF法的Kinect 2.0[3]在不同的颜色、材质情况下其深度测量精度的变化情况未有研究.这对将便携式RGB-D传感器应用于测绘近景领域的场景测量与三维重建很不利,为此有必要从理论与实验两方面对其实际深度量测精度和最终模型重建精度进行深入与定量的研究.
本文以常用的Kinect 2.0为研究对象从两方面对RGB-D相机的测量建模精度进行研究:(1)深度测量精度的定量分析,侧重于深度测量精度与目标距离、颜色、材质间的关系研究;(2)场景及模型三维重建结果的精度定量分析与评估.在此基础上得出Kinect场景重建精度在不同环境下的适用性、确定其最佳应用范围.
1 Kinect 2.0深度测量误差来源及建模精度的评定方法Kinect 2.0进行三维重建时,深度值为该物点到深度相机像平面的垂直距离d(点云Z坐标值),根据相机标定参数由深度图转换得到目标的三维点云;参数的准确性会影响生成点云的精度且会产生系统性偏差,需通过相机的精确标定来消除该影响[4].而最根本的误差来源是深度d的测量误差,直接影响点云的精度及最终重建场景模型的精度.
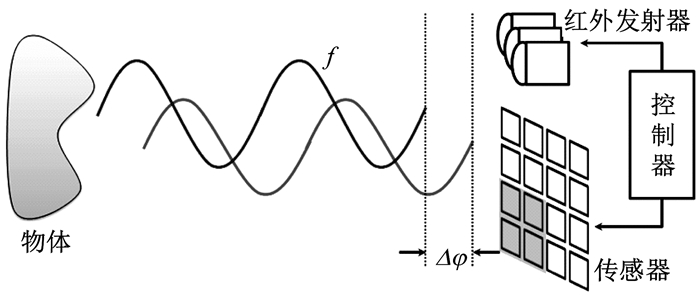
1.1 ToF深度测量原理与误差来源Kinect 2.0深度测量采用ToF中的调制连续波法(continuous wave modulation,CWM) [2, 5],其发射红外光波长为830~950 nm,原理如图 1所示.其中f是调制频率,Δφ为相位偏移.
式(1)为图 1中发射的电磁波信号s(t)(蓝),a为振幅,f为调制频率;式(2)为经过时延Δt后接收到的反射波r(t)(红),m为接受到的衰减后的振幅,n为接收的反射波信号中的偏置,其是环境光和系统内部偏移的函数;相位偏移Δφ与时延Δt间存在Δφ=2πf·Δt的关系.
| $ s(t) = a \cdot (1 + \sin (2{\rm{ \mathsf{ π} }}ft)) $ | (1) |
| $ \begin{array}{l} r(t) = m \cdot (1 + \sin (2{\rm{ \mathsf{ π} }}f(t - \Delta t))) + n = \\ \;\;\;\;\;\;\;\;\;m \cdot (1 + \sin (2{\rm{ \mathsf{ π} }}ft - \Delta \varphi )) + n \end{array} $ | (2) |
CWM通过测定相位偏移Δφ来确定时延Δt,物体与深度相机的距离d由式(3)确定,其中c为光速.
| $ d = c \cdot \Delta t/2 = c \cdot \Delta \varphi /(4{\rm{ \mathsf{ π} }}f) $ | (3) |
理论上深度测量的方差可用式(4)近似表示:
| $ {\sigma _d} \approx \frac{c}{{4\sqrt 2 {\rm{ \mathsf{ π} }}f}} \cdot \frac{{\sqrt {m + n} }}{{{c_d} \cdot m}} $ | (4) |
式(4)中cd为调制常量,描述ToF传感器分离和收集光电信号的好坏能力.当m,f较大时σd偏小精度高,n偏大时则会导致精度降低;但因f增大时调制对比度会衰减,所以其增大有上限;而m与距离d存在m∝1/d2的关系[6],即目标距相机越远m越小,对应的距离测量精度也随之降低.
根据本节上述原理,ToF深度测量误差的主要来源有:(1)传感器自身的误差.包括cd、f的影响以及深度相机标定误差造成物方坐标的系统性偏差.(2)几何因素产生的误差.一般由传感器与待测物之间的相对距离和位置等因素引起的;文献[2]指出,Kinect2.0在量测范围内(0.8~4.0 m)目标距相机越远精度越差;当目标与传感器像平面距离相等、在同一平面内时,精度与目标在深度图像上的成像位置到光轴中心的距离成反比呈辐射状.(3)测量环境造成的误差.包括两种情况:环境中存在电磁波干扰源,以及物体表面不同性状(颜色、材料、表面状况)影响反射率造成精度下降.环境中有干扰源时(对Kinect2.0是强红外波段辐射源或吸收源),会干扰反射红外光r(t)的正常接受,对Δφ、Δt测量产生很大影响,由式(3) Δφ、Δt的误差会直接造成深度值d的精度与可靠性降低.就物体具体的反射特性而言,具有较高漫反射率的表面可反射更多调制信号到传感器完成深度获取的卷积运算,这会提高信噪比对d的测量精度有利[7];而对易出现镜面反射或透明的目标则可能出现反射波几乎完全偏离相机或无反射波,导致深度图上出现孔洞.
在第1.1节误差来源中,(1)对给定的相机其cd与f已定,只能通过相机严格标定来减少残留的标定误差引起的系统偏差.(2)则是在数据获取时选择合适的成像范围与位置,重要物体应尽量位于深度图的中心位置,来减少影响.(3)中的环境影响,有关红外辐射源干扰,通过尽量避免来消除;其他方面研究,现在主要有针对不同距离以及不同表面状况下进行ToF深度测量的精度变化实验研究,指出当物体表面较为光亮时(如瓷砖和玻璃等)极易镜面反射红外光,无法测量对应区域的深度[2, 8-11].但对于不同颜色材质(木头、塑料等)状况下深度测量的精度不清楚,特别是对在不同距离下各种材质目标精度变化的定量变化规律未研究.真实的应用中建模物体与场景的材质、颜色都是多种多样的,本文为此展开研究.
1.2 建模精度的评定方法利用多帧深度图通过配准重建场景点云模型,重建参数与深度图精度共同影响了模型精度.目前对点云模型数据进行精度评价的方法主要有:①利用点云模型上检查点的已知理论值,计算点位中误差进行评估[12];②提取模型场景中目标的边长、面积、体积等属性值与参考理论值比较,用均方根误差、相对误差等参数进行评价[12-13];③在给定搜索距离阈值的前提下,确定重建模型与参考点云间的豪斯多夫距离,利用该值进行评估[14].
方法①需要已知检查点的准确的理论位置,不易获取且极易受点位判断误差影响,故较少使用.本文以精度更高的点云模型作为参考标准点云;利用方法②,比较两套模型属性值的绝对误差和相对误差;利用方法③,将Kinect点云模型和标准点云配准,并对豪斯多夫距离计算方法加以改进,比较两者间的相似程度;实现对建模精度的评估.
1.2.1 基于模型表面参数指标的绝对和相对误差一般采用目标的长、宽等可以明确判断的特征作为模型的表面属性参数,计算其绝对误差、相对误差.但对光滑曲面物体(如圆形物体等)难以选择这些参数时,可采用切面的一些属性参数,如圆切面曲线拟合的直径等.
(1) 绝对误差(absolute error)ε*是以同一量纲反映测量值偏离真值的实际大小:
| $ {\varepsilon ^*} = |L - \tilde L| $ | (5) |
式中:L为观测值(文中为待分析精度的点云上的属性特征值如长度);
(2) 相对误差(relative error)ε指测量的绝对误差与真值的比值,更能反映测量的精度:
| $ \varepsilon = \frac{{\left| {{\varepsilon ^*}} \right|}}{{\widetilde L}} \times 100\% $ | (6) |
第1.2.1节所述方法在模型场景中难以进行特征的判断和选择表面特征参数时无法采用(如无规则曲面),此时用豪斯多夫距离进行精度分析.
H-D是描述两组点集之间相似程度的一种度量,它不需建立两个点集间属性特征精确的对应关系,只需计算两者间的相似程度(最大距离);H-D越小相似程度越高.该方法更适于不易提取特征的点云精度评定,本文采用单向H-D法并对其进行改进,方法如下:
(1) 假设空间存在两个点集Ra={a1, a2, …, am}、Rb={b1, b2, …, bn},它们之间的单向H-D定义为
| $ h\left( {{R_a}, {R_b}} \right) = \mathop {\max }\limits_{{a_i} \in {R_a}} \left( {\min \left\| {\mathop a\limits_{{b_i} \in {R_b}} - b} \right\|} \right) $ | (7) |
式中:‖·‖为距离范数,文中采用点集Ra, Rb之间的欧式距离.对Ra中的每个点ai求出它到Rb的最小距离,h(Ra, Rb)为Ra中所有点到Rb的最小距离的最大值,一般用该值描述两集合间的相似程度.
(2) 考虑到实际点云模型会存在粗差,造成个别点到参考点云的最小距离很大,出现野值,对H-D计算产生极大影响,直接用式(7)的结果进行精度评定并不合理.为此对H-D方法进行如下改进:
对Ra中所有点到点集Rb的最小距离,从0到最大距离,以一定距离间隔Δ进行划分(δ根据Ra的精度情况确定),统计不同间隔内的点数占总点数的比例,生成直方图;并从0到某一距离累计点数i比例P,生成累计直方图,如式(8):
| $ P = \sum\limits_{i = 0}^I {{p_{{\delta _i}}}} ,{\mathit{\Delta} _i} = i \cdot \mathit{\Delta} ,I > 0 $ | (8) |
式中:pδi为最小距离落在Δi到Δi+1的点数占Ra总点数的比例.认为累计比例P达到某一百分比时,对应的距离D=Iδ才较合理地反映精度状况,该值称为改进的H-D.该值越大,表征两个模型之间的差异性越大,模型重建的质量越低.
采用改进的H-D方法,对重建的模型与参考点云的相似性程度进行定量评估,流程如图 2所示.

|
图 2 基于改进Hausdorff距离的精度评估流程图 Fig.2 Flowchart of accuracy evaluation based on the improved Hausdorff distance |
采用不同颜色、不同材质的自制平面靶标进行实验,获取距相机不同距离处靶标的深度数据并转化成点云.和深度测量精度相比,可视靶标平面为理想平面.对靶标处深度数据进行平面最佳拟合,得到靶标点云到拟合平面的中误差,分析不同颜色、材质、距离下该误差的变化,研究这些因素对深度测量的影响[1, 15].
实验所用平面靶标为A3大小,将其垂直设立并使其成像位于深度图的中心位置(以光轴中心为对称中心)且位置固定.架设相机获取数据时成像面应与靶标面平行,获取的一组数据包括彩色、红外与深度影像(图 3).为分析距离的影响,在Kinect深度量测范围内,距靶标1.0~4.0 m间每隔约0.5 m设置相机测站采集数据.为研究颜色的影响,在每一测站选择同一材质(纸)红、绿、蓝、白、黑5种典型颜色的靶标进行数据采集;为研究材质的影响,选择6种常见的材质(纸、玻璃、瓷砖、木头、布、塑料)的靶标进行实验,除木头为哑光漆漆成紫红色,玻璃透明外,其他接近白色.最终得到不同距离处的实验数据.

|
图 3 采集数据(彩色、红外、深度影像) Fig.3 Obtained data (color, infrared, depth image) |
文中共采集了10种靶标(5种颜色的纸质以及5种其他材质),在7种测程下共获得70组数据.
2.2 实验数据处理利用文献[15]的方法标定出相机的精确参数,对获得的深度图进行转换得到3D点云.然后对原始点云进行除噪、裁剪等预处理,保留平面靶标处的目标信息用于精度分析.
根据最小二乘原理利用靶标处点云数据拟合靶标平面,方程为aX+bY+cZ+e=0,其中a, b, c, e表示平面参数,
| $ \begin{array}{*{20}{c}} {{\varepsilon _d} = \frac{{a{X_i} + b{Y_i} + c{Z_i} + e}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} = }\\ {a{X_i} + b{Y_i} + c{Z_i} + e} \end{array} $ | (9) |
εd值反映了量测的靶标点云数据的误差.对所有误差进行分段统计分析,分别得到不同材质颜色在1~4 m中7种距离处的统计结果,分析表明εd都近似服从正态分布,即点云误差满足偶然误差的特性(透明玻璃无有效数据除外).
用标准差δd来表示靶标点深度值的误差.因实验中靶标面与Kinect相机成像面接近平行,拟合平面的a, b≈0,c≈1,可认为εd主要由Z(深度值)的量测误差δZ引起.由误差传播定律,δZ与δd之间的精度存在式(10)所示的关系:
| $ {\delta _d} = c{\delta _Z} $ | (10) |
因此可认为δZ≈δd.
2.3 深度测量精度分析利用2.2节方法计算不同颜色、材质标靶在距传感器不同距离d处深度值测量的δZ.以δZ为因变量, d为自变量,得到δZ与d的变化关系曲线,图 4为同材质不同颜色时的变化关曲线;图 5为不同材质时的情况.

|
图 4 不同颜色的误差随距离的变化关系 Fig.4 Errors of different colors varies with distance |

|
图 5 不同材质的误差随距离的变化关系 Fig.5 Error of different material varies with distance |
图 4、5中δZ与d的变化曲线类似式(11)的二次函数,故对其利用式(11)进行拟合.
| $ {\delta _Z} = {k_1} \cdot {d^2} + {k_2} $ | (11) |
得到k1、k2值及拟合的确定性系数R2.取深度量测值的误差在两倍中误差的置信区间内,偶然误差的极限值Δmax=2δZ,得到不同距离,不同颜色、材质平面靶标的深度量测值Z的精度变化范围(单位:mm),最终得到表 1.表 1中确定系数R2最差为0.879,大多数都在0.9以上,说明式(11)很好地反映了精度与距离的关系.综合表 1和图 4、5,首先有深度测量时δZ∝d2,误差值与深度距离平方成线性正比关系,这与1.1节理论分析中反射辐射m与距离d存在m∝1/d2关系一致,此外颜色和材质对深度量测值精度有很大影响.颜色影响:黑色精度最差,k1、k2都比其他颜色大,随距离增大误差增速远大于其他颜色,精度下降最剧烈,4 m时已达27 mm,远大于标称精度,这是因为黑色物体对工作波段反射率很低,反射信号弱且随距离增加衰减极快;②实验中其他颜色深度量测的精度差别较小,都优于黑色,基本在标称精度内.材质的影响:①木头、布与纸(白)的k1、k2值接近,误差范围为3~12 mm,木头的精度稍好;②塑料(半透明)与瓷砖的精度差,其k1值是①中材质的2倍,随距离增加精度下降速率也很快,此外塑料的k2值最大,即近距离时其深度测量精度也不高.玻璃材质因其透光性太强传感器无法接收到有效的反射信息.
| 下载CSV 表 1 深度量测值的精度变化范围 Tab.1 Accuracy of depth measurement |
综上,目标为漫反射时深度测量精度取决于其对工作波段的反射情况,反射率越低精度越差且误差随距离增加也增大越快;目标为镜面或材质具有透明性时精度会下降;即颜色材质对深度测量精度有很大影响.为保证精度达到标称要求,深度测量范围应小于2.5 m;对黑色、瓷砖及半透明材料场景时,距离应小于2 m.
3 Kinect场景重建精度实验分析Kinect建模精度除受深度数据精度影响还和模型重建算法有关,所以还应对最终重建的点云模型进行精度实验分析.这里选择了两种形状材质等有较大差异、较具代表性的实验对象:某会议室的一部分(约4 m×5 m),为亚光表面接近朗伯面的材质环境;常见的瓷质花瓶(约1 m×0.3 m),为易出现高光镜面反射的材质模型.
3.1 数据的采集获取 3.1.1 标准参考模型数据获取采用FARO Focus3d 120激光扫描仪进行场景模型扫描,获取高精度模型点云数据作为精度分析的参考标准,其测距误差在25 m内为±2 mm.
对实验模型场景进行先粗后精扫描,得到三维点云数据,利用配备的球形靶标作为测站间点云配准的依据,通过点云配准、拼接得到统一坐标下的结果.经统计配准点位精度达到2 mm,与标称精度一致.对拼接的结果进行去噪优化和兴趣区提取,删除不相关的点云信息,生成标准参考点云数据.
3.1.2 基于Kinect的模型点云数据获取利用标定得到的相机参数[15]对获得的深度图像进行转换得到3D点云.在预处理阶段,分别采用双边滤波对深度数据降噪平滑以及快速特征点与二进制特征描述子(oriented fast and rotated brief, ORB)特征检测算法提取彩色影像上的特征点.因为微软自带Kinect Fusion中的模型重建方法精度较差,为此在模型重建阶段,采用文献[16]的改进迭代最近邻法(iterative closest point, ICP)算法,引入多种约束减少点云配准误差的累积影响,进行多帧深度数据配准重建模型.实验中的花瓶及会议室场景进行Kinect建模的结果如图 6所示.

|
图 6 Kinect相机位姿恢复后的模型点云示意图 Fig.6 Overlay point cloud after Kinect pose estimation |
分别在Kinect和标准参考模型表面判断量取17段距离特征,比较两模型上对应的距离值差异,结果见表 2(注意:表中Absolute_Error未取绝对值,后表同).
| 下载CSV 表 2 两种传感器重建模型表面的长度参数对比 Tab.2 Comparison of the length parameters on the surface of the Kinect and reference models |
特征距离差异值中包含有因判断及滤波造成的深度图像边缘变平滑模糊而引入的手工量测误差,但总体这些误差较小.在特征点量测上,判断误差一般为0.5像素,考虑是利用多帧点云数据的配准结果进行建模,模型中点到相机的距离多在2 m左右,此时0.5像素的判断误差对应点云上为2 mm,与参考点云精度相当,可认为对后面精度分析不影响.
由表 2:①特征参数的比较,Kinect所建模型的绝对误差在10 mm的范围内,相对误差基本在2%的范围内.②编号1、2、3、4的绝对误差和相对误差都比较大;因这些特征与背景处同一平面,重建及测量判断的过程中都只利用了获得的光学信息,未利用深度信息,故精度较低;此外因其特征长度较小,同等误差下相对误差更大.③排除②中所列特征,距离特征长度大于1 m时,相对误差在0.5%左右;而长度小于1 m时,相对误差在1%~1.5%左右;短距离特征的相对精度更低.
3.2.2 花瓶模型(1) 基于模型表面参数指标
花瓶为光滑表面,无明显点特征用于判断距离特征.分别对花瓶的Kinect模型和标准参考模型切取对应位置的切片(这里取了17片).利用最小二乘法分别对两组离散的切片点云数据进行圆拟合,得到每一切片的直径,求Kinect数据与标准数据拟合直径的绝对、相对误差,结果见表 3.
| 下载CSV 表 3 Kinect和参考花瓶模型切片拟合直径的对比 Tab.3 The diameter comparison of vase slice obtained by the Kinect and reference models |
比较Kinect点云和参考点云拟合的结果发现:绝对误差最大有13 mm,且直径整体稍偏小(17组中有12组绝对偏差为正值).与会议室场景比花瓶模型的重建精度要低.
(2) 基于改进豪斯多夫距离的精度分析
因为花瓶点云上获取目标特征属性较困难,为此还利用1.2.2节中改进的豪斯多夫距离来进行精度分析.这两套点云模型分属不同的坐标系统,需将两者配准到同一坐标系统.以精度高的参考点云模型坐标系为参考坐标系,选少量对应点(5组)并结合算法[17]将Kinect点云模型转换到参考坐标系中.精确配准后结果如图 7所示,可见,除了花瓶顶部,Kinect重建的模型整体要稍小于参考点云模型.

|
图 7 Kinect点云(红色)与参考点云(绿色)精配准图 Fig.7 The fine registration result between Kinect point cloud (red) with the reference point cloud (green) |
利用配准结果,根据1.2.2节方法,首先计算Kinect点云上每一点到参考点云的最小欧式距离;然后取间隔δ=0.05 cm(Kinect的最高标称精度为1 mm,故δ取其一半),将点对之间的距离分为140段,统计最小距离在对应距离段内的点数,得到图 8,图中箭头标注为最小距离小于该距离的点数占总点数的比例.根据已有Kinect建模经验,点云模型上大多数点(超过80%)是可靠的,实验中计算累计比例达80%时其对应的距离D作为改进的H-D值.重建模型上80%的点到参考点云的最小距离小于21.9 mm,峰值在5~9 mm,与本节(1)中评定结果基本一致.

|
图 8 点对间的欧式距离分段统计 Fig.8 Euclidean distance section statistics of the point pair |
Kinect对花瓶建模精度较差的原因除文中分析的瓷质材质深度测量精度不高外,还有实验中背景复杂,生成点云中含大量背景干扰信息,滤波时边缘过平滑,背景信息被错当成场景内容使得点云建模受影响.而这些更多似乎会造成重建模型比例偏小.
综合这两种模型场景实验,并结合文中深度测量的精度分析有:①对一般材质的室内环境,模型重建的相对误差总体在2%之内.②瓷砖及透明材质环境下,建模精度会明显下降,对表面瓷质的目标建模会出现系统性偏差(实验是整体稍偏小);所以Kinect 2.0不适用于瓷砖材质目标场景的数据获取与建模.③利用Kinect进行近景测量建模时,目标到相机距离不应超过2.5 m.
4 结论本文通过理论分析与实验对ToF成像的RGB-D相机(Kinect 2.0)深度测量与建模精度进行了定量研究;得出在不同环境(颜色、材质、表面状况)下,深度测量精度与相机到目标距离变化之间的定量关系,以及三维建模精度状况的量化分析结果;给出其测量与建模的适用环境、条件;指出对黑色、微透明或瓷砖材质目标,要慎用其进行数据获取与建模.
本文虽然是针对kinect 2.0进行的研究,但所用方法也适用于其他光学与深度镜头相结合的双镜头传感器系统(如Creative、Senz3D等)数据获取与建模精度的分析研究.
| [1] |
KHOSHELHAM K, ELBERINK S O. Accuracy and resolution of kinect depth data for indoor mapping applications[J]. Sensors, 2012, 12(2): 1437 DOI:10.3390/s120201437 |
| [2] |
SHIM H, LEE S. Performance evaluation of time-of-flight and structured light depth sensors in radiometric/geometric variations[J]. Optical Engineering, 2012, 51(9): 4401 |
| [3] |
SARBOLANDI H, LEFLOCH D, KOLB A. Kinect range sensing: structured-light versus time-of-flight kinect[J]. Computer Vision and Image Understanding, 2015, 139(1): 1 |
| [4] |
SMISEK J, JANCOSEK M, PAJDLA T. 3D with Kinect[J]. Advance in Computer & Pattern Recognition, 2011, 21(5): 1154 |
| [5] |
XU Z, PERRY T, HILLS G. Method and system for multi-phase dynamic calibration of three-dimensional (3D) sensors in a time-of-flight system: US, 8587771[P]. 2013-11-19.
|
| [6] |
ZHANG Z. Microsoft Kinect Sensor and Its Effect[J]. IEEE Multimedia, 2012, 19(2): 4 DOI:10.1109/MMUL.2012.24 |
| [7] |
杨晶晶, 冯文刚. 连续调制ToF图像误差来源及降噪处理[J]. 合肥工业大学学报(自然科学版), 2012, 35(4): 485 YANG Jingjing, FENG Wengang. Research on error sources and denoising of ToF camera image with continuous modulation[J]. Journal of HeFei University Technology (Natural Science), 2012, 35(4): 485 |
| [8] |
李诗锐, 李琪, 李海洋, 等. 基于Kinect v2的实时精确三维重建系统[J]. 软件学报, 2016, 27(10): 2519 LI Shirui, LI Qi, LI Haiyang, et al. Real-time accurate 3D reconstruction based on Kinect v2[J]. Journal of Software, 2016, 27(10): 2519 |
| [9] |
林耀冬.基于Kinect的再制造零件三维表面建模系统[D].哈尔滨: 哈尔滨工业大学, 2015. LIN Yaodong. 3D surface modeling of remanufactured parts based on Kinect[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015982564.htm |
| [10] |
石广升.基于Kinect的物体三维模型构建和姿态估计方法研究[D].哈尔滨: 哈尔滨工业大学, 2015. SHI Guangsheng. Object 3D modeling and pose estimation based on Kinect[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015980780.htm |
| [11] |
王国利.单站地面激光点云精度影响因素研究[D].北京: 北京建筑大学, 2015. WANG Guoli. Research on the influence the accuracy of single station ground laser point cloud[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2015. |
| [12] |
王玉鹏, 卢小平, 葛晓天, 等. 地面三维激光扫描点位精度评定[J]. 测绘通报, 2011, 4(1): 10 WANG Yupeng, LU Xiaoping, GE Xxiaotian, et al. Point precision assessment for terrestrial 3D laser scanning[J]. Bulletin of Surveying and Mapping, 2011, 4(1): 10 |
| [13] |
胡鹏程, 郭焱, 李保国, 等. 基于多视角立体视觉的植株三维重建与精度评估[J]. 农业工程学报, 2015, 31(11): 209 HU Pengcheng, GUO Yan, LI Baoguo, et al. Three-dimensional reconstruction and its precision evaluation of plant architecture based on multiple view stereo method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(11): 209 DOI:10.11975/j.issn.1002-6819.2015.11.030 |
| [14] |
张小青. 基于三维激光扫描技术的变形监测方法研究[J]. 北京测绘, 2016(3): 53 ZHANG Xiao Qing. Research on deformation monitoring method based on terrestrial 3D laser scanning technology[J]. Beijing Surveying and Mapping, 2016(3): 53 DOI:10.3969/j.issn.1007-3000.2016.03.013 |
| [15] |
叶勤, 桂坡坡. 一种新的深度传感器内部参数标定方法研究[J]. 光电子·激光, 2015, 26(6): 1146 YE Qin, GUI Popo. A new calibration method for depth sensor[J]. Journal of Optoelectronics·Laser, 2015, 26(6): 1146 |
| [16] |
叶勤, 姚亚会, 桂坡坡. 基于极线及共面约束条件的Kinect点云配准方法[J]. 武汉大学学报·信息科学版, 2017, 42(9): 1271 YE Qin, YAO Yahui, GUI Popo. Kinect point cloud registration method based on epipolar and point-to-plane constraints[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1271 |
| [17] |
BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 586 |
 2019, Vol. 47
2019, Vol. 47