2. 同济大学 中德学院, 上海 201804
2. Chinesisch-Deutsches Hochschulkolleg, Tongji University, Shanghai 201804, China
4WIS电动汽车低速时具有较好的机动性, 高速时具有较优的操纵稳定性和安全性.除此之外, 通过控制转向角度, 它还能实现诸如斜行、蟹行和原地转向等功能[1], 并且在给定参考路径下具有较优的跟踪性能.
车辆自动转向系统在智能或无人驾驶车辆控制中占有非常重要的地位, 其中路径跟踪控制是自动转向过程中的基本控制问题.Goodarzi[2]等提出了一种新型的路径跟踪最优控制律, 将主动前轮转向(AFS)和直接横摆力矩控制(DYC)组合起来, 实现了横向偏移和航向误差的最小化.Salehpour等[3]采用粒子游动优化(PSO)方法, 对线性二次控制器(LQR)进行了优化, 提高了乘用车路径跟踪能力.Hu等[4]设计了一种路径跟踪控制器, 即使在大曲率路径下也能使横向偏移和航向误差同时收敛至零.基于LQR方法, Mashadi等[5]采用反馈/前馈路径控制实现了AFS、4WIS和带有DYC系统的AFS三种转向模式.
模型预测控制(MPC)具有预测、滚动优化和反馈校正的基本功能, 尤其适用于不易建立精确被控对象模型、不确定环境干扰下且存在约束条件的控制系统, 对解决无人驾驶车辆在复杂路况下的路径跟踪控制问题具有独特的优势[6].传统的前轴主动转向已经有众多学者研究,Falcone等[7-8]分别基于预测控制算法使用车辆的非线性模型和线性时变模型设计无人驾驶车辆模型预测控制器,解决了车辆在高速低附着路面上的路径跟踪问题.本文提出了四轮独立转向汽车的六自由度动力学状态空间表达式,使用线性时变MPC算法设计了四轮主动转向路径跟踪控制器,并分析了该控制算法的鲁棒性和实时性.
本文涉及4WIS电动汽车路径跟踪的模型预测控制.首先, 根据力学原理及轮胎特性模型, 推导出一种近似的非线性四轮转向车辆动力学状态空间描述模型;其次, 基于对上述非线性动力学模型的线性化, 提出了线性时变(linear time-varying, LTV)MPC算法, 并结合约束条件和优化目标函数将相应的最优问题转化为便于计算机求解的标准二次规划问题;随后, 针对4WIS设计了相应的LTV MPC路径跟踪控制器, 并利用Matlab/Carsim联合仿真平台对双移线工况下路径跟踪进行了仿真验证;最后, 对LTV MPC算法的鲁棒性及实时性进行仿真分析.
1 4WIS车辆路径跟踪模型图 1为惯性坐标系XOY和车辆坐标系xoy下4WIS车辆相关变量的示意图.其中, 令i=fl, fr, rl, rr分别表示前左轮、前右轮、后左轮、后右轮, δi为车轮i的转向角, φ为车身横摆角; vxi、vyi和Fxi、Fyi分别为车辆坐标系下轮胎纵向速度、侧向速度和纵向力、侧向力; vli、vci和Fli、Fci分别为轮胎坐标系下轮胎纵向速度、侧向速度和纵向力、侧向力.

|
图 1 4WIS车辆示意图 Fig.1 4WIS Vehicle schematic |
由图 1可知, 在XOY下和在xoy下的车辆质心速度满足如式(1)的转换关系.
| $ \left\{\begin{array}{l}{\dot{X}=\dot{x} \cos \varphi-\dot{y} \sin \varphi} \\ {\dot{Y}=\dot{x} \sin \varphi+\dot{y} \cos \varphi}\end{array}\right. $ | (1) |
在轮胎坐标系下和在xoy下的轮胎纵向速度、侧向速度满足式(2)的转换关系.
| $ \left\{ {\begin{array}{*{20}{l}} {{v_{{\rm l}i}} = {v_{xi}}\cos {\delta _i} + {v_{yi}}\sin {\delta _i}}\\ {{v_{{\rm{c}}i}} = {v_{yi}}\cos {\delta _i} - {v_{xi}}\sin {\delta _i}} \end{array}} \right. $ | (2) |
在xoy下和在轮胎坐标系下的轮胎纵向力、侧向力满足式(3)的转换关系.
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{{\rm{l}}i}} = {F_{xi}}\cos {\delta _i} + {F_{yi}}\sin {\delta _i}}\\ {{F_{{\rm{c}}i}} = {F_{yi}}\cos {\delta _i} - {F_{xi}}\sin {\delta _i}} \end{array}} \right. $ | (3) |
车辆实际行驶过程中车轮运动状态比较复杂, 不仅有纵向滑移, 车辆转弯时还会发生轮胎侧偏;轮胎模型描述了车辆运动与地面相互作用关系, 即联合纵向和侧偏工况下的轮胎力特性, 如图 2所示.

|
图 2 轮胎与地面作用示意图 Fig.2 Tire and ground action diagram |
研究4WIS车辆路径跟踪控制问题时(图 3), 假定不同工况下各轮胎转矩使车辆曲线匀速运行.因此, 4WIS车辆路径跟踪系统控制变量可设为四轮线控主动转向角(转角)δi, i=fl, fr, rl, rr, 即:

|
图 3 路径跟踪控制系统 Fig.3 Path tracking control system |
| $ \boldsymbol{u}_{\mathrm{dyn}}=\left[u_{1}, u_{2}, u_{3}, u_{4}\right]^{\mathrm{T}}=\left[\delta_{\mathrm{fl}}, \delta_{\mathrm{fr}}, \delta_{\mathrm{rl}}, \delta_{\mathrm{rr}}\right]^{\mathrm{T}}. $ |
式中:u1~u4为控制变量.
系统状态变量为
| $ {\mathit{\boldsymbol{\xi }}_{{\rm{dyn}}}} = {\left[ {{\xi _1}, {\xi _2}, {\xi _3}, {\xi _4}, {\xi _5}, {\xi _6}} \right]^{\rm{T}}} = {[\dot y, \dot x, \varphi , \dot \varphi , Y, X]^{\rm{T}}}, $ |
系统输出量(实际路径)为
| $ \boldsymbol{\eta}=[\varphi, Y, X]^{\mathrm{T}}, $ |
参考路径为
| $ \boldsymbol{\eta}_{\mathrm{ref}}=\left[\varphi_{\mathrm{ref}}, Y_{\mathrm{ref}}, X_{\mathrm{ref}}\right], $ |
其中, X为XOY坐标系下车辆质心的横坐标, 路径规划层给定的参考路径由式(4)的关系确定.
| $ \left\{\begin{array}{l}{X_{\mathrm{ref}}=X} \\ {\varphi_{\mathrm{ref}}=f_{\varphi}\left(X_{\mathrm{ref}}\right), Y_{\mathrm{ref}}=f_{Y}\left(X_{\mathrm{ref}}\right)}\end{array}\right. $ | (4) |
因此, 作为路径跟踪控制系统的输出量可简化为:ηdyn=[ξ3, ξ5]T=[φ, Y]T, 相应的期望输出量(或期望路径)可简化为
| $ \boldsymbol{\eta}_{\mathrm{ref}}=\left[\varphi_{\mathrm{ref}}, Y_{\mathrm{ref}}\right]^{\mathrm{T}}. $ |
路径跟踪控制器根据ηdyn和ηref的信息, 给出控制变量udyn, 实现车辆对期望路径的跟踪.
在侧向加速度ay≤0.4g和侧偏角/纵向滑移率较小的情况下, 常规轮胎的侧向力Fc和纵向力Fl可以分别用式(5)和式(6)近似表示.
| $ F_{\mathrm{cfl}}=C_{\mathrm{cll}}\left(\delta_{\mathrm{fl}}-\frac{\dot{y}+l_{\mathrm{f}} \dot{\varphi}}{\dot{x}}\right) $ | (5a) |
| $ F_{\mathrm{cfr}}=C_{\mathrm{cfr}}\left(\delta_{f l}-\frac{\dot{y}+l_{\mathrm{f}} \dot{\varphi}}{\dot{x}}\right) $ | (5b) |
| $ F_{\mathrm{crl}}=C_{\mathrm{crl}}\left(\frac{\dot{y}-l_{\mathrm{r}} \dot{\varphi}}{\dot{x}}-\delta_{\mathrm{rl}}\right) $ | (5c) |
| $ F_{\mathrm{crr}}=C_{\mathrm{crl}}\left(\frac{\dot{y}-l_{\mathrm{r}} \dot{\varphi}}{\dot{x}}-\delta_{\mathrm{rr}}\right) $ | (5d) |
| $ {F_{{\rm{l}}i}} = {C_{{\rm{l}}i}}{S_i}, i = {\rm{fl}}, {\rm{fr}}, {\rm{rl}}, {\rm{rr}} $ | (6) |
式中:lf和lr分别为前轮中心和后轮中心到质心的距离; Cli和Cci分别为轮胎i的纵向刚度和侧偏刚度; Si为轮胎i的滑移率.
根据牛顿第二定律并结合式(1)~(6),可得到近似的4WIS非线性车辆动力学状态空间描述模型,如式(7)所示.
| $ \left\{ \begin{array}{l} {{\dot \xi }_1} = - {\xi _2}{\xi _4} + \frac{1}{m}\left[ {{C_{{\rm{cfl}}}}\left( {{u_1} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right) + {C_{{\rm{cfr}}}}\left( {{u_2} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right) + } \right.\\ \left. {{C_{{\rm{crl}}}}\left( {\frac{{{\xi _1} - {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}} - {\xi _3}} \right) + {C_{{\rm{crr}}}}\left( {\frac{{{\xi _1} - {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}} - {u_4}} \right)} \right]\\ {{\dot \xi }_2} = {\xi _1}{\xi _4} + \frac{1}{m}\left[ {{C_{{\rm{lfl}}}}{S_{{\rm{fl}}}} + {C_{{\rm{cfl}}}}\left( {{u_1} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right){u_1} + } \right.\\ {C_{{\rm{lfr}}}}{S_{{\rm{fr}}}} + {C_{{\rm{cfr}}}}\left( {{u_2} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right){u_2} + {C_{{\rm{lrl}}}}{S_{{\rm{rl}}}} + \\ \left. {{C_{{\rm{crl}}}}\left( {{u_3} - \frac{{{\xi _1} + {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}}} \right){u_3} + {C_{{\rm{lrr}}}}{S_{{\rm{rr}}}} + {C_{{\rm{crr}}}}\left( {{u_4} - \frac{{{\xi _1} + {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}}} \right){u_4}} \right]\\ {{\dot \xi }_3} = {\xi _4}\\ {{\dot \xi }_4} = \frac{1}{{{I_z}}}\left[ {{l_{\rm{f}}}\left( {{C_{{\rm{cfl}}}}\left( {{u_1} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right) + {C_{{\rm{cfr}}}}\left( {{u_2} - \frac{{{\xi _1} + {l_{\rm{f}}}{\xi _4}}}{{{\xi _2}}}} \right)} \right) - } \right.\\ \left. {{l_{\rm{r}}}\left( {{C_{{\rm{crl}}}}\left( {\frac{{{\xi _1} - {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}} - {u_3}} \right) + {C_{{\rm{crr}}}}\left( {\frac{{{\xi _1} - {l_{\rm{r}}}{\xi _4}}}{{{\xi _2}}} - {u_4}} \right)} \right)} \right]\\ {{\dot \xi }_5} = {\xi _2}\sin {\xi _3} + {\xi _1}\cos {\xi _3}\\ {{\dot \xi }_6} = {\xi _2}\cos {\xi _3} - {\xi _1}\sin {\xi _3} \end{array} \right. $ | (7) |
| $ \boldsymbol{\eta}_{\mathrm{dyn}}=\left[\xi_{3}, \xi_{5}\right]^{\mathrm{T}} $ |
式(7)中4个车轮转角为控制变量(系统输入)、6个整车变量为状态变量、车身横摆角及惯性坐标系下侧向位移为系统输出的非线性状态空间表达式用于设计参考路径跟踪控制算法.
2 预测模型的设计 2.1 线性时变模型的转化相比于非线性模型预测控制, LTV MPC具有计算量小, 易求解等特点[9-12].为了便于控制器的设计, 将式(7)转化为离散形式(8).
| $ \mathit{\boldsymbol{\xi }}(k + 1) = \mathit{\boldsymbol{\xi }}(k) + T \cdot f(\mathit{\boldsymbol{\xi }}(k) $ | (8a) |
| $ \boldsymbol{u}_{\mathrm{dyn}}(k) )=F\left(\boldsymbol{\xi}(k), \boldsymbol{u}_{\mathrm{dyn}}(k)\right) $ | (8b) |
式中:T为离散系统采样时间.
考虑离散系统在k时刻的工作点为(ξ(k), u(k-1)),
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\tilde \xi }}(k + 1) = F(\mathit{\boldsymbol{\tilde \xi }}(k), \mathit{\boldsymbol{\tilde u}}(k))}\\ {\mathit{\boldsymbol{\tilde \xi }}(k) = \mathit{\boldsymbol{\tilde \xi }}(k)}\\ {\mathit{\boldsymbol{\tilde u}}(k) = \mathit{\boldsymbol{u}}(k - 1)} \end{array}} \right. $ | (9) |
将非线性离散系统F在工作点(ξ(k), u(k-1))用泰勒公式展开, 只保留一阶项, 可得到式(10).
| $ \mathit{\boldsymbol{\tilde \xi }}(k + 1) = {\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{\tilde \xi }}(k) + {\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{\tilde u}}(k) $ | (10) |
式中:
至此, 将非线性连续模型转化成了离散线性时变模型, 便于MPC控制器的设计.
2.2 预测模型的推导根据离散的时变线性系统设计模型预测控制器, 将式(10)中的控制量u(k)转变为控制增量Δu(k), 将各个变量进行相应的变换, 即可得到新的状态空间表达式如式(11).
| $ \hat{\boldsymbol{\xi}}(k+1)=\hat{\boldsymbol{A}}_{k} \hat{\boldsymbol{\xi}}(k)+\hat{\boldsymbol{B}}_{k} \Delta \boldsymbol{u}(k)+\hat{\boldsymbol{d}}(k) $ | (11a) |
| $ \hat{\boldsymbol{\eta}}(k)=\hat{\boldsymbol{C}}_{k} \hat{\boldsymbol{\xi}}(k)+\hat{\boldsymbol{D}}_{k} \Delta \boldsymbol{u}(k) $ | (11b) |
其中设定:
| $ \begin{array}{c} \mathit{\boldsymbol{\hat \xi }}(k) = {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\xi }}(k)}\\ {\mathit{\boldsymbol{u}}(k - 1)} \end{array}} \right)_{(n + m) \times 1}}, \mathit{\boldsymbol{\hat d}}(k) = {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{d}}(k)}\\ {{0_m}} \end{array}} \right)_{(n + m) \times 1}}\\ \Delta \mathit{\boldsymbol{u}}(k) = \mathit{\boldsymbol{u}}(k) - \mathit{\boldsymbol{u}}(k - 1)\\ \mathit{\boldsymbol{d}}(k) = \mathit{\boldsymbol{\tilde \xi }}(k + 1) - {\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{\tilde \xi }}(k) - {\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{\tilde u}}(k), k \ge 0\\ {{\mathit{\boldsymbol{\hat A}}}_k} = {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_k}}&{{\mathit{\boldsymbol{B}}_k}}\\ {{\mathit{\boldsymbol{0}}_{m \times n}}}&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right)_{(n + m) \times (n + m)}}{{\mathit{\boldsymbol{\hat B}}}_k} = {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_k}}\\ {{\mathit{\boldsymbol{I}}_m}} \end{array}} \right)_{(n + m) \times m}}\\ {{\mathit{\boldsymbol{\hat C}}}_k} = {\left( {{\mathit{\boldsymbol{C}}_k}\quad {\mathit{\boldsymbol{D}}_k}} \right)_{p \times (n + m)}}, {{\mathit{\boldsymbol{\hat D}}}_k} = {\left( {{\mathit{\boldsymbol{D}}_k}} \right)_{p \times m}} \end{array} $ |
其中:n为状态量个数; m为控制量个数; p为输出量个数.
若已知k时刻的状态量
设定:Δu(k+i)=0, i=Nc, Nc+1, …, Np-1
即:u(k+Nc-1)=u(k+Nc)=…=u(k+Np-1)
其中, Np是预测时域,指系统控制过程中状态量的预测步长; Nc是控制时域,指系统控制过程中控制量的预测步长, 且Nc≤Np.
则在预测时域Np内系统输出量可用式(12)计算.
| $ \mathit{\boldsymbol{\hat Y}} = {\mathit{\boldsymbol{\psi }}_k}\mathit{\boldsymbol{\widehat \xi }}(k) + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_k}\Delta \mathit{\boldsymbol{U}}(k) + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}\mathit{\boldsymbol{\phi}}(k) $ | (12) |
其中,
| $ \begin{array}{c} \mathit{\boldsymbol{\hat Y}} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \eta }}(k + 1)}\\ {\mathit{\boldsymbol{\hat \eta }}(k + 2)}\\ \vdots \\ {\mathit{\boldsymbol{\hat \eta }}\left( {k + {N_{\rm{p}}}} \right)} \end{array}} \right]_{{N_{\rm{p}}} \times 1}}, \Delta \mathit{\boldsymbol{U}}(k) = {\left[ {\begin{array}{*{20}{c}} {\Delta u(k)}\\ {\Delta u(k + 1)}\\ \vdots \\ {\Delta u\left( {k + {N_{\rm{c}}}} \right)} \end{array}} \right]_{{N_{\rm{c}}} \times 1}}, \\ \phi (k) = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat d}}(k)}\\ {\mathit{\boldsymbol{\hat d}}(k + 1)}\\ \vdots \\ {\mathit{\boldsymbol{\hat d}}\left( {k + {N_{\rm{p}}} - 1} \right)} \end{array}} \right]_{{N_{\rm{p}}} \times 1}}, \end{array} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_k} = {\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat C}}}_k}{{\mathit{\boldsymbol{\hat B}}}_k}}&{{{\mathit{\boldsymbol{\hat D}}}_k}}& \cdots & \cdots &{{\mathit{\boldsymbol{0}}_{p \times m}}}\\ {\mathit{\boldsymbol{\hat C}}{{\mathit{\boldsymbol{\hat A}}}_k}{{\mathit{\boldsymbol{\hat B}}}_k}}&{{{\mathit{\boldsymbol{\hat C}}}_k}{{\mathit{\boldsymbol{\hat B}}}_k}}&{{{\mathit{\boldsymbol{\hat D}}}_k}}& \cdots &{{\mathit{\boldsymbol{0}}_{p \times m}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{{\mathit{\boldsymbol{\hat C}}}_k}\mathit{\boldsymbol{\hat A}}_k^{{N_{\rm{p}}} - 1}{{\mathit{\boldsymbol{\hat B}}}_k}}&{{{\mathit{\boldsymbol{\hat C}}}_k}\mathit{\boldsymbol{\hat A}}_k^{{N_{\rm{p}}} - 2}{{\mathit{\boldsymbol{\hat B}}}_k}}& \cdots & \cdots &{{{\mathit{\boldsymbol{\hat C}}}_k}\mathit{\boldsymbol{\hat A}}_k^{{N_{\rm{p}}} - {N_{\rm{c}}}}{{\mathit{\boldsymbol{\hat B}}}_k}} \end{array}\\ \end{array} \right]_{{N_{\rm{p}}} \times {N_{\rm{c}}}}}, $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k} = {\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat C}}}_k}}&{{\mathit{\boldsymbol{0}}_{p \times (n + m)}}}& \cdots &{{\mathit{\boldsymbol{0}}_{p \times (n + m)}}}\\ {{{\mathit{\boldsymbol{\hat C}}}_k}{{\mathit{\boldsymbol{\hat A}}}_k}}&{{{\mathit{\boldsymbol{\hat C}}}_k}}& \cdots &{{\mathit{\boldsymbol{0}}_{p \times (n + m)}}}\\ \vdots & \vdots & \ddots & \vdots\\ {{{\mathit{\boldsymbol{\hat C}}}_k}\mathit{\boldsymbol{\hat A}}_k^{{N_{\rm{p}}} - 1}}&{{{\mathit{\boldsymbol{\hat C}}}_k}\mathit{\boldsymbol{\hat A}}_k^{{N_{\rm{p}}} - 2}}& \cdots &{{{\mathit{\boldsymbol{\hat C}}}_k}} \end{array} \end{array} \right]_{{N_{\rm{p}}} \times {N_{\rm{p}}}}}, $ |
| $ \boldsymbol{\psi}_{k}=\left[\begin{array}{c}{\hat{{\bf C}}_{k} \hat{\boldsymbol{A}}_{k}} \\ {\hat{\boldsymbol{C}}_{k} \hat{\boldsymbol{A}}_{k}^{2}} \\ {\vdots} \\ {\hat{\boldsymbol{C}}_{k} \hat{\boldsymbol{A}}_{k}^{N_{\mathrm{p}}}}\end{array}\right]_{N_{\mathrm{p}} \times 1}. $ |
通过式(12)可知, 预测时域Np内控制输出量的预测值
系统的控制增量是未知的, 需要通过设计合理的目标函数来进行最优求解, 得到控制时域内的控制序列.路径跟踪问题对于控制量变化要求较为严格, 可以把控制增量作为目标函数的状态量, 目标函数设计为如式(13)的形式.
| $ \begin{array}{l} J = \sum\limits_{j = 1}^{{N_{\rm{p}}}} {{{\left( {\mathit{\boldsymbol{\hat \eta }}(k + j) - {\mathit{\boldsymbol{\eta }}_{{\rm{ref}}}}(k + j)} \right)}^{\rm{T}}}} {q_j}(\mathit{\boldsymbol{\hat \eta }}(k + j) - \\ {\mathit{\boldsymbol{\eta }}_{{\rm{ref}}}}(k + j)) + \sum\limits_{j = 1}^{{N_{\rm{c}}} - 1} {{{(\Delta \mathit{\boldsymbol{u}}(k))}^{\rm{T}}}} {r_j}(\Delta \mathit{\boldsymbol{u}}(k)) \end{array} $ | (13) |
式中:第1项反映了系统对参考路径的跟随能力; 第2项反映了对控制量平稳变化的要求.qj和rj为权重矩阵Q和R中的权重因子.同时, 在实际控制过程中, 需要满足控制量和输出量约束条件, 如式(14), 其中i=0, 1, …Nc-1.
控制量约束:
| $ u_{\min }(k+i) \leqslant u(k+i) \leqslant u_{\max }(k+i) $ | (4a) |
控制增量约束:
| $ \Delta u_{\min }(k+i) \leqslant \Delta u(k+i) \leqslant \Delta u_{\max }(k+i) $ | (14b) |
输出约束:
| $ \hat{\boldsymbol{\eta}}_{\min }(k+i) \leqslant \hat{\boldsymbol{\eta}}(k+i) \leqslant \hat{\boldsymbol{\eta}}_{\max }(k+i) $ | (14c) |
式(14)形成了一个完整的约束条件表达式.由于系统是时变模型, 并不能保证在每个时刻都能得到可行解.因此, 在目标函数中加入相应的松弛因子, 如式(15)所示.
| $ \begin{array}{l} J = \sum\limits_{j = 1}^{{N_p}} {{{\left( {\mathit{\boldsymbol{\hat \eta }}(k + j) - {\mathit{\boldsymbol{\eta }}_{{\rm{esf}}}}(k + j)} \right)}^T}} {q_j}(\mathit{\boldsymbol{\hat \eta }}(k + j) - \\ {\mathit{\boldsymbol{\eta }}_{{\rm{ref}}}}(k + j)) + \sum\limits_{j = 1}^{{N_{\rm{c}}} - 1} {{{(\Delta \mathit{\boldsymbol{u}}(k))}^{\rm{T}}}} {r_j}(\Delta \mathit{\boldsymbol{u}}(k)) + \rho {\varepsilon ^2} \end{array} $ | (15) |
式中:ρ为权重系数; ε为松弛因子.
将式(11)代入目标函数式(15), 并设定预测时域内的输出量偏差如式(16).
| $ \boldsymbol{e}_{k}=\boldsymbol{\psi}_{k} \hat{\boldsymbol{\xi}}(k)+{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k} \boldsymbol{\phi}_{k}-\boldsymbol{Y}_{\mathrm{ref}}(k) $ | (16) |
经过相应的计算, 可将优化目标调整如式(17).
| $ J=\Delta \boldsymbol{U}(k)^{\mathrm{T}}\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}^{\mathrm{T}} \boldsymbol{Q} \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}+R\right) \Delta \boldsymbol{U}(k)+2 \boldsymbol{e}_{k} \boldsymbol{Q} \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k} \Delta \boldsymbol{U}(k)+\\ \boldsymbol{e}_{k}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{e}_{k}=\frac{1}{2}\left[\begin{array}{c}{\Delta \boldsymbol{U}(k)} \\ {\varepsilon}\end{array}\right]^{\mathrm{T}} \boldsymbol{H}\left[\begin{array}{c}{\Delta \boldsymbol{U}(k)} \\ {\varepsilon}\end{array}\right]+\\ f\left[\begin{array}{c}{\Delta \boldsymbol{U}(k)} \\ {\varepsilon}\end{array}\right]+\boldsymbol{e}_{k}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{e}_{k} $ | (17) |
其中,
| $ \begin{array}{c} \boldsymbol{H}=\left[\begin{array}{cc}{2\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}^{\mathrm{T}} \boldsymbol{Q} \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}+\boldsymbol{R}\right)} & {0} \\ {0} & {2 \boldsymbol{e}_{k}}\end{array}\right]_{\left(1+m N_{\mathrm{c}}\right) \times\left(1+M N_{\mathrm{c}}\right)}\\ \boldsymbol{f}=\left[\begin{array}{cc}{2 \boldsymbol{e}_{k}^{\mathrm{T}} \boldsymbol{Q} \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}} & {} & {0}\end{array}\right]_{1 \times m N_{\mathrm{c}}} \end{array} $ |
又令:U(k)=[u(k), u(k+1), …u(k+Nc-1)]T
| $ \boldsymbol{K}=\left(\begin{array}{cccc}{1} & {0} & {0} & {0} \\ {1} & {1} & {0} & {0} \\ {\vdots} & {\vdots} & {\ddots} & {0} \\ {1} & {1} & {\cdots} & {1}\end{array}\right)_{N_{{\rm c}} \times N_{{\rm c}}}, \quad \boldsymbol{M}=\boldsymbol{K} \otimes \boldsymbol{I}_{m} $ |
则:
| $ \boldsymbol{U}(k)=\boldsymbol{M} \Delta u(k)+\boldsymbol{u}(k-1) $ | (18) |
模型预测控制在每一步的带约束优化求解问题都等价于求解如式(19)的二次规划问题.
| $ \operatorname{Min} J(\boldsymbol{\xi}(k), \boldsymbol{u}(k-1), \Delta \boldsymbol{U}(k)) $ |
| $ \mathrm{s. t} \left[\begin{array}{c}{\Delta \boldsymbol{U}_{\min }} \\ {0}\end{array}\right] \leqslant\left[\begin{array}{c}{\Delta \boldsymbol{U}(k)} \\ {\varepsilon}\end{array}\right] \leqslant\left[\begin{array}{c}{\Delta \boldsymbol{U}_{\max }} \\ {\rho}\end{array}\right] $ | (19) |
| $ \left[\begin{array}{cc}{\boldsymbol{M}} & {{\bf 0}_{m N_{\mathrm{c}}} \times 1} \\ {-\boldsymbol{M}} & {{\bf 0}_{m N_{\mathrm{c}}} \times 1} \\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}} & {{\bf 0}_{p N_{\mathrm{p}} \times 1}} \\ {-\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{k}} & {{\bf 0}_{p N_{\mathrm{p}} \times 1}}\end{array}\right]\left[\begin{array}{c}{\Delta \boldsymbol{U}(k)} \\ {\varepsilon}\end{array}\right] \leqslant \left[\begin{array}{c}{\boldsymbol{U}_{\max }-\boldsymbol{U}(k)} \\ {-\boldsymbol{U}_{\min }-\boldsymbol{U}(k)} \\ {\hat{\boldsymbol{Y}}_{\max }-\boldsymbol{\psi}_{k} \mathit{\boldsymbol{\hat \xi }}-\mathit{\boldsymbol{ \boldsymbol{\varGamma}}}_{k} \boldsymbol{\phi}(k)} \\ {-\hat{\boldsymbol{Y}}_{\max }+\boldsymbol{\psi}_{k} \mathit{\boldsymbol{\hat \xi }}+\mathit{\boldsymbol{ \boldsymbol{\varGamma}}}_{k} \boldsymbol{\phi}(k)}\end{array}\right] $ |
在每个控制周期完成对式(19)的求解后, 得到了控制时域内的一系列控制输入增量如式(20).
| $ \Delta \boldsymbol{U}_{k}^{*}=\left[\Delta u_{k}^{*}, \Delta u_{k+1}^{*}, \cdots, \Delta u_{k+N_{{\rm c}}-1}^{*}\right]^{\mathrm{T}} $ | (20) |
将该控制序列中第一个元素作为实际的控制输入增量作用于系统, 如式(21)所示.
| $ u(k)=u(k-1)+\Delta u_{k}^{*} $ | (21) |
系统执行这一控制量直到下一时刻.在新的时刻, 系统根据状态信息重新预测下一段时域的输出, 通过优化过程得到一个新的控制增量序列.如此循环往复, 直至系统完成控制过程.
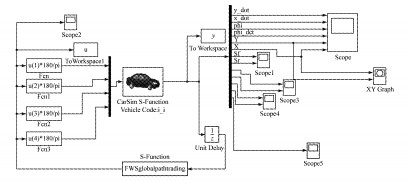
3 4WIS车辆路径跟踪控制器 3.1 平台及模型参数基于Matlab/Carsim建立4WIS动力学模型, 并进行路径跟踪控制器设计如图 4所示, 把LTV MPC算法以S函数形式进行封装, 将所设计控制器用于双移线工况的仿真验证.主要的车辆参数见表 1.
|
图 4 Matlab/Carsim联合仿真模型 Fig.4 Matlab/Carsim joint simulation model |
| 下载CSV 表 1 车辆模型参数 Tab.1 Vehicle model parameters |
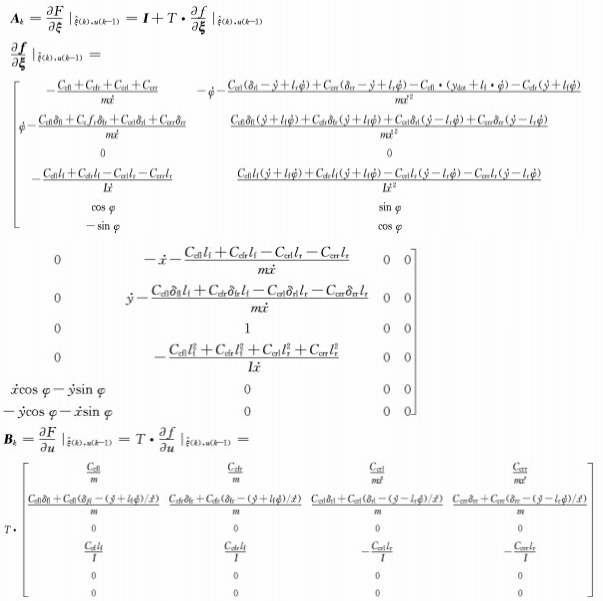
考虑式(10), 求出4WIS动力学模型中的参数A和B如下:
|
主要控制器参数设置如下:
| $ \begin{array}{c} \boldsymbol{u}_{\min }=\left[-10^{\circ}, -10^{\circ}, -10^{\circ}, -10^{\circ}\right]^{\mathrm{T}} \\ \boldsymbol{u}_{\max }=\left[10^{\circ}, 10^{\circ}, 10^{\circ}, 10^{\circ}\right]^{\mathrm{T}} \\ \Delta \boldsymbol{u}_{\min }=\left[-0.3^{\circ}, -0.3^{\circ}, \right.-0.3^{\circ}, -0.3^{\circ} ]^{\mathrm{T}} \\ \Delta \boldsymbol{u}_{\max }=\left[0.3^{\circ}, 0.3^{\circ}, \right. 3^{\circ}, 0.3^{\circ} ]^{\mathrm{T}} \end{array} $ |
双移线路径由参考的横向位置Yref和参考的航向角ϕref构成, 具体路径函数[7]如式(22)所示:
| $ \left\{\begin{array}{l}{Y_{\mathrm{ref}}(X)=\frac{d_{y 1}}{2}\left(1+\tanh \left(z_{1}\right)\right)-\frac{d_{2}}{2}\left(1+\tanh \left(z_{2}\right)\right)} \\ {\varphi_{\mathrm{ref}}(X)=\arctan \left(d_{y 1}\left(\frac{1}{\cosh \left(z_{1}\right)}\right)^{2}\left(\frac{1.2}{d_{x 1}}\right)-\right.} \\ {d_{y 2}\left(\frac{1}{\cosh \left(z_{2}\right)}\right)^{2}\left(\frac{1.2}{d_{x 2}}\right) )}\end{array}\right. $ | (22) |
其中, dx1=25, dx2=21.95,dy1=4.05, dy2=5.7,
试验平台中, 控制对象为Carsim中的整车模型, 实时输出车辆的各个状态量;MPC控制器结合预测模型、目标函数和约束条件进行最优化求解, 得到当前时刻的最优控制序列u*(t), 输入到被控平台.为了验证控制算法对路况和速度的鲁棒性, 以及研究控制参数对路径跟踪能力的影响, 本文进行了在不同路面、不同速度以及不同设计参数下双移线跟踪验证.
图 5为不同路况下以30 km·h-1的车速的路径跟踪结果, 其中预测时域Np=25, 控制时域Nc=10.根据图 5对比仿真结果可以看出, 控制器对不同路面下的跟踪效果都能保持较好的鲁棒性.若附着条件变差(摩擦系数μ=0.2), 则质心侧偏角具有较大的变化, 会影响车辆行驶的稳定性.控制系统能够在不同附着条件下, 较好地跟踪期望路径, 但实际车辆在低附着路面(μ=0.2)上一定会打滑,分析原因为在建模时考虑不同工况下各轮胎转矩使车辆曲线匀速行驶, 未考虑车轮打滑.因此可以考虑加入相应的转矩控制,提高算法在工程上的适用性.

|
图 5 不同路况下仿真结果 Fig.5 Simulation results under different road conditions |
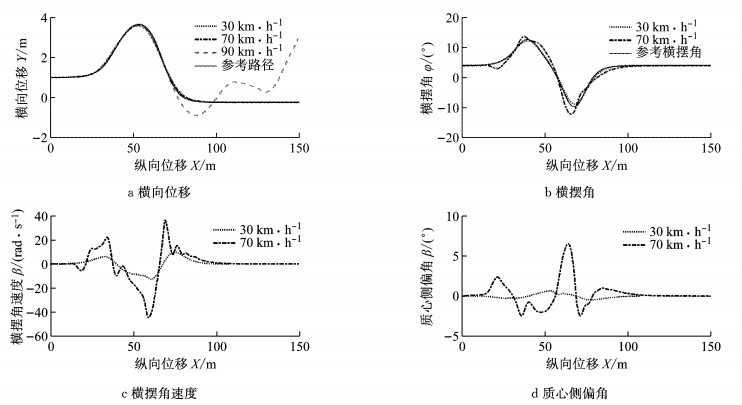
图 6是设置车辆分别以30、70、90 km·h-1的车速进行双移线路径跟踪, 道路附着条件良好, 预测时域Np=25, 控制时域Nc=10.通过对比图 6中的横向位移、横摆角、横摆角速度和质心侧偏角的变化可知, 车速在30和70 km·h-1时, 横向位移和横摆角都能较好地跟踪双移线路径; 30 km·h-1时车辆的横摆角速度和质心侧偏角都保持在较小的范围内, 而70 km·h-1时车速稳定性不太好.另外, 车速在90 km·h-1时, 在双移线参考路径的出口处, 车辆不再沿参考路径行驶, 出现失稳现象.分析其原因, 高速引起较大的侧向加速度使得车轮侧偏特性进入非线性区域, 控制算法无法计算出最优控制量, 产生非可行解.此种情况下, 可以通过以下方法改善:
|
图 6 不同车速下的仿真结果 Fig.6 Simulation results under different vehicle speeds |
① 不再单纯通过四轮转角作为输入控制量, 联合直接横摆力矩控制车辆横摆角速度, 实现高速时的路径跟踪;
② 在二次规划问题转化时, 加入质心侧偏角约束;
③ 经仿真验证, 在减小采样时间T时, 同时提高可控车速, 这也提高了对试验硬件的要求.
为了研究控制器参数设计对路径跟踪能力的影响, 设定车辆以30 km·h-1的车速行驶在μ=0.8的良好路面上, 在不同预测时域Np和不同控制时域Nc下对比仿真结果.
图 7为不同预测时域下的动力学状态变化和仿真运算时间.可以看出, Np=20、Np=30时车辆能较好地跟踪期望路径, 行驶稳定性也比较好; 当Np=5时, 在双移线参考路径的出口处, 车辆不再沿参考路径行驶, 出现失稳现象.分析其原因, 预测时域较小时, 控制器难以准确预测未来的输出, 导致控制量出现非可行解; 降低车速有利于提高路径的跟踪能力, 这是符合驾驶员实际驾驶行为的.因此在路径跟踪问题中,预测时域的设定和车速有关.经仿真验证本算法应用于车速30 km·h-1的工况时, 预测时域Np大于15才能保证行驶的稳定性.

|
图 7 不同预测时域下的仿真结果 Fig.7 Simulation results of different prediction horizon |
对运算时间积分, Np=5的运算时间为19.89 s, Np=20的运算时间为25.51 s, Np=30的运算时间为41.08 s.预测时域的减小能明显减小运算时间, 有助于提高控制器的实时性.
综合上述分析, 预测时域的减小会增大车辆转向时的偏差, 但实时性会明显改善.稳态行驶时, 较小的预测时域偏差较大, 在双移线出口处控制器会逐渐减小偏差直至收敛为零.因此, 在控制器设计时需根据实时性和跟踪精度选择合适的预测时域.
之后, 验证不同控制时域参数对控制器性能的影响.设定控制器的预测时域Np=25, 分别验证控制时域Nc=5、10、20时的路径跟踪能力.图 8为不同控制时域Nc下的仿真结果, 分析结果可知, 控制时域对实时性影响不大; 同时, 控制时域对路径跟踪能力影响不大, 这是因为预测算法通过求解满足目标函数以及各种约束的优化问题, 得到在控制时域内一系列的控制序列, 总是将该控制序列的第1个元素作为受控对象的实际控制量.

|
图 8 不同控制时域下的仿真结果 Fig.8 Simulation results under different control time domain |
(1) 4WIS车辆动力学模型建立.车辆动力学模型和轮胎模型是设计控制器的模型基础, 以六自由度的四轮转向车辆动力学状态空间描述模型作为预测模型, 实现路径跟踪.非线性模型需要进行适当的降维和简化, 使用小角度转向时的特性来描述轮胎模型.
(2) 线性时变模型预测控制算法的研究.非线性模型和约束会大大增加模型预测控制问题的求解难度, 在线实时求解较难实现.推导了线性时变预测模型控制算法的公式, 以及将LTV MPC最优问题转化为便于计算机求解的标准二次规划问题.基于此, 设计了4WIS电动汽车路径跟踪模型预测控制算法, 并结合约束条件和优化目标函数进行控制器设计.
(3) 双移线工况下路径跟踪控制算法的仿真验证和性能分析.利用Matlab/Carsim的联合仿真, 将LTV MPC算法以S函数形式进行封装, 在Carsim里建立合适的整车模型, 对算法进行验证.通过对控制器在不同路况、不同车速、不同设计参数下的分析, 验证了控制器在不同车速和不同附着系数下对路径跟踪的鲁棒性, 保证了车辆的稳定行驶; 并且分析了预测时域和控制时域对控制器的准确性、实时性的影响.
(4) 算法约束优化.设计的算法约束只有控制量、控制增量和输出量的范围, 在实际仿真过程中可能会出现非可行解或使整车失稳的控制量序列.因此, 可以考虑加入软约束或设计动力学状态约束(如质心侧偏角), 使算法具有更广泛的应用性.
| [1] |
肖志文.四轮独立驱动、独立转向电动汽车: 用于路径控制的车辆动力学建模及分析[D].上海: 同济大学, 2017. XIAO Zhiwen. Four-wheel independent drive, independent steering electric vehicle: vehicle dynamics modeling and analysis for trajectory Control [D]. Shanghai: Tongji University, 2017. |
| [2] |
GOODARZI A, SABOOTEH A, ESMAILZADEH E. Automatic path control based on integrated steering and external yaw-moment control[J]. Proceedings of the Institution of Mechanical Engineers Part K: Journal of Multi-body Dynamics, 2008, 222(2): 189 DOI:10.1243/14644193JMBD120 |
| [3] |
SALEHPOUR S, POURASAD Y, TAHERI S H. Vehicle path tracking by integrated chassis control[J]. Journal of Central South University, 2015, 22(4): 1378 DOI:10.1007/s11771-015-2655-y |
| [4] |
HU C, WANG R, YAN F, et al. Should the desired heading in path following of autonomous vehicles be the tangent direction of the desired path[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3084 DOI:10.1109/TITS.2015.2435016 |
| [5] |
MASHADI B, AHMADIZADEH P, MAJIDI M.Integrated controller design for path following in autonomous vehicles[R]. [S.l.]: SAE, 2011.
|
| [6] |
HANG P, LUO F, FANG S, et al. Path tracking control of a four wheel independent steering electric vehicle based on model predictive control[C]//Proceedings of the 36th Chinese Control Conference. Dalian: IEEE, 2017: 9360-9366. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZLL201707006193.htm
|
| [7] |
FALCONE P, BORRELLI F, ASGARI J, et al. Predictive active steering control for autonomous vehicle systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 566 DOI:10.1109/TCST.2007.894653 |
| [8] |
FALCONE P.Nonlinear model predictive control for autonomous vehicles[D].Benevento: [s.n.], 2007.
|
| [9] |
张济民, 张继彤, 任利慧. 摆式客车倾摆控制系统神经网络预测控制[J]. 同济大学学报(自然科学版), 2006(7): 947 ZHANG Jimin, ZHANG Jitong, REN Lihui. Predictive control of tilting control system for pendulum-train buses based on neural network[J]. Journal of Tongji University(Natural Science), 2006(7): 947 DOI:10.3321/j.issn:0253-374X.2006.07.020 |
| [10] |
胡长健.电动轮驱动车辆的驱动力助力转向技术研究[D].长春: 吉林大学, 2008. HU Changjian. Research on power steering assisted by driving force of electric wheel driven vehicle[D]. Changchun: Jilin University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10183-2008060853.htm |
| [11] |
FALCONE P, TUFO M, BORRELLI F, et al.A linear time varying model predictive control approach to the integrated vehicle dynamics control problem in autonomous systems[C]//2007 46th IEEE Conference on Decision and Control.[S.l.]: IEEE, 2008: 2980-2985.
|
| [12] |
陈虹, 刘志远, 解小华. 非线性模型预测控制的现状与问题[J]. 控制与决策, 2001(4): 385 CHEN Hong, LIU Zhiyuan, XIE Xiaohua. Present situation and problems of nonlinear model predictive control[J]. Control and Decision, 2001(4): 385 DOI:10.3321/j.issn:1001-0920.2001.04.001 |
 2019, Vol. 47
2019, Vol. 47

