随着我国城市化进程的加快,市郊客流日益增大,轨道交通市郊线路(以下简称“市郊线路”)发挥着越来越重要作用.由于市郊客流在时空分布上的差异性,快慢列车运行模式(以下简称“快慢车模式”)可以较好地适应市郊客流的需要,为长距离乘客节省了在途时间.然而,与站站停的平行运行图相比,快慢车模式下的非平行运行图,使得线路通过能力的计算变得复杂,越行站数量和位置、快慢列车开行比例等,都对通过能力有一定程度的影响.
关于通过能力的研究:VUCHIC[1]在运输能力计算方面,推荐了一种计算追踪间隔时间的方法,考虑了列车停站时间等因素对地铁通过能力的影响,但未考虑行车组织的要求,因此计算的通过能力偏大.KHISTY[2]提出了轨道交通线路通过能力的一般公式,但未对追踪间隔时间的计算方法作进一步说明.张国宝等[3]分析三种非站站停车方案的适用条件,并提出判定列车是否越行及越行站的设置数量和位置的方法.潘寒川等[4]研究了市域轨道交通快慢车开行比例与通过能力之间的关系,以实例验证可通过改变快慢车的发车比例提高线路通过能力.陈福贵等[5]在传统平图基础上,提出快慢车组合运行对系统能力损失的建议计算公式.丁小兵和徐行方等[6]研究了基于不同快慢车开行比例的线路通过能力计算方法,并给出了根据时段客流量的列车建议开行比例.李明高、毛保华等[7]研究了直通运营下,受异质与同质列车间追踪间隔不同的影响下,直通区段通过能力计算方法.
综上研究成果表明,虽然已有针对快慢车模式下通过能力计算的研究,但从系统角度分析,对通过能力随越行站分布、快慢车开行比例、发车间隔等众多相互渗透、相互影响的要素进行深入的研究仍然缺乏.因此,本文将寻求快慢车模式不同要素对通过能力的影响规律,研究不同要素组合条件下线路通过能力的计算与表达.
1 快慢车线路通过能力计算方法城市轨道交通线路通过能力是指在采用一定的车辆类型、信号设备和行车组织方法条件下,线路各项固定设备在单位时间(通常是高峰小时)所能通过的最大列车数[8],通常计算如下:
| $ N_{\max }=3600 / \mathrm{h} $ | (1) |
式中:h为追踪列车间隔时间,s.
然而,快慢车共线的线路通过能力不仅仅取决于追踪间隔时间,还受快慢车停站次数、停站时间、开行比例(以下简称快慢比)、越行站数量及位置、不同发车间隔等因素的影响.
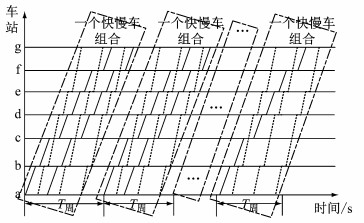
因此,提出以下快慢车模式下线路通过能力的计算思路,如图 1所示.假设快慢比为m:n,将这(m+n)列车看作一个快慢车组合,该组合的周期时间为T周.图中,实线表示慢车,虚线表示快车,下同.
|
图 1 快慢车模式下通过能力计算思路 Fig.1 Calculating idea of carrying capacity under fast-slow mode |
由此,快慢车组合运行线路的通过能力为
| $ N = K \times 3\;600/{T_{周}} = \left( {m + n} \right) \times 3\;600/{T_{周}} $ | (2) |
式中:T周为一个快慢车组合的周期时间,s;K为一个快慢车组合周期内所包含的快慢车列数和,即(m+n)列.
2 快慢车组合的通过能力分析为探索不同快慢车组合情况下线路通过能力的计算分析方法,下面将讨论不同快慢车开行比例及越行次数与通过能力之间的关系.运行图按照最密集方式、快慢车按照阶段均衡原则铺画,且越行时快车不停站.列举相邻列车间追踪间隔时间种类如表 1所示,以下简称追踪间隔[9].
| 下载CSV 表 1 相邻列车间追踪间隔时间种类 Tab.1 Types of tracking intervals between adjacent trains |
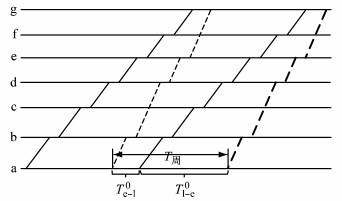
无越行、快慢比1:1时,列车如图 2所示.
|
图 2 无越行、快慢比1:1时列车运行周期 Fig.2 Train diagram without overtaking and with the proportion of fast and slow 1:1 |
可知,为求解T周,关键在于求解满足在始发站最小的快慢发车间隔Te-l0以及最小的慢快发车间隔Tl-e0.可借助编程语言由计算机遍历各个站点求解.由此可得
| $ {T_{周}} = T_{{\rm{e}} - 1}^0 + T_{{\rm{l}} - {\rm{e}}}^0 $ | (3) |
基于快慢车均衡铺画的原则,对于快慢车成组开行的情况,本文不作考虑,如图 3所示快慢车隔列开行的运行图.

|
图 3 无越行、快慢比m:n的列车运行周期 Fig.3 Train diagram without overtaking and with the proportion of fast and slow vehicles m:n |
其中,T周1=T周2=Te-l0+Tl-e0,则无越行、均衡铺画方式下快慢比m:n时,T周为
| $ {T_{周}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} m \times \left( {T_{{\rm{e}} - 1}^0 + T_{1 - {\rm{e}}}^0} \right) + \left( {n - m} \right) \times T_{{\rm{l}} - {\rm{l}}}^0\\ n \times \left( {T_{{\rm{e}} - 1}^0 + T_{1 - {\rm{e}}}^0} \right) + \left( {m - n} \right) \times T_{{\rm{e}} - {\rm{e}}}^0 \end{array}&\begin{array}{l} m < n\\ m > n \end{array} \end{array}} \right. $ | (4) |
综上,在无越行情况下:
| $ \begin{array}{*{20}{c}} {{T_{周}} = \min \left( {m,n} \right) \times \left( {T_{{\rm{e - l}}}^0 + T_{{\rm{l - e}}}^0} \right) + }\\ {\left( {{\rm{abs}}\left( {m - n} \right)} \right) * \left\{ {\begin{array}{*{20}{c}} {T_{{\rm{l - l}}}^0}&{m \le n}\\ {T_{{\rm{e - e}}}^0}&{m \ge n} \end{array}} \right.} \end{array} $ | (5) |
式中:Te-l0、Tl-e0、Te-e0、Tl-l0分别表示在无越行情况下,快慢、慢快、快快、慢慢列车在始发站的最小发车间隔.
因此,根据式(2)和式(5),可求无越行情况下,线路的通过能力.
2.2 越行1次通过能力计算 2.2.1 快慢比m:n=1:1假设快车在c站越行慢车1次,快慢比1:1时列车运行图如图 4所示.

|
图 4 越行1次、快慢比1:1的列车运行周期 Fig.4 Train diagram with one overtaking and the proportion of fast and slow vehicles 1:1 |
越行1次情况下,铺画最密集运行图的步骤为:①继上一周期慢、快车运行线段HLI-JLK之后,按照表 1所示的追踪间隔,求解在越行站c之前所有站点,与前行快车运行线段JL之间的时间间隔均满足要求的本周期第1列慢车的运行线段AB(暂定);②求解在越行站c之前所有站点,与前行慢车运行线段AB之间的时间间隔均满足要求的快车运行线段CE,确定慢快车在始发站最小发车间隔Tl-e1;③求解在越行站c之后所有站点,与前行慢车LI之间的时间间隔均满足要求的快车运行线段ED,若在某站点不符合,则同时移动线段AB、CD,最终得出本周期与上一周期的快慢车在始发站的发车间隔Te-l1;④铺画与前行快车运行线ED之间的时间间隔均满足要求的慢车运行线段EFG.
由此,越行1次、快慢比1:1时,T周为
| $ {T_{周}} = {T_{{\rm{AC}}}} + {T_{{\rm{JA}}}} = T_{{\rm{l - e}}}^{\rm{l}} + T_{{\rm{e - l}}}^{\rm{l}} $ | (6) |
式中:Tl-e1、Te-l1分别表示越行1次时,慢快、快慢列车在始发站的最小发车间隔.
2.2.2 快慢比=m:n(m>1,n>1)如图 5所示为快慢比m:n(m < n)的列车运行图,此时m列快、慢车均衡铺画,剩余n-m列慢车成组铺画.

|
图 5 越行1次、快慢比m:n(m < n)时列车运行周期 Fig.5 Train diagram with one overtaking and the proportion of fast and slow vehicles m :n(m < n) |
由图 5可知,越行1次、快慢比m:n(m < n)时,T周为
| $ \begin{array}{*{20}{c}} {{T_{周}} = T_{{\rm{e - l}}}^{1**} + \left( {n - m - 1} \right) \times T_{{\rm{1 - 1}}}^0 + T_{{\rm{1 - 1}}}^1 + }\\ {\left( {m - 1} \right) \times {T_{周\;i}} + T_{{\rm{1 - e}}}^1\;\;\;\;m < n} \end{array} $ | (7) |
进一步,图 6为快慢比m:n(m>n)的列车运行图,此时n列快、慢车均衡铺画,剩余m-n列快车成组铺画.

|
图 6 越行1次、快慢比m:n(m>n)时列车运行周期 Fig.6 Train diagram with one overtaking and the proportion of fast and slow vehicles m:n(m>n) |
由图 6可知,越行1次、快慢比m:n(m>n)时,T周为
| $ \begin{array}{*{20}{c}} {{T_{周}} = T_{{\rm{e - e}}}^1 + \left( {m - n - 1} \right) \times T_{{\rm{e - e}}}^0 + T_{{\rm{e - l}}}^{1 * } + }\\ {\left( {n - 1} \right) \times {T_{周\;i}} + T_{{\rm{l - e}}}^1\;\;\;m > n} \end{array} $ | (8) |
综上,在越行1次的情况下
| $ {T_{周}} = \left\{ \begin{array}{l} T_{{\rm{e - l}}}^{1 * * } + \left( {n - m - 1} \right) \times T_{{\rm{l - l}}}^0 + T_{{\rm{l - l}}}^1 + \\ \;\;\;\;\;\;\left( {m - 1} \right) \times {T_{周\;i}} + T_{{\rm{l - e}}}^1\;\;\;\;\;\;\;\;\;\;\;\;m < n\\ m \times {T_{周\;i}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n\\ T_{{\rm{e - e}}}^1 + \left( {m - n - 1} \right) \times T_{{\rm{e - e}}}^0 + T_{{\rm{e - l}}}^{1 * } + \\ \;\;\;\;\;\;\left( {n - 1} \right) \times {T_{周\;i}} + T_{{\rm{l - e}}}^1\;\;\;\;\;\;\;\;\;\;\;\;\;m > n \end{array} \right. $ | (9) |
式中:T周i=Tl-e1+Te-l1.
根据式(2)和式(9)可求越行1次情况下线路的通过能力.
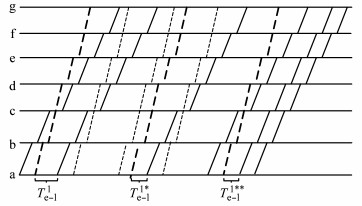
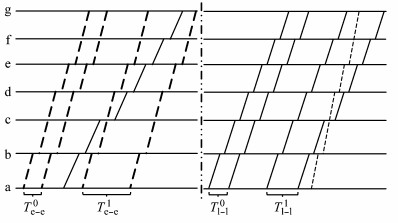
式(9)中,除了在越行1次、快慢比1:1描述的变量Tl-e1、Te-l1,新增变量Te-l1*,Te-l1**,Te-e1,Tl-l1.其中Te-l1*, Te-l1**均表示前快后慢列车的发车间隔,将其与前述变量Te-l1的区别如图 7所示,Te-e1,Tl-l1分别表示两列快车、两列慢车之间的发车间隔,其与前述变量Te-e0, Tl-l0的区别如图 8所示.
|
图 7 Te-l1、Te-l1*和Te-l1**的关系 Fig.7 Relationship of Te-l1, Te-l1* and Te-l1** |
|
图 8 Te-e0与Te-e1和Tl-l0与Tl-l1的关系 Fig.8 Relationship of Te-e0 and Te-e1, Tl-l0 and Tl-l1 |
对于图 7,①为求解Te-l1*,需要对越行站c站之前的所有站点,考虑后行慢车与前行快车的追踪时间间隔,对越行站c站之后的所有站点,考虑后行快车与前行快车的追踪时间间隔;②为求解Te-l1**,需要对越行站c站之前的所有站点,考虑后行慢车与前行快车的追踪时间间隔,对越行站c站之后的所有站点,考虑后行慢车与前行慢车的追踪时间间隔.Te-l1、Te-l1*、Te-l1**三者的区别在于,Te-l1的前行快车越行慢车,后行慢车被越行,Te-l1*仅有后行慢车被越行,前行快车不越行慢车,Te-l1**仅有前行快车越行慢车,后行慢车不被越行.
对于图 8,①为求解Te-e1,需要对越行站c站之前的所有站点,考虑后行快车与前行快车的追踪时间间隔,对越行站c站之后的所有站点,考虑后行快车与前行慢车的追踪时间间隔.与Te-e0的区别在于,Te-e0中前后行快车均不越行慢车,而Te-e1的前行快车越行慢车.②为求解Tl-l1,需要对越行站c站之前的所有站点,考虑后行慢车与前行慢车的追踪时间间隔,对越行站c站之后的所有站点,考虑后行快车与前行慢车的追踪时间间隔.与Tl-l0的区别在于,Tl-l0中前后行慢车均不被越行,而Tl-l1的后行慢车被越行.显然有,Te-e0≤Te-e1,Tl-l0≤Tl-l1.
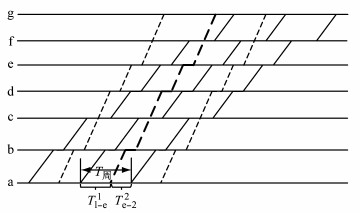
2.3 越行2次通过能力计算 2.3.1 快慢比=1:1(m=n)假设快车分别在c, f站越行慢车1次.快慢比1:1时,除第1列快车仅越行慢车1次,其余每列快车越行慢车2次,每列慢车被越行2次,列车运行如图 9所示.
|
图 9 越行2次、快慢比1:1的列车运行周期 Fig.9 Train diagram with two overtaking and the proportion of fast and slow vehicles 1:1 |
后行快车与前行慢车在始发站的最小发车间隔Tl-e1,可参照慢车被越行1次的情况求解;后行慢车与前行快车之间的发车间隔Te-l2,需要确保越行站c之前的每个站点,第2列慢车与前行第1列快车之间的时间间隔满足表 1所列的追踪间隔,同时在越行站c之后每个站点,第2列快车与前行第1列慢车的时间间隔满足表 1所列的追踪时间间隔.
由此,越行2次、快慢比1:1时,T周为
| $ {T_{周}} = T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^2 $ | (10) |
式中:Tl-e1同前,Te-l2为越行2次,后行慢车与前行快车在始发站的最小发车间隔,下同.
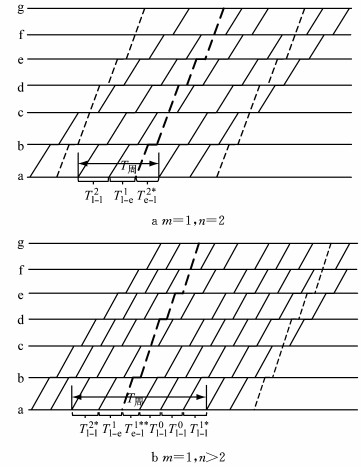
2.3.2 快慢比=m:n(1≤m < n)快慢比增至1:2时,周期内每列慢车被越行1次,每列快车越行慢车2次;而快慢比增至1:n时,周期内前2列慢车分别被越行1次,其余慢车不被越行, 如图 10所示.
|
图 10 越行2次,快慢比1:n(n≥2)的列车运行周期 Fig.10 Train diagram with two overtaking and the proportion of fast and slow vehicles 1:n(n≥2) |
同理快慢比1:1的分析,可得越行2次,快慢比1:n时,T周为
| $ {T_{周}} = \left\{ \begin{array}{l} T_{{\rm{l - l}}}^2 + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{2 * }\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = 1,n = 2\\ T_{{\rm{l - l}}}^{2 * } + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{1 * * } + \\ \;\;\;\left( {n - m - 2} \right) \times T_{{\rm{l - l}}}^0 + T_{{\rm{l - l}}}^{1 * }\;m = 1,n > 2 \end{array} \right. $ | (11) |
式中:Te-l2*与Te-l1**均代表前快后慢列车的发车间隔,Tl-l0、Tl-l2、Tl-l2*、Tl-l1*均代表前后行慢车之间的时间间隔.
继续增加快车的数量,形成如图 11所示的快慢比m:(m+1)、m:n(n>m+1)的列车运行图,此时周期内,除首、列和末列慢车被越行1次,其余慢车均被越行2次.

|
图 11 越行2次、快慢比m:n(m < n)的列车运行周期图 Fig.11 Train diagram with two overtaking and the proportion of fast and slow vehicles m:n(m < n) |
参照快慢比1:n的分析,可得越行2次、快慢比m:n(m < n)时,T周为
| $ \begin{array}{l} {T_{周}} = \\ \left\{ \begin{array}{l} T_{{\rm{l - l}}}^2 + \left( {m - 1} \right) \times {T_{周{\rm{i}}}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{2 * }\;\;\;\;\;\;n = m + 1\\ T_{{\rm{l - l}}}^{2 * } + \left( {m - 1} \right) \times {T_{周{\rm{i}}}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{1 * * } + \\ \;\;\;\;\left( {n - m - 2} \right) \times T_{{\rm{l - l}}}^0 + T_{{\rm{l - l}}}^{1 * }\;\;\;\;\;\;\;\;\;\;\;\;\;n > m + 1 \end{array} \right. \end{array} $ | (12) |
进一步对比式(12)与式(11),可知前后两式是包含和被包含的关系,即对于快慢比为m:n(m < n),统一用式(12)表达.
式(11)和式(12)中新增变量Te-l2*与前述变量Te-l1**、Te-l2的关系如图 12所示.新增变量Tl-l2、Tl-l2*和Tl-l1*三者的关系示意如图 13所示.

|
图 12 Te-l2、Te-l2*和Te-l1**的关系 Fig.12 Relationship of Te-l2, Te-l2* and Te-l1** |

|
图 13 Tl-l2, Tl-l2*和Tl-l1*的关系 Fig.13 Relationship of Tl-l2, Tl-l2* and Tl-l1* |
对于图 12Te-l2*的求解,需要在越行站c站前每个站点,考虑后行慢车与前行快车的追踪时间间隔,在越行站c站及f站之间每个站点,考虑前后行慢车之间的时间间隔,同时在越行站f站之后的每个站点,考虑后行快车与前行慢车之间的追踪时间间隔.图 12中3个变量的区别在于,Te-l1**的后行慢车不被越行,Te-l2的后行慢车分别在c、f站被快车越行,而Te-l2*的后行慢车仅在f站被快车越行.显然有Te-l1**≤Te-l2*≤Te-l2.
对于图 13,Tl-l2、Tl-l2*和Tl-l1*均表示编号②③的慢车在始发站的发车间隔,其中:Tl-l2和Tl-l2*中,后行第1列快车(编号为④)分别在c, f站越行慢车②、③,因此两者的求解均需要确保编号为④的快车在越行站c, f之间与编号为②的慢车,以及在第2个越行站f之后与编号为①的慢车,保持相应的追踪间隔同时, 在越行站c之前, 保证前慢后慢列车必要的追踪间隔;两者的区别在于,Tl-l2中编号①②的慢车之间还开行了1列快车,而Tl-l2*中无其他列车;Tl-l1*中,后行第1列快车仅在f站越行慢车③,因此在越行站f之前, 在保证前慢后慢列车必要的追踪间隔基础上, 只需要保证编号为④的快车在第2个越行站f之后与编号为②的慢车保持相应的追踪间隔.显然有Tl-l2*≥Tl-l2≥Tl-l1*.
2.3.3 快慢比=m:n(1≤n < m)进一步分析快车多于慢车的情况.如图 14所示为快慢比2:1、m:1(m>2)的列车运行图,此时周期内前2列快车分别越行慢车1次,每列慢车均被越行2次.

|
图 14 越行2次,快慢比m:1(m≥2)的列车运行周期 Fig.14 Train diagram with two overtaking and the proportion of fast and slow vehicles m:1(m≥2) |
同理快慢比1:n的分析,可得越行2次,快慢比m:1时,T周为
| $ {T_{周}} = \left\{ \begin{array}{l} T_{{\rm{l - e}}}^{\rm{1}} + T_{{\rm{e - e}}}^{\rm{2}} + T_{{\rm{e - l}}}^{{\rm{2}} * * }\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = 2,n = 1\\ T_{{\rm{l - e}}}^{\rm{1}} + T_{{\rm{e - e}}}^{\rm{2}} + T_{{\rm{e - l}}}^{{\rm{1}} * } + \\ \;\;\;\;\left( {n - m - 2} \right) \times T_{{\rm{e - e}}}^{\rm{0}} + T_{{\rm{e - e}}}^{{\rm{2}} * }\;m > 2,n = 1 \end{array} \right. $ | (13) |
继续增加慢车的数量,形成如图 15所示的快慢比(n+1):n、m:n(m>n+1)的列车运行图,此时周期内,首列和末列快车越行慢车1次,其余快车均越行2次,每列慢车均被越行2次.

|
图 15 越行2次、快慢比m:n(m>n)的列车运行周期 Fig.15 Train diagram with two overtaking and the proportion of fast and slow vehicles m:n(m>n) |
参照快慢比m:n(m < n)的分析,可得快慢比m:n(m>n)时,T周为
| $ {T_{周}} = \left\{ \begin{array}{l} \left( {n - 1} \right) \times {T_{周\;i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - e}}}^2 + T_{{\rm{e - l}}}^{2 * * }\;\;\;m = n + 1\\ \left( {n - 1} \right) \times {T_{周\;i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - e}}}^2 + T_{{\rm{e - l}}}^{1 * } + \\ \;\;\;\;\left( {n - m - 2} \right) \times T_{{\rm{e - e}}}^0 + T_{{\rm{e - e}}}^{2 * }\;\;\;\;\;\;\;\;\;\;m > n + 1 \end{array} \right. $ | (14) |
式中:T周=Tl-e1+Te-l2为快慢比1:1时的T周.
式(13)和式(14)中新增变量Te-l2**与前述变量Te-l1*的关系如图 16所示;新增变量Te-e2、Te-e2*的关系示意如图 17所示.

|
图 16 Te-l1*与Te-l2**的关系 Fig.16 Relationship of Te-l1* and Te-l2** |
|
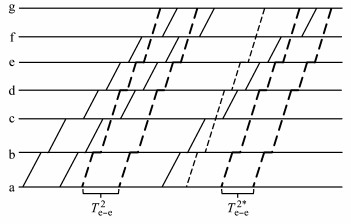
图 17 Te-e2和Te-e2*的关系 Fig.17 Relationship of Te-e2 and Te-e2* |
对于图 16Te-l2**的求解,需要在越行站c站前,考虑后行慢车与前行快车的追踪时间间隔,在越行站c站及f站之间,考虑前后行快车之间的时间间隔,在越行站f站之后,考虑后行快车与前行慢车之间的追踪时间间隔.Te-l2**与Te-l1*的区别在于,Te-l1*前行快车不越行慢车,而Te-l2**的前行快车在f站越行慢车.
对于图 17,①为求解Te-e2,需要在越行站c站前每个站点,考虑前后行快车之间的追踪时间间隔,在越行站c站及f站之间每个站点,考虑后行快车与前行第1列慢车之间的时间间隔,在越行站f站之后的每个站点,考虑后行快车与前行第2列慢车之间的时间间隔;②为求解Te-e2*,需要在越行站f站之前的每个站点,考虑前后行快车之间的追踪时间间隔,同时在越行站f站之后的每个站点,考虑后行快车与前行慢车之间的追踪时间间隔.Te-e2、Te-e2*的区别在于,Te-e2中前后两列快车分别在f, c站越行慢车1次;Te-e2*中前行快车在f站越行慢车1次,后行快车不越行慢车.
综上,在越行2次的情况下:
| $ \begin{array}{l} {T_{周}} = \\ \left\{ \begin{array}{l} \left\{ \begin{array}{l} T_{{\rm{l - l}}}^2 + \left( {m - 1} \right) \times {T_{周i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{2 * }\;\;\;\;\;\;\;n = m + 1\\ T_{{\rm{l - l}}}^{2 * } + \left( {m - 1} \right) \times {T_{周i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^{1 * * } + \;\;\;\;\;\;\;\;\;m < n\\ \;\;\;\left( {n - m - 2} \right) \times T_{{\rm{l - l}}}^0 + T_{{\rm{l - l}}}^{1 * }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n > m + 1 \end{array} \right.\\ m \times \left( {T_{{\rm{l - e}}}^1 + T_{{\rm{e - l}}}^2} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n\\ \left\{ \begin{array}{l} \left( {n - 1} \right) \times {T_{周i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - e}}}^2 + T_{{\rm{e - l}}}^{2 * * }\;\;\;m = n + 1\\ \left( {n - 1} \right) \times {T_{周i}} + T_{{\rm{l - e}}}^1 + T_{{\rm{e - e}}}^2 + T_{{\rm{e - l}}}^{1 * } + \;\;\;\;\;\;\;\;\;m > n\\ \;\;\;\left( {n - m - 2} \right) \times T_{{\rm{e - e}}}^0 + T_{{\rm{e - e}}}^{2 * }\;\;\;\;\;\;\;\;\;\;\;m > n + 1 \end{array} \right. \end{array} \right. \end{array} $ | (15) |
式中:T周i=Tl-e1+Te-l2.
2.4 寻优求解算法总结基于以上的分析,对于T周的求解,最重要的是求解以下几个关键变量:①无越行情况下,快慢、慢快、快快、慢慢列车在始发站的最小发车间隔Te-l0、Tl-e0和Te-e0、Tl-l0;②越行1次情况下,慢快列车在始发站的最小发车间隔Tl-e1,不同快慢列车在始发站的最小发车间隔Te-l1、Te-l1*和Te-l1**,快快列车在始发站的最小发车间隔Te-e1,慢慢列车在始发站的最小发车间隔Tl-l1;③越行2次情况下,不同快慢列车在始发站的最小发车间隔Te-l2、Te-l2*和Te-l2**,不同快快列车在始发站的最小发车间隔Te-e2和Te-e2*,不同慢慢列车在始发站的最小发车间隔Tl-l2、Tl-l2*和Tl-l1*.
因此,对于快慢车不同开行比例,无越行、越行1次及2次情况下,快速求解线路通过能力的算法为
(1) 结合线路数据及客流情况,预先设定快慢车开行比例、越行次数及越行站,确定一个快慢车组合内,快慢车的开行方式(如图 1所示);
(2) 列出不同快慢车开行比例、越行次数下,T周的总结式(5)、式(9)和式(15);
(3) 利用计算机语言实现T周表达式中关键变量的计算,最后应用式(2)计算得到不同快慢车开行比例、越行次数下线路的通过能力.
虽然本文只分析了越行0—2次情况,但对于更多越行次数,该方法同样适用,只是需要重新总结不同越行次数下快慢车组合的周期时间T周.
3 实例验证以上海轨道交通16号线为例,将滴水湖至龙阳路车站依次编号为A~M.线路选用快慢车组合运行方案,慢车站站停,快车中途停靠E、G和K站,越行站为D、I站.快、慢车停站时间均设为30 s,区间运行和起车、停车时分如表 2所示.追踪间隔时间,除Iat、Itd、Ida和Idt分别取60、90、90和150 s,其他均取120 s[9].
利用计算机编程语言求解出无越行、越行1次及越行2次情况下的关键变量,具体为
(1) 无越行情况下,Te-l0=120、Tl-e0=857、Te-e0=120、Tl-l0=120,代入式(2)、式(5),可得通过能力为
| $ N = \frac{{3\;600\left( {m + n} \right)}}{{\left( {857 \times \min \left( {m,n} \right) + 120 \times \max \left( {m,n} \right)} \right)}} $ | (16) |
(2) 越行1次情况下,Tl-e1=316,Te-l1=371、Te-l1*=120、Te-l1**=120,Te-e1=687,Tl-l1=541,代入式(2)、式(9),可得通过能力为
| $ N = \left\{ \begin{array}{l} \frac{{3\;600\left( {m + n} \right)}}{{\left( {120n + 567m + 170} \right)}}\;\;\;\;\;m < n\\ \frac{{3\;600\left( {m + n} \right)}}{{687m}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n\\ \frac{{3\;600\left( {m + n} \right)}}{{\left( {120m + 567n + 316} \right)}}\;\;\;\;\;m > n \end{array} \right. $ | (17) |
(3) 越行2次情况下,Tl-e1=316、Te-l2=146、Te-l2*=120、Te-l2**=120、Te-e2=462、Te-e2*=379、Tl-l2=316、Tl-l2*=421、Tl-l1*=120,代入式(2)、式(15),可得通过能力为
| $ N = \left\{ \begin{array}{l} \left\{ \begin{array}{l} \frac{{3\;600\left( {m + n} \right)}}{{\left( {462m + 290} \right)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = m + 1\\ \frac{{3\;600\left( {m + n} \right)}}{{\left( {342m + 120n + 275} \right)}}\;\;\;\;\;\;\;\;\;n > m + 1 \end{array} \right.\\ \frac{{3\;600\left( {m + n} \right)}}{{462m}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n\\ \left\{ \begin{array}{l} \frac{{3\;600\left( {m + n} \right)}}{{\left( {462n + 436} \right)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m = n + 1\\ \frac{{3\;600\left( {m + n} \right)}}{{\left( {342n + 120m + 575} \right)}}\;\;\;\;\;\;\;\;\;m > n + 1 \end{array} \right. \end{array} \right. $ | (18) |
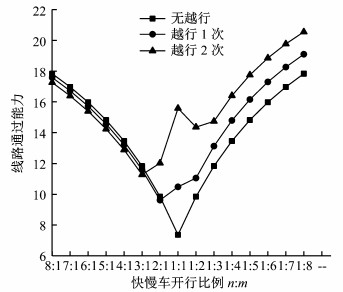
简要列举快慢车比例从8:1变化至1:8,不同越行情况下线路通过能力的演变趋势,绘制如图 18所示.
|
图 18 不同越行次数快慢车开行比例下线路通过能力 Fig.18 Carrying capacity under different quantity of overtaking and different proportion of fast and slow vehicles |
从图 18可以看出,线路通过能力随着列车越行次数和快慢车开行比例的变化而变化.具体有
(1) 对于相同越行次数,随着同种类列车(快车或慢车)开行列车的增加,线路通过能力不断上升,使得图形呈现“V”字型;
(2) 对于不同越行次数:当慢车开行列数相等,快车多于慢车时,对于相同的快慢比(如m:n=8:1),快车越行慢车2次时线路的通过能力最小,无越行时线路通过能力最大,说明慢车由于被越行增加的停站时间对于线路通过能力有一定的损失;当快车数开行列车相等,且快车少于慢车时时,对于相同的快慢比(如m:n=1:8),无越行时线路通过能力最小,快车越行慢车2次时线路通过能力最大,说明随着快车越行慢车次数的增加,前行慢车和后行快车之间的发车间隔逐渐缩短,从而带来线路通过能力的增加.
与既有文献[6]和文献[10]相比,本文的方法直接在通过能力计算公式中包含不同快慢车开行比例、越行次数,并将每个站点各列车之间所有可能的追踪间隔时间都考虑其中,与既有文献相比能更准确地计算线路通过能力.
4 结语在快慢车模式下,市郊线路越行站数量和位置、快慢车开行比例、列车发车间隔等因素,都会对通过能力产生不同程度的影响,研究通过能力随不同参数演变的影响机理变得尤为重要.
因此,提出了快慢车模式下线路通过能力的计算思路,并对不同越行次数、快慢车开行比例、发车间隔等要素对通过能力的影响程度及影响规律进行了分析和归纳,得出了快慢车模式下市郊线路通过能力的求解方法及表达公式.通过实例分析表明本文计算方法的有效性.
| [1] |
VUCHIC V R.Urban public transportation system and technology[J].[S.l.]: Prentice Hall Inc., 1981.
|
| [2] |
KHISTY C J, LALL B K.Transportation engineering: an introduction[M].Englewood: Prentice Hall Inc., 2002.
|
| [3] |
张国宝, 傅嘉, 刘明姝. 城轨列车非站站停车及派生的越行问题研究[J]. 都市快轨交通, 2005, 18(5): 18 ZHANG Guobao, FU Jia, LIU Mingshu. Research on skip-stop running patterns of urban rail transit and the derived problem of train overtaking[J]. Urban Rapid Rail Transit, 2005, 18(5): 18 DOI:10.3969/j.issn.1672-6073.2005.05.005 |
| [4] |
潘寒川, 杨涛. 市域轨道交通快慢车组合运营的通行能力研究[J]. 城市轨道交通研究, 2009(10): 48 PAN Hanchuan, YANG Tao. Express/slow train on urban rail transit line based on carrying capacity[J]. Urban Mass Transit, 2009(10): 48 DOI:10.3969/j.issn.1007-869X.2009.10.015 |
| [5] |
陈福贵, 汤珏. 地铁快慢车模式系统能力损失原则研究[J]. 铁道工程学报, 2014, 31(12): 96 CHENG Fugui, TANG Jue. Research on the loss principle of subway's system capacity under express-local mode[J]. Journal of Railway Engineering Society, 2014, 31(12): 96 DOI:10.3969/j.issn.1006-2106.2014.12.020 |
| [6] |
DING Xiaobing, ZHANG Shenrun, LIU Zhigang, et al. The analysis and calculation method of urban rail transit carrying capacity based on express-slow mode[J]. Mathematical Problems in Engineering, 2016(1): 1 |
| [7] |
李明高, 毛保华, 杜鹏, 等. 城市轨道交通与市郊铁路直通运营下通过能力研究[J]. 交通运输系统工程与信息, 2016, 16(1): 111 LI Minggao, MAO Baohua, DU Peng, et al. Capacity calculation under through operation between urban aail transit and suburban railway[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(1): 111 DOI:10.3969/j.issn.1009-6744.2016.01.018 |
| [8] |
徐瑞华, 张国宝, 徐行方. 轨道交通系统行车组织[M]. 上海: 中国铁道出版社, 2005 XU Ruihua, ZHANG Guobao, XU Xingfang, et al. Traffic organization of rail transit system[M]. Shanghai: China Railway Publishing House, 2005 |
| [9] |
赵欣苗.城市轨道交通市域线快慢车开行方案优化研究[D].北京: 北京交通大学, 2017. ZHAO Xinmiao.Optimization of the operational schemes with express/local trains on regional rail transit[D].Beijing: Beijing Jiaotong University, 2017. |
| [10] |
陈秋任.快慢车组合开行条件下的城市轨道交通线路运输组织优化研究[D].上海: 同济大学, 2016. CHEN Qiuren.Transportation organization optimization for fast-slow operation model in urban rail transit[D].Shanghai: Tongji University, 2016. |
 2019, Vol. 47
2019, Vol. 47

