智能化是减少交通事故,降低驾驶员操作负荷,提高交通效率的重要途径之一.目前,以ADAS (advanced driver assistance systems)为代表的驾驶辅助系统已经在量产车上有很多应用.但完全自动驾驶或高等级自动驾驶实现起来仍有较大困难.因此人机共驾成为了近些年来的一个研究热点[1-5].
广义上的人机共驾指所有驾驶员和智能系统共同驾驶车辆的系统.从这个意义上讲,人机共驾可以根据控制模式分为单驾双控、双驾单控和双驾双控.单驾双控是指驾驶指令只来源于驾驶员或控制系统其中之一,而实际车辆控制由驾驶员和控制系统共同完成.ABS(anti-lock brake system)和ESP(electronic stability program)都是典型的单驾双控系统.在ABS中所有的制动指令都来源于驾驶员踩制动踏板的行为,即单驾;ABS系统根据车轮角加速度传感器获得的轮胎滑移率信息和驾驶员的制动行为进行制动操作,即双控.单驾双控可以较好的补偿驾驶员在控制层[6]的不足.但单驾双控仍然将驾驶员作为理想驾驶员来考虑,即驾驶员的所有操作都是正确的.统计表明[7],93%的事故是由于驾驶员和驾驶环境之间的信息交互错误和驾驶员的误操作导致的.双驾单控和双驾双控系统可以在一定程度上对驾驶员予以预先纠正,因此可以获得更大的安全收益.
双驾单控是指驾驶指令可以来源于驾驶员和控制系统,但同一时刻只执行驾驶员和控制系统其中之一的驾驶指令.ACC(adaptive cruise control)和AEB(autonomous emergency braking)都是典型的双驾单控系统.关于智能汽车事故的研究表明,在自动驾驶系统完全成熟之前保持驾驶员时刻在环是非常重要的[8-9].双驾单控不能保证驾驶员始终在环,并且双驾单控系统的驾驶权是在驾驶员和控制系统之间无过度转换的.这些都带来一定的安全隐患.双驾双控是指驾驶指令来源于驾驶员和控制系统,且同一时刻按照某种策略同时执行驾驶员和控制系统的驾驶指令.双驾双控可以保证驾驶员始终对车辆保持控制,同时又可以在驾驶员操作失误时在一定程度上予以纠正.相比于在驾驶员和控制系统之间无过度的转换,双驾双控是一种更好的模式.
由于人机共驾的双驾双控策略中的驾驶指令来源于驾驶员和智能车的控制系统,如何根据两者的指令控制车辆成为一个难题.触觉共享控制是一种较早的双驾双控模式.当触觉共享控制的控制系统期望接管驾驶权时,会在方向盘上作用一个附加力矩来控制车辆[10].在触觉共享控制中,从方向盘到前轮的传力路径仍然是机械连接.文献[11]基于触觉共享控制提出一种人机共驾策略,虚拟驾驶员根据驾驶员作用在方向盘上的力矩来感知驾驶员的驾驶意图,并且通过方向盘力矩来辅助驾驶员.文献[12]使用驾驶模拟器研究了触觉共享控制对驾驶员弯道通过的辅助效果.最近发展起来的线控转向(steer-by-wire)技术为驾驶权分配提供了新的可能.文献[13]提出一种使用驾驶员和控制系统操作的加权和来得到智能车的实际控制输入的方法.文献[14]基于加权和与MPC(model predictive control)来实现人机共驾的双驾双控.
在双驾双控的驾驶权分配中,驾驶员和控制系统都希望智能车沿自己的期望轨迹行驶.人机共驾双控双驾策略是要在两者期望轨迹之间根据某一规则找到一个最优解.非合作动态博弈主要用来解决多个决策者共同作用于同一个动力系统的问题[15],因而双驾双控中的驾驶权分配问题可以使用动态博弈理论来描述.动态博弈在车辆系统中的应用仍相当有限.文献[16]和文献[17]使用动态博弈研究了在恶劣工况下车辆评价方法,并使用卡车侧翻和折叠这两个极端工况验证了其评价方法.文献[18]和文献[19]使用纳什均衡策略研究了将驾驶员行为考虑在内的车辆控制策略.文献[20]使用动态博弈对驾驶员和前轮主动转向系统共同进行轨迹跟踪时的控制行为进行了建模.
本文基于非合作MPC(model predictive control)提出了一种人机共驾双控双驾策略.本文的主要创新点包括:①证明了非合作MPC存在唯一的纳什均衡解的条件,并表明在求解非合作MPC时文献[20]中的迭代是没有必要的.②使用驾驶员和控制系统的置信度矩阵更新实现了驾驶员与控制系统之间驾驶权的逐渐交接.本文提出的非合作MPC人机共驾策略可以在智能车遇到危险时实现智能汽车由驾驶员驾驶到系统控制驾驶的平稳过度,从而实现在提高车辆安全性的同时保持驾驶员时刻在环.
1 人机共驾系统模型基于车辆单轨模型构建一个人机共驾车辆侧向控制模型,以实现驾驶员和控制系统同时对车辆转向的控制.记系统状态变量为x=[y, vy, ψ, ω]T.其中,y车辆侧向位移; vy为车辆侧向速度; ψ为车辆朝向角; ω为车辆横摆角速度.系统状态方程可以表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_{\rm{c}}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_{1,{\rm{c}}}}{\mathit{\boldsymbol{u}}_{\rm{D}}} + {\mathit{\boldsymbol{B}}_{2,{\rm{c}}}}{\mathit{\boldsymbol{u}}_{\rm{A}}}}\\ {\mathit{\boldsymbol{z}} = \mathit{\boldsymbol{Cx}}} \end{array} $ | (1) |
式中,
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&0&1&0 \end{array}} \right],{a_{11}} = - \frac{{2{C_{\rm{f}}} + 2{C_{\rm{r}}}}}{{m{v_x}}}, $ |
| $ {a_{12}} = - {v_x} - \frac{{2a{C_{\rm{f}}} - 2b{C_{\rm{r}}}}}{{m{v_x}}},\;{a_{21}} = - \frac{{2a{C_{\rm{f}}} - 2b{C_{\rm{r}}}}}{{{I_z}{v_x}}}, $ |
| $ {a_{22}} = - \frac{{2{a^2}{C_{\rm{f}}} + 2{b^2}{C_{\rm{r}}}}}{{{I_z}{v_x}}},{b_1} = \frac{{2{C_{\rm{f}}}}}{m},{b_2} = \frac{{2a{C_{\rm{f}}}}}{{{I_z}}}. $ |
式中:vx为车辆纵向速度;Cf为车辆前轮侧偏刚度;Cr为车辆后轮侧偏刚度;m为车辆质量;a为车辆前轴中心到质心距离;b为车辆后轴中心到质心距离;Iz为车辆绕z轴转动惯量;uD为非合作MPC人机共驾策略中驾驶员的输入;uA为非合作MPC人机共驾策略中控制系统的输入;z为系统可量测状态.
将连续系统离散化可以得到
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + {\mathit{\boldsymbol{B}}_1}{\mathit{\boldsymbol{u}}_{\rm{D}}}\left( k \right) + {\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{u}}_{\rm{A}}}\left( k \right)}\\ {\mathit{\boldsymbol{z}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right)} \end{array} $ | (2) |
式中:A为系统离散化之后Ac对应的矩阵;B1和B2为系统离散化之后B1, c和B2, c对应的矩阵.
通过离散系统模型的连续迭代可以得到
| $ \mathit{\boldsymbol{Z}}\left( k \right) = \mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}{\mathit{\boldsymbol{U}}_1}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}{\mathit{\boldsymbol{U}}_2}\left( k \right) $ | (3) |
式中,
| $ {\mathit{\boldsymbol{U}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{D}}}\left( k \right)}\\ {{\mathit{\boldsymbol{u}}_{\rm{D}}}\left( {k + 1} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{u}}_{\rm{D}}}\left( {k + {N_{\rm{u}}} - 2} \right)}\\ {{\mathit{\boldsymbol{u}}_{\rm{D}}}\left( {k + {N_{\rm{u}}} - 1} \right)} \end{array}} \right],{\mathit{\boldsymbol{U}}_2} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{A}}}\left( k \right)}\\ {{\mathit{\boldsymbol{u}}_{\rm{A}}}\left( {k + 1} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{u}}_{\rm{A}}}\left( {k + {N_{\rm{u}}} - 2} \right)}\\ {{\mathit{\boldsymbol{u}}_{\rm{A}}}\left( {k + {N_{\rm{u}}} - 1} \right)} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CA}}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^2}}\\ \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - 1}}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}}}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_1}}&0& \cdots &0\\ {\mathit{\boldsymbol{CA}}{\mathit{\boldsymbol{B}}_1}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_1}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{u}}} - 1}}{\mathit{\boldsymbol{B}}_1}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{u}}} - 2}}{\mathit{\boldsymbol{B}}_1}}& \cdots &{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_1}}\\ \vdots & \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - 1}}{\mathit{\boldsymbol{B}}_1}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - 2}}{\mathit{\boldsymbol{B}}_1}}& \cdots &{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - {N_{\rm{u}}}}}{\mathit{\boldsymbol{B}}_1}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_2}}&0& \cdots &0\\ {\mathit{\boldsymbol{CA}}{\mathit{\boldsymbol{B}}_2}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_2}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{u}}} - 1}}{\mathit{\boldsymbol{B}}_2}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{u}}} - 2}}{\mathit{\boldsymbol{B}}_2}}& \cdots &{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_2}}\\ \vdots & \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - 1}}{\mathit{\boldsymbol{B}}_2}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - 2}}{\mathit{\boldsymbol{B}}_2}}& \cdots &{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{N_{\rm{p}}} - {N_{\rm{u}}}}}{\mathit{\boldsymbol{B}}_2}} \end{array}} \right]. $ |
式中:Np为所谓的优化域(preview horizon),Nu为所谓的控制域(control horizon).系统根据Np步的信息来求解局部最优解,U1和U2可以在Nu步内调节,因而有Nu≤Np.
2 非合作MPC人机共驾策略基于非合作MPC提出一种人机共驾策略,实现人机共驾中的双驾双控.在人机共驾策略中,智能车根据驾驶员的操作输入、驾驶员模型、和车辆模型得到驾驶员的期望轨迹.同时,智能车根据环境感知系统构建的环境模型得到车辆可行域.通过比较车辆可行域和驾驶员期望轨迹,智能车可以判定当前车辆处于安全域、过渡域、或危险域.过渡域通常指虽然不危险但安全裕量已经较小.

|
图 1 人机共驾策略原理 Fig.1 Schematic diagram of cooperative driving |
对于驾驶辅助系统而言,当车辆从安全域到过渡域再到危险域的过程中通常有两个工作点.即当车辆从安全域进入过渡域时,包括FCW(forward collision warning)和LDW(lane departure warning)在内的预警系统开始工作;当车辆在危险域进入预碰撞状态时,AEB或AEC(autonomous emergency control)系统开始工作.驾驶辅助系统可以在一定程度上降低事故风险.但驾驶辅助系统的这种在某一工作点突然介入的模式让很多驾驶员感到不适应或不习惯.同时,如何准确确定预警系统和辅助系统的工作点时刻或位置成为一个难题.这些都限制了驾驶辅助系统的接受程度和安全收益.
在非合作MPC人机共驾策略中,智能车在行驶过程中驾驶指令同时来源于驾驶员和控制系统.智能车根据两者的驾驶指令来规划运动轨迹.当智能车处于安全驾驶状态时,智能车根据驾驶员的操作来控制车辆.当由于驾驶员操作失误或分心导致车辆进入过度域或危险域时,非合作MPC人机共驾策略可以将驾驶权从驾驶员逐渐交接给控制系统,来避免危险.这种逐渐过渡的方式可以较好地兼顾舒适性和安全性,同时保证驾驶员时刻在环.
非合作MPC人机共驾策略中的两个参与者(驾驶员和控制系统)都期望使关于自身目标的代价函数尽可能小,即
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{U_1}} {\mathit{\boldsymbol{V}}_1}\left( k \right),\;\;\;\;\;\mathop {\min }\limits_{{U_2}} {\mathit{\boldsymbol{V}}_2}\left( k \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\mathit{\boldsymbol{Z}}\left( k \right) = \mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}{\mathit{\boldsymbol{U}}_1}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}{\mathit{\boldsymbol{U}}_2}\left( k \right)} \end{array} $ | (4) |
式中,V1(k)为驾驶员的代价函数,V2(k)为控制系统的代价函数.
两个参与者的代价函数定义为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\left( k \right) = \left\| {\mathit{\boldsymbol{Z}}\left( k \right) - {\mathit{\boldsymbol{T}}_1}\left( k \right)} \right\|_{{Q_1}\left( k \right)}^2 + \left\| {{\mathit{\boldsymbol{U}}_1}\left( k \right)} \right\|_{{R_1}}^2}\\ {{\mathit{\boldsymbol{V}}_2}\left( k \right) = \left\| {\mathit{\boldsymbol{Z}}\left( k \right) - {\mathit{\boldsymbol{T}}_2}\left( k \right)} \right\|_{{Q_2}\left( k \right)}^2 + \left\| {{\mathit{\boldsymbol{U}}_2}\left( k \right)} \right\|_{{R_2}}^2} \end{array} $ | (5) |
式中,
| $ {\mathit{\boldsymbol{T}}_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{t}}_2}\left( {k - {N_{\rm{p}}} + 1} \right)}\\ {{\mathit{\boldsymbol{t}}_2}\left( {k - {N_{\rm{p}}} + 2} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{t}}_2}\left( {k - 1} \right)}\\ {{\mathit{\boldsymbol{t}}_2}\left( k \right)} \end{array}} \right],{\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{r}}_1}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{r}}_1}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_2}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{r}}_2}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{r}}_2}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{Q}}_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_1}\left( {k + 1} \right)}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{q}}_1}\left( {k + 2} \right)}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{q}}_1}\left( {k + {N_{\rm{p}}}} \right)} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{Q}}_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_2}\left( {k + 1} \right)}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{q}}_2}\left( {k + 2} \right)}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{q}}_2}\left( {k + {N_{\rm{p}}}} \right)} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{q}}_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\kappa _1}\left( k \right)}&0\\ 0&{{\lambda _1}\left( k \right)} \end{array}} \right],{\mathit{\boldsymbol{q}}_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\kappa _2}\left( k \right)}&0\\ 0&{{\lambda _2}\left( k \right)} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{t}}_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\rm{D}}}\left( k \right)}\\ {{\psi _{\rm{D}}}\left( k \right)} \end{array}} \right],{\mathit{\boldsymbol{t}}_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\rm{A}}}\left( k \right)}\\ {{\psi _{\rm{A}}}\left( k \right)} \end{array}} \right]. $ |
在人机共驾非合作MPC模型中,有以下两个要点:
(1) Q1(k)和Q2(k)均为时变矩阵.q1(k)为驾驶员置信度矩阵,q2(k)为智能车控制系统置信度矩阵.通过Q1(k)和Q2(k)中的两个置信度矩阵随时间的变化可以实现驾驶员与智能车控制系统之间驾驶权的转换.通过后文仿真分析可知,κ1(k)和κ2(k)是与驾驶权分配相关的参数,因此称其为分配系数;λ1(k)和λ2(k)是与动态特性相关的参数,因此称其为动态调整系数.当智能车感知到车辆进入危险状态时,可以通过逐渐调低κ1(k)并逐渐调高κ2(k),使车辆沿着智能车控制系统的规划轨迹行驶以躲避危险.而当车辆躲避危险逐渐进入正常行驶状态时,可以通过逐渐调高κ1(k)并逐渐调低κ2(k),将驾驶权逐渐交还给驾驶员.这样就实现了驾驶员与控制系统之间驾驶权的平缓交接.
(2) MPC需要根据未来Np步内的预测信息来求局部最优解.但在非合作MPC人机共驾策略中,期望使用驾驶员实时转向操作实现双驾双控.因此,使用一种预测域提前的方法,即将预测域取为当前时刻向前Np步的区间.这样可以较好地解决非合作MPC的实时求解,但会产生Np步的延迟.因此预测域Np不能取得过大.本文选取Np=10,而每一步的时长为0.01 s.这样产生的0.1 s延迟仍在可接受范围之内.
T1(k)和T2(k)是两个参与者的局部目标轨迹,在每一次优化前都需要滚动更新.其更新方程为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( {k + 1} \right) = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{T}}_1}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{t}}_1}\left( {k + 1} \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( {k + 1} \right) = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{T}}_2}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{t}}_2}\left( {k + 1} \right)} \end{array} $ | (6) |
式中,
定义两个误差变量ε1(k)和ε2(k)为
| $ \begin{array}{*{20}{c}} {{\varepsilon _1}\left( k \right) = {\mathit{\boldsymbol{T}}_1}\left( k \right) - \mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}\left( k \right) - {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}{\mathit{\boldsymbol{U}}_2}\left( k \right)}\\ {{\varepsilon _2}\left( k \right) = {\mathit{\boldsymbol{T}}_2}\left( k \right) - \mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}\left( k \right) - {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}{\mathit{\boldsymbol{U}}_1}\left( k \right)} \end{array} $ | (7) |
则有
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_i}\left( k \right) = \left\| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}{\mathit{\boldsymbol{U}}_i}\left( k \right) - {\varepsilon _i}\left( k \right)} \right\|_{{Q_i}\left( k \right)}^2 + \left\| {{\mathit{\boldsymbol{U}}_i}\left( k \right)} \right\|_{{R_i}}^2,}\\ {i = 1,2} \end{array} $ | (8) |
Vi(k)对Ui(k)的偏导为
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{V}}_i}\left( k \right)}}{{\partial {\mathit{\boldsymbol{U}}_i}\left( k \right)}} = - 2\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_i}\left( k \right){\varepsilon _i}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;2\left[ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_i}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} + {\mathit{\boldsymbol{R}}_i}} \right]{\mathit{\boldsymbol{U}}_i}\left( k \right) \end{array} $ | (9) |
由于Qi(k)都是半正定矩阵且Ri都是正定矩阵,因此Vi(k)对Ui(k)的二阶偏导始终大于0.则Vi(k)对Ui(k)的偏导等于0的解即为代价函数最小的最优控制序列.因此有
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_i^{\rm{o}}\left( k \right) = {\mathit{\boldsymbol{F}}_i}\left( k \right){\varepsilon _i}\left( k \right)}\\ {\mathit{\boldsymbol{U}}_i^{\rm{o}}\left( k \right) \in \mathit{\boldsymbol{ \boldsymbol{\varPi} }}_i^{\rm{o}}} \end{array} $ | (10) |
其中
| $ {\mathit{\boldsymbol{F}}_i}\left( k \right) = {\left[ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_i}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} + {\mathit{\boldsymbol{R}}_i}} \right]^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_i}\left( k \right) $ | (11) |
Uio(k)表示第i个(i=1, 2)控制输入Ui(k)的最优控制序列.Πio表示Ui(k)的所有可能最优控制序列的集合.通过式(7)可知,式(10)中一个参与者的最优控制序列总与另一个参与者的控制决策有关.即U1o(k)是与U2(k)相关的,U2o(k)是与U1(k)相关的.因此式(10)表示了一簇最优控制序列,这一簇最优控制序列组成的集合可以表示为Π1o×Π2o.符号×表示集合的直积.
非合作博弈问题可以通过所谓的纳什均衡(Nash equilibrium)[21]来求解.不失一般性的,我们以两个参与者的动态博弈来说明这个问题.记博弈中第i个参与者的控制为Ui(i=1, 2).其中Ui∈Πi,Πi为第i个参与者全部可行控制的集合.若存在一组控制{U1*, U2*}(Ui*∈Πi, i=1, 2)使得关于控制的代价函数式(12)成立,那么{U1*, U2*}就称为一组纳什均衡解[15].
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\left( {\mathit{\boldsymbol{U}}_1^ * ,\mathit{\boldsymbol{U}}_2^ * } \right) \le {\mathit{\boldsymbol{V}}_1}\left( {{\mathit{\boldsymbol{U}}_1},\mathit{\boldsymbol{U}}_2^ * } \right),\forall {\mathit{\boldsymbol{U}}_1} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_1}}\\ {{\mathit{\boldsymbol{V}}_2}\left( {\mathit{\boldsymbol{U}}_1^ * ,\mathit{\boldsymbol{U}}_2^ * } \right) \le {\mathit{\boldsymbol{V}}_1}\left( {\mathit{\boldsymbol{U}}_1^ * ,{\mathit{\boldsymbol{U}}_2}} \right),\forall {\mathit{\boldsymbol{U}}_2} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_2}} \end{array} $ | (12) |
纳什均衡表明,当一个参与者执行纳什均衡策略时,其他参与者无法通过选择非纳什均衡的其他策略来增加自己的收益.因此对每一个参与者来说,纳什均衡解是当前博弈条件下的最优解.
对于非合作博弈MPC人机共驾策略,其纳什均衡解可以由定理1给出.
定理1 对于如式(2)所描述的博弈系统和式(4)所描述的代价函数,当且仅当I-L(k)可逆时系统具有唯一的纳什均衡解.且该纳什均衡解为
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_1^ * \left( k \right)}\\ {\mathit{\boldsymbol{U}}_2^ * \left( k \right)} \end{array}} \right] = \mathit{\boldsymbol{K}}\left( k \right)\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\} $ |
式中,K(k)=[I-L(k)]-1M(k),
| $ \mathit{\boldsymbol{M}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1}\left( k \right)}&0\\ 0&{{\mathit{\boldsymbol{F}}_2}\left( k \right)} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{L}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} 0&{ - {\mathit{\boldsymbol{F}}_1}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}}\\ { - {\mathit{\boldsymbol{F}}_2}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}}&0 \end{array}} \right]. $ |
证明:
(1) 存在性与唯一性.Vi(k)(i=1, 2)为一个二次型函数的博弈通常也被称为二次博弈(quadratic game).二次博弈是否存在唯一纳什均衡解可以通过矩阵的可逆性来判别.文献[15]表明,存在一个矩阵P(k),当且仅当P(k)可逆时,二次博弈存在唯一的纳什均衡解.其中
| $ \mathit{\boldsymbol{P}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^{\rm{T}}{\mathit{\boldsymbol{Q}}_1}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1} + {\mathit{\boldsymbol{R}}_1}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^{\rm{T}}{\mathit{\boldsymbol{Q}}_1}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2^{\rm{T}}{\mathit{\boldsymbol{Q}}_2}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2^{\rm{T}}{\mathit{\boldsymbol{Q}}_2}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2} + {\mathit{\boldsymbol{R}}_2}} \end{array}} \right] $ |
对P(k)进行变换可得
| $ \begin{array}{l} \mathit{\boldsymbol{P}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^{\rm{T}}{\mathit{\boldsymbol{Q}}_1}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1} + {\mathit{\boldsymbol{R}}_1}}&0\\ 0&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2^{\rm{T}}{\mathit{\boldsymbol{Q}}_2}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2} + {\mathit{\boldsymbol{R}}_2}} \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{L}}\left( k \right)} \right] \end{array} $ |
因为Qi(k)都是半正定矩阵且Ri都是正定矩阵,所以P(k)的可逆性等价于I-L(k)的可逆性.因此当且仅当I-L(k)的可逆性,非合作MPC具有唯一的纳什均衡解.
(2) 构造性.当I-L(k)可逆时,非合作MPC的唯一纳什均衡解可以直接求得闭式解析表达而不需要迭代.下面来构造非合作MPC的纳什均衡解.
将U1o(k)与U2o(k)表示为矩阵形式可得
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_1^{\rm{o}}\left( k \right)}\\ {\mathit{\boldsymbol{U}}_2^{\rm{o}}\left( k \right)} \end{array}} \right] = \mathit{\boldsymbol{M}}\left( k \right)\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{L}}\left( k \right)\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{U}}_2}\left( k \right)} \end{array}} \right] \end{array} $ | (13) |
通过式(13)得到的U1(k)和U2(k)的一对最优控制序列满足
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\left( {\mathit{\boldsymbol{U}}_1^{\rm{o}},{\mathit{\boldsymbol{U}}_2}} \right) \le {\mathit{\boldsymbol{V}}_1}\left( {{\mathit{\boldsymbol{U}}_1},{\mathit{\boldsymbol{U}}_2}} \right),\forall {\mathit{\boldsymbol{U}}_1} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_1},\forall {\mathit{\boldsymbol{U}}_2} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_2}}\\ {{\mathit{\boldsymbol{V}}_2}\left( {{\mathit{\boldsymbol{U}}_1},\mathit{\boldsymbol{U}}_2^{\rm{o}}} \right) \le {\mathit{\boldsymbol{V}}_2}\left( {{\mathit{\boldsymbol{U}}_1},{\mathit{\boldsymbol{U}}_2}} \right),\forall {\mathit{\boldsymbol{U}}_1} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_1},\forall {\mathit{\boldsymbol{U}}_2} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_2}} \end{array} $ | (14) |
当且仅当I-L(k)可逆时,非合作MPC有唯一的纳什均衡解.记系统的纳什均衡解为(U1*(k), U2*(k)).系统的纳什均衡解应满足最优反应函数式(13),即{U1*(k), U2*(k)}∈Π1o×Π2o.因此有
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_1^ * \left( k \right)}\\ {\mathit{\boldsymbol{U}}_2^ * \left( k \right)} \end{array}} \right] = \mathit{\boldsymbol{M}}\left( k \right)\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\} + }\\ {\mathit{\boldsymbol{L}}\left( k \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_1^ * \left( k \right)}\\ {\mathit{\boldsymbol{U}}_2^ * \left( k \right)} \end{array}} \right]} \end{array} $ | (15) |
式(15)得到的U1*(k)和U2*(k)满足
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\left( {\mathit{\boldsymbol{U}}_1^ * ,\mathit{\boldsymbol{U}}_2^ * } \right) \le {\mathit{\boldsymbol{V}}_1}\left( {{\mathit{\boldsymbol{U}}_1},\mathit{\boldsymbol{U}}_2^ * } \right),\forall {\mathit{\boldsymbol{U}}_1} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_1}}\\ {{\mathit{\boldsymbol{V}}_2}\left( {\mathit{\boldsymbol{U}}_1^ * ,\mathit{\boldsymbol{U}}_2^ * } \right) \le {\mathit{\boldsymbol{V}}_2}\left( {\mathit{\boldsymbol{U}}_2^ * ,{\mathit{\boldsymbol{U}}_2}} \right),\forall {\mathit{\boldsymbol{U}}_2} \in {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_2}} \end{array} $ | (16) |
因此,通过式(15)得到的最优控制序列对{U1*(k), U2*(k)}即为系统的一组纳什均衡解.当I-L(k)可逆时,式(15)有解.非合作博弈MPC的纳什均衡解为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_1^ * \left( k \right)}\\ {\mathit{\boldsymbol{U}}_2^ * \left( k \right)} \end{array}} \right] = {\left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{L}}\left( k \right)} \right]^{ - 1}}\mathit{\boldsymbol{M}}\left( k \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\} \end{array} $ | (17) |
证毕.
在MPC中,通常采取一种域后退的策略.即在每一个优化域中求解局部最优MPC控制策略,但优化域随时间一直向后推移进行滚动优化,因此只有控制序列的第一个控制输入起作用.两个参与者的反馈增益K1(k)和K2(k)为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{K}}_2}\left( k \right)} \end{array}} \right] = \left[ {\underbrace {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_l}}&0& \cdots &0\\ 0&0& \cdots &0 \end{array}}_{{N_{\rm{p}}}}\left| {\underbrace {\begin{array}{*{20}{c}} 0&0& \cdots &0\\ {{\mathit{\boldsymbol{I}}_l}}&0& \cdots &0 \end{array}}_{{N_{\rm{p}}}}} \right.} \right]\mathit{\boldsymbol{K}}\left( k \right) $ | (18) |
式中:Il为l维单位矩阵,l为每个参与者控制输入的个数.
人机共驾中两个参与者的非合作博弈MPC控制输入可以表示为
| $ \begin{array}{l} \mathit{\boldsymbol{u}}_{\rm{D}}^ * \left( k \right) = {\mathit{\boldsymbol{K}}_1}\left( k \right)\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\}\\ \mathit{\boldsymbol{u}}_{\rm{A}}^ * \left( k \right) = {\mathit{\boldsymbol{K}}_2}\left( k \right)\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}\left( k \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( k \right)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\\ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right)} \right\} \end{array} $ | (19) |
非合作MPC人机共驾策略的控制输入是综合考虑驾驶员操作,控制系统规划轨迹,和当前危险状态后对车辆的控制.即根据危险程度在驾驶员和控制系统之间动态的分配驾驶权,因此可以兼顾舒适性和安全性.
文献[22]表明,虽然通过式(10)推导MPC的最优控制序列比较直观方便,但使用式(10)计算矩阵Fi(k)的方法通常数值不稳定.文献[22]提供了一种较好的解决方法,本文使用该方法来计算Fi(k).则F1(k)和F2(k)可以表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1}\left( k \right) = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{Q_1}}}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}}\\ {{\mathit{\boldsymbol{S}}_{{R_1}}}} \end{array}} \right]}^ + }\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{Q_1}}}\left( k \right)}\\ 0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{F}}_2}\left( k \right) = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{Q_2}}}\left( k \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}}\\ {{\mathit{\boldsymbol{S}}_{{R_2}}}} \end{array}} \right]}^ + }\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{Q_2}}}\left( k \right)}\\ 0 \end{array}} \right]}\\ {\left\{ \begin{array}{l} {\mathit{\boldsymbol{S}}_{{Q_1}}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{S}}_{{Q_1}}}\left( k \right) = {\mathit{\boldsymbol{Q}}_1}\left( k \right)\\ \mathit{\boldsymbol{S}}_{{R_1}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{R_1}}} = {\mathit{\boldsymbol{R}}_1} \end{array} \right.}\\ {\left\{ \begin{array}{l} {\mathit{\boldsymbol{S}}_{{Q_2}}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{S}}_{{Q_2}}}\left( k \right) = {\mathit{\boldsymbol{Q}}_2}\left( k \right)\\ \mathit{\boldsymbol{S}}_{{R_2}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{R_2}}} = {\mathit{\boldsymbol{R}}_2} \end{array} \right.} \end{array} $ | (20) |
式中:A+表示矩阵A的广义逆.
4 仿真结果及分析使用Matlab软件对非合作MPC人机共驾策略进行仿真验证.根据实际车辆参数选取车辆参数如表 1所示.
| 下载CSV 表 1 车辆参数 Tab.1 Vehicle parameters |
使用驾驶员期望向左侧变道而智能车控制系统期望直行的场景验证非合作MPC人机共驾策略的效果.驾驶员变道轨迹使用5次多项式变道轨迹拟合[23].变道轨迹长度为50 m,宽度为3.5 m.仿真中车辆行驶速度为20 m·s-1.预测域Np=10,控制域Nu=10,仿真步长T=0.01 s.与最优控制类似,在非合作MPC中,只有q1(k)和q2(k)与r1和r2的相对值会对控制结果产生影响.本文中每个参与者只有一个输入,r1和r2均为标量.因此在仿真中均设定r1=1,r2=1.
第1组仿真验证分配系数κ1(k)和κ2(k)对控制结果的影响.这一组5个工况的参数设置如下:
(1) 仿真工况1.1:κ1(k)=0.1,λ1(k)=10;κ2(k)=0.1,λ2(k)=10.
(2) 仿真工况1.2:κ1(k)=0.4,λ1(k)=40;κ2(k)=0.1,λ2(k)=10.
(3) 仿真工况1.3:κ1(k)=0.1,λ1(k)=10;κ2(k)=0.3,λ2(k)=30.
(4) 仿真工况1.4:κ1(k)=0,λ1(k)=0;κ2(k)=0.1,λ2(k)=10.
(5) 仿真工况1.5:κ1(k)=0.1,λ1(k)=10;κ2(k)=0,λ2(k)=0.
第1组仿真中,q1(k)和q2(k)均为常数,仿真结果如图 2所示.通过图 2可以看出,改变q1(k)和q2(k)的相对比例(即等比例的缩放κi(k)和λi(k).(i=1, 2)),会使最终的规划轨迹处于驾驶员期望轨迹和控制系统期望轨迹之间.当q1(k)为0时,最终规划轨迹会与控制系统期望轨迹完全相同,此时智能车完全受系统控制;当q2(k)为0时,最终规划轨迹会与驾驶员期望轨迹完全相同,此时智能车完全受驾驶员控制.

|
图 2 第1组仿真工况结果 Fig.2 Results of the first group of simulations |
第2组仿真验证动态调整系数λ1(k)和λ2(k)对控制结果的影响.这一组5个工况的参数设置如下:
(1) 仿真工况2.1:κ1(k)=0.1,λ1(k)=10;κ2(k)=0.1,λ2(k)=10.
(2) 仿真工况2.2:κ1(k)=0.1,λ1(k)=2;κ2(k)=0.1,λ2(k)=10.
(3) 仿真工况2.3:κ1(k)=0.1,λ1(k)=6;κ2(k)=0.1,λ2(k)=10.
(4) 仿真工况2.4:κ1(k)=0.1,λ1(k)=10;κ2(k)=0.1,λ2(k)=2..
(5) 仿真工况2.5:κ1(k)=0.1,λ1(k)=10;κ2(k)=0.1,λ2(k)=6.
第2组仿真中,q1(k)和q2(k)同样均为常数,仿真结果如图 3所示.通过图 3可以看出,在κ1(k)和κ2(k)保持不变的情况下,改变λ1(k)和λ2(k)对规划轨迹的最终结果不产生影响.即5个工况的规划轨迹最终收敛到同样的位置.改变λ1(k)和λ2(k)主要影响了规划轨迹的动态特性.当λ1(k)比λ2(k)大时,规划轨迹表现出一种超调特性,并且λ1(k)与λ2(k)的差值越大这种超调特性越明显;当λ1(k)比λ2(k)小时,规划轨迹表现出一种过阻尼特性,并且λ1(k)与λ2(k)的差值越大这种过阻尼特性越明显.
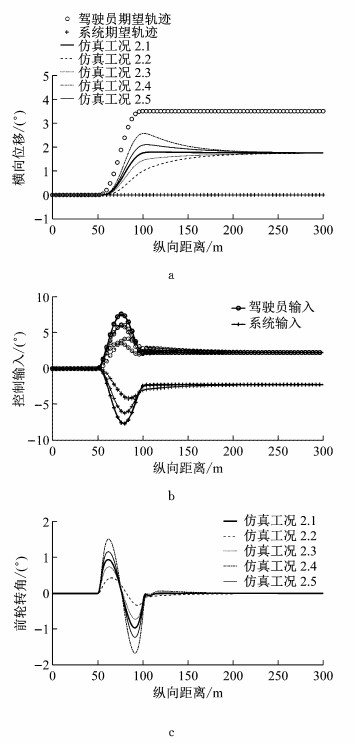
|
图 3 第2组仿真工况结果 Fig.3 Results of second group of simulations |
第1组和第2组仿真使我们对κi(k)和λi(k)(i=1, 2)对规划轨迹的影响有了较为清晰的了解.接下来的第3组仿真将表示非合作MPC人机共驾策略最为明显的优点,即实现驾驶员和控制系统之间驾驶权的逐渐交接.这主要通过κ1(k)和κ2(k)的逐渐变化来实现.
第3组仿真中,λ1(k)和λ2(k)设为常数,即λ1(k)=2,λ2(k)=2.3个工况中开始均设定κ1(k)=0.1,κ2(k)=0.在某一时刻,κ1(k)逐渐线性的减小到0,同时κ2(k)逐渐线性的增大到0.1.第3组仿真3个工况κ1(k)和κ2(k)的变化如图 4所示.仿真工况3.1是在3 s时(60 m处)开始驾驶权交接,并在1 s内(20 m内)完成从驾驶员驾驶到系统驾驶的转换.注意到仿真工况设定是在50 m处驾驶员期望开始变道,并在100 m处变道结束.因此仿真工况3.1表示了在变道过程中进行驾驶权交接的结果.仿真工况3.2是在9 s时(180 m处)开始驾驶权交接,并在6 s内(120 m内)完成从驾驶员驾驶到系统驾驶的转换.仿真工况3.3是在9 s时(180 m处)开始驾驶权交接,并在1 s内(20 m内)完成从驾驶员驾驶到系统驾驶的转换.仿真工况3.2和3.3表示了当驾驶员和控制系统存在分歧的稳定状态时进行驾驶权转换的结果.

|
图 4 分配系数的变化 Fig.4 Assignment coefficients in the third group of simulations |
第3组仿真3个工况结果如图 5所示.通过图 5a可以看出,当驾驶员与控制系统发生分歧时进行驾驶权的转换,3个工况都可以规划出一条非常符合车辆动力学的稳定轨迹.并且3个工况都实现了平稳的从驾驶员控制转换到系统控制.在仿真工况3.1中,变道进行到一半时进行驾驶权转换,车辆可以平顺的由向左变道逐渐回到本车道.在仿真工况3.2和3.3中,当车辆已经按照驾驶员的操作进行左变道后进行驾驶权交接,车辆可以平顺的右变道回到本车道.且驾驶权交接时间越短,变道轨迹越紧急.通过图 5c可以看出,3个工况在驾驶权交接的过程中,车辆前轮转角输入始终保持在较小范围内,没有较大范围的突然剧烈变化.这对保持车辆稳定是非常有利的.
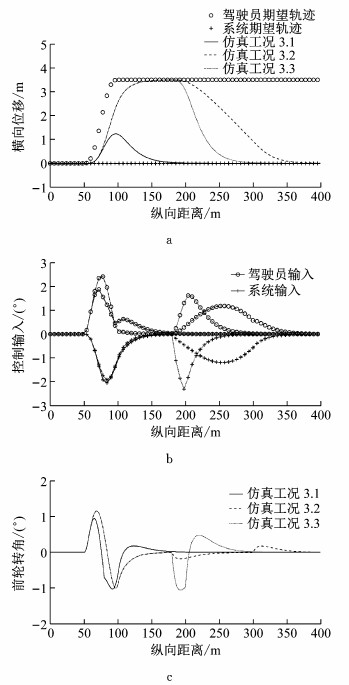
|
图 5 第三组仿真工况结果 Fig.5 Results of the third group of simulations |
第3组仿真工况是有其实际意义的.当驾驶员左转方向盘期望左变道时,智能车在之前可以由于感知系统的遮挡等没有检测到左侧车道的障碍物.在车辆左变道过程中,智能车在检测到左侧车道障碍物的危险后在变道过程中马上进行驾驶权交接,使本车回到原车道以避免危险.
5 结语使用非合作MPC实现了一种人机共驾的双驾双控策略.即驾驶员和智能车控制系统同时发出驾驶指令,智能车根据车辆当前状态和两者的控制指令依某一规则规划车辆运动轨迹.之前关于非合作MPC求解的文献中均使用了迭代法,本文表明非合作MPC可以通过非迭代的方法求解.非合作MPC人机共驾策略的主要优点是可以实现驾驶员和控制系统之间驾驶权的逐渐交接.这样,既能保证驾驶员实时在环,又不会在智能车控制系统接管车辆时过于突兀,给驾驶员带来不适感.非合作MPC的这种驾驶权逐渐交接是通过驾驶员和控制系统置信度矩阵的实时更新实现的.Matlab仿真验证表明在危险工况时,非合作MPC人机共驾策略可以完成驾驶权从驾驶员到智能车控制系统的平稳交接.
| [1] |
Da LIO M, BIRAL F, BERTOLAZZI E, et al. Artificial co-drivers as a universal enabling technology for future intelligent vehicles and transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 244 DOI:10.1109/TITS.2014.2330199 |
| [2] |
ROSENSTATTER T, ENGLUND C. Modelling the level of trust in a cooperative automated vehicle control system[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(4): 1237 DOI:10.1109/TITS.2017.2749962 |
| [3] |
SAWADE O, SCHULZE M, RADUSCH I. Robust communication for cooperative driving maneuvers[J]. IEEE Intelligent Transportation Systems Magazine, 2018, 10(3): 159 DOI:10.1109/MITS.2018.2842241 |
| [4] |
WU Jian, CHENG Shuo, LIU Binhao, et al. A human-machine-cooperative-driving controller based on AFS and DYC for vehicle dynamic stability[J]. Energies, 2017, 10(11): 1737 DOI:10.3390/en10111737 |
| [5] |
MENG Yue, LI Li, WANG Feiyue, et al. Analysis of cooperative driving strategies for nonsignalized intersections[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 2900 DOI:10.1109/TVT.2017.2780269 |
| [6] |
MICHON J A.A critical view of driver behavior models: what do we know, what should we do?[C]//Human Behavior and Traffic Safety.New York: Springer, 1985: 485-520.
|
| [7] |
RUMAR K.The role of perceptual and cognitive filters in ohserved hehavior[M].Human Behavior and Traffic Safety.New York: Springer, 1985.
|
| [8] |
KHOSRAVANI S, KHAJEPOUR A, FIDAN B, et al.Development of a robust vehicle control with driver in the loop[C]//American Control Conference.Portland: IEEE, 2014: 3482-3487.
|
| [9] |
LI Renjie, LI Shengbo, GAO Hongbo, et al.Effects of human adaptation and trust on shared control for driver-automation cooperative driving[C]//SAE Technical Paper Series.Detroit: SAE Publication Group, 2017: 2017-01-1987.
|
| [10] |
ABBINK D A, MULDER M, BOER E R. Haptic shared control:smoothly shifting control authority?[J]. Cognition Technology&Work, 2012, 14(1): 19 |
| [11] |
SOUALMI B, SENTOUH C, POPIEUL J C, et al. Automation-driver cooperative driving in presence of undetected obstacles[J]. Control Engineering Practice, 2014, 24(1): 106 |
| [12] |
MULDER M, ABBINK D A, BOER E R. sharing control with haptics:seamless driver support from manual to automatic control[J]. Human Factors, 2012, 54(5): 786 DOI:10.1177/0018720812443984 |
| [13] |
OMAE M, FUJIOKA T, HASHIMOTO N, et al. The application of RTK-GPS and steer-by-wire technology to the automatic driving of vehicles and an evaluation of driver behavior[J]. IATSS Research, 2006, 30(2): 29 DOI:10.1016/S0386-1112(14)60167-9 |
| [14] |
LI Renjie, LI Yanan, LI Shengbo, et al.Driver-automation indirect shared control of highly automated vehicles with intention-aware authority transition[C]//Intelligent Vehicles Symposium.Los Angeles: IEEE, 2017: 26-32.
|
| [15] |
BASAR T, OLSDER G J. Dynamic noncooperative game theory[M]. Philadelphia: SIAM, 1999
|
| [16] |
MA W H, PENG H. Worst-case vehicle evaluation methodology?examples on truck rollover/jackknifing and active yaw control systems[J]. Vehicle System Dynamics, 1999, 32(4/5): 389 |
| [17] |
MA W H, PENG H. A worst-case evaluation method for dynamic systems[J]. Journal of Dynamic Systems Measurement and Control, 1999, 121(2): 191 DOI:10.1115/1.2802454 |
| [18] |
TAMADDONI S H, TAHERI S, AHMADIAN M.Optimal VSC design based on nash strategy for differential 2-player games[C]//International Conference on Systems, Man and Cybernetics.San Antonio: IEEE, 2009: 2415-2420.
|
| [19] |
TAMADDONI S H, TAHERI S, AHMADIAN M. Optimal preview game theory approach to vehicle stability controller design[J]. Vehicle System Dynamics, 2011, 49(12): 1967 DOI:10.1080/00423114.2011.565778 |
| [20] |
NA X, COLE D J. Linear quadratic game and non-cooperative predictive methods for potential application to modelling driver-AFS interactive steering control[J]. Vehicle System Dynamics, 2013, 51(2): 165 DOI:10.1080/00423114.2012.715653 |
| [21] |
ENGWERDA J. LQ dynamic optimization and differential games[M]. London: John Wiley&Sons Ltd, 2005
|
| [22] |
MACIEJOWSKI J M. Predictive control with constraints[M]. London: Pearson Education, 2001
|
| [23] |
SLEDGE N H, MARSHEK K M.Comparison of ideal vehicle lane-change trajectories[C]//SAE Technical Paper Series.Detroit: SAE Publication Group, 1997: 971062.
|
 2019, Vol. 47
2019, Vol. 47

