超高层建筑由于刚度小和低阻尼的特点,抗风是超高层建筑设计中的主导因素.但在结构设计过程中,阻尼比难以准确获得,一般是按照规范取经验值.对于超限建筑结构,通常需要进行振动台试验和风洞试验评估结构的设计方案.随着监测技术的发展,原型实测正成为研究结构风效应的最直接和最有效的手段.国外,圣母大学和西安大略大学对芝加哥四栋高楼进行了实测研究[1-2].国内,香港城市大学和香港理工大学对广州西塔、帝王大厦和广州塔等国内十几栋超高层建筑进行了实测[3-9],同济大学对上海环球金融中心[10-12]、上海中心大厦[13]等进行了实测分析.目前,对台风等极端环境下结构高振幅的动力特性研究较少,而日常良态风下结构监测时间跨度长,包含风事件充足,能够全面了解结构在低振幅下的动力特性规律.但目前将台风和良态风下的动力特性进行对比研究的文献和成果很少.因此,对日常监测数据进行分析,全面掌握结构低振幅下的动力响应特性,以及台风时高振幅下的动力特性变化规律十分必要.
Zhang等[13]利用Bayesian FFT方法对上海中心大厦施工期间及施工后的结构动力特性进行了评估,指出结构阻尼比随振幅增大而增大的现象并不如文献[3-9]所述明显,但该文所用评估数据仅是日常数据且时间跨度短,同时,Bayesian FFT方法决定了评估结果受数据量限制,所得结论仍需进一步验证.本文基于上海中心大厦2016—2017年日常监测数据,对低振幅下结构的动力特性规律进行分析,同时基于2018年7月台风“安比”登陆时的监测数据,对高振幅下结构的动力特性规律进行分析,得出了一些结构动力参数随振幅的变化规律.
1 上海中心大厦简介上海中心大厦位于上海市浦东新区陆家嘴金融中心,总高632 m,结构高度580 m,由地上121层主楼、5层裙楼和5层地下室组成,是目前中国已建成的最高建筑,其周边高层众多,地貌极其复杂,如图 1所示.

|
图 1 上海中心及周边建筑 Fig.1 Panorama and surrounding of Shanghai Tower |
上海中心大厦抗侧力体系为“巨型框架-核心筒-外伸臂”结构体系.大厦顶部125层安装了1 000 t的电涡流阻尼器,用以减小结构在台风作用下的振幅以提高舒适性.为了对结构的施工指导、设计验证和性能评估提供支持,同济大学、香港理工大学和同济大学设计院等单位建立了较为完备的结构健康监测系统,对上海中心大厦从施工阶段到运营阶段进行长期监测[14].由于传感器数量众多,硬件系统设置了7个采集子站和1个采集总站,保证了数据传输的信号强度和效率.其中,加速度传感器详细参数见表 1, 布置见图 2.整个健康监测系统包括4个子系统,分别为数据采集控制子系统、数据管理子系统、远程监测子系统和模态识别分析评估子系统.
| 下载CSV 表 1 加速度传感器参数 Tab.1 Specific parameters of acceleration sensor |

|
图 2 117层加速度传感器布置 Fig.2 Layout of accelerometers on the 117th floor |
本文基于2016—2017年良态风和2018年7月台风“安比”作用下的上海中心大厦第117层的加速度实测数据,选取了南北向(X向)4 390 h和东西向(Y向)3 864 h的日常监测数据,以及72 h台风“安比”登陆期间的监测数据,进行结构动力参数分析.
采用包络随机减量法[15]识别上海中心大厦的第一阶频率和阻尼比,具体步骤如下:
(1) 运用解析模态分解法[16]对时程数据进行滤波,求得一阶模态加速度响应时程a(t),采用Hillbert变换获得时程a(t)的包络线幅值A(t).
(2) 截取包络线幅值A(t)累计概率分布30%以上的点A(ti),对应到时程上的点为a(ti),i为截取点数,i=1, 2, …, N.
(3) 对于每个时间点ti,获得其后连续20个周期的时程a(ti+τ),共获得N个时程.
(4) 将加速度时程a(t)和包络线幅值A(t)的符号反转, 即乘以负号,按照步骤(2)和(3)获得N个时程a′ (ti+τ).
(5) 计算待拟合的自由衰减曲线.
(6) 对自由衰减曲线D(τ)进行拟合,得到一阶自振频率和一阶阻尼比.
3 上海中心大厦动力特性分析考虑到随机减量技术在识别系统参数时对于数据量的要求,本文均以1 h为分析时距.对每段1 h加速度响应时程,采用随机减量法识别出一阶自振频率和一阶阻尼比,并以1 h响应时程加速度标准差为振幅,分析一阶自振频率和振幅、一阶阻尼比和振幅的相关性.
3.1 良态风作用下的结构动力参数分析 3.1.1 一阶自振频率随振幅的变化规律图 3显示了一阶自振频率随振幅的变化趋势,采用式(1)对图 3中的实测数据进行线性拟合.

|
图 3 一阶自振频率随振幅的变化规律 Fig.3 Fundamental natural frequencies versus vibration amplitude |
| $ f=\alpha_{0} {z}+\alpha_{1} $ | (1) |
式中:f为一阶自振频率;z为振幅;α0和α1为回归系数,其中α0表示一阶自振频率随振幅的变化速度,α1表示振幅为0时结构的一阶自振频率.
从图 3可看出,一阶自振频率随着振幅的增加而减小.根据拟合直线可知,X方向振幅由0.01×10-3g增大到0.40×10-3g时,一阶自振频率由0.107 0 Hz下降到0.106 0 Hz,降幅为0.934 6%;Y方向振幅由0.01×10-3g增大到0.40×10-3g时,一阶自振频率由0.107 3 Hz下降到0.106 4 Hz,降幅为0.838 7%.本文所述良态风下的一阶自振频率略小于Zhang等[13]利用Bayesian FFT方法所测得X向和Y向的一阶自振频率0.108 0 Hz和0.109 0 Hz,这可能是由于分析方法的不同所致.利用MIDAS/Gen有限元软件对上海中心大厦进行数值分析得到其X向和Y向的自振频率分别为0.111 6 Hz和0.110 4 Hz,比本文和文献[13]的结果略大,这是由于数值模拟时未考虑非结构部分的影响、单元参数为预估值以及连接部分模拟理想化,导致数值模拟的结构刚度比实际结构偏大,结构质量偏小,自振频率偏大.
表 2给出了上海中心大厦、上海环球金融中心和广州塔的拟合参数α0及α1值.从表 2中可看出,3栋超高层建筑的α0基本接近,都在-4×10-3~-2×10-3 Hz·g-1之间,表明3栋超高层建筑的一阶频率随振幅减小的速率基本一致.引起结构自振频率随振幅的增大而降低的可能原因是:结构振动较大时,结构产生的非线性响应、刚节点滑移以及结构构件和非结构构件的相互作用[17].3栋超高层建筑的系数α1基本在0.090~0.160范围内,表明超高层建筑的刚度较小.另外,上海中心大厦的系数α1小于环球金融中心,这是由于前者的结构高度大于后者所致.虽然上海中心大厦的主体结构比广州塔高126 m,但其系数α1却大于广州塔,说明上海中心大厦的结构刚度略高于广州塔.
| 下载CSV 表 2 上海中心大厦及其他超高层拟合参数α0和α1值 Tab.2 Coefficients α0 and α1 of Shanghai Tower and those of other super-tall buildings |
图 4显示了一阶阻尼比随振幅的变化趋势.采用式(2)对图 4中的实测数据进行线性拟合.

|
图 4 一阶阻尼比随振幅的变化规律 Fig.4 Fundamental damping ratios versus vibrationamplitude |
| $ \xi=\beta_{0} z+\beta_{1} $ | (2) |
式中:ξ为一阶阻尼;z为振幅;β0和β1为回归系数,其中β0表示一阶阻尼比随振幅的变化速度,β1表示振幅为0时的结构一阶阻尼比.
图 4说明,上海中心在正常使用状态下,结构的阻尼比在0.3%~1.0%范围内,与Zhang等[13]利用Bayesian FFT方法所测结果相似.根据拟合结果,当结构振幅由0.01×10-3g增加到0.40×10-3g时,X向一阶阻尼比由0.574 3%增加到0.669 8%,Y向一阶阻尼比由0.495 6%增加到0.594 6%.但是,考虑到数据的随机性和离散程度,上海中心大厦在正常使用状态下阻尼比取0.3%~1.0%较为合理.
表 3给出了上海中心大厦、上海环球金融中心和广州塔的拟合参数β0和β1值.从表 3中可看出,上海中心大厦的β0小于上海环球金融中心和广州塔,这说明与其他两座超高层相比,上海中心大厦的阻尼比随振幅的增大而增大的现象并不明显,这与Zhang等[13]的结论一致.β1基本在0.3%~0.6%左右,表明3栋超高层建筑的一阶阻尼比较小.
| 下载CSV 表 3 上海中心大厦及其他超高层拟合参数β0和β1值 Tab.3 Coefficients β0 and β1 of Shanghai Tower and those of other super-tall buildings |
台风“安比”登陆上海时间是2018年7月22日,本文选取2018年7月21日至2018年7月23日作为结构动力参数的分析时间段.
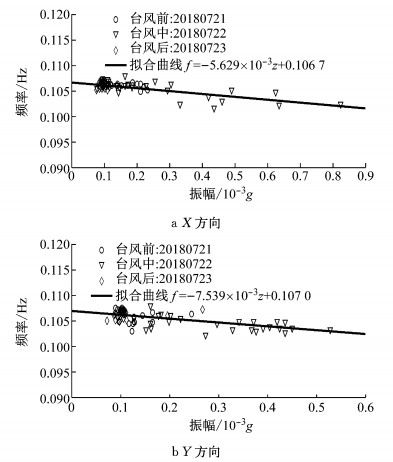
3.2.1 一阶自振频率随振幅的变化规律图 5显示了一阶自振频率随振幅的变化趋势.仍然采用式(1)对图 5中的数据进行拟合,拟合参数α0和α1取值见表 4.根据拟合公式,当振幅由0.01×10-3g增加到0.90×10-3g时,X向一阶自振频率由0.106 7 Hz下降到0.101 6 Hz,降幅为4.78%,Y向一阶自振频率由0.107 0 Hz下降到0.100 2 Hz,降幅为6.35%.
|
图 5 台风“安比”登陆期间频率随振幅的变化规律 Fig.5 Variation of fundamental damping ratios with vibration amplitude under typhoon "Ampil" |
| 下载CSV 表 4 台风“安比”登陆期间上海中心大厦拟合参数α0和α1值 Tab.4 Coefficients α0 and α1 of Shanghai Tower in typhoon 'Ampil' |
图 5表明,一阶自振频率随振幅的增大而减小,同时一阶自振频率在台风前后保持一致,说明上海中心大厦在台风前后刚度保持一致.此外,图 5间接地反映出结构的响应随着风速的增大而增大.从表 4可以看出,上海中心大厦在台风期间, α0是良态风时的2~3倍,说明台风期间结构的一阶频率随振幅降低较快,这一方面是由于高振幅下阻尼器的启动增加了结构的阻尼,导致频率随振幅降低的速率有一定的增大;另一方面,良态风下的数据量多,α0具有一般性的统计意义,考虑了频率参数的随机性,而根据台风“安比”所拟合的α0仅代表这一特殊事件的值,高振幅数据稀少,对拟合结果有一定的影响;另外,图 3和图 5对比显示,台风下的频率随振幅的趋势变化并不违背良态风下的一般规律.拟合系数α1在台风和良态风下基本一致,这是由于结构振幅为0时,动力参数不受非线性响应、刚节点滑移、阻尼器以及结构构件和非结构构件相互作用等因素的影响.
3.2.2 一阶阻尼比随振幅的变化规律与良态风下的阻尼比随振幅的变化规律不同,台风“安比”作用时阻尼比与振幅的关系曲线采用式(3)进行拟合.
| $ \zeta=k_{0} z^{k_{1}}+k_{2} $ | (3) |
式中:ζ为一阶阻尼比;z为振幅;k0、k1和k2为回归系数,其中k0和k1反映了阻尼比ζ随振幅的增长速率,k2反映阻尼比ζ的上限值.
表 5给出了式(3)的拟合结果.从表 5中可以看出,结构X向和Y向的k0、k1和k2基本相同,说明在台风作用下,结构在X和Y两个方向的耗能能力基本相同.
| 下载CSV 表 5 台风“安比”登陆期间上海中心大厦拟合参数k0、k1和k2值 Tab.5 Coefficients k0, k1, and k2 of Shanghai Tower in typhoon "Ampil" |
图 6显示了台风“安比”作用下结构的一阶阻尼比随振幅的变化趋势.从图 6中可看出,由于受到阻尼器启动的影响,上海中心大厦的一阶阻尼比随振幅的增大呈非线性增大,最终X向和Y向的阻尼比稳定在4.0%和5.0%左右.大厦在风荷载设计阶段取4%的阻尼比,与实测结果接近.与台风期间(7月22日)的一阶自振频率相似,台风前(7月21日)和台风后(7月23日)的一阶阻尼比保持一致,回落到0.5%~1.0%之间,而台风期间大厦的阻尼比随振幅的增大持续增加,且无数据突变,表明大厦的阻尼器在触发状态下具有良好的工作性能.根据拟合结果,阻尼器触发的振幅阈值大致为0.1×10-3g.此外,台风期间,实测平均风向在230°~290°之间(大致为东西向,即Y向,见图 2),大厦纵向(Y向)和横向(X向)的最大振幅分别为0.53×10-3g和0.82×10-3g,纵横向最大振幅之比为1:1.55.横向振幅大于纵向振幅的原因是当气流通过大厦时,在其横向产生了卡门涡流,一旦卡门涡流的频率与结构的振动频率一致时会发生“共振”,导致出现横向振动大于纵向振动的现象.

|
图 6 台风“安比”登陆期间一阶阻尼比随振幅的变化规律 Fig.6 Fundamental damping ratios versus vibration amplitude in typhoon "Ampil" |
本文基于2016—2017年日常监测数据和2018年7月台风“安比”登陆期间的监测数据,对上海中心大厦动力参数变化规律进行对比分析,主要结论如下:
(1) 在良态风作用下,阻尼器未启动时,上海中心大厦的一阶自振频率随振幅的增加而增加.根据拟合直线可知,X方向振幅由0.01×10-3g增大到0.40×10-3g时,一阶自振频率由0.107 0 Hz下降至0.106 0 Hz,降幅为0.93%;Y方向振幅由0.01×10-3g增大到0.4×10-3g时,一阶自振频率由0.107 3 Hz下降至0.106 4 Hz,降幅为0.84%.
(2) 在良态风作用下,阻尼器未启动时,上海中心大厦的阻尼比在0.25%~1.00%范围内.根据拟合结果,当结构振幅由0.01×10-3g增大到0.40×10-3g时,X向一阶阻尼比由0.574 3%增加至0.669 8%,Y向一阶阻尼比由0.495 6%增加至0.594 6%.考虑到数据的随机性和离散程度,大厦在正常使用状态下, 阻尼比取0.3%~1.0%较为合理.
(3) 台风作用下,阻尼器开始运行,上海中心大厦的一阶自振频率与振幅之间仍可以用线性关系来描述,但频率降低的速率是良态风下的2~3倍.当振幅由0.01×10-3g增加到0.90×10-3g时,X向一阶自振频率由0.106 7 Hz下降至0.101 6 Hz,降幅为4.78%,Y向一阶自振频率由0.107 0 Hz下降至0.100 2 Hz,降幅为6.35%.
(4) 台风期间,由于受到阻尼器启动的影响,上海中心大厦的一阶阻尼比随振幅的增大呈现非线性增大,最终X和Y方向的阻尼比稳定在4.0%~5.0%左右;大厦在风荷载设计阶段,阻尼比取4.0%较为合理.
| [1] |
KIJEWSKI-CORREA T L. Full-scale measurements and system identification: a time-frequency perspective [D]. Notre Dame: The University of Notre Dame, 2003.
|
| [2] |
KIJEWSKI-CORREA T L, PIRNIA J D. Dynamic behavior of tall buildings under wind: insights from full-scale monitoring[J]. The Structural Design of Tall and Special Buildings, 2007, 16(16): 471 |
| [3] |
LI Q S, FU J Y, XIAO Y Q, et al. Wind tunnel and full-scale study of wind effects on China's tallest building[J]. Engineering Structures, 2006, 28(12): 1745 DOI:10.1016/j.engstruct.2006.02.017 |
| [4] |
LI Q S, ZHI L H, TUAN A Y, et al. Dynamic behavior of Taipei 101 Tower: field measurement and numerical analysis[J]. Journal of Structural Engineering, 2011, 137(1): 143 DOI:10.1061/(ASCE)ST.1943-541X.0000264 |
| [5] |
FU J Y, WU J R, XU A, et al. Full-scale measurements of wind effects on Guangzhou West Tower[J]. Engineering Structures, 2012, 35(1): 120 |
| [6] |
YI J, ZHANG J W, LI Q S. Dynamic characteristics and wind-induced responses of a super-tall building during typhoons[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 121(5): 116 |
| [7] |
HE Y C, LI Q. Dynamic responses of a 492-m-high tall building with active tuned mass damping system during a typhoon[J]. Structural Control & Health Monitoring, 2014, 21(5): 705 |
| [8] |
XU Y L, CHEN S W, ZHANG R C. Modal identification of Di Wang Building under typhoon York using the Hilbert-Huang transform method[J]. The Structural Design of Tall and Special Buildings, 2003, 12(1): 21 |
| [9] |
GUO Y L, KAREEM A, NI Y Q, et al. Performance evaluation of Canton Tower under winds based on full-scale data[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104 |
| [10] |
AN Y, QUAN Y, GU M. Field measurement of wind characteristics of typhoon Muifa on the Shanghai World Financial Center[J]. International Journal of Distributed Sensor Networks, 2012, 8(9): 1 |
| [11] |
QUAN Y, WANG S, GU M, et al. Field measurement of wind speeds and wind-induced responses atop the Shanghai World Financial Center under normal climate conditions[J]. Mathematical Problems in Engineering, 2013, 2013(1056): 469 |
| [12] |
黄雅君, 顾明, 黄子逢. 上海环球金融中心顶部风速和加速度实测[J]. 同济大学学报(自然科学版), 2017, 45(6): 821 HUANG Yajun, GU Ming, HUANG Zifeng. Field measurement of wind and acceleration on Shanghai World Financial Center[J]. Journal of Tongji University (Natural Science), 2017, 45(6): 821 |
| [13] |
ZHANG F L, XIONG H B, SHI W X, et al. Structural health monitoring of Shanghai Tower during different stages using a Bayesian approach[J]. Structural Control & Health Monitoring, 2016, 23(11): 1366 |
| [14] |
胡笳, 李晗, 杨晖柱, 等. 上海中心大厦结构健康监测软件集成设计及应用[J]. 同济大学学报(自然科学版), 2014, 42(3): 460 HU Jia, LI Han, YANG Huizhu, et al. Integrated design and application of structural health monitoring software system of Shanghai Tower[J]. Journal of Tongji University (Natural Science), 2014, 42(3): 460 DOI:10.3969/j.issn.0253-374x.2014.03.021 |
| [15] |
HUANG Z, GU M. Envelope random decrement technique for identification of nonlinear damping of tall buildings[J]. Journal of Structural Engineering, 2016, 142(11): 1 |
| [16] |
CHEN G, WANG Z. A signal decomposition theorem with Hilbert transform and its application to narrow band time series with closely spaced frequency components[J]. Mechanical Systems & Signal Processing, 2012, 28(2): 258 |
| [17] |
LELEBI M, PHAN L T, MARSHALL R D. Dynamic characteristics of five tall buildings during strong and low-amplitude motions[J]. Structural Design of Tall Buildings, 1993, 2(1): 1 |
 2019, Vol. 47
2019, Vol. 47

