转向架作为轨道车辆的唯一走行部件,具有牵引、制动、支撑、导向、减振五大功能,对轨道车辆动力学性能起着决定性作用,其参数的准确性对动力学性能的设计、预测、故障诊断都有着极为重要的作用[1-3].为此,我国对轨道车辆转向架检测做出了相关规定[4-7].
研究转向架参数的测试方法和转向架参数测试台,对于提升轨道列车运行性能、降低转向架研发周期有巨大意义.鉴于转向架参数对轨道车辆运行性能的重要影响,国内外越来越多的科研机构投入到转向架参数试验台的研制工作中.德国Windhoff公司开发了转向架测试试验台[8], 该试验台可以对不同轴距、不同轨距的动车转向架和拖车转向架进行测试,可以实现对转向架一系、二系悬挂横向刚度值的测量.瑞士NENCKI公司研制的转向架测试台适用于多种轴距的转向架的测试[9].文献[10]在已知转向架质量的前提下,提出了基于激振法的转向架三轴向转动惯量试验方法,建立了基于欧拉角及向量范数的转向架运动平台位姿反解模型.文献[11]以转向架参数测试台为基础开发了基于坡道模拟器的转向架质心高度测量系统.文献[12]在转向架参数测定试验台上实现了铁道车辆转向架的三向刚度同时测定及几何结构尺寸参数测定功能.文献[13]对高速列车转向架悬挂参数的测试方法进行了研究,建立了转向架悬挂参数测试模型.文献[14]设计了用来测试转向架动力学参数的试验台,对转向架轮对间的抗弯刚度及抗剪刚度、三大件式转向架的抗菱刚度、减振器相对摩擦系数、心盘旁承回转摩擦力矩、转向架一系及二系悬挂刚度等参数的测试方法进行了探讨.文献[15]探讨了三大件式转向架抗菱刚度在参数测试台上的测试方法和计算公式.文献[16]实现了整车转向架及独立转向架刚度参数的动态和静态测试.
综上所述,以往的转向架参数测试试验台主要是对转向架系统整体的惯量参数和悬挂参数进行测试.然而长期以来,转向架系统簧上质量物理参数的准确性无法校验,目前国内外尚未有专家学者针对此问题进行研究.因此,本文提出了基于质量感应法、状态空间理论和模态空间理论的转向架系统簧上质量物理参数识别方法, 设计了用于参数识别的定向激励测试工况,利用系统自由振动加速度响应信号,对转向架系统簧上质量的质量参数、惯量参数、结构参数、一系垂向刚度及阻尼参数同时识别进行了研究.这3种方法均无需已知系统任何参数,不依赖专业试验装置,操作简便,实用性强,是可用于现场实验测试的物理参数识别方法.
1 转向架动力学方程以转向架系统簧上质量的质量参数、惯量参数、结构参数、一系垂向刚度及阻尼参数为识别对象,构建如图 1所示的转向架动力学模型,并推导系统的动力学方程.模型中,m为转向架系统的簧上质量,转向架系统簧上质量的侧滚转动惯量、点头转动惯量、摇头转动惯量分别为Ixx、Iyy、Izz,其浮沉自由度、侧滚自由度、点头自由度、摇头自由度分别为z、α、β、θ,ki(i=x,y,z)分别为转向架一系纵向刚度、一系横向刚度和一系垂向刚度,ci(i=x,y,z)分别为转向架一系纵向阻尼、一系横向阻尼和一系垂向阻尼,a为垂向悬挂的横向距离之半,b为垂向悬挂的纵向距离之半,h为转向架簧上质量质心与一系悬挂下作用点位置的高度差.

|
图 1 转向架动力学模型 Fig.1 Bogie dynamics model |
根据牛顿定律,转向架系统的动力学方程为
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = \mathit{\boldsymbol{F}} $ | (1) |
其中
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{l}} z&\alpha &\beta &\theta \end{array}} \right]^{\rm{T}}} $ | (2) |
| $ $ | (3) |
| $ \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{P}}}\mathit{\boldsymbol{L}} $ | (4) |
| $ \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{\rm{P}}}\mathit{\boldsymbol{L}} $ | (5) |
式(1)~式(5)中,M、C和K分别为转向架系统簧上质量的质量矩阵、阻尼矩阵和刚度矩阵; X,
| $ {\mathit{\boldsymbol{K}}_{\rm{p}}} = {\rm{diag}} \left( {{k_z}\;{k_z}\;{k_z}\;{k_z}\;{k_y}\;{k_y}\;{k_y}\;{k_y}\;{k_x}\;{k_x}\;{k_x}\;{k_x}} \right) $ | (6) |
| $ {\mathit{\boldsymbol{C}}_{\rm{p}}} = {\rm{diag}} \left( {{c_z}\quad {c_z}\quad {c_z}\quad {c_z}\quad {c_y}\quad {c_y}\quad {c_y}\quad {c_y}\quad {c_y}\quad {c_x}\quad {c_x}\quad {c_x}\quad {c_x}\quad {c_x}\quad {c_x}} \right) $ | (7) |
| $ \mathit{\boldsymbol{L}} = {\left[ {\begin{array}{*{20}{c}} 1&1&1&1&0&0&0&0&0&0&0&0\\ a&{ - a}&a&{ - a}&h&{ - h}&h&{ - h}&0&0&0&0\\ b&{ - b}&b&b&0&0&0&0&{ - h}&{ - h}&h&h\\ 0&0&0&0&{ - b}&b&b&{ - b}&a&{ - a}&{ - a}&a \end{array}} \right]^{\rm{T}}} $ | (8) |
利用上述转向架系统动力学方程,提出基于质量感应法、状态空间理论和模态空间理论的物理参数识别方法,这3种方法均无需已知系统任何参数.
2.1 质量感应法质量感应法[17]是通过在主系统中附加一个已知的质量,利用附加质量前后系统固有频率的关系来推算出主系统的等效质量.
由转向架系统的动力学方程(1)可知,转向架系统簧上质量的固有振动频率为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i} = \sqrt {\frac{{{\mathit{\boldsymbol{K}}_i}}}{{{\mathit{\boldsymbol{M}}_i}}}} (i = z,\alpha ,\beta ,\theta ) $ | (9) |
式中:Ki(i=z,α,β,θ)为转向架系统簧上质量在浮沉运动、侧滚运动、点头运动、摇头运动中的等效刚度矩阵; Mi(i=z,α,β,θ)是转向架系统簧上质量的质量矩阵.为获得质量矩阵M,可将式(10)所示的特定质量矩阵ΔM附加到系统中.
| $ \Delta \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{l}} {\Delta m}&{\Delta {I_{xx}}}&{\Delta {I_{yy}}}&{\Delta {I_{zx}}} \end{array}} \right] $ | (10) |
其中,Δm、ΔIxx、ΔIyy、ΔIzz分别表示相对于构架质心处坐标系附加的质量、侧滚转动惯量、点头转动惯量、摇头转动惯量.则附加质量后转向架系统簧上质量的固有振动频率为
| $ {\mathit{\boldsymbol{\omega }}_i} = \sqrt {\frac{{{\mathit{\boldsymbol{K}}_i}}}{{{\mathit{\boldsymbol{M}}_i} + \Delta {\mathit{\boldsymbol{M}}_i}}}} (i = z,\alpha ,\beta ,\theta ) $ | (11) |
联立式(9)和式(11)可得
| $ {\mathit{\boldsymbol{M}}_i} = \frac{{\Delta {\mathit{\boldsymbol{M}}_i}\mathit{\boldsymbol{\omega }}_i^2}}{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i^2 - \mathit{\boldsymbol{\omega }}_i^2}}(i = z,\alpha ,\beta ,\theta ) $ | (12) |
由式(12)可求得转向架系统簧上质量的质量矩阵M.
由于附加质量法物理意义明确,该方法在工程实际中得到广泛的应用.但是,该方法无法对系统的刚度矩阵和阻尼矩阵进行识别,因此,无法求得系统的悬挂刚度参数、悬挂阻尼参数及结构参数.
2.2 状态空间理论状态空间理论[18]是基于物理坐标系下的时域参数识别方法.在式(1)中引入状态变量
| $ \mathit{\boldsymbol{\dot Y}} = \mathit{\boldsymbol{AY}} $ | (13) |
其中,A为状态矩阵.
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{O}}_{{\rm{4}} \times 4}}}&{{\mathit{\boldsymbol{I}}_{{\rm{4}} \times 4}}}\\ { - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{K}}}&{ - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{C}}} \end{array}} \right] $ | (14) |
状态矩阵A的子矩阵A21和Α22分别为
| $ {\mathit{\boldsymbol{A}}_{21}} = - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{K}} $ | (15) |
| $ {\mathit{\boldsymbol{A}}_{22}} = - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{C}} $ | (16) |
由于车辆系统状态矩阵中包含车辆物理参数,所以识别车辆系统的状态矩阵是获得车辆物理参数的前提.
根据微分方程理论[19]可知,式(13)的解为
| $ \mathit{\boldsymbol{Y}}(t) = {\mathit{\boldsymbol{Y}}_0}{{\rm{e}}^{\mathit{\boldsymbol{A}}t}} $ | (17) |
其中
| $ \mathit{\boldsymbol{Y}}\left( {{t_k}} \right) = {\mathit{\boldsymbol{Y}}_0}{{\rm{e}}^{\mathit{\boldsymbol{A}}kT}} $ | (18) |
| $ \mathit{\boldsymbol{Y}}\left( {{t_{k + 1}}} \right) = {\mathit{\boldsymbol{Y}}_0}{{\rm{e}}^{\mathit{\boldsymbol{A}}(k + 1)T}} = {\mathit{\boldsymbol{Y}}_0}{{\rm{e}}^{\mathit{\boldsymbol{A}}T}}{{\rm{e}}^{\mathit{\boldsymbol{A}}kT}} $ | (19) |
将Y(tk)和Y(tk+1)分别记为Y(k)和Y(k+1).
| $ \mathit{\boldsymbol{Y}}(k) = {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}(k)\quad {\mathit{\boldsymbol{X}}^T}(k + 1)} \right)^{\rm{T}}} $ | (20) |
| $ \mathit{\boldsymbol{Y}}(k + 1) = {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}(k + 1)\quad {\mathit{\boldsymbol{X}}^{\rm{T}}}(k + 2)} \right)^{\rm{T}}} $ | (21) |
比较式(20)和(21)可得
| $ \mathit{\boldsymbol{Y}}(k + 1) = \mathit{\boldsymbol{GY}}(k) $ | (22) |
其中G为系统的传递矩阵.
| $ \mathit{\boldsymbol{G}} = {{\rm{e}}^{\mathit{\boldsymbol{A}}T}} $ | (23) |
由式(23)可以知道系统的传递矩阵G的特征值si和特征向量Φi与状态矩阵A的特征值λi和特征向量pi存在以下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {{s_i} = {{\rm{e}}^{{\lambda _i}T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} = {\mathit{\boldsymbol{p}}_i}} \end{array}\quad (i = 1,2, \cdots ,2n)} \right. $ | (24) |
根据式(24)可通过系统传递矩阵的特征值和特征向量求得系统状态矩阵的特征值和特征向量.然后由矩阵的谱分解理论[20]可知,系统状态矩阵A和其特征值矩阵Λ、特征向量矩阵P存在以下关系:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{P \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}^{ - 1}} $ | (25) |
其中
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\rm{diag}} \left( {{\lambda _1}\quad {\lambda _2}\quad \cdots \quad {\lambda _n}} \right) $ | (26) |
| $ \mathit{\boldsymbol{P}} = \left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_1}}&{{\mathit{\boldsymbol{p}}_2}}& \cdots &{{\mathit{\boldsymbol{p}}_n}} \end{array}} \right) $ | (27) |
根据式(14)所示的系统状态矩阵,为获得质量矩阵M、阻尼矩阵C和刚度矩阵K,可将式(28)所示的特定质量矩阵ΔM附加到系统状态矩阵中.
| $ \Delta \mathit{\boldsymbol{M}} = {\rm{diag}} \left( {\Delta m\quad \Delta {I_{xx}}\quad \Delta {I_{yy}}\quad \Delta {I_{zz}}} \right) $ | (28) |
其中,Δm、ΔIxx、ΔIyy、ΔIzz分别表示相对于构架质心处坐标系附加的质量、侧滚转动惯量、点头转动惯量、摇头转动惯量.则附加质量后的系统状态矩阵为
| $ \mathit{\boldsymbol{\bar A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{O}}_{{\rm{4}} \times {\rm{4}}}}}&{{\mathit{\boldsymbol{I}}_{{\rm{4}} \times {\rm{4}}}}}\\ { - {{(\mathit{\boldsymbol{M}} + \Delta \mathit{\boldsymbol{M}})}^{ - 1}}\mathit{\boldsymbol{K}}}&{ - {{(\mathit{\boldsymbol{M}} + \Delta \mathit{\boldsymbol{M}})}^{ - 1}}\mathit{\boldsymbol{C}}} \end{array}} \right] $ | (29) |
此时,系统状态矩阵
| $ {\mathit{\boldsymbol{\overline A}} _{21}} = - {(\mathit{\boldsymbol{M}} + \Delta \mathit{\boldsymbol{M}})^{ - 1}}\mathit{\boldsymbol{K}} $ | (30) |
| $ {\mathit{\boldsymbol{\overline A}} _{22}} = - {(\mathit{\boldsymbol{M}} + \Delta \mathit{\boldsymbol{M}})^{ - 1}}\mathit{\boldsymbol{C}} $ | (31) |
对比式(15)和(16)可得
| $ \mathit{\boldsymbol{M}} = \Delta \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{\overline A}} _{21}}{\left( {{\mathit{\boldsymbol{A}}_{21}} - {{\mathit{\boldsymbol{\overline A}} }_{21}}} \right)^{ - 1}} $ | (32) |
或
| $ \mathit{\boldsymbol{M}} = \Delta {\mathit{\boldsymbol{M}}_{22}}{\left( {{\mathit{\boldsymbol{A}}_{22}} - {{\mathit{\boldsymbol{\overline A}} }_{22}}} \right)^{ - 1}} $ | (33) |
依据式(32)或式(33)可求得系统的质量矩阵M,随后,通过求解式(30)可得系统刚度矩阵K,同样,通过求解式(31)可得系统阻尼矩阵C.最后,应用最小二乘法由识别的质量矩阵、阻尼矩阵、刚度矩阵计算得到系统相应的物理参数.
值得注意的是,根据式(32)或式(33)可知,附加质量矩阵ΔM的选取会直接影响附加质量法的参数识别结果.
2.3 模态空间理论模态空间理论[21]基于模态坐标系下的时域参数识别方法.Ibrahim提出一种基于模态空间理论的时域模态参数识别方法[22].基于识别的模态参数,可重构系统状态矩阵.对于式(1),由振动方程的复模态理论可知,一个n自由度的有阻尼系统含有n对复共轭的特征值,这n对复共轭的特征值与系统的n个模态对应,振动方程的解可以表示成n个模态的解的叠加, 则微分方程的解可以表示为
| $ \left( {\begin{array}{*{20}{c}} {{x_1}(t)}\\ {{x_2}(t)}\\ \vdots \\ {{x_n}(t)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\Phi }_{11}}}&{{\mathit{\Phi }_{12}}}& \cdots &{{\mathit{\Phi }_{12(n)}}}\\ {{\mathit{\Phi }_{21}}}&{{\mathit{\Phi }_{22}}}& \cdots &{{\mathit{\Phi }_{2(2n)}}}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{\Phi }_{n1}}}&{{\mathit{\Phi }_{n1}}}& \cdots &{{\mathit{\Phi }_{n(2n)}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\lambda _1}t}}}\\ {{{\rm{e}}^{{\lambda _2}t}}}\\ \vdots \\ {{{\rm{e}}^{{\lambda _{2n}}t}}} \end{array}} \right) $ | (34) |
其中xit表示系统第i个自由度的位移响应,λi表示系统的第i个特征值,Φij表示第j个特征值对应第i个自由度的振型系数.
为了求解系统的n对复共轭特征值,构造以下信号矩阵:
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{x_1}\left( {{t_1}} \right)}&{{x_1}\left( {{t_2}} \right)}& \cdots &{{x_1}\left( {{t_m}} \right)}\\ {{x_2}\left( {{t_1}} \right)}&{{x_2}\left( {{t_2}} \right)}& \cdots &{{x_2}\left( {{t_m}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{x_{2n}}\left( {{t_1}} \right)}&{{x_{2n}}\left( {{t_2}} \right)}& \cdots &{{x_{2n}}\left( {{t_m}} \right)} \end{array}} \right) = \\ \left( {\begin{array}{*{20}{c}} {{\mathit{\Phi }_{11}}}&{{\mathit{\Phi }_{12}}}& \cdots &{{\mathit{\Phi }_{1(2n)}}}\\ {{\mathit{\Phi }_{21}}}&{{\mathit{\Phi }_{22}}}& \cdots &{{\mathit{\Phi }_{2(2n)}}}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{\Phi }_{(2n)1}}}&{{\mathit{\Phi }_{(2n)1}}}& \cdots &{{\mathit{\Phi }_{(2n)(2n)}}} \end{array}} \right) \cdot \\ \left( {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\lambda _1}{t_1}}}}&{{{\rm{e}}^{{\lambda _1}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _1}{t_m}}}}\\ {{{\rm{e}}^{{\lambda _2}{t_1}}}}&{{{\rm{e}}^{{\lambda _2}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _2}{t_m}}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\rm{e}}^{{\lambda _{2n}}{t_1}}}}&{{{\rm{e}}^{{\lambda _{2n}}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _{2n}}{t_m}}}} \end{array}} \right) \end{array} $ | (35) |
式(35)可以用矩阵形式表示为
| $ {\mathit{\boldsymbol{Z}}_{2n \times m}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2n \times 2n}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{2n \times m}} $ | (36) |
将式(35)表示的信号矩阵延时Δt后为
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{x_1}\left( {{t_1} + \Delta t} \right)}&{{x_1}\left( {{t_2} + \Delta t} \right)}& \cdots &{{x_1}\left( {{t_m} + \Delta t} \right)}\\ {{x_2}\left( {{t_1} + \Delta t} \right)}&{{x_2}\left( {{t_2} + \Delta t} \right)}& \cdots &{{x_2}\left( {{t_m} + \Delta t} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{x_{2n}}\left( {{t_1} + \Delta t} \right)}&{{x_{2n}}\left( {{t_2} + \Delta t} \right)}& \cdots &{{x_{2n}}\left( {{t_m} + \Delta t} \right)} \end{array}} \right) = \\ \left( {\begin{array}{*{20}{c}} {{{\mathit{\bar \Phi }}_{11}}}&{{{\mathit{\bar \Phi }}_{12}}}& \cdots &{{{\mathit{\bar \Phi }}_{1(2n)}}}\\ {{{\mathit{\bar \Phi }}_{21}}}&{{{\mathit{\bar \Phi }}_{22}}}& \cdots &{{{\mathit{\bar \Phi }}_{2(2n)}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\mathit{\bar \Phi }}_{(2n1)}}}&{{{\mathit{\bar \Phi }}_{(2n)1}}}& \cdots &{{{\mathit{\bar \Phi }}_{(2n)(2n)}}} \end{array}} \right) \cdot \\ \left( {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\lambda _1}{t_1}}}}&{{{\rm{e}}^{{\lambda _1}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _1}{t_m}}}}\\ {{{\rm{e}}^{{\lambda _2}{t_1}}}}&{{{\rm{e}}^{{\lambda _2}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _2}{t_m}}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\rm{e}}^{{\lambda _{2n}}{t_1}}}}&{{{\rm{e}}^{{\lambda _{2n}}{t_2}}}}& \cdots &{{{\rm{e}}^{{\lambda _{2n}}{t_m}}}} \end{array}} \right) \end{array} $ | (37) |
用矩阵形式表示为
| $ {\mathit{\boldsymbol{\overline Z}} _{2n \times m}} = {\mathit{\boldsymbol{ \boldsymbol{\overline \varPhi} }} _{2n \times 2n}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{2n \times m}} $ | (38) |
通过比较式(35)和(37)可知,满足以下关系:
| $ {\mathit{\boldsymbol{\overline Z}} _{2n \times m}} = {\mathit{\boldsymbol{G}}_{2n \times 2n}}{\mathit{\boldsymbol{Z}}_{2n \times m}} $ | (39) |
其中G为系统的传递矩阵,且满足以下关系:
| $ {\mathit{\boldsymbol{G}}_{2n \times 2n}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2n \times 2n}} {\rm{diag}} \left( {{{\rm{e}}^{{\lambda _1}\Delta t}}\quad {{\rm{e}}^{{\lambda _2}\Delta }}\quad \cdots \quad {{\rm{e}}^{{\lambda _{2n}}\Delta }}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2n \times 2n}^{ - 1} $ | (40) |
由上式可以知道系统的传递矩阵G的特征值si和特征向量Φi与状态矩阵A的特征值λi和特征向量pi存在以下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {{s_i} = {{\rm{e}}^{{\lambda _i}{\cal L}}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} = {\mathit{\boldsymbol{p}}_i}} \end{array}\quad (i = 1,2, \cdots ,2n)} \right. $ | (41) |
根据上式可求得系统状态矩阵的特征值和特征向量.然后系统状态矩阵A可以通过式(25)~(27)求得.最后,基于获得的系统状态矩阵对系统物理参数进行识别,过程与状态空间理论相同,如式(28)~(33)所示,不再赘述.
3 物理参数识别方法验证及对比分析为了验证上述物理参数识别方法的有效性,针对第1节所述转向架系统动力学方程,基于表 1所示的CRH3动车组列车转向架参数,采用Matlab/simulink仿真平台搭建转向架系统模型,利用质量感应法、状态空间理论和模态空间理论对转向架系统簧上质量的物理参数进行识别.
| 下载CSV 表 1 CRH3动车组列车转向架参数 Tab.1 CRH3 EMU train bogie parameters |
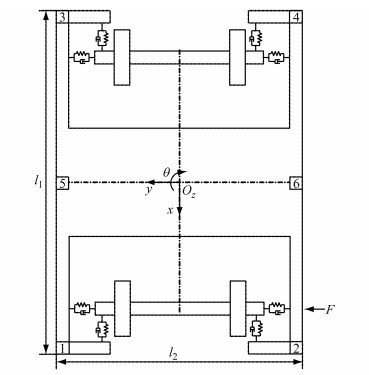
根据式(22)和式(39)可知,在参数识别过程中,为构造系统传递函数矩阵,首先需分别获得浮沉响应信号、侧滚响应信号、点头响应信号及摇头响应信号.为此,设计如下4种定向激励测试工况:①浮沉模态激励(令转向架4个车轮同时通过同一高度的楔块后垂直落地,模拟阶跃激励输入,如图 2所示); ②侧滚模态激励(令转向架左侧(或右侧)2个车轮同时通过同一高度的楔块后垂直落地,模拟阶跃激励输入,如图 3所示); ③点头模态激励(令转向架前轮对(或后轮对)2个车轮同时通过同一高度的楔块后垂直落地,模拟阶跃激励输入,如图 4所示); ④摇头模态激励(对转向架前端左侧(或右侧)或后端左侧(或右侧)进行横向激励,模拟阶跃激励输入,如图 5所示).上述4种定向激励测试工况不受专用的转向架参数识别试验装置所限,易于在转向架存放现场实施.本文通过仿真模型分别模拟实现上述4种定向激励.

|
图 2 浮沉模态激励 Fig.2 Bounce modal excitation |

|
图 3 侧滚模态激励 Fig.3 Rolling modal excitation |

|
图 4 点头模态激励 Fig.4 Pitch modal excitation |
|
图 5 摇头模态激励 Fig.5 Yaw modal excitation |
激励测试试验的加速度响应测点位置如图 5中1、2、3、4、5、6所示,其中测点1、2、3、4为垂向加速度响应测点位置,测点5、6为纵向加速度响应测点位置,则构架质心处浮沉、侧滚、点头和摇头加速度响应为
| $ \left\{ {\begin{array}{*{20}{l}} {\ddot z = \left( {{{\ddot z}_1} + {{\ddot z}_2} + {{\ddot z}_3} + {{\ddot z}_4}} \right)/4}\\ {\ddot \alpha = \left( {{{\ddot z}_1} - {{\ddot z}_2} + {{\ddot z}_3} - {{\ddot z}_4}} \right)/\left( {2{l_2}} \right)}\\ {\ddot \beta = \left( {{{\ddot z}_1} + {{\ddot z}_2} - {{\ddot z}_3} - {{\ddot z}_4}} \right)/\left( {2{l_1}} \right)}\\ {\ddot \theta = \left( {{{\ddot x}_6} - {{\ddot x}_5}} \right)/\left( {2{l_2}} \right)} \end{array}} \right. $ | (42) |
由于附加质量的大小可能会对识别结果的精度产生影响,且如果附加质量过大,会增加测试成本及难度,因此合理选择附加质量大小十分必要.
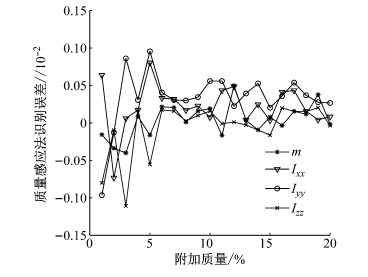
对所建立的转向架模型施加4种定向激励,模拟阶跃激励所使用的楔块高度为16 mm,依次获得浮沉响应信号、侧滚响应信号、点头响应信号及摇头响应信号,然后,分别采用质量感应法、状态空间理论和模态空间理论对转向架系统簧上质量物理参数进行识别.图 6所示为采用质量感应法时附加质量大小对识别参数误差的影响,其中,附加质量ΔM以系统质量M的百分比为参考,选取范围为1%至20%.从图 6中可以看到,当附加质量小于系统质量的6%时,随着附加质量的增大,全部参数识别误差均在较大范围内波动; 当附加质量大于系统质量的6%时,随着附加质量的增大,全部参数识别误差收敛至较小范围内波动; 当附加质量为系统质量的8%时,总体参数识别误差达到最小值.
|
图 6 附加质量对质量感应法识别误差的影响 Fig.6 Influence of additional mass on identification error of mass induction method |
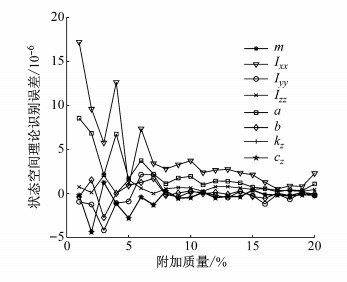
图 7所示为采用状态空间理论时附加质量大小对识别参数误差的影响.其中,附加质量大小选取范围为系统质量的1%至20%.从图 7中可以看到,随着附加质量的增大,全部参数识别误差均逐渐收敛至较小范围内波动; 当附加质量为系统质量的17%时,总体参数识别误差达到最小值.
|
图 7 附加质量对状态空间理论识别误差的影响 Fig.7 Influence of additional mass on identification error of state space theory |
图 8所示为采用模态空间理论时附加质量大小对识别参数误差的影响.其中,附加质量大小选取范围为系统质量的1%至20%.从图 8中可以看到,随着附加质量的增大,全部参数识别误差均逐渐收敛至较小范围内波动; 当附加质量为系统质量的7%时,总体参数识别误差达到最小值.

|
图 8 附加质量对模态空间理论识别误差的影响 Fig.8 Influence of additional mass on identification error of modal space theory |
综上所述,基于质量感应法、状态空间理论和模态空间理论的物理参数识别方法对转向架系统簧上质量物理参数的识别误差均在可接受范围内,因此,采用以上方法进行转向架系统簧上质量物理参数识别是有效的.当采用质量感应法时,附加质量大小选取为系统质量的8%时识别精度最高; 当采用状态空间理论时,附加质量大小选取为系统质量的17%时识别精度最高; 当采用模态空间理论时,附加质量大小选取为系统质量的7%时识别精度最高.
3.3 识别方法对比分析对质量感应法、状态空间理论和模态空间理论3种物理参数识别方法进行对比分析.其中,在采用附加质量法、状态空间理论和模态空间理论进行参数识别时,附加质量大小分别选取为系统质量的8%、17%和7%.
表 2所示为质量感应法、状态空间理论和模态空间理论3种方法的识别结果及相应误差.对比表 2的识别结果,可以看出:
| 下载CSV 表 2 转向架系统簧上质量物理参数识别结果 Tab.2 Physical parameters identification result of the mass above the suspension of the bogie system |
(1) 质量感应法无法识别结构参数、一系垂向刚度及阻尼参数.
(2) 就转向架系统簧上质量的质量参数、侧滚转动惯量参数、点头转动惯量参数和摇头转动惯量参数识别而言,模态空间理论的识别精度最高,状态空间理论次之,质量感应法最低.
(3) 就结构参数、一系垂向刚度及阻尼参数识别而言,模态空间理论的识别精度高于状态空间理论.
4 转向架系统簧上质量质心与一系悬挂下作用点位置的高度差对识别结果的影响在第3节的仿真试验中,转向架系统簧上质量质心与一系悬挂下作用点位置的高度差h为零,而对于不同的转向架系统,其结构参数h的值是不同的,因此,下面讨论结构参数h的大小对识别结果的影响.
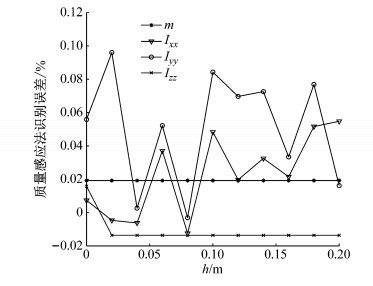
对所建立的转向架模型施加4种定向激励,模拟阶跃激励所使用的楔块高度为16 mm,分别采用质量感应法、状态空间理论和模态空间理论对转向架系统簧上质量物理参数进行识别,其中,附加质量大小分别选取为系统质量的8%、17%和7%.图 9所示为采用质量感应法时结构参数h的大小对物理参数识别误差的影响,其中,结构参数h的选取范围为0~0.2 m.从图 9中可以看到,当不考虑结构参数h进行参数识别时,在结构参数h从零增加到0.2 m的过程中,转向架簧上质量的质量参数、惯量参数的识别精度在0.1%范围内波动.
|
图 9 结构参数对质量感应法识别误差的影响 Fig.9 Influence of structural parameter on iden- tification error of mass induction method |
图 10所示为采用状态空间理论时结构参数h的大小对物理参数识别误差的影响,其中,结构参数h的选取范围为0~0.2 m.从图 10中可以看到,当不考虑结构参数h进行参数识别时,在结构参数h从零增加到0.2 m的过程中,转向架簧上质量的质量参数、惯量参数、一系垂向刚度及阻尼参数均无明显变化; 结构参数a、b的识别误差越来越大; 当结构参数h达到0.2 m时,结构参数a的识别误差为2.069 5%,结构参数b的识别误差为0.924 9%.

|
图 10 结构参数h对状态空间理论识别误差的影响 Fig.10 Influence of structural parameter h on identification error of state space theory |
图 11所示为采用模态空间理论时结构参数h的大小对物理参数识别误差的影响,其中,结构参数h的选取范围为0~0.2 m.从图 11中可以看到,当不考虑结构参数h进行参数识别时,在结构参数h从零增加到0.2 m的过程中,转向架簧上质量的质量参数、惯量参数、一系垂向刚度及阻尼参数均无明显变化; 结构参数a、b的识别误差越来越大; 当结构参数h达到0.2 m时,结构参数a的识别误差为2.069 4%,结构参数b的识别误差为0.925 0%.

|
图 11 结构参数h对模态空间理论识别误差的影响 Fig.11 Influence of structural parameter h on identification error of modal space theory |
综上所述,利用质量感应法、状态空间理论和模态空间理论对转向架系统簧上质量物理参数进行识别时,转向架簧上质量质心与一系悬挂下作用点位置的高度差h对质量参数、惯量参数、一系垂向刚度及阻尼参数的识别误差几乎没有影响; 结构参数a、b的识别误差会随着结构参数h的增大而增大; 若结构参数h的值较小,结构参数a、b的识别误差保持在较小范围内.在设计制造过程中,结构参数h通常控制在0.1 m以内,如某高速动车组列车的结构参数h为0.06 m,此时采用状态空间理论和模态空间理论对结构参数a、b的识别误差分别为0.187 9%、0.083 6%和0.188 0%、0.083 5%,均在可接受范围内.因此,就转向架系统簧上质量的质量参数、惯量参数、一系垂向刚度及阻尼参数识别而言,可以不考虑转向架簧上质量质心与一系悬挂下作用点位置的高度差h的影响; 在h较小时,也可忽略其对结构参数识别误差的影响.
5 结论提出了基于质量感应法、状态空间理论和模态空间理论的物理参数识别方法,对转向架系统簧上质量的质量参数、惯量参数、结构参数、一系垂向刚度及阻尼参数同时识别进行了研究,设计了用于参数识别的定向激励测试工况,并通过仿真试验对以上参数识别方法的有效性进行了验证, 得到以下主要结论:
(1) 当采用质量感应法时,附加质量大小选取为系统质量的8%时识别精度最高; 当采用状态空间理论时,附加质量大小选取为系统质量的17%时识别精度最高; 当采用模态空间理论时,附加质量大小选取为系统质量的7%时识别精度最高.
(2) 质量感应法无法识别结构参数、一系垂向刚度及阻尼参数; 状态空间理论和模态空间理论可以识别全部物理参数.
(3) 就质量参数、侧滚转动惯量参数、点头转动惯量参数和摇头转动惯量参数识别而言,模态空间理论的识别精度最高,状态空间理论次之,质量感应法最低.
(4) 就结构参数、一系垂向刚度及阻尼参数识别而言,模态空间理论的识别精度高于状态空间理论.
(5) 就质量参数、惯量参数、一系垂向刚度及阻尼参数识别而言,可以不考虑转向架簧上质量质心与一系悬挂下作用点位置的高度差h的影响; 在h较小时,也可忽略其对结构参数识别误差的影响.
提出的3种物理参数识别方法均无需已知系统任何参数,不依赖专业试验装置,可用于现场试验测试,具有工程应用价值,后续将进行现场测试与验证.
| [1] |
周劲松. 铁道车辆振动与控制[M]. 北京: 中国铁道出版社, 2012 ZHOU Jinsong. Vibration and control of railway vehicles[M]. Beijing: China Railway Press, 2012 |
| [2] |
张兆丰.铁道客车动力学性能灵敏度分析及稳健设计[D].长沙: 中南大学, 2012. ZHANG Zhaofeng. Sensitivity analysis and robust design of dynamic performance of railway passenger vehicle[D]. Changsha: Central South University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10533-1012477849.htm |
| [3] |
SUAREZ B, FELEZ J, RODRIGUEZ J M P. Sensitivity analysis to assess the influence of the inertial properties of railway vehicle bodies on the vehicle's dynamic behaviour[J]. Vehicle System Dynamics, 2013, 51(2): 251 DOI:10.1080/00423114.2012.725851 |
| [4] |
国家标准局.铁道车辆动力学性能评定和试验鉴定规范: GB 5599—1985[S].北京: 中国标准出版社, 1986. Standardization Administration. Railway vehicles- specification for evaluation the dynamic performance and accreditation test: GB 5599—1985[S]. Beijing: Standards Press of China, 1986. |
| [5] |
铁道部标准计量研究所.铁道客车转向架通用技术条件: TB/T 1490—2004[S].北京: 中国铁道出版社, 2004. Ministry of Railways Institute of Standard Metrology. General technical specification for the bogies of railway passenger coach: TB/T 1490—2004[S]. Beijing: China Railway Publishing House, 2004. |
| [6] |
铁道部标准计量研究所.铁道机车动力学性能试验鉴定方法及评定标准: TB/T 2360—1993[S].北京: 中国铁道出版社, 1994. Ministry of Railways Institute of Standard Metrology. Railway locomotive dynamic performance test identification method and evaluation standard: TB/T 2360—1993[S]. Beijing: China Railway Publishing House, 1994. |
| [7] |
铁道部车辆研究所. 200 km·h-1及以上速度级电动车组动力学性能试验鉴定方法及评定标准[S].北京: 中国铁道出版社, 2001. Ministry of Railways Vehicle Research Institute. Test method and evaluation standard for dynamic performance test of electric vehicles with speed class of 200 km·h-1 and above[S]. Beijing: China Railway Publishing House, 2001. |
| [8] |
苏明. 新型转向架试验台[J]. 国外内燃机车, 1996, 33(7): 43 SU Ming. New bogie test bench[J]. Foreign Diesel Locomotive, 1996, 33(7): 43 |
| [9] |
王兴宇.高速列车转向架刚度测试模型及新型动态测试系统研究[D].长春: 吉林大学, 2010. WANG Xingyu. Research on testing model and novel dynamic test system of high-speed train bogie stiffness[D]. Changchun: Jilin University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10183-2010107077.htm |
| [10] |
王秀刚, 苏建, 曹晓宁, 等. 转向架三轴向转动惯量测试方法[J]. 华南理工大学学报(自然科学版), 2012, 40(11): 71 WANG Xiugang, SU Jian, CAO Xiaoning, et al. Test method of three-axis moment of inertia of bogies[J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(11): 71 DOI:10.3969/j.issn.1000-565X.2012.11.010 |
| [11] |
曹晓宁, 刘玉梅, 苏建, 等. 转向架质心高度的测定[J]. 吉林大学学报(工学版), 2013, 43(2): 329 CAO Xiaoning, LIU Yumei, SU Jian, et al. Determination of mass center height of bogie[J]. Journal of Jilin University(Engineering Edition), 2013, 43(2): 329 |
| [12] |
高云鹤, 张卫华. 新型转向架参数测定试验台的研制[J]. 电力机车与城轨车辆, 2010, 33(1): 37 GAO Yunhe, ZHANG Weihua. Development of a new bogie parameter measurement test bench[J]. Electric Locomotive & Urban Rail Vehicles, 2010, 33(1): 37 DOI:10.3969/j.issn.1672-1187.2010.01.012 |
| [13] |
李雪海.高速列车转向架悬挂参数测试方法研究[D].长春: 吉林大学, 2011. LI Xuehai. Research on measuring methods of high-speed train bogie suspension parameters[D]. Changchun: Jilin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011099980.htm |
| [14] |
魏培虎.货车转向架动力学参数测试方法研究[D].成都: 西南交通大学, 2002. WEI Peihu. Research on test method of dynamic parameters of freight car bogies[D]. Chengdu: Southwest Jiaotong University, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10613-2003060303.htm |
| [15] |
任利惠, 张辉, 胡用生. 货车转向架动力学参数测试台研究与试验[J]. 中国铁道科学, 2001, 22(3): 72 REN Lihui, ZHANG Hui, HU Yongsheng. Research and experiment of dynamic parameter test bench for freight car bogies[J]. China Railway Science, 2001, 22(3): 72 DOI:10.3321/j.issn:1001-4632.2001.03.014 |
| [16] |
王兴宇, 苏建, 刘玉梅, 等. 一种新型转向架刚度试验台设计及测试方法研究[J]. 铁道车辆, 2009, 47(10): 6 WANG Xingyu, SU Jian, LIU Yumei, et al. Research on design and test method of a new type of bogie stiffness test bench[J]. Railway Vehicles, 2009, 47(10): 6 DOI:10.3969/j.issn.1002-7602.2009.10.002 |
| [17] |
背户一登.动力吸振器及其应用[M].任明章, 译.北京: 机械工业出版社, 2013. KAZUTO Seto. Dynamic vibratin absorber and its applications[M]. Translated by REN Mingzhang. Beijing: Mechanical Industry Press, 2013. |
| [18] |
刘豹, 唐万生. 现代控制理论[M]. 北京: 机械工业出版社, 2006 LIU Bao, TANG Wansheng. Modern control theory[M]. Beijing: Mechanical Industry Press, 2006 |
| [19] |
林鹤. 机械振动理论及应用[M]. 北京: 冶金工业出版社, 1990 LIN He. Mechanical vibration theory and application[M]. Beijing: Metallurgical Industry Press, 1990 |
| [20] |
同济大学应用数学系. 矩阵分析[M]. 上海: 同济大学出版社, 2005 Department of Applied Mathematics of Tongji University. Matrix analysis[M]. Shanghai: Tongji University Press, 2005 |
| [21] |
曹树谦. 振动结构模态分析:理论、实验与应用[M]. 天津: 天津大学出版社, 2001 CAO Shuqian. Modal analysis of vibration structure: Theory, experiment and application[M]. Tianjin: Tianjin University Press, 2001 |
| [22] |
IBRAHIM S R. Random decrement technique for modal identification of structures[J]. Journal of Spacecraft & Rockets, 1977, 14(11): 696 |
 2019, Vol. 47
2019, Vol. 47

