2. 同济大学 土木工程学院,上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
自从英国1986年首次提出钢-混凝土组合结构沉管隧道方案以来,该组合结构因在近海和海洋中具有较好的工作性能,成为了具有竞争力的隧道结构形式之一[1].该沉管隧道主要有以下三方面优势:合理的力学性能,钢板对内部混凝土有约束作用,同时混凝土能够有效地防止受压区钢板的失稳;良好的施工性能,隧道的内外层钢板可以作为混凝土浇筑的模板,同时又能够提供良好的防水性能;较好的经济效益,构造上无钢筋,减少了因钢筋绑扎等造成的人力成本.因此,钢-混凝土组合结构被认为是一种具有应用前景的沉管隧道结构.隧道横断面的抗剪受力性能对结构安全性来说至关重要,而混凝土的受剪破坏往往是以脆性破坏为主,因此确保钢-混凝土组合沉管结构的抗剪性能是隧道结构设计的关键问题之一.
近年来,针对实际应用中采用的设置纵隔板、横隔板的组合沉管结构,目前仅有日本开展了相关研究并形成设计标准草案[2].文献[3]以桁架模型为基础,系统地阐释了日本标准的设计思路,并提出了分别计算受拉钢板失效、受压混凝土失效并取两者较小值作为设计值的计算方法.文献[4]采用四点弯剪加载研究了腹板为不连续钢板的组合沉管结构的弯剪性能,并分析了不同腹板厚度条件下的抗剪承载力.文献[5]采用四点纯剪加载研究了连接件形式为板肋的组合结构的抗剪性能,并探讨了腹板厚度及间距、横隔板间距等因素对结构抗剪承载力的影响.Zahran等[6]采用四点弯剪加载研究了设置不连续腹板的组合沉管结构的剪切疲劳试验性能.Nakamura等[7]针对工字钢梁内衬混凝土结构进行了四点加载纯剪试验,并同样采用了桁架结构分析模型.
以深圳至中山跨海通道(下文简称深中通道)沉管隧道设计方案为研究背景,通过沉管抗剪节段的精细化三维实体非线性有限元模型,进行四点反弯矩剪切试验的仿真数值模拟;分析钢板、混凝土、角钢连接件在承载过程中的受力特点,揭示组合沉管结构抗剪传力机理,为结构计算、理论分析及工程实践提供参考.
1 工程结构概况深中通道隧道采用钢-混凝土组合沉管结构,隧道总长6.845 km,沉管段总长5.035 km,由32个管节组成,单个管节纵向标准长度为165 m.
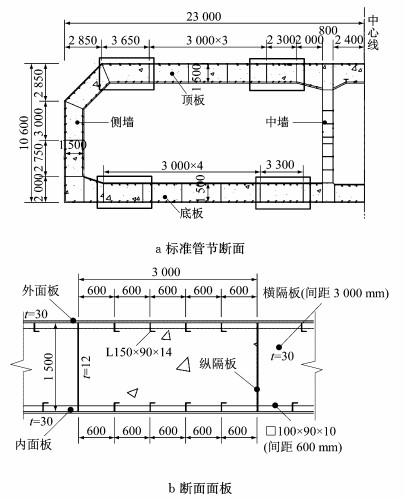
图 1为沉管隧道断面及顶、底板抗剪区间标准节段的尺寸.横截面高10.6 m,宽46.0 m,顶、底板厚度均为1.5 m.图 1中,t表示板件厚度.
|
图 1 断面构造与尺寸(单位:mm) Fig.1 Configuration and details of cross-section (unit:mm) |
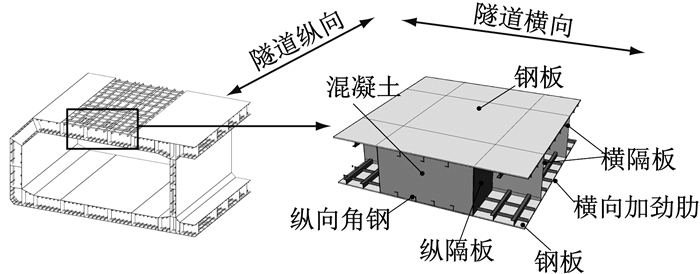
如图 2所示,沉管隧道的顶、底板,侧墙,中墙均由钢-混凝土组合结构构成.组合沉管结构包括钢结构格室及格室内部混凝土,钢结构格室由内、外层钢板及横、纵隔板组成,面板纵向布置角钢加劲肋,横向布置板肋加劲肋.隧道受力体系主要为横向,纵向角钢作为横向受力的剪力连接件承担钢板与混凝土的界面作用.
|
图 2 组合沉管结构示意图 Fig.2 Schematic diagram of composite tunnel structure |
沉管隧道结构以横向受力为主,而隧道结构的主要受剪区段在顶、底板靠近中墙和边墙的区段.为探讨沉管隧道受剪区段的抗剪承载性能,以如图 1所示的结构尺寸,建立抗剪节段的三维实体非线性有限元模型.
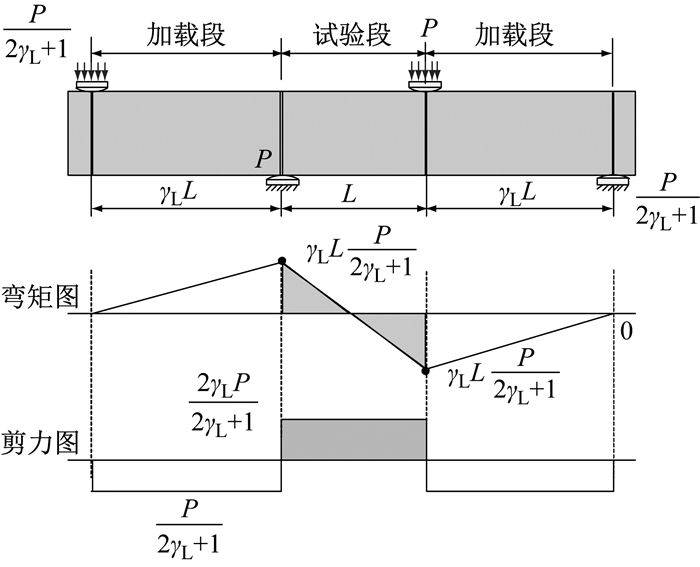
图 3为纯剪试验加载示意图.其中,L为试验段长度,γL为加载段与试验段的长度比值,P为荷载值.相比于弯剪试验,纯剪试验中试验段的受力性能更接近于连续梁、框架结构等实际结构中受剪区段的力学性能,也与沉管隧道抗剪段的受力相近.为此,模型主要对试验段进行有限元模拟,试验段的支点截面和加载点截面边界条件简化为沿受力方向的对称约束.对于顶板受剪区段,格室间距为3.0 m,顶板厚度为1.5 m,剪跨比为2.0.
|
图 3 加载示意图 Fig.3 Schematic diagram of loading |
图 4为离散化有限元模型.模型顶、底面设置一对200 mm宽的加载端.上部加载端施加竖向荷载,下部加载端约束固定.采用通用有限元计算软件Abaqus进行计算分析,采用六面体缩减积分单元C3D8R进行网格划分.

|
图 4 离散化有限元模型 Fig.4 Discretization of finite element models |
为保证计算精度,探究了网格尺寸、网格形状对结构的影响.当网格小于40 mm(试件高度的1/20)时,极限承载力趋于稳定,误差小于2%.为此,沿钢板厚度方向划分为四层,混凝土单元长度25 mm,钢结构单元长度20 mm.为精确计算混凝土开裂,对角钢附近混凝土网格进行加密,以保证可靠的局部受力计算.模型中钢结构单元约20万个,混凝土单元约40万个,加载端和固定端单元共约2万个.
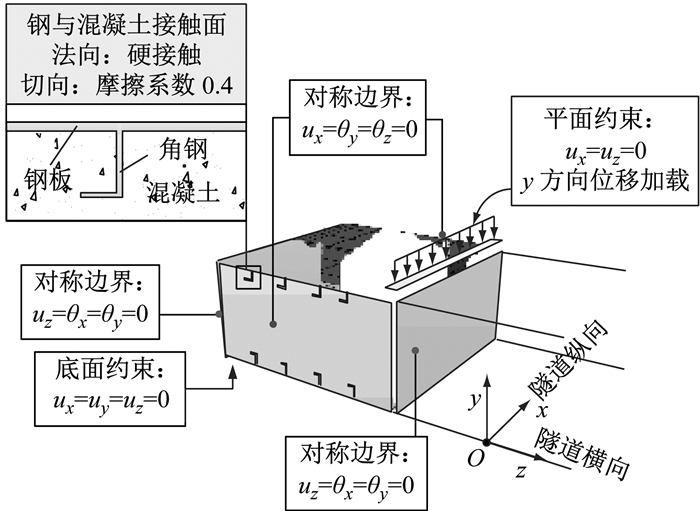
2.2 接触、加载及边界条件图 5为抗剪模型的接触、加载与边界条件.组合沉管节段模型与上、下两个加载端建立耦合,节段模型内部面板,角钢,横、纵隔板与两侧混凝土之间均采用面-面接触模拟.接触面法向力学行为采用“硬”接触,以模拟接触时不穿透并可分离的法向状态;切向采用罚刚度法描述结合面的黏结、滑移与摩擦.切向摩擦系数为0.4[8].
|
图 5 接触、加载及边界条件 Fig.5 Interaction behavior, loading and boundary condition |
节段模型顶部加载端顶面施加竖向位移荷载,底部支承加载端为固定约束.模型节段纵向长度为3 m,由于沿隧道纵向结构具有相似性和连续性,模型施加x方向对称约束.隧道横向顶板构造一致,由于横、纵隔板两侧均为混凝土,模型施加z方向对称约束.坐标轴绘于图 5中,其中ux、uy、uz为沿x、y、z轴平动,θx、θy、θz为绕x、y、z轴转动.
2.3 本构关系混凝土屈服准则采用Abaqus软件提供的塑性损伤模型[9].该塑性损伤模型的多轴受力屈服面是基于Lubliner等[10]和Lee等[11]提出的破坏准则,由参数Kc、剪胀角θc、强度比值fb0/fc0、单轴应力-应变关系、损伤模型等因素共同确定.
参数Kc表示静水压力轴与拉、压子午面距离之比,剪胀角θc为静水压力轴与破坏面的角度,fb0/fc0为二轴等压强度与单轴受压强度的比值.根据Kmiecik等[12]的研究,Kc取0.667,θc取30°,fb0/fc0取1.16.
损伤模型采用的是Kachanov[13]所提出的弹性损伤模型,采用损伤因子d反映材料弹性模量的损伤,并满足下式:
| $ \sigma=E_{0}(1-d)\left(\varepsilon-\varepsilon_{\mathrm{pl}}\right) $ |
式中:σ、ε分别为材料的应力、应变;εpl为材料塑性应变;E0为初始弹性应变.
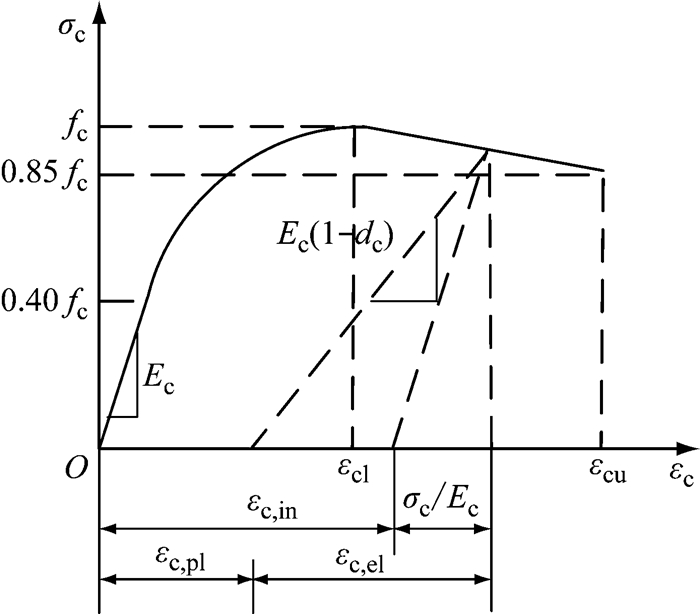
图 6为混凝土材料单轴受压应力-应变关系,曲线分成三个阶段.其中,σc为压应力,εc为压应变,fc为混凝土轴心抗压强度,Ec为混凝土弹性模量,εc1为混凝土轴心抗压强度对应峰值压应变,dc为混凝土压缩破坏损伤因子,εc, el为混凝土受压弹性应变,εc, pl为混凝土塑性应变,εc, in为受压非弹性应变;εcu为极限压应变.
|
图 6 混凝土受压应力-应变关系 Fig.6 Relation between strain and stress under compression for concrete |
受压本构曲线的第一个阶段近似假定为弹性受力阶段,混凝土的压应力随压应变增加而增大.当混凝土单轴压应力大于0.40fc时,混凝土受力进入塑性强化阶段.为较合理地模拟混凝土结构的上升段,此时压应力与压应变的关系为[14]
| $ \sigma_{\mathrm{c}}=f_{\mathrm{c}} \frac{E_{\mathrm{c}} \frac{\varepsilon_{\mathrm{c}}}{f_{\mathrm{c}}}-\left(\frac{\varepsilon_{\mathrm{c}}}{\varepsilon_{\mathrm{cl}}}\right)^{2}}{1+\left(E_{\mathrm{c}} \frac{\varepsilon_{\mathrm{cl}}}{f_{\mathrm{c}}}-2\right) \frac{\varepsilon_{\mathrm{c}}}{\varepsilon_{\mathrm{cl}}}} $ |
弹性模量Ec、峰值压应变εc1取值为
| $ \begin{aligned} E_{\mathrm{c}}=& 22 \times\left(0.1 f_{\mathrm{c}}\right)^{0.3} \\ \varepsilon_{\mathrm{cl}} &=0.7 f_{\mathrm{c}}^{0.31} \end{aligned} $ |
第三阶段为混凝土塑性软化阶段.假定压应力随压应变增加而减小,并在极限压应变εcu处下降至0.85fc[15].
在混凝土的加载过程中,混凝土的受压损伤因子取值满足下式:
| $ d_{\mathrm{c}}=1-\frac{\sigma_{\mathrm{c}}}{E_{\mathrm{c}} \varepsilon_{\mathrm{cl}}\left(1 / b_{\mathrm{c}}-1\right)+\sigma_{\mathrm{c}}} $ |
式中:bc为塑性应变与非弹性应变的比值,根据Birtel等[16]的研究结果取0.7.
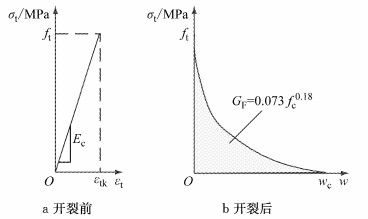
图 7为混凝土材料单轴受拉本构模型,受拉曲线分成两个阶段.其中,σt为拉应力,εt为拉应变,w为混凝土开裂后裂缝宽度,ft为混凝土轴心抗拉强度,εtk为混凝土轴心抗拉强度对应峰值拉应变,wc为混凝土应力完全释放时的裂缝宽度.
|
图 7 混凝土受拉本构关系 Fig.7 Constitutive laws of concrete under tension |
混凝土受拉开裂前假定为线性,开裂后的混凝土本构关系采用应力-裂缝宽度曲线表示,如下所示[17]:
| $ \begin{array}{*{20}{c}} {\frac{{{\sigma _{\rm{t}}}}}{{{f_{\rm{t}}}}} = \left( {1 + {{\left( {{c_1}\frac{w}{{{w_{\rm{c}}}}}} \right)}^3}} \right){{\rm{e}}^{ - \frac{{{c_2}w}}{{{w_{\rm{c}}}}}}} - \frac{w}{{{w_{\rm{c}}}}}\left( {1 + c_1^3} \right){{\rm{e}}^{ - {c_2}}}}\\ {{w_{\rm{c}}} = 5.14\frac{{{G_{\rm{F}}}}}{{{f_{\rm{t}}}}}} \end{array} $ |
式中:GF为产生单位面积无应力裂缝所需的断裂能,GF=0.073fc0.18;c1、c2为常数,普通混凝土c1取3.0、c2取6.93.
在混凝土的加载过程中,混凝土的受拉损伤因子dt与塑性裂缝宽度wp相关.假定塑性裂缝宽度wp与裂缝宽度w的关系为线性,则受拉损伤因子dt计算式如下所示:
| $ d_{\mathrm{t}}=1-\frac{\sigma_{\mathrm{t}} l_{0}}{E_{\mathrm{c}} w_{\mathrm{p}}\left(1 / b_{\mathrm{t}}-1\right)+\sigma_{\mathrm{t}} l_{0}} $ |
式中:l0是单元长度;bt是塑性应变与非弹性应变的比值,根据Birtel等[16]的研究结果取0.1.
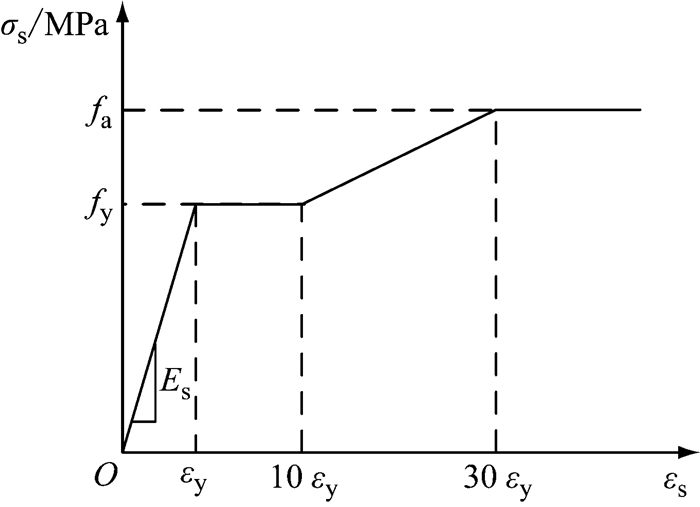
图 8为钢材本构曲线.图 8中,σs为钢板应力,εs为钢板应变,fy、Es、εy和fa分别为钢材屈服强度、弹性模量、屈服强度对应应变以及钢板极限抗拉强度.假定屈服平台长度为10εy,材料屈强比fy/fa取0.78,极限抗拉强度对应应变取30εy.
|
图 8 钢材本构关系 Fig.8 Constitutive laws of structural steel |
加载端、固定端的本构采用钢材材性,并且仅考虑弹性.混凝土强度等级设为C50,钢材设为Q390,计算中fc、Ec、ft、fy、Es等根据规范取相似等级材料的强度标准值.
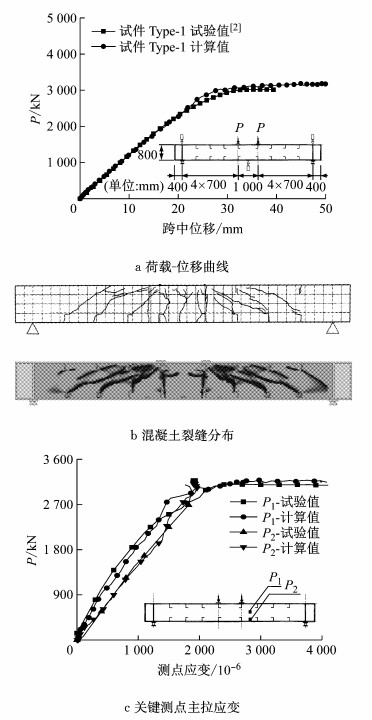
2.4 模型验证为验证建模方法的合理性,首先对文献[2]中的弯剪试验进行仿真分析,并将模型计算结果与试验数据进行比较,如图 9所示.有限元计算结果的刚度、抗剪承载力与试验结果相近,并且具有良好的延性.混凝土裂缝分布、开裂角度相近,钢结构主拉应变及应力发展相近,有限元仿真计算能够较好地模拟试验加载过程.
|
图 9 有限元模型验证 Fig.9 Validation of finite element model |
为排除单个模型计算的偶然性,以上述方法模拟文献[5]中开展的纯剪试验.试验结果表明,破坏形态相近,承载力误差较小.计算结果如表 1所示.表 1中,bw、h、a、tw、ttop、tbottom分别为构件宽度、高度、加载点距支点中心距、钢腹板厚度、顶板厚度、底板厚度,Vu-exp、Vu-FEM分别为极限抗剪承载力的试验值和有限元计算值.有限元计算结果与多组试验数据具有较好的吻合度,说明该建模方法能够较良好地模拟组合沉管结构的抗剪性能.
| 下载CSV 表 1 计算值与试验结果比较 Tab.1 Comparison between test results and computational results |
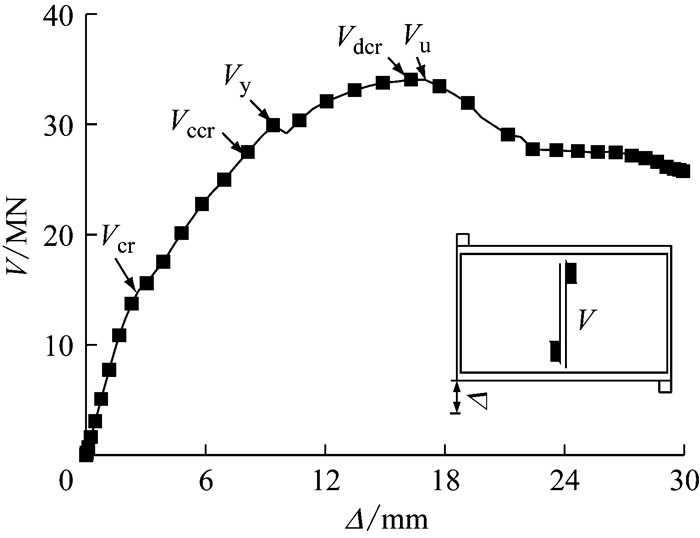
截面剪力V随加载位移Δ的变化曲线如图 10所示.图 10中, 初裂荷载Vcr、连接件失效荷载Vccr、全截面屈服荷载Vy、斜裂荷载Vdcr、极限荷载Vu分别对应模型加载至破坏过程中,初始弯剪裂缝贯通、角钢附近混凝土开裂、横隔钢板屈服、斜裂缝贯通、混凝土进一步受压开裂至结构失效时的截面剪力.
|
图 10 剪力-位移曲线 Fig.10 Shear force-displacement curves |
剪力-位移曲线存在较明显的弹性段、弹塑性段和屈服段,加载至极限承载力后有良好的延性.混凝土的开裂、横隔钢板的屈服对结构的刚度均有明显影响.混凝土对角斜裂缝贯通,是结构达到极限承载力Vu的主要标志.
3.2 混凝土受力机理混凝土裂缝发展过程如图 11所示.塑性损伤因子是裂缝宽度的函数,塑性损伤分布一定程度上反映混凝土的裂缝进展.混凝土的初始裂缝发生在受弯区角钢尖端附近,是明显的弯曲裂缝;增大外荷载至Vcr,混凝土弯剪裂缝贯通,并在贯通的弯剪裂缝附近出现分散的细微裂缝;当外荷载增大至Vccr时,由于角钢的拉拔作用,导致角钢间混凝土层状开裂;当外荷载增大至Vdcr时,混凝土核心受压区中心出现对角剪切斜裂缝,并随着斜裂缝的贯通,截面剪力达到极限承载力.

|
图 11 混凝土裂缝发展 Fig.11 Development of cracks in concrete |
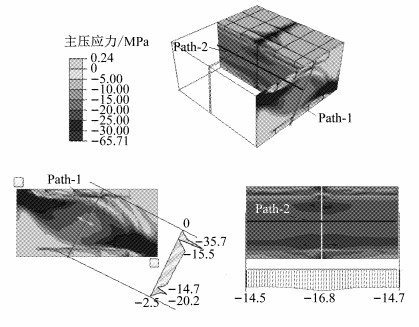
图 12为截面剪力达到Vdcr时混凝土主压应力分布.选取路径Path-1、Path-2上的主压应力,并标识应力路径上的特征值.
|
图 12 极限荷载下混凝土主压应力分布 Fig.12 Distribution of principal compressive stresses in concrete at ultimate capacity |
路径Path-1与主压应力方向垂直.混凝土的裂缝发展导致角钢附近混凝土与核心区混凝土分离,而截面剪力主要由核心区混凝土承担,分布区域呈梭形.混凝土主压应力幅值分布均匀,约为15 MPa,此时混凝土核心区类似斜向压杆.
路径Path-2与横隔钢板垂直,并通过Path-1路径中点.Path-2上的混凝土主压应力分布均匀,远离横隔钢板位置的混凝土主压应力比靠近横隔钢板位置的低约10%.横隔钢板对附近的混凝土应力分布存在影响,但范围较小.混凝土应力横向分布不均匀现象并不明显.
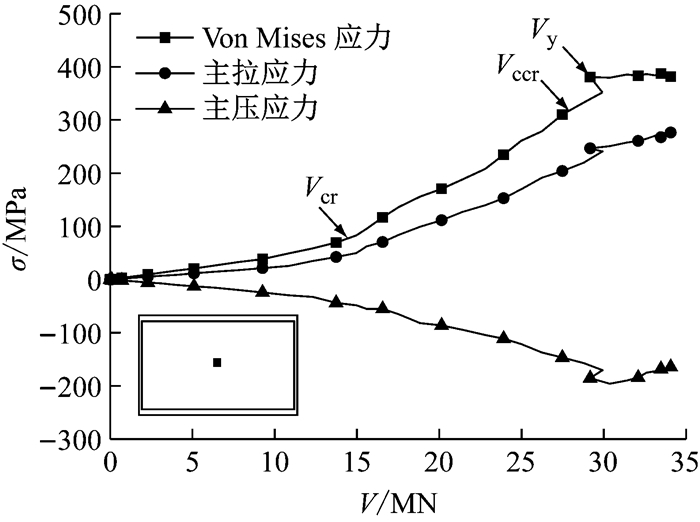
3.3 钢结构受力机理横隔钢板中心点的应力变化曲线如图 13所示.截面剪力达到Vcr前,横隔钢板应力水平较低;超过Vcr后,混凝土不再承受拉应力,横隔钢板应力快速增大至屈服.开裂前,钢板主拉应力与主压应力水平相当,横隔钢板中心主要处于纯剪状态;开裂后,主拉应力略有增加,与主压应力水平仍相近.
|
图 13 横隔钢板应力变化 Fig.13 Stress variation in transverse steel diaphragm |
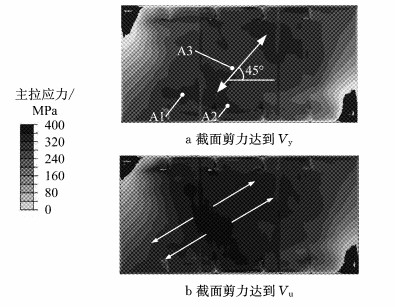
图 14为横隔钢板主拉应力分布.截面剪力未达到Vy时,因承受弯矩作用,A1区域主拉应力较大;当截面剪力达到Vy时,钢腹板Von Mises应力达到屈服强度,此时A1区域主拉应力增加至300 MPa以上,并向A2、A3区域逐步扩展,以承担混凝土弯剪开裂、连接件层间开裂后的拉应力.随着荷载进一步增加,由于截面剪力逐渐由混凝土和钢结构承受,混凝土的协同作用改变了钢板纯剪状态,钢板的主拉应力角度逐渐发生改变.当截面剪力达到Vu时,A1、A2、A3区域的主拉应力接近屈服材料单向受拉强度,说明接近极限状态时,钢板主要承担拉应力.
|
图 14 横隔钢板主拉应力方向及分布 Fig.14 Direction and distribution of principal tension stress in transverse steel diaphragm |
采用不等边角钢作为钢与混凝土间的连接件,角钢既传递格室面板与内部混凝土之间的剪力作用,又承担着防止面板与内部混凝土分离的拉拔作用.
日本标准[2]中给出了角钢剪力承载力VL的计算式,如下所示:
| $ \begin{aligned} V_{\mathrm{L}}=& 5.590 h_{\mathrm{sc}} w_{\mathrm{sc}} f_{\mathrm{c}}^{1 / 2} k_{1} k_{2} k_{3} \\ k_{1} &=2.2 \times\left(\frac{t_{\mathrm{sc}}}{h_{\mathrm{sc}}}\right)^{2 / 3} \\ k_{2}=& 0.4 \times\left(\frac{t_{\mathrm{f}}}{t_{\mathrm{sc}}}\right)^{1 / 2}+0.43 \\ k_{3} &=\left(\frac{s_{\mathrm{sc}}}{10 t_{\mathrm{sc}}}\right)^{1 / 2} \end{aligned} $ |
式中:hsc为角钢高度;wsc为角钢长度;k1、k2、k3分别为考虑角钢腹板高厚比的系数、考虑面板厚度引起边界效应的系数、考虑连接件间距影响的系数;tsc为角钢腹板厚度;tf为面板厚度;ssc为角钢间距.以各参数计算角钢承载力,得到面板角钢每延米承载的最大剪力为1 539 kN·m-1左右.
根据文献[18]的角钢连接件推出试验结果,当连接件破坏不是由于根部钢材剪断时,连接件的开口方向对连接件抗剪承载力有影响,对应本研究的角钢布置,外表面角钢的抗剪承载力比内表面角钢的抗剪承载力低约10%.
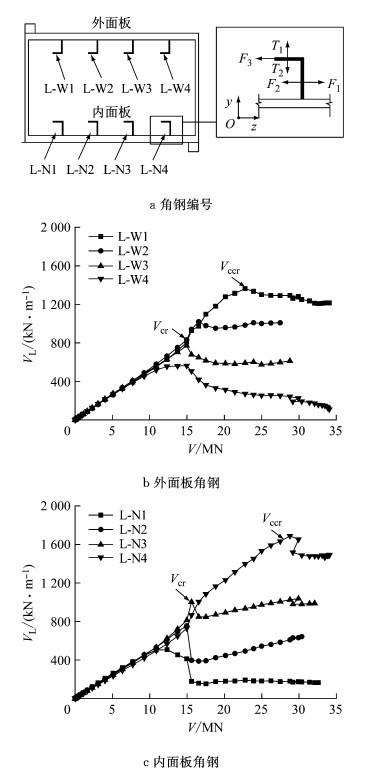
图 15为各角钢承担的剪力VL随截面剪力V的变化曲线.图 15a中给出了各个角钢的编号和角钢剪力、拉拔力计算方法。图 15中,F1、F2、F3、T1、T2分别表示角钢各个面的法向合力,以yoz方向为正.对每个焊钉,其承担的剪力VL=F1+F2+F3,承担的拉拔力TL=T1+T2.
|
图 15 角钢剪力随截面剪力变化 Fig.15 Shear force variation of angle steel with load |
开裂前,各角钢承担的剪力分布均匀,假定弹性节段连接件刚度相近,说明开裂前各连接件的相对滑移分布均匀.随着荷载增加,角钢L-N1、L-W4位置处混凝土出现弯剪开裂,连接件刚度下降并退出工作.当荷载达到Vcr时,弯剪裂缝贯通,L-N2和L-N3、L-W2和L-W3逐渐退出工作,但破坏时各连接件承担的剪力均未达到规范建议值.当荷载继续增加至Vccr时,连接件L-W1、L-N4承担的剪力逐渐增大,相继达到连接件承载力.当剪力达到极限承载力Vu时,连接件L-W1、L-N4仍承担较大剪力.截面剪力进一步由斜压杆混凝土和斜拉杆横隔钢板承担.
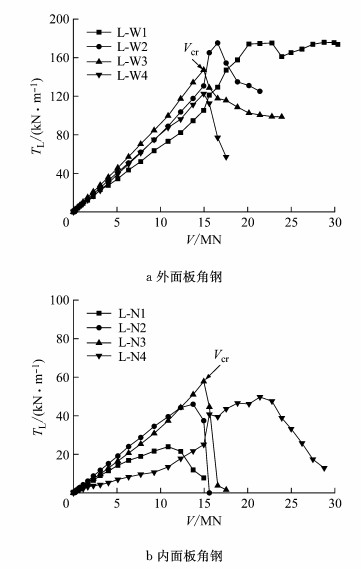
图 16为角钢承担的拉拔力TL随截面剪力V的变化曲线.开裂前,各连接件承担的拉拔力分布不均,位于节段中部的角钢L-W2、L-W3、L-N2、L-N3承担的拉拔力较大,其中外面板上角钢承担的力又明显大于内面板,假定弹性状态拉拔刚度相同,则说明各连接件的相对分离与受力状态、边界条件相关.开裂后,弯剪裂缝导致角钢的拉拔作用减弱.
|
图 16 角钢拉拔力随截面剪力变化 Fig.16 Uplift force variation of angle steel with load |
(1) 钢-混凝土组合沉管结构在剪切破坏过程中,依次发生混凝土弯剪开裂、连接件附近混凝土开裂、横隔钢板屈服,最终因混凝土剪切斜裂缝贯通达到结构极限承载力.
(2) 结构加载存在明显的弹性段、弹塑性段和屈服段,加载至极限承载力后有良好的延性,并未出现明显的脆性破坏.横隔钢板的屈服、混凝土的开裂对结构刚度均有明显的影响.
(3) 在结构受剪方向,横隔钢板主要承担斜向拉力,混凝土主要承担斜向压力,两者形成主要受力承载体系;同时,在结构受剪的垂直方向,混凝土内应力没有明显的横向分布不均匀现象.
(4) 角钢主要承担格室面板与内部混凝土之间剪力的传递作用,拉拔力作用较小.开裂前,各连接件抗剪刚度相近,截面剪力分布均匀.加载至极限状态时,连接件附近混凝土已开裂,但并不影响结构继续承载.
| [1] |
KIMURA H, KOJIMA I, MORITAKA H. Development of sandwich-structure submerged tunnel tube production method[J]. Nippon Steel Technical Report, 2002, 86: 86 |
| [2] |
日本土木学会.鋼コンクリートサンドイッチ構造設計指針(案)[M].东京: 土木学会, 1992.
|
| [3] |
上田多門, 塩屋俊幸. 鋼コンクリート系サンドイッチ構造[J]. コンクリート工学, 1992, 30(5): 5 |
| [4] |
淺沼芳雄, 中井勝彥, 古內仁, 等. 鋼コンクリートサンドイッチはりのせん断耐カ[J]. 構造工學論文集, 1996, 42A: 1139 |
| [5] |
鬼頭宏明, 山脇学, 園田恵一郎. 鋼·コンクリ-トサンドイッチ部材のせん断耐荷機構[J]. 土木学会論文集, 1998, 591(43): 53 |
| [6] |
ZAHRAN M, UEDA T, KAKUTA Y. A study on fatigue strength of steel-concrete sandwich beams without shear reinforcement[J]. Journal of Materials, Concrete Structure, Pavements: JSCE, 1998, 38: 205 |
| [7] |
NAKAMURA S, NARITA N. Bending and shear strengths of partially encased composite Ⅰ:girders[J]. Journal of Constructional Steel Research, 2003, 59: 1435 DOI:10.1016/S0143-974X(03)00104-4 |
| [8] |
COOK R A, KINGER R. Behavior and design of ductile multiple anchor steel-to-concrete connections[R]. Austin: University of Texas at Austin, 1989.
|
| [9] |
Dassault System. Abaqus documentation: version 6.13[M]. Providence: Dassault Systèmes Simulia Corporation, 2010.
|
| [10] |
LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete[J]. International Journal of Solids Strucutres, 1989, 25(3): 299 DOI:10.1016/0020-7683(89)90050-4 |
| [11] |
LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892 DOI:10.1061/(ASCE)0733-9399(1998)124:8(892) |
| [12] |
KMIECIK P, KAMINSKI M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration[J]. Archives of Civil and Mechanical Engineering, 2011, 11(3): 623 DOI:10.1016/S1644-9665(12)60105-8 |
| [13] |
KACHANOV L M. Introduction to continuum damage mechanics[M]. Dordrecht: Martinus Nijhoff Publishers, 1986
|
| [14] |
CEN. Eurocode 4, design of composite steel and concrete structures, Part 1-1: general rules and rules for buildings[S]. Brussels: CEN, 2006.
|
| [15] |
ZHENG S, LIU Y, YODA T, et al. Parametric study on shear capacity of circular-hole and long-hole perfobond shear connector[J]. Journal of Constructional Steel Research, 2017, 117: 64 |
| [16] |
BRITEL V, MARK P. Parameterised finite element modelling of RC beam shear failure[C]//Proceeding of 2006 ABAQUS Users' Conference. Boston: Abaqus Inc., 2006: 95-107.
|
| [17] |
CORNELISSEN H, HORDIJK D, REINHARDT H. Experimental determination of crack softening characteristics of normal weight and lightweight concrete[J]. Heron, 1986, 31(2): 45 |
| [18] |
清宫理, 横田弘, 铃木操, 等. 合成構造におけるシアーコネクターの基本的な力学性状[J]. コンクリート工学年次講演会論文集, 1986, 8: 609 |
 2019, Vol. 47
2019, Vol. 47

