随着我国轨道交通的迅速发展,轨道车辆的运行速度、载重以及发车频次大幅提升,致使轨道车辆振动问题日益凸显,轴箱及转向架上因振动导致的结构裂纹、断裂和部件脱落现象日趋严重,危及行车安全.为了设计和考核装备在振动环境中的安全性及可靠性,必须依据实测数据、振动环境和规范标准制定振动环境归纳谱.我国在航空机载设备振动环境谱归纳方面较早地开展了研究[1-2],同时也制定了振动、冲击环境数据归纳方法的军用标准[3],运用正态假设下的数理统计原理来归纳特征样本,并以此计算实测谱和规范谱.研究发现,振动环境数据归纳方法在轨道交通领域的运用很少.
轨道交通装备需要经过标准[4]检验后方可装车,而国内轨道交通装备在载重、运行速度和振动环境等方面的检验标准各自迥异,装备开发者希望掌握国内实际车辆运行环境振动谱,并与振动试验标准比较,以提高轨道交通装备的设计准确性和运行可靠性.丁杰等[5]采用军用标准GJB/Z126-99对实测数据进行归纳,获得实测1类A级功率谱曲线,并据此对车载设备进行疲劳分析.然而,在实际运用中轨道车辆装备振动数据存在大量的非正态样本,正态假设导致归纳谱误差的产生.Slifker等[6]提出了Johnson法则,利用正态拟合函数方法对非正态数据进行转换.罗敏等[7]利用Johnson法则对非正态振动数据进行转换,解决了飞行器的非正态振动数据问题.
本研究利用Johnson法则对军用标准归纳方法进行改进,处理非正态振动数据,并运用于实测数据中;计算某线路车辆不同振动部位和方向的振动加速度归纳谱,与国际标准[4]IEC 61373-2010进行对比,分析改进前后的差异.
1 归纳方法原理 1.1 非正态处理Slifker等[6]提出,使用一簇分布可将数据正态化,如下所示:
| $ \widetilde{x}=\gamma+\eta k_{a}(x ; \lambda, \varepsilon) $ | (1) |
其中,
| $ k_{a}(x ; \lambda, \varepsilon)=\left\{\begin{array}{ll}{\sinh ^{-1}\left(\frac{x-\varepsilon}{\lambda}\right), } & {a=1} \\ {\ln \left(\frac{x-\varepsilon}{\lambda+\varepsilon-x}\right), } & {a=2} \\ {\ln \left(\frac{x-\varepsilon}{\lambda}\right), } & {a=3}\end{array}\right. $ | (2) |
式中:x为原样本数个体,其转换结果为
对于给定的z,计算标准正态分位点(-3z, -z, z, 3z)的分位数,并以此确定原样本的四个分位点(x1, x2, x3, x4).通常z的取值[8]在0.25到1.25范围内.令o=x4-x3,n=x2-x1,r=x3-x2.根据on/r2的大小选择方程ka的形式,即:当on/r2=1时,a=1;当on/r2>1时,a=2;当on/r2 < 1时,a=3.选定方程后,根据估计法则[6]对其中的参数γ、η、λ和ε进行估计.
选取转换后数据集的规定水平下的分位点,实现对原始数据样本的上限系数的估计.
1.2 时域处理时域数据可分成不同样本和不同通道,各自形成独立的样本,因此对样本进行正态检验[9]是很有必要的.振动过程中,外界环境的突然变化带来误差较大的数据,如果这些数据不排除,就会降低结果的精度,甚至得出错误的结论[10].
处理过程中,由于采样频率高且样本容量大,因此采用Jarque-Bera检验法对样本数据进行正态检验.对于数据集中的每个样本,若满足正态分布,则认为不存在偏差数据;若不满足正态分布,在将数据正态化后,通过下式估计上限:
| $ x_{1}=\bar{x}+Q_s $ | (3) |
式中:xl、x和s分别为样本的估计上限、样本均值和样本标准差;Q为原样本在正态转换后规定水平下的分位数.去除超限的数据点,并重置为该分布下的随机数.
1.3 频域处理 1.3.1 特征样本计算所有样本的功率谱数据,记为Gk(i, j)(i=1, 2, 3, …, L1; j=1, 2, 3, …, M1; k=1, 2, 3, …, N1).其中,L1表示通道数,M1表示样本数,N1表示谱线数.Gk(i, j)的均方根值为αRMS(i, j),并按下式对均值Xi和方差Si2进行参数估计:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_i} = \frac{1}{{{M_1}}}\sum\limits_{j = 1}^{{M_1}} {{\alpha _{{\rm{RMS}}}}} (i, j)}\\ {S_i^2 = \frac{1}{{{M_1} - 1}}\sum\limits_{j = 1}^{{M_1}} {{{\left( {{\alpha _{{\rm{RMS}}}}(i, j) - {X_i}} \right)}^2}} } \end{array}} \right. $ | (4) |
选取第i个和第m个数据通道,根据均值和方差计算统计量F(i, m)和t(i, m),如下所示:
| $ \left\{\begin{array}{l}{F(i, m)=\frac{S_{i}^{2}}{S_{m}^{2}}, \quad i \neq m} \\ {t(i, m)=\frac{X_{i}-X_{m}}{\sqrt{\left(S_{i}^{2}+S_{m}^{2}\right) / M_{1}}}, \quad i \neq m}\end{array}\right. $ | (5) |
假设数据通道i和m的功率谱属于同一总体,则F(i, m)服从自由度为(M1-1, M1-1)的F分布,t(i, m)服从自由度为2(M1-1)的中心t分布.
在给定置信度(1-α)下,若
| $ \left\{\begin{array}{l}{F_{\left(M_{1}-1, M_{1}-1\right) ; \alpha / 2} \leqslant F(i, m) \leqslant F_{\left(M_{1}-1, M_{1}-1\right) ;(1-\alpha / 2)}} \\ {|t(i, m)| \leqslant t_{2\left(M_{1}-1\right) ;(1-\alpha / 2)}}\end{array}\right. $ | (6) |
成立,则假设成立,即数据通道i和m的功率谱属于同一总体;反之,则不属于同一总体.
归并属于同一通道的数据,形成特征样本
令
| $ x_{k}(p, q)=\sqrt{\widetilde{G}_{k}(p, q)} $ | (7) |
并对样本xk(p, q)进行均值Xk(p)和方差Sk2(p)的参数估计,如下所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_k}(p) = \frac{1}{{{Q_p}}}\sum\limits_{q = 1}^{{Q_p}} {{x_k}} (p, q)}\\ {S_k^2(p) = \frac{1}{{{Q_p} - 1}}\sum\limits_{q = 1}^{{Q_p}} {{{\left( {{x_k}(p, q) - {X_k}(p)} \right)}^2}} } \end{array}} \right. $ | (8) |
计算置信度为(1-α)、分位点为β的容差上限系数F11,如下所示:
| $ {F_{11}} = \frac{{{t_{\left( {{Q_p} - 1} \right);(1 - \alpha )}}}}{{\sqrt {{Q_p}} }} + {Z_\beta }\sqrt {\frac{{{Q_p} - 1}}{{\chi _{\left( {{Q_q} - 1} \right);\alpha }^2}}} $ | (9) |
式中:Zβ为满足P(Z≤Zβ) =β的正态分布分位点;χ(Qp-1)2为自由度是(Qp-1)的χ2分布α分位点.
对第p个样本进行容差上限估计,如下所示:
| $ G_{k}(p)=\left(X_{k}(p)+F_{11} S_{k}(p)\right)^{2} $ | (10) |
从而得到每个特征样本的随机振动实测谱Gk(p).
1.3.3 规范谱按特征样本频段分布情况进行划分,对样本xk(p, q)相邻谱线进行假设检验,如下所示:
| $ \left\{\begin{array}{l}{F(k, k+1)=\frac{S_{k}^{2}(p)}{S_{k+1}^{2}(p)}} \\ {t(k, k+1)=\frac{X_{k}(p)-X_{k+1}(p)}{\sqrt{\left(S_{k}^{2}(p)+S_{k+1}^{2}(p)\right) / Q_{p}}}}\end{array}\right. $ | (11) |
假设相邻谱线k和(k+1)的功率谱属于同一总体,则F(k, k+1)服从自由度为(Qp-1, Qp-1)的F分布,t(i, m)服从自由度为2(Qp-1)的中心t分布.
在给定置信度(1-α)下,若
| $ \left\{\begin{array}{l}{F_{\left(Q_{q}-1, Q_{q}-1\right) ; a / 2} \leqslant F(k, k+1) \leqslant F_{\left(Q_{q}-1, Q_{q}-1\right) ;(1-\alpha / 2)}} \\ {|t(k, k+1)| \leqslant t_{2\left(Q_{q}-1\right) ;(1-\alpha / 2)}}\end{array}\right. $ | (12) |
成立,则假设成立,即相邻谱线k和(k+1)的功率谱属于同一总体;反之,则不属于同一总体.
归并属于同一总体的相邻谱线,形成H1个频段,第h(h=1, 2, …, H1)频段两端的谱线分别为kh1和kh2,谱线数为Nh.对第h频段的数据xk(p, q)进行均值Xh(p)和方差Sh2(p)的参数估计,如下所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_h}(p) = \frac{1}{{{Q_p}{N_h}}}\sum\limits_{q = 1}^{{Q_p}} {\sum\limits_{k = {k_{h1}}}^{{k_{h2}}} {{x_k}} } (p, q)}\\ {S_h^2(p) = \frac{1}{{{Q_p}{N_h} - 1}}\sum\limits_{q = 1}^{{Q_p}} {\sum\limits_{k = {k_{h1}}}^{{k_{h2}}} {{{\left( {{x_k}(p, q) - {X_k}(p)} \right)}^2}} } } \end{array}} \right. $ | (13) |
计算置信度为(1-α)、分位点为β的容差上限系数F12,如下所示:
| $ {F_{12}} = \frac{{{t_{\left( {{Q_p}{N_h} - 1} \right);(1 - \alpha )}}}}{{\sqrt {{Q_p}{N_h}} }} + {Z_\beta }\sqrt {\frac{{{Q_p}{N_h} - 1}}{{\chi _{\left( {{Q_q}{N_h} - 1} \right);\alpha }^2}}} $ | (14) |
对第h个样本进行容差上限估计,如下所示:
| $ G_{h}(p)=\left(X_{h}(p)+F_{12} S_{h}(p)\right)^{2} $ | (15) |
从而得到每个特征样本的随机振动规范谱Gh(p).
图 1为数据归纳流程.在时域数据处理中,利用非正态转换获取上下限,剔除出野点;在谱线归纳中,对非正态的数据进行转换,求得上限谱.

|
图 1 谱归纳流程 Fig.1 Flow chart of spectral induction |
某线路地铁车辆运营时,一运行公里数约为18万的车辆(旧车)出现提吊装置振裂现象.据实测现场反馈,旧车轴箱明显比新上线车辆(新车)振动剧烈,并且提吊装置振裂现象只出现在旧车中.分析时,对比了新旧两车的振动数据,归纳了多通道数据的频谱.实测中,在一测试车辆的轴箱上均布置了测点,垂横每向各8个通道;同时,在对应的构架中部和端部布置了6个测点,在车体地板上布置了4个测点.轴箱测点的采样频率为2 048 Hz,构架和车体的采样频率分别为1 024 Hz和512 Hz.测试时,全程上下行共行驶5次.
表 1为振动加速度数据统计结果.由表 1可知, 车辆的振动加速度数据均为非正态数据.
| 下载CSV 表 1 数据样本统计值对比 Tab.1 Comparison of statistical values of data samples |
选取5 s轴箱垂向振动的数据片段进行计算,计算得到偏度和峰度分别为0.04和17.47,根据
| $ J=\frac{N}{6}\left(\gamma_{\mathrm{s}}^{2}+\frac{\left(\gamma_{\mathrm{k}}-3\right)^{2}}{4}\right) $ | (16) |
计算得到的统计量J远大于自由度为2的χ2分布在显著性水平0.05下的分位点,故正态假设不成立.式(16)中,J、N、γs和γk分别表示检验统计量、样本容量、偏度和峰度.根据式(3)在正态转换后求取上限,用该分布下的随机数代替超限的数据点.图 2显示了处理前后轴箱振动的部分数据.表 2对比了处理前后振动加速度数据统计值.

|
图 2 处理前后部分时域数据对比 Fig.2 Comparison of time domain data before and after processing |
| 下载CSV 表 2 处理前后统计值对比 Tab.2 Comparison of statistical values before and after processing |
由表 2可知,处理数据的最大绝对值比原数据小,但其均方根值几乎保持不变,未改变数据整体的能量特征,并且偏度更接近于零,峰度大大减小.处理方法不改变样本分布,对振动信号能量的影响很小,能极大程度保留原始数据特征,并剔除部分振动野点.
2.3 频域分析根据第1.3节所述,归纳谱为实测谱和规范谱的总称,表示由GJB/Z126-99原方法和Johnson法则改进法2种方法所求的功率谱.实测谱为频率轴连续的功率谱,规范谱是由实测谱中相邻同分布的谱线合并而成的平直谱图.标准谱为IEC 61373-2010中轨道车辆装备振动[4]的上限谱.
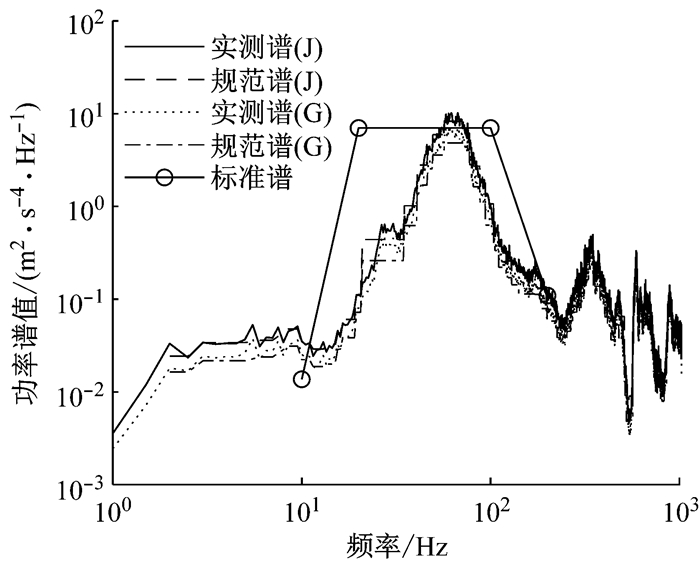
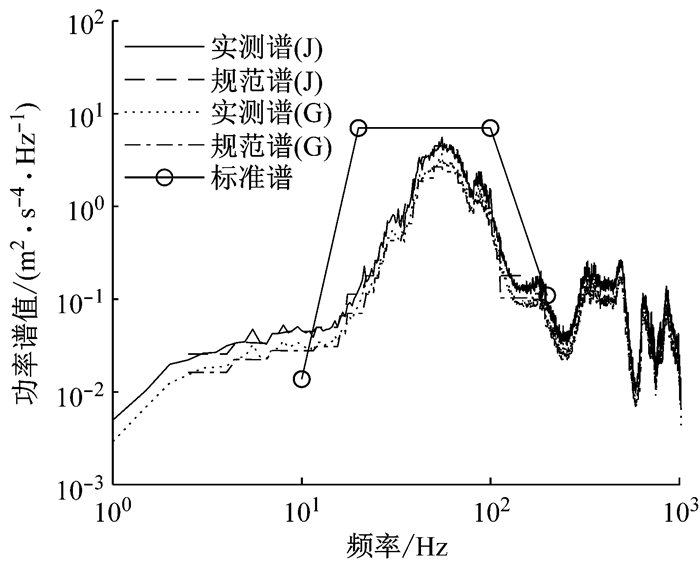
图 3和图 4分别显示了旧车和新车轴箱的垂向振动归纳谱.原方法和改进法所求的归纳谱分别用G和J表示.
|
图 3 旧车轴箱垂向振动归纳谱与标准谱对比 Fig.3 Comparison between induced spectrum and standard spectrum of axle box's vertical vibration of old vehicle |
|
图 4 新车轴箱垂向振动归纳谱与标准谱对比 Fig.4 Comparison between induced spectrum and standard spectrum of axle box's vertical vibration of new vehicle |
由图 3可知,改进法所求得归纳谱值略大于原方法,原因是非正态数据某一分位点比转换后数据同一水平下的分位点小.原始数据中单个样本的统计值不能准确地估计样本总体,转换后求得的容差上限系数更能反映总体的真实情况.对比归纳谱中的实测谱和规范谱.实测谱是频率轴连续的谱图,规范谱则形成了频段.实测谱能清楚地显示每一个谱线,规范谱则将相邻同分布的谱线合并,便于归纳比较.对比归纳谱和标准谱,原方法所求的旧车和新车的归纳谱在主频段部分都未超过标准谱,而从改进法所求的归纳谱中可以看出, 旧车轴箱振动在部分主频段超过标准谱,与实测中旧车轴箱提吊振裂现象一致.
2.4 偏差分析记原方法和改进法所求的实测谱分别为Gko和Gkj.计算偏差比δk,如下所示:
| $ \delta_{k}=\frac{G_{k {\rm o}}-G_{k {\rm j}}}{G_{k {\rm o}}} \times 100 \% $ | (17) |
对于同一样本,分别使用2种方法计算归纳谱并计算两者的偏差比.整个谱线中偏差的平均值为29%,同时存在偏差较大的谱线,最大值为35%.
图 5为2种方法所求谱线值偏差比的分布.由图 5可知,偏差比的分布大部分维持在29.1%左右.

|
图 5 偏差分布 Fig.5 Deviation distribution |
选取某个频段的谱线值,对比2种方法的估计结果.表 3对比了该频段2种方法所求得的上限系数和上限值.其中,改进法所求得上限系数比原方法所求得的高28.1%,上限值高17.9%.
| 下载CSV 表 3 上限系数和上限值对比 Tab.3 Upper bound coefficient and upper bound value |
图 6显示了该频段原始谱线值的分布,谱线值样本是非正态的.由图 6可知,改进法所求得的上限值要大于原方法的计算结果.对于具有大量非正态样本的数据集,2种方法的计算结果存在明显差别.

|
图 6 谱线值分布 Fig.6 Distribution of spectral line values |
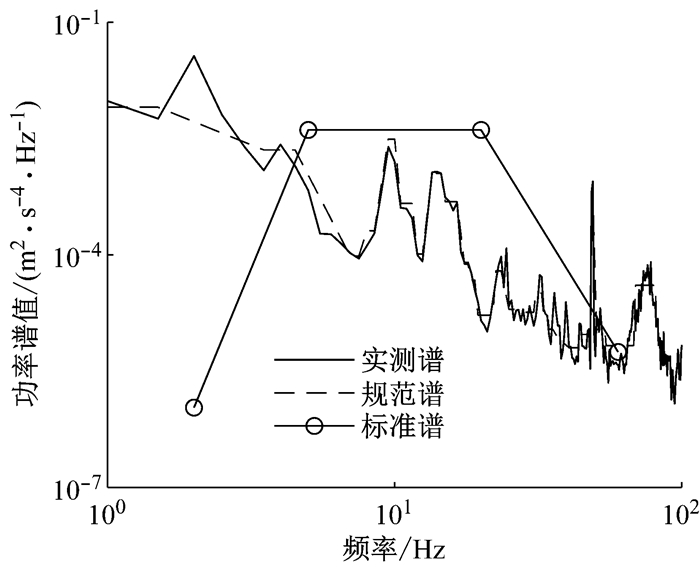
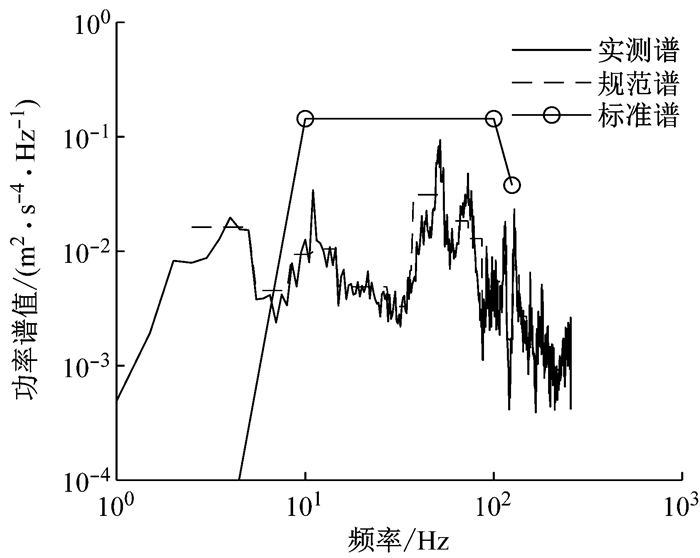
图 7和图 8分别显示了旧车车体横向和构架横向振动归纳谱.由图 7可知,旧车车体横向振动能量主要在10 Hz以内,低频振动十分明显并超过标准谱,反映了实测过程中低频晃车和舒适性的劣化.由图 8可知,旧车构架横向振动在低频部分超过标准谱,主要是在2 Hz到5 Hz有较大的振动谱值.在50 Hz频段附近,谱线出现峰值,并且与车体振动峰值是对应的.谱分析方法在不同实测部位的振动数据上均能使用,得出的结果基本符合实测现象,可以验证该方法具有处理轨道车辆振动实测环境的普适性.
|
图 7 旧车车体横向振动归纳谱 Fig.7 Induced spectrum of body's lateral vibration of old vehicle |
|
图 8 旧车构架横向振动归纳谱 Fig.8 Induced spectrum of frame's lateral vibration of old vehicle |
基于GJB/Z126-99军用标准,提出了适用于轨道车辆振动环境数据归纳的方法和流程.原方法计算的非正态样本上限偏小,并用Johnson法则对原方法进行了改进,使得上限值更接近实际.研究的数据归纳技术可用于非正态数据、多通道、不同部位和不同振动方向,具有更好的普适性和准确性.利用归纳得出的实测谱和规范谱,可对振动情况做出可靠和准确的判断.
| [1] |
丰志强, 阎楚良, 张书明. 飞机机载设备振动环境谱的数据处理与编制[J]. 航空学报, 2006, 27(1): 465 FENG Zhiqiang, YAN Chuliang, ZHANG Shuming. Data processing and compilation of vibration environmental spectrum for aircraft airborne equipment[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(1): 465 |
| [2] |
田永卫, 阎楚良, 张书明, 等. 飞机随机振动环境实测试验数据的归纳方法[J]. 振动、测试与诊断, 2014, 34(6): 1129 TIAN Yongwei, YAN Chuliang, ZHANG Shuming, et al. Inductive method of flight test data measured from aircraft random vibration environment[J]. Journal of Vibration, Measurement and Diagnosis, 2014, 34(6): 1129 DOI:10.3969/j.issn.1004-6801.2014.06.025 |
| [3] |
振动、冲击环境测量数据归纳方法: GJB/Z126-99[S].北京: 中国标准出版社, 1999. The inductive methods for environmental measured data of vibration and shock: GJB/Z126-99[S]. Beijing: Standards Press of China, 1999. |
| [4] |
International Electrotechnical Commission Technical Committee 9. Railway applications, rolling stock equipment-shock and vibration test: IEC 61373—2010[S]. Geneva: Standards Press of International Electrotechnical Commission, 2010.
|
| [5] |
丁杰, 张平, 王鹏. 机车车辆设备振动试验标准与实测数据的分析[J]. 机械工程学报, 2016, 52(22): 129 DING Jie, ZHANG Ping, WANG Peng. Analysis of vibration test standard and field measurement data for rolling stock equipment[J]. Journal of Mechanical Engineering, 2016, 52(22): 129 |
| [6] |
SLIFKER J F, SHAPIRO S S. The Johnson system: selection and parameter estimation[J]. Techno-metrics, 1980, 22(2): 239 DOI:10.1080/00401706.1980.10486139 |
| [7] |
罗敏, 姜同敏, 袁宏杰. 一种可靠性试验实测振动数据的处理方法[J]. 北京航空航天大学学报, 2007(10): 1237 LOU Min, JIANG Tongmin, YUAN Hongjie. Method for inducing reliability test measured vibration data[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007(10): 1237 DOI:10.3969/j.issn.1001-5965.2007.10.026 |
| [8] |
OWEN D B, LI H. The starship for point estimates and confidence intervals on a mean and for percentiles[J]. Communication in Satistic Simulation and Computation, 1998, 17: 325 |
| [9] |
谭炳麟. 随机振动数据的数字功率谱分析[J]. 上海交通大学学报:自然科学版, 1979(1): 93 TAN Binglin. The date digital spectral analysis in random vibration[J]. Journal of Shanghai Jiaotong University: Natural Science Edition, 1979(1): 93 |
| [10] |
姜兴渭, 石伟, 张跃民. 随机振动数据处理数字化方法研究[J]. 哈尔滨工业大学学报, 1985(3): 54 JIANG Xingwei, SHI Wei, ZHANG Yuemin. A study of the digitization method of data processing for random vibration[J]. Journal of Harbin Institute of Technology, 1985(3): 54 |
 2019, Vol. 47
2019, Vol. 47

