2. 上海城建市政工程(集团)有限公司,上海 200065
2. Shanghai Urban Construction Municipal Engineering (Group) Co., Ltd., Shanghai 200065, China
节段预制拼装混凝土桥梁已成为当前混凝土桥梁发展的重要方向.混凝土节段之间布置通长的预应力钢束,但不设置连续的抗剪分布钢筋,节段间剪力主要通过受压的接缝面上的剪力键来传递.因此,剪力键接缝面的受力性能和传力机理是节段预制拼装混凝土桥梁设计和施工的关键.国内外大量学者对接缝面抗剪承载力的影响因素和计算方法进行了深入研究[1-12].
根据美国AASHTO[1]规范,接缝面的抗剪承载力包括两个部分:一是剪力键提供的抗剪贡献,二是接触部分的混凝土提供的摩擦贡献.抗剪承载力计算式如下所示:
| $ V_{\mathrm{u}}=A_{\mathrm{k}} \sqrt{f_{\mathrm{ck}}}\left(0.2048 \sigma_{\mathrm{n}}+0.9961\right)+0.6 \mathrm{A}_{\mathrm{sm}} \sigma_{\mathrm{n}} $ | (1) |
式中:Ak为剪力键根部面积;Asm为接触部分的混凝土面积;fck为混凝土标准抗压强度;σn为接缝面平均压应力水平.从式(1)的表达形式上来看,剪力键提供的抗剪承载力是均匀分布在接缝面所有剪力键根部面积上的.这是因为式(1)是由单齿剪力键试件的荷载试验结果提出的回归公式[2],没有考虑接缝面上多齿剪力键中可能存在的剪应力分布不均匀现象.对于多齿剪力键接缝面,应用式(1)计算的抗剪承载力偏大[2-4].
已有研究表明,多齿剪力键中存在剪力分布不均匀现象[2, 4-6].Zhou等[2]基于试验结果提出, 应用AASHTO规范建议公式计算多齿剪力键接缝面抗剪承载力时应考虑强度折减系数,但未对该强度折减效应的机理以及折减系数的具体计算方法做进一步说明.Alcalde等[3]的数值分析结果表明,剪力键数量的增加导致接缝面抗剪承载力降低,并提出了抗剪承载力的回归公式.Jiang等[4]在试验中观察到,剪力键的布置形式对接缝面抗剪承载力也有影响,这一影响因素在之前的研究中未被考虑.
上述研究结果均表明,多齿剪力键存在剪应力分布不均匀现象,但对这一不均匀现象的理论解释十分匮乏.当节段预制拼装混凝土桥梁接缝面的抗剪承载力计算忽略剪应力的非均匀分布特征时,将使得抗剪承载力计算结果偏不安全.通过对单腹板剪力键接缝面的受力分析,建立接缝面上脱离体的受力平衡方程,对多齿剪力键根部剪应力分布规律进行研究,进而提出剪力键根部剪应力的计算方法.采用数值分析方法,对轴力剪力比、剪力键的数量及其分布形式进行了参数分析.
1 多齿剪力键剪应力分布理论分析 1.1 脱离体受力分析节段预制拼装混凝土桥梁通常采用箱型截面,多齿剪力键沿箱型截面腹板的高度方向布置.取箱型截面一个腹板厚度为dz的部分作为脱离体(见图 1),腹板宽度为b,单个剪力键在腹板宽度方向上通长布置.取左侧连续面中心处为原点,x轴取为截面宽度方向,y轴取为截面高度方向,z轴取为梁长方向.

|
图 1 腹板脱离体 Fig.1 Free body of web |
对剪力键从上至下进行排序,序号i=1, 2, …, N,N为剪力键数量.定义yi为第i个剪力键中心到截面中心的距离,hi为第i个剪力键根部高度,s为剪力键间距,如图 1所示.
取距离截面中心高度ys(见图 2)以上的部分为脱离体进行分析,坐标系沿用图 1中的定义.考虑到单个剪力键剪力分析中的整体化处理,ys的取值区间取为相邻剪力键之间,即ys∈[yi-hi/2, yi+1+hi/2].A*为脱离体左侧连续面的面积,Ai、τi分别为右侧剪力键根部的面积与剪应力,Asm、τsm分别为右侧混凝土面的面积与剪应力,σz为z方向正应力.
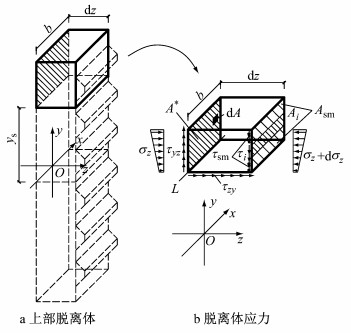
|
图 2 上部脱离体应力 Fig.2 Stress of upper free body |
引入以下基本假定:
(1) 接缝面全程受压,紧密贴合无脱离,接缝面左右侧纤维共同变形,满足平截面假定.
(2) 梁的上下层纤维间剪应力τzy均匀地分布在截面宽度b方向上.
(3) 剪力键根部剪应力τi均匀地分布在剪力键根部面积Ai上.
对脱离体的上部进行分析,取z方向受力平衡得
| $ \int_{A^{*}} \sigma_{z} \mathrm{d} A-\int_{A_{i}+A_{\mathrm{sm}}}\left(\sigma_{z}+\mathrm{d} \sigma_{z}\right) \mathrm{d} A+\tau_{z y} b \mathrm{d} z=0 $ |
代入
| $ \tau_{z y}=\frac{1}{b \mathrm{d} z} \frac{\mathrm{d} M_{x}}{I_{x}} S_{A^{*}}=\frac{Q}{I_{x} b} S_{A^{*}} $ | (2) |
式中:Q为截面上剪力;SA*为A*相对x轴的静矩,即材料力学Zhuravsky公式;Mx为截面上对x轴的弯矩;Ix为截面对x轴的惯性矩.
考虑脱离体弯矩平衡,取脱离体左下方的一条棱边L轴的弯矩平衡得
| $ \begin{array}{l} \sum {{M_L}} = \int_{{A^*}} {{\sigma _z}} \left( {y - {y_{\rm{s}}}} \right){\rm{d}}A + \int_{{A_i}} {{\tau _i}{\rm{d}}z{\rm{d}}A} + \\ \;\;\;\;\;\;\int_{{A_{\rm{m}}}} {{\tau _{{\rm{ma}}}}} {\rm{d}}z{\rm{d}}A - \int_{{A_i} + {A_{\rm{m}}}} {\left( {{\sigma _z} + {\rm{d}}{\sigma _z}} \right)} \left( {y - {y_{\rm{s}}}} \right){\rm{d}}A = \\ \;\;\;\;\;\sum {{\tau _i}} {A_i}{\rm{d}}z + \mu \left( {{\sigma _z} + {\rm{d}}{\sigma _z}} \right){\rm{d}}z{A_{{\rm{sm}}}} - \\ \;\;\;\;\;\;\frac{{{\rm{d}}{M_x}}}{{{I_x}}}\left( {{I_{{A^*}}} - {y_{\rm{s}}}{S_{{A^*}}}} \right) = 0 \end{array} $ |
式中:μ为剪力键间接触部分的混凝土表面摩擦系数;IA*为A*对x轴的惯性矩.忽略二阶小量μdσzdzAsm,有
| $ \sum {{\tau _i}} {A_i} = \frac{Q}{{{I_x}}}\left( {{I_{{A^*}}} - {y_{\rm{s}}}{S_{{A^*}}}} \right) - \mu {\sigma _z}{A_{{\mathop{\rm sm}\nolimits} }} $ | (3) |
式中:∑τiAi为脱离体前i个剪力键的合剪力.对于矩形截面腹板,式(3)可表达为
| $ \sum \tau_{i} A_{i}=f\left(\frac{2 y_{\mathrm{s}}}{h}\right) Q-\mu \sigma_{z} A_{\mathrm{sm}} $ | (4) |
其中,
| $ \sum \tau_{i} A_{i}=f\left(\frac{2 y_{\mathrm{s}}}{h}\right) Q $ | (5) |
当剪力键接缝面几何尺寸确定后,应用式(4)计算剪力键根部剪应力τi的唯一参数为脱离体上部距截面中心距离ys.ys可能的取值区间如图 3所示.偏保守考虑,推荐采用如图 3b所示ys上限取值.

|
图 3 ys取值区间 Fig.3 Value interval of ys |
当计算第i个剪力键根部剪应力时,采用以下几个步骤:
(1) 将ys=yi+1+hi/2代入式(4),得到前i个剪力键上合剪力∑τiAi.
(2) 将ys=yi+hi/2代入式(4),得到前(i-1)个剪力键上合剪力∑τi-1Ai-1.
(3) 两者相减得到第i个剪力键根部剪应力
| $ \tau_{i}=\frac{\sum \tau_{i} A_{i}-\sum \tau_{i-1} A_{i-1}}{A_{i}} $ | (6) |
在接缝面抗剪承载力计算中,光滑混凝土面上的摩擦力对抗剪承载力的贡献远小于剪力键的贡献,取摩擦系数为零进行简化计算.
(1) 典型的剪力键均匀分布的接缝面如图 4所示,其中A面为凸面,B面为凹面.
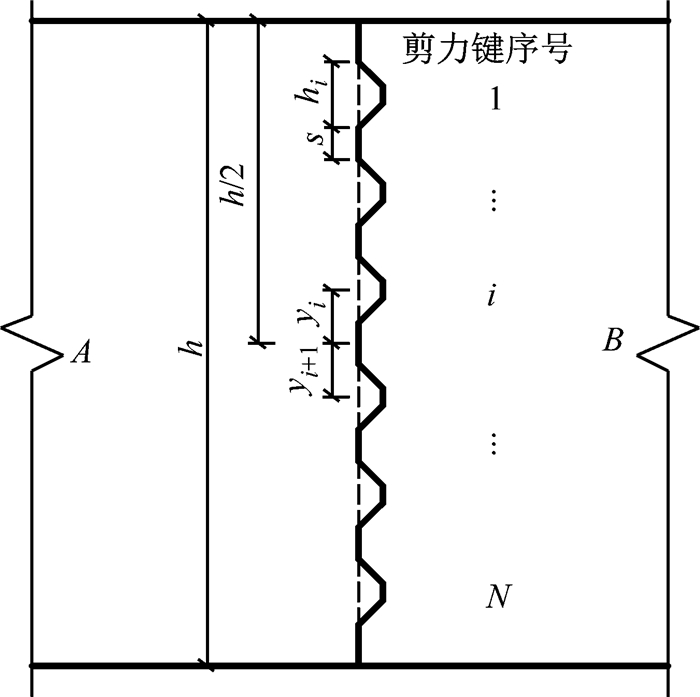
|
图 4 均匀分布剪力键的接缝面 Fig.4 Joint with uniformly distributed keys |
根据上述理论分析,剪应力最大值可能出现在最靠近接缝面中心处的剪力键根部,计算式如下所示:
| $ \left(\tau_{i}\right)_{\max }=\frac{Q}{b h_{i}}\left(f\left(\frac{2 y_{i+1}+h_{i}}{h}\right)-f\left(\frac{2 y_{i}+h_{i}}{h}\right)\right) $ |
剪力键根部剪应力的平均值
| $ \bar{\tau}=\frac{Q}{b \sum h_{i}} $ | (7) |
定义剪应力分布不均匀系数
| $ k=\frac{\left(\tau_{i}\right)_{\max }}{\bar{\tau}} $ | (8) |
对于剪力键均匀分布的接缝面,剪应力分布不均匀系数为
| $ \left\{ {\begin{array}{*{20}{l}} {k = N\left( {f\left( {\frac{{ - {h_i} - 2s}}{h}} \right) - f\left( {\frac{{{h_i}}}{h}} \right)} \right), N为奇数}\\ {k = N\left( {f\left( {\frac{{ - s}}{h}} \right) - f\left( {\frac{{2{y_i} + {h_i}}}{h}} \right)} \right), N为偶数} \end{array}} \right. $ | (9) |
(2) 典型的剪力键靠一侧分布的接缝面如图 5所示.
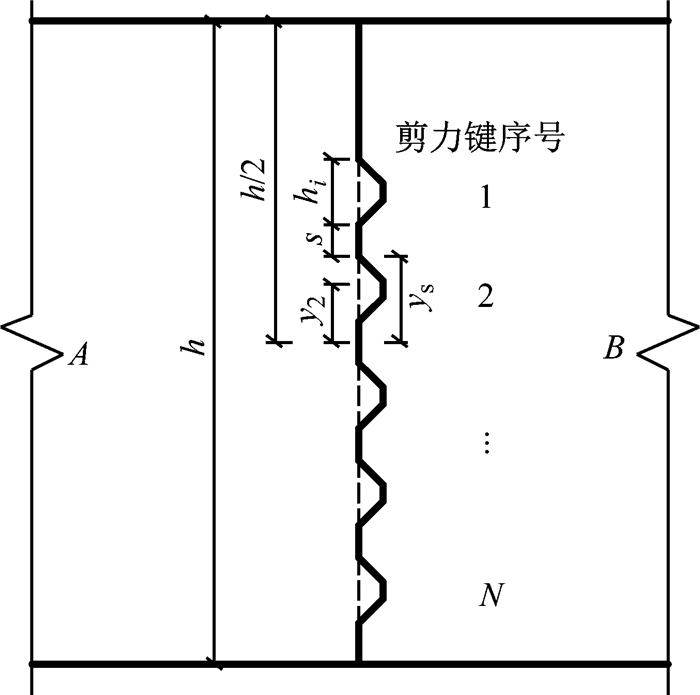
|
图 5 剪力键靠一侧分布的接缝面 Fig.5 Joint with non-uniformly distributed keys |
剪应力最大值可能出现在剪力键稀疏一侧的最边缘剪力键根部(如图 5所示的1号剪力键),计算式如下所示:
| $ \left(\tau_{i}\right)_{\max }=\frac{Q}{b h_{i}} f\left(\frac{2 y_{2}+h_{i}}{h}\right) $ |
剪应力分布不均匀系数
| $ k=N f\left(\frac{2 y_{2}+h_{i}}{h}\right) $ | (10) |
若剪力键靠上分布,则对剪力键从下至上进行编号.
(3) 分别计算(1)、(2)两种情况下的剪应力分布不均匀系数k,取较大值作为最终的剪应力分布不均匀系数k.
1.3 考虑剪应力不均匀分布的抗剪承载力(1) 施工阶段应力计算时,节段预制拼装混凝土桥梁剪力键接缝面上的剪应力应考虑剪力键中的剪应力不均匀分布效应.施工阶段剪力键中的剪应力峰值可表达为
| $ \tau=\bar{\tau}_{\max } $ | (11) |
式中:
(2) 运营阶段承载能力计算时,可沿用AASHTO规范建议公式并进行修正.考虑了剪应力分布不均匀系数修正后的抗剪承载力计算式可表达为
| $ V_{\mathrm{u}}=A_{\mathrm{k}} \frac{\sqrt{f_{\mathrm{ck}}}}{k}\left(0.2048 \sigma_{\mathrm{n}}+0.9961\right)+0.6 A_{\mathrm{sm}} \sigma_{\mathrm{n}} $ | (12) |
因k值反映了剪力键中剪应力的峰值效应,由此得到修正后的抗剪承载力为塑性下限解.
2 数值分析 2.1 分析参数及有限元模型以混凝土箱梁的单个多剪力键腹板作为研究对象,混凝土弹性模量为34.5 GPa,泊松比为0.2.腹板高度为3.0 m,宽度为0.5 m,固定端梁段与自由端梁段均长为6.0 m.在梁段间接缝面上设置剪力键,剪力键在宽度方向通长布置,厚度均为40 mm.在保证剪力键根部总面积不变的基础上调整剪力键的数量、根部高度及间距,布置形式分为均布与靠上、靠下分布,如表 1和图 6所示.
| 下载CSV 表 1 接缝面类型参数 Tab.1 Parameters of joint type |
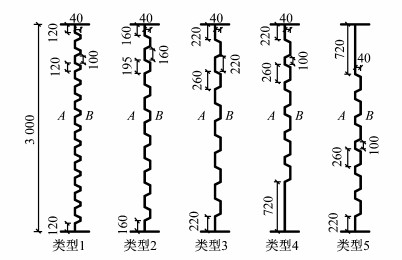
|
图 6 多剪力键接缝面几何参数(单位:mm) Fig.6 Geometries of multi-keyed joints(unit:mm) |
剪力由自由端梁段重力提供,通过给予不同的轴力P来模拟不同的轴力剪力比荷载工况.轴力P作用存在一定偏心,保证接缝面所受压力基本均匀,如表 2所示.
| 下载CSV 表 2 模型加载参数 Tab.2 Parameters of loading on models |
在通用有限元软件中建立三维实体有限元模型(见图 7).模型为两节段悬臂梁,悬臂梁总长6 m,每个悬臂节段长3 m.节段接缝位于悬臂梁跨中.网格划分尺度分为两部分:接缝的凹面和凸面附近100 mm深度内, 单元网格大小为20 mm;其余部分单元网格大小为200 mm.两种网格尺度之间采用绑定约束(tie-constraint)连接.接缝的凸面和凹面之间考虑硬接触(hard contact),摩擦系数取为零.

|
图 7 有限元模型(单位:mm) Fig.7 Finite element model(unit:mm) |
接缝面类型1~3的剪力键在接缝面上均布,剪力键数量分别为13、8、6个,加载类型1作用下数值模拟结果如图 8所示.剪应力分布符合抛物线规律,剪应力最大值在靠中间的剪力键根部;接缝面类型1、2、3的剪应力峰值分别为0.30、0.28、0.27 MPa,即剪力键数量越多,剪应力分布的“抛物线特性”越显著,剪力键根部剪应力峰值越大.
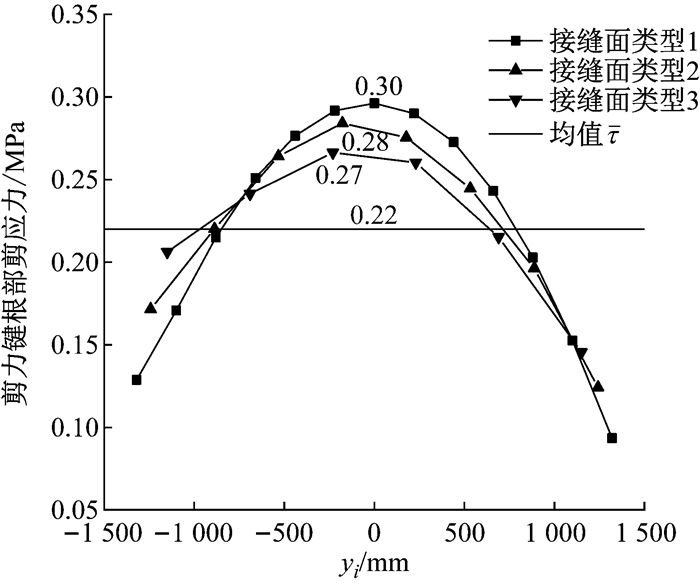
|
图 8 剪力键数量的影响 Fig.8 Effect of key's number |
理论分析所得剪应力峰值位置与数值模拟结果相一致,式(9)和式(10)中剪应力分布不均匀系数k与剪力键数量N成正比,能够反映剪力键数量的影响.
2.2.2 剪力键布置形式影响接缝面类型3、4、5剪力键数量均为6个,布置形式分别为均布及靠上、靠下分布,加载类型1作用下数值模拟结果如图 9所示.剪力键均布(接缝面类型3)的剪力键根部剪应力分布呈现出抛物线规律,峰值为0.27 MPa,出现在最靠中间的剪力键根部;剪力键靠一侧分布(接缝面类型4、5)的剪力键根部剪应力峰值分别为0.21 MPa、0.27 MPa,均出现在剪力键稀疏一侧的最边缘剪力键根部.

|
图 9 剪力键布置形式影响 Fig.9 Effect of keys' layout |
理论分析与数值模拟结果均表明,剪力键根部剪应力峰值可能出现在最靠近接缝面中心处的剪力键根部或者剪力键稀疏一侧的最边缘剪力键根部,故应用式(9)和式(10)计算两种情况下的剪应力分布不均匀系数k时,取较大值作为最终的剪应力分布不均匀系数k是有效的.
2.2.3 轴力剪力比影响如图 10所示,轴力剪力比对剪力键根部剪应力分布的影响较小,故剪应力分布不均匀系数k的计算式中不对轴力剪力比进行修正.
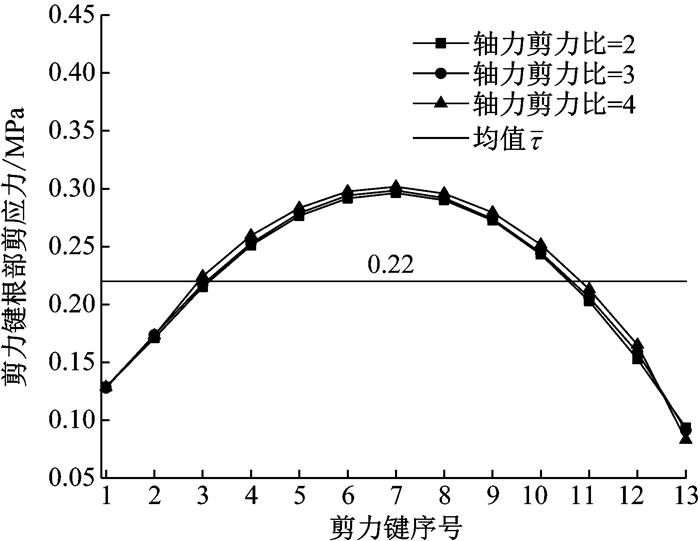
|
图 10 轴力剪力比影响 Fig.10 Effect of axial force to shear ratio |
以文献[4]中的三齿剪力键试件模型K3-01(见图 11)作为计算模型,将各文献计算所得抗剪承载力进行比较,如表 3所示.比较结果表明,AASHTO规范建议公式对三齿剪力键接缝面抗剪承载力的计算结果偏大,比试验结果大10%左右.Rombach[5]建议公式为
| $ V_{\mathrm{u}}=0.14 f_{\mathrm{c}} A_{\mathrm{k}}+0.65 \sigma_{\mathrm{n}} A_{\mathrm{joint}} $ | (13) |
| 下载CSV 表 3 抗剪承载力试验值和计算值对比 Tab.3 Comparison between experimental and calculated values of shear strength |
式中:fc为混凝土强度;Ajoint为截面总面积, Ajoint=Ak+Asm.文献[5]中公式计算的接缝面抗剪承载力比试验结果小20%,本研究提出的考虑剪应力分布不均匀系数的修正公式与试验结果误差在5%以内.
3.2 与Alcalde等[3]的有限元结果比较Alcalde等[3]以Zhou等[2]的试验模型为基础建立有限元模型(见图 12),取剪力键数量为主要参数,研究了从单齿到七齿剪力键接缝面的受力性能.通过对有限元结果进行系数回归给出了考虑剪力键数量影响的抗剪承载力计算公式,该公式仅适用于混凝土标准抗压强度为50 MPa、接缝面压应力水平为3 MPa的情况, 如下所示:
| $ \begin{aligned} V_{\mathrm{u}}=& 7.118 {A}_{\mathrm{k}}\left(1-0.064 N_{\mathrm{k}}\right)+\\ & 2.436 {A}_{\mathrm{sm}} \sigma_{\mathrm{n}}\left(1+0.127 N_{\mathrm{k}}\right) \end{aligned} $ | (14) |
式中:Nk为剪力键数量.以Alcalde等[3]的七齿剪力键有限元模型作为计算模型,将各文献计算所得抗剪承载力进行比较,如表 4所示.比较结果表明,AASHTO规范建议公式对七齿剪力键接缝面抗剪承载力的计算结果偏大,比有限元结果大35%左右.结合第3.1节中AASHTO规范建议公式,对三齿剪力键接缝面抗剪承载力的计算结果比试验结果大10%左右,说明当剪力键数量增多时,剪应力在剪力键中的不均匀分布效应更显著,剪应力不均匀分布效应对接缝面抗剪承载力的影响不可忽视.
| 下载CSV 表 4 抗剪承载力计算值对比 Tab.4 Comparison between calculated values of shear strengh |
文献[5]中公式计算所得接缝面抗剪承载力比试验结果大20%左右.结合第3.1节文献[5]中公式对三齿剪力键接缝面抗剪承载力的计算结果比试验结果小20%,说明文献[5]公式对于多齿剪力键接缝面抗剪承载力的计算误差较大且计算结果可能偏危险.本研究提出的考虑剪应力分布不均匀系数的修正公式与有限元结果误差在5%以内.该公式能够反映剪力键数量对抗剪承载力的影响,并且计算误差在5%以内.
4 结论(1) 通过对单腹板剪力键接缝面脱离体的受力分析,从理论上阐释了剪力键接缝面上剪应力不均匀分布的受力机理,提出了多齿剪力键接缝面上剪力键根部剪应力的计算方法以及考虑剪应力不均匀分布的抗剪承载力计算方法.
(2) 多剪力键接缝面剪应力及抗剪承载力的计算中均应考虑剪应力在剪力键中的不均匀分布效应.本研究采用剪应力分布不均匀系数k来反映剪力键中剪应力分布的峰值效应,并给出了k的简化计算方法.
(3) 通过数值分析方法,讨论了轴力剪力比、剪力键数量及剪力键分布形式对剪力键根部剪应力的影响.结果表明:剪力键数量增多会增加剪力键根部剪应力分布的不均匀程度,当剪力键靠一侧分布时,剪应力峰值由梁中心向剪力键稀疏侧转移,而轴力剪力比对剪应力分布的影响较小.所提出的剪应力分布计算公式可准确反映剪力键中剪应力的变化趋势和峰值效应.
(4) 将考虑剪应力不均匀分布的抗剪承载力计算结果分别与文献[4]的试验结果及文献[3]的有限元结果进行比较.结果表明:AASHTO规范建议公式对三齿剪力键接缝面抗剪承载力的计算结果比试验结果偏大10%左右,对七齿剪力键接缝面抗剪承载力的计算结果比有限元结果偏大35%左右;所提出的考虑了剪应力不均匀分布的修正公式对抗剪承载力的计算结果与试验、有限元结果相比,误差均在5%以内.
| [1] |
American Association of State Highway and Transportation Officials. Guide specifications for design and construction of segmental concrete bridges (1999)[S]. Washington DC: AASHTO, 1999.
|
| [2] |
ZHOU X, MICKLEBOROUGH N, LI Z. Shear strength of joints in precast concrete segmental bridges[J]. ACI Structural Journal, 2005, 102(1): 901 |
| [3] |
ALCALDE M, CIFUENTES H, MEDLINA F. Influence of the number of keys on the shear strength of post-tensioned dry joints[J]. Materiales de Construcción, 2013, 63: 297 DOI:10.3989/mc.2013.07611 |
| [4] |
JIANG H, CHEN L, MA Z J, et al. Shear behavior of dry joints with castellated keys in precast concrete segmental bridges[J]. Journal of Bridge Engineering, 2015, 20(2): 04014062 DOI:10.1061/(ASCE)BE.1943-5592.0000649 |
| [5] |
ROMBACH G A. Dry joint behavior of hollow box girder segmental bridges[C]//Proceedings of the FIP Symposium "Segmental Construction in Concrete". New Delhi: [s.n.], 2004: 1-8.
|
| [6] |
汪双炎. 悬臂拼装节段梁剪力键模型试验研究[J]. 铁道建筑, 1997(3): 23 WANG Shuangyan. Model test study on keyed joints of cantilever assembled segmental bridges[J]. Railway Architecture, 1997(3): 23 |
| [7] |
BUYUKOZTURK O, BAKHOUM MOURAD M, MICHAEL BEATTIE S. Shear behavior of joints in precast concrete segmental bridges[J]. Journal of Structural Engineering, 1990, 116(12): 3380 DOI:10.1061/(ASCE)0733-9445(1990)116:12(3380) |
| [8] |
TURMO J, RAMOS G, APARICIO A C, et al. Shear strength of match cast dry joints of precast concrete segmental bridges: proposal for Eurocode 2[J]. Materiales de Construcción, 2006, 56: 45 |
| [9] |
The International Federation for Structural Concrete. Model code for concrete structures (2010)[S]. Hoboken: Wiley, 2013.
|
| [10] |
SHAMASSS R, ZHOU X, ALFANO G. Finite-element analysis of shear-off failure of keyed dry joints in precast concrete segmental bridges[J]. Journal of Bridge Engineering, 2015, 20(6): 04014084 DOI:10.1061/(ASCE)BE.1943-5592.0000669 |
| [11] |
王景全, 刘桐旭, 王震. 考虑弯距影响的混凝土键齿接缝抗剪承载力计算方法[J]. 东南大学学报:自然科学版, 2017(3): 553 WANG Jingquan, LIU Tongxu, WANG Zhen. Calculation method for shear strength of concrete keyed joints considering bending effects[J]. Journal of Southeast University: Natural Science Edition, 2017(3): 553 |
| [12] |
DOVZHENKO O, POHRIBNYI V, KARABASH L. Experimental study on the multikeyed joints of concrete and reinforced concrete elements[J]. International Journal of Engineering and Technology, 2018, 7: 354 |
 2019, Vol. 47
2019, Vol. 47