为适应货运列车(以下简称列车)快速、重载的发展需求,急需对重载列车制动系统进行研究.传统的列车制动试验台无法适应多种制动性能,在进行不同种类列车的制动试验时,需要更换不同的制动阀.对于长大列车而言,拆卸并更换制动阀的工作量十分巨大,大大增加了新产品研发或出口列车产品试验实物成本以及周期.
国内外多个团队针对列车空气制动系统进行了研究并取得了一定的成果.文献[1]中建立了装有ABDW系列阀的仿真模型,并进行了制动特性模拟;文献[2]中建立了空气制动系统的仿真模型并对其进行了研究;文献[3-6]中根据试验台的试验结果建立了气动模型,并结合算法对空气制动系统进行了研究;文献[7-8]中运用AMESim软件对城轨列车制动系统进行了分析;文献[9]中对F8型空气制动机进行了制动性能分析,研究了阀内参数对制动性能的影响;文献[10]中通过半实物半仿真系统对列车制动系统进行了分析,但没有对再充气特性进行分析.
建立智能化仿真试验平台的目标是结合少量制动机试验, 验证计算机控制的可真实模拟列车空气制动系统的虚拟试验系统.核心的制动过程模型研究,分成气管路对缸体、气室与缸体以及多气室缸体之间等气动方程特性分析和解算,偏微分方程的气动方程大多采用特征线法[3],无法实现虚拟试验系统的实时控制及制动试验的实现.再充气过程是非常典型的多气室缸体之间流体的传递过程,如能解决这种复杂结构建模的各种难点,建立反映再充气工况的数学模型,对实际的制动机控制模拟具有重要意义.因此,从气体流动连续方程入手,建立再充气工况的数学模型,并讨论再充气缓解特性.最后,对150辆编组列车不同位置处的再充气特性和列车管与制动缸作用时间进行分析.
1 再充气缓解工况仿真模型的建立 1.1 再充气缓解工况为了解除制动系统对列车施加的与列车运行相反的阻力,列车风源系统通过列车管再次向储存一部分空气的列车管、副风缸等充气的过程称为“再充气缓解”.再充气缓解工况下,各关联缸室间压力流动情况及平衡关系与初充气工况基本一致.再充气缓解使列车管、副风缸压力再次恢复至定压p0,而制动缸则排大气以达到缓解列车制动的作用.
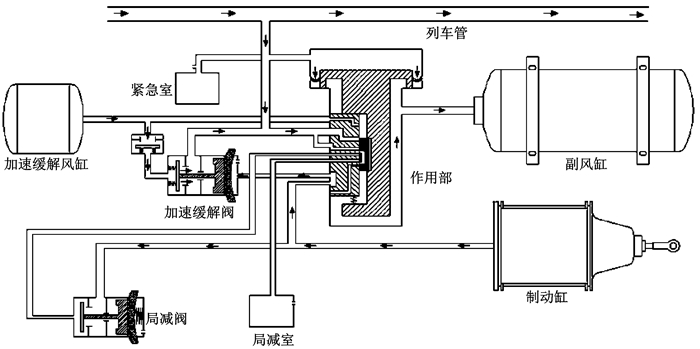
“再充气缓解”是加速缓解风缸对列车管的局部增压.列车再充气缓解时,首先让制动缸里的空气打开加速缓解风缸向列车管逆流的充气通路,然后排入大气.初充气工况下,加速缓解风缸与列车管的压力相同;制动时,加速缓解风缸由于止回阀的作用空气不能逆流回副风缸而保持压力恒定.列车管在制动过程中排气使得列车管压力降低,导致列车管压力低于加速缓解风缸压力.当制动系统再充气缓解时,两者的压力差使得加速缓解风缸内空气可以通过加速缓解阀逆流到列车管,形成对列车管的局部增压作用.加速缓解作用提高了后部车辆制动系统列车管的增压速度,从而缩短了再充气缓解的时间.再充气缓解简化模型如图 1所示.
|
图 1 再充气缓解模型 Fig.1 Re-inflation mitigation model |
列车的120型空气制动阀属于气动阀,阀路之间的信号主要靠空气进行传递.由于制动管路和缸室与外界散热良好,压力与体积变化可以视为等温过程,气体状态方程都是适用的.完全气体状态方程为
| $ p V=m R T $ | (1) |
式中:p为绝对压强;V为体积;m为质量;R为气体常数,R=287 N·m·(kg·K)-1;T为热力学温度.
在dt时间内,充入容器内的气体质量
| $ \mathrm{d} m_{2}=-q_{m_{2}} \mathrm{d} t $ | (2) |
式中:qm1是单位时间内进气回路流入的质量流量.
在dt时间内,从容器内放出的气体质量
| $ \mathrm{d} m_{2}=-q_{m_{2}} \mathrm{d} t $ | (3) |
式中:qm2为单位时间内排气回路流出的质量流量.
质量流量qm1和qm2的大小与气动回路中的流动状态有关.当回路处于亚声速流动时,回路中通过的气体质量流量[11]
| $ q_{m}=q_{m}^{*} \sqrt{1-\left(\frac{p_{2} / p_{1}-b}{1-b}\right)^{2}}, 1 \geqslant \frac{p_{2}}{p_{1}}>b $ | (4) |
式中:qm*为节流孔质量流量最大值,qm*=0.04(p1/
亚声速流动时,气体的质量流量
| $ q_{m}=0.04 S \frac{p_{1}}{\sqrt{T}} \sqrt{1-\left(\frac{p_{2} / p_{1}-b}{1-b}\right)^{2}}, 1 \geqslant \frac{p_{2}}{p_{1}}>b $ | (5) |
式中:S为修正系数.
缓解时,制动缸内的空气排入大气,松开闸瓦或制动夹钳,以达到缓解效果.实际再充气状态时制动缸容积不断变化,推导出的偏微分方程难以进行实时仿真计算.因此,将制动缸充放气预先视为定容积容器充放气,通过气容放气特性来近似模拟制动缸排气特性,其误差通过S修正.
在制动缸缓解时,将制动缸模型简化为如图 2所示的模型.图 2中,左边表示初始压力为pz的制动缸等效风缸,右边表示标准大气压pa下的大气,制动缸容积为Vz,制动缸排气的复杂通路简化为一个等效的节流孔.

|
图 2 制动缸放气简化模型 Fig.2 Simplified model of brake cylinder venting |
将式(1)代入式(3)可得
| $ q_{m}=-\frac{\mathrm{d} m}{\mathrm{d} t}=-\frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{p_{{\rm z}} V_{{\rm z}}}{R T}\right)=-\frac{V_{{\rm z}}}{R T} \frac{\mathrm{d} p_{{\rm z}}}{\mathrm{d} t} $ | (6) |
制动缸初始压力与常用制动时列车管减压量r有关,pz0=(Vf/Vz)r-100(绝对压力为(Vf/Vz)r,其中Vf为副风缸容积).再充气过程开始,风源系统缓慢向列车管充气,主活塞在两侧压力差作用下移动至再充气及缓解位,历时t1,制动缸才开始缓解.
当列车管开始再充气,主活塞还未移至再充气及缓解位时,制动缸保持初始压力不变,即t≤t1时,pz=pz0=(Vf/Vz)r-100.当该辆车开始缓解时,制动缸向大气排气,即t>t1时,制动缸开始减压.由于制动缸内可达到的最大绝对压力不超过500 kPa,根据声速与亚声速流动的判定条件,制动缸缓解过程为亚声速放气过程.
当放气过程为亚声速放气过程时,即1≥pa/pz>b时,消去式(5)和(6)中的qm,经积分运算后,由pz0降至pz所需的放气时间
| $ t=\frac{1.4603 V_{z}(1-b)}{S \sqrt{1-2 b} \sqrt{R T}}\left(\ln \left(\frac{\sqrt{\left(1-\frac{p_{\mathrm{a}}}{p_{\mathrm{z} 0}}\right)\left(1-2 b+\frac{p_{\mathrm{a}}}{p_{\mathrm{z0}}}\right)}+\sqrt{1-2 b}}{p_{\mathrm{a}} / p}+\frac{b}{\sqrt{1-2 b}}\right)-\right.\\ ~~~~~\left. {\ln \left( {\frac{{\sqrt {\left( {1 - \frac{{{p_{\rm{a}}}}}{{{p_{\rm{z}}}}}} \right)\left( {1 - 2b + \frac{{{p_{\rm{a}}}}}{{{p_{\rm{z}}}}}} \right)} + \sqrt {1 - 2b} }}{{{p_{\rm{a}}}/{p_{\rm{z}}}}} + \frac{b}{{\sqrt {1 - 2b} }}} \right)} \right) $ | (7) |
由式(7)倒推可知,在容器放气时,容器内的压力随时间变化的关系式为
| $ {p_{\rm{z}}} = \frac{{2{p_{\rm{a}}}}}{{\sqrt {\frac{{A_1^2}}{{{{\rm{e}}^{2{A_2}\left( {t - {t_1}} \right)}}}} - 1.3164\frac{{{A_1}}}{{{{\rm{e}}^{{A_2}\left( {t - {t_1}} \right)}}}} + 5.93162} - \frac{{{A_1}}}{{{{\rm{e}}^{{A_2}\left( {t - {t_1}} \right)}}}} + 0.658}} $ | (8) |
其中,
| $ \begin{aligned} A_{1}=& \frac{\sqrt{\left(1-\frac{p_{{\rm a}}}{p_{{\rm z} 0}}\right)\left(0.6+\frac{p_{{\rm a}}}{p_{{\rm z} 0}}\right)}+0.7746}{p_{\mathrm{a}} / p_{{\rm z0}}}+\\ & 0.2582 \\ A_{2}=& \frac{S \sqrt{T}}{8.9026 \times 10^{-2} V_{{\rm z}}} \end{aligned} $ |
再充气过程中,列车管的空气除了来自风源系统外,还来自加速缓解风缸,即列车管“局部增压”,目的在于加速列车的缓解作用,提高缓解波速.
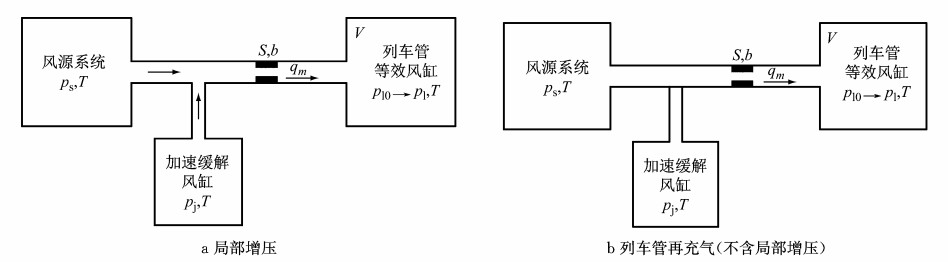
再充气过程开始,风源系统缓慢向列车管充气,主活塞在两侧压力差作用下移动至再充气及缓解位,历时t1,于是制动缸开始缓解.加速缓解风缸中的空气进入列车管,使得列车管内压力在短时间内有一个明显的跃升,“局部增压”作用时间很短,设置该时间为t2.此后, 列车管空气主要来自风源系统.将列车管再充气及局部增压模型简化为如图 3所示的模型.通过气容充气特性来近似模拟列车管等效风缸的充气特性,误差通过S修正.图 3a表示列车管局部增压时风源系统和加速缓解风缸同时向列车管充气的简化模型,图 3b表示列车管局部增压作用结束后风源系统向列车管充气的简化模型.列车管再充气时的复杂通路初步简化为一个等效的节流孔.
|
图 3 列车管再充气简化模型 Fig.3 Simplified model of train tube refilling |
将式(1)代入式(2)可得
| $ q_{m}=\frac{\mathrm{d} m}{\mathrm{d} t}=\frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{p_{2} V}{R T}\right)=\frac{V}{R T} \frac{\mathrm{d} p_{2}}{\mathrm{d} t} $ | (9) |
当充气过程为1 ≥ p2/p1>b时,即亚声速充气时,消去式(5)和(9)中的qm,经积分运算后,由pz0充至pz所需的充气时间
| $ t=\frac{1.4603 V(1-b)}{S \sqrt{R T}}\left(\sin ^{-1}\left(\frac{p_{2} / p_{1}-b}{1-b}\right)-\sin ^{-1}\left(\frac{p_{{\rm z0}} / p_{1}-b}{1-b}\right)\right) $ | (10) |
由式(10)倒推可知,在向容器充气时,容器内的压力随时间变化的关系式为
| $ p_{2}=p_{1}\left(\begin{array}{c}{\left.(1-b) \arcsin \frac{1.4603 V(1-b)}{S \sqrt{R T }t-1.4603 V(1-b) \sin ^{-1}\left(\frac{p_{{\rm 00}} / p_{1}-b}{1-b}\right)}+b\right)}\end{array}\right. $ | (11) |
列车管容积
| $ V = \frac{{{\rm{ \mathsf{ π} }}D_1^2}}{4}N{L_1} + \frac{{{\rm{ \mathsf{ π} }}D_2^2}}{4}N{L_2} $ | (12) |
式中:D1为列车管主管直径;D2为列车管支管直径;N为车辆位置;L1为单车列车管主管长度;L2为单车列车管支管长度.
在制动缸缓解之前,风源系统就开始向列车管再充气,即t < t1时,根据声速与亚声速流动的判定条件,此时列车管再充气过程为亚声速充气过程.由式(11)可知,列车管内压力pl随时间t的变化为
| $ {p_1} = {p_{\rm{s}}}\left( {0.8\arcsin \frac{{{\rm{ \mathsf{ π} }}{D^2}NL}}{{58.0055S\sqrt T t - {\rm{ \mathsf{ π} }}{D^2}NL{{\sin }^{ - 1}}\left( {\frac{{{p_{{\rm l}0}}}}{{0.8{p_{\rm{s}}}}} - 0.25} \right)}} + 0.2} \right) $ | (13) |
式中:pl0为列车管初始压力;ps为风源压力;D为列车管直径;L为列车管长度.
在制动缸缓解的同时,加速缓解风缸开始向列车管充气,即t1≤t≤ t1+t2时.根据声速与亚声速流动的判定条件,此时列车管再充气过程是亚声速充气过程.列车管局部增压作用开始时的压力为pl1,即t=t1时pl的值.由式(11)可知,列车管内压力pl随时间t的变化为
| $ \begin{array}{l} {p_1} = \left( {{p_{\rm{s}}} + {p_{\rm{j}}}} \right)\\ \left( {\begin{array}{*{20}{c}} {0.8\arcsin }&{\frac{{{\rm{ \mathsf{ π} }}{D^2}NL}}{{58.0055S\sqrt T \left( {t - {t_1}} \right) - {\rm{ \mathsf{ π} }}{D^2}NL{{\sin }^{ - 1}}\left( {\frac{{{p_{{\rm{l}}1}}}}{{0.8\left( {{p_{\rm{s}}} + {p_{\rm{j}}}} \right)}} - 0.25} \right)}} + 0.2} \end{array}} \right) \end{array} $ | (14) |
式中:加速缓解风缸压力为pj.
当加速缓解作用结束时,列车管空气依旧主要来自风源系统充气,即t>t1+t2时.根据声速与亚声速流动的判定条件,此时列车管再充气过程为亚声速充气过程,并且加速缓解作用结束时列车管的压力为pl2,即t=t1+t2时pl的值.由式(11)可知,列车管内压力pl随时间t的变化为
| $ \begin{array}{l} {p_1} = {p_{\rm{s}}}\\ \left( {0.8\arcsin \frac{{{\rm{ \mathsf{ π} }}{D^2}NL}}{{58.0055S\sqrt T \left( {t - \left( {{t_1} + {t_2}} \right)} \right) - {\rm{ \mathsf{ π} }}{D^2}NL{{\sin }^{ - 1}}\left( {\frac{{{p_{{\rm{l}}2}}}}{{0.8{p_{\rm{s}}}}} - 0.25} \right)}} + 0.2} \right) \end{array} $ | (15) |
与“制动波速”不同,国内还没有对“缓解波速”有过明确定义.依据与制动波速相同的定义方法[11],将缓解波速定义为单位时间内缓解波沿列车管的传播长度.与制动波速一样,缓解波速可以用试验的方法进行测定,计算式如下所示:
| $ W_{\mathrm{a}}=\frac{L_{\mathrm{HB}}}{t_{\mathrm{HB}}}=\frac{L_{\mathrm{HB}}}{\left(t_{\mathrm{e}}-t_{\mathrm{s}}\right)} $ | (16) |
式中:Wa为平均缓解波速,m·s-1;LHB为缓解波传播距离,m,可取为机车后第一辆车与最后一辆车之间的列车管长度;tHB为缓解波传播时间,s,当风源系统经机车自动制动阀排气时,从列车管开始充气到最后一个制动缸压力开始降低为止;ts为机车后第一辆车列车管开始增压时间,s;te为机车最后一辆车制动缸开始减压时间,s.
2 单车模型仿真与试验图 4为智能化仿真试验平台,运用该智能化仿真试验平台测试单车和150辆编组列车不同位置处车辆实际制动效果.

|
图 4 智能化仿真试验平台 Fig.4 Intelligent simulation test platform |
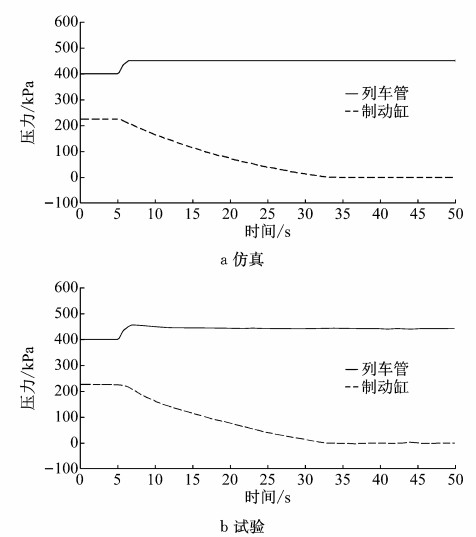
再充气缓解仿真曲线与试验曲线如图 5所示.
|
图 5 再充气缓解曲线 Fig.5 Re-inflation relief curve |
制动缸缓解前保压5.20 s,制动缸从225 kPa完全缓解需要27.71 s,总用时32.91 s.列车管压力曲线出现了一次明显的跃升,加速缓解风缸对列车管具有明显的局部增压作用.再充气缓解工况的仿真结果和试验数据吻合,仿真的准确性得到了验证.
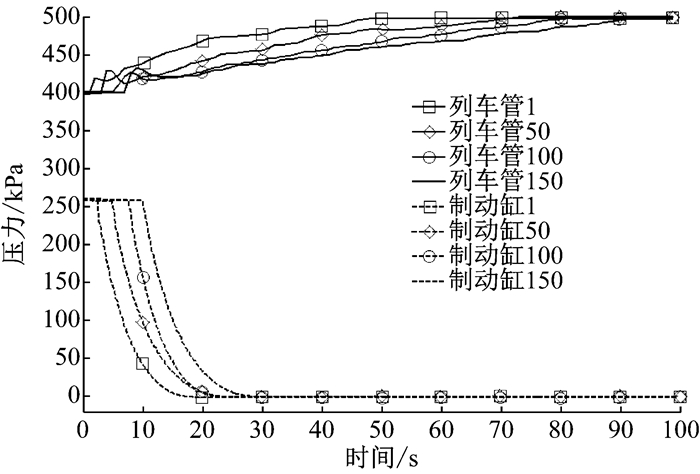
3 150辆编组列车模型仿真分析为了研究列车在再充气缓解工况下不同车辆的缓解特性,常用制动减压70、100、140 kPa后进行再充气缓解试验,其中减压100 kPa后的试验曲线如图 6所示.
|
图 6 不同位置处车辆列车管与制动缸压力试验曲线 Fig.6 Pressure curve of vehicle train pipe and brake cylinder at different positions |
从图 6可以看出:
(1) 第1、50、100、150辆车列车管开始增压的时间分别为1.0、3.2、5.5、7.6 s,基本呈均匀分布,说明缓解工况下空气波在列车管内具有均匀传播的特性.
(2) 各个位置处车辆制动缸开始减压时间比相同位置处列车管开始增压时间略晚.四个位置处车辆制动缸与列车管作用时间差约为1.2、1.7、2.0、2.2 s,这是由于120阀主活塞两侧需要一定的压力差才能发生规定的动作.
(3) 第1、50、100、150辆车列车管达到系统平衡压力的时间分别约为48、69、82、91 s.造成这种现象的根本原因是制动系统列车管内壁、折角塞门及连接软管的阻尼使得空气波沿着列车车长方向能量越来越弱,导致由前至后列车管增压速度越来越慢.
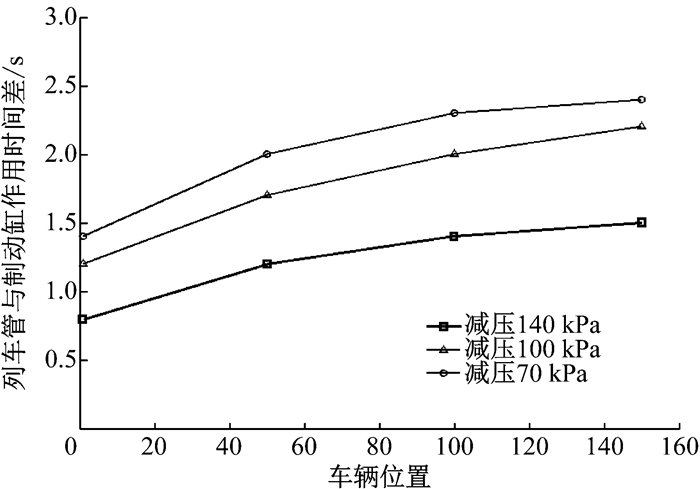
图 7为列车管减压70、100、140 kPa后再充气缓解工况下,第1、50、100、150辆车列车管与制动缸作用时间差的试验结果.
|
图 7 不同位置处车辆列车管与制动缸作用时间差 Fig.7 Time difference of vehicle train pipe and brake cylinder at different positions |
在相同的减压条件下,随着车辆位置后移,列车管与制动缸作用时间差逐渐增加,但增加的幅度越来越小;相同位置处车辆作用时间差随着列车管减压量的增加而逐渐减小.列车管与制动缸作用时间差的存在,说明缓解波在制动系统内不是均匀传播的,当减压量一定时,具有先慢后快的传播特性.
4 结语结合制动机在再充气缓解工况下的工作原理,分析列车制动机在再充气工况下的工作过程,推导气体状态方程,建立列车制动系统再充气缓解工况的数学模型.
利用智能化仿真试验平台进行再充气缓解工况试验,试验所得曲线与仿真曲线基本吻合,再充气缓解数学模型能准确地模拟再充气缓解过程.
结合模型和试验,得到150辆编组列车首车和尾车的再充气缓解过程特征,并测试出不同位置处车辆列车管与制动缸的作用时间差.
| [1] |
MURTAZA M A. Railway air brake simulation: an empirical approach[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 51 DOI:10.1243/PIME_PROC_1993_207_226_02 |
| [2] |
BELFORTE G, CARELLO M, FERRARESI C, et al. Modelling and identification methodology of components for train braking systems[C]//Fluid Power Conference. Dresden: IFK, 2008: 393-405.
|
| [3] |
魏伟. 120阀及试验台的计算机模拟[J]. 铁道学报, 2000, 22(1): 31 WEI Wei. Computer simulation of 120 valve and test bench[J]. Journal of the China Railway Society, 2000, 22(1): 31 DOI:10.3321/j.issn:1001-8360.2000.01.007 |
| [4] |
胡杨, 魏伟, 张渊. 机车编组方式对列车再充气特性的影响[J]. 交通运输工程学报, 2017, 17(3): 111 HU Yang, WEI Wei, ZHANG Yuan. Influence of locomotive grouping method on train re-inflation characteristics[J]. Journal of Traffic and Transportation Engineering, 2017, 17(3): 111 DOI:10.3969/j.issn.1671-1637.2017.03.012 |
| [5] |
魏伟, 李文辉. 列车空气制动系统数值仿真[J]. 铁道学报, 2003, 25(1): 38 WEI Wei, LI Wenhui. Numerical simulation of train air braking system[J]. Journal of the China Railway Society, 2003, 25(1): 38 DOI:10.3321/j.issn:1001-8360.2003.01.008 |
| [6] |
刘金朝, 王成国, 马大炜, 等. 长大列车空气管系充气特性数值仿真研究[J]. 中国铁道科学, 2004(1): 14 LIU Jinchao, WANG Chengguo, MA Dawei, et al. Numerical simulation study on inflating characteristics of air trains in long trains[J]. China Railway Science, 2004(1): 14 |
| [7] |
杨璨.货运列车制动系统的建模及仿真研究[D].成都: 西南交通大学, 2010. YANG Can.Modeling and simulation of freight train braking system[D]. Chengdu: Southwest Jiaotong University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10613-2010122576.htm |
| [8] |
BHARATH S, NAKRA B C, GUPTA K N. Modeling and analysis of railway brake system[J]. Journal of the Institution of Engineers, 1989, 70(5): 12 |
| [9] |
刁亮. F8阀列车空气制动系统数值仿真[D].大连: 大连交通大学, 2007. DIAO Liang. Numerical simulation of air brake system for F8 valve train [D]. Dalian: Dalian Jiaotong University, 2007. http://cdmd.cnki.com.cn/article/cdmd-10150-2007213230.htm |
| [10] |
应之丁, 高伟航, 顾灵燕. 基于气动系统流体方程的货车制动性能分析[J]. 铁道学报, 2017, 39(11): 59 YING Zhiding, GAO Weihang, GU Lingyan. Analysis of truck braking performance based on fluid equation of pneumatic system[J]. Journal of the China Railway Society, 2017, 39(11): 59 DOI:10.3969/j.issn.1001-8360.2017.11.009 |
| [11] |
卡洛瓦茨基 B P. 自动制动抽基本理论[M]. 北京: 人民铁道出版社, 1959 KALOVATZJI B P. Automatic brake pumping basic theory[M]. Beijing: People's Railway Publishing House, 1959 |
 2019, Vol. 47
2019, Vol. 47

