2. 国家机动车产品质量监督检验中心(上海), 上海 201805
2. National Center of Supervision and Inspection on Motor Vehicle Products Quality (Shanghai), Shanghai 201805, China
研究紧急工况下的驾驶员行为是开发先进驾驶辅助系统(advanced driver assistant systems, ADAS)的前提.在紧急工况下驾驶员存在制动和转向两种避撞行为[1], 相对于制动避撞, 紧急转向变道避撞在高相对速度、低附着系数、低重叠率等工况下所需的纵向距离更小, 避撞效能更高[2-4]; 但紧急转向变道是驾驶员容易操作失误, 引发交通事故的一种驾驶行为.目前国际上已经开始了对紧急转向变道技术的研究[1-5], 但如何准确分析真实驾驶员的紧急转向变道行为特征, 并建立相应的驾驶员模型, 是目前开发紧急转向避撞系统的难点.
紧急工况下的驾驶员转向模型往往是基于经典控制或现代控制理论建立的, 通过简化驾驶员转向操作或预瞄最优变道路径来实现转向控制.简化的驾驶员转向模型有利于快速得到驾驶员的紧急转向避撞轨迹和驾驶员操纵特征, 典型的简化方法如Lee等[6]、Chovan等[7]、Bascunana[8]都是用正弦函数对驾驶员紧急转向进行建模; Nelson[9]则是用多项式对驾驶员的紧急转向进行建模.上述的简化模型过于理想化, 无法很好地复原驾驶员的紧急转向特征, 有一定的局限性.
大量的研究表明, 驾驶员在转向过程中采用目标点的视觉导向来进行转向控制.根据国外学者[10]的研究, 驾驶员在转向过程中通过预瞄车辆前方的近点区域(near point)和远点区域(far point)来控制车辆的运动; Salvucci等[11-12]利用远近两个目标点的视觉导向建立了驾驶员转向模型.上述驾驶员模型能很好地表现驾驶员的转向机理, 但仅适用于正常驾驶工况, 并未开展对紧急转向工况模型建立的研究.
为了建立更加符合实际驾驶员紧急转向特征的变道模型, 本文利用中国自然驾驶数据中的紧急转向变道工况, 提出了驾驶员紧急转向变道驾驶侧向运动轨迹的规划方法.基于此, 利用远、近目标点的转向理论, 建立了紧急转向变道工况的驾驶员转向模型.研究表明, 所建立的驾驶员转向模型能较好地复现驾驶员紧急转向变道行为.
1 自然驾驶数据的采集和筛选为了研究驾驶员在真实交通环境中的驾驶行为, 本文所使用的数据全部来自中国大型实车路试(China field operational test, China-FOT)的自然驾驶工况数据.自然驾驶数据包含:① CAN(controller area network, 控制器局域网络)总线数据; ②外接传感器, 包括独立加速度传感器, 用于保证数据的完整性和准确性; ③摄像头数据, 分别为前置摄像头、前置广角摄像头、车内驾驶员面部摄像头、踏板摄像头(图 1).数据采集从人、车、路3个方面出发, 采集驾驶员日常驾驶行为数据、车辆行驶运动状态参数和道路交通环境信息.项目采集了32名驾驶员的驾驶数据, 共计约3 559 h, 总行程129 109 km.

|
图 1 自然驾驶工况采集中的摄像头视角 Fig.1 Imaging view of cameras in naturalistic driving data |
在紧急转向变道工况中驾驶员的方向盘转速和碰撞时间(time to collision, TTC)值是衡量变道过程是否紧急的重要因素[13-14].当TTC小于2 s, 且两车相对速度大于30 km·h-1时, 驾驶员更易用转向变道的方式来避免碰撞的发生, 并伴随较大的方向盘转速[15-16].本文参考国外研究, 将最大方向盘转速
在本文的研究中将危险场景的行车环境定义为驾驶危险域, 驾驶危险域分为主观危险域、物理极限危险域以及碰撞减轻域.China-FOT自然驾驶数据中采集到50例紧急转向危险场景, 都属于主观危险域的行车环境(未发生碰撞), 主观危险域为大部分驾驶员可通过紧急制动和紧急转向来避免碰撞发生的区域; 物理极限危险域为一般驾驶员无法避免碰撞区域, 需要通过车辆的紧急控制来避免碰撞的发生; 碰撞减轻区域为碰撞无法避免, 只能通过车辆控制减轻碰撞的程度.
2 驾驶员紧急变道侧向轨迹模型人体行为学研究表明:一般情况下人类在进行运动路径的规划时都遵循最优控制原则, 保证运动路径的平顺性[18].但在紧急变道过程的路径轨迹中, 驾驶员不仅要考虑轨迹平顺性的要求, 同时还要考虑与前车避撞的约束条件.本文研究在短时间内紧急转向变道的路径规划, 引入碰撞时间TTC, 采用最优控制方法来建立紧急变道侧向轨迹模型.
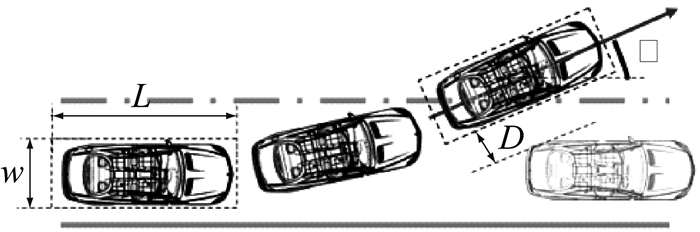
不失一般性, 以图 2向左转向避撞的变道工况为例, 将两车视作相同的矩形, 车辆长L=5.2 m, 宽w=2.0 m, 重叠率为100%.对车辆进行简化处理, 质心到前轴的距离Lf=2.5 m, 到后轴距离为Lr=2.7 m.图中, D为距离, φ为航向角.
|
图 2 紧急转向避撞示意图 Fig.2 Collision avoidance by steering |
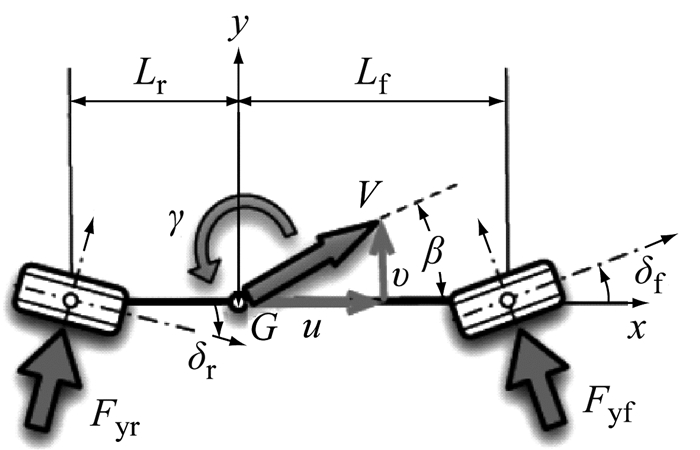
考虑到车辆侧向位移的复杂性, 同时为了获取更准确的计算结果, 选取二自由度单轨车辆模型如图 3所示.图中, 质心侧偏角β和横摆角速度γ为状态变量, V为车辆行驶速度, v、u分别为车辆侧向、纵向速度.
|
图 3 二自由度单轨车辆模型 Fig.3 Model of two-degree-of-freedom single track vehicle |
通过自然驾驶数据分析表明, 驾驶员在紧急转向变道过程中车速变化量很小, 故在模型中选取恒定车速v0, 即不考虑在转向过程中驾驶员纵向操纵的影响.车辆状态方程可表达为
| $ \begin{array}{l} m{v_0}(\dot \beta (t) + \gamma (t)) = {F_{y{\rm{f}}}}(t) + {F_{y{\rm{r}}}}(t)\\ \;\;\;\;{I_z}\dot \gamma (t) = {L_{\rm{f}}}{F_{\mathit{y}{\rm{f}}}}(t) - {L_{\rm{r}}}{F_{y{\rm{r}}}}(t) \end{array} $ | (1) |
式中:m为车辆的质量; Iz为车辆绕z轴的转动惯量; Fyf和Fyr分别表示左、右两个前轮、后轮的轮胎力在车辆坐标系下的分量, 在此假设左、右两个轮胎力相等.
采用Pacejka轮胎模型, 将车辆坐标系变量转换到大地坐标系, 得到非线性单轨车辆模型为
| $ \dot \xi (t) = f(\xi (t), U(t)) $ | (2) |
式中:ξ=[β, γ, φ, X, Y, δf]; X, Y, φ分别为车辆在大地坐标系中沿x轴的位置、沿y轴的位置以及航向角; δf为驾驶员方向盘转角.输入
避免与前方障碍物发生碰撞, 车辆质心在大地坐标系中坐标为(X, Y), 航向角为φ, 图 2中右前顶点坐标(xLf, yLf)可表述为
| $ \left\{\begin{array}{l}{x_{\mathrm{Lf}}=X+L_{\mathrm{f}} \cos \varphi-\frac{w}{2} \sin \varphi} \\ {y_{\mathrm{Lf}}=Y+L_{\mathrm{f}} \sin \varphi+\frac{w}{2} \cos \varphi}\end{array}\right. $ | (3) |
以图 2所示工况为例, 在本车通过目标车时, 目标车左后角(x0, y0)到本车右侧边界距离D大于一定的安全距离Dsm, 即
| $ D = \frac{{c{x_0} - {y_0} + {y_{{\rm{rf}}}} - c{x_{{\rm{rf}}}}}}{{\sqrt {1 + {c^2}} }} \ge {D_{{\rm{sm}}}} $ | (4) |
式中:c为本车右侧边界所在直线斜率, c=tan φ; (xrf, yrf)为本车矩形边界的右上顶点坐标.
2.2.2 驾驶员输入特性的约束驾驶员在转向避撞时车辆的侧向加速度不能超过一定的限制, 过高的侧向加速度会导致车辆的失稳, 侧向加速度满足|ay|≤ay, max, 即
| $ \left| {{v_0}(\dot \beta + \gamma )} \right| \le {a_{y, \max }} $ | (5) |
式中:ay, max为车辆的极限侧向加速度.
驾驶员转向避撞操纵, 受到驾驶员进行方向盘转速的操作能力限制, 驾驶员的方向盘转角操纵不能超过一定的限值, 即
| $ \left| {{{\dot \delta }_{\rm{f}}}} \right| \le {\dot \delta _{{\rm{f}}, {\rm{max}}}} $ | (6) |
式中:
驾驶员在紧急转向变道的路径规划时, 优化目标是保证轨迹的平顺性, 紧急转向变道避撞的路径优化目标函数表达式如下:
| $ J = S\left( {\xi \left( {{t_{\rm{f}}}} \right), {t_{\rm{f}}}} \right) + \int_{{t_0}}^{{t_{\rm{f}}}} L (\xi , U, t){\rm{d}}t $ | (7) |
式中:t0表示变道的起始时刻; tf表示变道的终止时刻.等号右边第一项表示终值目标函数, 目的是控制结果使最终得到的结果更加接近目标集, 为Mayer型目标函数.等号右边第二项代表过程目标函数, 目的是对整个过程进行控制, 使其满足一定的状态条件, 为Lagrange型目标函数.
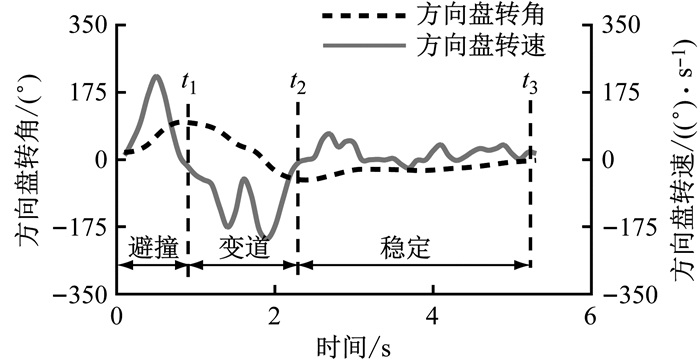
依据驾驶员变道过程中的方向盘转角和转速特征, 将紧急转向变道分成3个阶段, 如图 4所示.
|
图 4 紧急转向变道的阶段划分 Fig.4 Phase division of emergency lane changing |
第1阶段是避撞阶段, 从驾驶员开始转向避撞的时刻t0开始, 以方向盘转角达到最大值时刻t1为终点.从自然驾驶数据分析避撞阶段的持续时间约为0.8 s, 起始时刻t0开始到t1=0.8 s[19]结束.避撞阶段目的是避免碰撞发生, 满足避撞的几何条件约束.
第2阶段是侧移阶段, 从方向盘转角达到最大值时刻t1开始, 以方向盘转角到达反方向最大值时刻t2为终点.从自然驾驶数据分析侧移阶段的持续时间为2 s[19], 从t1开始到t2=2.8 s结束.侧移阶段保证车辆的侧向位移, 防止侧向位移过小(不能进入车道), 防止侧向位移过大(超出车道边界线).
第3阶段是稳定阶段, 从t2开始结束时间不限, 该阶段是降低车辆的横摆角速度, 车道保持的过程[19].
将紧急变道分为上述3个阶段规划车辆侧向位移轨迹, 将其转换为最优控制问题.采用高斯维普法计算该最优化问题, 并采用GPOPS软件进行求解.自然驾驶测试车型为沃尔沃S60, Lf=2.5 m, Lr=2.7 m, w=2.0 m, 方向盘与转动轮之间的转速比ist=16.25, 不足转向系数0.003;车道宽度Yref=3.5 m; 道路状态良好摩擦系数μ=0.8, 最大侧向加速度ay, max=μg; 最大方向盘转速
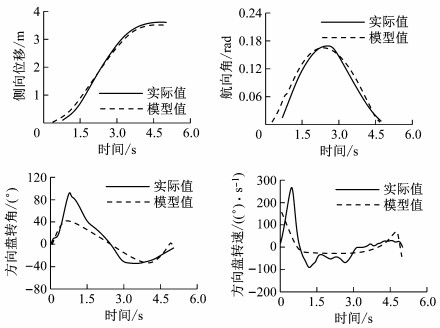
随机选取两个紧急变道工况进行拟合分析, 求解最优方程, 参数如表 1所示.通过轨迹模型可得车辆航向角、理想的驾驶员方向盘转角和方向盘转速.将车辆的拟合轨迹、拟合航向角、理想方向盘转角和转速与实际的紧急转向操作进行比较, 如图 5和图 6所示.
| 下载CSV 表 1 工况A2260-59和A2211-22的相关参数 Tab.1 Parameters of Case A2260-59 and A2211-2 |
|
图 5 工况A2260-59的拟合结果 Fig.5 Fitting results of Case A2260-59 |
|
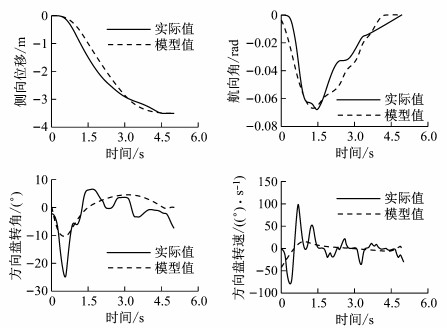
图 6 工况A2211-22的拟合结果 Fig.6 Fitting results of Case A2211-22 |
紧急变道侧向位移轨迹的模型拟合结果表明, 该轨迹模型可准确描述驾驶员在紧急变道过程的变道侧向位移曲线, 同时该模型也能很好地拟合车辆的航向角, 车辆的侧向位移参数和航向角参数可作为驾驶员紧急转向模型的输入.
从上述比较结果可知, 驾驶员在实际的紧急变道过程中所使用的方向盘转角要比轨迹模型中得到的理想方向盘转角要大, 结合自然驾驶工况的数据和视频可知, 驾驶员在紧急转向操作时由于工况比较紧急, 驾驶员通常会较大幅度地转动方向盘以避免碰撞的发生, 与驾驶员正常变道有所不同, 无法用理想模型来表征一般驾驶员的紧急转向操纵.
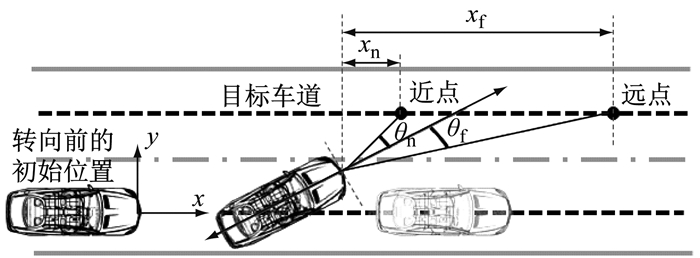
3 紧急变道驾驶员模型建立和分析 3.1 紧急转向变道避撞阶段的行为分析驾驶员进行转向过程中, 与转向目标点的角度偏差以及角度变化率是驾驶员的视觉信息感知源, 驾驶员转向控制所需获得的视觉信息包含了远、近两个区域.如图 7所示, 近点距离车辆前端较近, 驾驶员通过近点区域来控制车辆的侧向位移, 近点控制产生的方向盘转速峰值较高; 远点距离车辆前端较远, 驾驶员通过远点区域来保持车辆的稳定, 并感知路面的曲率变化情况, 远点控制产生的方向盘转速峰值较低, 且曲线平滑[20].
|
图 7 紧急转向变道的近点和远点 Fig.7 Far and near aimed point of emergency lane changing |
在紧急转向变道阶段驾驶员通过远、近目标点的选择切换完成转向.在避撞、侧移阶段驾驶员方向盘转速幅值较大, 驾驶员通过近点来控制车辆的侧向位移:在避撞阶段, 驾驶员选择的近点与本车前端水平距离为两车的初始距离, 以此控制车辆的转向避免碰撞的发生; 在侧移阶段, 驾驶员选择的近点与本车前端的水平距离为6~10 m[10, 20], 以此控制车辆的转向确保车身进入目标车道; 在稳定阶段, 驾驶员总体上转向控制更平滑, 驾驶员通常选择与本车前端的水平距离为80~150 m[10, 20]的远点来控制车辆保持在目标车道内, 并保证车辆的稳定.
3.2 基于近、远目标点的紧急转向模型建立 3.2.1 避撞和侧移阶段分析驾驶员通过目标近点来控制车辆转向.以车辆变道前转向初始位置车辆前端的中点作为坐标的原点, 纵向行驶方向为x轴, 侧向位移方向为y轴, 向左转向为正.在此忽略驾驶员在车内的位置误差, 本车前端中点的坐标为C(XC, YC), 目标近点坐标为On(XOn, YOn), 车辆行驶方向与目标近点On角度差为
| $ {\theta _{\rm{n}}} = \arctan \frac{{{Y_{\rm{n}}}}}{{{X_{\rm{n}}}}} - \varphi $ | (8) |
式中:θn为车辆位置与近点On的角度偏差; Xn=XOn-XC; Yn=YOn-YC; Xn表示近点距离车前端的水平距离, 在避撞和侧移阶段取值不同, 在避撞阶段Xn选取为两车之间的距离, 在侧移阶段选取Xn=10 m; 本文选取的自然驾驶工况是在城市路况下, 根据道路宽度的国家标准YOn=3.5 m(如车辆未行驶在车道中心线, 则根据实际情况选取).
驾驶员通过车辆与目标近点的位置角度偏差以及角度偏差的变化率来控制转向, 故所需方向盘转速
| $ {\dot \delta _{\rm{f}}} = {k_{{\rm{np}}}}{\dot \theta _{\rm{n}}} + {k_{{\rm{ni}}}}{\theta _{\rm{n}}} $ | (9) |
式中:knp、kni均为增益参数, 对于每个驾驶员都有所不同, 表征了驾驶员对于车辆和环境的综合感知程度, 在避撞和侧移阶段取值也有所变化, 优化范围为0~50[10].
3.2.2 稳定阶段远点的选择分析本车前端中点坐标C(XC, YC), 目标远点坐标为Of(XOf, YOf), 车辆行驶方向与目标远点间的角度差为
| $ {\theta _{\rm{f}}} = \arctan \left( {{Y_{\rm{f}}}/{X_{\rm{f}}}} \right) - \varphi $ | (10) |
式中:Xf=XOf-XC, Yf=YOf-YC; Xf表示了远点距离车前端的水平距离; 同样根据道路宽度的国家标准YOf=3.5 m.驾驶员通过与目标远点的角度变化率来控制转向, 所需方向盘转速
| $ {\dot \delta _{\rm{f}}} = {k_{\rm{f}}}{\dot \theta _{\rm{f}}} $ | (11) |
式中:kf为增益参数.
稳定阶段的Xf区间范围是80~150 m[10, 20], 在此为了避免模型复杂化, 选取稳定阶段的Xf=123 m; 增益参数kf优化范围为0~50[10].
利用MATLAB中的优化工具箱, 采用非线性多变量函数的极小值优化方法对驾驶员模型进行求解, 优化目标是方向盘转角和方向盘转速的操作与实际驾驶员的方向盘转速和转角拟合度.
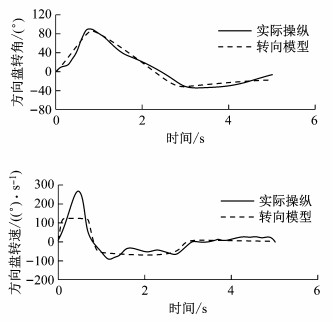
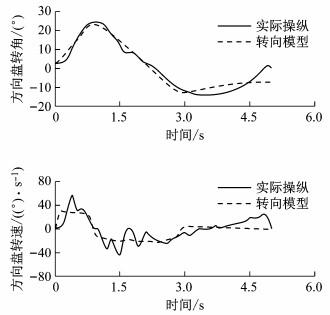
随机挑选3个紧急转向变道的危险工况, 表 2为该危险工况的本车、环境以及拟合参数, 图 8~10为3个紧急转向变道工况的拟合情况.
| 下载CSV 表 2 紧急变道工况的参数表 Tab.2 Parameters of emergency changing case |
|
图 8 工况A2260-59转向模型拟合结果 Fig.8 Fitting results of Case A2260-59 |
|
图 9 工况A2176-24转向模型拟合结果 Fig.9 Fitting results of Case A2176-24 |
|
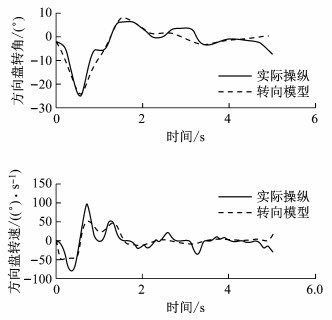
图 10 工况A2211-22转向模型拟合结果 Fig.10 Fitting results of Case A2211-11 |
对50例驾驶员紧急转向变道操作进行参数拟合, 近、远目标点的紧急转向变道连续模型方向盘转角拟合度比方向盘转速拟合度要高, 方向盘转角拟合度平均值大于0.8, 方向盘转速拟合优度平均值大于0.5.分析转向模型的近、远点增益因子的分布, 以及驾驶员紧急转向变道的特征.
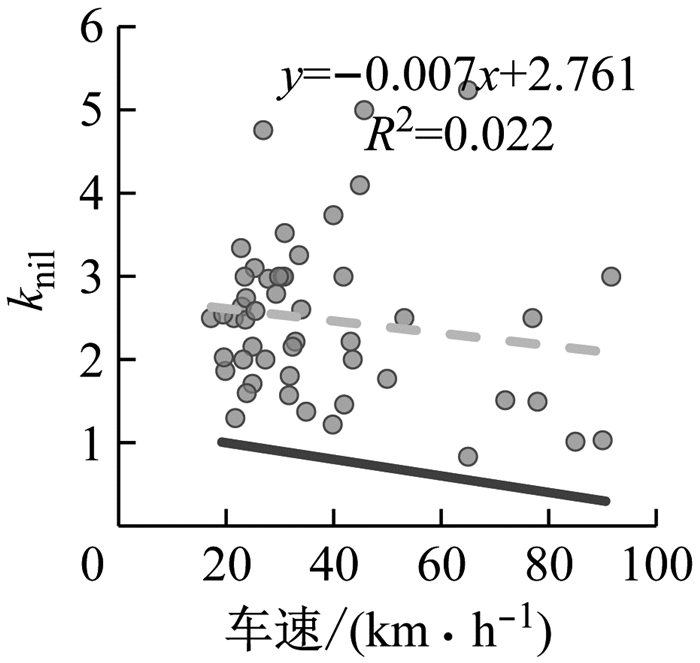
图 11是避撞阶段增益因子kni1随车速分布情况, kni1与车速并不显著相关, 但随本车速度的增大有呈现减小的趋势.kni1增益因子值越小, 避撞阶段的方向盘转角和转速幅度越小, 即本车车速越高方向盘转角与转速峰值越低, 与从自然驾驶数据库驾驶特征分析中得到的规律相符.图 11中实线为正常变道中拟合的增益因子kni1随车速变化的线性关系曲线, 可明显发现紧急变道过程驾驶员的增益因子kni1相对于正常变道取值偏大.
|
图 11 kni1随车速的分布 Fig.11 kni1 distribution with speed |
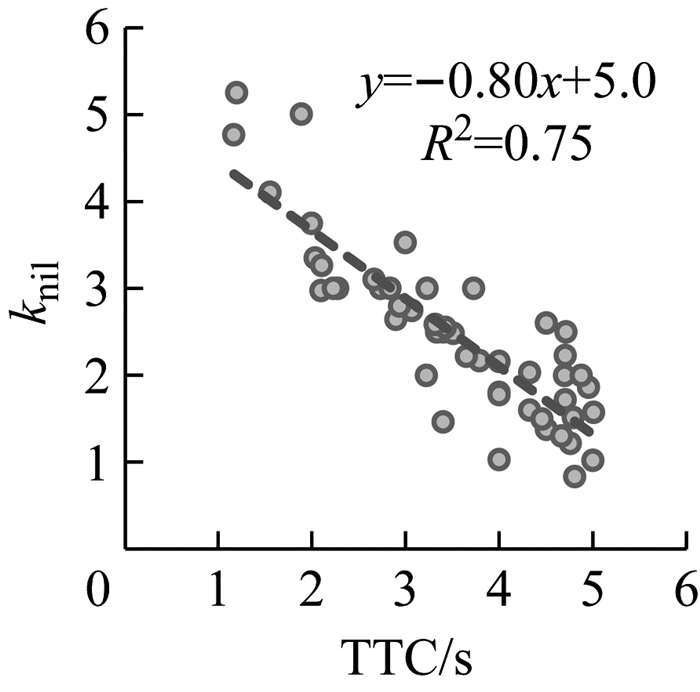
在紧急转向变道避撞阶段中受碰撞时间TTC的影响较大, 变道工况越紧急, 驾驶员的操纵就越剧烈.图 12是避撞阶段增益因子kni1随TTC分布情况, 随着TTC减小, 增益因子kni1逐渐增加, 且两者显著线性相关.由于紧急变道中的TTC小于5 s, 故kni1大于1.0.利用皮尔森检验方法, 对避撞阶段的增益因子kni1与TTC、行车车速之间的关系进行分析, 表明kni1与TTC在95%置信区间内显著相关, 而与行车车速并不显著相关.
|
图 12 kni1随TTC的分布 Fig.12 kni1 distribution with TTC |
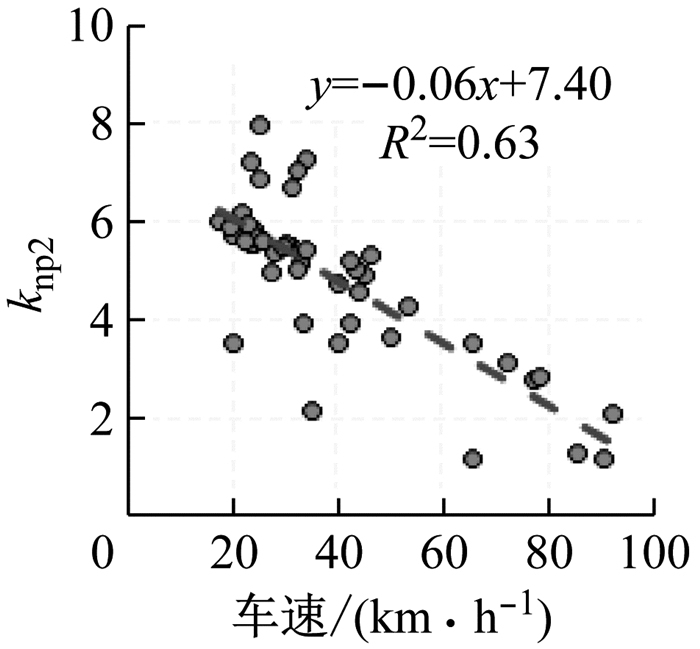
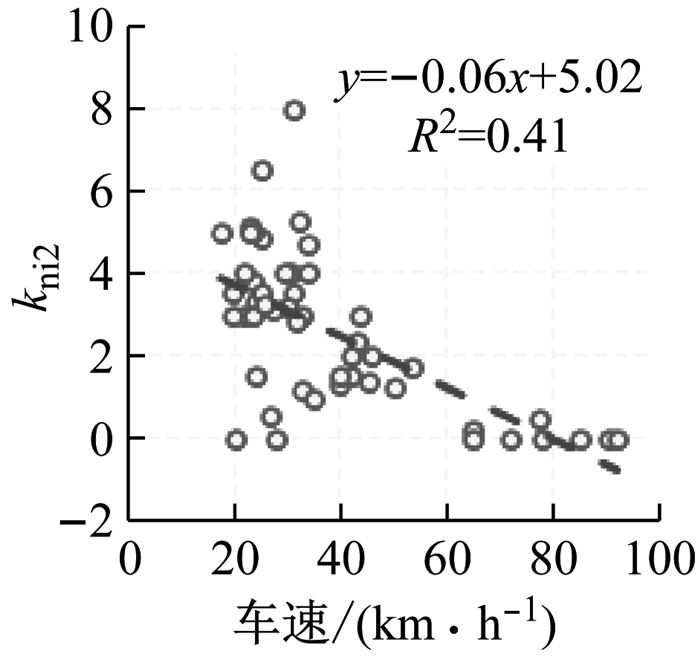
利用皮尔森检验方法, 分析侧移阶段的增益因子knp2、kni2的关系, knp2与本车的行驶车速有较强的相关性, 与kni2也有较显著的相关性.两者与TTC并不显著相关, 在侧移阶段转向的主要目的是保证车辆顺利进入目标车道, knp2、kni2主要与车辆动力学性能相关.图 13、图 14是侧移阶段增益因子knp2、kni2随车速分布情况, knp2、kni2与行驶车速显著相关, 随本车速度的增大有呈现减小的趋势, knp2≥1.0, kni2≥0.与避撞阶段类似, 增益因子knp2、kni2值越小, 侧移阶段的方向盘转角和转速幅值越小, 即车速越高方向盘转角与转速峰值越低, 与从自然驾驶数据库驾驶特征分析中得到规律相符.
|
图 13 knp2随车速的分布 Fig.13 knp2 distribution with speed |
|
图 14 kni2随车速的分布 Fig.14 kni2 distribution with speed |
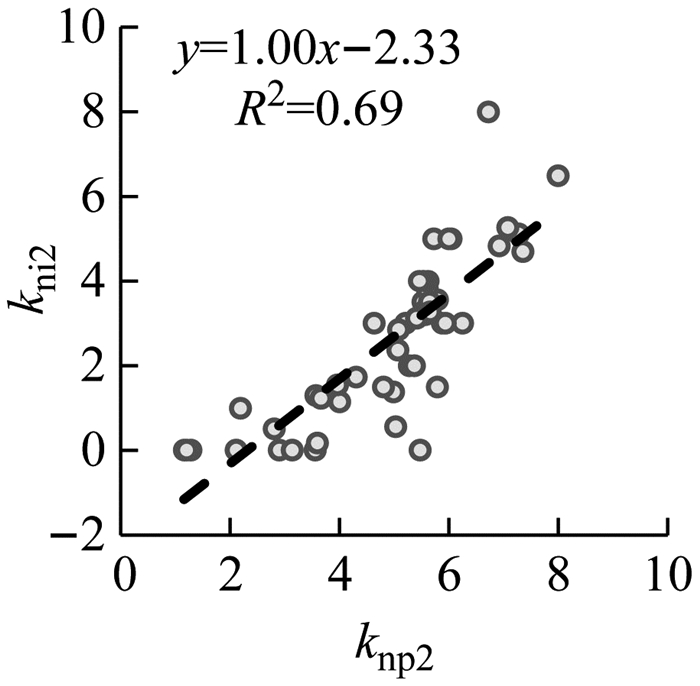
图 15是侧移阶段增益因子knp2与kni2相互关系的分布图, 随着knp2的增大, 增益因子kni2逐渐增大, 且两者显著线性相关.
|
图 15 knp2随kni2的分布 Fig.15 knp2 distribution with kni2 |
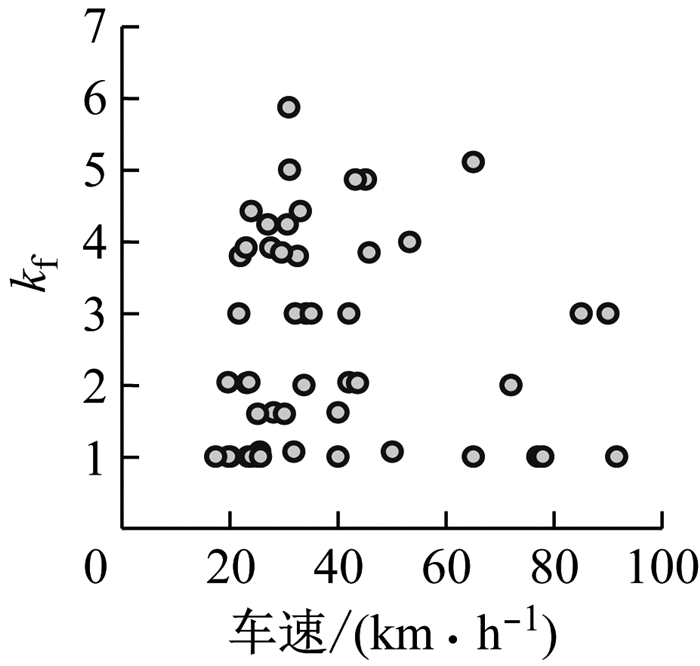
图 16是稳定阶段增益kf与车速的分布情况, 稳定阶段转向的作用是使车辆保持最小的横摆角速度, 保持车辆在车道内稳定行驶.实际驾驶中, 该阶段驾驶员操作与驾驶风格密切相关.
|
图 16 kf随车速的分布 Fig.16 kf distribution with speed |
避撞阶段增益因子kni1与碰撞时间TTC显著相关, 侧移阶段增益因子knp2与行车车速显著相关, 而增益因子kni2和knp2相关, 故在此可通过线性拟合关系得到避撞阶段和侧移阶段的驾驶员转向模型的增益参数表达.
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{{\rm{np}}1}} = 0}\\ {{k_{{\rm{ni}}1}} = - 0.8{t_{{\rm{TTC}}}} + 5.0, \;{t_{{\rm{TTC}}}} < 5.0\;{\rm{s}}}\\ {{k_{{\rm{np}}2}} = \max \{ - 0.06V + 7.0, 1\} }\\ {{k_{{\rm{ni}}2}} = \max \left\{ {{k_{{\rm{np}}2}} - 2.33, 0} \right\}} \end{array}} \right. $ | (12) |
式中:tTTC为碰撞时间TTC.
式(12)表征了驾驶员紧急变道转向模型增益参数的平均分布表达.
5 结论本文提出了紧急转向变道的驾驶侧向运动轨迹的规划方法, 通过二自由度单轨模型和高斯伪谱法求解最优控制问题, 得到了驾驶员紧急转向避撞的侧向运动轨迹.验证结果表明, 该规划方法能够较好地拟合驾驶员紧急转向变道的侧向运动轨迹.
通过驾驶员的紧急转向特征, 分析了驾驶员在紧急转向变道各阶段的远、近目标点的选择, 基于远、近目标点理论, 建立了紧急转向变道工况的驾驶员转向模型.对50例紧急转向变道模型进行了拟合验证.对避撞、侧移和稳定阶段的增益因子的分布特征进行了研究, 避撞阶段的增益因子kni1与碰撞TTC显著相关, 侧移阶段的增益因子kni2和knp2与车速显著相关, 通过线性拟合建立了参数之间的计算模型.本文建立的紧急转向模型能够真实地预测自然驾驶中的紧急转向变道行为.
| [1] |
ECKERT A, SEVENICH M, RIETH P E. Emergency steer & brake assist-a systematic approach for system integration of two complementary driver assistance systems[J]. European Journal of Political Research, 2011, 50(4): 441 |
| [2] |
BEVAN G P, GOLLEE H, O'REILLY J. Trajectory generation for road vehicle obstacle avoidance using convex optimization[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2010, 224(4): 455 |
| [3] |
HATTORI Y, ONO E, HOSOE S. Optimum vehicle trajectory control for obstacle avoidance problem[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(5): 507 |
| [4] |
李霖, 朱西产, 陈海林. 驾驶员制动和转向避撞极限[J]. 同济大学学报(自然科学版), 2016, 44(11): 1743 LI Lin, ZHU Xichan, CHEN Hailin. Drivers' collision avoidance limit by braking and steering[J]. Journal of Tongji University(Natural Science), 2016, 44(11): 1743 |
| [5] |
FAUSTEN M. Accident avoidance by evasive maneuvers[R]. Munich: [s.n.], 2010.
|
| [6] |
LEE T, KIM B, YI K, et al. Development of lane change driver model for closed-loop simulation of the active safety system[C]//International IEEE Conference on Intelligent Transportation Systems. Washington D C: IEEE, 2011: 56-61.
|
| [7] |
CHOVAN J D, TIJERINA L, ALEXANDER G, et al. Examination of lane change crashes and potential IVHS countermeasures[R]. Washington D C: National Highway Traffic Safety Administration, 1994.
|
| [8] |
BASCUNANA J L. Analysis of lane change crash avoidance[C]//SAE International Future Transportation Technology Conference & Exposition. Costa Mesa: National Highway Traffic Safety Administration. 1995: 33-38.
|
| [9] |
NELSON W. Continuous-curvature paths for autonomous vehicles[C]//IEEE International Conference on Robotics and Automation. Scottsdale: IEEE, 1989: 1260-1264.
|
| [10] |
Markkula G, Benderius O, Wahde M. Comparing and validating models of driver steering behavior in collision avoidance and vehicle stabilization[J]. Vehicle System Dynamics, 2014, 52(12): 1658 |
| [11] |
SALVUCCI D D, GRAY R. A two-point visual control model of steering[J]. Perception, 2004, 33(10): 1233 |
| [12] |
SALVUCCI D D, LIU A. The time course of a lane change: driver control and eye-movement behavior[J]. Transportation Research Part F Traffic Psychology & Behaviour, 2002, 5(2): 123 |
| [13] |
BENDERIUS O, MARKKULA G. Evidence for a fundamental property of steering[C] // Proceedings of the Human Factors and Ergonomics Society Annual Meeting. Goteborg: SAGE Publications, 2014: 884-888.
|
| [14] |
BENDERIUS O, MARKKULA G, WOLFF K, et al. Driver behaviour in unexpected critical events and in repeated exposures-a comparison[J]. European Transport Research Review, 2014, 6(1): 51 |
| [15] |
BENDERIUS O. Modelling driver steering and neuromuscular behavior[D]. Goteborg: Chalmers University of Technology, 2014.
|
| [16] |
HONG T, KWON J, PARK K, et al. Development of a driver's intention determining algorithm for a steering system based collision avoidance system[J]. Applied Microbiology & Biotechnology, 2013, 38(5): 443 |
| [17] |
GALVANI M. Optimal control based ADAS for driver warning and autonomous intervention using maneuver jerks for risk assessment[D]. Trento: University of Trento, 2013.
|
| [18] |
BRANNSTROM M, COELINGH E, SJOBERG J. Model-based threat assessment for avoiding arbitrary vehicle collisions[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(3): 658 |
| [19] |
MORASSO P. Spatial control of arm movements[J]. Experimental Brain Research, 1981, 42(2): 223 |
| [20] |
吴斌, 朱西产, 沈剑平, 等. 自然驾驶工况的驾驶员紧急转向变道行为[J]. 同济大学学报(自然科学版), 2017, 45(4): 554 WU Bin, ZHU Xichan, SHEN Jianping, et al. Analysis of driver emergency steering lane changing behavior based on naturalistic driving data[J]. Journal of Tongji University(Natural Science), 2017, 45(4): 554 |
 2019, Vol. 47
2019, Vol. 47

