随着全球金融衍生品市场的快速发展, 交易对手信用风险(counterparty credit risk, CCR)逐渐成为全球金融机构面临的主要风险之一, 其定义为交易对手未能履行约定契约中的支付义务而造成经济损失的风险.自2008年金融危机之后, 金融衍生品合约的定价考虑CCR逐渐成为全球共识. 2010年出台的巴塞尔协议Ⅲ^[1]则首次增添新的资本计提量, 即信用估值调整(credit valuation adjustment, CVA).

CVA是度量由于交易对手违约而造成的期望潜在损失, 定义为无交易对手违约风险的金融衍生品价格与含违约风险的价格之差.因此, 从定价角度来讲, CVA的计算即是对CCR的风险中性定价^[2], 其主要由3部分组成：贴现期望暴露、交易对手违约概率和违约损失率^[2-3].通常的CVA计算多数是基于交易对手违约概率与暴露互相独立的假设, 如巴塞尔协议Ⅲ中所给出的CVA计算公式^[1].然而, 交易对手违约概率与决定金融衍生品价格的市场风险因子之间会存在相关性, 即存在错向风险(wrong way risk, WWR):暴露越大, 交易对手违约概率越大.错向风险的存在会增大CVA, 因此对于CCR的定价非常重要.

对于欧式期权, 由于到期日之前无法行权, 若不考虑WWR, CVA在几何布朗运动^[4](geometric Brownian motion, GBM)和Merton跳扩散模型^[5]下存在解析公式^[2-3].但对于百慕大期权, 由于其路径依赖性, CVA的计算过程将变得非常复杂.目前, 多数文献中CVA是通过基于模拟的方法来计算. Breton等^[6]在GBM和跳扩散模型^[5]下提出了一种基于函数插值的动态规划方法, 对高斯Copula^[3]和Hull-White强度模型^[7]两种WWR模型下的百慕大期权进行了定价研究.但该方法仅适用于低维标的模型, 同时对Hull-White模型也无法做到拟合市场上信用违约互换价差数据.之后, Bavier等^[8]基于Hull-White强度模型, 首先利用二叉树方法将违约强度通过价差数据校准得到, 然后通过蒙特卡洛模拟研究了GBM下百慕大期权的提前行权特性对于CVA的影响. Graaf等^[9]在随机波动率模型^[10]下提出了基于蒙特卡洛模拟的SGBM(stochastic grid bundling method)方法用于定价百慕大期权下无WWR的CVA. Feng等^[11]利用同样方法研究了包含WWR的百慕大期权下的CVA计算, 但其中WWR是由额外的随机过程进行刻画, 形式较为复杂.近年来, 国内学者对于交易对手违约风险也有研究, 如蒋昇^[12]基于Copula函数利用复杂的嵌套蒙特卡洛模拟对交易对手风险进行了实证分析; 奚扬阳^[13]计算了欧式期权下的CVA.更多关于CVA和WWR模型的内容可参见文献[3].

本文基于以上现有方法的诸多限制, 首次提出了一种基于柳树树状结构能应用于各种标的资产模型并且快速有效计算带有Hull-White-WWR的CVA的数值算法.该方法主要包括两部分.第一部分, 柳树法在无WWR时计算CVA.此时假设违约概率分布是确定的, 根据文献[2-3], 对于欧式期权, 计算CVA等价于计算欧式期权在零时刻的价格, 则根据文献[14]柳树法可快速求得欧式期权价格从而直接求得CVA.而对于百慕大期权, 假设交易对手在期权所有可行权时间节点均可能发生违约, 则根据文献[9]中关于百慕大期权下暴露的定义:期权行权, 暴露为零; 期权持有, 暴露等于该时刻的持有价值.因此无WWR下CVA的计算是一个路径依赖的过程, 需要用柳树法倒向归纳计算期权在所有可行权时刻的持有价值, 并判断是否行权, 以确定当前时刻的贴现期望暴露.第二部分, 柳树法在Hull-White模型刻画WWR时计算有错向风险的CVA, 此时与无WWR区别在于违约概率分布需要用市场上信用违约互换价差数据校准得到.柳树法基于Bavier^[8]的思想, 通过自身柳树结构在给定价差数据时精确校准Hull-White模型中的时间依赖函数a(t), 从而得到新的违约概率分布, 用于最后计算有WWR的CVA.

本文基于柳树法计算错向风险下欧式和百慕大期权的CVA, 主要贡献体现在以下几方面:第一, 以树状结构计算CVA在现有文献中尚属首次; 第二, 所提出的柳树法计算CVA的算法不依赖于标的资产模型, 容易从常见的GBM^[4]、Merton跳扩散模型^[5]扩展到更复杂的随机波动率^[10]或Lévy过程^[15]等, 适用范围更广; 第三, 柳树法基于Hull-White模型刻画WWR能拟合市场上信用互换价差数据, 实用性更强; 第四, 柳树法在欧式和百慕大期权的CVA计算中计算效率高, 存储空间较少, 维护成本更低.

1 无错向风险的CVA计算

考虑一份权益类衍生品合约, 如欧式和百慕大期权, 到期日为T, 其CVA定义如下^[3]:

$ \begin{gathered} {\text{CVA}} = \left( {1 - R} \right)\mathbb{E}\left[ {{1_{\left\{ {0 < \tau < T} \right\}}},{B^\tau }{E^\tau }} \right] = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\left( {1 - R} \right)\int_0^T {\mathbb{E}\left[ {{B^\tau }{E^\tau }|\tau = t} \right]{P_{\text{D}}}\left( {{\text{d}}t} \right)} \hfill \\ \end{gathered} $

(1)

式中: $ \mathit{\mathbb{E}} $[·]代表风险中性测度下的期望; τ为交易对手违约时间; R为回收率, 1－R即违约损失率; B^t为t时刻的贴现因子, 在无风险利率r为常数假设下, B^t=e^－rt; 1_{·}为示性函数; E^t代表t时刻的暴露, 非负; P_D(dt)代表交易对手在时段[t, t+dt]内违约的风险中性概率(假设时刻t之前没有违约).

式(1)是CVA一般化的表达式, 没有对风险暴露和交易对手违约概率之间的相关性做任何的假设.事实上, 业界普遍采用二者是互相独立的假设, 从而得到以下简化的CVA表达式:

$ {\rm{CVA}} = \left( {1 - R} \right)\int_0^T {{B^t}E_{\rm{E}}^t{P_{\rm{D}}}\left( {{\rm{d}}t} \right)} $

(2)

其中：$ {{E}_{\text{E}}^t}=\mathit{\mathbb{E}}\left[ {{E}^{t}} \right] $, 代表t时刻暴露的期望, 称之为期望暴露.根据文献[3], 准确计算CVA的3要素(回收率、贴现期望暴露和违约概率).

一般来讲, 式(2)中积分表达式不具有显式解, 需要借助于数值积分近似求解.首先, 不失一般性, 将区间[0, T]等分为0=t₀ < t₁ < … < t_N=T, 等分间隔Δt=T/N, 然后确定{t_n}_n=1^N时刻的期望暴露$ E_{\text{E}}^{n}\overset{\text{def}}{\mathop{=}}\, E_{{{\text{E}}^{n}}}^{t} $, 最后用违约概率加权求和计算CVA.若利用矩形公式计算数值积分, 式(2)近似求解如下:

$ {\rm{CVA}} = \left( {1 - R} \right)\sum\limits_{n = 1}^N {{B^n}E_{\rm{E}}^nP_{\rm{D}}^n} $

(3)

式中：Bⁿ=e^－rt_n, P_Dⁿ是[t_n－1, t_n]内违约的概率.特别地, 巴塞尔协议Ⅲ利用梯形公式计算数值积分^[1], 即

$ \begin{array}{l} {\rm{CVA}} = \left( {1 - R} \right)\sum\limits_{n = 1}^N {\frac{{{B^n}E_{\rm{E}}^n + {B^{n - 1}}E_{\rm{E}}^{n - 1}}}{2}P_{\rm{D}}^n} = \\ \frac{1}{2}\left[ {\left( {1 - R} \right)\sum\limits_{n = 1}^N {{B^n}E_{\rm{E}}^nP_{\rm{D}}^n} + \left( {1 - R} \right)\sum\limits_{n = 1}^N {{B^{n - 1}}E_{\rm{E}}^{n - 1}P_{\rm{D}}^n} } \right] \end{array} $

因此, 巴塞尔协议要求的CVA可通过计算式(3)间接得到.假设交易对手违约时刻的概率分布具有如下形式^[6-8]:

$ {P_{\rm{D}}}\left( t \right) = 1 - \exp \left( { - \lambda t} \right) $

(4)

其中违约强度参数λ通常由市场上的信用违约互换价差数据进行估计^[3], 如假设违约互换期限结构恒为常数^{[6, 8]}, 则λ=θ/1－R, 其中θ为信用违约互换价差.从而, 由式(3)可知, 计算CVA的核心是计算期望暴露E_Eⁿ.

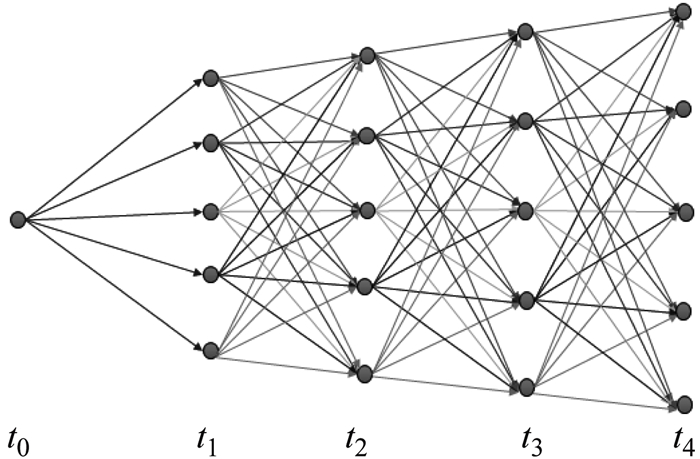
1.1 柳树法期权定价

柳树法通过构造离散的马尔科夫过程来刻画布朗运动, 能处理各种标的资产模型, 如GBM^{[4, 14]}、Merton跳扩散模型^{[5, 16]}、随机波动率模型^[10]以及Lévy过程^[15-16]等等, 现已经被广泛用于各种期权的定价^{[14, 16-17]}. 图 1展示了一个柳树结构的简单示意图.该柳树结构从初始时刻0到T, 有5个离散的时刻, 从第2个时刻起, 每个时刻都有5个可能的资产价格节点.因此, 柳树法的一个优点在于每个离散时刻上的资产价格节点个数是常数, 从而总的节点个数随时间步长N呈线性增长.

根据图 1和文献[14, 16-17]可知，给定资产价格模型, 如本文采用的GBM和Merton跳扩散模型，记S⁰为零时刻资产价格，S_iⁿ为t_n时刻第i个节点上可能的价格, Pⁿ=[p_ijⁿ]^m×m为相邻时刻[t_n, t_n+1]之间状态转移概率矩阵, 其中p_ijⁿ代表从S_iⁿ转移到S_jⁿ⁺¹的转移概率, n=1, …, N－1；i, j=1, 2, …, m, 其中m为柳树在每一时刻可能的资产价格节点个数, V_iⁿ为期权在t_n时刻第i个节点上的价格.则根据倒向归纳法, 柳树法百慕大期权定价框架可写为

$ V_i^n = \left\{ {\begin{array}{*{20}{l}} {\varphi \left( {S_i^n} \right),}&{n = N}\\ {\max \left[ {c_i^n,\varphi \left( {S_i^n} \right)} \right],}&{n = N - 1, \cdots ,1}\\ {{c^0},}&{n = 0} \end{array}} \right. $

(5)

式中：φ(S_iⁿ)=max(δ(S_iⁿ－K), 0);参数δ为1(或-1)代表看涨(或看跌); K为敲定价格; c_iⁿ为期权在t_n时刻第i个节点上的持有价值.由柳树法倒向归纳计算如下:

$ c_i^n = {{\rm{e}}^{ - r\Delta t}}\sum\limits_{j = 1}^m {p_{ij}^nV_j^{n + 1}} $

1.2 欧式期权的E_Eⁿ

考虑欧式期权, 由于其只在到期日T时刻有现金流, 在无WWR情况下, 任意时刻期权期望暴露E_Eⁿ等于该时刻期权价格^[2].此时式(2)中的CVA简化为^[2-3]

$ {\rm{CVA}} = \left( {1 - R} \right)E_{\rm{E}}^{\rm{0}}{P_{\rm{D}}}\left( T \right) $

(6)

式中：E_E⁰为欧式期权在零时刻的价格, 即E_E⁰=V⁰; P_D(T)为到期日T之前违约概率.

则由式(6)可知, 柳树法计算无WWR时欧式期权的CVA等价于定价欧式期权.

1.3 百慕大期权的E_Eⁿ

考虑一份百慕大期权, 在任意行权时刻, 根据文献[9]中百慕大期权暴露的定义:期权行权, 暴露为0;期权持有, 暴露等于持有价值.因此, 对于柳树法每一节点上的暴露E_iⁿ, 有

$ E_i^n = \left\{ \begin{array}{l} 0,\;\;\;期权在\;S_i^n\;行权\\ c_i^n,\;\;期权在\;S_i^n\;继续持有 \end{array} \right.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 1, \cdots ,N - 1 $

式中：c_iⁿ代表t_n时刻期权在第i个节点上的持有价值, 边界条件为E⁰=c⁰, E_i^N=0, i=1, 2, …, m.由于$ E_{\mathrm{E}}^{n}=\mathit{\mathbb{E}}\left[E^{n}\right] $, 如何基于柳树法计算E_Eⁿ是计算百慕大期权CVA的关键.

给定柳树结构上t_n时刻某个资产价格节点S_iⁿ, 当期权行权时, 因为合约已经终止, 未来不再存在暴露, 则该点暴露为0, 因此, 该点转移到t_n+1时刻所有状态的转移概率均为0, 即p_ijⁿ=0, j=1, 2, …, m; 若未行权, 则转移概率保持不变.记新的转移概率$ \widetilde{p}_{i j}^{n} $为

$ \tilde p_{ij}^n = \left\{ \begin{array}{l} 0,\;\;\;\;\;期权在\;S_i^n\;行权\\ p_{ij}^n,\;\;\;期权在\;S_i^n\;继续持有 \end{array} \right.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1,2, \cdots ,m $

则t_n时刻, 相应的转移概率矩阵Pⁿ被调整为$ \tilde{\boldsymbol{P}}^{n}=\left[\widetilde{p}_{i j}^{n}\right]^{m \times m}$.由此, 柳树法可迭代计算期望暴露, 即在t_n时刻, 计算数学期望E_Eⁿ=qⁿEⁿ, 其中$\boldsymbol{q}^{n}=\boldsymbol{q} \mathop \prod \limits_{k = 1}^{n - 1} \widetilde{\boldsymbol{P}}^{k} $, q=[q₁, q₂, …, q_m], 代表柳树从S⁰转移到暴露Eⁿ的转移概率向量, 暴露向量Eⁿ=[E₁ⁿ, E₂ⁿ, …, E_mⁿ]^T, 其中E_iⁿ代表t_n时刻柳树上第i个节点上的暴露, i=1, 2, …, m.在t_n+1时刻, 更新概率向量$ {{\boldsymbol{q}}^{n+1}}=\boldsymbol{q}^{n} \widetilde{\boldsymbol{P}}^{n} $, 则t_n+1时刻期望暴露为

$ E_E^{n + 1} = {\mathit{\boldsymbol{q}}^{n + 1}}{\mathit{\boldsymbol{E}}^{n + 1}} $

(7)

2 有错向风险的CVA计算

错向风险是描述暴露与交易对手违约概率之间的正相关性, 即违约概率随着交易对手暴露的增加而增加.在柳树框架下主要考虑Hull-White强度模型对于CVA计算的影响.此时由于违约概率与暴露的相关性, CVA无法再通过式(2)和(3)简化计算.

Hull-White强度模型是指:假设式(4)违约强度是一个关于时间t和t时刻无违约风险下期权价格V的函数, 记为λ(t), 即

$ \lambda \left( t \right) = \exp \left( {a\left( t \right) + b{V^t}} \right) $

(8)

式中：V^t是t时刻对应的期权价格, 如后续数值试验中欧式或百慕大看跌期权的价格; b∈$ \mathscr{R} $⁺是WWR参数; a(t)是标准化函数.

当WWR由式(8)刻画时, 结合式(2)和式(3), Hull-White模型下的CVA的计算表达式修正为^[7-8]

$ {\text{CVA}} = \left( {1 - R} \right)\sum\limits_{n = 1}^N {{B^n}\mathbb{E}\left[ {{E^n}P_{\text{D}}^n} \right]} $

(9)

式中：P_Dⁿ代表此模型下[t_n－1, t_n]内违约概率.时间依赖函数a(t)通常在给定参数b后由市场上信用违约互换价差数据在所有时间节点{t_n}_n=1^N校准确定, 从而形成以下校准问题:

$ \exp \left( { - \frac{\theta }{{1 - R}}{t_n}} \right) = \mathbb{E}\left[ {\exp \left( { - \int_0^{{t_n}} {\lambda \left( t \right){\text{d}}t} } \right)} \right] $

(10)

问题(10)是一个路径依赖的复杂问题^[8].由式(8), 对于任意区间[t_n－1, t_n], n=1, 2, …, N, 定义过程ηⁿ满足$ \eta^{n} \stackrel{\text { def }}{=} \exp \left(-\lambda^{n} \Delta t+\frac{\theta}{1-R} \Delta t\right) $, 其中λⁿ≜λ(t_n), 是一个随机变量.同时, 式(10)可进一步写为

$ \begin{gathered} \exp \left( { - \frac{\theta }{{1 - R}}n\Delta t} \right) = \mathbb{E}\left[ {\exp \left( { - \sum\limits_{k = 1}^n {\int_{{t_{n - 1}}}^{{t_n}} {\lambda \left( t \right){\text{d}}t} } } \right)} \right] = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathbb{E}\left[ {\exp \left( { - \sum\limits_{k = 1}^n {{\lambda ^n}\Delta t} } \right)} \right] \hfill \\ \end{gathered} $

(11)

若令式(11)等号两端同时除以左端项, 则成立

$ 1 = \mathbb{E}\left[ {\prod\limits_{k = 1}^n {\exp } \left( { - {\lambda ^k}\Delta t + \frac{\theta }{{1 - R}}\Delta t} \right)} \right] = \mathbb{E}\left[ {\prod\limits_{k = 1}^n {{\eta ^k}} } \right] $

(12)

基于式(12), 本文有以下定理, 用于迭代校准a(t).

定理1  在柳树法定价期权框架(5)下, 给定转移概率矩阵Pⁿ=[p_ijⁿ]^m×m, 期权价格V_iⁿ, ∀i, j=1, 2, …, m；n=1, 2, …, N, 信用违约互换价差θ, 回收率R和参数b, 校准问题(10)等价于:对时间节点n=1, 2, …, N, 柳树节点i=1, 2, …, m, 成立

$ \sum\limits_{i = 1}^m {w_i^n\eta _i^n} = 1 $

(13)

式中：$ \eta_{i}^{n}=\exp \left(-\lambda_{i}^{n} \Delta t+\frac{\theta}{1-R} \Delta t\right) $, 系数w_iⁿ表示概率, 由下式迭代给出:

$ w_i^n = \left\{ {\begin{array}{*{20}{l}} {{q_i},}&{n = 1}\\ {\sum\limits_{j = 1}^m {p_{ji}^{n - 1}\eta _j^{n - 1}w_j^{n - 1}} ,}&{n > 1} \end{array}} \right. $

证明  首先, 当n=1时, 即对于区间[t₀, t₁], 由式(12)数学期望可知

$ \sum\limits_{i = 1}^m {{q_i}\eta _i^1} = \mathbb{E}\left[ {{\eta ^1}} \right] = 1 $

令$ \omega _{i}^{1}\triangleq {{q}_{i}} $, 则定理成立.当n>1时, 一方面, 计算$ \sum\limits_{i=1}^{m}{w_{i}^{n}}\eta _{i}^{n} $如下:

$ \begin{array}{l} \sum\limits_{i = 1}^m {w_i^n\eta _i^n} = \sum\limits_{i = 1}^m {\eta _i^n} \left[ {\sum\limits_{{j_{n - 1}} = 1}^m {p_{{j_{n - 1}}i}^{n - 1}} \eta _{{j_{n - 1}}}^{n - 1}w_{{j_{n - 1}}}^{n - 1}} \right] = \\ \sum\limits_{i = 1}^m {\eta _i^n} \left[ {\sum\limits_{{j_{n - 1}} = 1}^m {p_{{j_{n - 1}}i}^{n - 1}} \eta _{{j_{n - 1}}}^{n - 1}\left[ {\sum\limits_{{j_{n - 2}} = 1}^m {p_{{j_{n - 2}}{j_{n - 1}}}^{n - 2}} \eta _{{j_{n - 2}}}^{n - 2}w_{{j_{n - 2}}}^{n - 2}} \right]} \right] \end{array} $

以此类推, 通过连续代入w_jn－2^n－2直至w_j1¹可得

$ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^m {w_i^n} \eta _i^n = \sum\limits_{i = 1}^m {\eta _i^n} \left[ {\sum\limits_{{j_{n - 1}} = 1}^m {p_{{j_{n - 1}}i}^{n - 1}} \eta _{{j_{n - 1}}}^{n - 1} \cdots } \right.}\\ {\left. {\left[ {\sum\limits_{{j_1} = 1}^m {p_{{j_1}{j_2}}^1} \eta _{{j_1}}^1w_{{j_1}}^1} \right]} \right]} \end{array} $

(14)

另一方面, 在柳树结构下, $ \prod\limits_{k=1}^{n}{{{\eta }^{k}}} $可写成离散形式$ \prod\limits_{k=1}^{n}{\eta _{{{j}_{k}}}^{k}} $, ∀j_k=1, 2, …, m, 在柳树结构下对应的转移概率为$ {{q}_{{{j}_{1}}}}\prod\limits_{k=1}^{n-1}{p_{{{j}_{k}}{{j}_{k+1}}}^{k}} $.因此成立

$ \begin{gathered} \mathbb{E}\left[ {\prod\limits_{k = 1}^n {{\eta ^k}} } \right] = \sum\limits_{{j_n} = 1}^m \cdots \sum\limits_{{j_1} = 1}^m {\left( {\prod\limits_{k = 1}^n {\eta _{{j_k}}^k} } \right)} \left( {{q_{{j_1}}}\prod\limits_{k = 1}^{n - 1} {p_{{j_k}{j_{k + 1}}}^k} } \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{{j_n} = 1}^m {\eta _{{j_n}}^m} \left[ {\sum\limits_{{j_{n - 1}} = 1}^m {p_{{j_{n - 1}}{j_n}}^{n - 1}} \eta _{{j_{n - 1}}}^{n - 1} \cdots } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[ {\sum\limits_{{j_1} = 1}^m {p_{{j_1}{j_2}}^1} \eta _{{j_1}}^1{q_{{j_1}}}} \right]} \right] \hfill \\ \end{gathered} $

由于当n=1时, w_j1¹≜q_j1, ∀j₁=1, 2, …, m, 则结合式(14), 可以得到

$ \sum\limits_{i = 1}^m {w_i^n\eta _i^n} = \mathbb{E}\left[ {\prod\limits_{k = 1}^n {{\eta ^k}} } \right] $

从而由式(12)可以得到$ \sum\limits_{i=1}^{m}{w_{i}^{n}}\eta _{i}^{n}=1 $, 即定理式(13)得证.最后, 由w_iⁿ定义可知w_iⁿ>0, ∀i=1, 2, …, m, 对n=1, 成立

$ \sum\limits_{i = 1}^m {w_i^1} = \sum\limits_{i = 1}^m {{q_i}} = 1 $

对n>1, 成立

$ \begin{array}{l} \sum\limits_{i = 1}^m {w_i^n} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {p_{ji}^{n - 1}} } \eta _j^{n - 1}w_j^{n - 1} = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^m {\eta _j^{n - 1}w_j^{n - 1}} \left[ {\sum\limits_{i = 1}^m {p_{ji}^{n - 1}} } \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^m {\eta _j^{n - 1}w_j^{n - 1}} = 1 \end{array} $

这是因为, 一方面柳树结构中转移概率矩阵每行的和等于1, 即$ \mathop \sum \limits_{i = 1}^m p_{j i}^{n-1}=1 $, ∀j=1, 2, …, m成立；另一方面, $ \mathop \sum \limits_{j = 1}^m \eta_{j}^{n-1} w_{j}^{n-1}=1 $已经证明成立, 从而说明{w_iⁿ}是概率, 定理证毕.

综上, 本文通过柳树结构迭代计算a(t), 避免了Hull和White^[7]所给算法的路径依赖性.因此，该WWR模型一旦在给定参数b下, 由算法1校准得到一系列aⁿ后, 则对于t_n时刻柳树节点i=1, 2, …, m处暴露对应的[t_n－1, t_n]内违约概率P_Diⁿ可写作

$ P_{{\rm{D}}i}^n = 1 - \exp \left( { - \exp \left( {{a^n} + bV_i^n} \right)\Delta t} \right) $

(15)

式中：V_iⁿ为该点期权价格.式(15)说明t_n时刻柳树上每一节点暴露对应的违约概率是不同的, 因此, 由无WWR下期望暴露的计算公式(7)可知, 式(9)中含有WWR的期望暴露可计算为

$ \mathbb{E}\left[ {{E^n}P_{\text{D}}^n} \right] = {\mathit{\boldsymbol{q}}^n}\left( {{\mathit{\boldsymbol{E}}^n}, * \mathit{\boldsymbol{P}}_{\text{D}}^n} \right) $

其中暴露向量Eⁿ与无WWR时一致, 而违约概率P_Dⁿ=[P_D1ⁿ, P_D2ⁿ, …, P_Dmⁿ]^T, 由式(15)给出.从而Hull-White错向风险模型下柳树法计算CVA如下:

$ {\rm{CVA}} = \left( {1 - R} \right)\sum\limits_{n = 1}^N {{B^n}\left[ {{\mathit{\boldsymbol{q}}^n}\left( {{\mathit{\boldsymbol{E}}^n}, * \mathit{\boldsymbol{P}}_{\rm{D}}^n} \right)} \right]} $

3 CVA数值实验

基于不同标的资产模型, 以GBM和Merton跳扩散模型为例, 其他资产模型同理，对Hull-White错向风险模型中不同参数下的CVA进行定价分析, 同时以欧式和百慕大看跌期权为产品(看涨期权同理), 比较柳树法与解析公式或蒙特卡洛模拟方法的数值结果.所有数值实验的程序均在操作系统为64位Windows 10家庭版的计算机上运行, 内存为8 GB, 处理器为Intel(R) Core(TM) i7-6700U CPU@2.80 GHz, 使用的软件版本为Matlab R2018a.

实验中, 对于GBM, 柳树法中资产价格节点个数m=30；对于复杂的Merto跳扩散模型, m=50.离散时间步数N=100, 蒙特卡洛方法的模拟路径数为5×10⁴.回收率R=0.4.实验比较了不同的股票价格S⁰, 不同的信用互换价差θ下柳树法和蒙特卡洛方法的表现.记号WT代表柳树法, MC代表蒙特卡洛模拟, 以运行10次求平均值作为参考值, s.d.代表蒙特卡洛的标准差, B-S、M-J分别代表由Gregory^[3]列出的在GBM和Merton跳扩散模型下无WWR的欧式期权的CVA解析公式.

首先, 考虑GBM, 固定欧式和百慕大期权的敲定价格K=100, 利率r=0.05, 波动率σ=0.1, 到期日T=1.然后选取了不同的价格S⁰和不同的信用价差θ, 从表 1可以看出, 在无WWR时, 对于欧式期权, 柳树法的定价结果与文献[3]解析公式非常接近; 而对于百慕大期权, 柳树法数值结果与文献常用的最小二乘蒙特卡洛结果相近, 相对误差均低于1%, 其中蒙特卡洛的标准差至少为10^－3量级.这充分说明了柳树法的准确性.从计算时间上来看, 在给定资产价格节点个数m和时间节点个数N时, 其他参数的变化并没有影响柳树法的计算时间, 但是, 柳树法的计算时间则少于蒙特卡洛方法.

接下来, 讨论错向风险对于CVA计算的影响, 其中Hull-White模型参数b以文献[6, 8]中b=0.01为参考.从表 2可以看出, 柳树法在欧式期权和百慕大期权下定价CVA的数值结果与蒙特卡洛模拟相比均十分接近, 同样, 柳树法在计算时间上均具有明显优势.

其次, 从GBM拓展到带跳跃的Merton跳扩散模型.欧式和百慕大期权的敲定价格K=100, 利率r=0.05, 波动率σ=0.1, 到期日T=1, 跳跃强度为0.1, 跳跃幅度满足对数正态分布, 均值为-0.05, 标准差为0.05^[16].从表 3可以看出, 选取不同的S⁰和不同的信用价差θ, 柳树法在欧式和百慕大期权下的无WWR的CVA数值结果与蒙特卡洛相比十分接近, 其中蒙特卡洛标准差至少为10^－3量级, 同时在计算时间上有一定优势.这说明柳树法在复杂的资产模型下同样表现优秀.进一步, 将Hull-White错向风险模型应用到Merton跳扩散模型.从表 4可以看出, 柳树法在欧式和百慕大期权下的CVA计算与蒙特卡洛相比十分接近, 其中蒙特卡洛标准差同样至少为10^－3量级, 但柳树法在计算时间上有优势.

最后, 考虑CVA在两种期权同样参数下以及有无WWR下的数值比较.一方面, 从表 1到表 4, 可以看出, 欧式期权下的CVA与百慕大期权下的CVA在数值上明显不同, 并且欧式期权下的CVA数值较大, 这是因为百慕大期权给与期权持有者更多主动行使期权的机会, 从而降低了持有者将来时刻的暴露, 降低了CVA.另一方面, 考虑WWR的Hull-White模型下的CVA比无WWR下的CVA数值要大.通过计算, 其比值介于1.02~1.40之间, 这与巴塞尔协议Ⅲ^[1]中WWR系数所在区间[1.2, 1.4]较为吻合, 也证实了错向风险会增大CVA的结论.

4 结语

本文首次提出了一种基于柳树树状结构快速计算错向风险下CVA的算法.一方面, 文中指出在无WWR时计算CVA的核心是计算期望暴露, 并详细给出了欧式和百慕大期权下柳树法计算期望暴露的算法；另一方面, 用Hull-White模型刻画WWR时, 通过柳树结构校准该模型中的时间依赖函数a(t)从而调整新的违约概率.数值实验以几何布朗运动和跳扩散模型下欧式和百慕大看跌期权的CVA计算为例, 表明柳树法与现有方法相比有相同的计算精度, 但计算速度更快, 同时柳树法能拟合市场上信用违约互换价差数据, 实用性较高.此外, 该算法较容易扩展到更复杂的标的资产价格模型，适用范围广.下一步将研究更多WWR模型对于CVA计算的影响，以及计算欧式和百慕大互换期权下的CVA.