2. 北京民用飞机技术研究中心, 北京 102211;
3. 同济大学 机械与能源工程学院, 上海 201804
2. Beijing Aeronautical Science and Technology Research Institute, Beijing 102211, China;
3. School of Mechanical Engineering, Tongji University, Shanghai 201804, China
热舒适性是汽车舒适性的一个重要方面, 并与空调能耗紧密相关, 近年来受到越来越多的关注.在车内热环境中, 人体各节段所处的微环境差异较大, 人与环境之间的热交换情况复杂.Nillson[1]指出, 人体并不能区分热交换的方式, 只对各种形式的热交换结果即热损失量产生热感觉.Wyon等[2]则指出, 人体总热损失影响人的精神状态与工作效率, 而局部热损失决定了人体热舒适度, 同时影响局部吹风感, 局部过冷甚至会导致肌肉损伤.因此, 热舒适研究中, 人体整体与各节段热损失量至关重要, 而整合皮肤温度与热损失的热舒适客观指标EHT(equivalent homogenous temperature, 等效均匀温度)是一个能够代表人与热环境各热交换作用结果的综合参数.
为得到EHT数值, 传统方法是根据定义, 通过热损失、皮肤温度及传热系数计算整体与各节段EHT, 但该方法依赖于暖体假人的车内实验, 无法在开发前期评价车内热环境或用于空调控制策略设计.
以往学者的研究[3-5]多聚焦于空调送风条件与太阳辐射对车内热环境温度与人体皮肤温度的影响, 并未得到其对人体舒适性的影响.
文章通过基于CFD(computational fluid dynamics, 计算流体力学)与人体热调节模型的耦合仿真, 以空调送风速度、送风温度及太阳辐射强度作为分析因素, 设计3水平全因子矩阵, 计算得到EHT, 对比分析空调送风速度、送风温度与太阳辐射强度对整体与局部EHT、平均皮肤温度及换热损失量的影响, 并得到以此三者作为参数预测整体与局部EHT的拟合方程, 为研究汽车热舒适条件提供参考, 有助于基于EHT的空调控制策略开发.
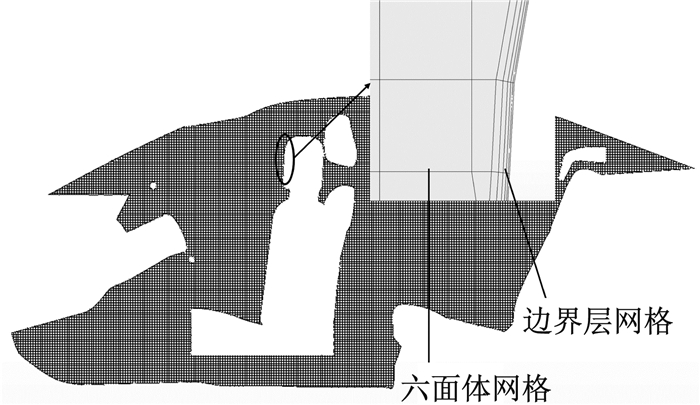
1 CFD验证 1.1 仿真方法乘员舱几何模型由试验用车三维扫描后通过软件CATIA逆向建模并简化得到, 之后在驾驶员位置加入人体几何模型, 使用软件Hypermesh生成面网格, 在软件STAR-CCM+中使用Trimmed Mesher生成体网格, 加Prism Layer Mesher生成边界层网格, 如图 1所示, 体网格数量为400万.车内气流计算采用Boussinesq假设, 以Realizable k-ε湍流模型, 结合2阶迎风格式完成数值计算.为较为精确地模拟太阳辐射对车内热环境的影响辐射, 计算采用区分长短波段的S2S(surface-to-surface)辐射模型.
|
图 1 CFD网格模型 Fig.1 CFD grid model |
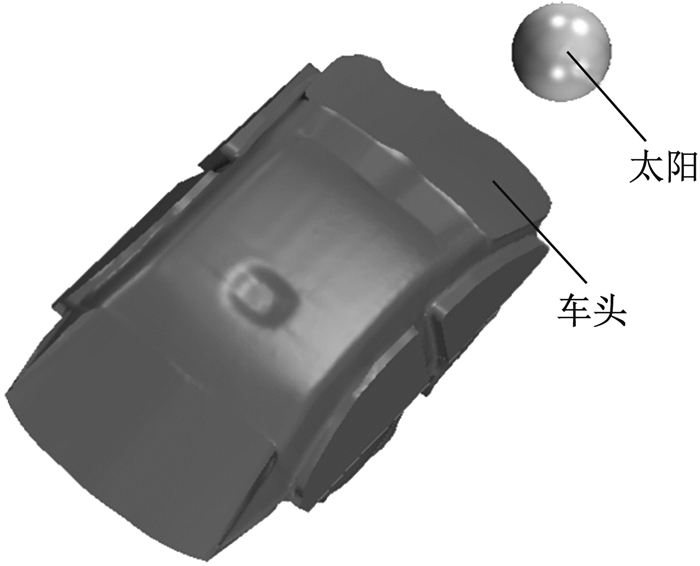
验证试验以荣威350为试验用车, 试验地点在同济大学试车场, 场地内太阳辐射不受建筑物遮挡.试验时间为2018年7月中旬, 环境空气温度为34~36 ℃, 为排除人体个体差异的影响进行了3组单人的驾驶员位置试验.试验中空调温度档设置为最低温档, 风速档位设置为最高风速档, 4个出风口均固定在吹面模式下运行.试验中测量车内热环境温度与人体14节段皮肤温度.环境温度测点如图 2所示, 包括4个出风口温度、仪表板温度、前挡风玻璃温度、车内顶部温度、呼吸点温度、脚部周围空气温度和车外环境温度.人体皮肤温度测点包括头部、胸部、左上臂、右上臂、左下臂、右下臂、左手、右手、左大腿、右大腿、左小腿、右小腿、左脚、右脚14个节段的皮肤温度.试验时车辆与太阳的相对位置如图 3所示, 在试验过程中用太阳辐射仪测量外部车顶及内部仪表板太阳辐射强度.

|
图 2 环境温度测点 Fig.2 Monitoring points of ambient temperature |
|
图 3 车与太阳的相对位置 Fig.3 Relative position of car and sun |
以该单人驾驶员位置的车内热环境试验为基础, 仿真计算边界条件使用试验测得的数据, 包括空调送风速度与送风温度、车外空气温度、相对湿度, 太阳辐射强度及太阳高度与方位角, 3组试验所测得的数据如表 1所示.其中4个出风口的位置如图 4所示.在仿真中, 设置模型入口为质量流量入口, 根据出风口面积与出风速度计算得到.出口设置为压力出口.内壁面设置为耦合边界条件, 相关的汽车物理性能设置参数如表 2所示.
| 下载CSV 表 1 仿真计算边界条件 Tab.1 Boundary conditions of simulation |

|
图 4 出风口与车窗位置 Fig.4 Positions of air outlets and windows |
| 下载CSV 表 2 相关物理性能设置参数 Tab.2 Parameters of related settings |
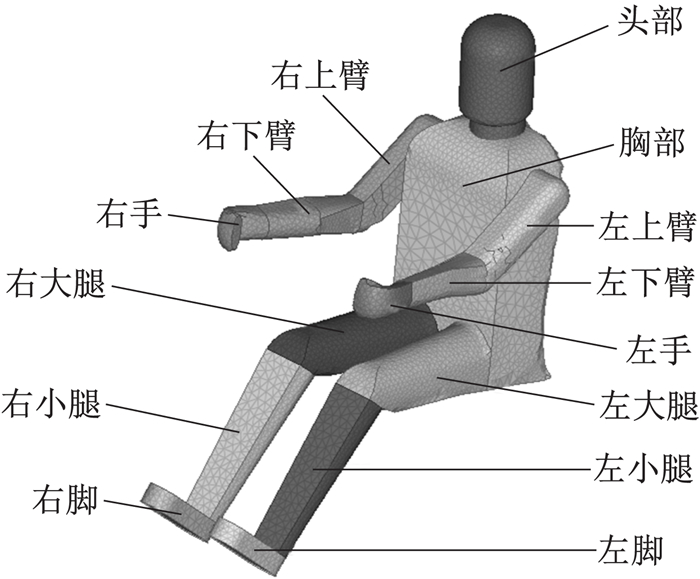
人体热调节计算使用Stolwijk等[6]提出的人体生理热调节模型, 将人体分为14个节段, 分节段示意图如图 5所示, 每个节段又分为皮肤、脂肪、肌肉与核心4层.该模型将人体热调节系统分为被动系统与主动系统.被动系统计算人体与热环境间的对流、辐射、传导热交换量, 主动系统通过调节散热与产热维持人体热平衡.该模型能较好地模拟非均匀热环境下的人体皮肤温度值.
1.2 模型验证计算收敛时, 车内温度场如图 6所示, 可见车内热环境的不均匀性显著.

|
图 6 车内温度场 Fig.6 Temperature field inside the car |
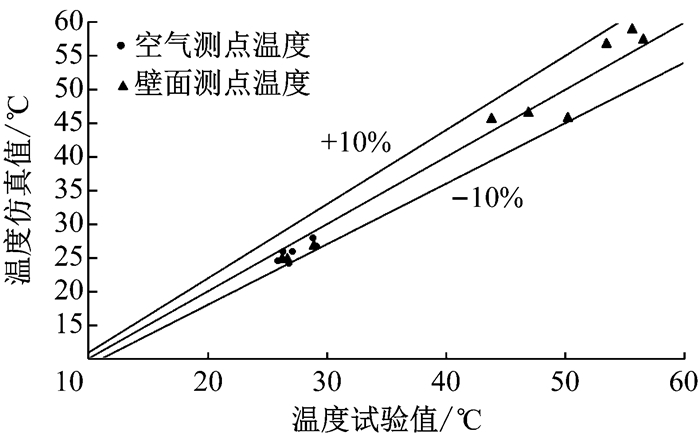
图 7为试验与仿真人体各个部位的皮肤温度值.图 8为试验与仿真的壁面与空气测点温度值.通过3组试验与仿真的对比发现, CFD计算结果误差均在10%以内, 可认为CFD仿真能较好地模拟车内热环境与人体热调节.

|
图 7 试验与仿真皮肤温度 Fig.7 Skin temperature of experiment and simulation |
|
图 8 试验与仿真壁面与空气测点温度 Fig.8 Wall and air temperature of experiment and simulation |
EHT是Wyon[7]使用暖体假人评价车内热环境时提出的人体热舒适评价指标, 其定义是:设定一个理想等效均匀环境, 空气流速为0, 空气温度等于平均辐射温度, 在衣着量和代谢强度相同的情况下, 如果非均匀环境下身体某一部位的干热损失与其在该均匀环境下的干热损失相等, 就称均匀环境下的空气温度为非均匀环境下该部位的EHT.该定义中的干热损失后被Han等[8]通过下式来表示:
| $ C+R+Q_{\mathrm{sun}}=C_{\mathrm{EHT}}+R_{\mathrm{EHT}} $ | (1) |
式中:C为实际对流换热损失; R为实际壁面辐射换热损失; Qsun为太阳辐射造成的换热损失; CEHT为等效环境下的对流换热损失; REHT为等效环境下的辐射换热损失.
可以看出, 实际环境下的干热损失总量等于等效无风环境下的干热损失总和.
EHT综合了风速、风温、壁面温度、太阳辐射及人体与固体接触面导热等众多环境参数的影响, 物理意义清晰, 使用单一的量描述热交换的综合作用结果, 容易解释也便于理解[9].EHT的值较大则热损失较少, 人体将具有较热的热感觉; 反之, EHT的值越小则干热损失越大, 人体将具有较冷的热感觉.此外, 还可以得到各节段的局部EHT, 对研究车内热环境这种非均匀热条件下的人体热舒适性十分适当、有效.
2.2 EHT计算EHT根据ISO 145052—2006[10]中的标准公式计算, 计算公式如下:
| $ {t_{{\rm{eq}}}} = {t_{\rm{s}}} - Q/{h_{{\rm{cal}}}} $ | (2) |
式中:teq为等效均匀温度EHT, ℃; ts为皮肤温度, ℃; Q为干热损失, 包括对流传热及辐射传热量, W·m-2; hcal为理想等效均匀热环境下相同坐姿及服装的人体表面综合换热系数, W·m-2·K-1, 人体各局部hcal如表 3所示, 取值来自文献[11].
整体EHT基于平均皮肤温度与整体总干热损失计算得来, 其中平均皮肤温度根据局部皮肤温度进行面积平均计算, 计算公式如下:
| $ {t_{{\rm{s}},{\rm{mean}}}} = \sum {\left( {{t_{s, i}}{A_i}} \right)} /\sum {{A_i}} $ | (3) |
式中:ts, mean为平均皮肤温度; ts, i为各节段皮肤温度; Ai为各节段面积.
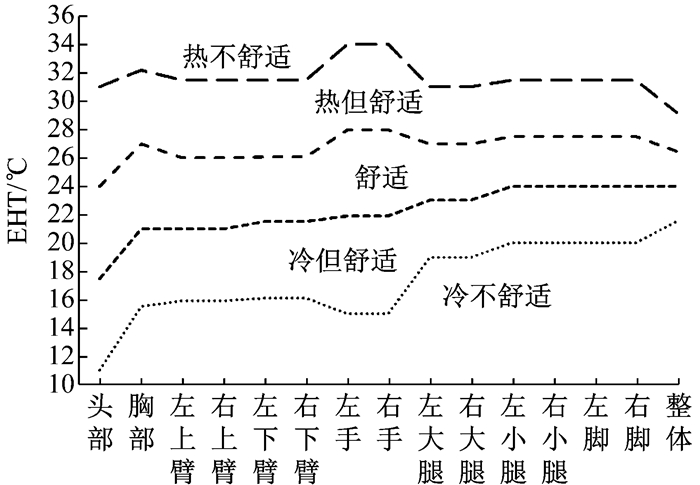
2.3 EHT舒适区人体对热环境有一定的适应范围, Wyon[7]根据试验得出EHT舒适区, Nilsson[1]则根据服装热阻的不同做了进一步改进.以Nilsson所得舒适区为参考, 根据本研究的参数条件与人体节段, 得到如图 9所示的人体14个节段与整体EHT舒适范围, 当计算所得的各节段或整体EHT值位于各区域内, 即得到不同的舒适程度.
|
图 9 EHT热舒适区 Fig.9 EHT thermal comfort zone |
为了比较空调送风条件(即送风速度、送风温度)与太阳辐射对EHT的影响, 进行DOE(design of experiment, 试验设计)全因子设计分析.DOE是一种通过建立数学模型(y=f(xi))来确定一个或多个输出响应y与输入因子xi之间关系的方法.使用DOE方法系统地改变输入因子, 应用统计学原理和方法, 分析确定它们对输出响应的影响, 以此能够确定输入因子对输出响应的影响程度, 识别输入因子设置以实现优化的输出响应, 此外还能够阐明输入因子之间的相互作用关系.
空调送风速度、送风温度及太阳辐射强度为设计因素, 耦合仿真得到的人体14个节段皮肤温度、平局皮肤温度与对应的干热损失量, 其中各节段皮肤温度及干热损失量可在人体热调节模型输出文件中直接读取, 根据式(2)计算人体各节段及整体EHT作为响应量, 进行DOE全因子水平设计, 如表 4所示, 据此得到33组因素组合.除3个设计因素的变化外, 仿真模型及边界条件设置均与仿真验证中的设置相同.
| 下载CSV 表 4 设计因素水平表 Tab.4 Level of design factor |
首先进行单因素分析.为了分析单因素与响应间的变化规律, 在全因子试验设计组上添加中间点, 共6组计算工况.分析送风速度时, 送风温度固定为10 ℃, 太阳辐射固定为800 W·m-2, 送风速度在5~9 m·s-1间变化; 分析送风温度时, 送风速度固定为7 m·s-1, 太阳辐射强度固定为800 W·m-2, 送风温度在6~14 ℃间变化; 分析太阳辐射时, 送风速度固定为7 m·s-1, 送风温度固定为10 ℃, 太阳辐射强度在600~1 000 W·m-2间变化, 以此观察各个因素与EHT的关系.
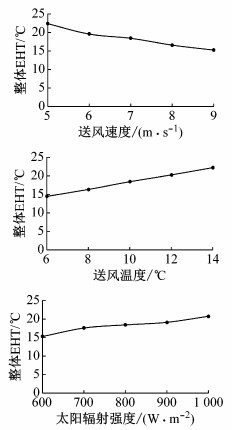
图 10为3个因素与整体EHT的关系.从图中可以看出, 送风速度变大时, 整体EHT逐渐变小; 而送风温度变大时整体EHT线性增大.当太阳辐射强度从600 W·m-2增大到700 W·m-2及从900 W·m-2增大到1 000 W·m-2时, EHT的变化较大, 而太阳辐射在700~900 W·m-2范围内对整体EHT几乎没有影响.
|
图 10 送风速度、送风温度及太阳辐射对整体EHT的影响 Fig.10 Effect of supply air velocity, temperature, and solar radiation on overall EHT |
进一步分析这3个因素对平均皮肤温度及对流、辐射、蒸发热损失的影响, 分别如图 11、图 12所示.从图 11中可以看出, 送风速度与送风温度对平均皮肤温度的影响都比较大, 风速增大, 平均皮肤温度下降, 送风温度升高平均皮肤温度也跟着升高; 而太阳辐射强度对平均皮肤温度的影响规律与对EHT的影响类似, 即太阳辐射强度在700~900 W·m-2范围内对平均皮肤温度的影响较小.

|
图 11 送风速度、送风温度及太阳辐射对平均皮肤温度的影响 Fig.11 Effect of supply air velocity, temperature, and solar radiation on mean skin temperature |
|
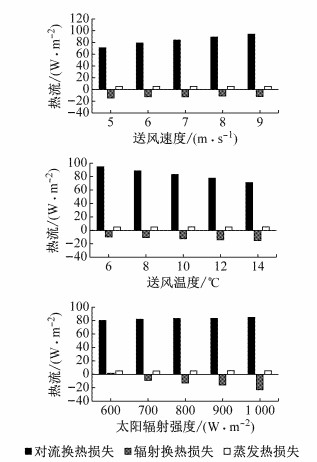
图 12 送风速度、送风温度及太阳辐射对各换热方式热流的影响 Fig.12 Effect of supply air velocity, temperature, and solar radiation on heat flux in different ways of heat-exchange |
从图 12中可以看出, 对流换热为人体与车内空调热环境换热的主要方式, 随着送风速度增大, 对流换热损失增大, 送风温度升高, 对流热损失减小, 而送风条件对辐射热流影响较小.此外, 太阳辐射强度变化对对流换热量几乎没有影响, 太阳辐射强度为600 W·m-2时, 人体通过辐射散热; 太阳辐射强度在700~1 000 W·m-2内变化时, 人体受辐射吸热, 且辐射吸热量逐渐增大, 但远小于对流散热量.总的来看, 蒸发散热量较小.
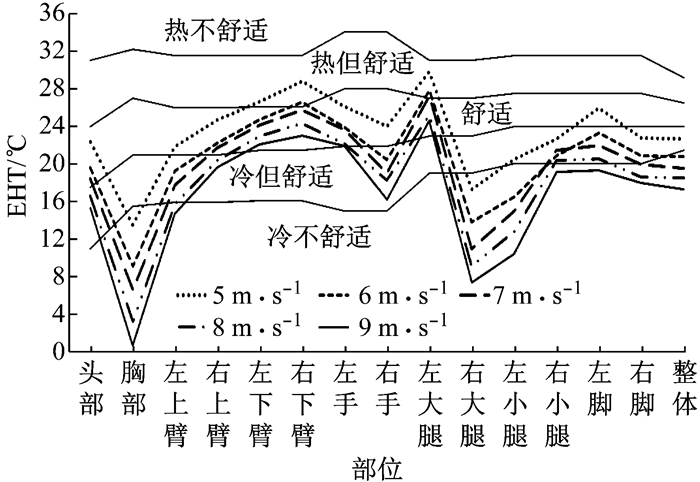
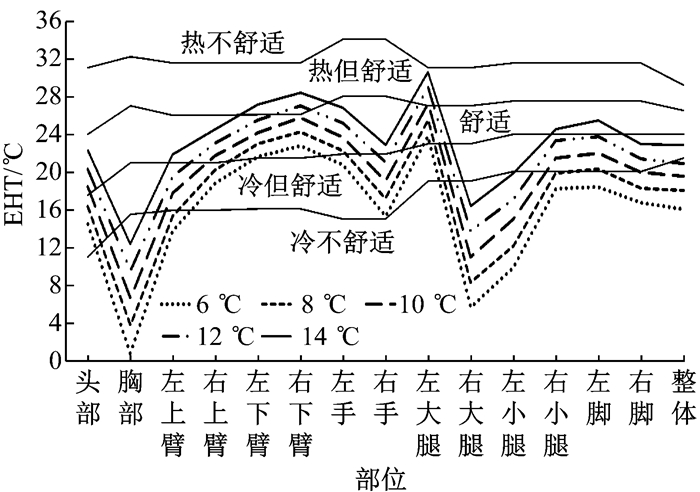
图 13至图 15分别为送风速度、送风温度及太阳辐射变化时各节段及整体EHT所处舒适区的变化情况.可以看出, 送风角度及太阳高度角与方位角不变的情况下, 人体各节段的热舒适分布几乎不变, 送风速度、送风温度及太阳辐射强度的变化仅改变舒适程度.
|
图 13 送风速度变化时所处的EHT热舒适区 Fig.13 EHT thermal comfort zone as supply air speed changes |
|
图 14 送风温度变化时所处的EHT热舒适区 Fig.14 EHT thermal comfort zone as supply air temperature changes |

|
图 15 太阳辐射强度变化时所处的EHT热舒适区 Fig.15 EHT thermal comfort zone as solar radiation intensity changes |
再根据全因子设计矩阵进行CFD仿真得到的人体皮肤温度及干热损失, 计算平均皮肤温度、整体与14个节段EHT值, 对结果进行方差分析, 根据式(4)计算各因素其两两交互作用对局部与整体EHT、平均皮肤温度与总干热损失的贡献率, 结果如表 5所示.表中, X1为送风速度, X2为送风温度, X3为太阳辐射强度, X1*X2为送风速度与送风温度交互作用, X1*X3为送风速度与太阳辐射强度交互作用, X2*X3为送风温度与太阳辐射强度交互作用.
| 下载CSV 表 5 各因素对整体EHT、平均皮肤温度及干热损失的贡献率 Tab.5 Contribution to overall EHT, mean skin temperature, and dry heat loss |
| $ {P_{\rm{A}}} = \left( {{S_{{\rm{SA}}}} - {F_{\rm{A}}}{M_{{\rm{SE}}}}} \right)/{S_{{\rm{ST}}}} $ | (4) |
式中:PA为因素A的贡献率; SSA为因素A的离差平方和; FA为因素A的自由度; MSE为误差均方; SST为总离差平方和.
从表 5中可以看出, 空调送风条件是影响整体EHT的关键因素, 其中送风温度影响最大.由于送风条件对人体平均皮肤温度和干热损失具有较大的影响, 而整体EHT通过平均皮肤温度和干热损失量求得, 因此, 送风温度对EHT影响最大.从表中还可以看出, 各因素对整体EHT和干热损失的贡献率基本相同, 送风速度、送风温度及太阳辐射强度之间几乎不存在交互作用.
表 6为送风速度、送风温度及太阳辐射强度对各局部EHT的影响权重.可以看出, 仅有右手受太阳辐射强度影响大于空调送风参数, 各因素对左手和右手影响权重的不同主要是因为左、右手所处的位置不同, 根据太阳方位角与高度角可知, 太阳位于驾驶员的右上方, 对右手的照射面积较大, 而左手更多地受出门风口送风的影响.此外, 头部、胸部、左右大腿受送风速度影响较大.而送风温度对各个节段EHT均有显著影响.
| 下载CSV 表 6 3个因素对局部EHT的贡献率 Tab.6 Contribution rate of the 3 factors to local EHT |
在以上分析的基础上, 对3个因素与EHT的关系进行线性拟合, 得到各节段及整体EHT拟合方程, 其中整体、头部、胸部及右大腿EHT(分别表示为teq, e、teq, h、teq, c、teq, rt)的拟合方程如式(5)~(8)所示.根据拟合公式可以通过送风速度、送风温度及太阳辐射强度预测整体及局部的EHT值.
| $ \begin{array}{l} {t_{{\rm{eq}}, {\rm{e}}}} = 10.210 - 1.7572{X_1} + 0.9404{X_2} + \\ \;\;\;\;\;\;\;\;{\rm{0}}{\rm{.013827 }}{\mathit{X}_{\rm{3}}} \end{array} $ | (5) |
| $ \begin{array}{l} {t_{{\rm{eq}}, {\rm{h}}}} = 1.92 - 3.1681{X_1} + 1.4083{X_2} + \\ \;\;\;\;\;\;\;\;\;{\rm{0}}{\rm{.015953 }}{\mathit{X}_{\rm{3}}} \end{array} $ | (6) |
| $ \begin{array}{l} {t_{{\rm{eq}}, {\rm{c}}}} = 9.46 - 1.996{X_1} + 0.9554{X_2} + \\ \;\;\;\;\;\;\;\;{\rm{0}}{\rm{.01610 }}{\mathit{X}_{\rm{3}}} \end{array} $ | (7) |
| $ \begin{array}{l} {t_{{\rm{eq}}, {\rm{rt}}}} = 4.11 - 2.527{X_1} + 1.2127{X_2} + \\ \;\;\;\;\;\;\;\;\;{\rm{0}}{\rm{.02060 }}{\mathit{X}_{\rm{3}}} \end{array} $ | (8) |
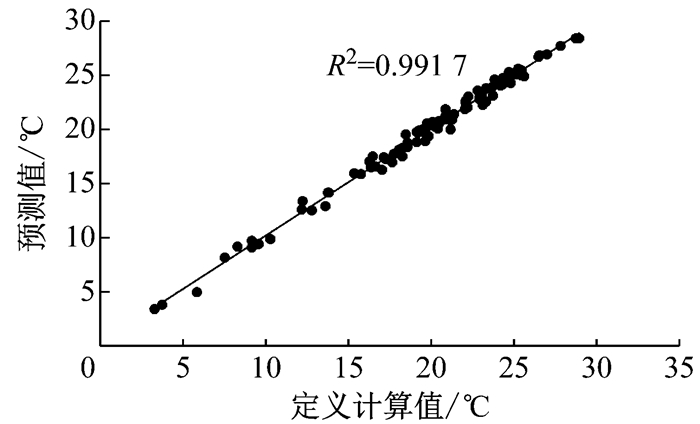
为了验证拟合公式的准确性, 在全因子设计试验组外, 以相同CFD仿真方法计算不同送风速度、送风温度及太阳辐射下的人体皮肤温度与热损失, 即单因素分析中增加的6组计算工况, 将得到的局部及整体EHT预测值与根据定义计算出来的EHT值进行比较, 结果如图 16所示.
|
图 16 局部及整体EHT定义计算值与预测值对比 Fig.16 Defined value of local and whole EHT compared with predicted value |
从图 16中可以看出, 拟合公式的预测准确度很高, 相关系数达到0.991 7.说明可以通过送风速度、送风温度及太阳辐射强度预测人体整体及各节段EHT值, 而不需要得到人体皮肤温度与干热损失量.这将有助于新型空调系统控制策略设计, 即将空调送风速度、送风温度及太阳辐射强度数据应用于拟合公式, 预测局部与整体EHT, 以EHT舒适区图(图 9)中舒适范围内的EHT为调节指标, 进行反馈控制, 能够更加合理地为乘员提供车内热舒适环境.
4 结论基于EHT基本概念, 采用DOE试验设计因素分析法及方差分析法, 得到的主要结论如下:
(1) 除受到太阳大面积直射的节段右手外, 空调送风条件对人体各节段与整体EHT的影响大于太阳辐射.其中送风温度的影响最大.送风条件一致时, 太阳辐射强度的升高仅使EHT小幅度上升, 而太阳辐射强度相同时, 空调送风速度或温度的改变都使EHT的值有较为明显的增大.
(2) 送风速度、送风温度及太阳辐射三者对EHT的影响不存在交互作用, 而送风速度、送风温度对平均皮肤温度及干热损失量的影响大于太阳辐射, 因而对EHT的影响权重更大.
(3) 根据EHT拟合公式, 可以通过空调送风速度、送风温度及太阳辐射强度较为准确地预测人体整体及局部EHT值, 以此更好地设计车内空调控制策略.
在今后的研究中, 可以增加空调出风角度及太阳方位角作为考虑因素, 再配合全球定位系统, 为车内空调控制提供更精确的方案.
| [1] |
NILSSON H O. Thermal comfort evaluation with virtual manikin methods[J]. Building and Environment, 2007, 42(12): 4000 DOI:10.1016/j.buildenv.2006.04.027 |
| [2] |
WYON D P, LARSSON S, FORSGREN B, et al. Standard Procedures for Assessing Vehicle Climate with a Thermal Manikin[C]//SAE International, 1989. DOI: 10.4271/890049.
|
| [3] |
宋亚军, 赵兰萍, 杨志刚, 等. 太阳辐射对车室内热舒适性的影响分析与改进[J]. 计算机仿真, 2014(7): 148 SONG Yajun, ZHAO Lanping, YANG Zhigang, et al. Analysis and improvement of the effect of solar incidence on cabin thermal comfort[J]. Computer Simulation, 2014(7): 148 DOI:10.3969/j.issn.1006-9348.2014.07.034 |
| [4] |
赵树恩, 朱冰, 王荣, 等. 太阳辐射对汽车舱内热环境舒适性的影响研究与改善[J]. 流体机械, 2016(7): 70 ZHAO Shuen, ZHU Bing, WANG Rong, et al. Study of influence on the comfort of cabin thermal environment and improve cabin thermal environment comfort[J]. Fluid Machinery, 2016(7): 70 DOI:10.3969/j.issn.1005-0329.2016.07.015 |
| [5] |
张文灿, 陈吉清, 兰凤崇. 太阳辐射下车窗玻璃特性对车内温度场的影响研究[J]. 机械工程学报, 2011, 47(22): 119 ZHANG Wencan, CHEN Jiqing, LAN Fengchong. Research on windshield glazing property effect on cabin temperature under solar radiation[J]. Journal of Mechanical Engineering, 2011, 47(22): 119 |
| [6] |
STOLWIJK J A, HARDY J D. Temperature regulation in man—a theoretical study[J]. Pflugers Arch Gesamte Physiol Menschen Tiere, 1966, 291(2): 129 |
| [7] |
WYON D P. Use of thermal manikins in environmental ergonomics[J]. Scandinavian Journal of Work Environment & Health, 1989, 15(S1): 84 |
| [8] |
HAN T, HUANG L. A model for relating a thermal comfort scale to EHT comfort index[C]//SAE International, 2004. DOI: 10.4271/2004-01-0919.
|
| [9] |
NILSSON H O, HOLMER I. Comfort climate evaluation with thermal manikin methods and computer simulation models[J]. Indoor Air, 2003, 13(1): 28 |
| [10] |
International Standard Organization. Ergonomic of the environment-evaluation of thermal environments in vehicles-part 2: determination of equivalent temperature: ISO 14505-2—2006[S]. Geneva: ISO, 2006.
|
| [11] |
FODA E, SIRÉN K. A thermal manikin with human thermoregulatory control: implementation and validation[J]. International Journal of Biometeorology, 2012, 56(5): 959 DOI:10.1007/s00484-011-0506-6 |
 2019, Vol. 47
2019, Vol. 47