2. 中交第二公路勘察设计研究院有限公司,湖北 武汉 430056
2. CCCC Second Highway Consultants Co., Ltd., Wuhan 430056, China
盾构壁后注浆技术源自于岩土工程注浆,但盾构壁后注浆施工需考虑管片结构受力、接头螺栓抗剪、周边地层变形、管片环位移等因素的影响,盾构壁后注浆与岩土工程注浆具有一定的差异性.岩土工程注浆理论主要包括:渗透注浆、劈裂注浆、压密注浆等,盾构隧道壁后注浆施工考虑盾尾间隙和管片衬砌的影响,盾构壁后注浆浆液扩散过程可概括为:充填注浆、渗透注浆、压密注浆、劈裂注浆4个阶段.针对盾构壁后注浆过程,叶飞等[1-2]提出利用等效孔隙率替代土体原始孔隙率,分析了牛顿流体、宾汉姆流体、幂律流体等不同流型流体的扩散过程.於昌荣[3]基于分形分维非线性理论,建立了宾汉姆流型浆液在砂卵地层的分形渗透本构模型.刘健等[4]考虑浆液黏度时变特性,分析了浆液扩散规律和管片结构受力特征.陈治[5]系统分析了浆液流变性、粘度时变性、自重对浆液扩散过程的影响.
目前针对盾构壁后注浆过程的研究主要关注了浆液流型、浆液粘度时变性、地层渗透率、注浆压力等因素的影响.这些研究中对地层中地下水的影响进行了过度简化,将浆液周边的地下水考虑为确定的边界.但实际注浆施工中,浆液渗透扩散过程会挤压地下水,引起地下水体内压力分布的变化,且在浆水交界面处存在平衡关系.针对该现象,本文考虑浆液和地下水在分界面处的连续条件,根据广义达西定律,分析驱水注浆过程中宾汉姆流型浆液的渗透扩散特征.
1 宾汉姆流体渗透扩散方程 1.1 驱替效应盾构壁后注浆施工中,由于浆液和地下水性质的差异,浆液扩散过程并不能简单地归结为单一液体在多孔介质中的渗流.在注浆压力的驱动作用下,浆液驱赶地层孔隙中的自由水并取而代之,完成扩散与加固的过程,即所谓驱替效应.驱替效应表现为两种具有不同物理化学特性的液体,在多孔介质地层中依据不同的规律同时运动.盾构壁后注浆中,由于浆液驱水扩散时两种流体存在混溶的现象,所以并不存在突变界面,而是存在一相对较薄的混相过渡区,但该过渡区与浆液扩散半径相比较小,可简化为突变界面进行处理(有该理想突变界面的驱替效应也称为活塞式驱替),浆液球形驱水扩散过程如图 1所示.

|
图 1 浆液球形扩散驱水示意图 Fig.1 Sketch of spherical diffusion grout displacing groundwater |
宾汉姆流体的流变曲线为在剪切应力轴上存在截距的直线,该截距表示屈服应力.在流体所受剪切应力τ达到屈服应力(启动压力梯度)τ0前,流体是不运动的,当τ>τ0流体开始流动,之后其切应力与剪切速率关系类似于牛顿流体,该类流体的流变方程为
| $ \tau=\tau_{0}+u \gamma $ | (1) |
式中:τ0为屈服应力,Pa;μ为黏度系数,N·s·m-2;γ为剪切速率,s-1.
根据文献[6],水灰比(W/C)0.8~1.0的单液水泥基浆液属于宾汉姆流体,水泥复合浆液和水泥黏土浆液也显现出宾汉姆流体的性质,流变方程见表 1.
| 下载CSV 表 1 宾汉姆流体流变方程 Tab.1 Rheological equation of Binghamian fluid |
针对盾构隧道管片注浆中宾汉姆型浆液的扩散过程,本文做如下基本假设:
① 受注砂卵石土层为均匀、各向同性介质;②所注浆液为宾汉姆流体,忽略浆液的黏度时效性;③采用恒压注浆;④不考虑浆液重力的影响;⑤忽略管片曲率的影响.
1.4 浆液渗透微分方程宾汉姆流体渗流运动不符合狭义上的Darcy定律,前苏联学者弗洛林[7]在1951年提出了启动压力梯度的概念.根据启动压力梯度的概念,孔祥言等[8]利用不均匀毛细管组模型,基于非牛顿幂律流体和宾汉姆流体遵从广义达西定律的原则,推导了非牛顿流体的一般渗流方程.基于此,本文进一步分析宾汉姆浆液的渗透微分方程.
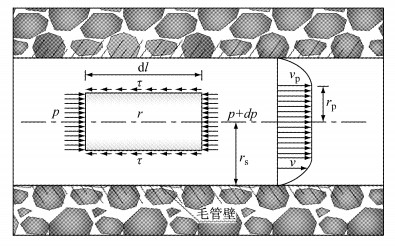
由于多孔介质砂卵石地层孔隙尺寸较小,因此浆液的渗流状态可近似认为是层流.根据毛细管组理论,假设单个毛细管道的半径为rs,选取与毛细管道同轴的长度为dl,半径为r的柱形微元体,则微元体受力状况如图 2所示(图中p和p+dp分别为柱形微元体两端所受的压力,rp为宾汉姆流体的流核半径,vp为流核半径范围内的浆液流速,v为流核半径范围外的浆液流速).
|
图 2 管内流体受力示意图 Fig.2 Force analysis of grout in tube |
对该微元受力分析,其平衡方程可简化为
| $ \tau=-\frac{r}{2} \frac{\mathrm{d} p}{\mathrm{d} l} $ | (2) |
根据式(1)、式(2)在毛细管截面上积分,可得截面平均流速v为
| $ {\bar{v}=\frac{Q}{\mathsf{π} r_{\mathrm{s}}^{2}}=-\frac{r_{\mathrm{s}}^{2}}{8 \mu}\left[1-\frac{4}{3}\left(\frac{2 \tau_{0} / r_{\mathrm{s}}}{-\mathrm{d} p / \mathrm{d} l}\right)+\frac{1}{3}\left(\frac{2 \tau_{0} / r_{\mathrm{s}}}{-\mathrm{d} p / \mathrm{d} l}\right)^{4}\right]} \\ {\frac{\mathrm{d} p}{\mathrm{d} l}} $ | (3) |
式中:Q为毛细管道内浆液总流量.
使管道内流体流量为零即可解得流体的启动压力梯度λ,其值为
| $ \lambda=-\frac{\mathrm{d} p}{\mathrm{d} l}=2 \tau_{0} / r_{\mathrm{s}} $ | (4) |
利用Dupuit-Forchheimer关系V=φv(V为渗流速度,v为实际流速,φ为孔隙度)和毛细管渗透率关系式K=φrs2/8(K为水在砂卵石地层的渗透率),即可将式(3)化为
| $ \begin{aligned} V=&-\frac{K}{\mu}\left[1-\frac{4}{3}\left(\frac{\lambda}{-\mathrm{d} p / \mathrm{d} l}\right)+\frac{1}{3}\left(\frac{\lambda}{-\mathrm{d} p / \mathrm{d} l}\right)^{4}\right] \frac{\mathrm{d} p}{\mathrm{d} l}, \\ &\left|\frac{\mathrm{d} p}{\mathrm{d} l}\right|>\lambda \end{aligned} $ | (5) |
宾汉姆流体在克服启动压力梯度后与牛顿流体类似,根据不均匀毛细管组理论,宾汉姆流体透过多孔介质的有效渗透率Kp与牛顿流体通过多孔介质的渗透率K相等,即为介质的绝对渗透率K.
将式(5)推广到三维情形,宾汉姆流体渗流的广义达西定律可表示为
| $ V=-\frac{K}{\mu} \nabla p\left[\left(1-\frac{\lambda}{|\nabla p |}\right)-\\~~~~~\frac{1}{3} \frac{\lambda}{\nabla p}\left(1-\frac{\lambda^{3}}{|\mathbb{\nabla} p|^3}\right)\right] $ | (6) |
为简化计算,将式(6)中括号内的高次项省略,该简化的合理性在参数确定部分给出,式(6)可简化为
| $ V=-\frac{K}{\mu} \nabla p\left[1-\frac{\lambda}{|\nabla p |}\right] $ | (7) |
根据质量守恒原理,弱压缩流体球面不定常渗流连续性方程可表示为
| $ -\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \cdot v_{r}\right)=\phi c_{\mathrm{f}} \frac{\partial p}{\partial t} $ | (8) |
式中:vr为流体球形扩散时的径向流速;cf为流体的压缩系数.
对于稳态渗流,式(8)中∂p/∂t=0,因此稳态渗流球面连续性方程可写成
| $ \frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \cdot v_{\mathrm{r}}\right)=0 $ | (9) |
将式(7)代入式(9),可求得宾汉姆流体球面渗流微分方程为
| $ \frac{\partial^{2} p}{\partial r^{2}}+\frac{2}{r} \frac{\partial p}{\partial r}+\frac{2 \lambda}{r}=0, \left|\frac{\partial p}{\partial r}\right|>\lambda $ | (10) |
壁后注浆过程中,假设注入浆液属于宾汉姆流体,而地下水属于牛顿流体,忽略流体重力和压缩性,该模型渗流微分方程和边界条件如下:
| $ \left.\begin{array}{ll}{\frac{\partial^{2} p_{1}}{\partial r^{2}}+\frac{2}{r} \frac{\partial p_{1}}{\partial r}+\frac{2 \lambda}{r}=0, } & {r_{0}<r \leqslant r(t)} \\ {\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial p_{2}}{\partial r}\right)=0, } & {r(t) \leqslant r<r_{{\rm w}}} \\ {p_{1}=p_{0}, } & {r=r_{0}} \\ {p_{2}=p_{{\rm w}}, } & {r=r_{{\rm w}}}\end{array}\right\} $ | (11) |
式中:下标1代表浆液渗流区域,下标2代表地下水渗流区域;r0为注浆管半径,p0为r0处的注浆压力;rw为注浆扰动范围,pw为rw处的地下水压力.
在浆液锋面r=r(t)处,压力和流量连续,有
| $ \left.\begin{array}{c}{2 \mathsf{π} r^{2}\left[-\frac{K_{1}}{\mu_{1}} \frac{\partial p_{1}}{\partial r}\left(1-\lambda\left(-\frac{\partial p_{1}}{\partial r}\right)^{-1}\right)\right]=} \\ {-2 \mathsf{π} r^{2} \frac{K_{2}}{\mu_{2}} \frac{\partial p_{2}}{\partial r}} \\ {p_{1}=p_{2}}\end{array}\right\} $ | (12) |
式中:μ1、μ2分别为浆液、水的黏度系数,K1、K2分别为浆液渗流区域、地下水渗流区域渗透率.
令∂p1/∂r=Y1, ∂p2/∂r=Y2,据式(11)可得:
| $ \left.\begin{array}{l}{\frac{\partial Y_{1}}{\partial r}+\frac{2}{r} Y_{1}+\frac{2 \lambda}{r}=0} \\ {\frac{\partial Y_{2}}{\partial r}+\frac{2}{r} Y_{2}=0}\end{array}\right\} $ | (13) |
解得Y1=-λ-C1/r2, Y2=C2/r2,故
| $ \left.\begin{array}{l}{p_{1}=C_{1} r^{-1}-\lambda r+C_{3}} \\ {p_{2}=-C_{2} r^{-1}+C_{4}}\end{array}\right\} $ | (14) |
根据式(11)、(12)、(14)得出:
| $ \left.\begin{array}{l}{p_{0}=} {C_{1} \frac{1}{r_{0}}-\lambda r_{0}+C_{3}} \\ {p_{\mathrm{w}}=} {-C_{2} \frac{1}{r_{\mathrm{w}}}+C_{4}} \\ {C_{1} \frac{1}{r(t)}-\lambda r(t)+C_{3}=-C_{2} \frac{1}{r(t)}+C_{4}-} \\ {\quad \frac{K_{1}}{\mu_{1}}\left(-\frac{C_{1}}{r(t)^{2}}\right)=-\frac{K_{2}}{\mu_{2}} \frac{C_{2}}{r(t)^{2}}}\end{array}\right\} $ | (15) |
令K1/μ1/K2/μ2=M,当浆流区和水流区地层渗透率相同时,则M为水的黏度与浆液的黏度比,M=μ2/μ1,根据式(11)中的边界条件解得:
| $ C_{1}=\frac{p_{\mathrm{w}}-p_{0}-\lambda\left(r_{0}-r(t)\right)}{\left(\frac{1}{r(t)}-\frac{1}{r_{0}}\right)-M\left(\frac{1}{r(t)}-\frac{1}{r_{\mathrm{w}}}\right)} $ | (16) |
令式(16)中A=pw-p0-λr0,B=1-M,D=M/rw-1/r0,则式(16)可改写为
| $ C_{1}=\frac{A+\lambda r(t)}{D+B / r(t)} $ | (17) |
将式(17)代入式(14)、(15),可解得浆液扩散区域和地下水分布区域的压力分布如下:
| $ \begin{aligned} p_{1}=& \frac{A+\lambda r(t)}{[D+B / r(t)] r}-\lambda r+p_{0}-\\ & \frac{A+\lambda r(t)}{[D+B / r(t)] r_{0}}+\lambda r_{0} \end{aligned} $ | (18) |
| $ \begin{aligned} p_{2}=& \frac{M[A+\lambda r(t)]}{[D+B / r(t)] r}+p_{\mathrm{w}}-\\ & \frac{M[A+\lambda r(t)]}{[D+B / r(t)] r_{\mathrm{w}}} \end{aligned} $ | (19) |
为保证计算结果的准确性,计算浆液流量时采用未简化的广义达西定律进行计算,因此根据式(18)及式(6)可以求得流量Q(r)为
| $ \begin{aligned} Q(r)=&-\frac{A K_{1}}{\mu_{1}}\left[\frac{\lambda}{3}-\frac{A+\lambda r(t)}{(D+B / r(t)) r(t)^{2}}-\right.\\ &\left.\frac{\lambda^{4}}{3}\left(\lambda+\frac{A+\lambda r(t)}{(D+B / r(t)) r(t)^{2}}\right)^{-3}\right] \end{aligned} $ | (20) |
将式(20)所表示的Q(r)除以有效过水面积,得到:
| $ \begin{aligned} \frac{\mathrm{d} r(t)}{\mathrm{d} t}=&-\frac{K_{1}}{\varphi \mu_{1}}\left[\frac{\lambda}{3}-\frac{A+\lambda r(t)}{(D+B / r(t)) r(t)^{2}}-\right.\\ &\left.\frac{\lambda^{4}}{3}\left(\lambda+\frac{A+\lambda r(t)}{(D+B / r(t)) r(t)^{2}}\right)^{-3}\right] \end{aligned} $ | (21) |
该微分方程的原函数无法用基本函数表示,因此该方程无解析解,可采用数值方法求数值解.
由式(18)和式(19)可得浆液对管片产生的压力Fg为
| $ F_{\mathrm{g}}=\int_{r_{0}}^{r(t)} 2 \mathsf{π} r p_{1} \mathrm{d} r+\int_{0}^{r_{0}} 2 \mathsf{π} r p_{0} \mathrm{d} r $ | (22) |
针对盾尾间隙的影响,本文采用文献[1]提出的等效孔隙度代替土层本身孔隙率,盾尾间隙体积为πr2d,考虑浆液球形扩散,则土体等效孔隙度为
| $ \phi=\eta'=\eta+\frac{3 d(1-\eta)}{2 R} $ | (23) |
式中:R为盾构间隙对周边地层扰动的影响范围,根据黎春林等[9]相关研究,地层扰动范围可取5 m;d为盾尾间隙厚度;η为原始土体孔隙率.
2.2.2 渗透率K广义达西定律中的渗透率K与地层的渗透系数k有一定的区别.渗透率K是揭示土体或岩体本身传导液体能力的参数,其与孔隙率、渗流方向上孔隙形态、粒度及排列方向等有关,而与液体自身性质无关;渗透系数k(水力传导系数)表征流体通过孔隙的难易程度,与液体自身性质有关.地层的渗透率可通过地层的渗透系数计算:
| $ K=\frac{k \mu}{\gamma} $ | (24) |
式中:K为地层的渗透率;k为地层的渗透系数;μ为流体粘度系数;γ为流体重度.
2.2.3 渗流速度V为验证式(6)简化为式(7)的合理性,结合盾构施工过程,取基本计算参数如表 2所示.
| 下载CSV 表 2 基本参数 Tab.2 Basic parameters |
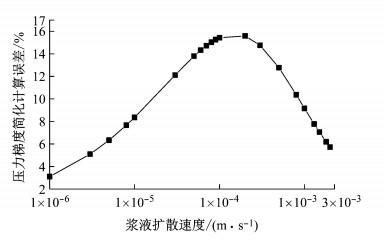
根据表 2的基本参数,通过式(18)、式(6)、式(7)可试算浆液的扩散速度.试算表明:注浆时间为10 s时,浆液的扩散速度分别为0.001 4 m·s-1(未简化)、0.001 5 m·s-1(简化),之后随着时间的增加浆液扩散速度逐渐减小.为检验浆液扩散速度式(6)的简化对计算压力梯度的影响,在浆液扩散速度1×10-6~2×10-3m·s-1范围内选取代表值,计算式(6)简化前后的压力梯度,结果如图 3所示.
|
图 3 压力梯度简化计算误差 Fig.3 Deviation of the simplified calculation of pressure gradient |
由图 3可知,根据式(7)计算得到的压力梯度误差随浆液扩散速度的增加呈先增大后减小趋势,在浆液扩散的局部阶段误差较大,在注浆初期和后期误差较小,基本满足工程要求,因此认为在推导浆液压力分布函数时,采用式(7)是合理的.
3 驱替效应分析 3.1 浆流区与水流区压力分布浆液驱替渗透扩散模型基于浆液与地下水界面的压力、流量连续的条件建立,首先针对浆液(浆流区)和地下水(水流区)渗透扩散区内流体压力的分布情况展开分析,基本参数如表 2所示.选取注浆时间分别为10、20、40、80、160、320、640、1 280、2 560、5 120 s,计算浆流区和水流区内的流体压力,如图 4所示.

|
图 4 注浆时间对流体压力分布的影响 Fig.4 Influence of grouting time effect on the distribution of the fluid in strata |
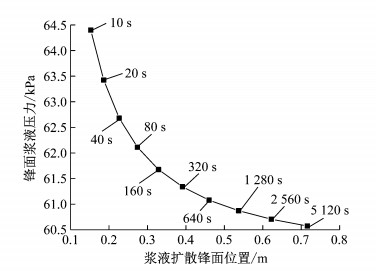
由图 4可知,浆液扩散区内的浆液压力随距注浆孔距离的增加而逐渐减小,同一注浆时刻浆液压力曲线呈下凹形;随着注浆时间的增加,距注浆孔同一距离处浆液压力逐渐升高,浆液压力提高幅度随距离注浆孔距离的增加而逐渐增大.不同注浆时间浆液扩散的锋面位置及锋面压力如图 4中矩形框标注,锋面处浆液压力值基本接近于地下水压力值.为进一步说明锋面处地下水压力的分布,绘制浆液锋面压力与扩散距离的关系曲线,如图 5所示.
|
图 5 不同注浆时刻锋面浆液压力 Fig.5 Grout pressure of different grouting time in the front |
由图 5可以看出,考虑浆液渗透扩散过程中的驱替效应时,浆液锋面压力随注浆时间的增加以及浆液扩散距离的增加而逐渐减小,浆液锋面压力曲线也呈下凹形.
3.2 浆液驱替效应对比分析基于3.1节对浆液压力分布函数的分析,结合文献[5]对比分析考虑浆液驱替效应时对浆液扩散半径、管片受力等的影响.不考虑浆液驱替效应时,地下水压力取为0.06 MPa,其余参数如表 2所示.
考虑浆液驱替效应时,浆液扩散过程所受的阻力增大.根据图 5可知,由于地下水压力的影响,浆液锋面压力与初始地下水压力的差值相对于注浆压力与初始地下水压力的差值较小,但驱替效应减缓了浆液的渗流扩散.由图 6可以看出,随着注浆时间的增加,浆液驱替效应对浆液扩散距离的影响逐渐明显.因此,在浆液渗透扩散分析中,引入浆液对地下水的驱替效应具有重要意义.

|
图 6 驱替效应对浆液扩散距离的影响 Fig.6 Influence of grout displacement effect on diffusion radius |
在考虑驱替效应的基础上,本节进一步分析地下水压力、注浆压力对浆液渗透扩散过程的影响,并结合相关试验进行讨论说明.
4.1 地层地下水压力的影响考虑浆液驱替效应,取rw=5 m处地下水压力分别为:0、0.02、0.04、0.06、0.08、0.10 MPa,其他参数如表 2所示,分析地下水压力对浆液扩散半径、管片受力的影响.
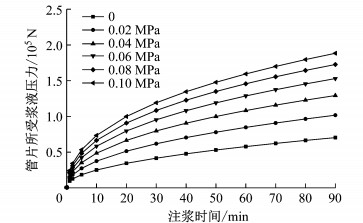
由图 7可知,浆液扩散速率随注浆时间的增加而减小,相同注浆时间内浆液的扩散距离随地下水压力的增加而减小.根据式(21),当浆液扩散距离的变化率趋于0时,浆液最终扩散距离分别为:3.41、3.22、3.02、2.83、2.64、2.44 m,即地下水压力每增加0.02 MPa时,浆液最终扩散距离减小约0.2 m.由图 8可以看出,地下水压力对壁后注浆在管片上产生的浆液压力影响较大,当地下水压力由0增加到0.10 MPa时,管片所受压力增大1倍以上.

|
图 7 浆液扩散距离与注浆时间的关系 Fig.7 Grout diffusion radius vs. grouting time |
|
图 8 管片所受注浆压力与注浆时间关系 Fig.8 Total pressure in segments vs. grouting time |
取rw=5 m处地下水压力pw=0.02 MPa,其他参数见表 2,计算注浆压力为0.25、0.30、0.35、0.40、0.45和0.50 MPa时浆液扩散半径、管片结构受力.
由图 9可以看出,随注浆时间的增加,不同注浆压力下浆液扩散半径的差值逐渐增加,由式(21)可知,浆液最终扩散距离分别为:4.67、4.18、3.70、3.22、2.73、2.25 m,注浆压力每增加0.05 MPa,浆液最终扩散距离约增大0.5 m.管片结构受力随注浆时间的变化与图 8基本相似,当注浆压力由0.25增加到0.50 MPa时,浆液对管片压力增加了约1倍,注浆压力的变化对管片结构的受力有显著影响.
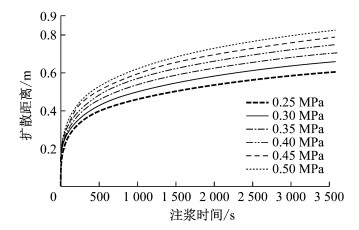
|
图 9 浆液扩散距离与注浆时间的关系 Fig.9 Grout diffusion radius vs. grouting time |
第3节分析表明:考虑浆液驱替效应时,浆液的扩散距离显著减小(注浆时间1 h,浆液扩散距离减小约23%),因此在分析盾构壁后注浆扩散过程时需考虑浆液驱替效应.根据对地下水压力、注浆压力等因素的分析,可以看出浆液扩散距离、管片结构受力等受地下水压力等因素的影响显著.另外,本文中浆液扩散距离、管片结构受力等随各影响因素的变化规律与文献[5]中所描述的规律相似,说明本文在考虑浆液驱替效应影响下,所建立的浆液驱替扩散模型能较好地反映浆液的扩散过程.
为进一步说明本文模型的合理性,选取文献[10]描述的室内盾构壁后同步注浆模型试验进行对比分析.文献[10]描述了均匀级配透明土(孔隙比0.6)中浆液的渗透扩散过程,试验结果表明:各注浆孔附近浆液的扩散范围基本呈半球形;注浆压力为3.0 kPa时,浆液的扩散范围约为1.3~1.5 cm;注浆压力为4.0 kPa时,浆液的扩散范围约为1.6~1.8 cm;模型试验的几何相似比为100:1,注浆压力0.35 MPa时,浆液的扩散范围约为1.5~1.7 m.4.1节计算表明:注浆压力为0.35 MPa,地下水压力为0时,浆液的最终扩散半径为3.41 m,该种情况考虑了在恒定注浆压力浆液的最大扩散距离.本文计算结果和试验结果具有一定差异,主要是由于试验地层的孔隙率(η=0.375)与本文采用的孔隙率(η=0.3)不同,另外浆液在地层中的扩散距离与注浆压力并非呈线性关系,采用相似比进行外推会有一定的差异性,以及试验中浆液的扩散时间有限.虽然目前针对盾构隧道壁后注浆的现场实测、室内试验等相关研究较多,但这些研究主要关注了壁后注浆施工引起的地层、管片的受力变形等,对浆液在地层中扩散形态的关注较少,本文尝试从浆液扩散形态方面对盾构壁后注浆浆液扩散过程进行验证说明.
5 结论基于砂卵石地层盾构壁后注浆过程中浆液对地下水的驱替效应,通过理论推导及参数分析研究了宾汉姆流型浆液的渗透扩散过程及浆液扩散在管片表面产生的压力等.主要得出如下结论:
(1) 根据砂卵石地层盾构壁后注浆施工过程,考虑浆液对地下水的驱替效应,以宾汉姆流体为研究对象,对其渗流运动方程广义达西定律进行简化,运用渗流力学相关理论推导了盾构壁后注浆浆液驱替渗透球形扩散模型.
(2) 考虑浆液驱替效应时,浆液扩散区内浆液压力、浆液扩散锋面压力呈下凹曲线,随着浆液扩散距离的增加,驱替效应对浆液扩散的影响更加显著,注浆时间1h时浆液扩散距离减小约23%.
(3) 盾构壁后注浆施工中,地下水压力、注浆压力的变化对浆液扩散距离、管片受力具有显著影响,盾构壁后注浆参数设计时需考虑浆液驱替效应的影响.
| [1] |
叶飞.软土盾构隧道施工期上浮机理分析及控制研究[D].上海: 同济大学, 2007. YE Fei. Analysis and control for upward movement of shield tunnel during construction[D].Shanghai: Tongji University, 2007. |
| [2] |
叶飞, 苟长飞, 刘燕鹏, 等. 盾构隧道壁后注浆浆液时变半球面扩散模型[J]. 同济大学学报(自然科学版), 2012, 40(12): 1789 YE Fei, GOU Changfei, LIU Yanpeng, et al. Half-spherical surface diffusion model of shield tunnel back-filled grouts[J]. Journal of Tongji University (Natural Science), 2012, 40(12): 1789 DOI:10.3969/j.issn.0253-374x.2012.12.008 |
| [3] |
於昌荣.砂砾地层盾构施工注浆效应及作用机理研究[D].上海: 上海交通大学, 2011. YU Changrong. Research on grouting influence and mechanism of shield tunneling in the sand-gravel stratum [D]. Shanghai: Shanghai Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011298101.htm |
| [4] |
刘健, 张载松, 韩烨, 等. 考虑黏度时变性的水泥浆液盾构壁后注浆扩散规律及管片压力模型的试验研究[J]. 岩土力学, 2015, 36(2): 361 LIU Jian, ZHANG Zaisong, HAN Ye, et al. Backfilled grouting diffusion law and model of pressure on segments of shield tunnel considering viscosity variation of cement grout[J]. Rock and Soil Mechanics, 2015, 36(2): 361 |
| [5] |
陈治.砂性地层盾构隧道同步注浆浆液渗透扩散机理研究[D].西安: 长安大学, 2016. CHEN Zhi. Study on mechanism of penetration and diffusion of synchronous grouting for shield tunnel in sandy stratum [D].Xi'an: Chang'an University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10710-1016749846.htm |
| [6] |
阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报, 2005, 27(1): 69 RUAN Wenjun. Research on diffusion of grouting and basic properties of grouts[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69 DOI:10.3321/j.issn:1000-4548.2005.01.011 |
| [7] |
戈尔布诺夫A T.异常油田开发[M].张树宝译.北京: 石油工业出版社, 1987. ГОРЪУНОВ А Т. The development of the singular oil field[M]. Translated by ZHANG Shubao. Beijing: Petroleum Industry Press, 1987. |
| [8] |
孔祥言, 陈峰磊, 陈国权. 非牛顿流体渗流的特性参数及数学模型[J]. 中国科学技术大学学报, 1999, 29(2): 141 KONG Xiangyan, CHEN Fenglei, CHEN Guoquan. Mathematical models and feature parameters of non-newtonian liquid flows in porous media[J]. Journal of University of Science and Technology of China, 1999, 29(2): 141 |
| [9] |
黎春林, 缪林昌. 盾构隧道施工土体扰动范围研究[J]. 岩土力学, 2016, 37(3): 759 LI Chunlin, MIAO Linchang. Determination of the range of shield tunneling-induced soil disturbance[J]. Rock and Soil Mechanics, 2016, 37(3): 759 |
| [10] |
李文涛.基于人工合成透明土盾构隧道壁后同步注浆模型试验研究[D].北京: 北京交通大学, 2015. LI Wentao. Model test of shield tunnel backfill grouting using synthetic transparent soil[D]. Beijing: Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015593693.htm |
 2019, Vol. 47
2019, Vol. 47

