2. 安徽明天氢能科技股份有限公司,安徽 六安 237000;
3. 同济大学 机械与能源工程学院,上海 201804
2. Anhui Mingtian Hydrogen Energy Technology Co., Ltd., Lu'an 237000, China;
3. School of Mechanical Engineering, Tongji University, Shanghai 201804, China
质子交换膜燃料电池(PEMFC, proton exchange membrane fuel cell)因其零污染、能量转换效率高、启动响应迅速和燃料来源广泛等特点被视为未来最有前景的车用动力来源之一[1-2].作为动力源的燃料电池欲实现大规模应用须经受高电位、启停、反极、极限电流和冷启动等严苛工况.其中,零下冷启动问题来源于低温启动过程中冰的形成覆盖电化学活性位点和阻塞反应气传输通道,造成电化学反应启动失败和耐久性降低[3-4].目前,有关燃料电池低温启动过程的数值模拟研究均聚焦在宏观尺度下的水热传递、反应气传质和相变等行为,以求解一维和三维微分或偏微分方程组为主要形式.如Jiao等[5-6]采用有限体积法的思想对燃料电池内的物理和化学现象建立一系列偏微分方程组,实现对输出电压和冰体积分数等宏观量的直接观察;许等[7]基于分层集总参数方法对燃料电池单电池进行一维冷启动数值建模,在单电池内每一个组件中心处进行建模和研究.但上述文献[5-7]研究考察现象均为整片单电池宏观尺度下的物理和化学行为.此外,目前有关燃料电池低温启动实验研究中可挖掘数据较少,除输出电压、欧姆阻抗和温度等结果参数外,若不借助X射线成像等高成本手段无法观察电池内部机理.再者,介观模拟尺度下燃料电池多孔介质内低温结冰研究和报道还未见.
相较宏观方法,由于演化方程简单、易并行计算和边界条件处理简单等优势,格子Boltzmann(LB)方法在多孔介质两相流等方面逐渐发挥了广泛应用[8-10].作为介观模拟尺度的代表之一,格子Boltzmann方法观察流体分子的速度分布函数,通过考察分子的时空演化过程并根据分布函数与宏观量之间的关系来获得宏观流体信息.格子Boltzmann方法与宏观模型的相同点是两者都为微观分子的统计学量,不在乎分子对描述对象的影响,不同之处在于前者没有连续性假设;与微观分子模型的相同点在于两者都从微观层次观察流体分子的运动状态,不同之处在于后者表现单个分子的行为,前者是微观分子的统计行为.
近年来,格子Boltzmann在多孔介质液固相变研究领域有些发展,主要有表征体元(REV)尺度和孔隙尺度.REV尺度的研究对象为一个控制体,求解控制体内体积平均宏观物理量,不关心微观结构,仅依赖于统计参数;孔隙尺度下的格子Boltzmann方法研究对象为流体分子团,多孔介质的骨架为流场和温度场的边界.目前有关格子Boltzmann方法在多孔介质相变领域的研究较少,且多数集中在REV尺度下的融化过程[11-14],如Gao等[12]对REV尺度下多孔介质方腔内的融化过程进行建模研究,考察孔隙率、Darcy数和Rayleigh数对自然对流的影响.此外,最近一些学者[15-17]对孔隙尺度下多孔介质内融化相变问题展开了相关研究,如杲东彦等[15]研究了正方形有序排列组成的多孔介质中Rayleigh数和Prandtl数对融化的影响.上述研究中所构建的多孔介质结构缺乏真实物理背景;此外,由于相变储能系统中液固两相的热物理参数差别较小,一些研究中假设液固两相热物理参数相同,但液态水对应液相和固相的比热容和导热系数差异较大,因此上述研究缺乏对液固两相不同热物理性参数的考察.本文通过构造燃料电池用真实气体扩散层三维微孔隙结构,严格考察凝固模型中液态水、固体冰和燃料电池用碳纤维的热物理参数,首次采用基于格子Boltzmann方法的液固相变模型研究了燃料电池气体扩散内液态水的结冰过程,从介观角度加深对燃料电池多孔介质内结冰机理的理解.
1 Boltzmann模型 1.1 速度场格子Boltzmann模型目前,基于格子Boltzmann方法的相变模型主要有相场法和焓方法.本文采用Huang学者[18-19]提出的固液相变总焓格子Boltzmann方法,该方法可以高效处理非线性潜热源项,避免焓值迭代计算和线性方程组求解,且可以实现相界面处变热物性的处理.由于结冰为相变问题,计算区域涉及液相和固相,需特殊处理以实现固相速度无滑移条件.网格点处的固相率实质上为单元内的平均固相率,因此,Huang学者提出了体积格子Boltzmann格式处理固相速度无滑移条件.鉴于LB方程的多松弛时间(MRT)处理可以使用多个松弛时间参数,具备多个调节参数,在数值稳定性和基本物理原理等方面具有明显优势,本研究中对于速度场和温度场,都采用MRT形式.
首先,未考虑固相效应的临时速度分布函数fi*的MRTLB方程为
| $ \begin{array}{*{20}{c}} {f_i^*\left( {\mathit{\boldsymbol{x}} + {e_i}{\delta _t},t + {\delta _t}} \right) = {f_i}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}}\left[ {{f_j}\left( {\mathit{\boldsymbol{x}},t} \right) - } \right.}\\ {\left. {f_j^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] + \left( {{\delta _{ij}} - \frac{{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}}}}{2}} \right){\delta _t}{F_{vj}}\left( {\mathit{\boldsymbol{x}},t} \right)} \end{array} $ | (1) |
式中:fi(x, t)为对应地点x处和时间t的速度分布函数;ei为离散速度;δt为格子时间步长;Λij为碰撞矩阵;fjeq(x, t)为当前时空下平衡态分布函数;Fvj(x, t)为外力项;δij为克罗内克符号.
格子Boltzmann方程一般分为碰撞过程和迁移过程.在计算过程中,碰撞步在矩空间执行,迁移步在速度空间执行.碰撞步在矩空间的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{\bar m}}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{m}}\left( {\mathit{\boldsymbol{x}},t} \right) - \mathit{\boldsymbol{S}}\left[ {\mathit{\boldsymbol{m}}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{m}}^{{\rm{eq}}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\delta _t}\left( {\mathit{\boldsymbol{I}} - \frac{\mathit{\boldsymbol{S}}}{2}} \right){\mathit{\boldsymbol{F}}_{\rm{m}}}\left( {\mathit{\boldsymbol{x}},t} \right) \end{array} $ | (2) |
式中:m (x, t)= Mf(x, t)= M [fi(x, t)]T为速度分布函数矩;m (x, t)为碰撞步执行以后的矩,在此基础上通过式
| $ \mathit{\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}} 1&1&1&1&1&1&1&1&1\\ { - 4}&{ - 1}&{ - 1}&{ - 1}&{ - 1}&2&2&2&2\\ 4&{ - 2}&{ - 2}&{ - 2}&{ - 2}&1&1&1&1\\ 0&1&0&{ - 1}&0&1&{ - 1}&{ - 1}&1\\ 0&{ - 2}&0&2&0&1&{ - 1}&{ - 1}&1\\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1}\\ 0&0&{ - 2}&0&2&1&1&{ - 1}&{ - 1}\\ 0&1&{ - 1}&1&{ - 1}&0&0&0&0\\ 0&0&0&0&0&1&{ - 1}&1&{ - 1} \end{array}} \right) $ | (3) |
| $ \mathit{\boldsymbol{S}} = {\rm{diag}}\left( {{s_0},{s_e},{s_\varepsilon },{s_j},{s_q},{s_p},{s_p}} \right) $ | (4) |
迁移步在速度空间下的表达式为
| $ {f_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}{\delta _t},t + {\delta _t}} \right) = {{\bar f}_i}\left( {\mathit{\boldsymbol{x}},t} \right) $ | (5) |
平衡态矩函数meq(x, t)为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{m}}^{{\rm{eq}}}} = \left( {\rho , - 2\rho + 3\frac{{{\mathit{\boldsymbol{u}}^2}}}{{{c^2}}},\rho - 3{\rho _0}\frac{{{\mathit{\boldsymbol{u}}^2}}}{{{c^2}}},{\rho _0}\frac{{{u_x}}}{c}, - {\rho _0}\frac{{{u_x}}}{c},} \right.}\\ {{{\left. {{\rho _0}\frac{{{u_y}}}{c}, - {\rho _0}\frac{{{u_y}}}{c},{\rho _0}\frac{{u_x^2 - u_y^2}}{{{c^2}}},{\rho _0}\frac{{{u_x}{u_y}}}{{{c^2}}}} \right)}^{\rm{T}}}} \end{array} $ | (6) |
式中:ρ0为参考密度;c为格子速度,c=δx/δt, δx为格子单位长度;u为速度矢量.矩空间的离散作用力项为
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_{\rm{m}}}\left( {\mathit{\boldsymbol{x}},t} \right) = \left( {0,6\frac{{\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{u}}}}{{{c^2}}}, - 6\frac{{\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{u}}}}{{{c^2}}},\frac{{{F_x}}}{c}, - \frac{{{F_x}}}{c},\frac{{{F_y}}}{c},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. { - \frac{{{F_y}}}{c},2\frac{{{F_x}{u_x} - {F_y}{u_y}}}{{{c^2}}},\frac{{{F_x}{u_x} + {F_y}{u_y}}}{{{c^2}}}} \right)^{\rm{T}}} \end{array} $ | (7) |
固相的出现不影响任意格点处的质量守恒关系,格点处的宏观密度根据临时速度分布函数计算,表达式为
| $ \rho = \sum\limits_0^8 {f_i^*} $ | (8) |
由于固相不运动,假设介观尺度下固相对应的速度分布函数一直处于平衡状态,固相使得临时速度分布函数中固相对应的部分趋于平衡态.因此,格点处速度分布函数表示为
| $ {f_i} = \left( {1 - {f_{\rm{s}}}} \right)f_i^* + {f_{\rm{s}}}f_i^{{\rm{eq}}}\left( {\rho ,{\mathit{\boldsymbol{u}}_{\rm{s}}}} \right) $ | (9) |
式中:fs为固相率; us为固相速率.
根据速度分布函数计算宏观速度,即:
| $ {\rho _o}\mathit{\boldsymbol{u}} = \sum\limits_{i = 0}^8 {{e_i}{f_i}} + \frac{{{\delta _t}}}{2}\mathit{\boldsymbol{F}} $ | (10) |
格子Boltzmann方程可以通过Chapman-Enskog多尺度分析推导出宏观方程.速度分布函数的格子Boltzmann方程对应的二阶近似宏观方程为
| $ {\partial _{\rm{t}}}\rho + \nabla \cdot \left( {{\rho _0}\mathit{\boldsymbol{u}}} \right) = 0 $ | (11) |
| $ \begin{array}{l} {\partial _t}\left( {{\rho _0}\mathit{\boldsymbol{u}}} \right) + \nabla \cdot \left( {{\rho _0}\mathit{\boldsymbol{uu}}} \right) = - \nabla p + \mathit{\boldsymbol{F}} + \nabla \cdot \left[ {{\rho _0}\nu \left( {\nabla \mathit{\boldsymbol{u}} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\mathit{\boldsymbol{u}}\nabla } \right)} \right] + \nabla \left[ {{\rho _0}\left( {\zeta - \nu } \right)\nabla \cdot \mathit{\boldsymbol{u}}} \right] \end{array} $ | (12) |
式中:压力p=ρc2/3;运动粘度ν=c2δt(sp-1-0.5)/3;体积粘度ζ=c2δt(se-1-0.5)/3.
1.2 总焓格子Boltzmann模型在Jiaung等[20-21]的固液相变LB模型中,潜热源项以离散源项的形式添加在LB方程中,显式LB方程变为隐式,故而需要采用焓值迭代计算或线性方程组求解,计算量巨大.Huang等学者[18-19]构建了一种新的总焓LB模型,总焓分布函数gi(x, t)的MRTLB方程为
| $ \begin{array}{l} {g_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}{\delta _t},t + {\delta _t}} \right) = \\ \;\;\;\;\;\;\;\;\;{g_i}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ij}}\left[ {{g_j}\left( {\mathit{\boldsymbol{x}},t} \right) - g_j^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] \end{array} $ | (13) |
与速度分布函数的计算过程类似,总焓分布函数的碰撞步亦在矩空间进行,迁移步亦在速度空间进行,即:
| $ \mathit{\boldsymbol{\bar n}}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{n}}\left( {\mathit{\boldsymbol{x}},t} \right) - \mathit{\boldsymbol{R}}\left[ {\mathit{\boldsymbol{n}}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{n}}^{{\rm{eq}}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] $ | (14) |
| $ {g_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}{\delta _t},t + {\delta _t}} \right) = {{\bar g}_i}\left( {\mathit{\boldsymbol{x}},t} \right) $ | (15) |
式中: n (x, t)= Mg(x, t)= M [gi(x, t)]T为总焓分布函数的矩;n(x, t)为碰撞步执行以后的矩,在此基础上通过式
| $ \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} {{\sigma _0}}&0&0&0&0&0&0&0&0\\ 0&{{\sigma _e}}&0&0&0&0&0&0&0\\ 0&0&{{\sigma _\varepsilon }}&0&0&0&0&0&0\\ 0&0&0&{{\sigma _j}}&{\left( {{\sigma _j}/2 - 1} \right){\sigma _q}}&0&0&0&0\\ 0&0&0&0&{{\sigma _q}}&0&0&0&0\\ 0&0&0&0&0&{{\sigma _j}}&{\left( {{\sigma _j}/2 - 1} \right){\sigma _q}}&0&0\\ 0&0&0&0&0&0&{{\sigma _q}}&0&0\\ 0&0&0&0&0&0&0&{{\sigma _e}}&0\\ 0&0&0&0&0&0&0&0&0 \end{array}} \right) $ | (16) |
总焓平衡态矩函数neq(x, t)和参考比热容Cp, ref、总焓H、温度T和比热容Cp有关,表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{n}}^{{\rm{eq}}}} = \left( {H, - 4H + 2{C_{{\rm{p}},{\rm{ref}}}}T,4H - 2{C_{{\rm{p}},{\rm{ref}}}}T,{C_{\rm{p}}}T\frac{{{u_x}}}{c},} \right.\\ \;\;\;\;\;\;\;\;{\left. { - {C_{\rm{p}}}T\frac{{{u_x}}}{c},{C_{\rm{p}}}T\frac{{{u_y}}}{c}, - {C_{\rm{p}}}T\frac{{{u_y}}}{c},0,0} \right)^{\rm{T}}} \end{array} $ | (17) |
与之对应的总焓平衡态分布函数为
| $ g_i^{{\rm{eq}}} = \left\{ \begin{array}{l} H - \frac{4}{9}{C_{{\rm{p}},{\rm{ref}}}}T,i = 0\\ \frac{1}{{18}}{C_{{\rm{p}},{\rm{ref}}}}T + \frac{1}{3}{C_{\rm{p}}}T\frac{{{e_i} \cdot \mathit{\boldsymbol{u}}}}{{{c^2}}},i = 1,2,3,4\\ \frac{1}{{18}}{C_{{\rm{p}},{\rm{ ref }}}}T + \frac{1}{{12}}{C_{\rm{p}}}T\frac{{{e_i} \cdot \mathit{\boldsymbol{u}}}}{{{c^2}}},i = 5,6,7,8 \end{array} \right. $ | (18) |
总焓H的计算式为
| $ H = \sum\limits_{i = 0}^8 {{g_i}} $ | (19) |
温度T和固相率fs由总焓H确定,即:
| $ T = \left\{ \begin{array}{l} {T_{\rm{s}}} - \frac{{{H_{\rm{s}}} - H}}{{{C_{{\rm{p}},{\rm{s}}}}}},H \le {H_{\rm{s}}}\\ \frac{{{H_{\rm{l}}} - H}}{{{H_{\rm{l}}} - {H_{\rm{s}}}}}{T_{\rm{s}}} + \frac{{H - {H_{\rm{s}}}}}{{{H_{\rm{l}}} - {H_{\rm{s}}}}}{T_{\rm{l}}},{H_{\rm{s}}} < H \le {H_{\rm{l}}}\\ {T_{\rm{l}}} + \frac{{H - {H_{\rm{l}}}}}{{{C_{{\rm{p,l}}}}}},H \ge {H_1} \end{array} \right. $ | (20) |
| $ {f_{\rm{s}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{H_1} - H}}{{{H_1} - {H_{\rm{s}}}}},{H_{\rm{s}}} < H \le {H_1}}\\ {0,H \ge {H_1}} \end{array}} \right. $ | (21) |
式(20)~(21)中:Hs、Hl分别为固态和液态的总焓.
与速度分布函数类似,总焓MRT LB模型亦可以通过Chapman-Enskog分析推出宏观方程,即:
| $ {\partial _t}H + \nabla \cdot \left( {{C_{\rm{p}}}Tu} \right) = \nabla \cdot \left[ {\frac{{{C_{{\rm{p}},{\rm{ref}}}}}}{3}\left( {\frac{1}{{{\sigma _j}}} - \frac{1}{2}} \right)\nabla T} \right] $ | (22) |
宏观热扩散系数为
| $ \lambda /\left( {{\rho _0}{C_{{\rm{p}},{\rm{ref}}}}} \right) = {c^2}{\delta _t}\left( {\sigma _j^{ - 1} - 0.5} \right)/3 $ | (23) |
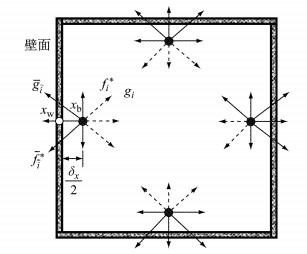
边界条件在数值模拟研究中至关重要.由于格点处的物理量通常代表网格单元内的平均值,基于半步长反弹思想,本文对速度无滑移边界条件和温度边界条件分别采用半步长反弹格式[22-23]和镜像半步长反弹格式[24-25]处理.如图 1所示,壁面格点xw离边界网格点xb半个网格步长,为δx/2,以图 1中左边边界网格点xb为例,第5方向的未知速度分布函数fi(xb, t+δt)和未知总焓分布函数gi(xb, t+δt)可以表示为
| $ {f_i}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t + {\delta _t}} \right) = {{\bar f}_{\bar i}}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t} \right) $ | (24) |
| $ {g_i}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t + {\delta _t}} \right) = - {{\bar g}_{\bar i}}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t} \right) + g_i^{{\rm{eq}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{w}}},t} \right) + g_i^{{\rm{eq}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{w}}},t} \right) $ | (25) |
|
图 1 边界条件处理示意图 Fig.1 Schematic of boundary condition treatment |
式中: i代表离散速度方向i和i相反,
| $ {g_i}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t + {\delta _t}} \right) = - {{\bar g}_{\bar i}}\left( {{\mathit{\boldsymbol{x}}_{\rm{b}}},t} \right) $ | (26) |
对于多孔介质微观结构的重构主要有两种方法:基于“图像”的重构方法和基于“随机”的重构方法[26].前者通常采用激光扫描显微镜和X射线断层摄影术等方法对多孔介质材料进行扫描,通过对扫描得到的二维图像进行计算机处理后得到微观结构,该方法基于实际材料,结构较为真实,但成本较高,受图像处理技术的限制;后者采用计算机的随机数字发生器生成材料典型的位置和方向特征,并提前设定规则来生成材料结构,该方法基于计算机,成本低,速度快,虽只能接近真实材料的微观孔隙结构,但对于目前的研究已足够.以下将介绍本文研究中气体扩散层微孔隙结构的重构方法及过程.
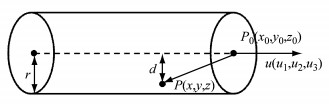
在孔隙尺度下,多孔介质可以看成由无数根半径相同的碳纤维杂乱无章的平铺层叠起来的.因此,在几何上可以简化为:无数根圆柱体重叠相交;圆柱体可以通过它的轴线方向向量u =(u1, u2, u3)、轴线通过的一点P0(x0, y0, z0)和圆柱体半径r唯一确定,如图 2所示;任意一根圆柱体可以定义为距离圆柱体轴线距离不大于圆柱体半径r的所有点的集合P(x, y, z);圆柱体内所有点的集合占据空间总体积比例为1与孔隙率ε的差值.
|
图 2 PEMFC碳纤维圆柱体模型 Fig.2 Cylindrical model for carbon fiber in proton exchange membrane fuel cell (PEMFC) |
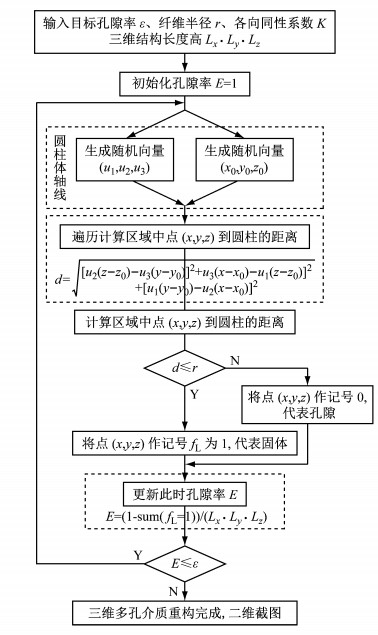
为了简化多孔介质孔隙结构的构建模型,作以下假设:①碳纤维呈笔直圆柱体形状;②所有碳纤维半径完全相同;③碳纤维存在重叠交叉的可能.图 3为本文多孔介质随机重构方法流程图.首先需要给出多孔介质的目标孔隙率ε、纤维半径r、各项同性系数K和三维结构的长宽高Lx·Ly·Lz,并且初始化孔隙率E=1.然后,利用Matlab中的随机函数rand随机生成圆柱体轴线的方向向量和通过轴线的一个点坐标,过程如下:
|
图 3 随机重构气体扩散层(GDL)微孔隙结构算法流程图 Fig.3 Flowchart of stochastic reconstruction algorithm for gas diffusion layer(GDL) micro-porous structure |
微尺度下碳纤维的重叠层交并不是均匀分布和各向同性的,多孔介质材料的各向异性可以看成制造过程中对材料施加外部压力导致的.如图 4所示,各向同性系数K可以定位为碳纤维最终厚度与初始厚度的比值,K=1代表完全各向同性,即最终厚度等于初始厚度.各向同性系数表达式为
| $ K = \frac{{\cos \theta }}{{\cos {\theta ^\prime }}} $ | (27) |

|
图 4 压缩对碳纤维方向角的影响 Fig.4 Effect of compression on orientation angle of carbon fiber |
在各向同性系数已知情况下,方向角度可从式(28)得到:
| $ \theta = {\cos ^{ - 1}}\left( {K\cos {\theta ^\prime }} \right) $ | (28) |
式中:θ′为初始碳纤维的方向角度,可由Matlab的rand函数给出;θ为碳纤维压缩后方向角度.
根据方向角度得出方向向量(u1, u2, u3),再通过圆柱体轴线的正交基准法向矢量和随机数rand函数,得到通过轴线的随机点(x0, y0, z0).在圆柱体方向向量、通过轴线的随机点以及碳纤维半径都确定后,通过while循环函数对三维空间中所有点遍历并判断当前点距离圆柱体轴线的距离是否小于碳纤维半径r,小于作记号f=1,否则作记号f=0,当前点距离圆柱轴线的距离公式见式(16).每生成一个圆柱体后,须判断当前孔隙率值,若E>ε,继续执行生成方向向量和随机点,反之,程序停止.
| $ d = \\ \sqrt {{{\left[ {{u_2}\left( {z - {z_0}} \right) - {u_3}\left( {y - {y_0}} \right)} \right]}^2} + {{\left[ {{u_3}\left( {x - {x_0}} \right) - {u_1}\left( {z - {z_0}} \right)} \right]}^2} + {{\left[ {{u_1}\left( {y - {y_0}} \right) - {u_2}\left( {x - {x_0}} \right)} \right]}^2}} $ | (29) |
本文取碳纤维半径r=3.5 μm,目标孔隙率分别为0.5、0.6、0.7、0.8和0.9,各向同性系数K=0.8,三维尺寸Lx·Ly·Lz=200 μm×200 μm×200 μm,模型比例为1个网格长度代表 1 μm.图 5为对应孔隙率分别为0.6的气体扩散层微孔隙三维结构视觉图,本文研究的二维气体扩散层为x方向1/2处的截取的平面.

|
图 5 孔隙率0.6气体扩散层微孔隙三维结构视图 Fig.5 Three-dimensional microporous structure view of gas diffusion layer with porosity 0.6 |
为了验证本文基于格子Boltzmann方法的燃料电池GDL内结冰模型的精确性和有效性,针对液、固和多孔介质三种材料的不同热物理参数进行了一维半无限大空间凝固热传导、二维直角区域凝固和二维介质方腔凝固的数值试验, 严格选取对应真实燃料电池GDL层内碳纤维、液态水和固体冰的热物理参数.注意,如没有特殊声明,本文涉及的数值皆为格子单位.
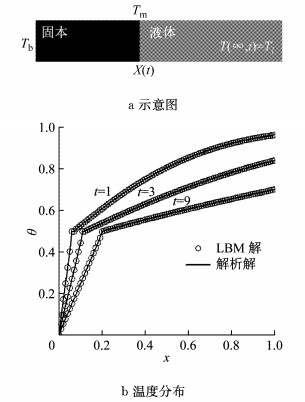
为了验证本文的凝固模型可以处理液固相变分界线两侧不同热物理参数问题,即液态水比热容Cpl和冰比热容Cps、液态水导热系数λl和冰λs不相同,进行了一维半无限大凝固热传导数值实验.如图 6所示,一维半无限大空间初始状态下充满温度Ti=1的液态,零时刻左侧壁面温度Tb骤降至0,液固分界线上的温度维持在Tm=0.5,液固分界线从左往右逐渐移动.相关参数设置如下:Cpl=1.0,Cps=2.0,Ss=0.004,Sl=0.008,λl=0.15,λs=0.6,其中液态水和冰Stefan数分别为Sl=Cpl(Ti-Tm)/L.Ss=Cps(Tm-Tb)/L.注意,本文所有的数值模拟均采用dx=dt=1,松弛因子设置为σ0=1.0,σ0=1/τg,σε=σe,σq=σj.图 6b为对应不同时刻下的温度θ随坐标x变化情况,LBM解和解析解[27]吻合良好.
|
图 6 一维半无限大空间凝固热传导数值实验 Fig.6 Temperature distribution for one-dimensional solidification test of half-space |
为了验证模型的使用适用于二维问题,进行了二维直角区域凝固数值试验.计算域和温度边界条件如图 7所示.初始状态下,方腔内充满温度Ti=0.3的液体,零时刻开始,方腔的左壁面和下壁面温度骤降至Tb=-1.0,方腔的上壁面和右壁面保持绝热状态,相关参数设置如下:Cpl=Cps=1.0,Sl=Ss=Cpl(Tm-Tb)/L=4.0,λl=λs=1.0.与Lin等的解析解[27]对比发现,Fo=0.25时刻的等温线和液固界面线吻合良好.

|
图 7 二维直角区域凝固数值试验 Fig.7 Two-dimensional solidification in semi-infinite corner |
为了验证本文模型适用于研究多孔介质方腔,进行了二维介质方腔凝固的数值试验.注意,由于引入了多孔介质,式(17)和式(18)中参考比热容Cp, ref定义为[28]:
| $ {C_{{\rm{p}},{\rm{ref}}}} = 3{C_{{\rm{ps}}}}{C_{{\rm{pl}}}}{C_{{\rm{pp}}}}/\left( {{C_{{\rm{ps}}}}{C_{{\rm{pl}}}} + {C_{{\rm{pl}}}}{C_{{\rm{pp}}}} + {C_{{\rm{ps}}}}{C_{{\rm{pp}}}}} \right) $ | (30) |
式中:Cpp多孔介质比热容.
如图 8a所示,在矩形方腔中心有一块矩形形状的介质,初始状态下,方腔内部充满温度为Ti=1.0的液相,方腔四周温度边界条件和二维直角区域凝固数值试验中相同.LBM数值模拟的相关参数设置如下:Cpl=Cps=1.0,Sl=Ss=Cpl(Tm-Tb)/L=0.251,λl=λs=0.575,Tm=0.5.Fluent数值模拟的相关参数设置如下:Cplphy=Cpsphy=4 182 J·kg-1·K-1,λlphy=λsphy=2.3 W·m-1·K-1,Sl=Ss=0.251.注意,由于Fluent相变模拟研究中,水的热物理参数液态和固态相同,为了简化处理,该数值试验部分假设液相和固相的热物理参数相同.图 8a为多孔介质方腔数值试验示意图,中间的黑色矩形区域为介质,初始状态下介质外充满液相,在左侧壁和下侧壁受低温影响下,液固分界线从左下逐渐往右上移动.图 8b为在Fo=0.01时刻的液固分界线,可以发现,LBM结果和Fluent结果吻合良好,说明本文模型可以准确地预测多孔介质中液态水、固体冰和碳纤维不同热物理参数条件下的凝固现象.

|
图 8 多孔介质方腔数值试验示意图和液固分界线 Fig.8 Schematic of solidification numerical experiment of cavity with porous and liquid-solid interface at Fo=0.01 |
首先,介绍格子单位和物理单位之间的换算关系.在本文的凝固相变模型中,Stefan数、量纲一温度θ和Fourier数F0的定义见式(31):
| $ {S_{\rm{l}}} = \frac{{{C_{{\rm{pl}}}}\left( {{T_i} - {T_{\rm{m}}}} \right)}}{L} $ | (31a) |
| $ \theta = \frac{{\left( {T - {T_{\rm{b}}}} \right)}}{{\left( {{T_i} - {T_{\rm{b}}}} \right)}} $ | (31b) |
| $ {F_0} = \frac{{\alpha t}}{{{L^2}}} $ | (31c) |
式中:α为导热系数; t为时间.
以量纲一温度θ和Fourier数F0为例, 说明格子单位和物理单位之间的换算过程,注意,以下表达式中的上标phy表示物理单位,不加上标为格子单位.本文研究初始温度Tiphy=20 ℃的液态水在GDL内的结冰过程,冰点Tmphy=0 ℃,外界低温Tbphy=-20 ℃,因此,根据式(31)中量纲一温度θ的表达式计算有初始温度θi=1,θb=0,θm=0.5.此外,本文选取二维GDL的长×宽为200 μm×200 μm,取1 μm=1 lu,即1个格子单位长度等于1 μm.根据Fophy=αphytphy/(Lphy)2=Fo=αt/L2可以得,实际时间tphy=αt(Lphy)2/(αphy(L)2),由于在格子Boltzmann相变研究领域,多数研究采用F0来间接表征时间进度,后续讨论亦采用该种方法.表 1为本文研究中碳纤维和液态水(冰)的热物理参数(LU代表格子单位,PU代表物理单位),其中碳纤维的热物理参数取自相关燃料电池三维宏观模拟的文献[5].
| 下载CSV 表 1 碳纤维、液态水和冰热物理参数 Tab.1 Thermophysical properties of carbon fiber, liquid water and ice |
在本文中,冰体积分数定义为孔隙内冰体积占据多孔介质中孔隙体积百分比.图 9表示不同孔隙率气体扩散层内结冰过程中冰体积分数随量纲一时间F0的变化关系.从图中可以看出,在冰体积分数小于0.1时,冰体积分数和量纲一时间F0呈现斜率较大的线性关系,大于0.1时,呈现斜率较低的线性关系.孔隙率越大,初始状态液态水体积分数越大,相同条件下完全结冰所用时间越长.

|
图 9 不同孔隙率气体扩散层内结冰过程中冰体积分数与F0变化关系 Fig.9 Variation of ice volume fraction with F0 in GDL with different porosity |
图 10为对应孔隙率0.6的气体扩散层方腔内50 %高度处自左侧壁向右侧壁的温度分布随时间变化情况,初始状态即F0 < 0时,自左至右温度都为θ=1,F0=0时,左侧壁温度骤降至θ=0.温度分布θ在不同时刻和不同区域表现出不同的变化趋势,比如当F0=0.01时,在θ < 0.5时为固相,且温度和位置呈现线性变化趋势,θ>0.5时为液相,温度θ < 1时表现出抛物线形状;F0=0.72时,θ < 0.5和θ>0.5区域温度都呈现线性变化趋势.此外,还可以发现,当某一时刻下的液相温度接近θ=0.5时,液固分界线右移速度放慢,原因是温度梯度较小,热传导放缓.

|
图 10 孔隙率为0.6气体扩散层结冰过程中方腔1/2高度处温度分布随时间变化情况 Fig.10 Variation of dimensionless temperature θ with time in 1/2 height for gas diffusion layer with porosity 0.6 |
对于均匀充满一种流体的方腔,在其左侧壁受低温热传导过程中,根据传热学原理,等温线应是垂直分布的.图 11为孔隙率0.6的GDL中在F0=0.72时刻的温度分布和液固分界线分布.由于相变温度θ=0.5,对应等温线中θ=0.5处为液固分界线点.对于等温线θ=0.5左侧的固体区域来说,由于碳纤维的导热系数大于固体冰的导热系数,导致碳纤维处的等温线比其他区域往右偏移,因此,对应等温线θ=0.5是凹凸不平的.图 11b为液固分界线示意图,分界线左侧为结冰区域,右侧为未结冰区域.

|
图 11 孔隙率为0.6的气体扩散层在F0=0.72的等温线和结冰情况 Fig.11 Isothermal curve and liquid-solid interface at F0=0.72 for gas diffusion layer with porosity 0.6 |
通过计算不同孔隙率的气体扩散层方腔内液态水结冰过程可以发现,对应气体扩散层孔隙率分别为0.5、0.6、0.7、0.8和0.9时,完全结冰所用量纲一时间F0分别为2.67、3.11、3.68、4.31和4.84.孔隙率越大,GDL完全结冰所用时间越久,因为孔隙率越大,液态水含量越多.此外,液固分界线基本呈现竖直状态并伴随凹凸不平现象逐渐从左向右移动.
自然对流是自然界中较为普遍的一种物理现象.由于流体内部存在温差,使得各部分流体的密度不同,温度较高的流体密度小会上浮,温度低的流体密度大会下沉,引起流体内的自然对流现象,自然对流现象在受热融化的相变问题中较为明显且研究较多.为了研究自然对流现象在燃料电池气体扩散层受冷凝固问题中的影响,本文对孔隙率从0.5~0.9气体扩散层方腔的左侧受冷凝固过程进行了研究.
研究发现,对应气体扩散层的孔隙率分别为0.5、0.6、0.7、0.8和0.9,有自然对流情况下的结冰时间比无自然对流时分别减少0、0、0.001、0.001和0.007.原因是GDL孔隙率越大,未被碳纤维封闭的液相区域越大,自然对流现象也越明显.图 12为对应孔隙率为0.6和0.36时刻的自然对流现象,箭头所指粗实线为液固分界线,带箭头细实线为流线.显然,流线主要集中在孔隙较大且密集的区域.

|
图 12 孔隙率为0.6气体扩散层内结冰过程中在F0=0.36时刻的自然对流现象 Fig.12 Natural convection phenomenon at F0=0.36 for gas diffusion layer with porosity 0.6 |
基于介观模拟尺度的格子Boltzmann方法,首次建立了孔隙尺度下燃料电池气体扩散层内液态水凝固模型,对孔隙率分别为0.5、0.6、0.7、0.8和0.9的二维200 μm×200 μm气体扩散层内微孔隙结构中液态水结冰过程进行数值模拟研究.主要成果如下:
(1) 引入格子Boltzmann方法到燃料电池用气体扩撒层内液态水结冰问题研究中,并且通过一维半无限大空间凝固热传导、二维直角区域凝固和二维介质方腔凝固三组数值试验验证了本文模型可以精确处理碳纤维、液态水和冰三种物质不同热物理参数的问题.
(2) 对应孔隙率分别为0.5、0.6、0.7、0.8和0.9时,气体扩散层孔中液态水完全结冰所用量纲一时间F0分别为2.67、3.11、3.68、4.31和4.84.气体扩散层孔隙率越大,完全结冰所用时间越多.
(3) 对应孔隙率分别为0.5、0.6、0.7、0.8和0.9时,有自然对流情况下的结冰时间F0比无自然对流时分别减少0、0、0.001、0.001和0.007.在燃料电池气体扩散层微孔隙内液态水结冰过程中,自然对流现象对结冰时间影响较小.
| [1] |
DAFALLA A M, JIANG F M. Stresses and their impacts on proton exchange membrane fuel cells: a review[J]. International Journal of Hydrogen Energy, 2018, 43(4): 2327 DOI:10.1016/j.ijhydene.2017.12.033 |
| [2] |
许澎, 高源, 许思传. 质子交换膜燃料电池停机后吹扫仿真[J]. 同济大学学报(自然科学版), 2017, 45(12): 1873 XU Peng, GAO Yuan, XU Sichuan. Numerical simulation on gas purge after shutdown in proton exchange membrane fuel cell[J]. Journal of Tongji University(Natural Science), 2017, 45(12): 1873 DOI:10.11908/j.issn.0253-374x.2017.12.019 |
| [3] |
LUO Y Q, JIAO K. Cold start analysis of proton exchange membrane fuel cell[J]. Progress in Energy and Combustion Science, 2018, 64: 29 DOI:10.1016/j.pecs.2017.10.003 |
| [4] |
YAO L, PENG J, ZHANG J B, et al. Numerical investigation of cold-start behavior of polymer electrolyte fuel cells in the presence of super-cooled water[J]. International Journal of Hydrogen Energy, 2018, 43(32): 15505 DOI:10.1016/j.ijhydene.2018.06.112 |
| [5] |
JIAO K, LI X. Three-dimensional multiphase modeling of cold start processes in polymer electrolyte membrane fuel cells[J]. Electrochimica Acta, 2009, 54(27): 6876 DOI:10.1016/j.electacta.2009.06.072 |
| [6] |
LUO Y, GUO Q, DU Q, et al. Analysis of cold start processes in proton exchange membrane fuel cell stacks[J]. Journal of Power Sources, 2013, 224(15): 99 |
| [7] |
许澎, 许思传, 郭鑫, 等. 一种质子交换膜燃料电池冷启动分层数值模型[J]. 同济大学学报(自然科学版), 2017, 47(1): 104 XU Peng, XU Sichuan, GUO Xin, et al. A layered numerical model for cold start in proton exchange membrane fuel cell[J]. Journal of Tongji University (Natural Science), 2017, 47(1): 104 |
| [8] |
郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009 GUO Zhaoli, ZHENG Chuguang. Theory and applications of Lattice Boltzmann method[M]. Beijing: Science Press, 2009 |
| [9] |
CHEN L, LUAN H B, HE Y L, et al. Pore-scale flow and mass transport in gas diffusion layer of proton exchange membrane fuel cell with interdigitated flow fields[J]. International Journal of Thermal Sciences, 2012, 51: 132 DOI:10.1016/j.ijthermalsci.2011.08.003 |
| [10] |
MOLAEIMANESH G R, GOOGARCHIN H S, MOQADDAM A Q. Lattice Boltzmann simulation of proton exchange membrane fuel cells-A review on opportunities and challenges[J]. International Journal of Hydrogen Energy, 2016, 41(47): 22221 DOI:10.1016/j.ijhydene.2016.09.211 |
| [11] |
GAO D, TIAN F B, CHEN Z, et al. An improved lattice Boltzmann method for solid-liquid phase change in porous media under local thermal non-equilibrium conditions[J]. International Journal of Heat and Mass Transfer, 2017, 110: 58 DOI:10.1016/j.ijheatmasstransfer.2017.03.014 |
| [12] |
GAO D Y, CHEN Z Q. Lattice Boltzmann simulation of natural convection dominated melting in a rectangular cavity filled with porous media[J]. International Journal of Thermal Sciences, 2011, 50(4): 493 DOI:10.1016/j.ijthermalsci.2010.11.010 |
| [13] |
LIU Q, HE Y L. Double multiple-relaxation-time lattice Boltzmann model for solid-liquid phase change with natural convection in porous media[J]. Physica A Statistical Mechanics and Its Applications, 2015, 438: 94 DOI:10.1016/j.physa.2015.06.018 |
| [14] |
WU W, ZHANG S, WANG S. A novel lattice Boltzmann model for the solid-liquid phase change with the convection heat transfer in the porous media[J]. International Journal of Heat and Mass Transfer, 2017, 104: 675 DOI:10.1016/j.ijheatmasstransfer.2016.08.088 |
| [15] |
杲东彦, 陈振乾, 孙东科. 泡沫金属内相变材料融化的格子Boltzmann方法孔隙尺度模拟研究[J]. 工程热物理学报, 2016, 37(2): 385 GAO Dongyan, CHEN Zhenqian, SUN Dongke. Lattice Boltzmann simulation of melting of phase change materials in metal foams at pore scale[J]. Journal of Engineering Thermophysics, 2016, 37(2): 385 |
| [16] |
王猛, 朱卫兵. 基于孔隙尺度的方腔内多孔介质融化模拟研究[J]. 哈尔冰工程大学学报, 2015, 36(6): 774 WANG Meng, ZHU Weibing. Simulation study for melting of porous media in a square cavity based on the pore scale[J]. Journal of Harbin Enginnering University, 2015, 36(6): 774 |
| [17] |
LI X Y, MA T, LIU J, et al. Pore-scale investigation of gravity effects on phase change heat transfer characteristics using lattice Boltzmann method[J]. Applied Energy, 2018, 222(15): 92 |
| [18] |
HUANG R, Wu H. Total enthalpy-based lattice Boltzmann method with adaptive mesh refinement for solid-liquid phase change[J]. Journal of Computational Physics, 2016, 315: 65 DOI:10.1016/j.jcp.2016.03.043 |
| [19] |
HUANG R, Wu H. Phase interface effects in the total enthalpy-based lattice Boltzmann model for solid-liquid phase change[J]. Journal of Computational Physics, 2015, 294: 346 DOI:10.1016/j.jcp.2015.03.064 |
| [20] |
JIAUNG W S, HO J R, KUO C P. Lattice Boltzmann method for the heat conduction problem with phase change[J]. Numerical Heat Transfer Part B Fundamentals, 2001, 39(2): 167 DOI:10.1080/10407790150503495 |
| [21] |
ChATTERJEE D, CHAKRABORTY S. An enthalpy-based lattice Boltzmann model for diffusion dominated solid-liquid phase transformation[J]. Physics Letters A, 2005, 341(1/4): 320 |
| [22] |
ZIEGLER D P. Boundary conditions for lattice Boltzmann simulations[J]. Journal of Statistical Physics, 1993, 71(5): 1171 |
| [23] |
HE X Y, ZOU Q, LUO L S, et al. Analytical solutions for simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model[J]. Journal of Statistical Physics, 1997, 87(1): 115 |
| [24] |
KUO L S, CHEN P H. Numerical implementation of thermal boundary conditions in the lattice Boltzmann method[J]. International Journal of Heat and Mass Transfer, 2009, 52(1/2): 529 |
| [25] |
ZHANG T, SHI B C, GUO Z L, et al. General bounce-back scheme for concentration boundary condition in the lattice-Boltzmann method[J]. Physical Review E, 2012, 85(1): 016701 DOI:10.1103/PhysRevE.85.016701 |
| [26] |
高源, 吴晓燕, 孙严博. 新型随机重构微孔隙介质模型与扩散特性[J]. 同济大学学报(自然科学版), 2017, 45(1): 109 GAO Yuan, WU Xiaoyan, SUN Yanbo. Characterization and diffusion in reconstruction gas diffusion layer based on stochastic method[J]. Journal of Tongji University(Natural Science), 2017, 45(1): 109 |
| [27] |
HAHN D W, OZISK M N. Heat conduction fundamentals, third edition[M].[S.l.]: John Wiley & Sons Inc, 2012.
|
| [28] |
黄荣宗.固液相变的格子Boltzmann方法及模拟研究[D].上海: 上海交通大学, 2017.
|
 2019, Vol. 47
2019, Vol. 47

