既有结构的定期检测和维护,是保障结构安全、正常服役的前提[1-3],而对结构损伤的准确识别则是进行检测和维护的基础.现有的损伤识别方法包括基于结构振动特性的识别方法和基于时频响应的识别方法[4-5].前者一般通过结构的模态参数进行损伤识别[6-13],然而,由于实际结构的高阶振型难以获取、高阶振型频率难以测量,此类方法的应用受到制约.后者是通过对结构的振动响应进行时域或频域处理,然后提取损伤特征量,进而评估结构的损伤状况.基于时频响应的识别方法因其具有数据样本易于获取、识别过程简单快速等特点,成为结构损伤识别领域的研究热点.
基于时频响应的识别方法需要对结构动态响应数据进行时域或频域处理.作为时域数据处理的重要方式,时间序列分析已被众多学者应用于结构损伤识别领域.刁延松等[14]利用计量经济学中的协整理论对时间序列的自回归模型(auto-regressive model, AR)系数进行处理,提取损伤指标并进行结构损伤识别.Noh等[15]采用NCREE标准模型建立AR模型,根据AR模型前三阶系数定义损伤因子并进行结构的损伤定位.上述方法仅利用模型的有限阶系数构造损伤特征参数,在数据处理过程中存在损伤信息遗漏问题,导致对部分损伤工况产生误判.Fugate等[16]基于AR模型残差的损伤识别方法,提出采用质量控制图形法监测结构状态.Sakellariou等[17]提出基于随机输出误差振动的地震激励下结构损伤检测与评估方法.这类方法仅考虑了单位置损伤识别,难以保证多位置损伤情况下的识别效果.Gul等[18-19]提出基于自回归滑动平均模型(auto-regressive moving average model, ARMA)的统计模式识别方法,以提高时间序列方法在损伤检测过程中的鲁棒性,并对不同结构的时间序列分析进行实测验证,但该方法仅验证了特定损伤程度下的损伤识别效果,难以保证不同损伤程度下的损伤识别效果.
分析现有研究文献可知,以时间序列分析作为时域数据处理方式的损伤识别方法,在应用过程中仍存在一些问题.产生这些问题的根本原因在于方法所建立的时间序列模型仅为统计意义上的数据序列规律总结,与结构本身的物理特性很难建立直接联系,进而导致数据处理过程中存在损伤信息遗漏,易产生误判现象,对多位置、多程度的复杂损伤工况难以进行有效处理,也难以实现结构损伤的定量识别.
针对上述问题,本文提出一种基于具有外部输入的自回归模型(auto-regressive model with eXogenous input, ARX)的损伤识别方法,通过建立考虑结构动力特性的ARX时间序列模型,对实测数据进行拟合,根据数据拟合度构造表征结构损伤的参数,即损伤因子,进而评估结构的损伤状态.以简支梁模型与桁架结构模型为例,通过一系列的损伤工况,分别对多位置和多程度的结构损伤进行识别,并分析激振位置和测量噪声对损伤识别结果的影响,证明了本文所提方法的有效性与适用性.
1 ARX模型基本原理 1.1 ARX模型一般表达式时间序列是指按照时间顺序或其他物理量顺序排列的一组随机数据[20],而时间序列模型则是揭示数据内部排列规律的系统函数.时间序列分析需要承认随机数据之间的有序性和相关性,并通过数据内部的相互关系来辨识系统的变化规律.常用的时间序列模型包括具有外部输入的自回归滑动平均模型(auto-regressive moving average model with eXogenous input, ARMAX)、ARX模型、AR模型等.ARMAX模型的基本形式[21]如式(1)所示:
| $ \begin{aligned} y(t) &+a_{1} y(t-\Delta t)+\cdots+a_{n_{a}} y\left(t-n_{a} \Delta t\right)=\\ & b_{1} u(t)+b_{2} u(t-\Delta t)+\cdots+b_{n_{b}} u\left(t-n_{b} \Delta t\right)+\\ & e(t)+c_{1} e(t-\Delta t)+\cdots+c_{n_{c}} e\left(t-n_{c} \Delta t\right) \end{aligned} $ | (1) |
式中:y(t)、u(t)和e(t)分别为模型的输出、输入和白噪声干扰项,a1, …, ana、b1, …, bnb、c1, …, cnc均为待定系数; Δt表示时间序列数据点的时间间隔.
式(1)可采用更简洁的方式进行表达,即:
| $ A(q) y(t)=B(q) u(t)+C(q) e(t) $ | (2) |
式中:A(q)、B(q)和C(q)均为包含模型系数的多项式:
| $ A(q)=1+a_{1} q^{-1}+\cdots+a_{n_{a}} q^{-n_{a}} $ | (3) |
| $ B(q)=b_{1}+b_{2} q^{-1}+\cdots+b_{n_{b}} q^{-n_{b}} $ | (4) |
| $ C(q)=1+c_{1} q^{-1}+c_{2} q^{-2}+\cdots+c_{n_{c}} q^{-n_{c}} $ | (5) |
式(3)~(5)中:q为后移算子,如时间t的变量xij(t)乘以k阶后移算子后可得xij(t-k),即:
| $ x_{i j}(t) q^{k}=x_{i j}(t-k) $ | (6) |
根据各多项式阶数取值的不同,ARMAX模型可退化为常见的一些时间序列模型.例如,当nb和nc均为0时,式(1)将转化为AR模型;当na和nb均为0时,式(1)转化为滑动平均模型(moving average model, MA);仅当nc为0时,式(1)转化为ARX模型.ARX模型的基本形式为
| $ \begin{aligned} y(t) &+a_{1} y(t-\Delta t)+\cdots+a_{n_{a}} y\left(t-n_{a} \Delta t\right)=\\ & b_{1} u(t)+\cdots+b_{n_{b}} u\left(t-n_{b} \Delta t\right)+e(t) \end{aligned} $ | (7) |
当输入u(t)与其系数bt为向量时,该模型即为多输入单输出模型.以双输入单输出模型为例,此时bt为两元素的行向量,u(t)为两元素的列向量,模型的基本形式如式(8)所示:
| $ \begin{aligned} y(t)+a_{1} y(t-\Delta t)+\cdots+a_{n_{a}} y\left(t-n_{a} \Delta t\right) &=\\ b_{11} u_{1}(t)+\cdots+b_{1 n_{b 1}} u_{1}\left(t-n_{b 1} \Delta t\right)+& \\ b_{21} u_{2}(t)+\cdots+b_{2 n_{b 2}} u_{2}\left(t-n_{b 2} \Delta t\right)+e(t) \end{aligned} $ | (8) |
式中:bij为第i个输入变量的第j阶待定参数.
1.2 考虑结构动力特性的ARX模型多自由度体系粘滞阻尼系统的振动微分方程为
| $ \boldsymbol{M} \ddot{\boldsymbol{x}}+\boldsymbol{C} \dot{\boldsymbol{x}}+\boldsymbol{K} \boldsymbol{x}=\boldsymbol{F} $ | (9) |
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为荷载向量;x、
根据式(9),第i自由度的运动方程可表示为
| $ \sum\limits_{j=1}^{N} m_{i j} \ddot{x}_{j}(t)+\sum\limits_{j=1}^{N} c_{i j} \dot{x}_{j}(t)+\sum\limits_{j=1}^{N} k_{i j} x_{j}(t)=f_{i}(t) $ | (10) |
式中:N为体系自由度数,i为自由度编号.
式(10)对x求二阶导数,可得:
| $ \sum\limits_{j=1}^{N} m_{i j} x_{j}^{(4)}(t)+\sum\limits_{j=1}^{N} c_{i j} x_{j}^{(3)}(t)+\sum\limits_{j=1}^{N} k_{i j} \ddot{x}_{j}(t)=\ddot{f}_{i}(t) $ | (11) |
式中:括号内数值表示对变量求导的阶数,后同.
当结构运动形式为自由振动时,式(11)中右侧荷载项为0,即:
| $ \sum\limits_{j=1}^{N} m_{i j} x_{j}^{(4)}(t)+\sum\limits_{j=1}^{N} c_{i j} x_{j}^{(3)}(t)+\sum\limits_{j=1}^{N} k_{i j} \ddot{x}_{j}(t)=0 $ | (12) |
采用差分法将x(3)与x(4)表示为
| $ x_{i}^{(3)}=\left(\ddot{x}_{i}(t+\Delta t)-\ddot{x}_{i}(t-\Delta t)\right) / 2 \Delta t $ | (13) |
| $ x_{i}^{(4)}=\left(\ddot{x}_{i}(t+\Delta t)+\ddot{x}_{i}(t-\Delta t)-2 \ddot{x}_{i}(t)\right) /(\Delta t)^{2} $ | (14) |
式中:Δt为数据的时间间隔.
将式(13)和(14)代入式(12),整理可得:
| $ \begin{aligned} \sum\limits_{j=1}^{N}(&\left.\frac{m_{i j}}{(\Delta t)^{2}}+\frac{c_{i j}}{2 \Delta t}\right) \ddot{x}_{j}(t+\Delta t)=\\ & \sum\limits_{j=1}^{N}\left(\frac{2 m_{i j}}{(\Delta t)^{2}}-k_{i j}\right) \ddot{x}_{j}(t)+\\ & \sum\limits_{j=1}^{N}\left(\frac{c_{i j}}{2 \Delta t}-\frac{m_{i j}}{(\Delta t)^{2}}\right) \ddot{x}_{j}(t-\Delta t) \end{aligned} $ | (15) |
考虑到质量矩阵与刚度矩阵的稀疏性,只有当两个自由度相互关联时,对应的矩阵元素才不为0.以N = 3为例,此时与自由度i的相邻自由度数为2,则式(15)可表示为
| $ A_{1} \ddot{x}_{i}(t)+A_{2} \ddot{x}_{i}(t-\Delta t)+A_{3} \ddot{x}_{i}(t-2 \Delta t) =\\~~~ B_{1} \ddot{x}_{i-1}(t)+B_{2} \ddot{x}_{i-1}(t-\Delta t)+B_{3} \ddot{x}_{i-1}(t-2 \Delta t)+ \\~~~ C_{1} \ddot{x}_{i+1}(t)+C_{2} \ddot{x}_{i+1}(t-\Delta t)+C_{3} \ddot{x}_{i+1}(t-2 \Delta t) $ | (16) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} = \frac{{{m_{ii}}}}{{{{(\Delta t)}^2}}} + \frac{{{c_{ii}}}}{{2\Delta t}}, {A_2} = {k_{ii}} - \frac{{2{m_{ij}}}}{{{{(\Delta t)}^2}}}, }\\ {{A_3} = \frac{{{m_{ii}}}}{{{{(\Delta t)}^2}}} - \frac{{{c_{ii}}}}{{2\Delta t}}}\\ {{B_1} = - \frac{{{m_{i, i - 1}}}}{{{{(\Delta t)}^2}}} - \frac{{{C_{i, i - 1}}}}{{2\Delta t}}, {B_2} = \frac{{2{m_{i, i - 1}}}}{{{{(\Delta t)}^2}}} - {k_{i, i - 1}}, }\\ {{B_3} = \frac{{{c_{i, i - 1}}}}{{2\Delta t}} - \frac{{{m_{i, i - 1}}}}{{{{(\Delta t)}^2}}}}\\ {{C_1} = - \frac{{{m_{i, i + 1}}}}{{{{(\Delta t)}^2}}} - \frac{{{c_{i, i + 1}}}}{{2\Delta t}}, {C_2} = \frac{{2{m_{i, i + 1}}}}{{{{(\Delta t)}^2}}} - {k_{i, i + 1}}, }\\ {{C_3} = \frac{{{c_{i, i + 1}}}}{{2\Delta t}} - \frac{{{m_{i, i + 1}}}}{{{{(\Delta t)}^2}}}} \end{array}} \right. $ | (17) |
可以看出,式(16)与式(8)表达形式基本一致.当以
由1.2节分析可知,按式(16)建立的对应于自由度i的ARX模型包含结构的质量、刚度和阻尼等参数.在结构发生损伤后,伴随着结构动力特性的变化,由无损结构所建立的各节点ARX模型将无法反映损伤结构的节点加速度动态响应规律.因此,在建立考虑结构动力特性的ARX模型后,可利用此模型进行结构的损伤状态评估.
为了更好地理解ARX模型在损伤识别领域的应用机理,本节采用一个包含三个自由度的弹簧质点子系统进行说明,如图 1所示.该系统各质点均沿水平方向自由振动,其中k、c分别表示质点间弹簧的刚度系数和阻尼系数,m1、m2、m3表示各质点的质量.

|
图 1 弹簧质点系统 Fig.1 Spring mass subsystem |
各质点的加速度时程数据分别用
| $ \ddot{x}_{2}(t)+a_{1} \ddot{x}_{2}(t-\Delta t)+a_{2} \ddot{x}_{2}(t-2 \Delta t) =\\~~~ b_{11} \ddot{x}_{1}(t)+b_{12} \ddot{x}_{1}(t-\Delta t)+b_{13} \ddot{x}_{1}(t-2 \Delta t)+\\~~~ b_{21} \ddot{x}_{3}(t)+b_{22} \ddot{x}_{3}(t-\Delta t)+b_{23} \ddot{x}_{3}(t-2 \Delta t)+e(t) $ | (18) |
式(18)中各系数包含了结构的物理力学参数(k1、k2、c1、c2、m1、m2).当该系统出现损伤时,质点2的加速度响应将不再满足式(18).此时,以系统损伤后实测得到的
假设某节点实测加速度时程序列为Yi,平均值为Y;由ARX模型预测的加速度时程序列为yi.根据两序列的差异性,定义拟合度ξ为
| $ \xi=\frac{1}{100 \times\left(Z^{1 / p}\right)+1} $ | (19) |
式中:p为计算阶次;Z表达为式(20):
| $ Z=\frac{\sum\limits_{i=1}^{n}\left(\left|y_{i}-Y_{i}\right|^{p}\right)}{\sum\limits_{i=1}^{n}\left(\left|Y_{i}-\bar{Y}\right|^{p}\right)} $ | (20) |
式中:n为样本数量.
根据定义,可以得到拟合度ξ所在区间为(0, 1].拟合度越大,代表待识别结构与未损伤结构越接近.无损伤情况下,yi将与Yi完全相等;而当结构出现损伤时,式(16)中模型各系数也随之变化,由无损伤情况下计算得到的ARX模型预测得到的加速度时程数据,将与实测的加速度时程数据产生偏差.因此,可根据拟合程度定义损伤因子(damage factor, DF)数值大小为1-ξ.
2.3 损伤识别流程由2.1节分析可知,可将模型预测所得某一节点的加速度时程数据与实测加速度时程数据进行对比,根据两者拟合度的大小,评估该节点附近单元的损伤状态.由此,本文提出基于ARX时间序列模型的损伤识别方法,具体分析步骤如下:
(1) 针对损伤识别对象的结构形式,根据式(7)、(15),确定所采用ARX模型的各多项式阶数;
(2) 通过有限元数值模拟,获取无损伤结构在某瞬时荷载作用后的自由振动加速度响应{Y′1, Y′2, …, Y′i, …};
(3) 根据{Y′1, Y′2, …, Y′i, …}建立对应于各节点的ARX模型;
(4) 针对待测结构制定测量方案,布置加速度传感器,施加外界激励(如锤击),获取结构各节点实测加速度时程数据{Y1, Y2, …, Yi, …};
(5) 将Yi-1与Yi+1作为输入,代入对应于节点i的ARX模型,得到未损伤结构中节点i的加速度响应yi;
(6) 代入yi与Yi至式(19)、(20),计算节点i的损伤因子DF;
(7) 改变i,按步骤(5)~步骤(6)重复计算,最终得到各节点的损伤因子DF;
(8) 根据DF数值对结构损伤状态进行评估.
3 数值算例为验证所提方法的有效性与适用性,本文分别采用一简支梁结构和桁架结构作为数值算例进行模拟验算.
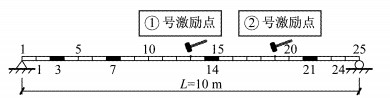
3.1 算例一 3.1.1 数值模型简支梁跨度L=10 m,采用箱型截面,截面尺寸为□300 mm×200 mm×10 mm×10 mm,弹性模量E=2.1×105 MPa,泊松比ν=0.3,材料密度ρ=7 850 kg·m-3,结构模型见图 2.采用ANSYS v17.0建立有限元模型,单元类型为Beam188单元,沿梁长度方向划分24个单元.阻尼类型采用Rayleigh阻尼,阻尼比取0.02.以瞬时冲击荷载作为激励,获取模型各节点竖向加速度响应作为仿真数据,加速度信号的采样频率为100 Hz.本文共选取2个位置(节点号13、19)作为激励点,并分别定义为①号激励点与②号激励点,冲击荷载大小为100 N,荷载作用时间0.000 1 s.图 2所示模型上方数字为节点编号,下方数字为单元编号.
|
图 2 简支梁模型 Fig.2 Simple-supported beam model |
由于既有结构构件的损伤类型较多,本文仅讨论钢结构中常见的材料腐蚀、截面畸变、壁板变形等缺陷所引起的杆件刚度削减,不考虑服役过程中构件的质量损失与阻尼变化.文中构件的损伤程度即为构件刚度削减的相对值.考虑到结构的对称性,假定简支梁损伤出现在4处不同的位置,损伤位置为图 2所示阴影区域,采用弹性模量折减的方式进行损伤模拟,弹性模量折减程度即为损伤程度.
需要说明的是,在利用相邻节点的加速度时程数据建立ARX模型预测某节点的加速度时,由于支座节点固定,不发生振动,因此,本文所提方法无法识别支座附近单元的损伤情况.
施加激励后,获取任意两个节点的加速度时程反应,并截取前2 s数据共200个数据点进行记录,如图 3所示.其中,示例1对应节点远离激振位置,示例2对应节点靠近激振位置.由图 3可知,本模型的自由振动在前2 s已基本衰减为0.此外,考虑到实际检测过程中可能出现人工操作引起的误差,需略去施加激励后一定时间段内的数据样本.因此,本文截取1~2 s时间区段的100个数据建立ARX模型,并进行损伤识别.在按式(19)计算损伤因子时,设定计算阶次p=2.

|
图 3 节点加速度时程数据 Fig.3 Acceleration time history data of nodes |
定义损伤工况如表 1所示,其中工况1~工况4为单位置损伤,工况5~工况8为多位置损伤.
| 下载CSV 表 1 数值模拟损伤工况(算例一) Tab.1 Damage cases of numerical simulation(example 1) |
实际工程中,实测输出响应信号通常会包含一定水平的测量误差.已有研究表明,测量误差具有一定同济规律,因此可以利用概率学理论和数理统计学方法对测量误差进行统计分析和数值模拟,从而弥补采用计算机数值模拟无法得到真实测量数据的不足.
本文采用文献[22]的方法,对测点的加速度响应施加正态分布的白噪声,作为测量噪声以引入测量误差,取噪声强度为n%,即测点加速度响应均方值R的n%,施加噪声后的响应为
| $ a_{t}=a_{t, 0}+r_{\mathrm{SN}} \cdot R \cdot n / 100 $ | (21) |
式中:at, 0和at分别为施加噪声前、后的加速度响应;rSN为符合标准正态分布的随机数.
本文数值算例中,噪声强度分别取0(无噪声)、1%、2%、4%.
3.1.4 结果与分析(1) 损伤位置识别
应用本文方法对工况1~工况8进行损伤识别.图 4为选择①号激振点进行激励,在不考虑测量噪声的情况下4种单位置损伤工况的损伤识别结果,图中阴影部分表示损伤位置.图 5为选择①号激振点进行激励,在不考虑测量噪声的情况下4种多位置损伤工况的损伤识别结果.以工况6为例,将识别结果与各位置单独发生损伤时的识别结果进行对比,如图 6所示.

|
图 4 单位置损伤识别结果(工况1~工况4,①号激振点,无噪声) Fig.4 Single-position damage identification results (condition 1~4, excitation point 1, without noise) |

|
图 5 多位置损伤识别结果(工况5~工况8,①号激振点,无噪声) Fig.5 Multi-position damage identification results (condition 5~8, excitation point 1, without noise) |
|
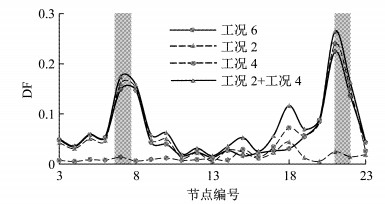
图 6 识别结果对比(工况6,①号激振点,无噪声) Fig.6 Comparison of identification result (condition 6, excitation point 1, without noise) |
图 4表明,对于单位置损伤工况,损伤杆件附近区域的DF值较大,并在与损伤杆件相连的节点达到峰值,由此可以对杆件损伤位置做出较为准确的判断.图 5表明,多位置损伤工况下各损伤位置处的DF显著高于其他位置,因此可以较为准确地判断损伤位置.图 6表明,多位置损伤识别结果近似为各单位置损伤识别结果的线性叠加,各位置损伤对识别结果的相互影响可忽略不计.
(2) 损伤程度识别
为考察不同杆件损伤程度的识别效果,本节以工况2和工况6为例,在原有20%损伤程度的基础上新增5组不同程度的损伤情况,损伤识别结果如图 7所示,损伤位置处相邻节点的DF值随损伤程度变化曲线如图 8所示.

|
图 7 不同损伤程度下的损伤识别结果(工况2、工况6,①号激振点,无噪声) Fig.7 Identification results of single-position damage under different degree of damage (condition 2 & 6, excitation point 1, without noise) |
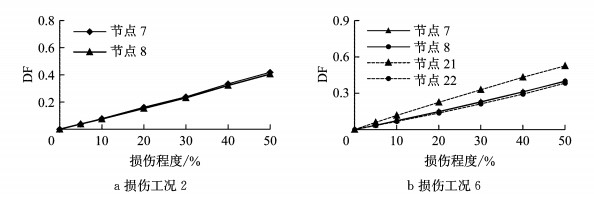
|
图 8 损伤单元相邻节点损伤因子-损伤程度曲线(工况2、工况6,①号激振点,无噪声) Fig.8 Damage factor-damage degree curve of nodes adjacent to damage element (condition 2 & 6, excitation point 1, without noise) |
图 7表明,不同损伤程度下各节点DF分布形式基本相同,即使在较小损伤程度的情况下,仍然能够较为准确地确定损伤位置.图 8表明,损伤位置相邻节点的DF值与损伤程度高度线性相关.因此,在进行结构损伤程度识别时,可将某一特定的损伤程度设定为基准损伤工况,并通过有限元数值模拟手段计算该损伤程度下节点的DF数值.根据DF与损伤程度的线性关系,通过对比实测结构与基准损伤工况下的DF数值,即可对损伤程度进行较为准确的判断.
(3) 激振位置对损伤识别结果的影响
为考察激励位置对杆件损伤识别效果的影响,本节以工况2和工况6为例,分别以激励点①和激励点②作为激励位置,应用本文方法对该简支梁结构进行损伤识别,得到不同激励位置的结构损伤识别结果如图 9所示.

|
图 9 不同激励位置下损伤识别结果(工况2、工况6,无噪声) Fig.9 Single-position damage identification results under different excitation positions (condition 2 & 6, without noise) |
图 9表明,不同激励位置的各节点DF值具有微小差异,但对损伤识别结果影响较小,可忽略不计.实际工程应用中,可根据不同激励位置所求得的DF数值进行综合判断,从而获得较为准确的识别结果.
(4) 测量噪声对损伤识别结果的影响
为考察测量噪声水平对杆件损伤识别效果的影响,本节以工况2和工况6为例,引入三组不同程度的测量噪声并将其识别结果与无噪声情况下的识别结果进行对比,对比结果如图 10所示.
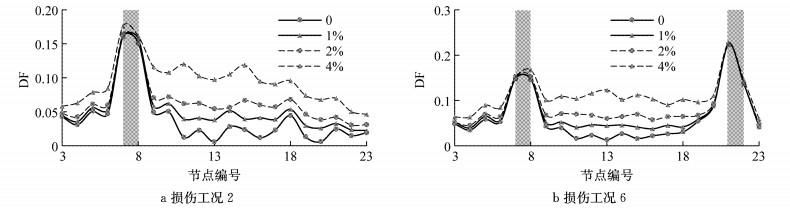
|
图 10 不同噪声水平下多位置损伤识别结果(工况2、工况6,①号激振点) Fig.10 Multi-position damage identification results under different noise levels(condition 2 & 6, excitation point 1) |
图 10表明,测量噪声对单位置及多位置损伤识别结果均具有一定程度的影响.随着测量噪声强度等级的不断提高,未损伤区域的节点DF变化显著,因此,可能存在高噪声环境下损伤位置的误判情况.不同噪声等级下损伤位置节点DF基本保持不变,因此,在准确识别损伤位置的情况下,测量噪声对损伤程度识别结果的影响较小,可忽略不计.
3.2 算例二 3.2.1 数值模型由1.1及1.2节理论推导部分可以看出,本文所提方法基于双输入单输出ARX模型,适用于梁式结构受力体系的损伤识别.桁架结构依据其实际受力形式可等效为普通梁结构,如图 11所示,因此可用本文所提方法对其进行损伤识别.
|
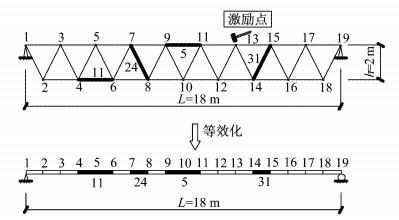
图 11 桁架结构模型 Fig.11 Truss structure model |
桁架结构为上弦支撑的平面静定钢桁架结构[12-13],跨度L=18 m,高度h=2 m.上下弦杆长度均为2 m,斜腹杆长度为2.24 m,采用圆钢管截面,截面面积为5×10-4 m2,弹性模量E=2.1×1011 Pa,泊松比ν=0.3,材料密度ρ=7 850 kg·m-3,结构模型如图 11所示.采用ANSYS v17.0建立有限元模型,单元类型为Link1单元.阻尼类型采用Rayleigh阻尼,阻尼比取0.02.以瞬时冲击荷载作为激励,获取模型各节点竖向加速度响应作为仿真数据,加速度信号的采样频率为100 Hz.本文选取节点13作为激励点,冲击荷载大小为100 N,荷载作用时间0.000 1 s.图 11所示模型节点位置处数字为节点编号,单元旁数字为单元编号.
考虑到结构的对称性,假定桁架结构损伤出现在4处不同的位置,损伤位置为图 11所示阴影区域(或称加粗区域),采用弹性模量折减的方式进行损伤模拟,弹性模量折减程度即为损伤程度.在识别过程中,上下弦杆的损伤可通过等效梁结构相应单元中部节点的DF值进行判断,如单元11可通过5号节点进行判断;斜腹杆的损伤可通过等效梁结构相应单元两侧节点的DF值进行判断,如单元24可通过7、8号节点进行判断.
3.2.2 损伤工况定义损伤工况如表 2所示,其中工况1、2为单位置损伤,工况3、4为多位置损伤.
| 下载CSV 表 2 数值模拟损伤工况(算例二) Tab.2 Damage cases of numerical simulation(example 2) |
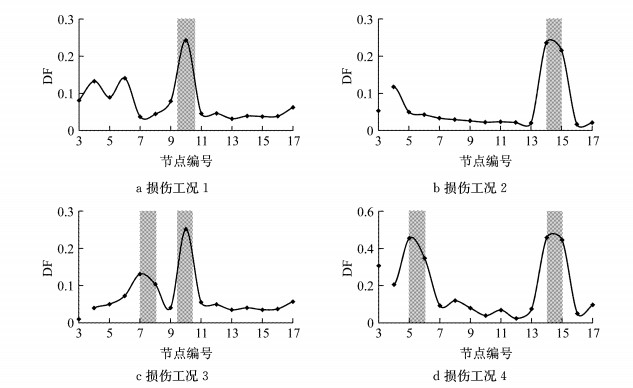
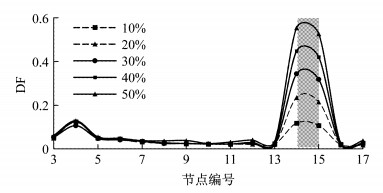
应用本文方法对工况1~工况4进行损伤识别,识别结果如图 12所示.为考察不同杆件损伤程度的识别效果,本节以工况2为例,在原有20%损伤程度的基础上新增4组不同程度的损伤情况,损伤识别结果如图 13所示,损伤位置处相邻节点的DF值随损伤程度变化曲线如图 14所示.
|
图 12 损伤位置识别结果 Fig.12 Damage location identification results |
|
图 13 不同损伤程度下的单位置损伤识别结果 Fig.13 Identification results of single-position damage under different degree of damage |

|
图 14 损伤因子-损伤程度曲线 Fig.14 Damage factor-damage degree curve |
图 12表明,各损伤工况下均可较为准确地识别损伤位置.值得注意的是,当损伤杆件为上下弦杆时,损伤区域中部节点的DF数值较大.同时可以看出,对于上下弦杆,若以原结构的单元相邻节点的DF值进行判断,识别效果不尽理想,原因在于在等效梁结构中,原结构弦杆的损伤相当于两个相邻单元同时发生损伤,此时两单元公共节点的DF值会高于端部的两节点DF值.因此,以中部节点的DF数值作为弦杆的损伤特征指标会获得更好的识别效果.
图 13表明,不同损伤程度下各节点DF分布形式基本相同,即使在较小损伤程度的情况下,仍然能够大致确定损伤位置,但其准确性会有所降低.图 14表明,与简支梁结构相同,桁架结构损伤区域内节点的DF值与损伤程度高度线性相关.因此,在进行结构损伤程度识别时,可将某一特定的损伤程度设定为基准损伤工况,并通过有限元数值模拟手段计算该损伤程度下节点的DF数值.根据DF与损伤程度的线性关系,通过对比实测结构与基准损伤工况下的DF数值,即可对损伤程度进行较为准确的判断.
在利用本文所提方法对桁架结构进行损伤识别时,激振位置与测量噪声对识别结果的影响程度仍需通过数值模拟进行评判.根据数值模拟结果,与算例一相同的是,激振位置和测量噪声两种因素对于桁架结构损伤识别结果准确性与精度的影响仍然较小,因此可以忽略.限于文献篇幅,本文不再赘述.
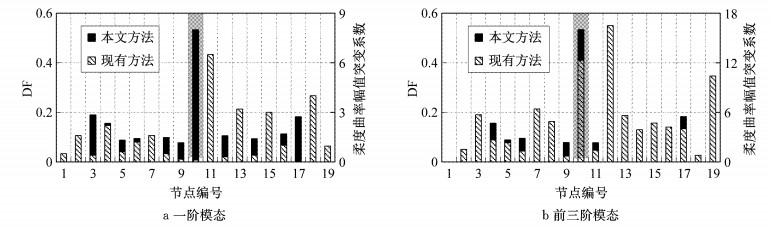
3.2.4 方法对比现有的桁架结构损伤识别方法主要为基于结构振动特性的识别方法,如应变模态法[9]、柔度阵法[10]、单元模态应变差法[12]、柔度曲率幅值突变系数法[13]等.柔度曲率幅值突变系数法通过计算结构各阶模态柔度曲率幅值突变系数,对结构的损伤状况进行综合判断.本节以柔度曲率幅值突变系数法为例,分别应用本文所提方法与此方法对算例二的桁架结构进行损伤识别,并对识别结果进行整理对比.以工况1为例,两种方法的损伤识别结果对比如图 15所示,其中图 15a为仅利用一阶柔度曲率幅值突变系数进行对比;图 15b为利用前三阶柔度曲率幅值突变系数的平均值进行对比.
|
图 15 与现有损伤识别方法的对比 Fig.15 Comparisons with existing damage identification methods |
图 15表明,应用现有损伤识别方法进行损伤位置识别时,未损伤区域处的节点柔度曲率幅值突变系数较大(如节点18、19),因此在实际工程应用中可能产生误判现象.此外,对于多位置损伤情况的识别以及损伤程度的判定,现有方法均不能较好地解决.本文所提方法在一定程度上提高了识别的精度,并在多位置损伤工况下以及损伤程度判定方面具有一定优势.
4 结论本文基于ARX时间序列模型,提出一种新的损伤识别方法.根据时间序列模型基本方程推导出双输入单输出ARX模型一般表达式,通过联立多自由度体系动力方程确定模型阶数,根据未损伤结构的加速度时程数据,建立考虑结构动力特性的各节点ARX时间序列模型,预测未损伤结构的节点加速度时程数据,通过对比理论预测数据和实测数据,根据拟合程度计算损伤因子DF,进而进行结构损伤评估.数值算例分析结果表明,根据本文方法计算得到的各节点DF数值分布可用于损伤位置的识别定位,并可根据损伤位置相邻节点的DF数值大小识别损伤程度.该方法具有以下优点:
(1) 应用本文所提方法建立的ARX模型符合动态数据的实际变化规律,模型拟合程度较高,拟合模型所需的样本数量较少;
(2) 可仅针对疑似损伤区域或重点检测区域进行损伤识别,无需对整体结构进行模态参数识别,所需传感器数量较少;
(3) 实际工程应用中,可通过有限元数值模拟计算基准损伤工况的节点DF数值,并将实测结构所得DF与其进行对比,即可较为准确地判断损伤程度;
(4) 多位置损伤工况下仍具有较好的识别效果.
| [1] |
罗永峰. 国家标准《高耸与复杂钢结构检测与鉴定技术标准》编制简介[J]. 钢结构, 2014, 29(4): 44 LUO Yongfeng. Brief introduction of composition of technical standard for inspection and appraisal of highrising and complex steel structures[J]. Steel Construction, 2014, 29(4): 44 |
| [2] |
罗永峰, 张立华, 贺明玄. 上海市《钢结构检测与鉴定技术规程》编制简介[J]. 钢结构, 2009, 24(10): 57 LUO Yongfeng, ZHANG Lihua, HE Mingxuan. Brief introduction of composition of technical specification for inspection and appraisal of steel structures of shanghai[J]. Steel Construction, 2009, 24(10): 57 DOI:10.3969/j.issn.1007-9963.2009.10.015 |
| [3] |
罗永峰, 刘俊. 既有空间结构位形推算的随机偏差方法[J]. 同济大学学报(自然科学版), 2017, 45(6): 791 LUO Yongfeng, LIU Jun. Stochastic deviation method of reckoning geometric shapes of existing spatial structures[J]. Journal of Tongji University (Natural Science), 2017, 45(6): 791 |
| [4] |
朱宏平, 余璟, 张俊兵. 结构损伤动力检测与健康监测研究现状与展望[J]. 工程力学, 2011, 28(2): 1 ZHU Hongping, YU Jing, ZHANG Junbin. A summary review and advantages of vibration-based damage identification methods in structural health monitoring[J]. Engineering Mechanics, 2011, 28(2): 1 |
| [5] |
韩大建, 王文东. 基于振动的结构损伤识别方法的近期研究进展[J]. 华南理工大学学报(自然科学版), 2003, 31(1): 91 HAN Dajian, WANG Wendong. Overview of vibration-based damage identification methods[J]. Journal of South China University of Technology (Natural Science Edition), 2003, 31(1): 91 DOI:10.3321/j.issn:1000-565X.2003.01.023 |
| [6] |
NDAMBI J M, VANTOMME J, HARRI K. Damage assessment in reinforced concrete beams using eigen frequencies and mode shape derivatives[J]. Engineering Structures, 2002, 24(4): 501 DOI:10.1016/S0141-0296(01)00117-1 |
| [7] |
RATCLIFFE C P. Damage detection using a modified laplacion operator on mode shape data[J]. Journal of Sound & Vibration, 1997, 204(3): 505 |
| [8] |
KO J M, SUN Z G, NI Y Q. Multi-stage identification scheme for detecting damage in cable-stayed Kap Shui Mun Bridge[J]. Engineering Structures, 2002, 24(7): 857 DOI:10.1016/S0141-0296(02)00024-X |
| [9] |
杜永峰, 邵云飞. 基于应变模态的桁架结构损伤指标研究[J]. 甘肃科学学报, 2007, 19(3): 127 DU Yongfeng, SHAO Yunfei. Study on damage index of truss structure based on strain modal[J]. Journal of Gansu Sciences, 2007, 19(3): 127 DOI:10.3969/j.issn.1004-0366.2007.03.037 |
| [10] |
綦宝晖, 邬瑞锋, 蔡贤辉, 等. 一种桁架结构损伤识别的柔度阵法[J]. 计算力学学报, 2001, 18(1): 42 QI Baohui, WU Ruifeng, CAI Xianhui, et al. A flexibility matrix method for damage identification of truss structure[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 42 DOI:10.3969/j.issn.1007-4708.2001.01.008 |
| [11] |
牛杰, 王龙花, 宗周红, 等. 考虑比例阻尼影响的梁式结构损伤识别方法[J]. 东南大学学报(自然科学版), 2018, 48(3): 120 NIU Jie, WANG Longhua, ZONG Zhouhong, et al. Damage identification method of beam type structures considering proportional damping[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(3): 120 |
| [12] |
李永梅, 郭磊, 孙国富, 等. 桁架结构损伤识别的单元模态应变差法[J]. 铁道学报, 2010, 32(6): 78 LI Yongmei, GUO Lei, SUN Guofu, et al. Identification of damages of truss structures using elemental modal strain method[J]. Journal of the China Railway Society, 2010, 32(6): 78 DOI:10.3969/j.issn.1001-8360.2010.06.013 |
| [13] |
张丽梅, 陈务军, 杜守军, 等. 钢桁架结构损伤检测的柔度曲率幅值突变系数法[J]. 东南大学学报(自然科学版), 2005, 35(S1): 133 ZHANG Limei, CHEN Wujun, DU Shoujun, et al. Testing damage on the steel truss structure using the method of the sudden change coefficient of flexibility of curvature[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(S1): 133 |
| [14] |
刁延松, 曹亚东, 孙玉婷. 环境变化下基于AR模型系数和协整的海洋平台结构损伤识别[J]. 工程力学, 2017, 34(2): 179 DIAO Yansong, CAO Yadong, SUN Yuting. Structural damage identification based on AR model coefficients and cointegration for offshore platform under environmental variations[J]. Engineering Mechanics, 2017, 34(2): 179 |
| [15] |
NOH H Y, NAIR K K, KIRERNIDJIAN A S, et al. Application of time series based damage detection algorithms to the benchmark experiment at the national center for research on earthquake engineering (NCREE) in Taipei[J]. Smart Structures and Systems, 2009, 5(1): 1 DOI:10.12989/sss.2009.5.1.001 |
| [16] |
FUGATE M L, SOHN H, FARRAR C R. Vibration-based damage detection using statistical process control[J]. Mechanical Systems & Signal Processing, 2001, 15(4): 707 |
| [17] |
SAKELLARIOU J S, FASSOIS S D. Stochastic output error vibration-based damage detection and assessment in structures under earthquake excitation[J]. Journal of Sound & Vibration, 2006, 297(3): 1048 |
| [18] |
GUL M, CATBAS F N. Statistical pattern recognition for structural health monitoring using time series modeling: theory and experimental verifications[J]. Mechanical Systems & Signal Processing, 2009, 23(7): 2192 |
| [19] |
GUL M, CATBAS F N. Structural health monitoring and damage assessment using a novel time series analysis methodology with sensor clustering[J]. Journal of Sound & Vibration, 2011, 330(6): 1196 |
| [20] |
王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2015 WANG Yan. Applied time series analysis[M]. Beijing: China Renmin University Press, 2015 |
| [21] |
BOX G E P, JENKINS G M, REINSEL G C. Time series analysis: forecasting and control[J]. Journal of Time, 2010, 31(4): 303 |
| [22] |
WANG D, HALDAR A. Element-level system identification with unknown input information[J]. Journal of Engineering and Mechanics, 1994, 120(1): 159 DOI:10.1061/(ASCE)0733-9399(1994)120:1(159) |
 2019, Vol. 47
2019, Vol. 47

