2. 东南大学 土木工程学院,江苏 南京 210096
2. College of Civil Engineering, Southeast University, Nanjing 210096, China
工程结构在服役期间可能遭受的灾害性动力作用,对结构非线性受力全过程分析提出了现实的需求.结构非线性分析的核心与灵魂,在于材料本构关系.事实上,工程材料的本构关系揭示了工程结构在外部或自身重力作用下的材料内部应力和应变之间的物理关系,构成了研究工程结构在外部作用下变形与运动的基础[1].
混凝土是工程结构的主要建筑材料.由于混凝土受力力学性质的高度复杂性,经典的弹性力学、塑性力学等理论很难客观、全面地反映混凝土的基本力学性质.20世纪80年代中期,混凝土损伤力学的出现及发展,给混凝土本构关系的研究提供了新的途径.连续介质-损伤理论以不可逆热力学理论为基础,通过引入损伤变量、建立相应的损伤演化法则,合理地解释了混凝土受力非线性行为的形成机制[1-5].然而,宏观损伤演化法则的经验性,导致了此类模型难以在物理本质上揭示混凝土的损伤演化规律[6-7].针对这一问题,从混凝土受力损伤的随机性入手,逐步研究建立了混凝土随机损伤本构模型[8-12].这一模型首先对经典的并联弹簧模型[13-14]加以改造,以细观断裂应变作为基本随机变量,考虑受拉、受剪两类细观损伤机制,建立了细观随机断裂模型[8-9].进而,将建立的双标量弹塑性损伤模型[5, 11]与细观随机断裂模型相结合,通过引入能量等效应变、建立了多维弹塑性随机损伤本构模型[12].这一模型,将混凝土材料内秉的随机性、非线性以及两者的耦合关系纳入到一个统一的模型中,不仅实现了非线性与随机性的综合反映,也在物理机制上对混凝土的损伤演化规律给出了合理的解释.
混凝土损伤本构关系已经纳入我国混凝土设计规范[15] .因此,从工程实用的角度考察,如何确定混凝土损伤本构模型中的基本参数,就成为一个亟待解决的问题.缘于此,本文试图建立一般工程参数与上述细观随机断裂模型参数之间的关系,并利用规范规定的混凝土一维受力均值本构关系,标定混凝土随机损伤本构模型中的基本参数.进而,考虑钢筋-混凝土之间的相互作用,对素混凝土本构模型加以修正,提出适用于钢筋混凝土结构分析的材料本构模型.通过自主研发、将混凝土随机损伤模型嵌入到结构分析软件ABAQUS和OpenSees之中,通过与试验结果的对比,验证了建议模型的有效性和实用性.
1 混凝土随机损伤本构关系 1.1 混凝土细观随机断裂模型在复杂外部应力作用下,混凝土的破坏形态可以概括为三种基本形式:拉伸破坏、剪切破坏及高静水压力下的压碎破坏.在不考虑高静水压力导致的应变强化前提下,混凝土材料的主要损伤机制可以分为两类:受拉损伤机制和受剪损伤机制[1].在受拉损伤机制中,混凝土细观单元的破坏是由骨料和水泥砂浆之间的界面被拉开、或集料及凝胶体中初始缺陷扩展造成;而在受剪损伤机制中,混凝土细观单元的破坏则源于骨料和水泥砂浆之间的界面滑移、或初始缺陷因剪应力而导致的位错.由于各相材料力学性质的随机性,上述损伤及其演化过程可视为受拉、受剪微弹簧的随机断裂过程.在单向轴向力(拉或压)作用下的混凝土细观单元可以由微弹簧构成的并联体系反映,如图 1所示.
|
图 1 并联弹簧系统 Fig.1 Parallel element system |
采用基于面积的损伤变量定义,有
| ${D^ \pm }{\rm{ = }}\frac{{A_D^ \pm }}{{{A^ \pm }}}$ | (1) |
式中:AD±为因微弹簧断裂而退出工作的面积;A±为微弹簧总面积;D±为损伤变量,上标“±”表示分别考虑受拉和受压两种情况.
假定图 1所示并联系统中的每根微弹簧面积相等、且满足理想弹脆性本构关系,根据此定义,可得损伤变量为
| ${D^ \pm }\left( {{\varepsilon ^{{\rm{e}} \pm }}} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {H\left( {{\varepsilon ^{{\rm{e}} \pm }} - \Delta _i^ \pm } \right)} $ | (2) |
式中:εe±为微弹簧弹性应变;N为弹簧个数;Δi±为第i个弹簧的断裂应变;H(·)为Heaviside函数,即
| $H\left( x \right) = \left\{ \begin{array}{l} 0,x \le 0\\ 1,x > 0 \end{array} \right.$ | (3) |
显然,当并联系统的弹簧数目N→∞时,有
| ${D^ \pm }\left( {{\varepsilon ^{{\rm{e}} \pm }}} \right) = \int_0^1 {H\left[ {{\varepsilon ^{{\rm {e}} \pm }} - {\Delta ^ \pm }\left( x \right)} \right]} {\rm{d}}x$ | (4) |
式中,Δ±(x)为一维断裂应变随机场.
事实上,式(4) 给出了混凝土损伤的演化法则,在微-细观尺度上解释了损伤发生和演化的基本物理机制,即:混凝土的损伤源于其微结构的随机断裂.
对式(4) 取均值,将给出确定性损伤演化律(用小写字母d表示损伤均值),即
| ${d^ \pm }\left( {{\varepsilon ^{{\rm{e}} \pm }}} \right) - E\left\{ {\int_0^1 {H\left[ {{\varepsilon ^{{\rm{e}} \pm }} - {\mathit{\Delta }^ \pm }\left( x \right)} \right]{\rm{d}}x} } \right\}$ | (5) |
显然,只要给定断裂应变Δ±(x)的随机场分布,就可以获得混凝土的损伤演化过程.
一般地,可假定断裂应变随机场的一维概率密度分布服从对数正态分布[12],此时,有
| ${d^ \pm } = \int_0^{{\varepsilon ^{{\rm{e}} \pm }}} {\frac{1}{{\sqrt {2\pi } {\zeta ^ \pm }}}} \exp \left( { - \frac{{{z^ \pm }}}{2}} \right){\rm{d}}{\varepsilon ^{{\rm{e}} \pm }}$ | (6) |
其中,
| ${z^ \pm } = \frac{{\ln {\varepsilon ^{{\rm{e}} \pm }} - {\lambda ^ \pm }}}{{{\zeta ^ \pm }}}$ | (7) |
式中:λ±、ζ±为随机场的均值参数,与材料细观物理特性直接相关.
实际上,式(6) 给出了随机损伤的均值演化规律,据此,容易给出混凝土一维受力均值本构关系:
| ${\sigma ^ \pm } = \left( {1 - {d^ \pm }} \right){E_c}{\varepsilon ^{{\rm{e}} \pm }}$ | (8) |
式中:σ±为混凝土应力;Ec为弹性模量.
1.2 塑性变形的考量塑性应变对混凝土本构关系的建模有不可忽略的影响.经验表明:在初始加载阶段,塑性应变占总应变的比例较小;而在后续加载阶段,塑性应变所占比例虽然不断增加,但其极限值为总应变的某一固定比例.考虑到受拉塑性变形相对较小,因此可以不考虑受拉塑性变形.而对受压的情况,塑性应变的演化应该建立在损伤和弹性应变的基础上.据此,李杰和杨卫忠[10]、Li和Ren[12]、曾莎洁[16]等基于试验数据提出了不同的经验塑性变形表达公式,然而这些模型仅能和各自试验数据匹配较好,在试验数据不同时则可能导致模型对塑性演化预测的精度大大下降.为此,本文提出了新的经验塑性变形εp+计算公式:
| $\left\{ \begin{array}{l} {\varepsilon ^{{\rm{p}} + }} = 0\\ {\varepsilon ^{{\rm{p}} - }} = {\left( {\frac{{\xi _{\rm{p}}^ - {d^ - }}}{{1 - {d^ - }}}} \right)^ {n_{\rm{p}}^ - }}{\varepsilon ^{{\rm{e}} - }} \end{array} \right.$ | (9) |
式中:ξp-与np-为控制受压加载下塑性演化的参数,可分别取0.2~0.5和0.3~0.5.
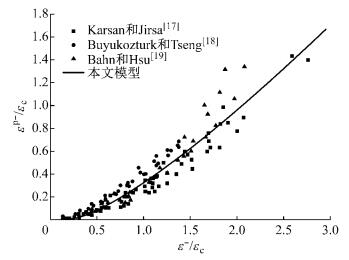
图 2给出了塑性模型式(9) (ξp-=0.4,np-=0.4) 与不同试验结果的对比.可见:本文提出的模型可以准确预测塑性变形的发展.
|
图 2 经验塑性变形 Fig.2 Emparical plastic strain |
上述细观随机断裂模型从细观层次揭示了混凝土损伤演化的基本规律,但仅适用于单轴加载的情况.为将随机损伤本构模型应用于复杂受力分析,需要将其拓展到多轴加载的情况.为此,引入文献[5, 11]提出的混凝土双标量弹塑性损伤模型:
| $\mathit{\boldsymbol{\sigma }} = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{D}}} \right): \mathit{\boldsymbol{\bar \sigma }}\\ = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{D}}) : \mathit{\boldsymbol{C}}_0 : (\mathit {\boldsymbol{\varepsilon}} - \mathit{\boldsymbol{\varepsilon}}^{\rm{P}})$ | (10) |
式中:σ与ε分别为应力与应变;εp为塑性应变;σ为有效应力;
| $\mathit{\boldsymbol{D}} = {d^ + }{\mathit{\boldsymbol{P}}^ + } + {d^ - }{\mathit{\boldsymbol{P}}^ - }$ | (11) |
式中:P+和P-为损伤张量的四阶投影张量.
式(10) 表明,只要确定了损伤演化法则和塑性演化法则,就可以建立多维弹塑性损伤本构关系.关于塑性演化,可以根据有效应力空间中的塑性力学或者经验塑性变形公式确立[12].而对于多维应力状态下的损伤演化,则可以利用前述细观随机断裂模型获得.
事实上,根据文献[5]的研究,受拉和受压损伤能释放率可以表示为
| $\left\{ \begin{array}{l} {Y^ + } = \frac{1}{2}{{\mathit{\boldsymbol{\bar \sigma }}}^ + }:{\mathit{\boldsymbol{C}}_0}:\mathit {\boldsymbol{\bar \sigma }}\\ {Y^ - } = \frac{1}{{2{b_0}}}{\left( {\alpha \mathit{\boldsymbol{\bar I}} + \sqrt {3{{\mathit {\boldsymbol{\bar J}}}_2}} } \right)^2} \end{array} \right.$ | (12) |
式中:σ+为受拉有效应力; I为有效应力分量的第一不变量;J2为有效应力分量的第二不变量; α和b0均为材料参数.
根据物理损伤一致性条件,Li和Ren[12]得到了在多维应力状态下的能量等效应变表达式:
| $\left\{ \begin{array}{l} \varepsilon _{{\rm{eq}}}^{{\rm{e + }}}{\rm{ = }}\sqrt {\frac{{2{Y^ + }}}{{{E_0}}}} \\ \varepsilon _{{\rm{eq}}}^{{\rm{e - }}}{\rm{ = }}\frac{1}{{\alpha - 1}}\sqrt {\frac{{2{Y^ - }}} {{{b_0}}}} \end{array} \right.$ | (13) |
据此,多维受力条件下的损伤演化可由能量等效应变直接代入一维损伤演化得到.即多维受力条件下的随机损伤演化法则为
| ${D^ \pm }\left( {\varepsilon _{{\rm{eq}}}^{{\rm{e}} \pm }} \right){\rm{ = }}\int_0^1 {H\left[ {\varepsilon _{{\rm{eq}}}^{{\rm{e}} \pm } - {\mathit{\Delta }^ \pm }\left( x \right)} \right]{\rm {d}}x} $ | (14) |
而对于均值损伤,有
| ${d^ \pm }\left( {\varepsilon _{{\rm{eq}}}^{{\rm{e}} \pm }} \right){\rm{ = }}\mathit{E}\left\{ {\int_0^1 {H\left[ {\varepsilon _{{\rm{eq}}}^{{\rm{e}} \pm } - {\mathit{\Delta }^ \pm }\left( x \right)} \right]{\rm{d}}x} } \right\}$ | (15) |
将式(14)~(15) 与式(10) 相结合,并适当考虑塑性变形的计算,即给出完整的混凝土多维弹塑性随机损伤本构关系.
2 细观随机断裂模型参数的工程标定在单轴受力情况下,一维混凝土应力应变曲线的均值为
| ${\sigma ^ \pm }{\rm{ = }}\left( {1 - {d^ \pm }} \right){E_c}\varepsilon _{{\rm{eq}}}^{{\rm{e}} \pm }$ | (16) |
而任一应变处的切线刚度为
| $\frac{{\partial {\sigma ^ \pm }}}{{\partial {\varepsilon ^ \pm }}} = \frac{{\partial {\sigma ^ \pm }}}{{\partial {\varepsilon ^{{\rm{e}} \pm }}}}\frac{{\partial {\varepsilon ^{{\rm{e}} \pm }}}} {{\partial {\varepsilon ^ \pm }}}{\rm{ = }}{E_c}\left[ {1 - {d^ \pm } - {\varepsilon ^{{\rm{e}} \pm }}f\left( {{\varepsilon ^{{\rm{e}} \pm }}} \right)} \right]\frac{{\partial {\varepsilon ^{{\rm{e}} \pm }}}}{{\partial {\varepsilon ^ \pm }}}$ | (17) |
事实上,由于混凝土存在天然的随机性,通常使用的混凝土的弹性模量Ec、受拉/受压应力应变曲线中的峰值强度ft/c以及峰值强度对应的应变εt/c(这里t/c表示受拉/受压)在本质上是试验均值,可以通过大样本试验确定.因此,可以利用式(16) 与式(17),由混凝土试验均值确立前述细观随机断裂模型中的基本参数.
将应力应变曲线上峰值点代入式(16),有
| ${f_{{\rm{t/c}}}}{\rm{ = }}\left( {1 - {d^ \pm }} \right){E_{\rm{c}}}\varepsilon _{{\rm{t/c}}}^{\rm {e}}$ | (18) |
注意到混凝土应力应变曲线为单峰值曲线,因此峰值点处切线刚度为0,由式(17) 有
| $1 - {d^ \pm } - \varepsilon _{{\rm{t/c}}}^{\rm{e}}f\left( {\varepsilon _{{\rm{t/c}}}^{\rm{e}}} \right) = 0$ | (19) |
结合式(6) 可知,在受拉和受压两种情况下,均可由式(18)、(19) 两个方程解出细观随机断裂模型的参数λ±、ζ±,即:
| $\left\{ \begin{array}{l} {\zeta ^ \pm } = \frac{{{E_{\rm{c}}}\varepsilon _{{\rm{t/c}}}^{\rm{e}}}}{{\sqrt {2\pi } {f_{{\rm {t}}/{\rm{c}}}}}}\exp \left\{ { - \frac{1}{2}{{\left[ {{\mathit{\Phi }^{ - 1}}\left( {1 - \frac{{{f_ {{\rm{t/c}}}}}}{{{E_{\rm{c}}}\varepsilon _{{\rm{t/c}}}^{\rm{e}}}}} \right)} \right]}^2}} \right\}\\ {\lambda ^ \pm }{\rm{ = }}\ln \varepsilon _{{\rm{t/c}}}^{\rm{e}} - {\zeta ^ \pm }{\mathit{\Phi }^{ - 1}}\left( {1 - \frac{{{f_{{\rm{t/c}}}}}}{{{E_{\rm{c}}}\varepsilon _{{\rm{t/c}}}^{\rm{e}}}}} \right) \end{array} \right.$ | (20) |
因此,只要给定混凝土的宏观参数Ec、ft/c、εt/c,便可以得到细观随机断裂模型参数λ±、ζ±.由此,不难确立随机损伤的均值演化规律.
我国《混凝土结构设计规范》(GB50010—2010)[15]中的混凝土本构关系,正是大量试验归纳总结的一类均值本构关系,因此,可以据之确定细观随机损伤模型的参数λ±、ζ±.根据规范给出的本构关系标定的细观随机损伤本构模型参数列于表 1.值得指出,这里采用的是材料参数均值而非设计值.
| 下载CSV 表 1 混凝土随机损伤本构模型参数 Tab.1 Parameter calibration of concrete micro stochastic fracture model |
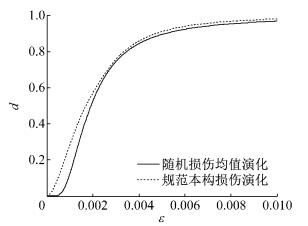
图 3为采用式(20) 参数确定方法给出混凝土单轴受压损伤和规范规定的受压损伤演化曲线,可见两者基本一致.
|
图 3 均值损伤演化 Fig.3 Mean value of damage evolution |
采用式(20) 参数确定方法给出混凝土单轴受拉、受压应力-应变曲线,并与规范本构曲线、文献[20]进行的大样本试验曲线均值作对比,结果如图 4所示.其中,随机断裂模型参数根据式(20) 计算,规范本构曲线中的下降段参数则按规范建议值选取.由图 4可见,本文模型结果与试验曲线符合良好,可以合理地反映混凝土的非线性特性.

|
图 4 细观随机断裂模型与规范本构模型对比 Fig.4 Comparison between stochastic fracture model and code model |
值得指出,现行规范本构关系需要7个参数(弹性模量Ec、受拉、受压峰值强度ft、fc以及对应的应变εt/c、受拉、受压下降段参数αt/c)才能确定混凝土受拉和受压的应力-应变全曲线,而细观随机断裂模型仅需要5个参数(Ec、λ±、ζ±)就可以确定混凝土受拉和受压的均值本构关系,不再需要下降段参数.这充分说明了理论模型较之经验模型的优势.事实上,随机损伤的发展,自然地反映了本构关系的下降段特性,这本质上缘于损伤机理得到了科学反映.与此同时,如果在随机损伤模型中加入受拉/受压相关长度系数,则可以反映混凝土的随机性,即力学性质的离散性[1].
在工程实际中,可以根据工程材料试验结果(弹模、强度和峰值应变)由式(20) 直接计算相应的细观参数,而在缺乏试验参数的情况下,可根据表 1直接确定随机损伤本构模型参数.显然,这一结果为在工程中应用混凝土损伤本构模型奠定了基础.
3 钢筋-混凝土复合效应的考虑在实际钢筋混凝土结构中,钢筋和混凝土之间存在着复杂的相互作用(如受拉刚化效应和箍筋约束效应).因此,需要对第1节素混凝土本构关系进行修正,以反映钢筋混凝土之间的相互作用.
3.1 受拉刚化效应受拉刚化效应是指混凝土开裂之后,裂缝间的混凝土对整个结构的贡献[21],其影响与配筋率密切相关.一般来讲,可以通过修正混凝土的软化段的应力-应变关系来反映受拉刚化.Stevens等[22]根据钢筋混凝土材料受拉试验,提出了考虑受拉刚化效应的混凝土软化段应力应变曲线:
| $\frac{{{\sigma ^ + }}}{{{f_{\rm{t}}}}}{\rm{ = }}\left( {1 - \theta } \right)\exp \left[ {\frac {{270}}{{\sqrt \theta }}\left( {{\varepsilon _{\rm{t}}} - {\varepsilon ^ + }} \right)} \right] + \theta $ | (21) |
式中:θ=0.075ρs/db,其中ρs为钢筋配筋率; db为钢筋直径.
吴建营参考式(21) 对损伤演化法则进行相应修正[23].本文采用类似的方式,将第1节素混凝土受拉损伤修正为
| $d_{{\rm{ts}}}^ + {\rm{ = }}1 - \frac{{{\varepsilon _{\rm{t}}}}}{{{\varepsilon ^ + }}}\left[ {\left( {1 - \theta } \right)\left( {1 - {d^ + }} \right) + \theta } \right]$ | (22) |
式中:θ仍按式(21) 计算.
3.2 箍筋约束效应箍筋的存在为混凝土提供了侧向约束力,因此可以显著地提高混凝土抗压强度和延性.从本质上考察,约束效应使得混凝土内部的损伤机制发生变化,表现为损伤演化、塑性应变的改变.事实上,约束效应的存在减缓了有效应变的发展、从而减缓了损伤的演化,提高了混凝土的强度和延性,而作为混凝土基本材料特性的细观断裂应变并未发生改变.因此,可将约束混凝土的损伤演化定义为
| $d_{{\rm{con}}}^ - {\rm{ = }}\int_0^1 {H\left[ {\gamma {\varepsilon ^{e - }} - {\mathit{\Delta }^ - }\left( x \right)} \right]} {\rm{d}}x$ | (23) |
式中:γ为减缓系数,与加载历程相关.
通过试验,发现约束效应的发展趋势与塑性应变的发展趋势比较接近,因此可以认为减缓系数γ是塑性应变εp-的函数[24].利用此试验、通过试验结果进行参数识别,得到γ的具体形式为
| $\gamma {\rm{ = }}1 - {\left( {\frac{{0.87\varepsilon _{\rm{p}}^ - }}{{\varepsilon _{\rm{p}}^ - + 1\;000\beta }}} \right)^\alpha }$ | (24) |
式中,α和β为模型参数,与有效约束力f ′l相关:
| $\left\{ \begin{align} & \alpha =-0.253f_{1}^{'}+0.862 \\ & \beta =0.713f_{1}^{'}+4.14 \\ \end{align} \right.$ | (25) |
有效约束力f′l可以根据Mander模型[25]计算.
采用式(25) 修正模型对不同配筋率的约束混凝土试验进行模拟,结果见图 5,可见该模型可以较好地模拟约束混凝土的应力应变曲线.

|
图 5 箍筋约束混凝土应力-应变曲线 Fig.5 Stress-strain curves of confined concrete |
钢筋混凝土结构受剪力作用时,主压方向的应力会被主拉方向的应变软化,即所谓的“正交软化”效应 [21, 26].采用类似转角裂缝模型[21]的方式,在随机损伤本构关系中引入软化系数可反映这一效应,即
| $\mathit{\boldsymbol{\sigma = }}\left( {1 - {d^ + }} \right){\mathit{\boldsymbol{\bar \sigma }}^ + } + \beta \left( {1 - {d^ - }} \right){\mathit{\boldsymbol{\bar \sigma }}^ - }$ | (26) |
式中:β为软化系数,可采用转角软化桁架模型[21]的表达形式:
| $\beta = \sqrt {\frac{1}{{1 + 400\varepsilon _{{\rm{eq}}}^ + }}} $ | (27) |
结合式(10),考虑拉压软化效应的混凝土随机损伤本构关系可表示为
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{\sigma }}{\rm{ = }}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{D}}^s}} \right):{\mathit{\boldsymbol{C}}_0}:{\varepsilon ^{\rm{e}}}\\ {\mathit{\boldsymbol{D}}^s}{\rm{ = }}{d^ + }{\mathit{\boldsymbol{P}}^ + } + \left[ {1 - \beta \left( {1 - {d^ - }} \right)} \right]{\mathit{\boldsymbol{P}}^ - } \end{array} \right.$ | (28) |
为了验证本文模型的实用性,将本文模型通过软件编程嵌入到有限元分析软件ABAQUS和OpneSees之中,对一批混凝土构件与结构试验进行了模拟.具体的开发流程可见相关文献[23-24],此处不展开讨论.分析中均假定钢筋与混凝土间完美黏结,不考虑两者间的滑移效应.
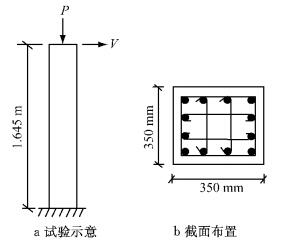
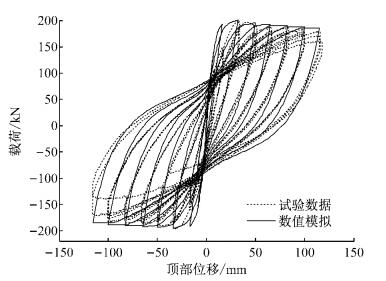
4.1 钢筋混凝土柱反复加载试验利用本文模型对文献[27]中的钢筋混凝土柱推覆试验(试件BG-8) 进行模拟,柱高1.645 m,截面350 mm×350 mm;混凝土保护层厚度29 mm;纵筋数目12根,直径19.5 mm;箍筋直径6.6mm,间距76 mm;轴压比0.231;混凝土强度为34 MPa;采用位移加载.试验示意图见图 6.图中, P为栓轴压力,V为剪力.数值模拟基于OpenSees软件,采用1个柔度法梁柱单元,柱底固接,柱顶采用力加载施加轴力,并采用位移加载施加侧向位移.模拟结果与试验数据对比见图 7,可以看出,本文模型能有效地反映柱在推覆过程中的非线性性能.
|
图 7 柱底剪力V-柱顶位移Δ曲线 Fig.7 Load-top displacement curve |
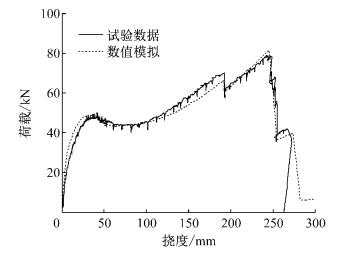
文献[28]进行了钢筋混凝土梁的模拟倒塌试验,具体试验装置如图 8所示.试验中通过上部作动器施加重力荷载,底部千斤顶分级卸载模拟中柱的渐进破坏.具体的配筋和材料参数可见文献[28].采用本文模型,基于OpenSees,利用两个柔度法梁柱单元对该试验进行模拟,梁端部固接,中部受集中荷载作用,采用位移加载.建模参数均按给定的材料参数选取,模拟结果与试验对比见图 9.可见:本文模型准确地反映了倒塌过程中的梁机制、悬链线机制以及两种机制之间的转变.

|
图 8 倒塌试验示意图(单位:mm) Fig.8 Collapse test setup(unit: mm) |
|
图 9 中柱荷载位移曲线 Fig.9 Loaddisplacement curve of middle column |
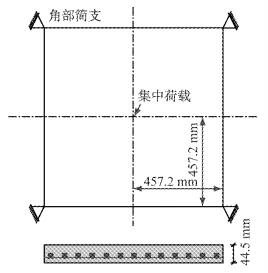
对McNeice[29]进行的4个角点竖向支撑的双向钢筋混凝土板在中点集中荷载作用下的静力试验进行模拟.试验如图 10所示,钢筋布置于75%的板厚度处,每个方向的体积配筋率为8.5×10-3.混凝土参数为:Ec=2.86 GPa,ft=2.9 MPa,εt=0.000 17,fc=38 MPa,εc=0.003,ξp-=0.3,np-=0.4;钢筋参数为:弹性模量Es=200 GPa,屈服强度fy=345 MPa.
|
图 10 钢筋混凝土双向板 Fig.10 Reinforced concrete two-way slab |
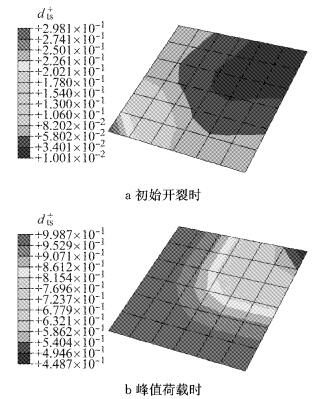
由于结构和荷载的对称性,可以只模拟1/4结构,分析基于ABAQUS,采用的是12×12个二次减缩积分壳单元,厚度方向采用9个积分点.图 11给出了计算所得初始开裂时和峰值荷载时对应的受拉损伤沿板底的分布;图 12给出了荷载位移曲线的对比.可见:这些数值模拟结果不但与试验结果符合较好,同时能够在一定程度上预测试验未达到的结果.
|
图 11 受拉损伤分布 Fig.11 Distribution of tensile damage |
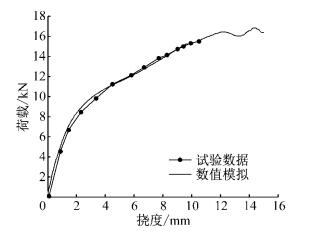
|
图 12 荷载位移曲线 Fig.12 Loaddisplacement curve |
对Thomsen和Wallace的进行的剪力墙反复加载试验试件RW2进行分析[30].如图 13所示,试件高3 658 mm,宽1 219 mm,高宽比为3,具体配筋如图.剪力墙中共2种钢筋:3号钢筋配置在两端暗柱,直径9.53 mm,屈服强度414 MPa;2号钢筋配置在墙体内部,直径6.35 mm,屈服强度448 MPa.混凝土抗压强度为34 MPa.试验中,剪力墙受到轴向压力378 kN,并根据预定的位移加载路径对剪力墙顶端框架梁施加低周反复水平荷载.

|
图 13 剪力墙几何与配筋信息(单位:mm) Fig.13 Geometric and reinforce information of the shear wall(unit: mm) |
基于ABAQUS,采用4节点平面应力单元并结合本文第1节所述多维随机损伤本构关系对混凝土进行模拟,钢筋用2节点桁架单元进行模拟并通过embeded的方式嵌入混凝土中,不考虑两者的粘结滑移.加载过程分两个步骤,首先采用力控制施加轴力,其次采用位移控制施加侧向位移.模拟结果与试验所得的荷载-位移曲线如图 14所示.从图中可见,本文模型分析的结果与试验结果在开裂前的刚度、开裂后的刚度、峰值承载力、残余位移以及能量耗散等方面都非常吻合,滞回曲线给出了准确的捏拢效应、残余位移、延性和耗能能力.
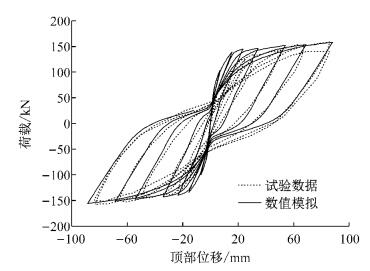
|
图 14 剪力墙荷载位移曲线 Fig.14 Loaddisplacement curve of the shear wall |
(1) 混凝土随机损伤本构关系具有客观的物理基础和完整的理论基础,可以科学地反映混凝土的受力力学行为;利用我国混凝土设计规范规定的本构关系标定了混凝土随机损伤本构模型的基本参数,所得结果可应用于实际工程;
(2) 通过修正素混凝土损伤本构模型,可以考虑实际结构中复杂的钢筋混凝土相互作用效应;
(3) 通过与不同类型试验结果的对比,表明混凝土随机损伤本构模型可以理想地模拟混凝土结构和钢筋混凝土结构的受力力学行为,具有实用性和可靠性.
| [1] |
李杰, 吴建营, 陈建兵. 混凝土随机损伤力学[M]. 北京: 科学出版社, 2014 LI Jie, WU Jianying, CHEN Jianbing. Stochastic damage mechanics of concrete structures[M]. Beijing: Science Press, 2014 |
| [2] |
MAZARS J. A description of micro-and macro-scale damage of concrete structures[J]. Engineering Fracture Mechanics, 1986, 25: 729 DOI:10.1016/0013-7944(86)90036-6 |
| [3] |
JU J W. On energy-based coupled elastoplastic damage theories: constitutive modeling and computational aspects[J]. International Journal of Solids Structures, 1989, 25(7): 803 DOI:10.1016/0020-7683(89)90015-2 |
| [4] |
FARIA R, OLIVER J, CERVERA M. A strain-based plastic viscous-damage model for massive concrete structures[J]. International Journal of Solids and Structures, 1998, 35(14): 1533 DOI:10.1016/S0020-7683(97)00119-4 |
| [5] |
WU J Y, LI J, FARIA R. An energy release rate-based plastic-damage model for concrete[J]. International Journal of Solids and Structures, 2006, 43(3): 583 |
| [6] |
李杰. 混凝土随机损伤力学的初步研究[J]. 同济大学学报(自然科学版), 2004, 32(10): 1270 LI Jie. Research on the stochastic damage mechanics for concrete materials and structures[J]. Journal of Tongji University(Natural Science), 2004, 32(10): 1270 DOI:10.3321/j.issn:0253-374X.2004.10.002 |
| [7] |
李杰, 任晓丹. 混凝土静力与动力损伤本构模型研究进展述评[J]. 力学进展, 2010, 40(3): 284 LI Jie, REN Xiaodan. A review on the constitutive model for static and dynamic damage of concrete[J]. Advances in Mechanics, 2010, 40(3): 284 DOI:10.6052/1000-0992-2010-3-J2008-043 |
| [8] |
李杰, 张其云. 混凝土随机损伤本构关系[J]. 同济大学学报(自然科学版), 2001, 29(10): 1135 LI Jie, ZHANG Qiyun. Stochastic damage constitutive law for concrete[J]. Journal of Tongji University(Natural Science), 2001, 29(10): 1135 DOI:10.3321/j.issn:0253-374X.2001.10.001 |
| [9] |
李杰. 混凝土随机损伤本构关系研究新进展[J]. 东南大学学报(自然科学版), 2002, 32(5): 750 LI Jie. Recent research progress on the stochastic damage constitutive law of concrete[J]. Journal of Southeast University(Natural Science), 2002, 32(5): 750 DOI:10.3969/j.issn.1001-0505.2002.05.016 |
| [10] |
李杰, 杨卫忠. 混凝土弹塑性随机损伤本构关系研究[J]. 土木工程学报, 2009, 42(2): 31 LI Jie, YANG Weizhong. Elastoplastic stochastic damage constitutive law for concrete[J]. China Civil Engineering Journal, 2009, 42(2): 31 |
| [11] |
李杰, 吴建营. 混凝土弹塑性损伤本构模型研究Ⅰ:基本公式[J]. 土木工程学报, 2005, 38(9): 14 LI Jie, WU Jianying. Elasto-plastic damage constitutive model for concrete based on damage energy release rates, part Ⅰ: basic formulations[J]. China Civil Engineering Journal, 2005, 38(9): 14 |
| [12] |
LI J, REN X D. Stochastic damage model of concrete based on energy equivalent strain[J]. International Journal of Solids and Structures, 2009, 46(11): 2407 |
| [13] |
KRAJCINOVIC D, SILVA M A G. Statistical aspects of the continuous damage theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551 DOI:10.1016/0020-7683(82)90039-7 |
| [14] |
KANDARPA S, KIRKNER D J, SPENCER B F. Stochastic damage model for brittle materials subjected to monotonic loading[J]. Journal of Engineering Mechanics, 1996, 122(8): 788 DOI:10.1061/(ASCE)0733-9399(1996)122:8(788) |
| [15] |
中华人民共和国建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. The Ministry of Construction of the People's Republic of China. Code for Design of Concrete Structures:GB 50010—2010[S]. Beijing: China Architecture & Buildings Press, 2010. |
| [16] |
曾莎洁. 混凝土随机损伤本构模型与试验研究[D]. 上海: 同济大学, 2012. ZENG Shajie. Dynamic experimental research and stochastic damage constitutive model of concrete[D]. Shanghai: Tongji University, 2012. |
| [17] |
KARSAN I K, JIRSA J O. Behaviour of concrete under compressive loadings[J]. ASCE Journal of the Structural Division, 1969, 95(12): 2543 |
| [18] |
BUYUKOZTURK O, TSENG T M. Concrete in biaxial cyclic compression[J]. Journal of Structural Engineering, 1984, 110(3): 461 DOI:10.1061/(ASCE)0733-9445(1984)110:3(461) |
| [19] |
BAHN B Y, HSU C T. Stress-strain behaviour of concrete under cyclic loading[J]. ACI Materials Journal, 1998, 95(2): 178 |
| [20] |
晏小欢, 任晓丹, 李杰. 混凝土单轴受压全过程变异性试验研究[J]. 同济大学学报(自然科学版), 2016, 44(5): 664 YAN Xiaohuan, REN Xiaodan, LI Jie. Experimental study on the full process variability of concrete under uniaxial compression[J]. Journal of Tongji University(Natural Science), 2016, 44(5): 664 |
| [21] |
HSU T T C, MO Y L. Unified theory of concrete structures[M]. New York: John Wiley & Sons, 2010
|
| [22] |
STEVENS N J, UZUMERI S M, WILL G T. Constitutive model for reinforced concrete finite element analysis[J]. ACI Structural Journal, 1991, 88(1): 49 |
| [23] |
吴建营. 基于损伤能释放率的混凝土弹塑性损伤本构模型及其在结构非线性分析应用[D]. 上海: 同济大学, 2004. WU Jianying. Damage energy release rate-based elastoplastic damage constitutive model for concrete and its application to nonlinear analysis of structures[D]. Shanghai: Tongji University, 2004. http://d.wanfangdata.com.cn/Thesis/Y675234 |
| [24] |
万增勇. 箍筋约束混凝土柱轴心与偏心受压试验及理论研究[D]. 上海: 同济大学, 2015. WAN Zengyong. Experimental and theoretical study on confined concrete columns bearing axial and eccentric compression[D]. Shanghai: Tongji University, 2015. |
| [25] |
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804 DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [26] |
VECCHIO F J, COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Structural Journal, 1986, 83(2): 219 |
| [27] |
SAATCIOGLU M, GRIRA M. Confinement of reinforced concrete columns with welded reinforced grids[J]. ACI Structural Journal, 1999, 96(1): 29 |
| [28] |
REN P, LI Y, ZHOU Y, et al. Experimental study on the progressive collapse resistance of RC slabs[C]//Structures Congress 2014. [S.l.]: ASCE, 2014: 868-879. http://ascelibrary.org/doi/10.1061/9780784413357.077
|
| [29] |
MCNEICE A M. Elastic-plastic bending of plates and slabs by the finite element method[D]. London: London University, 1967.
|
| [30] |
THOMSEN J H, WALLACE J W. Displacement-based design of slender reinforced concrete structural walls—Experimental Verification[J]. Journal of Structural Engineering, 2004, 130(4): 618 DOI:10.1061/(ASCE)0733-9445(2004)130:4(618) |
 2017, Vol. 45
2017, Vol. 45