Davenport[1-5]指出,极值风速的方向性对建筑风荷载有着重要的影响.Cook[6]是最早在处理风气候数据时考虑极值风速的风向问题的.他基于每年可能发生上百次的独立风暴记录开发出一种计算各风向极值风速的稳定的估算方法,该方法使得可用的样本不仅限于年极值,使得样本数量大大增加,每个风向下的风速极值规律可以进行独立统计.之后Cook[7-8]又对这种方法进行了不断更新改进,使之得到逐步完善.近年来,全涌等[9]对Cook方法的极值模型部分作出改进,使其由多元随机变量更准确地转化为一维随机变量,从而得出更精确的结果.但是,此类方法不便于讨论各方向极值风速的相关性.然而在此问题上,目前研究成果还很少.为了分析极值风速的风向相关性对总体风荷载评估的影响,Haraguchi和Kanda[10]以及Kanda和Itoi[11]分别提出了各风向极值风速的互相关Gumbel概率模型,但并没有将它运用到极值估计中.Haraguchi和Kanda[10]比较了这两个模型,指出上述两种方法还需要进一步优化.最近,Zhang和Chen[12]又提出一种应用高斯Copula函数的联合随机分布模型来考虑极值风速的风向相关性.这种方法用Copula函数将边缘分布函数组合成联合概率分布,得出多元极值风速模型.其后Zhang和Chen[13]考虑了使用不同的边缘概率分布模型对预测结果的影响,并讨论了风压的风向因子特性.
另一方面,在台风多发区,由于台风与良态风的极端风速概率特性完全不同,仍然对混合气候风速取样并拟合,通常会得到不真实的结果.Gomes和Vickery[14]给出了一种基于混合气候风速年极值估计方法,Cook,Harris和Whiting[15]对该方法进行了改进,Cook[16]进一步分析了根据该方法得到的混合气候风速极值的置信区间.但由于台风极值风速观测数据不易获得,目前还没有考虑风向的混合气候极值估计方法.现阶段,台风模拟的方法已经比较成熟.比如,Meng[17-18]建立的台风风场模型,并演化出了完整的解析解采用台风模拟的方法进行极值估计已成为可能.
本文首先根据风速风向分布模型,给出一种新的考虑风向的极值风速标准值.然后用Monte Carlo方法分别获取台风和良态风气候的风速极值.其中,台风气候极值风速采用Yan Meng模型模拟,良态风气候则利用气象站数据拟合极值分布后再模拟一定数量的极值风速数据,并对两者进行组合.最后以上海地区为例,分析了混合气候极值风速设计值,并对该方法中涉及到的极值风速的风向性和相关性等问题进行讨论.
1 风速风向理论与极值估计 1.1 极值风速标准值定义[19]这里沿用文献[19]中对于各个风向的极值风速的定义.任一风向d上重现期为R年的极值风速标准值为vR, d应满足两个基本要求:①一年中每个风向内的风速极值Vd, max都小于其各自风向的极值风速标准值vR, d的概率为1-
这里所定义的各个风向的极值风速标准值vR, d与传统意义上各个风向的重现期为R年的极值风速概念是不同的.传统意义上各个风向的极值风速是指单个风向扇区内,年超越概率为
结合上述定义及不同风向极值风速的相关性可得
| $ {\rm{Pr\{ }}{\mathit{V}_{\mathit{d}{\rm{, max}}}}{\rm{ < }}{\mathit{v}_{\mathit{R}{\rm{, }}\mathit{d}}}{\rm{\} = }}{\left( {{\rm{1 - }}\frac{1}{\mathit{R}}} \right)^{\frac{1}{{{\mathit{M}^\mathit{\gamma }}}}}} $ | (1) |
其中,Pr{·}表示事件的发生概率,d为风向编号,气象站通常将风向按每隔22.5°划分扇区,以正北方为1号风向,顺时针编号,共计16个风向,后文的讨论即采用这种风向划分方式;M为风向个数;Vd, max表示d风向内的风速年极值变量;γ为引入的相关性参数,0<γ<1,使得Mγ值为M个风向中极值风速完全独立的风向个数的平均值,此参数描述了不同风向极值风速之间的相关性,同时用以保证全风向的超越概率为
在参数γ的值及Vd, max的分布的已知情况下,根据式(1)就可以确定各个风向的极值风速vR, d.若每个风向都能获得一组风速极值数据且数据量足够大,Vd, max的经验分布很容易给出,本文将采用Monte Carlo方法来获得大量风速极值样本.关键在于如何估计参数γ的值.
1.2 相关性参数估计方法参数γ是用于描述所有风向同时发生指定重现期极值风速的可能性,显然不同风向的指定重现期极值风速不一定相同,因此这个数其实与指定重现期极值风速的大小没有直接关系,而只与极值风速值在各自风向内的概率分位数有关.因此,考虑可以用概率变换的方法从概率的角度计算参数γ值更加方便.
为了表达方便,令单风向不超越概率p=(1-
这里采用一种简单的概率变换,由于年极值风速值与不超越概率值可以一一对应,因此可将不超越概率值Pd视为一个随机变量,并替换各风向的年极值风速Vd, max.因而事件Vd, max<vR, d等价于事件Pd<p, 可得
| $ \begin{array}{l} {\rm{Pr\{ }}{\mathit{V}_{\mathit{d}{\rm{, max}}}}{\rm{ < }}{\mathit{v}_{\mathit{R}{\rm{, }}\mathit{d}}}{\rm{, }}\mathit{d}{\rm{ = 1, 2, }} \cdots {\rm{, }}\mathit{M}{\rm{\} = }}\\ \;\;\;{\rm{Pr\{ }}{\mathit{P}_\mathit{d}}{\rm{ < }}\mathit{p, d}{\rm{ = 1, 2, }} \cdots {\rm{, }}\mathit{M}{\rm{\} = }}\\ \;\;\;\;\;\;\;\;\;\;\;\;{\rm{Pr\{ }}\mathop {{\rm{max}}}\limits_\mathit{d} {\mathit{P}_\mathit{d}} < \mathit{p}{\rm{\} }} \end{array} $ | (2) |
由于每年全风向失效概率为1/R,可知,
| $ {\rm{Pr\{ }}\mathop {{\rm{max}}}\limits_\mathit{d} {\mathit{P}_\mathit{d}} < \mathit{p}{\rm{\} = 1 - }}\frac{1}{\mathit{R}} $ | (3) |
观察上式,可以发现该式中只有一个未知数p,非常容易求解.实际应用中,可以采用观测比例代替概率值.例如,若每个风向都能获得一组风速极值数据且数据量足够大,可以采用如下方法处理.
记vd, i为编号为d的风向内第i年的极值风速样本,其中d=1, 2, …, M,i=1, 2, …, N,N为年极值风速样本数量.对每个风向的极值风速样本vd, i做概率变换成pd, i.对于某个指定的风向d,pd, i的取值可表达如下:
| $ {\mathit{p}_{\mathit{d}{\rm{, }}\mathit{i}}}{\rm{ = }}\frac{{{\mathit{m}_{\mathit{d}{\rm{, }}\mathit{i}}}}}{{\mathit{N}{\rm{ + 1}}}} $ | (4) |
式中:md, i为风向d内极值样本的排序编号.若vd, i为风向d中的最小值,则md, i为1;若vd, i为风向d中的第2小的值,则md, i为2;以此类推.然后,对第i年的M个不超越概率值取最大值,即
| $ {\mathit{p}_\mathit{i}}{\rm{ = }}\mathop {{\rm{max}}}\limits_\mathit{d} {\rm{(}}{\mathit{p}_{\mathit{d}{\rm{, }}\mathit{i}}}{\rm{)}} $ | (5) |
再将序列{pi, i=1, 2, …, N}进行从小到大排序,取第round((N+1)(1-1/R))个值就是p=(1-1/R)1/Mγ的估计值,其中round(·)表示四舍五入取整.经过简单的代数运算即可求出γ的值.
2 不同气候下极值风速的Monte Carlo模拟由于台风与良态风的极值风速概率特性完全不同,若仍然对混合气候风速取样并拟合,通常会得到不真实的结果.另外,相比良态风而言,台风的数据记录十分稀少,不同风向之间的相关性信息极难获取,因此本文试图采用Monte Carlo的方法,分别模拟台风和良态风的极值风速后将两者混合,再根据本文风速风向模型估算混合气候极值风速.本节将以上海地区的混合气候极值风速估计为例,介绍该方法.
2.1 台风风速极值模拟由气象学的知识知道,虽然台风的真实结构非常复杂,但是所有台风的基本结构是非常相似的,台风移动过程中可以用一些关键参数及移动路径来描述,可以基于这些随机参数进行Monte Carlo抽样,得到给定位置的台风风速序列.
肖玉凤[20]总结了上海地区的台风关键参数的统计模型.其数据来源为中国气象局(CMA)提供的《台风年鉴》(1989年以后更名为《热带气旋年鉴》)(1949—2008)以及国家海洋局(SOA)第一海洋研究所.这些数据包括台风间隔6 h的位置和强度信息.这里涉及的具体关键参数包括:台风年发生率、台风移动方向、台风移动速度、中心压差、最小距离、最大风速半径、衰减模型、风压径向分布参数.
在确定了所有台风关键参数及其统计模型以后,就可基于Monte Carlo思想,采用Yan Meng[17-18]台风模型模拟目标地区年台风发生个数及每个台风在目标地区的风速大小时程.依据《建筑结构荷载规范》GB50009—2012的相关规定,本文以B类地貌10m高度处的平均风速为研究对象.模拟一年内台风极值风速,具体过程如下:
(1) 根据台风年发生率的参数分布抽取该年将会发生的台风个数,并为每个台风抽取其关键参数.
(2) 将每个台风按直线路径经过目标地点周围500 km的模拟圆,每隔1 h计算目标地点的风速,记录下风速大小和风向.
(3) 取一年内每个风向的最大值作为台风在该年的风速极值样本,记录下这些风速值.例如本文中将风向划分为16个,则此处需要记下16个风速值,若某风向无风,则将风速记为零.
2.2 良态风风速极值模拟为了与台风模拟进行数据组合,本文对良态风的年极值风速也将以Monte Carlo方法进行模拟.
本文所用的上海地区的风速风向样本来自上海龙华气象站1956-1-1—1990-12-31全部12 784 d的日最大风速值(10 min平均时距)和相应风向记录,由于当地经济发展,1990年以后气象站周围环境有所变化,我们没有采用了该站1990年以后的风速数据.
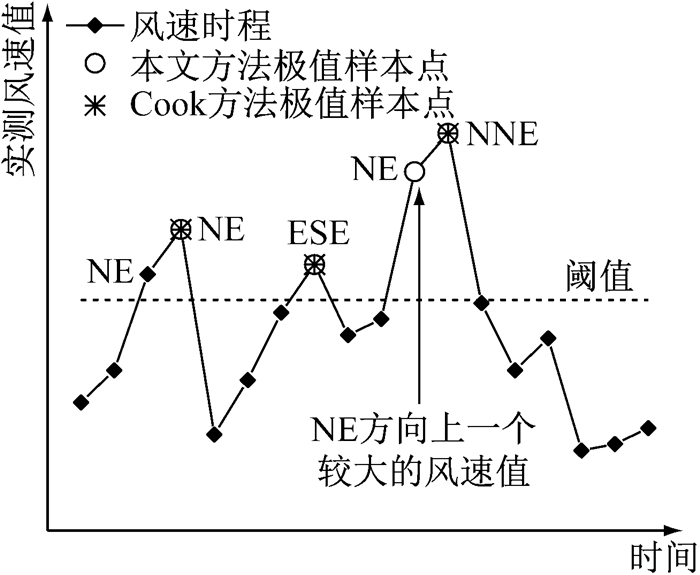
本文采用文献[19]中的考虑风向的独立风暴法进行统计处理.该方法与Cook[6]的独立风暴法略有不同,如图 1所示,需要将一个独立风暴内每个风向的最大值作为各个风向的极值样本.由于不会在一个独立风暴内取到同一风向的其他风速值,所以对于同一风向而言,取到的极值样本是独立的.另外,这样做的好处是,既提高了每个风向的样本数量,又能在样本中包含不同风向间极值风速的相关性信息,同时还避免了无法取到独立风暴内其他风向的风速较大值的问题,图 1中NE、ESE、NNE等均表示风向.
|
图 1 本文方法与Cook独立风暴法比较 Fig.1 Comparison between the proposed MIS and Cook's MIS |
本文取阈值为6.7 m·s-1,采用XIMIS方法[22]拟合各个风向年极值的分布函数.这里需要注意的是,在得到独立风暴样本后,须根据台风历史数据,去除上海地区受台风影响时的独立风暴样本,然后再进行统计.
根据各个风向良态风年极值的分布信息,可以对良态风做Monte Carlo模拟,即每个风向按对应的年极值分布随机抽取一个样本,记下16个风向的极值风速年极值.
2.3 混合气候极值样本获取对于每个风向,取上述Monte Carlo模拟得到良态风年极值和台风年极值中较大者为混合气候年极值,并记录下这些值.重复上述过程1×106次,我们就得到1×106年各个风向混合气候年极值样本,可保存成一个1×106行16列的矩阵.
在Monte Carlo模拟中需要说明以下两点:
(1) 良态风Monte Carlo模拟中不考虑风向之间的相关性,即默认良态风各个风向极值风速不相关,相关度参数γ值为1.文献[19]证实了良态风各个风向的风速是渐进独立的,这意味着在讨论极值问题时,不同风向的极值风速可以假设为完全独立.同时还证明了这一假设是偏于保守的,并且极值分析结果对微弱的相关性不敏感.
(2) 良态风Monte Carlo模拟中去除了受台风影响的日最大风速数据,这些台风风速数据在考虑风向相关性的极值估计中是没有用的.这是因为一个强台风在1 d内就可以使多个风向的风速达到极值的水平,用日最大风速来研究极值风向性是不合适的.但是,这些日最大风速可以用来检验台风模拟结果是否与实际相符.
2.4 混合气候极值样本合理性检验可以将混合气候极值样本与实测数据进行对比.根据上海龙华气象站所有日最大风速,取8 d最大风速或独立风暴极值风速[6](不考虑风向),将这组数据与混合气候年极值风速(同一年内取所有风向中风速最大值)一同绘制在Gumbel概率图中,如图 2和图 3所示,图中横坐标中的P为超越概率值.这里横坐标值采用Cook[16]描述的方法来计算.从图中看出,两者的经验分布相差不大.

|
图 2 模拟结果与实测数据对比(8 d极值) Fig.2 Comparison between the empirical distributions of the simulated results and the measured data (eight-day maxima) |

|
图 3 模拟结果与实测数据对比(独立风暴极值) Fig.3 Comparison between the empirical distributions of the simulated results and the measured data (storm maxima) |
除了从图中直接观察外,还可以用假设检验的方法来检验样本合理性.预先假设混合气候模拟结果为真实的极值风速分布,并设定的检验水准为α=0.05.令v1<v2<…<vm<…<vNs为排序后的8 d极值或独立风暴极值样本,其中vm为从小到大排序后第m个样本,Ns为实测样本数据总量.根据Harris[23],vm的真实不超越概率pm为一个随机变量,其概率密度函数为
| $ {\mathit{\varphi }_\mathit{m}}{\rm{(}}{\mathit{p}_\mathit{m}}{\rm{) = }}\frac{{\mathit{\Gamma }{\rm{(}}{\mathit{N}_\mathit{s}}{\rm{ + 1)}}}}{{\mathit{\Gamma }{\rm{(}}{\mathit{N}_{\rm{s}}}{\rm{ - }}\mathit{m}{\rm{ + 1)}}\mathit{\Gamma }\left( \mathit{m} \right)}}\mathit{p}_\mathit{m}^{\mathit{m} - 1}{{\rm{(1 - }}{\mathit{p}_\mathit{m}}{\rm{)}}^{{\mathit{N}_{\rm{s}}}{\rm{ - }}\mathit{m}}} $ | (6) |
其中Γ(·)为Gamma函数.pm的95%置信区间上下限值Pm, u和Pm, l分别由下列两式确定
| $ {\rm{1 - }}\frac{\mathit{\alpha }}{2}{\rm{ = }}\int_0^{{\mathit{P}_{\mathit{m}{\rm{, u}}}}} {{\mathit{\varphi }_\mathit{m}}\left( \mathit{p} \right){\rm{d}}\mathit{p}{\rm{ = }}{\mathit{I}_{{\mathit{P}_{\mathit{m}{\rm{, u}}}}}}{\rm{(}}\mathit{m}{\rm{, }}{\mathit{N}_{\rm{s}}}{\rm{ - }}\mathit{m}{\rm{ + 1)}}} $ | (7) |
| $ \frac{\mathit{\alpha }}{2}{\rm{ = }}\int_0^{{\mathit{P}_{\mathit{m}{\rm{, l}}}}} {} {\mathit{\varphi }_\mathit{m}}\left( \mathit{p} \right){\rm{d}}\mathit{p}{\rm{ = }}{\mathit{I}_{{\mathit{P}_{\mathit{m}{\rm{, l}}}}}}{\rm{(}}\mathit{m}{\rm{, }}{\mathit{N}_{\rm{s}}}{\rm{ - }}\mathit{m}{\rm{ + 1)}} $ | (8) |
式中,Ix(z, w)称为不完整的Beta函数(incomplete beta function),其表达式为
| $ {\mathit{I}_\mathit{x}}\left( {\mathit{z}{\rm{, }}\mathit{w}} \right){\rm{ = }}\frac{{\mathit{\Gamma }\left( {\mathit{z}{\rm{ + }}\mathit{w}} \right)}}{{\mathit{\Gamma }\left( \mathit{z} \right)\mathit{\Gamma }\left( \mathit{w} \right)}}\int_0^\mathit{x} {{\mathit{t}^{\mathit{z - }{\rm{1}}}}{{\left( {{\rm{1 - }}\mathit{t}} \right)}^{\mathit{w - }{\rm{1}}}}{\rm{d}}\mathit{t}} $ | (9) |
在Matlab软件中定义了Ix(z, w)的反函数(函数名为“betaincinv”),所以Pm, u和Pm, l很容易用Matlab编程求出,其对应的一年内的不超越概率为(Pm, u)r和(Pm, l)r,其中r为实测风速样本年平均个数.再结合混合气候年极值的经验分布(由模拟结果得到),可求出vm的95%置信区间上下限值vm, u和vm, l,画在图 2和图 3中.从图中看出,实测数据均不在拒绝域内,因此混合气候模拟结果是可信的.
3 考虑风向的混合气候极值风速估计方法通过Monte Carlo模拟获得混合气候各个风向年极值样本,该样本数量巨大,因此可以很容易地给出每个风向年极值风速的经验分布.另一方面,采用上文方法估算相关度参数γ值.确定上述两者后,就可以应用式(1)确定各个风向的重现期为R年的极值风速vR, d.实际计算时,可简单地将每个风向的年极值风速样本从小到大排序,取第round((N+1)p)个值就是此风向极值风速vR, d值,其中p=(1-1/R)1/Mγ为单风向不超越概率,N为模拟年份数量,本文中N=1×106.
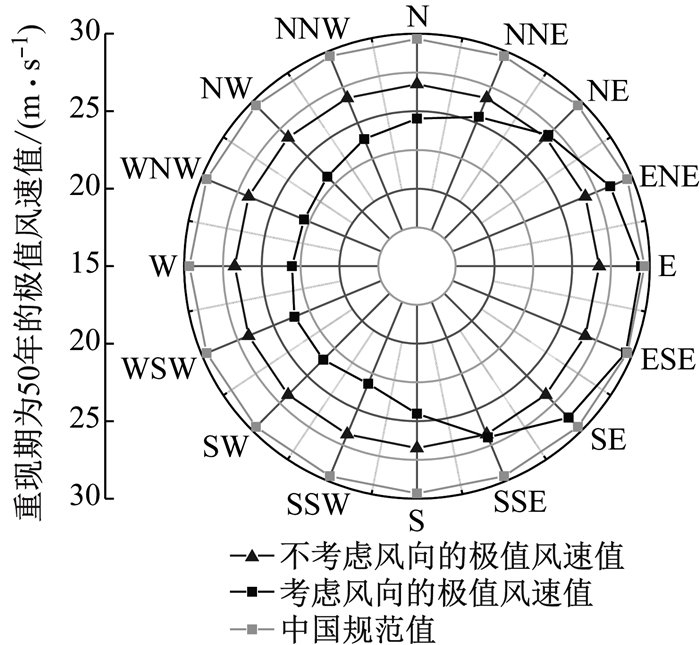
经计算,上海地区重现期为50年时,全风向极值风速标准值为26.74 m·s-1,极值风速标准值的最大值发生在东偏南(ESE)方向,大小为29.57 m·s-1,最小值发生在西偏北(WNW)方向,大小为22.87 m·s-1.图 4为上海地区重现期为50年的极值风速标准值玫瑰图,图中N、NNE、NE等均表示风向.该结果十分符合上海地区东南沿海的地理特性.
|
图 4 上海地区重现期为50年的极值风速玫瑰图 Fig.4 Characteristic values of wind speed under the return period of 50 years in Shanghai |
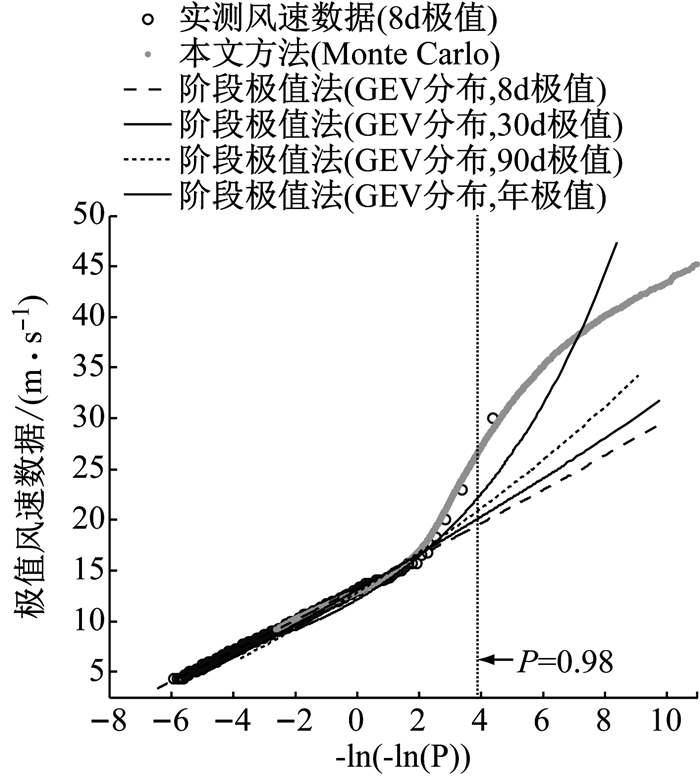
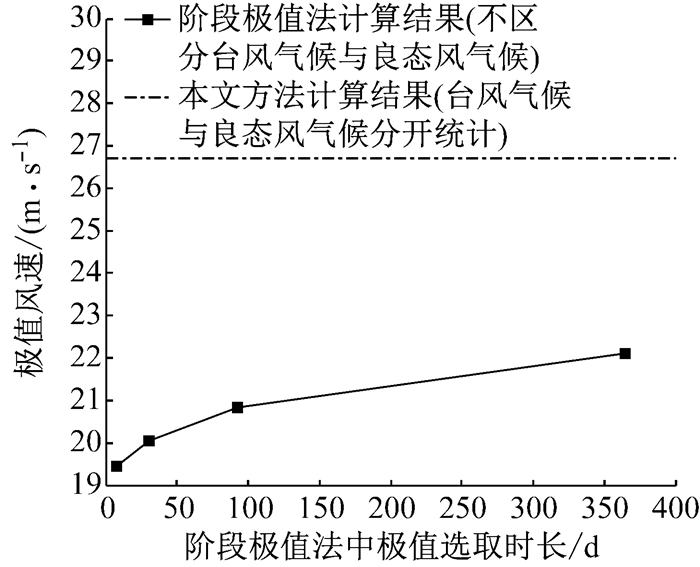
对于受台风影响较为显著的区域而言,不区分台风气候和良态风气候进行混合取样将导致不合理的结果,这是因为台风与良态风风速极值分布规律通常是有很大区别的.图 5和图 6以阶段极值法为例,给出了上海地区全风向本文方法(台风气候与良态风气候分开统计)与传统阶段极值拟合方法(直接统计混合气候数据,不区分台风气候与良态风气候)结果比较.从图中可以看出,基于8 d极值风速样本的结果在上尾段明显上扬,传统的阶段极值法很难处理这一现象,并且造成了观察时距越大极值风速估计值越大的错误结论.这是因为上海极值风速上尾部分由台风控制,而下尾部分由良态风控制,且良态风占大多数,延长观察时距实际上就是减小下尾部分的样本数量,也就是减小良态风数据样本在极值风速数据总样本中的权重,因而出现了观察时距越大极值风速估计值越大.本文方法由于台风和良态风分别处理,其结果较好地展现了两种气候的极值分布形态,且有合理的过渡,这种方法更加符合实际情况.
|
图 5 本文方法与不同观察时距下的阶段极法结果比较(年极值分布对比) Fig.5 Comparison between the proposed method and the traditional method (distributions on the Gumbel probability paper) |
|
图 6 本文方法与不同观察时距下的阶段极法结果比较(50年重现期基本风速对比) Fig.6 Comparison between the proposed method and the traditional method (characteristic values of wind speed under the return period of 50 years) |
现有的各类极值方法往往以一个单一的分布来描述极值,因而在不同气候混合而成的阶段性风速极值分布时可能出现困难.而Monte Carlo方法具有灵活的优点,其不依赖特定的极值分布.此外,极值方法的误差来源于函数拟合误差或分析误差以及样本误差,不同的方法性质不同因而各有特色及适用范围.Monte Carlo方法特色在于,只要模拟数量足够多,则可将分析误差无限缩小,在条件允许的情况下可以做到结果误差仅来源于样本误差.也就是说,本文中只要模拟样本数量足够多,则极值估计结果精度仅取决于输入数据的质量,即根据现有数据所得到的良态风和台风模拟样本的质量.
4.2 各个风向之间风速极值相关度参数从求解γ值的过程中可以看出,该值是会随着重现期R的大小而变化的.图 7展示了当单个风向的样本容量N=1×106时,计算得到的各种风气候下γ值随重现期R的变化情况.从图中可看出,对于较高的极值风速,混合气候的γ值主要由台风部分控制,并且显示出较强的相关性.

|
图 7 各种气候下γ值随重现期R的变化 Fig.7 Change in the value of γ with the return period R |
需要指出的是,本次模拟中良态风各个风向的年极值风速始终默认为互相独立,即良态风的γ应始终为1.图中当R>1 000时,良态风的γ产生波动而不再保持为1.即当N/R<1 000时,由于极值数量有限γ值将不再准确,进而使得极值风速产生误差.因此若要计算重现期为R年的各个风向的极值风速,建议将单个风向的样本容量N设定为1 000R以上.
5 结语对于目前尚没有考虑风向的混合气候极值估计方法的现状,本文试图采用Monte Carlo方法分别获取台风和良态风气候的风速极值样本,并结合风速风向分布模型,给出一种新的考虑风向的极值风速估计方法.该方法能较好地展现台风和良态风两种气候的极值分布形态,同时有效地结合了两者各自的极值风速特性,给出的结果较传统方法更为合理可信.
致谢: 感谢中国气象科学数据共享服务网(http://cdc.cma.gov.cn)提供气象数据支持.| [1] |
DAVENPORT A G. The application of statistical concepts to the wind loading of structures[J]. Proceedings of the Institution of Civil Engineers, 1961, 19(4): 449 DOI:10.1680/iicep.1961.11304 |
| [2] |
DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Proceedings of the Institution of Civil Engineers, 1964, 28(2): 187 DOI:10.1680/iicep.1964.10112 |
| [3] |
DAVENPORT A G. The buffeting of structures by gusts. Wind Effects on Buildings and Structures[C]//Proceedings of the Conference Held at the National Physical Laboratory. London, HMSO, 1965: 357-391.
|
| [4] |
DAVENPORT A G. The relationship of reliability to wind load[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 13(1-3): 3 DOI:10.1016/0167-6105(83)90125-3 |
| [5] |
DAVENPORT A G, SURRY D, STATHOPOULOS T. Wind loads on low rise buildings: final report of phases Ⅰ and Ⅱ BLWT-SS8-1977[R]. London: University of Western Ontario, 1977.
|
| [6] |
COOK N J. Towards better estimation of extreme winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 9(3): 295 |
| [7] |
COOK N J. Note on directional and seasonal assessment of extreme winds for design[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 12(3): 365 DOI:10.1016/0167-6105(83)90057-0 |
| [8] |
COOK N J, MILLER C A. Further note on directional assessment of extreme winds for design[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 79(3): 201 DOI:10.1016/S0167-6105(98)00109-3 |
| [9] |
全涌, 刘磊, 顾明. 考虑风向的极值风速估计的Cook方法改进[J]. 同济大学学报(自然科学版), 2015, 43(2): 189 QUAN Yong, LIU Lei, GU Ming. Improvement of Cook method considering directional extreme wind speed[J]. Journal of Tongji University(Natural Science), 2015, 43(2): 189 |
| [10] |
HARAGUCHI K, KANDA J. Probability model for annual maximum wind speeds in multi-direction[C]//Wind Engineering into 21st Century(ICWE). Copenhagen: [s. n. ], 1999: 205-212.
|
| [11] |
KANDA J, ITOI T. Correlated Gumbel probability model for directional wind speeds[C]// Structural Safety and Reliability: Proceedings of the Eighth International Conference, ICOSSAR'01. Newport Beach: CRC Press, 2001: 8-12.
|
| [12] |
ZHANG X, CHEN X. Assessing probabilistic wind load effects via a multivariate extreme wind speed model: A unified framework to consider directionality and uncertainty[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147: 30 |
| [13] |
ZHANG X, CHEN X. Influence of dependence of directional extreme wind speeds on wind load effects with various mean recurrence intervals[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 148: 45 |
| [14] |
GOMES L, VICKERY B J. Extreme wind speeds in mixed wind climates[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1978, 2(4): 331 |
| [15] |
COOK N J, HARRIS R I, WHITING R. Extreme wind speeds in mixed climates revisited[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(3): 403 DOI:10.1016/S0167-6105(02)00397-5 |
| [16] |
COOK N J. Confidence limits for extreme wind speeds in mixed climates[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(1): 41 DOI:10.1016/j.jweia.2003.09.037 |
| [17] |
MENG Y, MATSUI M, HIBI K. An analytical model for simulation of the wind field in a typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 56(2-3): 291 DOI:10.1016/0167-6105(94)00014-5 |
| [18] |
MENG Y, MATSUI M, HIBI K. A numerical study of the wind field in a typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67-68: 437 DOI:10.1016/S0167-6105(97)00092-5 |
| [19] |
张秉超. 建筑围护结构极值风压的全概率分析方法研究[D]. 上海: 同济大学, 2014. ZHANG Bingchao. Research on the fully probabilistic method of the extreme wind pressure on buildings[D]. Shanghai: Tongji University, 2014. |
| [20] |
肖玉凤. 基于数值模拟的东南沿海台风危险性分析及轻钢结构风灾易损性研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. XIAO Yufeng. Typhoon wind hazard analysis based on numerical simulation and fragility of light-gauge steel structure in southeast china coastal regions[D]. Harbin: Harbin Institute of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10213-1011279499.htm |
| [21] |
中华人民共和国国家标准. 建筑结构荷载规范: GB50009-2012[S]. 北京: 中国建筑工业出版社, 2012. Professional Standard of the People's Republic of China. Load code for the design of building structures: GB50009-2012[S]. Beijing: China Architecture and Building Press, 2012. |
| [22] |
HARRIS R I. XIMIS, a penultimate extreme value method suitable for all types of wind climate[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(5/6): 271 |
| [23] |
HARRIS R I. Gumbel re-visited-a new look at extreme value statistics applied to wind speeds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(1): 1 DOI:10.1016/0167-6105(95)00029-1 |
 2018, Vol. 46
2018, Vol. 46
