在目前的桥梁结构中,箱形截面是一种常见的截面形式.它的抗扭刚度大,整体稳定性好,可有效抵抗弯剪扭效应,是梁桥中应用最为广泛的一种截面形式.作为应用最普遍的预应力混凝土箱梁,在正常使用状态下,受拉区混凝土易开裂,混凝土的自重增加了结构负担.钢-混凝土组合梁是将钢梁和混凝土桥面板通过抗剪连接件连接成整体并考虑共同受力的结构形式[1],钢-混组合箱梁有利于材料强度的充分发挥,降低截面高度,减轻结构自重,实现结构的纤巧轻盈化,但是钢主梁的耐火性和耐腐蚀性较差,钢与混凝土连接件易破坏,钢主梁在反复交变应力下易疲劳失效.
超高性能混凝土(UHPC)具有超高强度、高应变强化行为[2]、高致密性、高裂纹自修复性、高耐久性以及良好施工性等突出优点, 是全新一代先进结构材料,已成为国内外研究的热点,欧美日韩等国均从国家战略高度将其列为21世纪关键结构材料.UHPC的基本力学性能优异,采用UHPC可以实现结构的轻盈化,提高结构的安全性,进一步延长结构的使用寿命,达到节约材料、减轻自重、增加耐久性、降低结构维护费用的目的,在土木工程领域有着广阔的应用前景.
UHPC-混凝土组合构件是UHPC在实际工程中应用的一个方向.UHPC-混凝土组合梁可以优化UHPC层厚度、减轻结构自重[3],UHPC与混凝土有良好的连接性能[4],UHPC的高耐久性减少了组合梁后期维护费用.当前UHPC-混凝土组合梁广泛应用在新建桥梁和旧桥加固领域.日本在2007年建造完成了一座跨径48 m的箱形组合桥梁[5],由预应力混凝土顶板和UHPC腹板、底板组成.瑞士自2004年起率先将UHPC应用于混凝土桥的加固,目前已完成10余座桥的加固工程[6].法国[7]、美国[8-9]等也将UHPC应用于混凝土桥梁的加固中.
近年来,一些学者对UHPC-混凝土组合梁的计算方法进行探索,但基本处于初始阶段,研究成果极少.Lampropoulos等[10]采用有限元方法对UHPC-混凝土矩形梁进行力学性能分析,Ferrier等[11]沿用传统理论保守估算UHPC-混凝土组合梁的抗剪极限承载力等.本文提出UHPC-混凝土新型组合截面,采用ANSYS软件对组合箱形截面简支梁的弯曲性能进行研究,分析不同组合形式梁的弯曲性能,为UHPC-混凝土组合箱梁的实际应用奠定基础.
1 ANSYS模型的验证性试验 1.1 UHPC材性试验UHPC中掺杂的纤维主要以细小的钢纤维为主(质量分数为2.5%),它与基体间的黏结滑移、纤维的拉拔、桥接和试验构件裂缝的偏转作用以及对混凝土基体的增强机理都有其自身的特性,因此它的力学特性介于普通混凝土和钢之间.UHPC-混凝土组合梁既区别于传统的混凝土箱梁又与当前的钢-混组合结构存在差异.当前对UHPC-混凝土组合箱梁缺乏成熟的计算方法,为了验证本文ANSYS模型计算方法的合理性,对1根矩形UHPC-混凝土组合梁进行试验对比分析.
试验所用UHPC材料由上海罗洋新材料科技有限公司提供,是一种常温养护高应变强化型超高性能混凝土,基体配合比见表 1,钢纤维特性见表 2.
| 下载CSV 表 1 UHPC基本配合比 Tab.1 Mix proportion of UHPC matrix |
| 下载CSV 表 2 钢纤维特征参数 Tab.2 Characteristic parameters of steel fiber |
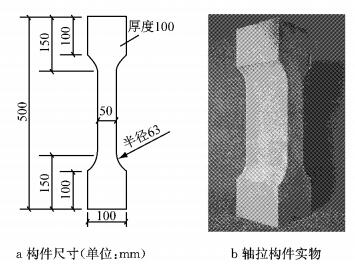
在浇筑试验梁时,测试材料的抗压和抗拉强度以及抗拉试件(尺寸如图 1a)如文献[12]所示.试件中间段为50 mm×100 mm×200 mm的棱柱体,各方向尺寸均大于纤维长度的3倍,这有助于纤维在试件中的三维均匀分布,降低纤维取向分布的影响.每组UHPC类型成型6根试件,室温下静置24 h后拆模,采用标准养护至28 d龄期后进行直接拉伸(抗压)试验.
|
图 1 轴拉试件 Fig.1 Axial tensile specimen |
在立方体抗压强度试验中,浇筑养护完成2组(6个)100 mm×100 mm×100 mm的立方体试块,按照标准养护条件(温度为20±2 ℃,湿度不小于95%)养护28 d后,进行试验.
抗压强度试验结果见表 3.在轴拉试验中,采用的轴拉试验装置有效避免了轴拉试验过程中的偏心失稳问题,对6根应力-应变曲线进行平均和离散性处理,如图 2所示.
| 下载CSV 表 3 UHPC的28 d抗压强度 Tab.3 28 days compressive strength of UHPC |

|
图 2 UHPC应力-应变曲线 Fig.2 Stress-strain curve of UHPC |
当立方体试块被压碎时,由于钢纤维的搭接作用,试块仍保持整体.根据试验确定的UHPC立方体抗压强度标准值为(试验均值-1.645倍的标准差)fcu, k=154.6-1.645×9.8=138.5 MPa.UHPC泊松比取0.2.
试验采用2种强度的钢筋,HRB400级钢筋的直径为18 mm和16 mm, 共2种.根据文献[13], 每种直径的钢筋分别预留3根450 mm长的试件做拉伸试验.拉伸试验得到的钢筋力学特性结果见表 4.
| 下载CSV 表 4 钢筋材料力学特性 Tab.4 Mechanical properties of steel |
矩形UHPC-混凝土组合梁的纵向受力钢筋为6φ18(HRB400,普通混凝土层),梁长3 m,跨中横断面见图 3.

|
图 3 横断面尺寸(单位:mm) Fig.3 Cross section size (unit:mm) |
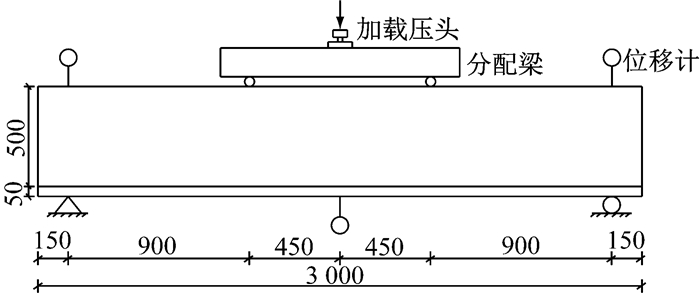
2根简支梁均按照三分点方式加载,加载示意图见图 4.试验加载初始阶段采用荷载控制(20 kN·级-1,加载速度10 kN·min-1),待裂缝发展到可视宽度,卸载后转位移控制.试验过程中通过钢筋和混凝土表面的应变片观测应变的变化,同步记录梁体裂缝的发展情况.
|
图 4 试验加载装置示意(单位:mm) Fig.4 Schematic test loading device (unit:mm) |
加载初期按照荷载控制,每个加载等级为20 kN,当加载到240 kN时,跨中纯弯段位置UHPC表层出现极微小裂缝(强光下),此时裂缝小于0.02 mm; 随着荷载的增大,初始微小裂缝跨过UHPC层,在普通C30混凝土表面显现,此时在C30混凝土表面出现新的裂缝;当荷载值到达460 kN时,裂缝宽度大于0.1 mm,肉眼可见;后续开始转位移控制(先卸载再加载),直到试验梁破坏.破坏形态为受拉区UHPC拉裂、受压区普通C30混凝土压碎,破坏荷载为868 kN.组合梁试验现场见图 5.

|
图 5 试验破坏图 Fig.5 Failure diagram of test |
有限元建模依据组合梁的实际尺寸,定义模型的纵向为x轴、横向为z轴、竖向为y轴,按照非线性材料计算结构的极限承载力.
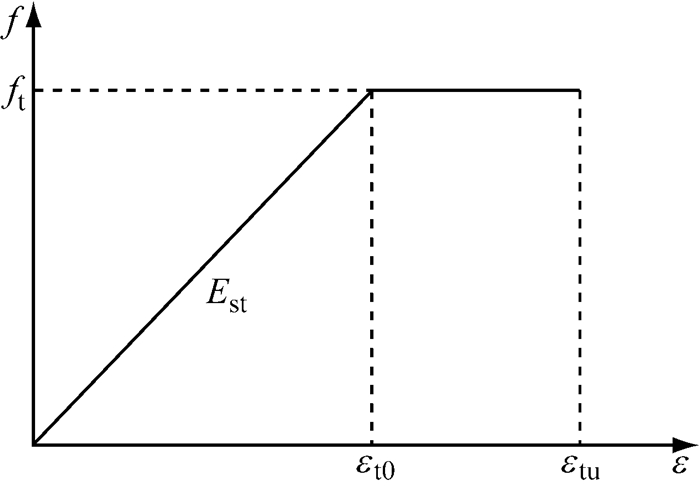
ANSYS模型采用SOLID65单元来模拟混凝土、LINK8单元来模拟钢筋,模型的非线性分析采用分离式模型进行模拟.在ANSYS软件中,钢筋选择BISO模型建立本构关系,即由弹性段和屈服段组成.力学特性由之前的钢筋材性试验得到.UHPC受压本构关系从实际应力应变曲线中选取相应的8个特征点,采用MISO模型建立本构关系,受拉本构与受压本构关于原点对称.钢材受拉本构关系见图 6.
|
图 6 钢材应力-应变曲线 Fig.6 Stress-strain curve of steel |
为保证非线性计算结果收敛和准确,在ANSYS软件中输入UHPC受拉和受压的本构关系,本构关系参照前述的实测材性值曲线,普通混凝土受拉受压本构关系采用实测曲线.ANSYS模型计算中采用力收敛法则,收敛精度为3%,共设置100个子步,每个子步进行50次迭代运算.
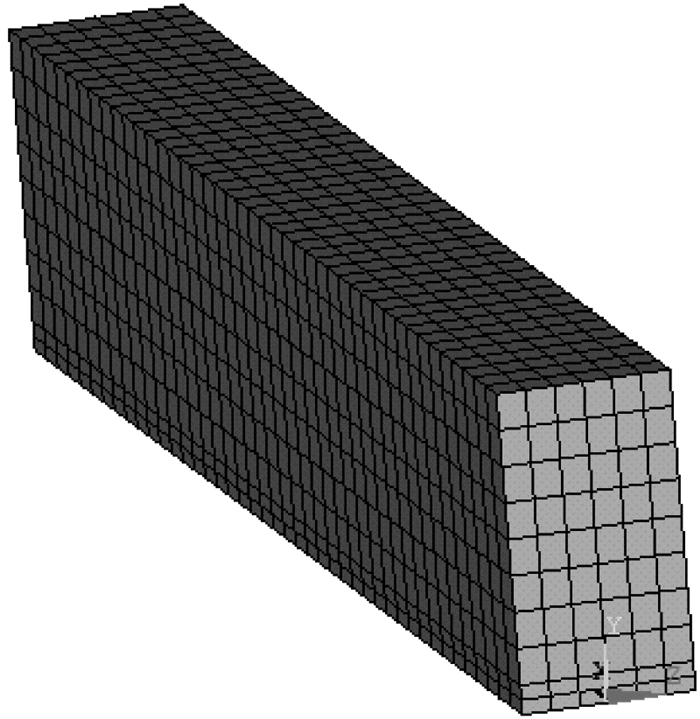
矩形UHPC-混凝土组合梁的ANSYS有限元模型如图 7所示.
|
图 7 有限元模型 Fig.7 Finite element mode |
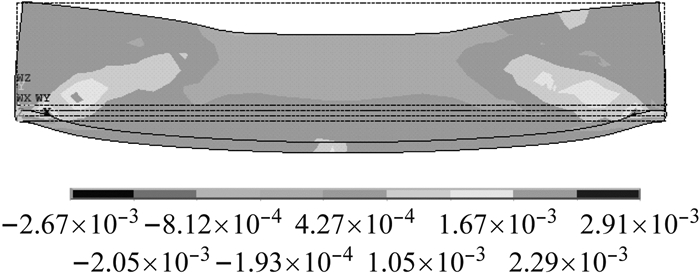
(1) 应变.在ANSYS模型中,裂缝的分析采用单元内部的分布裂缝模型,以分布裂缝来代替单独的裂缝.即某一个实体单元的应力(实际上是单元中某一代表点的应力)超过了开裂的应力,则认为整个单元(或这一个应力点周围的一定区域)开裂,并且认为是在垂直于引起开裂的拉应力方向形成了无数平行的裂缝,而不是1条裂缝.如果直接使用ANSYS模型中的裂缝结果, 它与真实情况有一定的差别,直接进行分析会造成较大的误差.因此采用读取ANSYS软件中的应变结果,用破坏时的极限应变来判断构件的开裂情况.此外根据材性试验的结果,钢筋应变达到2.300×10-3以上时基本达到了屈服时的强度,故2.300×10-3作为判断极限承载力的标准.最终ANSYS模型极限状态应变分布见图 8.从应变中可知:跨中应变值很大,组合梁的跨中极限应变值达到2.316×10-3.即认为裂缝由跨中出现并开始逐渐发展.通过实际试验发现,由ANSYS软件的应变计算结果分析出的裂缝发展趋势与现场实际裂缝发展形态基本一致.
|
图 8 ANSYS模型应变分布 Fig.8 Strain distribution in ANSYS |
(2) 抗弯极限承载能力. ANSYS软件计算结果和试验加载结果见表 5.达到极限状态时,组合梁荷载理论值与试验值的比值为1.03,说明ANSYS模型理论值与试验值相吻合,本文采用的ANSYS计算方法准确性高,可用来分析更加复杂的UHPC-混凝土组合箱梁.
| 下载CSV 表 5 组合梁试验值与有限元理论值对比 Tab.5 Comparison of experimental values with ANSYS theoretical values |
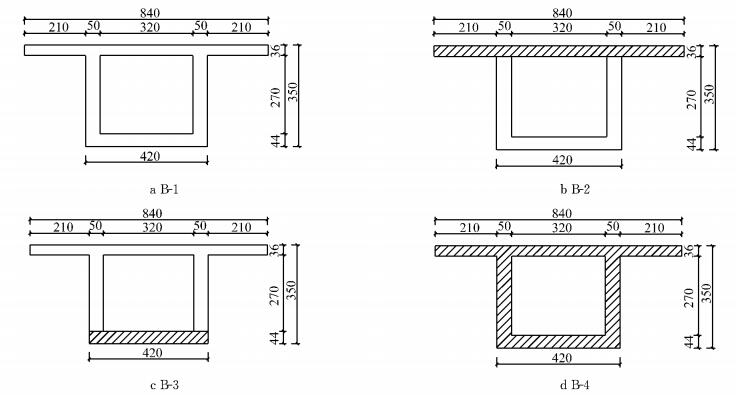
对某工程中的实际截面进行有限元法计算,建模时对截面进行简化处理,忽略腹板和顶底板连接处的承托构造,并且计算时忽略简支梁的自重.4种组合截面分别是:全截面C60(B-1)、顶板取代为UHPC(B-2)、底板取代为UHPC(B-3)、全截面UHPC(B-4),横截面具体尺寸见图 9.4种组合截面梁长是30 m,组合箱梁的纵向配筋率为2.69%,加载方式为四点加载法.
|
图 9 UHPC-混凝土组合箱形截面(单位:cm) Fig.9 UHPC-concrete composite box section (unit:cm) |
组合箱梁有限元模型的建立方法与1.5节相同,钢筋种类为HRB335.由钢筋的本构关系可以认为钢筋的拉应变达到1.675×10-3时钢筋屈服,并将此时所对应的荷载定义为试验模型箱梁的极限荷载.其中B-2和B-3组合箱梁作为优化组合截面箱梁,为防止发生斜截面剪切破坏,将这2种组合箱梁弯剪段的腹板更换为UHPC材料,纯弯段的腹板仍为C60普通混凝土.UHPC-混凝土组合箱梁的有限元模型如图 10所示.普通混凝土和钢筋本构关系参见文献[14].C60混凝土fck取38.5 MPa,ftk取2.85 MPa,极限拉应变取10-4,弹性模量取3.60×104 MPa.UHPC的抗拉和抗压本构关系采用前文中得到的曲线.受压本构输入时极限抗压强度设置为138.5 MPa,弹性模量为4.74×104 MPa.本构关系曲线仍参照第1节验证性试验中的材性值曲线.UHPC和C60混凝土泊松比均取0.2.

|
图 10 UHPC-混凝土组合箱梁有限元模型 Fig.10 Finite element mode of the UHPC-concrete composite box girder |
建模方法与前文对比试验中的有限元模型保持一致.
3 ANSYS模型计算结果分析 3.1 应力分析在ANSYS模型分析中,以箱梁发生弯曲破坏时钢筋屈服为计算终点,即受拉区拉应变达到1.7×10-3,记录此时受压区混凝土和钢筋的应力.试验梁计算结果见表 6.
| 下载CSV 表 6 4根梁极限状态下应力 Tab.6 Force value should be four beams under ultimate state |
由表 6可知:B-2(顶板取代为UHPC)与B-1(全截面C60)相比,在试验梁破坏时,底板、顶板和钢筋应力基本一致,UHPC顶板的压应力只有33.90 MPa,并未完全发挥UHPC的受压性能,试验梁的破坏由受拉区混凝土开裂和钢筋屈服控制;B-3(底板取代为UHPC)在梁体破坏时,底板的拉应力达到8.26 MPa,充分发挥了UHPC的受拉性能和C60的受压性能;B-4(全截面为UHPC)底板极限强度为9.65 MPa,顶板压应力为92.30 MPa.
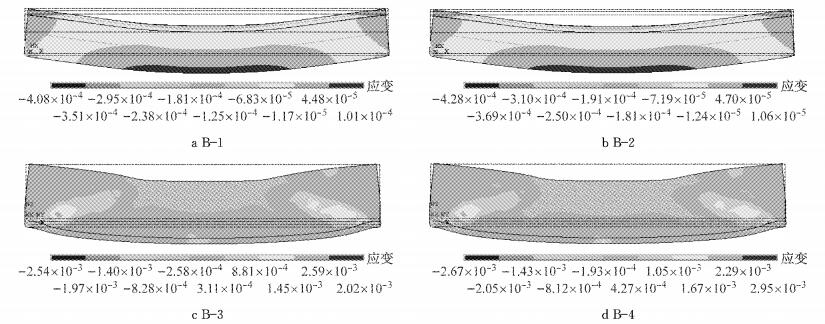
3.2 应变分析B-1:当施加荷载达到22 320 kN时,箱梁纯弯段底部的混凝土应变为57.6×10-6,随后沿着腹板向顶板发展.当总荷载达到89 280 kN时,ANSYS模型中底板处钢筋的应变值为1.681×10-3,梁体破坏.箱梁应变的分布见图 11a.
|
图 11 箱梁应变分布 Fig.11 Strain distribution diagram of box girder |
B-2:当荷载加载达到23 250 kN时,底板混凝土应变为58.8×10-6,开裂处混凝土逐渐退出工作.随着荷载的增加,裂缝继续发展.当施加荷载达到93 000 kN时,底板处的钢筋应变值为1.690×10-3,宣告梁体破坏.箱梁应变的分布见图 11b.
B-3:当荷载加载至37 200 kN时,底板处混凝土应变为177.9×10-6.由于UHPC混凝土的极限抗拉强度远大于C60普通混凝土,荷载加载至127 000 kN时,底板处的UHPC混凝土应变值达到极限值1.692×10-3.箱梁应变的分布见图 11c.
B-4:当施加荷载到66 308 kN时,纯弯段底部出现裂缝并迅速向上发展,此时箱梁由弹性工作状态转为混凝土开裂工作状态.当施加荷载到195 000 kN时,底板和腹板出现新的裂缝,并且裂缝向顶板继续发展,开裂处混凝土逐渐退出工作,钢筋参与受力,钢筋的应力迅速提高.ANSYS模型中底板处混凝土的极限应变值为1.701×10-3,此时箱梁破坏.箱梁应变的分布见图 11d.
由应变值的变化可以发现B-2与B-1裂缝发展速度基本一致,说明更换受压区混凝土对裂缝发展影响较小;B-3裂缝发展速度与B-1相比明显缓慢,说明更换受拉区(底板)可以改善组合箱梁的裂缝发展模态;由于钢纤维的掺入,B-4组合梁整体裂缝发展缓慢,裂缝沿梁高的发展速度明显变缓.
3.3 抗弯承载能力分析相应梁的荷载计算结果见表 7.由表 7可知:①开裂荷载.B-2梁与B-1梁的开裂荷载基本一致,B-3梁的开裂荷载为B-1梁的1.67倍,B-4梁是B-1梁开裂荷载的2.94倍.B-3梁和B-4梁更能体现出UHPC的抗拉性能优势. ②极限荷载.B-2梁与B-1梁的极限荷载基本一致,B-3梁的极限荷载为B-1梁的1.42倍,B-4梁是B-1梁极限荷载的2.18倍.全截面UHPC箱梁的极限承载能力最高,但仅更换底板也可大幅提高极限承载力.
| 下载CSV 表 7 4根简支梁荷载对比分析 Tab.7 Analysis of four beams load comparison |
(1) 顶板为UHPC组合梁的弯曲性能与C60箱梁基本一致,承载能力仅为C60箱梁的1.04倍.
(2) 底板为UHPC可以充分发挥UHPC的抗拉强度,提高截面的极限承载力(为C60箱梁极限承载力的1.42倍),该组合形式截面裂缝发展缓慢,梁体延性增加,可以显著改善裂缝发展模态.
(3) 全截面UHPC箱梁极限承载能力是C60箱梁的2.18倍,其安全储备远大于普通C60混凝土梁,还可以通过合理配筋来充分利用UHPC性能.
(4) 对比C60箱梁,底板为UHPC组合梁具有优异的裂缝宽度控制能力,同时UHPC可在钢筋屈服前与其全程协同工作,这使得钢筋在某些需要对裂缝宽度进行严格控制的结构类型中具有很高的应用价值.
(5) 对于简支箱梁结构,底板为受拉区,对比全截面更换UHPC,更换受拉区混凝土对于改善结构的受力性能效率更高.因此综合材料性能的发挥程度、裂缝发展模态、极限承载能力、普遍适用性和经济性等因素,推荐采用将受拉区混凝土代替为UHPC的组合截面进行设计应用.
| [1] |
聂建国. 钢-混凝土组合结构桥梁[M]. 北京: 人民交通出版社, 2011 NIE Jianguo. Steel-concrete composite structure bridge[M]. Beijing: People Communications Press, 2011 |
| [2] |
Association Francaise de Génie Civil. Ultra-high performance fiber reinforced recommendation[S]. [S. l. ]: Association Francaise de Génie Civil, 2013.
|
| [3] |
蒲心诚, 王志军. 超高强高性能混凝土的力学性能研究[J]. 建筑结构学报, 2002, 23(6): 49 PU Xincheng, WANG Zhijun. Study on mechanical properties of ultra high strength and high performance concrete[J]. Journal of Building Structures, 2002, 23(6): 49 |
| [4] |
TAYEH B A, BAKAR B H A, JOHARI M A M, et al. Evaluation of bond strength between normal concrete substrate and ultra high performance fiber concrete as a repair material[J]. Procedia Engineering, 2013, 54: 554 DOI:10.1016/j.proeng.2013.03.050 |
| [5] |
WATANABLE N, MUSHA H, YOSHINAGA K. Design and performance tests for bridge using ultra high strength fiber reinforced concrete[EB/OL]. [2017-10-01]. http://www.pwri.go.jp/eng/ujnr/tc/g/pdf/23/23-9-3watanabe.pdf.
|
| [6] |
BRUHWILER E, DENARIE E. Rehabilitation and strengthening of concrete structures using ultra-high performance fibre reinforced concrete[J]. Structural Engineering International, 2013, 23(4): 450 DOI:10.2749/101686613X13627347100437 |
| [7] |
THIBAUX T. Using UHPFRC for structural reinforcement of buildings and civil works[M]. [S.l.]: John Wiley & Sons Inc, 2013: 553-564
|
| [8] |
GRAYBEAL B. Ultra-high performance concrete[J]. Technote, 2011, 19(10): 848 |
| [9] |
HONARVAR E, SRITHARAN S, MATTHEWS R J, et al. Bridge decks with precast UHPC waffle panels: A field evaluation and design optimization[J]. Journal of Bridge Engineering, 2015, 21(1): 04015030 |
| [10] |
LAMPROPOULOS A P, PASCHALIS S A, TSIOULOU O T, et al. Strengthening of reinforced concrete beams using ultra high performance fibre reinforced concrete (UHPFRC)[J]. Engineering Structures, 2015, 106: 370 |
| [11] |
FERRIER E, CONFRERE A, MICHEL L, et al. Shear behaviour of new beams made of UHPC concrete and FRP rebar[J]. Composites Part B: Engineering, 2016, 90: 1 |
| [12] |
Maintenance Construction Sécurite, École Polytechnique Fédérale de Lausanne. Ultra-high performance fibre reinforced cement-based composites(UHPFRC)[S]. Lausanne: [s. n. ], 2016.
|
| [13] |
中华人民共和国国家质量监督检测检疫总局, 中国国家标准化管理委员会. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228. 1—2010 [S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. The first part of tensile test for metallic materials: Room temperature test method: GB/T 228. 1—2010 [S]. Beijing: China Standard Press, 2011. |
| [14] |
中国建筑科学研究院. 混凝土结构设计规范: GB50010—2010 [S]. 北京: 中国建筑工业出版社, 2010. China Academy of Building Research. Specification for design of concrete structure: GB50010—2010 [S]. Beijing: China Construction Industry Press, 2010. |
 2018, Vol. 46
2018, Vol. 46

