2. 武汉理工大学 汽车零部件技术湖北省协同创新中心, 湖北 武汉 430070;
3. 中国汽车技术研究中心, 天津 300300
2. Hubei Collaborative Innovation Center for Automotive Components Technology, Wuhan University of Technology, Wuhan 430070, China;
3. China Automotive Technology & Research Center, Tianjin 300300, China
目前, 由于汽车工业对车身轻量化的要求越来越高, 因此需要充分利用材料组合以达到最合理的性能.拼焊板技术可以将材料等级和厚度属性等进行灵活匹配[1-3].
为了达到车身性能要求, 必须以车身拼焊板结构设计中特定性能为开发目标, 对具体典型目标的车身拼焊板结构进行性能定制设计.针对此思路, 部分学者对拼焊板零件的设计进行了研究[4-5].Zhu等[6]和Pan等[7]研究了拼焊板车门和B柱的安全性优化设计, Xu等[8-9]研究了不同组合下拼焊板结构的压溃和弯曲性能, 段永川等[10]建立了拼焊板V形回弹解析预测模型并成功应用于自由弯曲成形过程.上述研究验证了拼焊板结构在吸能以及成形性方面的优越性.除此以外, 车身性能如刚度也需满足结构要求[11].其中, 车门系统作为汽车车身侧围结构中主要的相对独立的部件总成, 其刚度特性需满足特别的要求[12-13].
对于拼焊板车门结构来说, 在给定材料等级和厚度的前提下, 焊缝位置布局是否合理对刚度性能有着至关重要的作用, 所以需根据刚度性能要求对拼焊板车门的焊缝布局进行合理设计.该问题从本质上来讲是在材料等级或者厚度给定的情况下, 重新分布每种材料等级或者每种厚度所占有的区域, 各区域间的分界线自然就可以认为是焊缝的位置, 进而使得拼焊板性能达到最优, 是一种拓扑行为.
一般的拓扑优化方法所应用的对象是由不同弹性模量材料组成的结构, 这对于实施拓扑策略是有利的, 因为单位刚度矩阵与弹性模量成线性相关[14-15].然而, 若研究对象是由不同厚度的母板拼焊而成的结构, 情况会有所不同.对于不同的力学问题单位刚度矩阵与厚度之间的关系是不同的, 所以在对各厚度区域进行重新分布(分块)或者对焊缝位置重新布局时, 需要升级原始算法并重新进行针对厚度的插值函数构造及灵敏度分析.
本文采用双向渐进拓扑优化技术来实施多刚度性能要求下的拼焊板车门内板结构的焊缝布局.将传统的仅针对弹性模量的插值函数转换为基于厚度函数的插值模型, 根据不同的刚度工况要求推导出相应的灵敏度计算公式, 并提出了拼焊板车门结构焊缝布局设计方法.
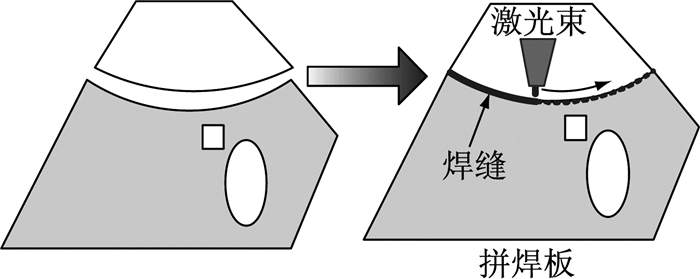
1 问题的提出对于实际的拼焊板结构, 除了由不同等级材料拼焊而成以外, 还可由不同厚度的部件组成, 这时就需要确定不同厚度区域的分界线, 即焊缝的位置, 也就是厚度区域的重新合理分布.在给定的载荷条件下使拼焊板结构具有最大的总体刚度, 以便在拼焊之前指导焊接过程(见图 1).
|
图 1 多厚度拼焊板结构的连续激光焊接过程示意图 Fig.1 Schematic diagram of continuous laser welding process for multi-thickness TWB structures |
在拼焊板结构的拓扑优化中, 需要用结构最小柔顺性或平均柔度指标作为目标响应.优化问题是对不同厚度区域进行重新布局, 或者在给定的设计空间内寻求最优的厚度分布, 不同厚度区域的交界线自然而然就是确定的最优焊缝位置.多厚度拼焊板结构拓扑优化方法的数学模型与一般拓扑优化问题相同, 即采用代表拼焊板结构总应变能或平均柔度作为目标函数, 如下所示:
| $ \begin{array}{l} \min C = \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{u}} = \frac{1}{2}{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ku}}\\ {\rm{s}}.\;{\rm{t}}.\;V_j^ * - \sum\limits_{i = 1}^N {{V_i}{x_{ij}}} - \sum\limits_{i = 1}^{j - 1} {V_i^ * } = 0,i = 1,2, \cdots ,N,\\ \;\;\;\;\;j = 1,2, \cdots ,n - 1 \end{array} $ | (1) |
式中:f为载荷向量; K和u分别为结构的全局刚度矩阵和位移向量; N为设计空间区域内的单元总数; Vi为第i个单元的体积; Vj*为第j种厚度的体积; xij为设计变量; n为总厚度个数.
拓扑优化问题中将有限元模型设计空间内每个单元的“单元密度”(xij)作为设计变量, 在优化迭代过程中改变单元密度并将其与刚度矩阵耦合.在数值实施过程中, 数字0用xmin(如0.001)来代替以避免数值不稳定.拼焊板结构的每个单元厚度值选择的原则是:若优化求解后目标单元的单元密度值为1, 则表示该单元位置处的厚度属性比较重要; 相反, 若单元密度值为xmin或者比较靠近xmin, 则说明该单元位置处的厚度不是特别重要, 需要赋予较小的厚度值.前者(较大厚度值)的单元保留, 后者的单元厚度值较小, 这样就能达到材料高效利用的目的, 进而实现拼焊板结构轻量化和性能设计最优化之间的最佳平衡.
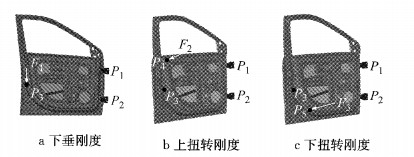
2 车门刚度性能及模型描述选择车身侧围结构的左前车门系统作为研究对象, 考虑到车门内板在保持系统刚度等静态特性中发挥着主要作用, 因此将车门内板作为拓扑优化的研究对象, 目的在于设计所有载荷情况下具有最小平均柔度(或者最大刚度)的车门系统.在每种载荷情况下, 通过施加载荷处的位移或者挠度来评价结构的刚度.通过商业有限元软件ABAQUS进行数值建模, 该模型定义了壳单元、单元属性、材料属性、载荷和边界条件等.本文考虑的载荷工况条件为下垂刚度、上扭转刚度和下扭转刚度, 有限元模型如图 2所示.
|
图 2 车门不同刚度的载荷和边界条件 Fig.2 Force and boundary conditions of door with different stiffnesses |
车门系统不同刚度性能目标所对应的载荷工况是不同的.对于下垂刚度, 铰链处(点P1和P2)的6个自由度被约束, 且门把手处(点P3)的水平位移即x和y方向上的位移被约束并在z方向施加F1=800 N的载荷; 对于上扭转刚度和下扭转刚度, 铰链处被完全固定, 门把手处除了旋转以外的自由度被约束, 2种载荷(F2=F3=200 N)沿着y方向被施加于车门内板的上下位置(点P4和P5).
可将上述3种刚度工况抽象为2种典型的力学问题.由于载荷主要集中在板内, 所以下垂刚度情况为平面应力问题, 上扭转刚度和下扭转刚度为弯曲问题.然后, 这3种工况的单位刚度矩阵与厚度之间的关系是不同的, 前者是一次方关系, 后者是三次方关系, 目前的算法还不能有效解决.本文将上述拓扑优化技术进行有效升级和拓展, 然后对多厚度拼焊板车门在多刚度工况条件下的焊缝位置进行合理布置, 进而使得拼焊板车门性能达到最优.
3 插值函数及灵敏度分析 3.1 插值函数的构造一般的拓扑优化方法是直接由2种或者多种材料的弹性模量插值函数进行灵敏度分析, 即中间或者相邻材料的弹性模量被定义为单元密度函数, 如下所示:
| $ E\left( {{x_{ij}}} \right) = x_{ij}^p{E_j} + \left( {1 - x_{ij}^p} \right){E_{j + 1}} $ | (2) |
式中:p为罚指数, p足够大时, 对优化设计结果几乎没有影响[16], 一般其值取为3;E为弹性模量.
假设设计变量xijp与泊松比不存在任何的内在关系, 那么就可以由设计变量xijp和单元刚度矩阵通过一定的插值技术得到全局刚度矩阵K, 如下所示:
| $ \mathit{\boldsymbol{K}} = \sum\limits_i {\left[ {x_{ij}^p{\mathit{\boldsymbol{K}}_{i,j}} + \left( {1 - x_{ij}^p} \right){\mathit{\boldsymbol{K}}_{i,j + 1}}} \right]} $ | (3) |
式中:Ki, j和Ki, j+1分别是由弹性模量Ej和Ej+1计算得到的第i个单元的刚度矩阵.
需要指出的是, 之所以给出式(3), 是因为对于本文所研究的多厚度拼焊板结构焊缝布局设计方法, 单元刚度矩阵与厚度呈现不同的函数关系, 不能给出统一的插值函数, 而是需要进行一定的变换.
由有限元知识可知, 对于任何力学问题, 单元刚度矩阵可以统一表达为
| $ {\mathit{\boldsymbol{K}}_i}\left( t \right) = T\left( t \right)\int_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{EB}}{\rm{d}}\mathit{\Omega }} = T\left( t \right){{\mathit{\boldsymbol{\hat K}}}_\mathit{\boldsymbol{i}}} $ | (4) |
式中:E和B分别分别为材料矩阵和应变位移矩阵; Ω为设计区域.对于平面应力问题和平板弯曲问题, 厚度t的函数
| $ T\left( t \right) = \left\{ \begin{array}{l} t,\;\;\;\;\;\;\;平面应力问题\\ \frac{{{t^3}}}{{12}},\;\;\;\;平板弯曲问题 \end{array} \right. $ | (5) |
为了清楚地表达, 本文直接对中间厚度的函数进行插值, 如下所示:
| $ T\left( {{t_{ij}}} \right) = x_{ij}^pT\left( {{t_j}} \right) + \left( {1 - x_{ij}^p} \right)T\left( {{t_{j + 1}}} \right) $ | (6) |
这样单元刚度矩阵
| $ {\mathit{\boldsymbol{K}}_i}\left( {{x_{ij}}} \right) = x_{ij}^p{\mathit{\boldsymbol{K}}_{i,j}} + \left( {1 - x_{ij}^p} \right){\mathit{\boldsymbol{K}}_{i,j + 1}} $ | (7) |
与式(3)不同的是, 在式(7)中Ki, j和Ki, j+1分别是由厚度Tj和Tj+1计算得到的第i个单元的刚度矩阵.
3.2 灵敏度分析当拼焊板结构厚度属性发生变化时, 其结构平均柔度也会随之发生变化.灵敏度用来分析和表达结构参数变化与响应变化之间的关系, 灵敏度系数可以表达为拼焊板结构响应对相应参数的梯度信息.
在有限元分析中, 静态结构平衡方程为
| $ \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{f}} $ | (8) |
当拼焊板车门结构给定载荷时, 结合式(1), 目标函数即平均柔度C的灵敏度可以通过对设计变量xij进行微分得到, 如下所示:
| $ \frac{{\partial C}}{{\partial {x_{ij}}}} = \frac{1}{2}\frac{{\partial {\mathit{\boldsymbol{f}}^{\rm{T}}}}}{{\partial {x_{ij}}}}\mathit{\boldsymbol{u}} + \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {x_{ij}}}} $ | (9) |
为了确定位移向量的灵敏度, 需要对目标函数引入Lagrangian乘子向量λ, 这样目标函数被修正为
| $ C = \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{Ku}}} \right) $ | (10) |
修正后的目标函数灵敏度
| $ \begin{array}{l} \frac{{\partial C}}{{\partial {x_{ij}}}} = \frac{1}{2}\frac{{\partial {\mathit{\boldsymbol{f}}^{\rm{T}}}}}{{\partial {x_{ij}}}}\mathit{\boldsymbol{u}} + \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {x_{ij}}}} + \\ \;\;\;\;\;\;\frac{{\partial {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}}}{{\partial {x_{ij}}}}\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{Ku}}} \right) + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\frac{{\partial \mathit{\boldsymbol{f}}}}{{\partial {x_{ij}}}} - \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_{ij}}}}\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{K}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {x_{ij}}}}} \right) \end{array} $ | (11) |
由于平衡方程的存在, 式(11)中等号右边的第3项就变为零.假设一个单元密度的变化对施加的载荷向量没有影响, 这样目标函数灵敏度
| $ \frac{{\partial C}}{{\partial {x_{ij}}}} = \left( {\frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{K}}} \right)\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {x_{ij}}}} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_{ij}}}}\mathit{\boldsymbol{u}} $ | (12) |
由式(10)可知, 因为(f-Ku)始终为零, 所以可以任意选择Lagrangian乘子向量λ.为了消除式(12)中的未知量
| $ \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{K}} = 0 $ | (13) |
再次结合平衡方程, 式(13)可以进一步表达为
| $ \mathit{\boldsymbol{\lambda }} = \frac{1}{2}\mathit{\boldsymbol{u}} $ | (14) |
将式(14)代入式(12), 可得目标函数的微分方程为
| $ \frac{{\partial C}}{{\partial {x_{ij}}}} = - \frac{1}{2}{\mathit{\boldsymbol{f}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_{ij}}}}\mathit{\boldsymbol{u}} = - \frac{1}{2}\mathit{\boldsymbol{u}}_i^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{K}}_i}}}{{\partial {x_{ij}}}}{\mathit{\boldsymbol{u}}_i} $ | (15) |
如果对n种厚度进行最优设计, 通过插值函数式(7), 可得单元灵敏度
| $ {\alpha _{ij}} = - \frac{1}{p}\frac{{\partial C}}{{\partial {x_{ij}}}} = \frac{1}{2}x_{ij}^{p - 1}\mathit{\boldsymbol{u}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}_{i,j}} - {\mathit{\boldsymbol{K}}_{i,j + 1}}} \right){\mathit{\boldsymbol{u}}_i} $ | (16) |
这样, 针对不同的力学问题, 灵敏度可以统一显式表达为
| $ {\alpha _{ij}} = \left\{ \begin{array}{l} \frac{1}{2}\left[ {1 - \frac{{T\left( {{t_{j + 1}}} \right)}}{{T\left( {{t_j}} \right)}}} \right]\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,j}}{\mathit{\boldsymbol{u}}_i},{x_{ij}} = 1\\ \frac{1}{2}x_{\min }^{p - 1}\left[ {\frac{{T\left( {{t_j}} \right)}}{{T\left( {{t_{j + 1}}} \right)}} - 1} \right]\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,j + 1}}{\mathit{\boldsymbol{u}}_i},{x_{ij}} = {x_{\min }} \end{array} \right. $ | (17) |
作为一种特殊和简单的算例, 对于2种厚度t1和t2的拼焊板结构, 单元灵敏度可以简化为
| $ {\alpha _{ij}} = \left\{ \begin{array}{l} \frac{1}{2}\left[ {1 - \frac{{T\left( {{t_2}} \right)}}{{T\left( {{t_1}} \right)}}} \right]\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,1}}{\mathit{\boldsymbol{u}}_i},{x_{ij}} = 1\\ \frac{1}{2}x_{\min }^{p - 1}\left[ {\frac{{T\left( {{t_1}} \right)}}{{T\left( {{t_2}} \right)}} - 1} \right]\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,2}}{\mathit{\boldsymbol{u}}_i},{x_{ij}} = {x_{\min }} \end{array} \right. $ | (18) |
将每个节点周围的单元灵敏度取平均值, 进而得到节点灵敏度, 如下所示:
| $ {\alpha _{j,{\rm{n}}}} = \sum\limits_{i = 1}^M {{\omega _i}{\alpha _{i,{\rm{e}}}}} $ | (19) |
式中:下标n和e分别表示节点和单元; M为与第j个节点连接的单元总数; ωi为第i个单元对于节点j的加权系数, 且
| $ {\omega _i} = \frac{1}{{M - 1}}\left( {1 - \frac{1}{{\sum\limits_{i = 1}^M {{r_{ij}}} }}} \right) $ | (20) |
式中:rij为第j个节点与第i个单元中心之间的直线距离.rij在物理意义上可以理解为单元的中心越靠近节点, 其对节点灵敏度的影响就会越大.
一般需把节点灵敏度映射到单元上, 过滤器的给定是为了找出设计区域内与第i个单元灵敏度有关联的每个节点, 该影响域中心就是第i个单元的中心.第i个单元的灵敏度给定为
| $ {\alpha _i} = \frac{{\sum\limits_{j = 1}^q {\omega \left( {{r_{ij}}} \right){\alpha _{j,{\rm{n}}}}} }}{{\sum\limits_{j = 1}^q {\omega \left( {{r_{ij}}} \right)} }} $ | (21) |
式中:q为影响域内节点的总数; ω(rij)为权重系数.ω(rij)的计算公式为
| $ \omega \left( {{r_{ij}}} \right) = {r_{\min }} - {r_{ij}} $ | (22) |
多刚度条件下的拼焊板车门结构设计其实可以视为一个多目标优化设计问题, 解决该问题的一个简单方式就是通过加权柔度将多目标转化为具有给定权系数的单目标问题.在拼焊板结构焊缝布局优化问题中, 将相应的目标响应看成每个子刚度工况相对应的柔度加权之和, 实际上就是一个定义在整个结构上的全局响应.
不同厚度组成的拼焊板结构在多刚度条件下的焊缝布局设计问题可以表示为
| $ \begin{array}{l} \min f\left( x \right) = \sum\limits_{k = 1}^m {{w_k}{C_k}} = \sum\limits_{k = 1}^m {{w_k}{{\left( {{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{u}}} \right)}_k}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{k = 1}^m {{w_k}{{\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ku}}} \right)}_k}} \\ {\rm{s}}.\;{\rm{t}}.\;\;V_j^ * - \sum\limits_{i = 1}^N {{V_i}{x_{ij}}} - \sum\limits_{i = 1}^{j - 1} {V_i^ * } = 0\\ \;\;\;\;\;\;{x_{ij}} = \left\{ \begin{array}{l} 1,\;\;t > {t_j}\\ {x_{\min }},\;\;t \le {t_{j + 1}} \end{array} \right. \end{array} $ | (23) |
式中:m是所有刚度情况总数; Ck是第k种刚度下的平均柔度; wk是第k种刚度的权系数, 其值依赖于每种刚度的相对重要性, 且
| $ {\alpha _{ij}} = \frac{1}{2}x_{ij}^{p - 1}\sum\limits_{k = 1}^m {{w_k}{{\left\{ {\left[ {T\left( {{t_j}} \right) - T\left( {{t_{j + 1}}} \right)} \right]\mathit{\boldsymbol{u}}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat K}}}_i}{\mathit{\boldsymbol{u}}_i}} \right\}}_k}} $ | (24) |
相似地, 对于第j种厚度的第i个单元的灵敏度可以显式表达为
| $ {\alpha _{ij}} = \left\{ \begin{array}{l} \frac{1}{2}\left[ {1 - \frac{{T\left( {{t_{j + 1}}} \right)}}{{T\left( {{t_j}} \right)}}} \right]\sum\limits_{k = 1}^m {{w_k}{{\left( {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,j}}{\mathit{\boldsymbol{u}}_i}} \right)}_k}} ,{x_{ij}} = 1\\ \frac{1}{2}x_{\min }^{p - 1}\left[ {\frac{{T\left( {{t_j}} \right)}}{{T\left( {{t_{j + 1}}} \right)}} - 1} \right]\sum\limits_{k = 1}^m {{w_k}{{\left( {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{i,j + 1}}{\mathit{\boldsymbol{u}}_i}} \right)}_k}} ,\\ \;\;\;\;\;\;{x_{ij}} = {x_{\min }} \end{array} \right. $ | (25) |
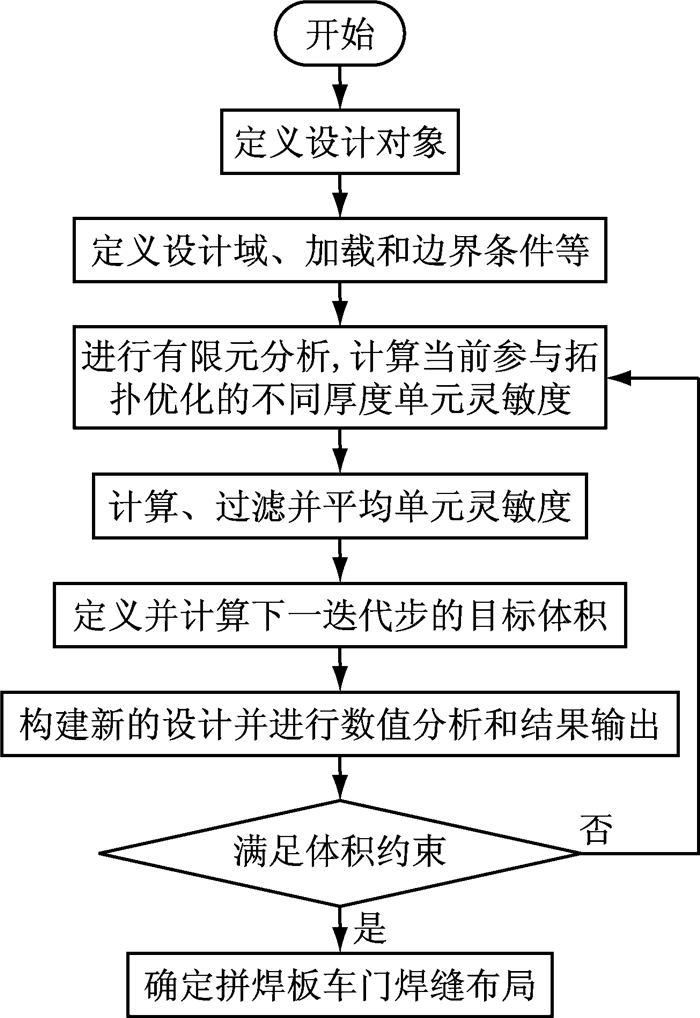
车身拼焊板车门结构在多刚度性能目标条件下的焊缝布局具体设计流程如图 3所示.
|
图 3 拼焊板车门焊缝布局拓扑设计流程 Fig.3 Topology design procedure of weld line layout of TWB door |
该算例是在固支方板中心承受一集中载荷(见图 4), 以验证该方法在处理拼焊板结构时的可行性.固支方板的几何尺寸为60 mm×60 mm, 弹性模量为210 GPa, 泊松比为0.3, 初始厚度为1 mm, 载荷p1为1 N.厚度分布情况为t1=1.0 mm、t2=0.8 mm和t3=0.5 mm, 体积分数分别为20%、30%和50%.

|
图 4 承受中心载荷的板结构示意图 Fig.4 Schematic diagram of plate structure subjected to central force |
图 5为不同厚度区域分布的渐进拓扑历史.可以看出, 优化后的拼焊板结构具有明显的对称性.由于在中心施加的是集中载荷, 最大厚度区域的大部分位于板结构的中心附近, 符合常理.从总体上来看, 得到的优化设计结果验证了采用该方法处理多厚度拼焊板结构的可行性, 不同厚度区域得到重新分布, 并能看出明显的焊缝位置.

|
图 5 本文方法优化迭代过程 Fig.5 Optimization iteration process of the proposed method |
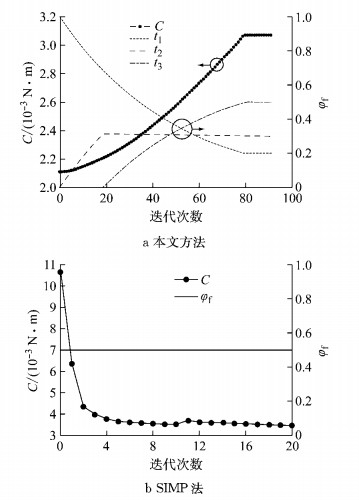
图 6a是平均柔度C和体积分数φf的渐进历史.可以看出, 拼焊板结构的平均柔度逐渐增加, 不同厚度区域的体积分数同时不断减小或增大, 达到预设值之后, 平均柔度和所有厚度的体积分数保持稳定并不再变化, 整个迭代过程较为平顺.
|
图 6 2种方法的平均柔度和体积分数的渐进历史 Fig.6 Evolutionary history of mean compliance and volume fraction of two methods |
作为对比, 这里也给出通过各向正交惩罚材料密度(SIMP)法得到的结果.为了明显看出SIMP法优化后的中间厚度过渡区域, 将SIMP法中的最小厚度参数设置为一个较小的值(如0.125 mm), 平均柔度C和体积分数φf的渐进历史以及拓扑结构渐进历程分别如图 6b和图 7所示.可以看出, 优化后的结构会出现中间厚度过渡区域, 不会产生清晰的不同厚度区域分界线, 从而不能确定真实的焊缝位置布局, 而这模糊的设计结果直接会给拼焊板结构的实际制造工艺带来很大的困难, 显示出SIMP法的局限性.与本文拓扑方法渐进历史不同的是, SIMP法从迭代过程开始, 结构最大厚度区域的体积分数就保持常量不变, 所以在SIMP法中平均柔度逐渐减小直至满足收敛条件, 而体积分数不会发生改变.

|
图 7 SIMP法优化迭代过程 Fig.7 Optimization iteration process of SIMP method |
对比图 5和图 7可以看出, 在给定设计空间和体积约束条件下, 2种方法得到的最大厚度区域的位置或者最优材料分布非常相似.相对于SIMP法, 本文基于刚度目标的多厚度拓扑优化方法得出的结果更合理, 材料分布更具有聚集性, 并且不存在棋盘效应和中间密度区域; 不同厚度区域的分界线更加明显, 即焊缝位置清晰可见, 使得优化后的拼焊板结构更容易解读, 能够较好地指导车身拼焊板零件如车门结构焊缝的布局设计.
5.2 拼焊板车门焊缝布局拓扑设计结果考虑以下2种典型工况:①下垂刚度, t1=1.3 mm (φf1=40%), t2=0.8 mm (φf2=30%), t3=0.5 mm (φf3=30%); ②上扭转刚度和下扭转刚度, t1=1.4 mm (φf1=50%), t2=1.0 mm (φf2=20%), t3=0.6 mm (φf3=30%).下垂刚度所施加的载荷主要集中在板内, 所以是平面应力问题; 上扭转刚度和下扭转刚度的载荷垂直于板, 故认为是弯曲问题.渐进优化参数设定为渐进率R=0.02, 过滤半径rmin =100 mm.对于情况②中的上扭转刚度和下扭转刚度权因子, 需根据试验结果或者重要程度确定.为了避免优化拼焊板车门出现较大的挠度, 在此取上扭转刚度和下扭转刚度的权因子比值为2 :1, 简单取为0.67和0.33.
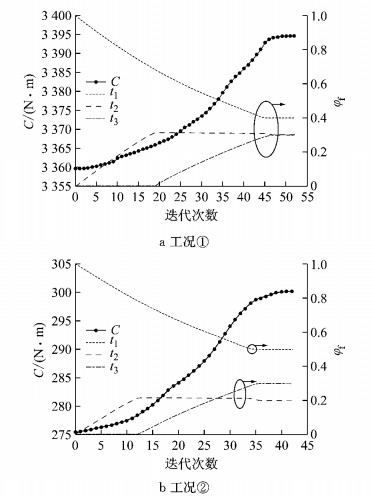
图 8为拼焊板车门内板的平均柔度和体积分数的拓扑渐进历史.优化后的工况①和工况②的平均柔度分别为3 394.62 N·mm和300.12 N·mm.体积分数的渐进历史表明:从厚度t1的初始设计开始, 逐渐从厚度t1转变到厚度t2, 直至厚度t2达到需满足的体积分数; 之后, 厚度t2的体积分数保持常量, 厚度t3的体积分数逐渐增加直到满足其体积约束为止; 目标函数和各个厚度区域的体积分数均保持稳定收敛时, 整个优化迭代过程停止.
|
图 8 拼焊板车门内板的平均柔度和体积分数的渐进历史 Fig.8 Evolutionary history of mean compliance and volume fraction of TWB door inner panel |
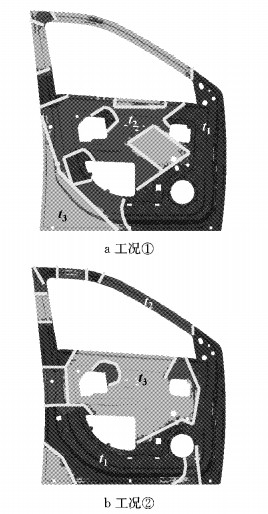
最优拓扑优化的车门内板形状如图 9所示.图中不同厚度的边界界面即焊缝位置用实线表示.可以明显看出, 在车门铰链固定处具有最大的厚度值.根据该拓扑优化结果, 可以通过激光焊接技术, 将不同厚度且合适的板结构焊接成整个零件, 再冲压成拼焊板车门内板, 最后通过电阻点焊等程序即可组成拼焊板车门系统.
|
图 9 不同刚度工况下拼焊板车门内板优化设计结果 Fig.9 Optimization design results of TWB door inner panel for different stiffness cases |
为了进一步评价优化结果, 表 1列出了初始设计和最优设计数值结果之间的对比.从最大厚度t1开始进行初始设计, 之后改变厚度从t1到t2再到t3, 逐渐降低总质量.由于结构总质量的大幅降低(20%以上), 得到的平均柔度仅有较小幅度的增加(不到9%), 尤其是工况①, 仅仅损失结构刚度的1%, 就能降低接近30%的质量, 这意味着通过本文提出的拓扑优化设计方法, 能在不牺牲结构总体刚度的前提下, 使拼焊板车门结构的总质量大幅降低, 表明该设计方法在拼焊板车门轻量化设计中是有效的.
| 下载CSV 表 1 优化前后拼焊板车门内板平均柔度和质量对比 Tab.1 Comparison of mean compliance and mass of TWB door inner panel before and after optimization |
(1) 将传统的只针对弹性模量的插值函数转换为对厚度函数的插值模型, 根据不同的刚度工况要求推导出相应的灵敏度计算公式.
(2) 在材料厚度和相应体积分数给定的情况下, 不同厚度区域重新分布, 分界线更加明显, 焊缝的布局位置清晰可见, 优化后的拼焊板结构更容易解读.
(3) 优化设计后的结构在不削弱总体刚度的前提下质量降低.
| [1] |
MIRAPEIX J, VILA E, VALDIANDE J J, et al. Real-time detection of the aluminum contribution during laser welding of Usibor1500 tailor-welded blanks[J]. Journal of Materials Processing Technology, 2016, 235: 106 DOI:10.1016/j.jmatprotec.2016.04.017 |
| [2] |
PARENTE M, SAFDARIAN R, SANTOS A D, et al. A study on the formability of aluminum tailor welded blanks produced by friction stir welding[J]. The International Journal of Advanced Manufacturing Technology, 2016, 83(9/10/11/12): 2129 |
| [3] |
徐峰祥, 田轩屹. 基于正交表的前纵梁拼焊板安全性设计[J]. 汽车工程, 2017, 39(2): 237 XU Fengxiang, TIAN Xuanyi. Safety design of TWB front side rail based on orthogonal array[J]. Automotive Engineering, 2017, 39(2): 237 |
| [4] |
SHIN J K, LEE K H, SONG S I, et al. Automotive door design with the ULSAB concept using structural optimization[J]. Structural and Multidisciplinary Optimization, 2002, 23(4): 320 DOI:10.1007/s00158-002-0189-z |
| [5] |
SONG S, PARK G. Multidisciplinary optimization of an automotive door with a tailored blank[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2006, 220(2): 151 DOI:10.1243/095440706X72772 |
| [6] |
ZHU P, SHI Y, ZHANG K, et al. Optimum design of an automotive inner door panel with a tailor-welded blank structure[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2008, 222(8): 1337 DOI:10.1243/09544070JAUTO763 |
| [7] |
PAN F, ZHU P, ZHANG Y. Metamodel-based lightweight design of B-pillar with TWB structure via support vector regression[J]. Computers & Structures, 2010, 88(1): 36 |
| [8] |
XU F X, SUN G Y, LI G Y, et al. Experimental study on crashworthiness of tailor welded blank (TWB) thin-walled high-strength steel (HSS) tubular structures[J]. Thin-Walled Structures, 2014, 74: 12 DOI:10.1016/j.tws.2013.08.021 |
| [9] |
XU F X, SUN G Y, LI G Y, et al. Experimental investigation on high strength steel (HSS) tailor-welded blanks (TWBs)[J]. Journal of Materials Processing Technology, 2014, 214(4): 925 DOI:10.1016/j.jmatprotec.2013.11.018 |
| [10] |
段永川, 官英平. 拼焊板V形自由弯曲精确回弹控制技术研究[J]. 机械工程学报, 2014, 50(10): 40 DUAN Yongchuan, GUAN Yingping. Development of precise spring-back control system of tailor welded blanks air bending process[J]. Journal of Mechanical Engineering, 2014, 50(10): 40 |
| [11] |
范文杰, 范子杰, 桂良进. 多工况下客车车架结构多刚度拓扑优化设计研究[J]. 汽车工程, 2008, 30(6): 531 FAN Wenjie, FAN Zijie, GUI Liangjin. Multi-stiffness topology optimization of bus frame with multiple conditions[J]. Automotive Engineering, 2008, 30(6): 531 |
| [12] |
朱茂桃, 钱洋, 顾娅欣, 等. 基于Kriging模型的车门刚度和模态优化[J]. 汽车工程, 2013, 35(11): 1047 ZHU Maotao, QIAN Yang, GU Yaxin, et al. Stiffness and modal optimization of car door based on Kriging model[J]. Automotive Engineering, 2013, 35(11): 1047 DOI:10.3969/j.issn.1000-680X.2013.11.019 |
| [13] |
高云凯, 申振宇, 冯兆玄, 等. 多目标优化在车门轻量化设计中的应用[J]. 同济大学学报(自然科学版), 2017, 45(2): 275 GAO Yunkai, SHEN Zhenyu, FENG Zhaoxuan, et al. Application of multi-objective optimization in vehicle door lightweight[J]. Journal of Tongji University (Natural Science), 2017, 45(2): 275 |
| [14] |
XIE Y M, STEVEN G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures, 1993, 49(5): 885 |
| [15] |
HUANG X, XIE Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J]. Computational Mechanics, 2009, 43(3): 393 DOI:10.1007/s00466-008-0312-0 |
| [16] |
HUANG X, XIE Y M. Evolutionary topology optimization of continuum structures:methods and applications[M]. Chichester: John Wiley & Sons, 2010
|
 2018, Vol. 46
2018, Vol. 46
