随着高速动车组运营速度的提升,车体振动加剧,诸多学者提出采用动力吸振器控制车体弹性振动.周劲松等[1]在车底安装动力吸振器,研究其对车体弹性振动的作用,提出动力吸振器质量越大,减振性能越好.Gong等[2]将车体视为均质弹性欧拉梁,安装动力吸振器,建立刚柔耦合模型,分析动力吸振器对车体振动的抑制作用,提出采用动力吸振器后,大大降低了对车体垂向一阶弯曲频率的要求.
以往的研究中,大多是将动力吸振器用于车体弹性振动控制,鲜见用于车体刚性振动控制,究其原因,是由于高速动车组车体刚性振动频率很低,针对刚性振动频率所设计的动力吸振器,其吊挂刚度很低,静挠度过大,难以直接安装于车体下方.为了解决吊挂刚度与静挠度这一矛盾,可采用高静刚度低动刚度(high static low dynamic stiffness, HSLDS)减振元件作为动力吸振器的吊挂元件.国内外学者对HSLDS减振元件进行过诸多研究.Carrella等[3-4]将一对线性弹簧水平放置,与垂向线性弹簧并联,得到HSLDS隔振系统,该系统在与等效线性系统有着同样静挠度的条件下,具有更低的固有频率.刘兴天等[5-7]通过并联具有负刚度特性的刀口支撑滑动梁和正刚度的线性弹簧,得到超低频非线性隔振系统,还将具有负刚度特性的欧拉屈曲梁结构与线性隔振器并联得到准零刚度隔振器.孟令帅等[8]分别采用等厚度和变厚度碟形弹簧与线性弹簧并联,得到准零刚度隔振器,并研究了其静态和动态特性,得到了激励幅值、质量比、阻尼比等参数对碟形弹簧准零刚度隔振器的影响特点.
本文首先分析了基于加速度的二维动力吸振器的工作原理,设计了安装于车体下方,同时吸收车体点头、浮沉振动的二维动力吸振器.然后,利用碟形弹簧的负刚度特性,将其与橡胶弹簧并联,设计了用于安装二维动力吸振器的HSLDS减振元件.最后,基于Matlab/Simulink软件,建立了车辆垂向非线性动力学模型,分析了二维动力吸振器对车体振动的作用.
1 基于加速度的二维动力吸振器设计动力吸振器是振动控制领域重要的制振装置,在建筑、机械等领域得到了广泛的应用[9-11].动力吸振器是由辅助质量、弹簧及阻尼组成,其工作原理是利用多自由度系统的反共振特性,当主系统振动时,动力吸振器也随之振动,由于吸振器的动力作用,使其施加到主系统上的力与外界激振力的方向相反,以致其与外界激励力叠加后,作用到主系统上的合力幅值减小,以达到抑制主系统振动的目的[12].
图 1是同时考虑主振动系统浮沉和点头振动的动力吸振器原理图.图中,m1、J1分别为主振动系统质量、转动惯量,m2、J2分别为动力吸振器质量、转动惯量,其振动微分方程为
| $ \begin{array}{*{20}{c}} {{m_1}{{\ddot x}_1} = - 2{k_1}{x_1} - 2{k_2}\left( {{x_1} - {x_2}} \right) - }\\ {2c\left( {{{\dot x}_1} - {{\dot x}_2}} \right) + {F_1}{{\rm{e}}^{{\rm{i}}\omega t}}} \end{array} $ | (1) |
| $ {m_2}{{\ddot x}_2} = - {k_2}\left( {{x_2} - {x_1}} \right) - 2c\left( {{{\dot x}_2} - {{\dot x}_1}} \right) $ | (2) |
| $ \begin{array}{*{20}{c}} {{J_1}{{\ddot \theta }_1} = - 2{k_1}l_1^2{\theta _1} - 2{k_2}l_2^2\left( {{\theta _1} - {\theta _2}} \right) - }\\ {2cl_2^2\left( {{{\dot \theta }_1} - {{\dot \theta }_2}} \right) + {T_1}{{\rm{e}}^{{\rm{i}}\omega t}}} \end{array} $ | (3) |
| $ {J_2}{{\ddot \theta }_2} = - 2{k_2}l_2^2\left( {{\theta _2} - {\theta _1}} \right) - 2cl_2^2\left( {{{\dot \theta }_2} - {{\dot \theta }_1}} \right) $ | (4) |

|
图 1 二维动力吸振器原理图 Fig.1 Theory of two-dimensional dynamic vibration absorber |
式中:x1、θ1、k1、l1分别为主振动系统的垂向位移、点头角度、悬挂刚度、悬挂跨距之半; x2、θ2、k2、c、l2分别为动力吸振器的垂向位移、点头角度、悬挂刚度、阻尼、悬挂跨距之半; F1、T1分别为作用在主振动系统上的力和力矩幅值.
由模型的振动微分方程可知,其浮沉与点头振动是独立的,并不耦合,因此,两种振动可单独描述.这里以点头振动为例,推导基于加速度的点头吸振原理,其动力学方程为式(3)与式(4),联立该两式,假设其解为
| $ {\theta _1}\left( t \right) = {\mathit{\Theta }_1}{{\rm{e}}^{{\rm{i}}\left( {\omega t - \phi } \right)}},\;\;\;\;\;\;{\theta _2}\left( t \right) = {\mathit{\Theta }_2}{{\rm{e}}^{{\rm{i}}\left( {\omega t - \phi } \right)}} $ | (5) |
式中:Θ1、Θ2分别为主振动系统和动力吸振器的响应幅值;
| $ {{\ddot \theta }_1}\left( t \right) = - {\omega ^2}{\mathit{\Theta }_1}{{\rm{e}}^{{\rm{i}}\left( {\omega t - \phi } \right)}} = {A_1}{{\rm{e}}^{{\rm{i}}\omega t}} $ | (6) |
式中:A1为复数,包含了加速度的幅值和相位信息.
将式(5)代入式(3)与式(4),并引入以下符号
| $ \begin{array}{*{20}{c}} {{\omega _1} = \sqrt {2{k_1}l_1^2/{J_1}} ,{\omega _2} = \sqrt {2{k_2}l_2^2/{J_2}} ,{\theta _{{\rm{st}}}} = {T_1}/2{k_1}l_1^2,}\\ {\mu = {J_2}/{J_1},\beta = {\omega _2}/{\omega _1},\lambda = \omega /{\omega _1},\zeta = cl_2^2/{J_2}{\omega _1}} \end{array} $ |
式中:ω1为主振动系统固有角频率; ω2为动力吸振器固有角频率; θst为主振动系统的静变形; μ为转动惯量比; β为动力吸振器与主振动系统的固有频率比; λ为强迫振动频率比; ζ为阻尼比.整理可得点头加速度放大倍数为
| $ \left| {\frac{{{A_1}}}{{{\theta _{{\rm{st}}}}}}} \right| = \sqrt {\frac{{{\lambda ^4}\left[ {{{\left( {{\beta ^2} - {\lambda ^2}} \right)}^2} + {{\left( {2\zeta \lambda } \right)}^2}} \right]}}{{{{\left[ {\left( {1 - {\lambda ^2}} \right)\left( {{\beta ^2} - {\lambda ^2}} \right) - \mu {\beta ^2}{\lambda ^2}} \right]}^2} + {{\left( {2\zeta \lambda } \right)}^2}{{\left( {1 - {\lambda ^2} - \mu {\lambda ^2}} \right)}^2}}}} $ | (7) |
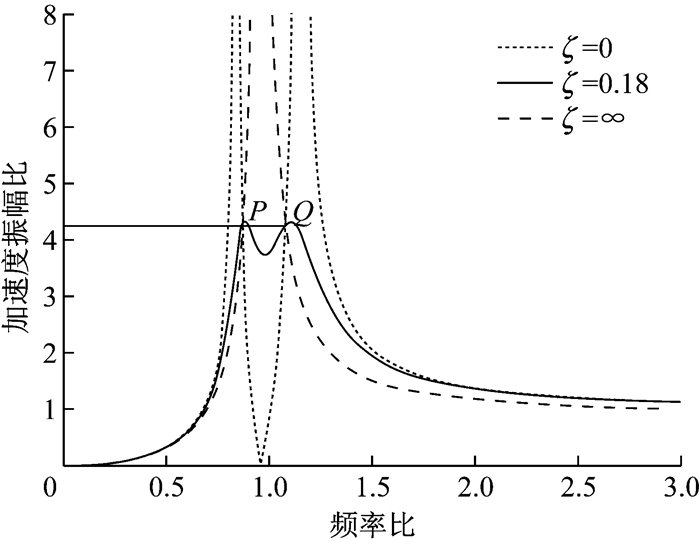
利用定点理论,令ζ=0及ζ=∞的两式相等,可得出两定点P、Q的坐标位置,再令二者等高,可得满足加速度响应的动力吸振器最优同调条件
| $ \beta = \frac{1}{{\sqrt {1 + \mu } }} $ | (8) |
图 2是基于加速度响应的最优同调得到满足时主振动系统的加速度响应与定点P、Q的关系.该图为转动惯量比μ=0.1的情况,其中ζ=0.18是动力吸振器最优阻尼,此时主振动系统加速度响应振幅比峰值位于定点P、Q附近.
|
图 2 主振动系统加速度响应曲线 Fig.2 Acceleration response of main vibration system |
目前的高速动车组通常采用轻量化技术,在车体底下吊挂重达数顿的动力吸振器是不现实的.一种可行的方法是将车下设备(如牵引变流器)视为动力吸振器,将车体视为主振动系统,如图 1所示.本研究中车辆动力学参数如表 1所示.
| 下载CSV 表 1 车辆动力学参数及其含义 Tab.1 Vehicle dynamics parameters and their meanings |
根据表 1所示车辆动力学参数,可计算得车体浮沉频率为0.678 Hz,点头频率为0.900 Hz,可得动力吸振器质量比μm、惯量比μJ分别为
| $ {\mu _{\rm{m}}} = \frac{6}{{40}} = 0.15,\;\;\;{\mu _{\rm{J}}} = \frac{{47}}{{1744}} = 0.027 $ | (9) |
可得满足动力吸振器浮沉、点头最优同调条件时,动力吸振器浮沉频率比βm、点头频率比βJ分别为
| $ {\beta _{\rm{m}}} = \frac{1}{{\sqrt {1 + {\mu _{\rm{m}}}} }} = 0.932,\;\;\;{\beta _{\rm{J}}} = \frac{1}{{\sqrt {1 + {\mu _{\rm{J}}}} }} = 0.987 $ | (10) |
可得动力吸振器浮沉频率fm、点头频率fJ分别为
| $ \left\{ \begin{array}{l} {f_{\rm{m}}} = 0.678{\beta _{\rm{m}}} = 0.632{\rm{Hz}}\\ {f_{\rm{J}}} = 0.900{\beta _{\rm{J}}} = 0.888{\rm{Hz}} \end{array} \right. $ | (11) |
根据图 1所示动力吸振器原理,可将动力吸振器视为2点吊挂,可得动力吸振器浮沉振动实现最优同调时,吊挂刚度ke为
| $ {k_{\rm{e}}} = {\left( {2{\rm{ \mathsf{ π} }}{f_{\rm{m}}}} \right)^2}{m_{\rm{e}}}/2 = 47.3\;{\rm{kN}} \cdot {{\rm{m}}^{ - 1}} $ | (12) |
动力吸振器点头振动实现最优同调时,吊挂跨距之半le为
| $ {l_{\rm{e}}} = \sqrt {\frac{{{{\left( {2{\rm{ \mathsf{ π} }}{f_{\rm{J}}}} \right)}^2}{J_{\rm{e}}}}}{{2{k_{\rm{e}}}}}} = 3.93\;{\rm{m}} $ | (13) |
如果采用传统橡胶元件作为动力吸振器悬挂元件,对于质量m、悬挂刚度kz、悬挂频率fz、静挠度δst的动力吸振器有
| $ {f_{\rm{z}}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sqrt {\frac{{{k_{\rm{z}}}}}{m}} ,\;\;\;\;{\delta _{{\rm{st}}}} = \frac{{mg}}{{{k_{\rm{z}}}}} = \frac{g}{{{{\left( {2{\rm{ \mathsf{ π} }}{f_{\rm{z}}}} \right)}^2}}} $ | (14) |
可见,悬挂频率直接决定了悬挂刚度及静挠度,如果悬挂频率过低,会使吸振器静挠度太大,导致超限界等问题.根据上节分析可知,抑制车体浮沉振动与点头振动的二维动力吸振器,其浮沉与点头固有频率均小于1 Hz,显然,仅采用传统橡胶元件作为悬挂元件是不行的.因此,本文基于碟形弹簧的负刚度特性,设计出一种碟型弹簧与传统橡胶件并联的HSLDS减振元件,以使动力吸振器以低频悬挂的同时,静挠度也控制在一定范围内.
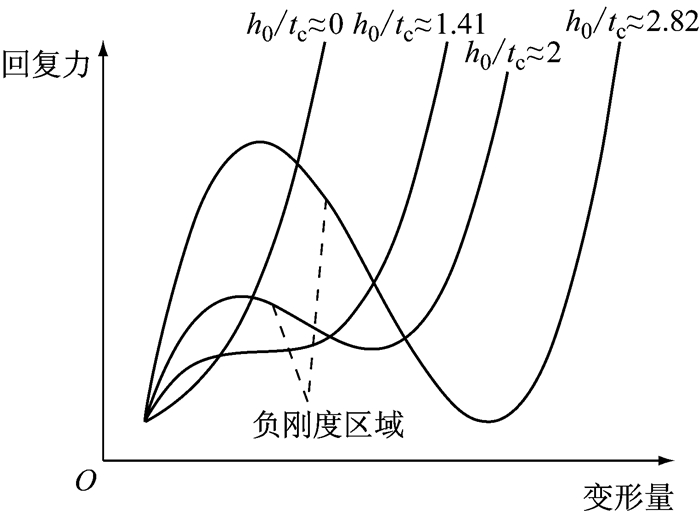
碟形弹簧根据其高厚比(h0/tc)不同,会表现出不同的受力特性,当高厚比大于
|
图 3 碟形弹簧力-变形特性曲线 Fig.3 Force characteristics of disc spring |

|
1—车体连接端; 2—设备连接端; 3—橡胶弹簧; 4—仅提供垂向刚度的碟形弹簧负刚度机构; 5—碟形弹簧; 6—滑动机构或润滑层 图 4 HSLDS减振元件示意图 Fig.4 Illustration of HSLDS element |
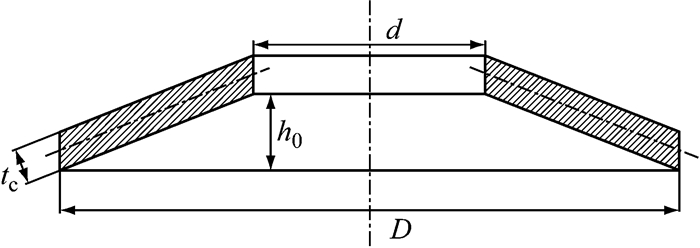
无支撑面碟形弹簧截面示意图如图 5所示.图中,D为外径,d为内径.通常,无支撑面碟形弹簧(外内径之比C=1~4)受力可表示为[13]
| $ {F_{\rm{d}}} = \frac{{4E}}{{{{\left( {1 - \nu } \right)}^2}}}\frac{{{t^4}}}{{{K_1}{D^2}}}\frac{x}{{{t_{\rm{c}}}}}\left[ {\left( {\frac{{{h_0}}}{{{t_{\rm{c}}}}} - \frac{x}{{{t_{\rm{c}}}}}} \right)\left( {\frac{{{h_0}}}{{{t_{\rm{c}}}}} - \frac{x}{{2{t_{\rm{c}}}}}} \right) + 1} \right] $ | (15) |
|
图 5 无支撑面碟形弹簧截面示意图 Fig.5 Illustration of the section of disc spring without supporting face |
式中:E为弹性模量; ν为泊松比,x为碟形弹簧从初始位置沿垂向产生的位移; K1与外内径之比C(C=D/d)有关
| $ {K_1} = \frac{1}{{\rm{ \mathsf{ π} }}}\frac{{{{\left( {\frac{{C - 1}}{C}} \right)}^2}}}{{\left( {\frac{{C + 1}}{{C - 1}}} \right) - \frac{2}{{\ln C}}}} $ | (16) |
为了研究碟形弹簧负刚度特性,令
| $ \kappa = \frac{{4E}}{{\left( {1 - {\mu ^2}} \right)}}\frac{{t_{\rm{c}}^4}}{{{K_1}{D^2}}},{x^ * } = \frac{x}{{{t_{\rm{c}}}}},\alpha = \frac{{{h_0}}}{{{t_{\rm{c}}}}} $ |
并代入式(15)有
| $ {F_{\rm{d}}} = \kappa \left[ {\frac{1}{2}{x^{ * 3}} - \frac{3}{2}\alpha {x^{ * 2}} + \left( {{\alpha ^2} + 1} \right){x^ * }} \right] $ | (17) |
将式(17)等号两侧对x进行求导,可得碟形弹簧刚度表达式为
| $ {k_{\rm{d}}} = \frac{{{\rm{d}}{F_{\rm{d}}}}}{{{\rm{d}}x}} = \frac{\kappa }{{{t_{\rm{c}}}}}\left[ {\frac{3}{2}{x^{ * 2}} - 3\alpha {x^ * } + {\alpha ^2} + 1} \right] $ | (18) |
可以看出,碟形弹簧刚度kd是变形量x的二次函数,其对称轴为x=αtc,最小值为kd0=κ(-0.5α2+1)/tc,要使碟形弹簧具有负刚度区间,必须满足Δ=(-3α)2-6(α2+1)>0,即
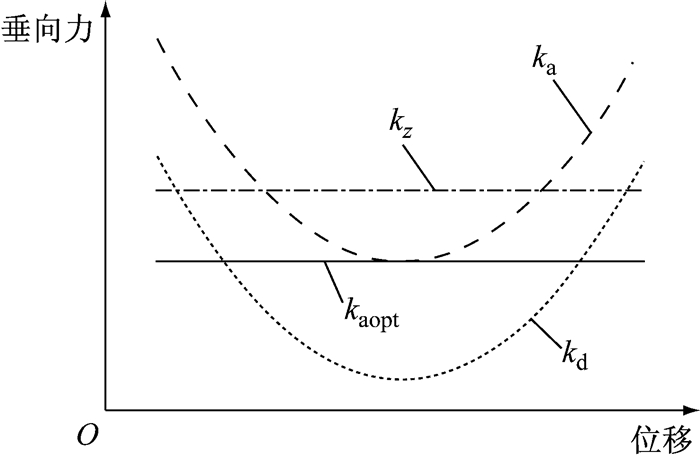
HSLDS减振元件垂向刚度位移曲线如图 6所示.图中,kaopt为动力吸振器垂向刚度目标设计值,
| $ {k_{{\rm{aopt}}}} = {\left( {2{\rm{ \mathsf{ π} }}{f_{{\rm{opt}}}}} \right)^2}{m_{\rm{e}}}/n $ | (19) |
|
图 6 HSLDS减振元件垂向刚度-位移曲线 Fig.6 Vertical stiffness-distance varve of HSLDS absorber |
fopt为设备的垂向目标固有频率; me为动力吸振器的质量; n为减振元件的个数; kd为通过式(18)计算得到的碟形弹簧垂向刚度; kz为并联的橡胶弹簧垂向刚度,并取平衡位置为z=0(z=x-h0); ka即为最终获得的HSLDS减振元件垂向刚度,
| $ {k_{\rm{a}}} = {k_{\rm{z}}} + {k_{\rm{d}}} = {k_{\rm{z}}} + \frac{\kappa }{{{t_{\rm{c}}}}}\left[ {\frac{3}{2}\frac{{{z^2}}}{{t_{\rm{c}}^2}} - \frac{1}{2}{\alpha ^2} + 1} \right] $ | (20) |
从图 6可以看出,当系统在平衡位置附近振动时,HSLDS减振元件垂向刚度ka可达到垂向刚度目标设计值kaopt.
根据上节所设计二维动力吸振器参数,HSLDS减振元件目标刚度值为kaopt=ke=47.3 kN·m-1,设吸振器仅在橡胶弹簧作用下吊挂静挠度为6 mm,采用4点吊挂的方式,可得橡胶弹簧垂向刚度值为
| $ {k_z} = \frac{{{m_{\rm{e}}}g}}{{0.006 \times 4}} = 2452.5\;{\rm{kN}} \cdot {{\rm{m}}^{ - 1}} $ | (21) |
根据式(19)可得平衡位置处碟形弹簧应提供的负刚度为
| $ {k_{\rm{d}}}\left( {z = 0} \right) = {k_z} - {k_{{\rm{aopt}}}} = 2405.2\;{\rm{kN}} \cdot {{\rm{m}}^{ - 1}} $ | (22) |
根据式(22)碟形弹簧平衡位置所需提供的负刚度值,可设计出碟形弹簧各参数如表 2所示.根据表 2所设计的碟形弹簧参数,校核设备在HSLDS吊挂下的实际静挠度为
| $ {\delta _{{\rm{st}}}} = \left( {{m_{\rm{e}}}g/4 - {F_{\rm{d}}}\left( {z = 0} \right)} \right)/{k_z} = 5.7{\rm{mm}} $ | (23) |
| 下载CSV 表 2 碟形弹簧各参数 Tab.2 Parameters of disc spring |
式中:Fd(z=0)为平衡位置时碟形弹簧提供的垂向力,此时碟形弹簧的压缩量等于其高度,结合表 2中碟形弹簧的高度可知,安装碟形弹簧时,需预压缩0.54 mm.
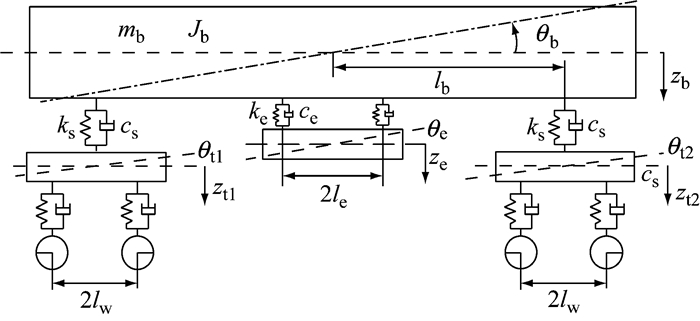
3 车辆垂向非线性动力学模型的建立与分析由以上分析可知,用于吊挂二维动力吸振器的HSLDS减振元件的刚度特性是非线性的,因此,本研究采用Matlab/Simulink建立车辆非线性垂向动力学模型,通过时间积分仿真,分析二维动力吸振器对车辆振动性能的影响.采用面向对象的建模方法[14],基于Matlab/Simulink建立车辆垂向动力学模型,可将车辆系统划分为5大类[15]:①结构类,②悬挂类,③功能模块类,④轮轨接触类,⑤轨道输入类.本研究中,结构类包含1个车体、1个动力吸振器、2个转向架,均考虑浮沉振动与点头振动,共8个自由度; 悬挂类包括4个一系悬挂、2个二系悬挂、2个动力吸振器悬挂; 轮轨接触假设车轮紧贴钢轨,将轨道谱垂向激励直接作用于轴箱作为系统激励输入,轨道谱采用空间域高速高干扰谱.输入到结构类的信息是广义悬挂力和广义惯性力,输出的是该结构的状态变量,如车体的浮沉、点头; 悬挂类包含一系、二系弹簧及阻尼器; 轨道谱输入垂向位移、速度激励.车辆垂向力学模型如图 7所示,各参数如表 1所示.其中,动力吸振器吊挂刚度ke为非线性,具体参数由所设计的碟形弹簧与橡胶弹簧决定.
|
图 7 车辆垂向力学模型 Fig.7 Vertical force model of vehicle |
通过所建车辆垂向非线性动力学模型进行时域仿真,计算车辆速度为350 km·h-1的车体振动响应情况.图 8为车体中部振动加速度功率谱密度(power spectral density, PSD).可以看出,无论有无采用二维动力吸振器,车体振动加速度功率谱密度峰值均在0.678 Hz与0.900 Hz处.这是分别由车体浮沉、点头振动所致,采用二维动力吸振器后,车体浮沉、点头振动得到明显降低,浮沉振动峰值降低50.6%,点头振动峰值降低49.0%.

|
图 8 车体中部垂向振动加速度PSD Fig.8 Vertical acceleration PSD in the middle of vehicle |
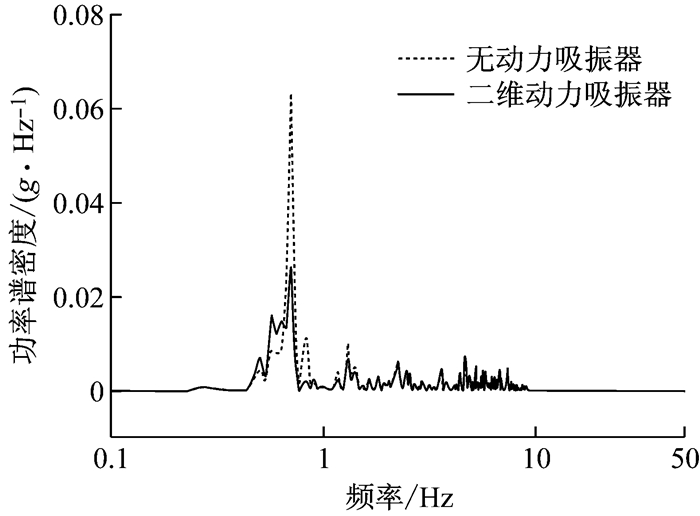
图 9为车体前转向架处振动加速度PSD,其与车体中部振动情况相似,采用二维动力吸振器后,浮沉、点头振动峰值分别降低约58.1%、47.6%.
|
图 9 前转向架处垂向振动加速度PSD Fig.9 Vehicle vertical acceleration PSD of front bogie |
图 10为车体后转向架处振动加速度PSD,采用二维动力吸振器后,浮沉、点头频率处峰值分别降低约43.8%、39.3%.

|
图 10 后转向架处垂向振动加速度PSD Fig.10 Vehicle vertical acceleration PSD of rear bogie |
综合图 8~10可得,车辆主要刚性振动能量来自于其浮沉及点头振动,在车体下方安装二维动力吸振器后,车体浮沉、点头振动均可得到有效降低.
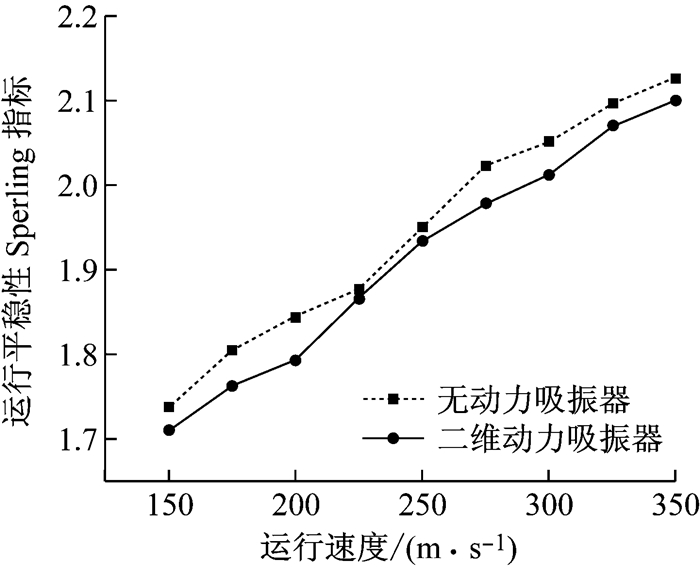
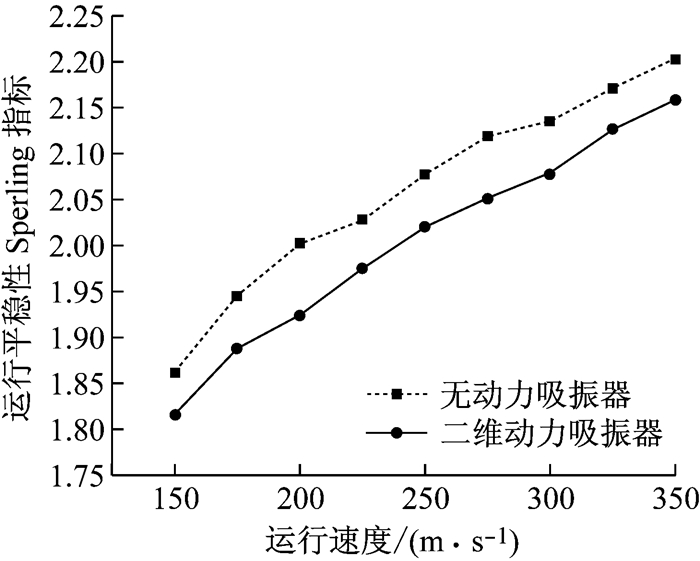
图 11、12、13分别为不同速度级下,无动力吸振器车体与采用二维动力吸振器车体中部、前转向架处、后转向架处的平稳性Sperling指标.采用动力吸振器后,车体中部、前转向架处、后转向架处运行平稳性Sperling指标均明显降低,速度为350 km·h-1时,车体中部、前转向架、后转向架处分别降低3.9%、1.2%、2.1%.这是由于采用二维动力吸振器后,车体浮沉、点头振动被二维动力吸振器所抑制,以致车体浮沉、点头振动加速度幅值降低,从而使运行平稳性得到提高,乘坐舒适度得到改善.

|
图 11 车体中部运行平稳性指标 Fig.11 Sperling indexes of in the middle of vehicle |
|
图 12 车体前转向架处运行平稳性指标 Fig.12 Sperling indexes of car body above front bogie |
|
图 13 车体后转向架处运行平稳性指标 Fig.13 Sperling indexes of car body above rear bogie |
本文首先分析了基于加速度的二维动力吸振器工作原理,将车体视为主振动系统,车下设备视为动力吸振器,设计了针对车体点头、浮沉振动的二维动力吸振器.为了使二维动力吸振器安装静挠度控制在一定范围的同时实现最优同调,基于碟形弹簧的负刚度特性,将其与橡胶弹簧结合,设计了用于二维动力吸振器吊挂的高静刚度低动刚度减振元件.基于Matlab/Simulink软件,建立了高速动车组垂向非线性动力学模型,分析了二维动力吸振器对车体振动的影响.基于本文所研究高速动车组,设计安装二维动力吸振器后,车体中部、前、后转向架处浮沉振动功率谱密度峰值分别降低50.6%、58.1%、43.8%;车体中部、前、后转向架处点头振动功率谱密度峰值分别降低49.0%、47.6%、39.3%;各速度级下车体中部、前、后转向架处运行平稳性Sperling指标明显降低.研究结果表明,二维动力吸振器可以有效抑制车体浮沉、点头振动,提高车辆运行平稳性,改善乘坐舒适度.
| [1] |
周劲松, 张伟, 孙文静, 等. 铁道车辆弹性车体动力吸振器减振分析[J]. 中国铁道科学, 2009, 30(3): 86 ZHOU Jinsong, ZHANG Wei, SUN Wenjing, et al. Vibration reduction analysis of the dynamic vibration absorber on the flexible carbody of railway vehicles[J]. China Railway Science, 2009, 30(3): 86 |
| [2] |
GONG D, ZHOU J S, SUN W J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber[J]. Journal of Vibration & Control, 2013, 19(5): 649 |
| [3] |
CARRELLA A, BRENNAN M J, WATERS T P. Optimization of a quasi-zero-stiffness isolator[J]. Journal of Mechanical Science and Technology, 2007, 21(6): 946 DOI:10.1007/BF03027074 |
| [4] |
CARRELLA A, BRENNAN M J, WATERS T P, et al. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness[J]. International Journal of Mechanical Sciences, 2012, 55(1): 22 DOI:10.1016/j.ijmecsci.2011.11.012 |
| [5] |
LIU X, HUANG X, HUA H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector[J]. Journal of Sound & Vibration, 2013, 332(14): 3359 |
| [6] |
HUANG X, LIU X, SUN J, et al. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: a theoretical and experimental study[J]. Journal of Sound & Vibration, 2014, 333(4): 1132 |
| [7] |
HUANG X, LIU X, SUN J, et al. Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator[J]. Nonlinear Dynamics, 2014, 76(2): 1157 DOI:10.1007/s11071-013-1199-7 |
| [8] |
MENG Lingshuai, SUN Jinggong, WU Wenjuan. Theoretical design and characteristics analysis of a quasi-zero stiffness isolator using a disk spring as negative stiffness element[J]. Shock & Vibration, 2015, 2015(4): 1 |
| [9] |
REN M Z. A variant design of the dynamic vibration absorber[J]. Journal of Sound and Vibration, 2001, 245(4): 762 DOI:10.1006/jsvi.2001.3564 |
| [10] |
GONG D, ZHOU J, SUN W. Influence of under-chassis-suspended equipment on high-speed EMU trains and the design of suspension parameters[J]. Journal of Rail & Rapid Transit, 2016, 230(8): 1790 |
| [11] |
GONG D, ZHOU J, SUN W, et al. Method of multi-mode vibration control for the carbody of high-speed electric multiple unit trains[J]. Journal of Sound & Vibration, 2017, 409: 94 |
| [12] |
背户一登. 动力吸振器及其应用[M]. 任明章, 译. 北京: 机械工业出版社, 2013. KAZUTO Seto. Dynamic vibration absorber and its applications[M]. Translated by REN Mingzhang. Beijing: China Machine Press, 2013. |
| [13] |
张英会, 刘辉航, 王德成. 弹簧手册[M]. 北京: 机械工业出版社, 2008 ZHANG Yinghui, LIU Huihang, WANG Decheng. Spring manual[M]. Beijing: China Machine Press, 2008 |
| [14] |
EICKHOFF B M, EVANS J R, MINNIS A J. A review of modelling methods for railway vehicle suspension components[J]. Vehicle System Dynamics, 1995, 24(6/7): 469 |
| [15] |
周劲松. 铁道车辆振动与控制[M]. 北京: 中国铁道出版社, 2012 ZHOU Jinsong. Railway vehicle vibration and control[M]. Beijing: China Railway Publication House, 2012 |
 2018, Vol. 46
2018, Vol. 46

