2. 上海财经大学 数学学院,上海 200433
2. School of Mathematical Sciences, Shanghai University of Finance and Economics, Shanghai 200433, China
随着经济的快速发展,期权作为金融风险管理、套利等工具变得越来越重要,而其定价及Greeks计算问题也成为现代金融理论的一个极其重要的研究领域.在当今国内外的金融市场上,一方面,由于市场的日益复杂,标的资产(如股票)、汇率及浮动利率等的变化过程也变得越来越复杂,因此想要更加准确地刻画这些特征,就需要提出比几何布朗运动更加复杂的模型来进行描述,例如随机利率、随机波动率模型、由Levy过程驱动的模型等.Robert Merton[1]最早考虑了随机利率下的期权定价,后来又出现了Vasieck和CIR(cox-ingersoll-ross)随机利率模型,Barndorff- Nielsen和Shephard[2]提出了Levy过程驱动的多因子模型.另一方面,为了满足客户对各类金融产品的个性化需求,期权的类型变得越来越复杂,如美式期权、与路径有关的亚式期权、提前实施条款等.金融市场也出现了一些具有复杂结构的高维期权.
除了标的资产价格以外,金融衍生品价格还取决于其他多个参数:市场无风险利率,标的资产价格波动率,产品期限等.而衍生产品对这些因素的变化率统称为敏感度,即为Greeks.Greeks值被广泛用于风险度量与风险控制中,因此准确地计算出Greeks值是一个非常有实际意义的问题,对于金融机构及保险公司构建对冲投资组合、进行风险管理非常重要.由于期权价格本身能在市场上观察得到,Greeks却不能,因此准确地计算Greeks甚至比计算期权价格本身更重要,难度也会更高.
根据现有的金融资产定价理论,很少一部分期权能通过偏微分理论求得解析解,因此往往需要借助于数值方法求解.金融衍生品定价数值方法大致分为:二叉树方法、有限差分与有限元方法、蒙特卡罗方法.其中,二叉树、有限差分方法对于低维模型能够快速有效地得到结果,但是存储量和计算量随着维数的增加呈指数增长,对于3维以上的问题基本无法解决.而蒙特卡罗方法的存储量和计算量随着维数的增加大体呈线性增长,且其收敛速度与维数无关,所以成为求解高维期权定价问题的重要方法.
最早使用蒙特卡罗方法进行金融资产定价的是Boyle[3],对标的资产为单一资产的欧式股票期权进行定价,而后Tilley[4]首先应用蒙特卡罗方法对可支付红利的美式看跌期权进行了估值, Baldi和Caramellino[5]利用蒙特卡罗方法对一般的障碍期权进行了定价分析.近些年蒙特卡罗方法在期权定价中的应用越加广泛,但其收敛速度慢,所以相继出现了一些对其进行加速的方法.本文所用的条件蒙特卡罗方法和控制变量法就是通过方差减小技术而达到加速效果的方法.此方法不仅适用于欧式期权定价,而且对亚式期权、一篮子期权和高维期权也同样具有显著效果.比较著名的例子是Kemma和Vorst利用几何平均的看涨和看跌期权都有解析解的特性,分别选择了几何平均亚式期权作为控制变量,为算术平均亚式期权定价.Shin和Svenstrup[6]使用控制变量技巧研究了LIBOR市场模型的百慕大互换的定价问题.Glasserman也指出条件蒙特卡罗方法可以减小模拟误差,但是缺少统一的实施方法.詹慧蓉和程乾生在蒙特卡罗模拟亚式期权定价过程中提出一个新的多元控制变量,得到了不错的结果.彭斌采用控制变量蒙特卡罗方法研究了两资产亚式彩虹期权的定价问题.梁义娟和徐承龙[7]使用条件蒙特卡罗方法及鞅方法研究了一般的两因子随机模型下欧式期权的定价问题,但是存在计算量较大的缺点.
目前计算Greeks大致有3大类方法:有限差分方法、基于轨道模拟的蒙特卡罗方法和基于似然的蒙特卡罗模拟方法.有限差分方法很容易理解,计算简单快捷,但其误差较大,为此Giles提出了多层蒙特卡罗方法用于提高计算速度.孙健兰[8]证明了多层蒙特卡罗算法的有效性,而这种方法近期只能针对几何布朗运动进行计算.基于轨道模拟的蒙特卡罗方法算法简单且通用性强.沿着此思路以及后续提出的IPA(infinitesimal perturbation analysis)方法,许多著名学者研究了其在运筹、优化及金融中的应用.第3种方法不出现对收益函数的导数,避免了收益函数仅为李-氏连续或者不连续的情形,但需已知其概率密度函数,而这对大部分复杂模型而言并不易求得.例如在金融中的应用见文献[9]等.以上3种方法各有优缺点.本文将在第2种方法基础上提出一种利用条件蒙特卡罗方法的求解思路,可以改进第2类方法的缺陷,同时具有减小方差的作用,特别是可以计算Γ值.与其他两种方法相比,利用条件蒙特卡罗方法计算Greeks值,提高了模拟效率.
本文主要以随机利率满足CIR模型下的欧式看涨期权为例,研究定价及Greeks值计算问题.首先建立了期权的条件期望表达式,以提高模拟效率.然后利用控制变量法对其进行进一步加速.接着运用本文所提出的条件期望表达式对Greeks值进行计算,进而通过比较说明本文所提出计算方法的优越性和有效性.最后讨论了本文方法可推广到其他适用的情形.
1 随机利率模型下期权定价对CIR随机利率模型下欧式期权的定价问题,由文献[10]可知此时无解析表达公式.本节结合条件期望表达式以及控制变量加速技巧对蒙特卡罗模拟进行加速处理.
1.1 随机利率下资产价格模型假设标的资产St满足波动率为常数σs>0的随机微分方程
| $ \frac{{{\rm{d}}{S_t}}}{{{S_t}}} = {r_t}{\rm{d}}t + {\sigma _s}{\rm{d}}{W_t} $ | (1) |
其中瞬时利率rt满足波动率为常数σr>0的随机方程
| $ {\rm{d}}{r_t} = \alpha \left( {\theta - {r_t}} \right){\rm{d}}t + {\sigma _r}\sqrt {{r_t}} {\rm{d}}{Z_t} $ | (2) |
式中:α、θ为正常数;Wt和Zt是标准布朗运动,且满足cov(dWt, dZt)=ρdt;ρ为两者之间的相关性系数.Wt和Zt之间的关系也可以写为
| $ {\rm{d}}{W_t} = \rho {\rm{d}}{Z_t} + \sqrt {1 - {\rho ^2}} {\rm{d}}{{\tilde Z}_t} $ | (3) |
其中标准布朗运动
| $ \begin{array}{l} {S_T} = {S_t}\exp \left[ {\int_t^T {{r_s}{\rm{d}}s} - \frac{1}{2}\sigma _s^2\left( {T - t} \right) + \rho {\sigma _s}\left( {{Z_T} - {Z_t}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{\sigma _s}\sqrt {1 - {\rho ^2}} \left( {{{\tilde Z}_T} - {{\tilde Z}_t}} \right)} \right] \end{array} $ | (4) |
式(4)也可以写成
| $ \begin{array}{l} {S_T} = {S_t}\xi \left( {t,T} \right)\exp \left[ {\left( {\bar r - \frac{1}{2}\sigma _s^2\left( {1 - {\rho ^2}} \right)} \right)\left( {T - t} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{\sigma _s}\sqrt {1 - {\rho ^2}} \left( {{{\tilde Z}_T} - {{\tilde Z}_t}} \right)} \right] \end{array} $ | (5) |
其中
| $ \bar r\left( {t,T} \right) = \frac{1}{{T - t}}\int_t^T {{r_s}{\rm{d}}s} $ | (6) |
| $ \xi \left( {t,T} \right) = \exp \left[ { - \frac{1}{2}{\rho ^2}\sigma _s^2\left( {T - t} \right) + \rho {\sigma _s}\left( {{Z_T} - {Z_t}} \right)} \right] $ | (7) |
给定敲定价格K在时刻t欧式看涨期权风险中性价格Vt可以写为
| $ {V_t} = {E^Q}\left[ {{{\rm{e}}^{ - \bar r\left( {T - t} \right)}} \cdot {{\left( {{S_T} - K} \right)}^ + }} \right] $ | (8) |
特别可得零时刻欧式看涨期权的价格为
| $ {V_0} = {E^Q}\left[ {{{\rm{e}}^{ - \bar rT}}{{\left( {{S_T} - K} \right)}^ + }} \right] $ | (9) |
蒙特卡罗期权定价方法的基本思想是利用随机变量的样本值估计期权价格:首先将时间间隔[0, T]等分为N份,步长为Δt=T/N,ti=i·Δt,记Si=Sti(i=0, 1, 2, …, N)为标的资产在时刻ti的价格,记ri=rti(i=0, 1, 2, …, N)为时刻ti的利率值,εk和
| $ {r_{k + 1}} = {r_k} + \alpha \left( {\theta - {r_k}} \right) \cdot \Delta t + {\sigma _r} \cdot \sqrt {{r_k} \cdot \Delta t} \cdot {\varepsilon _k} $ |
| $ \begin{array}{l} {S_{k + 1}} = {S_k}\exp \left\{ {{r_k} \cdot \Delta t - \frac{1}{2}\sigma _s^2 \cdot \Delta t + \rho {\sigma _s} \cdot \sqrt {\Delta t} \cdot {\varepsilon _k} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{\sigma _s}\sqrt {\left( {1 - {\rho ^2}} \right) \cdot \Delta t} \cdot {{\tilde \varepsilon }_k}} \right\} \end{array} $ |
令
| $ {{\tilde r}_0} = 0,{{\tilde r}_{k + 1}} = {{\tilde r}_k} + {r_k} \cdot \Delta t $ | (10) |
方程(9)中的期权价格可以用标准蒙特卡罗方法模拟:选取适当大的模拟次数M,用样本均值代替期望值,就可以得到无偏估计值:
| $ {{\bar V}_0} = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {{{\rm{e}}^{ - \bar rT}}{{\left( {S_T^{\left( i \right)} - K} \right)}^ + }} \right)} $ |
其中ST(i)表示ST的第i次模拟值.由大数定律可知,当模拟次数M趋近于正无穷,估计值
| $ P\left( {\left| {{{\bar V}_0} - {V_0}} \right| < \frac{{\sigma {\lambda _\alpha }}}{{\sqrt M }}} \right) = 1 - \alpha $ |
由上可知,蒙特卡罗方法的误差为
| $ \sigma _M^2 = \frac{1}{{M - 1}}\sum\limits_{i = 1}^M {{{\left( {\bar V_0^{\left( i \right)} - {{\bar V}_0}} \right)}^2}} $ |
蒙特卡罗估计量
利用条件蒙特卡罗方法估计随机利率满足CIR模型下的欧式看涨期权价格.由条件期望公式
| $ E\left[ Y \right] = E\left[ {E\left[ {Y\left| X \right.} \right]} \right] $ | (11) |
又由条件方差公式
| $ \begin{array}{l} {\rm{Var}}\left( Y \right) = {\rm{Var}}\left( {E\left[ {Y\left| X \right.} \right]} \right) + \\ \;\;\;\;\;\;\;E\left[ {{\rm{Var}}\left( {Y\left| X \right.} \right)} \right] > {\rm{Var}}\left( {E\left[ {Y\left| X \right.} \right]} \right) \end{array} $ |
可以看出条件蒙特卡罗方法是一种有效的方差减小技术.
给定随机过程{Zs:t < s < T},由期权风险中性定价公式(8),对随机过程{
| $ \begin{array}{*{20}{c}} {V\left( {S,t} \right) = {V_t} = E\left[ {E\left[ {{{\rm{e}}^{\int_t^T {{r_s}{\rm{d}}s} }} \cdot {{\left( {{S_T} - K} \right)}^ + }\left| {{{\tilde Z}_{\rm{t}}}} \right.} \right]} \right] = }\\ {E\left[ {{V_{{\rm{BS}}}}\left( {t,T,{S_t}\xi \left( {t,T} \right);\bar r\left( {t,T} \right),{\sigma _s}\sqrt {1 - {\rho ^2}} } \right)} \right]} \end{array} $ | (12) |
其中VBS(t, T, Stξ(t, T);
| $ {V_0} = E\left[ {{V_{{\rm{BS}}}}\left( {0,T,{S_0}\xi \left( {0,T} \right);\bar r\left( {0,T} \right),{\sigma _s}\sqrt {1 - {\rho ^2}} } \right)} \right] $ | (13) |
因此无需再对标的资产价格路径进行模拟,而只需对过程Zt及ξ(0, T)和
| $ \begin{array}{*{20}{c}} {{{\bar \xi }_0} = 0,{{\bar \xi }_{k + 1}} = {{\bar \xi }_k} - \frac{{{\rho ^2}\sigma _s^2}}{2}\Delta t + \rho {\sigma _s}\sqrt {\Delta t} \cdot {\varepsilon _k},}\\ {k = 0,1, \cdots ,N - 1} \end{array} $ |
式中:εk表示标准正态分布的样本值.由上可得,ξ(0, T)=
控制变量法是使用最广泛的方差减小技术之一,其原理是充分利用已知的方差量去缩小所求估计量的部分方差.在条件期望公式(13)的基础上再使用控制变量法,能够进一步消去计算过程中由于随机性产生的部分误差.采用两个控制变量为
| $ V\left( \mathit{\boldsymbol{b}} \right) = {V_{{\rm{BS}}}} - {\mathit{\boldsymbol{b}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}} - E\left[ \mathit{\boldsymbol{X}} \right]} \right) $ |
为式(12)中VBS的无偏估计,其中E[X]=(E[
| $ \begin{array}{*{20}{c}} {E\left[ {\bar r} \right] = \frac{1}{{T - t}}\int_t^T {E\left[ {{r_s}} \right]{\rm{d}}s} = \theta + \frac{{\left( {\theta - {r_0}} \right)}}{{\alpha \left( {T - t} \right)}}\left( {{{\rm{e}}^{ - \alpha T}} - {{\rm{e}}^{ - \alpha t}}} \right),}\\ {E\left[ \xi \right] = 1} \end{array} $ |
设(X, VBS)的协方差矩阵为
| $ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_X}}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{X{V_{{\rm{BS}}}}}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{X{V_{{\rm{BS}}}}}^{\rm{T}}}&{\sigma _{{V_{{\rm{BS}}}}}^2} \end{array}} \right) $ |
则M次模拟情形下,二元控制变量下的估计值为
| $ \begin{array}{*{20}{c}} {{{\bar V}_M}\left( \mathit{\boldsymbol{b}} \right) = {{\bar V}_{M,BS}} - {\mathit{\boldsymbol{b}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\bar X}} - E\left[ \mathit{\boldsymbol{X}} \right]} \right) = }\\ {\frac{1}{M}\sum\limits_{i = 1}^M {\left( {{V_{i,{\rm{BS}}}} - {b_1}\left( {{{\bar r}^{\left( i \right)}} - E\left[ {\bar r} \right]} \right) - {b_2}\left( {{\xi ^{\left( i \right)}} - E\left[ \xi \right]} \right)} \right)} } \end{array} $ | (14) |
式中:
| $ \begin{array}{l} {\rm{Var}}\left( {{{\bar V}_M}\left( \mathit{\boldsymbol{b}} \right)} \right) = {\rm{Var}}\left( {{{\bar V}_{M,\rm{BS}}} - {\mathit{\boldsymbol{b}}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\bar X}}}_M} - E\left[ \mathit{\boldsymbol{X}} \right]} \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sigma _{{V_{{\rm{BS}}}}}^2 - 2{\mathit{\boldsymbol{b}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{X{V_{{\rm{BS}}}}}} + {\mathit{\boldsymbol{b}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_X}\mathit{\boldsymbol{b}} \end{array} $ |
则使方差最小的最优控制系数向量为
| $ \mathit{\boldsymbol{b}} = \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_X^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{X{V_{{\rm{BS}}}}}} $ | (15) |
可用b模拟值近似计算,此时最小方差值为
| $ {\rm{Var}}\left( {{{\bar V}_M}\left( \mathit{\boldsymbol{b}} \right)} \right) = \left( {1 - R_{X{V_{{\rm{BS}}}}}^2} \right)\sigma _{{V_{{\rm{BS}}}}}^2 < \sigma _{{V_{{\rm{BS}}}}}^2 $ |
式中:RXVBS2= ΣXVBST ΣX-1 ΣXVBS/σVBS2.将式(15)中的b代入式(14)即可得到期权价格M次模拟估计值.
2 数值结果为比较本文中所提出方法的加速效果,选用标准误差减小倍数来判断加速效果
| $ {R_{{\rm{CMCC}}}} = \frac{{{\rm{st}}{{\rm{d}}_{{\rm{MC}}}}}}{{{\rm{st}}{{\rm{d}}_{{\rm{CMCC}}}}}} $ |
式中:stdMC和stdCMCC分别表示标准蒙特卡罗方法的标准误差和使用上节提出的基于条件期望的控制变量蒙特卡罗加速模拟后的标准误差.显然RCMCC越大,就表示加速效果越好,也说明方法的计算精度越高.
如果考虑时间成本因素,以标准蒙特卡罗方法为基准,加速方法的加速比还可以定义为
| $ s = \frac{{{\rm{std}}_{{\rm{MC}}}^2 \cdot {t_{{\rm{MC}}}}}}{{{\rm{std}}_{{\rm{CMCC}}}^2 \cdot {t_{{\rm{CMCC}}}}}} $ |
式中:tMC、tCMCC分别表示固定模拟次数时标准蒙特卡罗方法和加速后的方法计算所用时间.
给定离散时间点个数N=100,其他参数取值如下:标的资产价格与敲定价格相等,S0=K=30,标的资产的波动率σs=0.2,利率初值r0=0.05, 利率的波动率σr=0.2,利率的回复速度α=2, 利率均值θ=0.05,到期时间T=1.
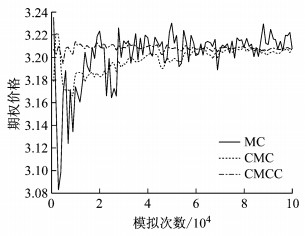
首先考虑欧式看涨期权价格关于模拟次数M的波动情况,结果见图 1.其中MC表示使用1.2.1节标准蒙特卡罗方法方法得到的价格,CMC表示利用1.2.2节条件蒙特卡罗得到的期权价格,CMCC表示利用1.2.3节结合控制变量为
|
图 1 期权价格与模拟次数关系图 Fig.1 Option price change for different simulation times |
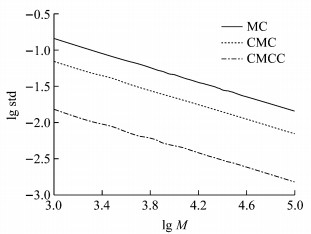
进一步地,图 2给出了模拟的标准误差与模拟次数M的关系,为了将结果显示更为直观,此处横纵坐标分别为标准误差和模拟次数的对数.由图 2可以看出,结合二元控制变量的条件蒙特卡罗方法的误差最小,而普通蒙特卡罗方法所得标准误差最大.所以条件蒙特卡罗方法及控制变量法可以达到减小标准误差的效果,从而提高蒙特卡罗模拟的效率.
|
图 2 标准误差与模拟次数关系图 Fig.2 Standard deviation change for different simulation times |
下面固定模拟次数M=100 000和其他参数,考虑相关系数ρ对计算效果的影响,结果见表 1和表 2,其中stdMC是普通蒙特卡罗方法得到的误差;stdCMC和stdCMCC分别表示条件蒙特卡罗方法和结合控制变量的条件蒙特卡罗加速方法得到的误差,RCMC和RCMCC表示其相对于普通蒙特卡罗方法的加速倍数.
| 下载CSV 表 1 不同方法模拟所得标准误差结果及加速倍数 Tab.1 Standard deviations and acceleration effects by different methods |
| 下载CSV 表 2 两种方法模拟所得Greeks值 Tab.2 Values of Greeks by using two different methods |
从表 1可以看出,误差随着相关系数|ρ|的增大而增大,即|ρ|越小,计算效果越好.从式(5)可知,条件蒙特卡罗方法消去了与利率过程不相关的部分随机性,该量与
综合考虑算法的加速效果,用普通蒙特卡罗方法计算所花时间为3.068 5 s,用条件蒙特卡罗方法计算所花时间为1.732 1 s,结合控制变量法之后所花时间为1.738 8 s.以ρ=0.4为例,基于条件蒙特卡罗的控制变量法对普通蒙特卡罗方法的综合加速倍数为
| $ s = \frac{{{\rm{std}}_{{\rm{MC}}}^2 \cdot {t_{{\rm{MC}}}}}}{{{\rm{std}}_{{\rm{CMCC}}}^2 \cdot {t_{{\rm{CMCC}}}}}} = {R^2}\frac{{{t_{{\rm{MC}}}}}}{{{t_{{\rm{CMCC}}}}}} = 347.726 $ |
另外,本文还对结合常用控制变量与普通蒙特卡罗方法的情况进行了模拟,此时控制变量利率为常数的标的资产,改变参数的值,发现其计算所得标准误差与普通蒙特卡罗方法基本一致;所花费的时间为3.084 3 s,与普通蒙特卡罗方法也基本一致;此时基于条件蒙特卡罗的控制变量法对其综合加速倍数与对普通蒙特卡罗的综合加速倍数基本一致.说明本文所提出的新的控制变量与条件蒙特卡罗方法结合具有显著的加速效果.
如果固定其他参数值,分别考虑K、r0、σS、σr、α、θ、T的影响,结果显示,期权价格随着标的资产波动率σS、利率的波动率σr、长期平均利率θ、到期时间T的增大而增大,随着敲定价格K、利率的回复速率α的增大而减小.而基于条件蒙特卡罗的控制变量法计算结果的标准误差及误差小于其他方法,这说明本文所提出的方法达到了较好的加速效果.尽管本文讨论的问题是一维欧式看涨期权价格,但实际上,对高维的多资产问题同样适用,并不影响模拟的效率,并且还可用于计算离散取样亚式期权及一篮子期权价格.例如,对于多资产的一篮子期权,SiT分别表示资产i在T时刻的值,设
| $ {\left( {A - K} \right)^ + } = \left( {A - K} \right)\left| {_{G \ge K}} \right. + \left( {A - K} \right)\left| {_{G < K < A}} \right. $ |
分解后的第1部分可求出期望公式,再用条件蒙特卡罗方法模拟,第2部分为小概率,可通过重要抽样模拟高效求解.
3 Greeks计算 3.1 Greeks介绍期权市场对市场参数的敏感度称为Greeks,也叫风险敏感度.计算Greeks值对于金融机构构建对冲投资组合,进行风险管理有重要作用.本文模型中,随机利率下欧式看涨期权Greeks值分别为:
对于随机利率模型和随机波动率模型等较复杂模型,由于期权价格没有对应的解析解,计算Greeks时需要借助数值方法.本文利用条件蒙特卡罗方法进行计算,使得计算过程更为简便和稳定, 也可以克服收益函数不能求二次导数的缺陷.
基于条件期望公式(12),可得随机利率模型下欧式看涨期权价格为
| $ {V_t} = E\left[ {{S_t}\xi N\left( {{{\hat d}_1}} \right) - K{{\rm{e}}^{ - \bar r\left( {T - t} \right)}} \cdot N\left( {{{\hat d}_2}} \right)} \right] $ | (16) |
其中:
| $ \begin{array}{*{20}{c}} {{{\hat d}_1} = \frac{{\ln \frac{{{S_t}\xi }}{K} + \left( {\bar r + \frac{{\sigma _s^2}}{2}\left( {1 - {\rho ^2}} \right)} \right)\left( {T - t} \right)}}{{{\sigma _s}\sqrt {\left( {1 - {\rho ^2}} \right)\left( {T - t} \right)} }},}\\ {{{\hat d}_2} = {{\hat d}_1} - {\sigma _s}\sqrt {\left( {1 - {\rho ^2}} \right)\left( {T - t} \right)} } \end{array} $ |
N(x)表示标准正态分布的分布函数.
从而由公式(16),计算可得其相关参数的Greeks公式为
| $ \Delta = \frac{{\partial V}}{{\partial S}} = E\left[ {\xi \cdot N\left( {{{\hat d}_1}} \right)} \right] $ |
| $ \mathit{\Gamma } = \frac{{\partial \Delta }}{{\partial S}} = \frac{{{\partial ^2}V}}{{\partial {S^2}}} = E\left[ {\frac{{\xi \cdot N'\left( {{{\hat d}_1}} \right)}}{{S{\sigma _s}\sqrt {\left( {1 - {\rho ^2}} \right)\left( {T - t} \right)} }}} \right] $ |
| $ \begin{array}{*{20}{c}} {\mathit{\Theta } = \frac{{\partial V}}{{\partial t}} = E\left[ { - \frac{{S\xi N'\left( {{{\hat d}_1}} \right) \cdot {\sigma _s}\sqrt {1 - {\rho ^2}} }}{{2\sqrt {T - t} }} - } \right.}\\ {\left. {K{r_t} \cdot {{\rm{e}}^{ - \bar r\left( {T - t} \right)}} \cdot N\left( {{{\hat d}_2}} \right)} \right]} \end{array} $ |
| $ \begin{array}{l} \upsilon = \frac{{\partial V}}{{\partial {\sigma _s}}} = E\left[ {S\xi N'\left( {{{\hat d}_1}} \right) \cdot \sqrt {\left( {1 - {\rho ^2}} \right)\left( {T - t} \right)} - } \right.\\ \left. {S\xi N\left( {{{\hat d}_1}} \right) \cdot \left( { - {\rho ^2}{\sigma _s}\left( {T - t} \right) + \rho \left( {{Z_T} - {Z_t}} \right)} \right)} \right] \end{array} $ | (17) |
相关参数取值与第2章相同,模拟次数M=100 000.Greeks值的计算结果以及模拟标准误差见表 2.
表 2中,CMC表示基于条件蒙特卡罗方法所求得的Greeks值,FD表示使用有限差分方法进行计算.基于条件蒙特卡罗方法求Greeks值时,由于期权价格表示为一个光滑函数的期望值,因此可以将价格对参数的求导与期望过程相互交换,使得计算过程更加简便快速,所得标准误差有明显的减小.由此可见,本文所提出的方法在计算Greeks值时有良好的效果.
接下来,固定其他值,改变标的资产的初始值S0,来观察不同的S0值对Δ值及计算时产生的误差的影响,结果分别见表 3和表 4.
| 下载CSV 表 3 不同标的资产的初始价格模拟出的Δ值 Tab.3 Values of Delta for different initial prices of underlying asset |
| 下载CSV 表 4 不同方法模拟出Δ值的标准误差 Tab.4 Standard deviations of Delta by using different methods |
由表 3和表 4可见,Δ值随着标的资产初始价格的增加而增加,而条件蒙特卡罗方法能更好地减小计算时产生的方差,从而产生加速效果,使得标准误差更小.为了使结果更为直观,图 3给出不同初始价格与标准误差的关系,可很明显看出条件蒙特卡罗法所得效果更好.

|
图 3 不同模拟方法下标的资产初始价格与Δ值的标准误差关系图 Fig.3 Comparison of standard deviations of Δ by using different methods |
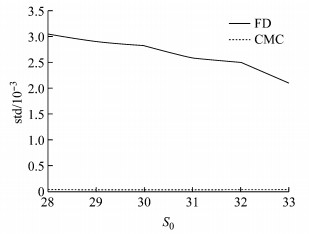
类似地,Γ的计算结果见表 5和表 6.由表可知,Γ值随着标的资产初始价格的增加而减小,而条件蒙特卡罗方法计算时能更好地减小标准误差.为了使结果更为直观,图 4给出不同初始价格与标准误差的关系,由此看出条件蒙特卡罗方法计算所得结果误差更小.
| 下载CSV 表 5 不同标的资产的初始价格模拟出的Γ值 Tab.5 Values of Gamma for different initial prices of underlying asset |
| 下载CSV 表 6 不同方法模拟出Γ值的标准误差 Tab.6 Standard deviations of Delta by using different methods |
|
图 4 不同模拟方法下标的资产初始价格与Γ值的标准误差关系图 Fig.4 Comparison of standard deviations of Γ by using different methods |
本文针对随机利率满足CIR模型的欧式期权定价问题,提出了一种基于条件期望的控制变量法进行蒙特卡罗加速模拟.计算结果显示,条件蒙特卡罗方法相对于普通蒙特卡罗方法而言能达到一定的方差减小效果,同时计算时间也更为节省;而在条件蒙特卡罗的基础上再使用控制变量法,能使得模拟误差进一步减小,且运行所需时间与条件蒙特卡罗方法基本一致,故能够达到更好的加速效果.最后,将条件蒙特卡罗方法应用于计算Greeks值,所得结果显示其可以达到较好的计算效果,但本文所提出的控制变量对Greeks值的加速计算基本无效.最后一点值得指出的是本文虽然讨论的问题是单资产问题,如果利用Green求积公式,固定利率的资产价格可以用公式表示出来,再用数值方法进行计算,则同样可以得到条件期望公式,从而条件蒙特卡罗方法同样适用.进一步地,该方法还可用于求解一篮子期权、离散取样的亚式期权等高维问题.
| [1] |
MERTON R C. The theory of rational option pricing[J]. The Bell Journal of Economics and Management Sciences, 1973, 4(1): 141 DOI:10.2307/3003143 |
| [2] |
BARNDORFFNIELSEN O E, SHEPHARD N. Econometric analysis of realised volatility and its use in estimating levy based non-gaussian OU type stochastic volatility models[J]. Economics, 2000, 64(2): 89 |
| [3] |
BOYLE P P. Options:a Monte Carlo approach[J]. Journal of Financial Economics, 1977, 4(3): 323 DOI:10.1016/0304-405X(77)90005-8 |
| [4] |
TILLEY J A. Valuing american options in a path simulation model[J]. Transactions of the Society of Actuarues, 1993, 45: 83 |
| [5] |
BALDI P, CARAMELLINO L, IOVINO M G. Pricing general barrier options:a numerical approach using sharp large deviations[J]. Mathematical Finance, 1999, 9(4): 293 |
| [6] |
SHIN J M, SVENSTRUP M. Efficient control variates and strategies for bermudan swaptions in a libor Market model[J]. Journal of Derivatives, 2002, 12: 2 |
| [7] |
梁义娟, 徐承龙. 两因子期权定价模型的条件蒙特卡罗加速方法[J]. 同济大学学报(自然科学版), 2014, 42(4): 645 LIANG Yijuan, XU Chenglong. Efiiecient accelerating method of conditional Monte-Carlo simulation for two-factor option pricing model[J]. Journal of Tongji University(Natural Science), 2014, 42(4): 645 DOI:10.3969/j.issn.0253-374x.2014.04.023 |
| [8] |
孙健兰.关于用多层蒙特卡罗方法模拟Greeks的分析[D].上海: 复旦大学, 2014. SUN Jianlan. Analysis of multilevel Monte Carlo path simulation for Greeks[D].Shanghai: Fudan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10246-1015412281.htm |
| [9] |
GLASSERMAN P, ZHAO X. Fast Greeks by simulation in forward LIBOR models[J]. Journal of Computational Finance, 1999, 3(1): 5 |
| [10] |
姜礼尚, 徐承龙, 任学敏, 等. 金融衍生产品定价的数学模型与案例分析[M]. 2版. 北京: 高等教育出版社, 2013 JIANG Lishang, XU Chenglong, REN Xuemin, et al. Mathematical modeling and cases analysis of pricing financial derivatives[M]. Beijing: Higher Education Press, 2013 |
 2018, Vol. 46
2018, Vol. 46

